Раздел 1. Приближенные числа и действия над ними
1.1 Виды погрешностей при приближенных вычислениях
Точное решение некоторых математических задач невозможно получить классическими методами, или это решение может быть получено в таком сложном виде, что неприемлемо для дальнейшего практического использования. Кроме того, точное решение задачи может потребовать очень большого количества (от нескольких десятков до многих миллиардов) действий. В таких случаях прибегают к приближенным и численным методам решения.
Появление компьютеров значительно расширило область применения этих методов. В настоящее время трудно себе представить инженера, не владеющего компьютером и методами приближённых вычислений.
Заметим, что любой компьютер способен запоминать большие, но конечные массивы чисел и производить над ними арифметические операции и сравнения с большой, но конечной скоростью. То есть машина способна выполнять очень большое, но конечное число операций. Поэтому при работе на компьютере можно использовать только те математические модели, которые описываются конечным набором чисел, и использовать только конечные последовательности арифметических действий.
Математическими моделями различных явлений служат функции, производные, интегралы, дифференциальные уравнения и т.п. При работе на компьютере эти исходные модели следует заменить такими, которые описываются конечными наборами чисел с указанием конечной последовательности действий для их обработки. Для этого функцию заменяют таблицей, определённый интеграл — суммой и т.д. Кроме того, вычислительная машина обладает конечной памятью и может оперировать с числами конечной длины, поэтому промежуточные результаты округляются. В результате этого даже точный метод с конечным числом действий становится приближенным.
Таким образом, решение, полученное численным методом, является приближенным.
Причинами появления погрешностей являются:
- Несоответствие математической модели изучаемому реальному явлению
- Погрешность исходных данных.
- Погрешность метода решения.
- Погрешности округлений в арифметических и других действиях над числами.
Погрешность решения, вызванная первыми двумя причинами, называется неустранимой — она не зависит от математика.
Погрешность метода возникает потому, что численным методом, как правило, решается не исходная задача, а более простая. Кроме того, обычно численный метод основан на бесконечном процессе, который приходится обрывать на некотором шаге.
Большинство численных методов зависит от одного или от нескольких параметров. Выбор параметров метода позволяет регулировать погрешность метода.
Погрешность округлений не должна быть существенно больше погрешности метода. А погрешность метода целесообразно выбирать в 2-5 раз меньше неустранимой погрешности.
1.2 Приближенные числа
На практике часто приходится иметь дело с числами, которые выражают истинную величину не точно, а приблизительно. Такие числа называются приближенными .
Обозначим точное числовое значение некоторой величины a , приближённое числовое значение этой же величины a * . Тогда a » a * .
Заменяя точное число a приближенным числом a * , мы совершаем ошибку (погрешность).
Определение 1.1. Абсолютной погрешностью приближенного числа a * называется абсолютная величина разности между этим числом и его точным значением | a - a * | .
Поскольку точное значение величины обычно бывает неизвестно, то невозможно вычислить и абсолютную погрешность. Но можно указать положительное число D (a *) , удовлетворяющее неравенству:
Любое число d (a *) , удовлетворяющее неравенству
Заметим, что чисел, удовлетворяющих неравенствам (1.2) и (1.3) множество. Поэтому величина предельной погрешности является не вполне определённой.
На практике обычно берётся по возможности меньшее значение предельной погрешности. Для каждого приближенного числа обязательно определяется его предельная погрешность (абсолютная или относительная). Предельная абсолютная погрешность позволяет установить пределы, в которых лежит число a , т.е.
Предельная относительная погрешность характеризует точность вычислений или измерений.
Примеры.
1.2.1 . При решении задач вместо точного числа p = 3,14159265... мы используем его приближенное значение 3,14 и совершаем ошибку:
p - 3,14 > 0,00159265
1.2.2 . При измерении длины пути получен результат 25,2 км с точностью до 2м . Вычислить предельную абсолютную и предельную относительную погрешности.
Решение
. В нашем случае предельная абсолютная погрешность равна
D = 0,002
км, а предельная относительная погрешность
Аналогично, вычисляем
означает, что a * является приближенным значением числа a с абсолютной погрешностью D (a *) . Если же a * является приближенным значением числа a с относительной погрешностью d (a *), то пишут так:
1.4 Значащие цифры, верные и сомнительные цифры
На практике используются различные приёмы, позволяющие уже только по записи самого приближенного числа судить о его погрешности.
Запись приближенных чисел и абсолютных погрешностей подчиняется определённым правилам.
В десятичной записи числа значащей цифрой называется любая цифра не равная нулю. Нуль считается значащей цифрой, если он расположен между значащими цифрами или стоит правее всех значащих
Пример 1.3.1. Приближенное число 0,38 имеет 2 значащих цифры, 0,308 — три, 0,3080 — четыре, 0,00308 — три. Значащими цифрами являются подчёркнутые цифры.
Определение
1.3.
Значащая цифра называется верной в широком смысле
если абсолютная погрешность числа не превосходит одной единицы разряда, соответствующего этой цифре.
Значащая цифра называется верной в узком смысле
если абсолютная погрешность числа не превосходит половины единицы разряда, соответствующего этой цифре.
В противном случае цифра считается сомнительной
.
Если приближенное число записывается без указания его абсолютной (предельной абсолютной) погрешности, то выписываются только его верные цифры. При этом верные нули на правом конце числа не отбрасывают. Числа 0,25 и 0,250 как приближенные различны. Если же мы пользуемся записями вида (1.4) или (1.5), то числа в правых частях этих равенств должны быть записаны с одинаковым количеством знаков после запятой.
Абсолютную или относительную погрешность принято записывать в виде числа, содержащего одну или две значащие цифры. При этом округление производится с избытком.
Может оказаться так, что у приближенного числа в его целой части значащих цифр больше, чем верных знаков. В этом случае используется запись в нормализованном виде a * = m ·10 n , при этом число m ≤ 1 должно содержать только верные цифры. В нормализованной записи число m называется мантисса , n —порядок числа
Заметим, что предельная абсолютная погрешность определяется числом десятичных знаков после запятой: чем меньше десятичных знаков после запятой, тем больше D (a *) .
Предельная относительная погрешность определяется числом значащих цифр: чем меньше значащих цифр, тем больше d (a *) .
1.5 Округление
Для записи приближенных чисел с верными цифрами применяется округление .
Точные числа также требуется округлить, если количество используемых разрядов ограничено.
Округлением (по дополнению) числа называется запись этого числа с меньшим количеством разрядов по следующему правилу: если первая отбрасываемая цифра больше или равна 5, то последнюю оставляемую цифру увеличивают на единицу. При округлении чисел возникает погрешность, которую также надо учитывать.
Погрешность округления по дополнению не превосходит по абсолютной величине половины единицы младшего оставляемого разряда. При вычислении результирующей погрешности, погрешность округления надо прибавлять к первоначальной абсолютной погрешности числа.
Пример 1.3.2. Число a * = 413287,51 имеет относительную погрешность d (a *) = 0,01 . Из (1.3) следует, что D (a *) = | a * | d (a *) .
Поэтому абсолютная погрешность данного числа равна 4133. Это означает, что четвёртый разряд числа a * уже может содержать ошибку. Следовательно, верными являются только первые две цифры числа. Тогда в нормализованном виде это число записывается так: a * = 0.41 ·10 6 .
Рассуждая аналогично, приближенное число b * = 0,0794 при d (b *) = 2% запишем в нормализованном виде b * = 0.8 ·10 - 1 .
Заметим, что здесь нам потребовалось округлить число.
При выполнении арифметических действий с приближенными числами возникают две взаимообратные задачи:
1. По известным погрешностям входных данных оценить погрешность результата.
2. Определить точность исходных данных, обеспечивающую заданную точность результата.
Кроме того, при работе с приближенными числами необходимо согласовывать точность различных входных данных, чтобы не тратить время на выписывание ненужных и неверных цифр.
В процессе вычислений также необходимо следить за точностью промежуточных результатов.
До начала выполнения арифметических действий применяется округление, чтобы все числа, участвующие в этих действиях, были записаны с одинаковым количеством десятичных знаков. Количество оставляемых десятичных знаков определяется наименьшим числом верных цифр у исходных данных.
При сложении и вычитании приближенных чисел, имеющих одинаковое число верных цифр после запятой, округление не производится.
При сложении и вычитании приближенных чисел с различным числом верных цифр после запятой результат округляется по наименьшему числу верных цифр после запятой у исходных данных.
При умножении и делении приближенных чисел с различным числом верных цифр производится округление результата по минимальному числу верных цифр у исходных данных.
1.6 Погрешности арифметических операций
Пусть a * и b * - приближенные числа, тогда их сумма c * = a * + b * также является приближенным числом.
Если обозначить абсолютные погрешности слагаемых D (a *) и D (b *) , соответственно, то абсолютная погрешность числа c * определяется формулой
|
Следовательно, при сложении двух приближенных чисел их предельные абсолютные погрешности складывают.
Это правило справедливо для любого конечного числа слагаемых. Кроме того, формула (1.6) справедлива и для разности двух чисел.
Действительно, разность двух чисел можно представить в виде суммы
a * - b * = a * + ( - b *),
а абсолютная погрешность числа (- b *) равна абсолютной погрешности числа b * .
Замечание При вычитании двух чисел одного знака относительная погрешность разности может оказаться значительно больше относительной погрешности каждого слагаемого. Особенно большая потеря точности происходит при вычитании близких между собой чисел.
Пример 1.4.1 . Пусть требуется найти разность 61,32 - 61,31 .
Абсолютные погрешности данных чисел, соответственно, равны D 1 = 0,01 и D 2 = 0,01. Найдём теперь относительные погрешности этих чисел:
При вычитании получится число 0,01
(замечаем, что произошла потеря
трёх значащих цифр). Его абсолютная погрешность равна сумме
абсолютных погрешностей слагаемых D 1 + D 2 = 0,02
.
Тогда относительная погрешность результата составляет Сравнивая погрешности исходных данных и результата, обнаруживаем
резкое возрастание относительной погрешности. Из примера 1.4.1. следует, что надо стараться избегать вычитания близких по
абсолютной величине чисел. Иногда этого можно добиться путём преобразования
расчётной формулы. Если же невозможно избежать такого вычитания, то надо
увеличить точность промежуточных вычислений с учётом потери значащих цифр. При умножении и делении двух приближенных чисел a * и b * погрешности определяются по формулам: Таким образом, при умножении и делении приближенных чисел
складывают их предельные относительные погрешности. Замечание
.
Если абсолютная погрешность
приближенного числа Δ (a *)
не превышает единицы разряда, выраженного n -ой значащей цифрой в десятичной записи этого числа, для предельной относительной погрешности верно неравенство: δ(a *) ≤ 1 / k 10 n - 1 где k - первая значащая цифра числа
a *
. Если абсолютная погрешность приближенного числа D
(a *)
не превышает половины единицы разряда, выраженного n -ой значащей
цифрой в десятичной записи этого числа, для предельной
относительной погрешности верно неравенство: δ(a *) ≤ 1 / 2 k 10 n − 1 где k - первая значащая цифра числа a * . В последнем случае справедливо и обратное утверждение: если d
(a *) Ј
1/ 2 (k + 1)10 n -
1 , то тогда a * является приближенным числом, имеющим n верных знаков. Пусть задана непрерывно дифференцируемая в области G функция u = f (x 1 , x 2 , ј
, x n). Оценка погрешности приближенного вычисления значения функции заменяется оценкой модуля ее отклонения от точного значения, вызванное ошибками аргументов. При этом отклонение функции заменяется ее полным дифференциалом, в котором прирашения аргументов заменяются их абсолютными погрешностями. Тогда предельная абсолютная погрешность значения функции определяется соотношением
d
=
0,02
0,01
= 2.
D
(a * b *) = |
b * | D
(a *) + |
a * | D
(b *),
d
(a * b *) = d
(a *) + d
(b *),
(1.7)
D
(a * /
b * ) =
|
b * |D
(a *) + |
a * |D
(b *)
|
b * |
2
d
(a * /
b *) = d
(a *) + d
(b *).
1.7 Погрешность функции
Для предельной относительной погрешности имеет место равенство
При помощи формул (1.11), можно определить точность аргументов, обеспечивающую заданную точность значения функции.
Пример 1.5.1.
Требуется измерить с точностью d
= 1%
площадь боковой поверхности усечённого конуса, радиусы оснований которого
r
1 »
2м, r
2 »
1м
, а образующая l
»
5м
.
С какой
абсолютной погрешностью нужно измерить радиусы и образующую и со сколькими
знаками, верными в широком смысле, нужно взять число p
?
Если D (a * ) не превышает единицы разряда, выраженного n -ой значащей цифрой, то a * называется числом, имеющим n верных знаков в широком смысле .)
Решение . Площадь боковой поверхности усечённого конуса вычисляется по формуле:
S = πl (r 1 + r 2).
Таким образом, имеем
функцию четырёх аргументов S
= S
(p
, l
, r
1 , r 2)
.
Найдём
частные производные и разделим на S .
Из формул (1.11) выразим абсолютные погрешности аргументов:
следует, что число p следует взять с количеством знаков n = 3 .
ПРОВЕРЬТЕ СЕБЯ
Дано приближенное число a * = 1,0754327 и его предельная абсолютная погрешность D (a *) = 0,0005 .
Округлите это число, оставив верные цифры. Учтите погрешность округления.
Портняжной сантиметровой лентой измеряют длину окружности меридиана, пушечного ядра Царь-пушки и теннисного мяча. Измерение какой величины даст большую относительную погрешность?
При измерении радиуса круга с точностью до 0,5 см получилось число 12 см . Найдите абсолютную и относительную погрешности площади круга.
Выполните арифметические действия над приближенными числами, все цифры которых верны:
130,6 + 0,255 + 1,15224 + 41,84 + 11,8216;
35,2 ·1,748;
Величиной называется то, что может быть в определенных единицах выражено числом. Например, длина, площадь, объем – это величины. Значение величины, в истинности которого мы не сомневаемся, называется точным (в дальнейшем х - точное число ). Но обычно на практике, отыскивая значение какой-либо величины, получают лишь ее приближенное значение (в дальнейшем а - приближенное число ). Например, при измерении физических величин с помощью измерительных приборов.
Модуль разности точного и приближенного значений величины называется абсолютной погрешностью
приближения Предельной абсолютной погрешностью приближения или границей погрешности или оценкой абсолютной
погрешности
называется число ![]() . Таких оценок может быть бесконечное число. Лучшей оценкой погрешности является наименьшая оценка.
. Таких оценок может быть бесконечное число. Лучшей оценкой погрешности является наименьшая оценка.
Краткая запись точного числа:
Отношение абсолютной погрешности приближения к модулю точного значения величины называется относительной погрешностью . На практике используется Для предельной относительной погрешности (оценки относительной погрешности): . Относительная погрешность обычно выражается в %.
В дальнейшем слово оценка опускается.
ПРИМЕР. Найти абсолютную и относительную погрешность приближения а=3,14 для х=π .
Известно, что 3,14 <π<3,15 .
Отсюда следует, что , т.е.
Если учесть, что 3,14 <π<3,142, то получим лучшую оценку
![]()
Цифра в десятичной записи приближенного значения величины х называется верной в широком смысле , если абсолютная погрешность приближения не превосходит единицы того разряда r , которому принадлежит эта цифра (Нулевым разрядом считается разряд единиц, десятичные цифры считаются отрицательными разрядами). Существует еще понятие верной цифры в узком смысле : . В дальнейшем будем рассматривать верные цифры в широком смысле. Остальные цифры числа называются сомнительными . Значащими цифрами числа, записанного в десятичной форме, называются все верные цифры числа, начиная с первой слева, отличной от 0. Все нули слева являются незначащими. По количеству значащих цифр можно легко оценить абсолютную погрешность приближенного числа. За оценку абсолютной погрешности можно взять 0,5 разряда, следующего за последней значащей цифрой. Предельную относительную погрешность можно принять равной дроби, числитель которой 1, а знаменатель – удвоенное целое число, записанное при помощи всех значащих цифр данного числа.
ПРИМЕР. а=0,065;
ЗАДАЧА 1.1. Объем помещения V определен с предельной относительной погрешностью δ Сколько значащих цифр в V ?
ЗАДАЧА 1.2. Известно, что приближенное значение а имеет n значащих цифр. Оценить абсолютную и относительную погрешность.
При решение задач, связанных с вычислениями, получаются числовые результаты, которые часто не являются точными, т.к. при постановке задачи и в ходе вычислений возникают погрешности.
Источниками погрешностей являются:
1) погрешности исходных данных;
2) погрешности округления промежуточных и окончательных результатов;
3) погрешности приближенного метода решения задачи.
При выполнении действий над приближенными числами надо:
1) зная точность исходных данных, уметь оценивать точность результата;
2) брать исходные данные с такой точностью, чтобы обеспечить заданную точность результата.
2.1 Погрешности приближенных чисел
Пусть число х является точным значением, а число а - приближенным значением некоторой величины.
Определение. Разность между числом x и его приближенным значением а называется погрешностью приближенного числа а: Δ = |х-а |.
Пусть х=10,5, а=10, тогда Δ=10,5-10=0,5.
Пусть х=9,5, а=10, тогда Δ=9,5-10=-0,5.
Определение. Абсолютная величина разности между числом x и его приближенным значением а называется абсолютной погрешностью приближенного числа а: Δа = |х-а|
Пусть х=10,5, а=10, тогда Δа =|10,5-10|=0,5.
Пусть х=9,5, а=10, тогда Δa=|9,5-10|=0,5.
Часто точное число х неизвестно. Тогда нельзя найти Δа = |х-а|, поэтому используют оценку абсолютной погрешности - предельную абсолютную погрешность Δ а ≥ Δа =x-а|. При этом число х заключено в границах:
а - Δ а х а + Δ а или кратко: х = а ± Δ а.
Читают: х равно а с точностью Δ а.
Для того, чтобы определить качество производимых вычислений, надо определить, какую долю составляет абсолютная погрешность от измеряемой величины. Для этого используют относительную погрешность.
Определение. Относительной погрешностью δа приближенного числа а называется отношение абсолютной погрешности Δа к модулю числа х:
или .
.
Оценкой относительной
погрешности ба является предельная
относительная погрешность:
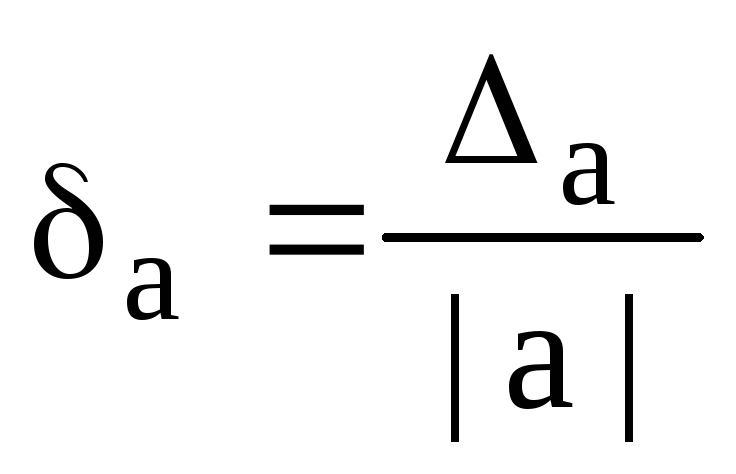
Пример. Дано число х=0,4287 и его приближенное значение а=0,4264. Найти абсолютную и относительную погрешности числа а.
Решение. Вычислим абсолютную погрешность числа а:
Δа=|0,4287- 0,4264| = 0,0023.
Вычислим относительную погрешность числа а:
 или
5,4%.
или
5,4%.
Замечания. 1. При записи погрешности принято оставлять 1-2 значащих цифры. Погрешности всегда округляют в сторону увеличения. При этом границы точного числа х расширяются.
2. Если число х неизвестно, то при нахождении относительной погрешности используют число а.
3. Относительную погрешность часто выражают в процентах, домножая ее на 100%.
2.2. Значащие и верные цифры приближенного числа
Для оценки точности приближенного числа а принято записывать его в виде десятичной дроби. Точность вычислений определяется не числом десятичных знаков (цифр после запятой), а числом верных значащих цифр результата.
Определение. Значащими цифрами числа а называются все его цифры, кроме нулей, записанных перед первой цифрой, отличной от нуля, и нули в конце записи, если они служат для сохранения разряда или точности числа.
Пример. Определить значащие цифры числа а.
а = 0,02701 => значащие цифры: 2,7,0,1.
а = 0,0270 => значащие цифры: 2,7,0.
а = 2700 => значащие цифры: 2,7,0,0.
Определение. Цифра α i приближенного числа а называется верной значащей цифрой в широком смысле (в строгом смысле), если предельная абсолютная погрешность числа а не превышает единицы (половины единицы) разряда, в котором записана цифра α i: Δ а 10 i (Δ а 0,5∙10 i).
Пример. Определить верные цифры приближенного числа а=0,7264, если абсолютная погрешность Δ а =0,0023.
Решение. Абсолютная погрешность Δ а =0,0023 0,005 = 0,5∙10 -2 . Следовательно, цифры 7 и 2 - верные в строгом смысле, цифры 6 и 4 – неверные (сомнительные). Так как Δ а = 0,0023 < 0,01 = 10 -2 , то цифры 7 и 2 являются верными в широком смысле.
Замечания. 1. В математических таблицах все значащие цифры являются верными в строгом смысле.
2. В окончательном результате принято оставлять только верные цифры. Тогда предельная абсолютная погрешность числа а определяется по единице младшего разряда. Например, пусть а=127,38, тогда Δ а =0,01, если все цифры являются верными в строгом смысле, и Δ а = 0,5∙ 0,01 = 0,005, если все цифры являются верными в широком смысле.
Пример.
Определить, какое равенство точнее
13/19=0,684 или
 =7,21?
=7,21?
Решение.
Обозначим а =0,684, в =7,21. Найдем абсолютные
погрешности этих чисел. Для этого возьмем
13/19 и
 с большим числом десятичных знаков:
13/39=0,68421...,
с большим числом десятичных знаков:
13/39=0,68421..., =7,2111...
=7,2111...
Тогда Δ а =|0,68421...-0,684| < 0,00022, Δ в = |7,2111...-7,21| < 0,0012.
Найдем относительные погрешности:
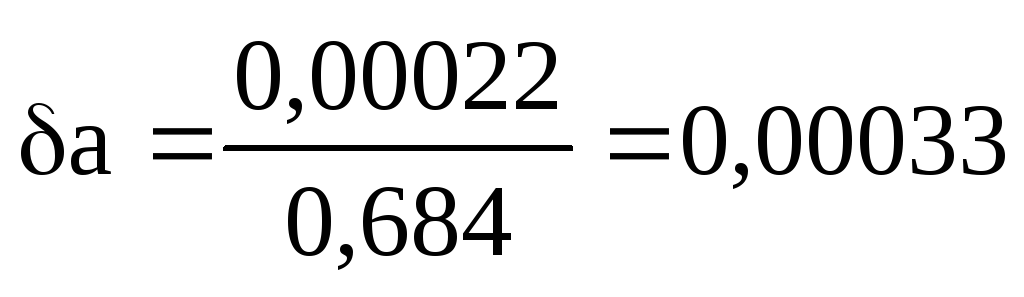 или
0,033%.
или
0,033%.
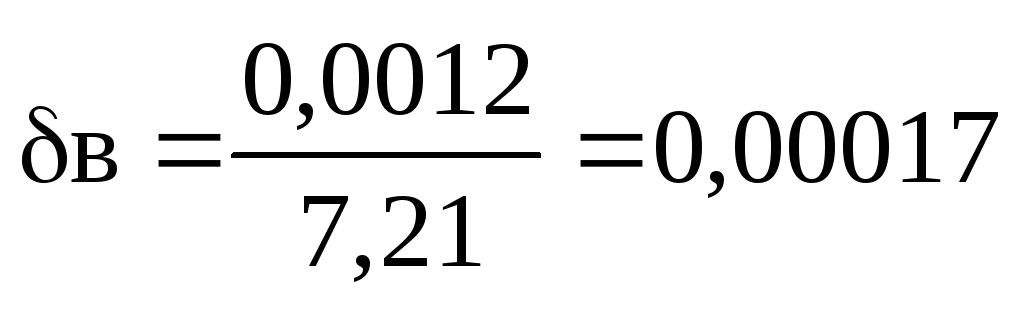 или
0,017%.
или
0,017%.
Второе равенство более
точное, так как
 .
.
2.3. Округление чисел
В приближенных вычислениях часто приходится округлять числа как приближенные, так и точные, т. е. отбрасывать одну или несколько последних цифр. При округлении числа мы заменяем его приближенным числом с меньшим количеством значащих цифр, в результате чего возникает погрешность округления. Чтобы эта погрешность была минимальной, нужно придерживаться некоторых правил округления.
Правило I . Если первая слева из отбрасываемых цифр больше 5, то последняя из сохраняемых цифр усиливается, т.е. увеличивается на единицу. Усиление производится и тогда, когда первая слева из отбрасываемых цифр равна 5, а за ней следуют отличные от нуля цифры.
Пример. Округляя до десятых долей число 73,473, получим 73,5. Последняя из оставшихся цифр усилена, так как 7 > 5.
Правило II . Если первая из отброшенных цифр меньше 5, то последняя из оставшихся цифр не усиливается, т. е. остается без изменения.
Пример. Округляя до сотых долей число 73,473, получим 73,47.
Правило III . Если первая слева из отброшенных цифр равна 5 и за ней не следуют отличные от нуля цифры, то последняя оставшаяся цифра усиливается, если она нечетная, и остается без изменения, если она четная (правило четной цифры).
Пример. Округляя число 5,785 до сотых долей, получаем 5,78. Усиления не делаем, так как последняя сохраняемая цифра 8 - четная. Округляя число 5,775 до второго десятичного знака, имеем 5,78. Последняя сохраняемая цифра 7 увеличивается на единицу, поскольку она нечетная.
При применении правила III к округлению одного числа мы фактически не увеличиваем точность вычислений, однако при многочисленных округлениях избыточные числа встречаются примерно так же часто, как и недостаточные. Происходит взаимная компенсация погрешностей, результат оказывается более точным.
Таким образом, при применении выше рассмотренных правил округления абсолютная погрешность округления не превосходит половины единицы разряда, определяемого последней оставленной значащей цифрой.
Если точное число х округляется до n значащих цифр, то получаемое приближенное число а имеет абсолютную погрешность, равную погрешности округления. В этом случае приближенное число а имеет n верных значащих цифр в узком смысле.
Пример. Округляя число х=26,837 до трех значащих цифр, получим а =26,8, откуда Δ а = |х-а | = | 26,837-26,8 |=0,037 < 0,05, т. е. число а имеет три верные значащие цифры в узком смысле.
При округлении приближенного числа a получаем новое приближенное число а 1 .
Определение. Число Δ а1 = Δ а +Δ окр называется погрешностью округления.
Абсолютная погрешность числа a 1 складывается из абсолютной погрешности первоначального числа Δ а и погрешности округления Δ окр, т. е.
Δ а1 = Δ а +Δ окр.
Пример. Округлить сомнительные цифры числа х=34,124 ± 0,021. Определить абсолютную погрешность результата.
Решение. Приближенное число a=34,124 имеет три верные цифры в узком смысле: 3, 4, 1, так как Δ а =0,021 < 0,05. Применяя правила округления, найдем приближенное значение а 1 , сохранив десятые доли: а 1 = 34,1. Погрешность округления Δ окр =|34,124-34,1|=0,024. Тогда абсолютная погрешность числа а 1 равна Δ а1 =Δ а +Δ окр =0,021+0,024 = 0,045 < 0,05.
Таким образом, все значащие цифры числа а 2 верные (в узком смысле).
Итак, х=34,1 ±0,045.
Однако при округлении приближенного числа а, имеющего n верных значащих цифр (в узком смысле), до n значащих цифр может оказаться, что округленное число а 1 будет иметь n верных значащих цифр в широком смысле.
Пример. Приближенное число a=15,3654 (± 0,0018) имеет четыре верные значащие цифры в узком смысле (1, 5, 3, 6), так как Δ а =0,0018 < 0,005. При округлении до четырех значащих цифр получим а 1 = 15,37 и Δ а1 =Δ а +Δ окр =0,0018+|15,3654-15,37|=0,0064.
Очевидно, что 0,005 < 0,0064 < 0,01. Следовательно, число 15,37 (± 0,0064) имеет четыре верные цифры в широком смысле.
Итак, х=15,37 ±0,0064.
Пример. Округлить сомнительные цифры числа а=26,7245 (± 0,0026), оставив верные знаки в узком смысле. Определить абсолютную погрешность результата.
Решение. По условию Δ а = 0,0026 < 0,005, следовательно, в числе 26,7245 верными в узком смысле являются цифры 2, 6, 7, 2. Используя правила округления, найдем приближенное значение а 1 , сохранив сотые доли:
Полученная погрешность больше 0,005 (0,005 < 0,0071), поэтому уменьшим число цифр в приближенном числе до трех; а 2 = 26,7. Находим Δ а2 = =Δ а +Δ окр =0,0026+|26,7245-26,7|=0,0271< 0,05. Следовательно, оставшиеся три цифры верны в узком смысле.
Итак, х=26,7 ±0,0271 => х=26,7 ±0,03, округляя погрешность до двух знаков.
Пример. Округлить сомнительные цифры числа а=22,7314, оставив верные знаки в узком смысле. Определить абсолютную погрешность числа, если δ а = 0,2%.
Решение. Запишем δ а в виде десятичной дроби: δа=0,002 и определим абсолютную погрешность . Так какΔ а = =0,0455 < 0,05, то верными в этом числе будут три цифры: 2, 2, 7. Округлим число 22,7314, сохранив в нем десятые доли: а 1 = 22,73. Тогда Δ а1 = =Δ а +Δ окр =0,0455+|22,7314-22,73|=0,0769>0,05, поэтому уменьшим число цифр в приближенном числе до двух: а 2 =23. Находим Δ а2 = =Δ а +Δ окр =0,0455+|22,7314-23|=0,3141< 0,05. Следовательно, оставшиеся две цифры верны в узком смысле.
Итак, х=23 ±0,3141 => х=23 ±0,32.
2.3. Правила действий над приближенными числами
Правило 1. Абсолютная погрешность алгебраической суммы нескольких приближенных чисел равна сумме абсолютных погрешностей этих чисел:
Δ а±в =Δ а + Δ в
Правило 2. Относительная погрешность произведения нескольких приближенных чисел равна сумме относительных погрешностей этих чисел:
δ ав = δ а +δ в.
Правило 3. Относительная погрешность частного приближенных чисел равна сумме относительных этих чисел: δ а/в = δ а +δ в.
Правило 4. Относительная погрешность степени приближенного числа а равна: δa n = nδ а.
Правило 5.
Относительная погрешность корня из
приближенного числа а равна:
 .
.
Правило 6. При вычислениях, если не проводится строгий подсчет погрешностей, рекомендуется пользоваться правилами подсчета цифр. Эти правила указывают, как следует проводить округление результатов, чтобы обеспечить заданную точность результата и при этом не производить вычислений с лишними знаками.
Правила предполагают, что числа, над которыми производятся действия, содержат только верные цифры, и число действий невелико.
I. При сложении и вычитании приближенных чисел в результате следует сохранить столько десятичных знаков, сколько их в числе, имеющем наименьшее число десятичных знаков.
II. При умножении и делении в результате следует сохранить столько значащих цифр, сколько их в числе с наименьшим числом значащих цифр.
III. При возведении приближенного числа в степень в результате следует сохранить столько значащих цифр, сколько их в основании степени.
IV. При извлечении корня из приближенного числа следует сохранить столько значащих цифр, сколько их в подкоренном числе.
V. В промежуточных результатах следует сохранять на 1-2 цифры больше, чем рекомендуют правилах I-IV. В окончательном результате "запасные цифры" отбрасываются с округлением числа.
VI. Если некоторые исходные данные имеют больше десятичных знаков (при сложении и вычитании) или больше значащих цифр (при других действиях), чем другие, то их предварительно следует округлить, сохраняя лишь одну "эапасную цифру".
VII. Для получения результата с N верными цифрами исходные данные следует брать с таким числом цифр, которые согласно предыдущим правилам обеспечивают N+1 цифру в результате.
Пример. Найдем s=2,35+11,8 без учета погрешностей. Применяя правило I, получим s=14,15. Результат округлим по числу 11,8 с наименьшим количеством десятичных знаков. Получим: s =14,2.
Решим задачу с учетом погрешностей. В числе s=14,15 надо оставить только верные цифры. Для этого найдем предельную абсолютную погрешность суммы s, используя правило 1. Учитывая, что все цифры в числах 2,35 и 11,8 являются верными, получим: Δ 14,15 =Δ 2,35 +Δ 11,8 =0,01+0,1=0,11 < 0,5. Последняя верная цифра в числе 14,15 находится в разряде единиц. Поэтому число s=14,15 надо округлить: s=14 и найти абсолютную погрешность округленного числа. Погрешность округления равна: |14,15-14|=0,15. Тогда абсолютная погрешность округленного числа Δ 14 =0,11+0,15=0,26 <0,5. Окончательный результат примет вид: s=14 ± 0,26.
Аналогично решаются задачи при выполнении других действий над приближенными числами.
Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
Размещено на http://www.allbest.ru/
Размещено на http://www.allbest.ru/
Московский институт экономики, менеджмента и права
Реферат
по дисциплине:
« Высшая м атематика »
« П риближенные вычисления и оценка погрешн о стей »
Выполнила: студентка
Янчук Людмила Александровна
Научный руководитель Питерцева Галина Александровна
Москва, 2000 год
План
Введение. Вычисления в современной науке и технике
1. Приближенные значения и погрешности приближений
2. Округление чисел. Погрешность округления
Заключение. Некоторые сведения о вычислительной технике
Литература
Введение. Вычисления в современной науке и технике
Измерения и вычисления с давних времен играют важную роль в жизни общества. Необходимость подсчитывать урожай, измерять емкость сосудов, размеры земельных участков, производить расчеты при строительстве крупных сооружений, выполнять различные астрономические расчеты -- вот неполный перечень задач, которые люди должны были решать еще в давние времена.
Одним из наиболее значительных событий последнего времени необходимо считать освоение человечеством космоса. Мы с волнением следим за полетами на Луну, Венеру, Марс, за созданием пилотируемых орбитальных станций. Запуск космического корабля был бы немыслим, если бы не был проведен точный расчет движения корабля, а для этого требуется выполнить колоссальную и сложную вычислительную работу.
В современный период, период научно-технической революции, роль математических методов все возрастает. Математические методы применяются не только в физике, но и в химии, биологии, медицине, экономике, истории и лингвистике
Большую вычислительную работу приходится выполнять математикам и инженерам в будничной, текущей деятельности промышленных предприятий, научных институтов, государственных учреждений, фермерских и коллективных хозяйствах.
Вычислительные методы в настоящее время широко применяются в экономических расчетах, в планировании работы отдельного предприятия, области и всего хозяйства страны.
Имеется много задач, в которых для получения численного результата требуются вычисления, превосходящие возможности одного человека. Расчет упругих напряжений в плотине, расчет сопротивлении, испытываемых самолетами при полете, или траекторий снарядов -- вот примеры таких задач. Десятки инженеров-вычислителей, используя различные вычислительные машины, выполняют эту сложную вычислительную работу.
Появление ЭВМ вызвало революцию в технике вычислений. Но для того чтобы довести решение математических задач до этапа, после которого они могут быть переданы на вычислительную машину для получения численных результатов, необходим тоже труд многих вычислителей. Создание ЭВМ стимулировало развитие самой математики, особенно ее прикладных направлений, вычисления теперь играют не вспомогательную, а основную роль во многих научных и технических достижениях. Во всех случаях, когда нужно довести до конца решение какой-либо математической задачи практического характера, необходимо получить численный результат. Если исходные данные приближенные, то нельзя добиться любой степени точности результата. Надо уметь оценивать точность исходных данных, а также определять, какая точность результата может быть достигнута и какая точность результата нужна при практическом использовании полученных численных результатов. В одних вычислениях требуется получить результат с очень большой точностью, а в других такая точность не требуется. Отсюда ясно, что нужно организовывать вычисления так, чтобы получать результаты с требуемой точностью при минимальной затрате вычислительного труда.
Для достижения этой цели необходимо:
изучить принципы и правила вычислений с приближенными данными;
овладеть необходимыми навыками рациональных вычислений с помощью доступных средств, к которым относятся различные приемы устных вычислений, математические таблицы, конторские счеты, счетные логарифмические линейки, арифмометры, полуавтоматические и автоматические вычислительные машины.
1. Приближенные значения и погрешности приближений
В практической деятельности человеку приходится измерять различные величины, учитывать материалы и продукты труда, производить различные вычисления. Результатами различных измерений, подсчетов и вычислений являются числа. Числа, полученные в результате измерения, лишь приблизительно, с некоторой степенью точности характеризуют искомые величины. Точные измерения невозможны ввиду неточности измерительных приборов, несовершенства наших органов зрения, да и сами измеряемые объекты иногда не позволяют определить их величину с любой точностью.
Так, например, известно, что длина Суэцкого канала 160 км, расстояние по железной дороге от Москвы до Ленинграда 651 км. Здесь мы имеем результаты измерений, произведенных с точностью до километра. Если, например, длина прямоугольного участка 29 м, ширина 12 м, то, вероятно, измерения произведены с точностью до метра, а долями метра пренебрегли,
Прежде чем произвести какое-либо измерение, необходимо решить, с какой точностью его нужно выполнить, т.е. какие доли единицы измерения надо при этом принять во внимание, а какими пренебречь.
Если имеется некоторая величина а, истинное значение которой неизвестно, а приближенное значение (приближение) этой величины равно х, то пишут а х .
При различных измерениях одной и той же величины будем получать различные приближения. Каждое из этих приближений будет отличаться от истинного значения измеряемой величины, равного, например, а, на некоторую величину, которую мы будем называть погрешностью. Определение. Если число x является приближенным значением (приближением) некоторой величины, истинное значение которой равно числу а, то модуль разности чисел, а и х называется абсолютной погрешностью данного приближения и обозначается a x : или просто a . Таким образом, по определению,
a x = a - x (1)
Из этого определения следует, что
a = x a x (2)
Если известно, о какой величине идет речь, то в обозначении a x индекс а опускается и равенство (2) записывается так:
a = x x (3)
Так как истинное значение искомой величины чаще всего бывает неизвестно, то нельзя найти и абсолютную погрешность приближения этой величины. Можно лишь указать в каждом конкретном случае положительное число, больше которого эта абсолютная погрешность быть не может. Это число называется границей абсолютной погрешности приближения величины a и обозначается h a . Таким образом, если x -- произвольное приближение величины а при заданной процедуре получения приближений, то
a x = a - x h a (4)
Из сказанного выше следует, что если h a является границей абсолютной погрешности приближения величины а , то и любое число, большее h a , также будет границей абсолютной погрешности приближения величины а .
На практике принято выбирать в качестве границы абсолютной погрешности возможно меньшее число, удовлетворяющее неравенству (4).
Решив неравенство a - x h a получим, что а заключено в границах
x - h a a x + h a (5)
Более строгое понятие границы абсолютной погрешности можно дать следующим образом.
Пусть X -- множество всевозможных приближений х величины а при заданной процедуре получения приближении. Тогда любое число h , удовлетворяющее условию a - x h a при любом х Х , называется границей абсолютной погрешности приближений из множества X . Обозначим через h a наименьшее из известных чисел h . Это число h a и выбирают на практике в качестве границы абсолютной погрешности.
Абсолютная погрешность приближения не характеризует качества измерений. Действительно, если мы измеряем с точностью до 1 см какую-либо длину, то в том случае, когда речь идет об определении длины карандаша, это будет плохая точность. Если же с точностью до 1 см определить длину или ширину волейбольной площадки, то это будет высокая точность.
Для характеристики точности измерения вводится понятие относительной погрешности.
Определение. Если a x : есть абсолютная погрешность приближения х некоторой величины, истинное значение которой равно числу а , то отношение a x к модулю числа х называется относительной погрешностью приближения и обозначается a x или x .
Таким образом, по определению,
Относительную погрешность обычно выражают в процентах.
В отличие от абсолютной погрешности, которая чаще всего бывает размерной величиной, относительная погрешность является безразмерной величиной.
На практике рассматривают не относительную погрешность, а так называемую границу относительной погрешности: такое число Е a , больше которого не может быть относительная погрешность приближения искомой величины.
Таким образом, a x Е a .
Если h a -- граница абсолютной погрешности приближений величины а , то a x h a и, следовательно,
Очевидно, что любое число Е , удовлетворяющее условию, будет границей относительной погрешности. На практике обычно известны некоторое приближение х величины а и граница абсолютной погрешности. Тогда за границу относительной погрешности принимают число
2. Округление чисел. Погрешность округления
При выполнении вычислений часто возникает необходимость в округлении чисел, т.е. в замене их числами с меньшим количеством значащих цифр.
Существуют три способа округления чисел:
Округление с недостатком до k -й значащей цифры состоит в отбрасывании всех цифр, начиная с (k +1) -й.
Округление с избытком отличается от округления с недостатком тем, что последняя сохраняемая цифра увеличивается на единицу.
Округление с наименьшей погрешностью отличается от округления с избытком тем, что увеличение на единицу последней сохраняемой цифры производится лишь в том случае, когда первая из отбрасываемых цифр больше 4.
Исключение: если округление с наименьшей погрешностью сводится к отбрасыванию только одной цифры 5, то последняя сохраняемая цифра не изменяется если она четная, и увеличивается на 1, если она нечетная.
Из вышеуказанных правил округления приближенных чисел следует, что погрешность, вызываемая округлением с наименьшей погрешностью, не превышает половины единицы последнего сохраняемого разряда, а при округлении с недостатком или с избытком погрешность может быть и больше половины единицы последнего сохраняемого разряда, но не более целой единицы этого разряда.
Рассмотрим это на следующих примерах.
1. Погрешность суммы. Пусть x а , у -- некоторое приближение величины b . Пусть х и у -- абсолютные погрешности соответствующих приближений х и у . Найдем границу абсолютной погрешности h a+b суммы х+у , являющейся приближением суммы а+b .
a = x + х,
b = y + y .
Сложим эти два равенства, получим
a + b = x + y + х + y .
Очевидно, что погрешность суммы приближений x и у равна сумме погрешностей слагаемых, т.е.
(x + y ) = x + y
Известно, что модуль суммы меньше или равен сумме модулей слагаемых. Поэтому
(x + y ) = x + y x + y
Отсюда следует, что абсолютная погрешность суммы приближений не превышает суммы абсолютных погрешностей слагаемых. Следовательно, за границу абсолютной погрешности суммы можно принять сумму границ абсолютных погрешностей слагаемых.
Обозначив границу абсолютной погрешности величины а через h a , а величины b через h b будем иметь
h a + b = h a + h b
2. Погрешность разности. Пусть х и у -- погрешности приближений x и у соответственно величин a и b .
a = x + х,
b = y + y .
Вычтем из первого равенства второе, получим
a - b = (x - y ) + ( x - y )
Очевидно, что погрешность разности приближений равна разности погрешностей уменьшаемого и вычитаемого, т. е.
(x - y ) = x - y ) ,
(x - y ) = x + (- y )
А тогда, рассуждая так же, как в случае сложения, будем иметь
(x - y ) = x + (- y ) x + y
Отсюда следует, что абсолютная погрешность разности не превышает суммы абсолютных погрешностей уменьшаемого и вычитаемого.
За границу абсолютной погрешности разности можно принять сумму границ абсолютных погрешностей уменьшаемого и вычитаемого. Таким образом.
h a - b = h a + h b (9)
Из формулы (9) следует, что граница абсолютной погрешности разности не может быть меньше границы абсолютной погрешности каждого приближения. Отсюда вытекает правило вычитания приближений, применяемое иногда при вычислениях.
При вычитании чисел, являющихся приближениями некоторых величин, в результате следует оставить столько цифр после запятой, сколько их имеет приближение с наименьшим числом цифр после запятой.
3. Погрешность произведения. Рассмотрим произведение чисел х и у , являющихся приближениями величин a и b . Обозначим через x погрешность приближения х , а через у -- погрешность приближения у ,
a = x + х,
b = y + y .
Перемножив эти два равенства, получим
Абсолютная погрешность произведения ху равна
И поэтому
Разделив обе части полученного неравенства на ху , получим
Учитывая, что модуль произведения равен произведению модулей сомножителей, будем иметь
Здесь левая часть неравенства представляет собой относительную погрешность произведения ху , -- относительную погрешность приближения х , а -- относительную погрешность приближения у . Следовательно, отбрасывая здесь малую величину, получим неравенство
Таким образом, относительная погрешность произведения приближений не превышает суммы относительных погрешностей сомножителей. Отсюда следует, что сумма границ относительных погрешностей сомножителей является границей относительной погрешности произведения, т.е.
E ab = E a + E b (10)
Из формулы (10) следует, что граница относительной погрешности произведения не может быть меньше границы относительной погрешности наименее точного из сомножителей. Поэтому здесь, как и в предыдущих действиях, не имеет смысла сохранять в сомножителях излишнее количество значащих цифр.
Иногда при вычислениях для сокращения объема работы полезно руководствоваться следующим правилом: При умножении приближений с различным числом значащих цифр в результате следует сохранить столько значащих цифр, сколько их имеет приближение с наименьшим числом значащих цифр.
4. Погрешность частного. Если x -- приближение величины а , погрешность которого x , а у -- приближение величины b с погрешностью y , то
Вычислим сначала абсолютную погрешность частного:
а затем относительную погрешность:
Принимая во внимание, что y мало по сравнению с y , абсолютную величину дроби можно считать равной единице. Тогда
из последней формулы вытекает, что относительная погрешность частного не превышает суммы относительных погрешностей делимого и делителя. Следовательно, можно считать, что граница относительной погрешности частного равна сумме границ относительных погрешностей делимого и делителя, т.е.
5. Погрешность степени и корня. 1) Пусть u = a n , где n -- натуральное число, и пусть а х. Тогда, если E a -- граница относительной погрешности приближения x величины a , то
и поэтому
Таким образом, граница относительной погрешности степени равна произведению границы относительной погрешности основания на показатель степени, т.е.
E u = n E a (11)
2) Пусть, где n -- натуральное число, и пусть а х .
По формуле (11)
и, следовательно,
погрешность вычитаемый вычисление
Таким образом, граница относительной погрешности корня n -й степени в n раз меньше границы относительной погрешности подкоренного числа.
6. Обратная задача приближенных вычислений. В прямой задаче требуется найти приближенное значение функции u= f (х,у,…, n ) по данным приближенным значениям аргументов
и границу погрешности h a , которая выражается через погрешности аргументов некоторой функции
h u = (h x , h y , …, h z ) (12)
На практике нередко приходится решать и обратную задачу, в которой требуется узнать, с какой точностью должны быть заданы значения аргументов х, у, …, z , чтобы вычислить соответствующие значения функции u = f (х, у, …, z ) с наперед заданной точностью h u .
Таким образом, при решении обратной задачи искомыми являются границы погрешностей аргументов, связанные с заданной границей погрешности функции h u уравнением (12), и решение обратной задачи сводится к составлению и решению уравнения h u = (h x , h y , …, h z ) относительно h x , h y , …, h z . Такое уравнение или имеет бесконечное множество решений, или совсем не имеет решений. Задача считается решенной, если найдено хотя бы одно решение такого уравнения.
Для решения обратной задачи, которая часто бывает неопределенной, приходится вводить добавочные условия об отношениях искомых погрешностей, например считать их равными и тем самым сводить задачу к уравнению с одним неизвестным.
Заключение. Некоторые сведения о вычислительной те х нике
В зависимости от точности исходных данных и целей проведения вычислений пользуются различными вычислительными средствами. Работникам многих массовых профессий значительно облегчают расчеты и позволяют экономить время и труд на производство различных вычислений русские счеты, счетные логарифмические линейки, арифмометры и всевозможные карманные и настольные электронные вычислители (микро- и миникалькуляторы).
К классу миникалькуляторов в настоящее время в нашей стране относятся семейство электронных настольных калькуляторов «Искра» и семейство калькуляторов «Электроника», в которое входит и несколько типов карманных калькуляторов. По очевидным причинам эти калькуляторы морально устарели, но, тем не менее, это единственные модели, выпускаемые отечественной промышленностью.
Машины семейств «Электроника» и «Искра» предназначены главным образом для решения несложных инженерных» бухгалтерских и учетных задач с точностью порядка 8--10 значащих цифр. Во многих из них предусмотрена возможность автоматического вычисления значений элементарных функций и имеются элементы программного управления.
С быстрым ростом технической оснащенности нашей промышленности и сельского хозяйства, с развитием науки все более и более увеличивается потребность во всевозможных вычислениях. Располагая быстродействующими электронными вычислительными машинами (ЭВМ) исследователь теперь может решать такие задачи, которые раньше даже не ставились, поскольку их решение требовало слишком много времени.
Электронные вычислительные машины применяются, например, для численного решения уравнений. Первые вычислительные машины разрабатывались именно для такого рода вычислений.
В настоящее время ЭВМ с успехом используются для управления технологическими процессами. Если управление быстропротекающим процессом требует сложных вычислений, основанных на данных, получаемых в ходе этого процесса, то без ЭВМ подобная задача была бы вообще неосуществима.
Литература
Алгебра и начала анализа. Ч. 1. Под ред. Г.Н. Яковлева. - М.: Наука, 1981. 336 с.
Выготский М.Я. Справочник по высшей математике. М.: 1987.
Введение в метрологию. Тюрин Н.И., М., Изд-во стандартов, 1976, 304 с.
Размещено на Allbest.ru
...Подобные документы
Определение абсолютной и относительной погрешностей приближенных чисел. Оценка погрешностей результата. Интерполирование и экстраполирование данных, интерполяционный многочлен Лагранжа и Ньютона, их основные характеристики и сравнительное описание.
лабораторная работа , добавлен 06.08.2013
Сущность и математическая интерпретация абсолютной и относительной погрешности, способы записи величины вместе с ними. Понятие приближенного значения и погрешности приближения, направления анализа данных категорий. Правило округления десятичных дробей.
реферат , добавлен 13.09.2014
Характеристика и особенности основных типов погрешностей, возникающих при численном решении математических и прикладных задач: задачи, метода, округлений. Понятие и причины возникновения погрешностей измерений. Описание случайных погрешностей, моменты.
контрольная работа , добавлен 13.01.2012
Классическая теория измерений по поводу истинного значения физической величины, ее главные постулаты. Классификация погрешностей по способу выражения, ее типы: абсолютная, приведенная и относительная. Случайные погрешности, закон их распределения.
реферат , добавлен 06.07.2014
Округление заданного числа до шести, пяти, четырех и трех знаков. Расчет погрешностей после каждого округления. Определение абсолютной и относительной погрешности вычисления значений функции u с учетом того, что все знаки операндов a, b, c и d верны.
контрольная работа , добавлен 02.05.2012
Исследование методов определения погрешностей и статистической оценки распределений. Построение эмпирической функции, определяющей частность события для каждого значения случайной величины. Расчеты по заданной выборке, ее анализ и определение параметров.
курсовая работа , добавлен 13.01.2011
Введение в численные методы, план построения вычислительного эксперимента. Точность вычислений, классификация погрешностей. Обзор методов численного интегрирования и дифференцирования, оценка апостериорной погрешности. Решение систем линейных уравнений.
методичка , добавлен 23.09.2010
Определение номера и значения членов прогрессии для бесконечно убывающей геометрической прогрессии. Вычисление относительной погрешности величины. Определение значений машинного нуля и бесконечности. Поведение погрешностей в зависимости от аргумента.
лабораторная работа , добавлен 15.11.2014
Исследование зависимости погрешности решения от погрешностей правой части системы. Определение корня уравнения с заданной точностью. Вычисление точностных оценок методов по координатам. Сплайн интерполяция и решение дифференциального уравнения.
контрольная работа , добавлен 26.04.2011
Решение задачи Коши для дифференциального уравнения. Погрешность приближенных решений. Функция, реализующая явный метод Эйлера. Вычисление погрешности по правилу Рунге. Решение дифференциальных уравнений второго порядка. Условие устойчивости для матрицы.
