المنتج المتجه أ ب. ناقلات للدمى. الإجراءات مع النواقل. إحداثيات المتجهات. أبسط مشاكل النواقل

7.1 تعريف المنتج المتقاطع

ثلاثة نواقل غير متحد المستوى أ ، ب ، ج ، مأخوذة بالترتيب المشار إليه ، تشكل ثلاثية يمنى إذا كان من نهاية المتجه الثالث c أقصر انعطاف من المتجه الأول أ إلى المتجه الثاني ب يكون عكس اتجاه عقارب الساعة ، و أيسر إذا كان في اتجاه عقارب الساعة (انظر الشكل 16).

يسمى منتج المتجه للمتجه a والمتجه b المتجه c ، والذي:

1. عمودي على المتجهين أ وب ، أي ج ^ أ وج ^ ب؛

2. له طول يساوي عدديًا مساحة متوازي الأضلاع المبنية على المتجهين a وبكما في الجوانب (انظر الشكل 17) ، أي

3. تشكل النواقل أ ، ب ، ج ثلاثية أيمن.

ناقلات المنتجتدل على أ س ب أو [أ ، ب]. من تعريف المنتج المتجه ، العلاقات التالية بين الأنواع التي أتبعها مباشرة ، يو ك(انظر الشكل 18):

i x j \ u003d k، j x k \ u003d i، k x i \ u003d j.
دعونا نثبت ذلك ، على سبيل المثالأنا xj \ u003d ك.

1) ك ^ ط ، ك ^ ي ؛

2) | ك | = 1 ، لكن | أنا x ي| = | أنا | | ي | الخطيئة (90 درجة) = 1 ؛

3) النواقل i و j و كتشكل ثلاثية أيمن (انظر الشكل 16).

7.2 عبر خصائص المنتج

1. عندما يتم إعادة ترتيب العوامل ، يتغير المنتج المتجه ، أي و xb \ u003d (ب xa) (انظر الشكل 19).

المتجهات a xb و b xa خطية ، ولها نفس الوحدات (تظل مساحة متوازي الأضلاع دون تغيير) ، ولكنها موجهة بشكل معاكس (ثلاثيات a ، b ، a xb و a ، b ، b x a ذات اتجاه معاكس). إنه اكسب = -(بكسا).

2. المنتج المتجه له خاصية مركبة فيما يتعلق بعامل قياسي ، أي l (a xb) \ u003d (l a) x b \ u003d a x (l b).

دع l> 0. المتجه l (a xb) عمودي على المتجهين a و b. المتجه ( لفأس بعمودي أيضًا على المتجهين a و ب(ناقلات أ ، للكن استلقي في نفس الطائرة). لذا فإن النواقل ل(أ x ب) و ( لفأس بعلاقة خطية متداخلة. من الواضح أن اتجاهاتهم تتوافق. لها نفس الطول:

لهذا ل(أ x ب) = لأ إكس ب. ثبت بالمثل ل ل<0.

3. متجهان غير صفريين أ و بتكون خطية متداخلة إذا وفقط إذا كان منتجها المتجه مساويًا للمتجه الصفري ، أي ، و || b<=>و xb \ u003d 0.

على وجه الخصوص ، i * i = j * j = k * k = 0.

4. للمنتج المتجه خاصية التوزيع:

(أ + ب) xs = a xs + ب xs.

تقبل بدون دليل.

7.3. عبر تعبير المنتج من حيث الإحداثيات

سوف نستخدم جدول الإنتاج المتجهي الأول ، يو ك:

إذا كان اتجاه أقصر مسار من المتجه الأول إلى الثاني يتزامن مع اتجاه السهم ، فإن المنتج يساوي المتجه الثالث ، وإذا لم يتطابق ، يتم أخذ المتجه الثالث بعلامة ناقص.

دع المتجهين a = a x i + a y ي+ az كو ب = ب س أنا+ بواسطة ي+ ب ك. لنجد حاصل الضرب المتجه لهذه المتجهات بضربها في صورة كثيرات حدود (وفقًا لخصائص منتج المتجه):

يمكن كتابة الصيغة الناتجة بشكل أقصر:

حيث أن الجانب الأيمن من المساواة (7.1) يتوافق مع توسيع محدد الدرجة الثالثة من حيث عناصر الصف الأول ، ومن السهل تذكر المساواة (7.2).

7.4. بعض تطبيقات المنتج المتقاطع

إنشاء علاقة خطية متداخلة من النواقل

إيجاد مساحة متوازي أضلاع ومثلث

وفقًا لتعريف المنتج المتقاطع للمتجهات أوب | a xb | =| أ | * | b | sin g ، ie S par = | a x b |. وبالتالي ، D S \ u003d 1/2 | a x b |.

تحديد لحظة القوة عند نقطة ما

دع القوة تطبق عند النقطة أ F = ABدعها تذهب عن- نقطة ما في الفضاء (انظر الشكل 20).

ومن المعروف من الفيزياء أن عزم الدوران F نسبة إلى هذه النقطة عنيسمى المتجه مالذي يمر بالنقطة عنو:

1) عموديًا على المستوى الذي يمر عبر النقاط س ، أ ، ب ؛

2) يساوي عدديًا ناتج القوة والذراع

3) تشكل ثلاثية صحيحة مع المتجهين OA و A B.

لذلك ، M \ u003d OA x F.

إيجاد السرعة الخطية للدوران

سرعة الخامسالنقطة M لجسم صلب يدور بسرعة زاوية ثحول محور ثابت ، يتم تحديده بواسطة صيغة أويلر v \ u003d w x r ، حيث r \ u003d OM ، حيث O هي نقطة ثابتة من المحور (انظر الشكل 21).

Yandex.RTB R-A-339285-1

قبل إعطاء مفهوم المنتج المتجه ، دعنا ننتقل إلى مسألة اتجاه الثلاثي المرتب من المتجهات a → ، b → ، c → في الفضاء ثلاثي الأبعاد.

بادئ ذي بدء ، دعنا نضع المتجهات a → ، b → ، c → من نقطة واحدة. اتجاه الثلاثي a → ، b → ، c → يمينًا أو يسارًا ، اعتمادًا على اتجاه المتجه c →. من الاتجاه الذي يتم فيه أقصر دورة من المتجه a → إلى b → من نهاية المتجه c → ، سيتم تحديد شكل الثلاثي a → ، b → ، c →.

إذا كان أقصر دوران هو عكس اتجاه عقارب الساعة ، فسيتم استدعاء ثلاثية المتجهات a → ، b → ، c → يمينإذا في اتجاه عقارب الساعة - غادر.

بعد ذلك ، خذ متجهين غير خطيين a → و b →. دعونا بعد ذلك نؤجل المتجهات A B → = a → و A C → = b → من النقطة A. دعونا نبني متجهًا A D → = c → ، وهو متعامد في نفس الوقت على كل من A B → و A C →. وبالتالي ، عند إنشاء المتجه A D → = c → ، يمكننا القيام بأمرين ، إما بإعطائه اتجاهًا واحدًا أو العكس (انظر الشكل التوضيحي).

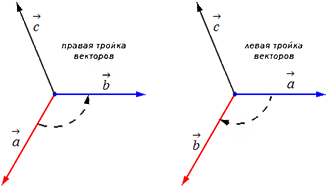
يمكن أن يكون الثلاثي المرتب للمتجهات a → ، b → ، c → ، كما اكتشفنا ، يمينًا أو يسارًا اعتمادًا على اتجاه المتجه.

مما سبق ، يمكننا تقديم تعريف المنتج المتجه. يتم إعطاء هذا التعريف لمتجهين محددين في نظام إحداثيات مستطيل للفضاء ثلاثي الأبعاد.

التعريف 1

المنتج المتجه لمتجهين a → و b → سوف نسمي مثل هذا المتجه المعطى في نظام إحداثيات مستطيل للفضاء ثلاثي الأبعاد مثل:

• إذا كانت النواقل a → و b → متداخلة ، فسيكون صفرًا ؛
• سيكون عموديًا على كل من المتجه a → والمتجه b → ie ∠ a → c → = ∠ b → c → = π 2 ؛
• يتم تحديد طوله بالصيغة: c → = a → b → sin ∠ a →، b →؛
• ثلاثية النواقل a → ، b → ، c → لها نفس اتجاه نظام الإحداثيات المحدد.

المنتج المتقاطع للمتجهات a → و b → له الترميز التالي: a → × b →.

عبر إحداثيات المنتج

نظرًا لأن أي متجه له إحداثيات معينة في نظام الإحداثيات ، فمن الممكن تقديم تعريف ثانٍ لمنتج المتجه ، والذي سيسمح لك بالعثور على إحداثياته ​​من الإحداثيات المحددة للمتجهات.

التعريف 2

في نظام إحداثيات مستطيل من الفضاء ثلاثي الأبعاد منتج متجه لمتجهين a → = (أ س ؛ أ ص ؛ أ ض) و ب → = (ب س ؛ ب ص ؛ ب ض) استدعاء المتجه c → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k → ، حيث i → ، j → ، k → هي متجهات إحداثية.

يمكن تمثيل منتج المتجه كمحدد لمصفوفة مربعة من الدرجة الثالثة ، حيث يكون الصف الأول هو متجهات orta i → ، j → ، k → ، الصف الثاني يحتوي على إحداثيات المتجه a → ، والصف الثالث هي إحداثيات المتجه b → في نظام إحداثيات مستطيل معين ، يبدو محدد المصفوفة هذا على النحو التالي: c → = a → × b → = i → j → k → a x a y a z b x b y b z

بتوسيع هذا المحدد على عناصر الصف الأول ، نحصل على المساواة: c → = a → × b → = i → j → k → a x a y a z b x b y b z = a y a z b y b z i → - a x a z b x b z j → + a x a y b x b y k → = = a → × b → = ( a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k →

عبر خصائص المنتج

من المعروف أن منتج المتجه في الإحداثيات يتم تمثيله كمحدد للمصفوفة c → = a → × b → = i → j → k → a x a y a z b x b y b z ، ثم على القاعدة خصائص محدد المصفوفةالأتى ناقلات خصائص المنتج:

1. anticommutativity a → × b → = - b → × a → ؛
2. التوزيعية a (1) → + a (2) → × b = a (1) → × b → + a (2) → × b → أو a → × b (1) → + b (2) → = a → × ب (1) → + أ → × ب (2) → ؛
3. الارتباط λ a → × b → = λ a → × b → أو a → × (λ b →) = λ a → × b → ، حيث λ هو رقم حقيقي تعسفي.

هذه الخصائص ليس لها براهين معقدة.

على سبيل المثال ، يمكننا إثبات الخاصية المضادة لمنتج متجه.

دليل على منع الحركة

بحكم التعريف ، a → × b → = i → j → k → a x a y a z b x b y b z and b → × a → = i → j → k → b x b y b z a x a y a z. وإذا تم تبادل صفين من المصفوفة ، فيجب أن تتغير قيمة محدد المصفوفة إلى العكس ، لذلك ، a → × b → = i → j → k → a x a y a z b x b y b z = - i → j → k → b x b y b z a x a y a z = - b → × a → ، والذي يثبت عدم قابلية التبادل للمنتج المتجه.

Vector Product - أمثلة وحلول

في معظم الحالات ، هناك ثلاثة أنواع من المهام.

في مسائل النوع الأول ، يتم تحديد أطوال متجهين والزاوية بينهما ، ولكن عليك إيجاد طول حاصل الضرب الاتجاهي. في هذه الحالة ، استخدم الصيغة التالية c → = a → b → sin ∠ a →، b →.

مثال 1

أوجد طول الضرب العرضي للمتجهات a → و b → إذا كان a → = 3 ، b → = 5 ، ∠ a → ، b → = π 4 معروف.

حل

باستخدام تعريف طول منتج المتجه للمتجهات a → و b → ، نحل هذه المشكلة: a → × b → = a → b → sin ∠ a → ، b → = 3 5 sin π 4 = 15 2 2 .

إجابة: 15 2 2 .

المهام من النوع الثاني لها اتصال بإحداثيات المتجهات ، فهي تحتوي على منتج متجه ، وطوله ، وما إلى ذلك. يتم البحث عنها من خلال الإحداثيات المعروفة للمتجهات المعينة أ → = (أ س ؛ أ ص ؛ أ ض) و ب → = (ب س ؛ ب ص ؛ ب ض) .

بالنسبة لهذا النوع من المهام ، يمكنك حل الكثير من خيارات المهام. على سبيل المثال ، ليس إحداثيات المتجهات a → و b → ، ولكن توسعاتها في متجهات تنسيق النموذج b → = b x i → + b y j → + b z k → و c → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k → ، أو يمكن إعطاء المتجهات a → و b → بواسطة إحداثياتهم نقطتا البداية والنهاية.

تأمل الأمثلة التالية.

مثال 2

يتم تعيين متجهين في نظام إحداثيات مستطيل a → = (2 ؛ 1 ؛ - 3) ، b → = (0 ؛ - 1 ؛ 1). ابحث عن منتجهم المتجه.

حل

وفقًا للتعريف الثاني ، نجد منتج المتجه لمتجهين في إحداثيات معينة: a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k → = = (1 1 - (- 3) (- 1)) i → + ((- 3) 0-2 1) j → + (2 (- 1) - 1 0) k → = = - 2 i → - 2 j → - 2 ك →.

إذا كتبنا منتج المتجه من خلال محدد المصفوفة ، فإن حل هذا المثال يكون كما يلي: a → × b → = i → j → k → a x a y a z b x b y b z = i → j → k → 2 1-3 0-1 1 = - 2 i → - 2 j → - 2 k →.

إجابة: a → × b → = - 2 i → - 2 j → - 2 k →.

مثال 3

أوجد طول الناتج المتقاطع للمتجهات i → - j → و i → + j → + k → ، حيث i → ، j → ، k → - orts من نظام إحداثيات ديكارتي مستطيل.

حل

أولاً ، لنجد إحداثيات منتج المتجه المحدد i → - j → × i → + j → + k → في نظام إحداثيات المستطيل المحدد.

من المعروف أن المتجهات i → - j → و i → + j → + k → لها إحداثيات (1 ؛ - 1 ؛ 0) و (1 ؛ 1 ؛ 1) على التوالي. أوجد طول منتج المتجه باستخدام محدد المصفوفة ، ثم لدينا i → - j → × i → + j → + k → = i → j → k → 1 - 1 0 1 1 1 = - i → - j → + 2 ك →.

لذلك ، فإن منتج المتجه i → - j → × i → + j → + k → له إحداثيات (- 1 ؛ - 1 ؛ 2) في نظام الإحداثيات المحدد.

نجد طول المنتج المتجه بالصيغة (انظر القسم الخاص بإيجاد طول المتجه): i → - j → × i → + j → + k → = - 1 2 + - 1 2 + 2 2 = 6.

إجابة: i → - j → × i → + j → + k → = 6. .

مثال 4

إحداثيات النقاط الثلاث أ (1 ، 0 ، 1) ، ب (0 ، 2 ، 3) ، ج (1 ، 4 ، 2) معطاة في نظام إحداثيات ديكارتي مستطيل. ابحث عن متجه عمودي على ب ← و ج ← في نفس الوقت.

حل

المتجهات A B → و A C → لها الإحداثيات التالية (- 1 ؛ 2 ؛ 2) و (0 ؛ 4 ؛ 1) على التوالي. بعد العثور على منتج المتجه للمتجهات A B → و A C → ، من الواضح أنه متجه عمودي بالتعريف لكل من A B → و A C → ، أي أنه الحل لمشكلتنا. ابحث عنه A B → × A C → = i → j → k → - 1 2 2 0 4 1 = - 6 i → + j → - 4 k →.

إجابة: - 6 i → + j → - 4 k →. هو أحد النواقل العمودية.

تركز مشاكل النوع الثالث على استخدام خصائص المنتج المتجه للمتجهات. بعد التقديم ، سنحصل على حل للمشكلة المحددة.

مثال 5

المتجهان a → و b → عموديان وأطوالهما 3 و 4 على التوالي. أوجد طول الضرب العرضي 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 a → × a → + 3 أ → × - 2 ب → + - ب → × أ → + - ب → × - 2 ب →.

حل

من خلال خاصية التوزيع لمنتج المتجه ، يمكننا كتابة 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 a → × a → + 3 a → × - 2 b → + - b → × a → + - b → × - 2 b →

من خلال خاصية الترابط ، نخرج المعاملات العددية التي تتجاوز علامة المنتجات المتجهة في التعبير الأخير: 3 أ → × أ → + 3 أ → × - 2 ب → + - ب → × أ → + - ب → × - 2 ب → = = 3 أ → × أ → + 3 (- 2) أ → × ب → + (- 1) ب → × أ → + (- 1) (- 2) ب → × ب → = = 3 a → × a → - 6 a → × b → - b → × a → + 2 b → × b →

منتجات المتجه a → × a → و b → × b → تساوي 0 ، حيث أن a → × a → = a → a → sin 0 = 0 و b → × b → = b → b → sin 0 = 0 ، ثم 3 a → × a → - 6 a → × b → - b → × a → + 2 b → × b → = - 6 a → × b → - b → × a →. .

من anticommutativity للمنتج المتجه يتبع - 6 a → × b → - b → × a → = - 6 a → × b → - (- 1) a → × b → = - 5 a → × b →. .

باستخدام خصائص منتج المتجه ، نحصل على المساواة 3 · a → - b → × a → - 2 · b → = = - 5 · a → × b →.

حسب الشرط ، يكون المتجهان a → و b → عموديين ، أي أن الزاوية بينهما تساوي π 2. الآن يبقى فقط استبدال القيم الموجودة في الصيغ المقابلة: 3 a → - b → × a → - 2 b → = - 5 a → × b → = = 5 a → × b → = 5 a → b → الخطيئة (أ → ، ب →) = 5 3 4 خطيئة π 2 = 60.

إجابة: 3 أ ← - ب ← × أ ← - 2 ب ← = 60.

طول الناتج المتقاطع للمتجهات حسب التعريف هو a → × b → = a → · b → · sin ∠ a →، b →. بما أنه معروف بالفعل (من مقرر المدرسة) أن مساحة المثلث تساوي نصف حاصل ضرب أطوال ضلعيه مضروبًا في جيب الزاوية بين هذين الضلعين. لذلك ، فإن طول منتج المتجه يساوي مساحة متوازي الأضلاع - مثلث مضاعف ، أي ناتج الجوانب في شكل متجهات a → و b → ، تم تسريحه من نقطة واحدة ، بواسطة الجيب للزاوية بينهما sin ∠ a → ، b →.

هذا هو المعنى الهندسي للمنتج المتجه.

المعنى المادي للمنتج المتجه

في الميكانيكا ، أحد فروع الفيزياء ، بفضل حاصل الضرب الاتجاهي ، يمكنك تحديد لحظة القوة بالنسبة إلى نقطة في الفضاء.

التعريف 3

تحت لحظة القوة F → ، المطبقة على النقطة B ، بالنسبة للنقطة A ، سوف نفهم المنتج المتجه التالي A B → × F →.

إذا لاحظت وجود خطأ في النص ، فيرجى تمييزه والضغط على Ctrl + Enter

تعريف. المنتج المتجه للمتجه a (المضاعف) بواسطة المتجه (المضاعف) غير المتصل به هو المتجه الثالث c (المنتج) ، والذي يتم إنشاؤه على النحو التالي:

1) معامله يساوي عدديًا مساحة متوازي الأضلاع في الشكل. 155) ، مبنية على متجهات ، أي أنها تساوي الاتجاه العمودي على مستوى متوازي الأضلاع المذكور ؛

3) في هذه الحالة ، يتم اختيار اتجاه المتجه c (من اثنين ممكنين) بحيث تشكل المتجهات c نظامًا لليمين (الفقرة 110).

التعيين: أو

إضافة إلى التعريف. إذا كانت المتجهات على خط واحد ، فعندئذٍ بالنظر إلى الشكل باعتباره متوازي أضلاع (مشروطًا) ، فمن الطبيعي تعيين منطقة صفرية. لذلك ، يعتبر منتج المتجه للمتجهات الخطية مساويًا للمتجه الصفري.

نظرًا لأنه يمكن تعيين المتجه الفارغ لأي اتجاه ، فإن هذا الاصطلاح لا يتعارض مع البندين 2 و 3 من التعريف.

ملاحظة 1. في المصطلح "منتج متجه" ، تشير الكلمة الأولى إلى أن نتيجة إجراء ما هي متجه (على عكس منتج قياسي ؛ راجع § 104 ، الملاحظة 1).

مثال 1. أوجد حاصل الضرب المتجه حيث المتجهات الرئيسية لنظام الإحداثيات الصحيح (الشكل 156).

1. نظرًا لأن أطوال المتجهات الرئيسية تساوي وحدة القياس ، فإن مساحة متوازي الأضلاع (المربع) تساوي واحدًا عدديًا. ومن ثم ، فإن معامل حاصل الضرب المتجه يساوي واحدًا.

2. بما أن المحور العمودي على المستوى هو المحور ، فإن المنتج المتجه المطلوب هو خط متجه متجه إلى المتجه k ؛ وبما أن كلاهما لهما المعامل 1 ، فإن حاصل الضرب العرضي المطلوب هو إما k أو -k.

3. من هذين المتجهين المحتملين ، يجب اختيار الأول ، حيث أن المتجهات k تشكل نظامًا صحيحًا (والمتجهات تشكل نظامًا يسارًا).

مثال 2. أوجد حاصل الضرب التبادلي

حل. كما في المثال 1 ، نستنتج أن المتجه إما k أو -k. لكننا الآن نحتاج إلى اختيار -k ، لأن المتجهات تشكل النظام الصحيح (والمتجهات تشكل اليسار). لذا،

مثال 3 أطوال المتجهات 80 و 50 cm ، على التوالي ، وتشكل زاوية 30 °. بأخذ المتر كوحدة للطول ، أوجد طول منتج المتجه أ

حل. مساحة متوازي الأضلاع المبنية على المتجهات تساوي طول منتج المتجه المطلوب يساوي

مثال 4. أوجد طول حاصل الضرب الاتجاهي لنفس المتجهات ، بأخذ سنتيمتر كوحدة طول.

حل. نظرًا لأن مساحة متوازي الأضلاع المبنية على المتجهات تساوي طول منتج المتجه 2000 سم ، أي

توضح المقارنة بين الأمثلة 3 و 4 أن طول المتجه لا يعتمد فقط على أطوال العوامل ، ولكن أيضًا على اختيار وحدة الطول.

المعنى المادي للمنتج المتجه.من بين الكميات الفيزيائية العديدة التي يمثلها حاصل الضرب المتجه ، سننظر فقط في لحظة القوة.

لنفترض أن A هي نقطة تطبيق القوة. تسمى لحظة القوة بالنسبة للنقطة O منتج المتجه. نظرًا لأن الوحدة النمطية لهذا المنتج المتجه تساوي عدديًا مساحة متوازي الأضلاع (الشكل 157) ، وحدة اللحظة تساوي ناتج القاعدة بالارتفاع ، أي القوة مضروبة في المسافة من النقطة O إلى الخط المستقيم الذي تعمل فيه القوة.

في الميكانيكا ، ثبت أنه بالنسبة لتوازن الجسم الصلب ، من الضروري ألا يكون مجموع المتجهات التي تمثل القوى المطبقة على الجسم فحسب ، بل أيضًا مجموع لحظات القوى مساويًا للصفر. في الحالة التي تكون فيها جميع القوى موازية لنفس المستوى ، يمكن استبدال إضافة المتجهات التي تمثل اللحظات بجمع وطرح وحداتها. لكن بالنسبة لتوجيهات القوات التعسفية ، فإن هذا الاستبدال مستحيل. وفقًا لهذا ، يتم تعريف الضرب التبادلي بدقة على أنه متجه وليس كرقم.

في هذه المقالة ، سوف نتناول مفهوم الضرب الاتجاهي لمتجهين. سنقدم التعريفات اللازمة ، ونكتب معادلة لإيجاد إحداثيات منتج متجه ، وسندرج خصائصه ونبررها. بعد ذلك ، سوف نتناول المعنى الهندسي للحاصل الضرب المتقاطع لمتجهين وننظر في حلول أمثلة نموذجية مختلفة.

التنقل في الصفحة.

تعريف منتج متجه.

قبل إعطاء تعريف لحاصل الضرب الاتجاهي ، دعنا نتعامل مع اتجاه ثلاثية مرتبة من المتجهات في الفضاء ثلاثي الأبعاد.

دعونا نؤجل المتجهات من نقطة واحدة. اعتمادًا على اتجاه المتجه ، يمكن أن يكون الثلاثي يمينًا أو يسارًا. لننظر من نهاية المتجه إلى كيفية دوران أقصر المتجه من المتجه إلى. إذا كان أقصر دوران في عكس اتجاه عقارب الساعة ، فسيتم استدعاء ثلاثية المتجهات يمين، خلاف ذلك - غادر.

الآن لنأخذ متجهين غير خطيين و. ضع المتجهات جانباً ومن النقطة أ. دعونا نبني متجهًا متعامدًا على وفي نفس الوقت. من الواضح ، عند إنشاء متجه ، يمكننا القيام بأمرين ، بإعطائه إما اتجاه واحد أو العكس (انظر الشكل).

اعتمادًا على اتجاه المتجه ، يمكن أن تكون النواقل الثلاثية المرتبة يمينًا أو يسارًا.

لذلك اقتربنا من تعريف المنتج المتجه. يتم إعطاؤه لمتجهين معطى في نظام إحداثيات مستطيل للفضاء ثلاثي الأبعاد.

تعريف.

حاصل ضرب متجهين متجهينويعطى في نظام إحداثيات مستطيل للفضاء ثلاثي الأبعاد ، يسمى ناقل مثل هذا

حاصل الضرب الاتجاهي للمتجهات ويشار إليه على أنه.

إحداثيات المنتج المتجه.

نعطي الآن التعريف الثاني للمنتج المتجه ، والذي يسمح لنا بإيجاد إحداثياته ​​من إحداثيات المتجهات المعطاة و.

تعريف.

في نظام إحداثيات مستطيل من الفضاء ثلاثي الأبعاد حاصل ضرب اثنين من النواقل و هو متجه ، حيث توجد متجهات إحداثيات.

يعطينا هذا التعريف حاصل الضرب التبادلي في شكل تنسيق.

من الملائم تمثيل حاصل الضرب المتجه كمحدد لمصفوفة مربعة من الرتبة الثالثة ، الصف الأول منها هو orts ، والصف الثاني يحتوي على إحداثيات المتجه ، والصف الثالث يحتوي على إحداثيات المتجه في نظام إحداثيات مستطيل معين:

إذا قمنا بتوسيع هذا المحدد بواسطة عناصر الصف الأول ، فإننا نحصل على المساواة من تعريف المنتج المتجه في الإحداثيات (إذا لزم الأمر ، راجع المقالة):

وتجدر الإشارة إلى أن الشكل الإحداثي للمنتج المتقاطع يتوافق تمامًا مع التعريف الوارد في الفقرة الأولى من هذه المقالة. علاوة على ذلك ، فإن هذين التعريفين للمنتج المتقاطع متكافئان. يمكن العثور على دليل على هذه الحقيقة في الكتاب المشار إليه في نهاية المقال.

خصائص المنتج المتجه.

نظرًا لأنه يمكن تمثيل منتج المتجه في الإحداثيات كمحدد للمصفوفة ، يمكن إثبات ما يلي بسهولة على أساس ناقلات خصائص المنتج:

كمثال ، دعنا نثبت الخاصية المضادة لمنتج ناقل.

الدير و . نعلم أن قيمة محدد المصفوفة تنعكس عند تبديل صفين ، لذلك ، ، مما يثبت الخاصية المضادة لمنتج المتجه.

منتج المتجهات - أمثلة وحلول.

هناك ثلاثة أنواع من المهام.

في مسائل النوع الأول ، يتم إعطاء أطوال متجهين والزاوية بينهما ، ومطلوب إيجاد طول حاصل الضرب الاتجاهي. في هذه الحالة ، يتم استخدام الصيغة .

مثال.

أوجد طول الضرب الاتجاهي للمتجهات وإذا كان معروفًا .

حل.

نعلم من التعريف أن طول حاصل الضرب الاتجاهي للمتجهات ويساوي حاصل ضرب أطوال المتجهات وضرب جيب الزاوية بينهما ، لذلك ، .

إجابة:

.

ترتبط مهام النوع الثاني بإحداثيات المتجهات ، حيث يتم البحث عن منتج المتجه أو طوله أو أي شيء آخر من خلال إحداثيات المتجهات المعينة و .

هناك العديد من الخيارات المختلفة المتاحة هنا. على سبيل المثال ، ليس إحداثيات المتجهات و لكن توسعاتها في متجهات إحداثيات للنموذج و ، أو المتجهات ويمكن تحديدها بواسطة إحداثيات نقطتي البداية والنهاية.

دعونا ننظر في الأمثلة النموذجية.

مثال.

يتم إعطاء متجهين في نظام إحداثيات مستطيل . ابحث عن منتجهم المتجه.

حل.

وفقًا للتعريف الثاني ، تتم كتابة الناتج المتقاطع لمتجهين في الإحداثيات على النحو التالي:

كنا سنصل إلى نفس النتيجة إذا كتبنا حاصل الضرب المتجه من خلال المحدد

إجابة:

.

مثال.

أوجد طول حاصل الضرب الاتجاهي للمتجهات وأين توجد أخطاء نظام الإحداثيات الديكارتية المستطيلة.

حل.

أولاً ، أوجد إحداثيات حاصل الضرب المتجه في نظام إحداثيات مستطيل معين.

نظرًا لأن المتجهات ولديها إحداثيات وعلى التوالي (إذا لزم الأمر ، راجع إحداثيات المقالة للمتجه في نظام إحداثيات مستطيل) ، ثم وفقًا للتعريف الثاني للمنتج المتقاطع ، لدينا

هذا هو ، منتج المتجه لديه إحداثيات في نظام إحداثيات معين.

نجد طول منتج المتجه كجذر تربيعي لمجموع مربعات إحداثياته ​​(حصلنا على هذه الصيغة لطول المتجه في القسم الخاص بإيجاد طول المتجه):

إجابة:

.

مثال.

يتم إعطاء إحداثيات النقاط الثلاث في نظام إحداثيات ديكارتي مستطيل. ابحث عن متجه عمودي عليه وفي نفس الوقت.

حل.

المتجهات ولها إحداثيات و ، على التوالي (انظر المقالة التي تبحث عن إحداثيات متجه من خلال إحداثيات النقاط). إذا وجدنا حاصل الضرب الاتجاهي للمتجهات ، ومن ثم فهو متجه عموديًا على كل من وعليه ، أي أنه الحل لمشكلتنا. لنجده

إجابة:

هو أحد النواقل العمودية.

في مهام النوع الثالث ، يتم التحقق من مهارة استخدام خصائص المنتج المتجه للمتجهات. بعد تطبيق الخصائص ، يتم تطبيق الصيغ المقابلة.

مثال.

المتجهات وعمودية وأطوالها 3 و 4 على التوالي. أوجد طول حاصل الضرب المتجه .

حل.

من خلال خاصية التوزيع لمنتج المتجه ، يمكننا الكتابة

بحكم الخاصية الترابطية ، نخرج المعاملات العددية لعلامة المنتجات المتجهة في التعبير الأخير:

منتجات المتجهات وتساوي الصفر ، منذ ذلك الحين و ، ثم .

بما أن منتج المتجه مضاد للتبديل ، إذن.

لذلك ، باستخدام خصائص المنتج المتجه ، وصلنا إلى المساواة .

حسب الشرط ، تكون المتجهات وعمودية ، أي أن الزاوية بينهما تساوي. أي ، لدينا جميع البيانات للعثور على الطول المطلوب

إجابة:

.

المعنى الهندسي للمنتج المتجه.

بحكم التعريف ، فإن طول المنتج المتقاطع للمتجهات هو . ومن دورة الهندسة في المدرسة الثانوية ، نعلم أن مساحة المثلث تساوي نصف حاصل ضرب ضلعي المثلث وجيب الزاوية بينهما. لذلك ، فإن طول حاصل الضرب الاتجاهي يساوي ضعف مساحة المثلث بأضلاع المتجهات ، وإذا تم تأجيلها من نقطة واحدة. وبعبارة أخرى ، فإن طول حاصل الضرب المتقاطع للمتجهات ويساوي مساحة متوازي أضلاع مع أضلاع وزاوية بينهما تساوي. هذا هو المعنى الهندسي للمنتج المتجه.

تعريف تسمى المجموعة المرتبة (× 1 ، × 2 ، ... ، × ن) من الأرقام الحقيقية ن ناقلات الأبعاد، والأرقام x i (i =) - عناصرأو إحداثيات

مثال. على سبيل المثال ، إذا كان على مصنع سيارات معين إنتاج 50 سيارة و 100 شاحنة و 10 حافلات و 50 مجموعة من قطع الغيار للسيارات و 150 مجموعة للشاحنات والحافلات لكل نوبة ، فيمكن كتابة برنامج الإنتاج لهذا المصنع باعتباره المتجه (50 ، 100 ، 10 ، 50 ، 150) ، والذي يتكون من خمسة مكونات.

الرموز. يتم الإشارة إلى المتجهات بأحرف صغيرة أو بأحرف صغيرة مع شريط أو سهم في الأعلى ، على سبيل المثال ، أأو. يتم استدعاء المتجهين متساويإذا كان لديهم نفس عدد المكونات والمكونات المقابلة لها متساوية.

لا يمكن تبادل مكونات المتجه ، على سبيل المثال (3 ، 2 ، 5 ، 0 ، 1)و (2 ، 3 ، 5 ، 0 ، 1) متجهات مختلفة.
العمليات على النواقل.عمل x= (x 1، x 2، ...، x n) لرقم حقيقيλ يسمى المتجهλ x= (λ x 1، λ x 2، ...، λ x n).

مجموعx= (x 1، x 2، ...، x n) و ذ= (y 1، y 2، ...، y n) يسمى متجه س + ص= (x 1 + y 1، x 2 + y 2، ...، x n + + y n).

مساحة النواقل.ن -الأبعاد ناقلات الفضاء صيتم تعريف n على أنها مجموعة من جميع المتجهات ذات الأبعاد n التي يتم من أجلها تحديد عمليات الضرب بالأرقام الحقيقية والإضافة.

التوضيح الاقتصادي. رسم توضيحي اقتصادي لمساحة متجهية ذات أبعاد n: مساحة البضائع (بضائع). تحت سلعةسوف نفهم بعض السلع أو الخدمات التي تم طرحها للبيع في وقت معين في مكان معين. افترض أن هناك عددًا محدودًا من السلع المتاحة n ؛ تتميز كميات كل منها المشتراة من قبل المستهلك بمجموعة من السلع

x= (× 1 ، × 2 ، ... ، × ن) ،

حيث تشير x i إلى مقدار السلعة i التي اشتراها المستهلك. سنفترض أن جميع السلع لها خاصية القابلية التعسفية للقسمة ، بحيث يمكن شراء أي كمية غير سلبية لكل منها. إذن ، فإن جميع مجموعات البضائع الممكنة هي ناقلات لمساحة البضائع C = ( x= (x 1، x 2، ...، x n)س أنا ≥ 0 ، أنا =).

الاستقلال الخطي. نظام ه 1 , ه 2 , ... , ه m ن نواقل الأبعاد يسمى تعتمد خطياإذا كان هناك مثل هذه الأرقامλ 1 ، λ 2 ، ... ، λ م ، منها واحد على الأقل غير صفري ، مما يرضي المساواةλ1 ه 1 + λ2 ه 2 + ... + ميكرون هم = 0 ؛ خلاف ذلك ، يسمى هذا النظام من النواقل مستقل خطيا، أي أن هذه المساواة ممكنة فقط في حالة وجود كل شيء . المعنى الهندسي للاعتماد الخطي للناقلات في ص 3 ، يتم تفسيرها على أنها شرائح موجهة ، اشرح النظريات التالية.

نظرية 1. النظام الذي يتكون من متجه واحد يعتمد خطيًا إذا وفقط إذا كان هذا المتجه صفرًا.

نظرية 2. لكي يكون متجهان معتمدين خطيًا ، من الضروري والكافي أن يكونا متصلين (متوازيين).

نظرية 3 . لكي تعتمد ثلاثة نواقل خطيًا ، من الضروري والكافي أن تكون متحد المستوى (مستلقية في نفس المستوى).

ثلاثة أضعاف اليسار واليمين من المتجهات. ثلاثية النواقل غير متحد المستوى أ ، ب ، جمُسَمًّى يمين، إذا تجاوز المراقب من أصلهم المشترك نهايات المتجهات أ ، ب ، جبهذا الترتيب يبدو أنه يسير في اتجاه عقارب الساعة. خلاف ذلك أ ، ب ، ج -ثلاثة أضعاف اليسار. يتم استدعاء جميع النواقل الثلاثية اليمنى (أو اليسرى) بالتساوي الموجهة.

الأساس والإحداثيات. الترويكا ه 1, ه 2 , ه 3 نواقل غير متحد المستوى في ص 3 دعا أساسوالنواقل نفسها ه 1, ه 2 , ه 3 - أساسي. أي ناقل أيمكن توسيعها بطريقة فريدة من حيث متجهات الأساس ، أي يمكن تمثيلها في النموذج

أ= س 1 ه 1 + × 2 ه 2 + × 3 ه 3, (1.1)

تسمى الأرقام × 1 ، × 2 ، × 3 في التوسع (1.1) إحداثياتأفي الأساس ه 1, ه 2 , ه 3 ويشار إليها أ(× 1 ، × 2 ، × 3).

أساس متعامد. إذا كانت النواقل ه 1, ه 2 , ه 3 هي زوجية متعامدة وطول كل منهما يساوي واحدًا ، ثم يسمى الأساس متعامد، والإحداثيات × 1 ، × 2 ، × 3 - مستطيلي.سيتم الإشارة إلى المتجهات الأساسية للأساس المتعامد أنا ، ي ، ك.

سوف نفترض ذلك في الفضاء ص 3 النظام الصحيح للإحداثيات المستطيلة الديكارتية (0 ، أنا ، ي ، ك}.

المنتج المتجه. ناقلات الفن ألكل متجه بيسمى المتجه ج، والتي تحددها الشروط الثلاثة التالية:

1. طول المتجه جيساوي عدديًا مساحة متوازي الأضلاع المبنية على المتجهات أو ب،أي.
ج= | أ || ب |الخطيئة ( أ^ب).

2. المتجهات جعمودي على كل من المتجهات أو ب.

3. النواقل أ، بو ج، المأخوذة بهذا الترتيب ، تشكل ثلاثية صحيحة.

لمنتج ناقل جتم تقديم التعيين ج =[أب] أو
ج = أ × ب.

إذا كانت النواقل أو بخطية متداخلة ، ثم الخطيئة ( أ ^ ب) = 0 و [ أب] = 0 ، على وجه الخصوص ، [ أأ] = 0. متجهات المنتجات ذات الصلة: [ اي جاي]=ك، [كيه] = أنا, [كي]=ي.

إذا كانت النواقل أو بنظرا في الأساس أنا ، ي ، كإحداثيات أ(أ 1 ، أ 2 ، أ 3) ، ب(ب 1 ، ب 2 ، ب 3) ، إذن

عمل مختلط. إذا كان حاصل الضرب الاتجاهي لمتجهين أو بالعددية مضروبة في المتجه الثالث ج ،ثم يسمى هذا المنتج من ثلاثة نواقل منتج مختلطويشار إليه بالرمز أ قبل الميلاد.

إذا كانت النواقل أ ، بو جفي الأساس أنا ، ي ، كالتي حددتها إحداثياتها
أ(أ 1 ، أ 2 ، أ 3) ، ب(ب 1 ، ب 2 ، ب 3) ، ج(ج 1 ، ج 2 ، ج 3) ، إذن

.

المنتج المختلط له تفسير هندسي بسيط - إنه عددي ، بقيمة مطلقة تساوي حجم خط متوازي مبني على ثلاثة متجهات معطاة.

إذا كانت المتجهات تشكل ثلاثية صحيحة ، فإن منتجها المختلط هو رقم موجب يساوي الحجم المشار إليه ؛ إذا كان الثلاثة أ ، ب ، ج -غادر ، إذن أ ب ج<0 и V = - أ ب ج، لذلك V =| أ ب ج |.

من المفترض أن يتم إعطاء إحداثيات المتجهات التي تمت مواجهتها في مشاكل الفصل الأول بالنسبة إلى الأساس الصحيح المتعامد. متجه الوحدة الاتجاهية إلى المتجه أ،يرمز له بالرمز أس. رمز ص=OMيُشار إليها بواسطة متجه نصف قطر النقطة M أو الرموز a أو AB أو| أ |, | AB |يتم الإشارة إلى وحدات المتجهات أو AB.

مثال 1.2. أوجد الزاوية بين المتجهات أ= 2م+4نو ب= م ن، أين مو ن-متجهات الوحدة والزاوية بينهما مو نيساوي 120 س.

حل. لدينا: كوس φ = أب/ أب ، أب =(2م+4ن) (م ن) = 2م 2 - 4ن 2 +2مليون=
= 2-4 + 2cos120 o = - 2 + 2 (-0.5) = -3 ؛ أ = ؛ أ 2 = (2م+4ن) (2م+4ن) =
= 4م 2 +16مليون+16ن 2 = 4 + 16 (-0.5) + 16 = 12 ، لذا أ =. ب = ؛ ب 2 =
= (م ن)(م ن) = م 2 -2مليون+ن 2 = 1-2 (-0.5) +1 = 3 ، لذا ب =. أخيرًا لدينا: cosφ \ u003d -1/2 ، φ \ u003d 120 درجة.

مثال 1.3.معرفة النواقل AB(-3 ، -2.6) و قبل الميلاد(-2،4،4) ، احسب ارتفاع AD للمثلث ABC.

حل. للدلالة على مساحة المثلث ABC بواسطة S ، نحصل على:
S = 1/2 قبل الميلاد. ثم AD = 2S / BC ، BC == = 6,
S = 1/2 | AB ×AC |. AC = AB + BC، وبالتالي فإن المتجه تيار مترددإحداثيات
. .

مثال 1.4 . نظرا اثنين من النواقل أ(11 ، 10 ، 2) و ب(4،0،3). أوجد متجه الوحدة ج ،متعامد مع النواقل أو بوتوجيهها بحيث يتم ترتيب النواقل الثلاثية أ ، ب ، جكان صحيحا.

حل.دعونا نشير إلى إحداثيات المتجه جفيما يتعلق بالأساس المتعامد الصحيح المعطى بدلالة x ، y ، z.

بسبب ال ج ⊥ أ ، ج ⊥ب، الذي - التي كاليفورنيا= 0، cb= 0. حسب حالة المشكلة ، يجب أن يكون c = 1 و أ ب ج >0.

لدينا نظام معادلات لإيجاد x ، y ، z: 11x + 10y + 2z = 0 ، 4x + 3z = 0 ، x 2 + y 2 + z 2 = 0.

من المعادلتين الأولى والثانية للنظام نحصل على z = -4/3 x ، y = -5/6 x. بالتعويض عن y و z في المعادلة الثالثة ، سيكون لدينا: x 2 = 36/125 ، من أين
س =± . باستخدام الشرط أ ب ج> 0 ، نحصل على عدم المساواة

مع الأخذ في الاعتبار تعابير z و y ، نعيد كتابة المتباينة الناتجة بالصيغة: 625/6 x> 0 ، ومن هنا يتبع ذلك x> 0. إذن x = ، y = - ، z = -.