Реферат
Абсолютная и относительная погрешность
Введение
Абсолютная погрешность - является оценкой абсолютной ошибки измерения. Вычисляется разными способами. Способ вычисления определяется распределением случайной величины. Соответственно, величина абсолютной погрешности в зависимости от распределения случайной величины может быть различной. Если - измеренное значение, а - истинное значение, то неравенство должно выполняться с некоторой вероятностью, близкой к 1. Если случайная величина распределена по нормальному закону, то обычно за абсолютную погрешность принимают её среднеквадратичное отклонение. Абсолютная погрешность измеряется в тех же единицах измерения, что и сама величина.
Существует несколько способов записи величины вместе с её абсолютной погрешностью.
·Обычно используется запись со знаком ± . Например, рекорд в беге на 100 метров, установленный в 1983 году, равен 9,930±0,005 с .
·Для записи величин, измеренных с очень высокой точностью, используется другая запись: цифры, соответствующие погрешности последних цифр мантиссы, дописываются в скобках. Например, измеренное значение постоянной Больцмана равно 1,380 6488 (13)×10 ?23 Дж/К , что также можно записать значительно длиннее как 1,380 6488×10 ?23 ± 0,000 0013×10 ?23 Дж/К .
Относительная погрешность - погрешность измерения, выраженная отношением абсолютной погрешности измерения к действительному или среднему значению измеряемой величины (РМГ 29-99):.
Относительная погрешность является безразмерной величиной, либо измеряется в процентах.
1. Что называется приближённым значением?
С избыточным и недостаточным? В процессе вычислений весьма часто приходится иметь дело с приближенными числами. Пусть А - точное значение некоторой величины, называемое в дальнейшем точным числом А. Под приближенным значением величины А, или приближенным числам, называется число а , заменяющее точное значение величины А. Если а < А, то а называется приближенным значением числа А по недостатку. Если а > А, - то по избытку. Например, 3,14 является приближенным значением числа ? по недостатку, а 3,15 - по избытку. Для характеристики степени точности данного приближения пользуются понятием погрешности или ошибки.
Погрешностью ?а приближенного числа а называется разность вида
?а = А - а,
где А - соответствующее точное число.
Из рисунка видно, что длина отрезка АВ заключена между 6 см и 7 см.
Значит, 6 - приближенное значение длины отрезка АВ (в сантиметрах) > с недостатком, а 7 - с избытком.
Обозначив длину отрезка буквой у, получим: 6 < у < 1. Если a < х < b, то а называют приближенным значением числа х с недостатком, a b - приближенным значением х с избытком. Длина отрезка АВ (см. рис. 149) ближе к 6 см, чем к 7 см. Она приближенно равна 6 см. Говорят, что число 6 получилось при округлении длины отрезка до целых.
. Что называется погрешностью приближения?
А) Абсолютной?
Б) Относительной?
А) Абсолютной погрешностью приближения называется модуль разности между истинным значением величины и её приближённым значением. |x - x_n|, где x - истинное значение, x_n - приближённое. Например: Длина листа бумаги формата А4 равна (29.7 ± 0.1) см. А расстояние от Санкт-Петербурга до Москвы равно (650± 1) км. Абсолютная погрешность в первом случае не превосходит одного миллиметра, а во втором - одного километра. Вопрос, сравнить точность этих измерений.
Если вы думаете, что длина листа измерена точнее потому, что величина абсолютной погрешности не превышает 1 мм. То вы ошибаетесь. Напрямую сравнить эти величины нельзя. Проведем некоторые рассуждения.
При измерении длины листа абсолютная погрешность не превышает 0.1 см на 29.7 см, то есть в процентном соотношении это составляет 0.1/29.7 *100% = 0.33% измеряемой величины.
Когда мы измеряем расстояние от Санкт-Петербурга до Москвы абсолютная погрешность не превышает 1 км на 650 км, что в процентном соотношении составляет 1/650 *100% = 0.15% измеряемой величины. Видим, что расстояние между городами измерено точнее, чем длинна листа формата А4.
Б) Относительной погрешностью приближения называется отношение абсолютной погрешности к модулю приближённого значения величины.
математический погрешность дробь
где x - истинное значение, x_n - приближённое.
Относительную погрешность обычно вызывают в процентах.
Пример. При округлении числа 24,3 до единиц получается число 24.
Относительная погрешность равна. Говорят, что относительная погрешность в этом случае равна 12,5%.
) Какое округление, называется округлением?
А) С недостатком?
Б) С избытком?
А) Округление с недостатком
При округлении числа, выраженного десятичной дробью, с точностью до 10^{-n} с недостатком сохраняют n первых знаков после запятой, а последующие отбрасываются.
Например, округляя 12,4587 до тысячных с недостатком, получим 12,458.
Б) Округление с избытком
При округлении числа, выраженного десятичной дробью, с точностью до 10^{-n} с избытком сохраняют n первых знаков после запятой, а последующие отбрасываются.
Например, округляя 12,4587 до тысячных с недостатком, получим 12,459.
) Правило округления десятичных дробей.
Правило. Чтобы округлить десятичную дробь до определенного разряда целой или дробной части, все меньшие разряды заменяются нулями или отбрасываются, а предшествующий отбрасываемой при округлении цифре разряд не изменяет своей величины, если за ним идут цифры 0, 1, 2, 3, 4, и увеличивается на 1 (единицу), если идут цифры 5, 6, 7, 8, 9.
Пример. Округлить дробь 93,70584 до:
десятитысячных: 93,7058
тысячных: 93,706
сотых: 93,71
десятых: 93,7
целого числа: 94
десятков: 90
Несмотря на равенство абсолютных погрешностей, т.к. различны измеряемые величины. Чем больше измеряемый размер, тем меньше относительная погрешность при постоянстве абсолютной.
Заказ работы
Наши специалисты помогут написать работу с обязательной проверкой на уникальность в системе «Антиплагиат»
Отправь заявку
с требованиями прямо сейчас, чтобы узнать стоимость и возможность написания.
Часто в жизни нам приходится сталкиваться с различными приближенными величинами. Приближенные вычисления - всегда вычисления с некоторой погрешностью.
Понятие абсолютной погрешности
Абсолютная погрешность приближенного значения это модуль разности точного значения и приближенного значения.
То есть из точного значения нужно вычесть приближенное значение и взять полученное число по модулю. Таким образом, абсолютная погрешность всегда величина положительная.
Как вычислять абсолютную погрешность
Покажем, как это может выглядеть на практике. Например, у нас имеется график некоторой величины, пускай это будет парабола: y=x^2.
По графику мы сможем определить приблизительное значение в некоторых точках. Например, при x=1.5 значение у приблизительно равно 2.2 (y≈2.2).
По формуле y=x^2 мы можем найти точное значение в точке x=1.5 у= 2.25.
Теперь вычислим абсолютную погрешность наших измерений. |2.25-2.2|=|0.05| = 0.05.
Абсолютная погрешность равна 0.05. В таких случаях еще говорят значение вычислено с точность до 0.05.
Часто бывает так, что точное значение не всегда можно найти, а, следовательно, абсолютную погрешность не всегда возможно найти.
Например, если мы будем вычислять расстояние между двумя точками с помощью линейки, или значение угла между двумя прямыми с помощью транспортира, то мы получим приближенные значения. А вот точное значение вычислить невозможно. В данном случае, мы можем указать такое число, больше которого значение абсолютной погрешности быть не может.
На практике обычно числа, над которыми производятся вычисления, являются приближенными значениями тех или иных величин. Для краткости речи приближенное значение величины называют приближенным числом. Истинное значение величины называют точным числом. Приближенное число имеет практическую ценность лишь тогда, когда мы можем определить, с какой степенью точности оно дано, т.е. оценить его погрешность. Напомним основные понятия из общего курса математики.
Обозначим: x - точное число (истинное значение величины), а -приближенное число (приближенное значение величины).
Определение 1 . Погрешностью (или истинной погрешностью) приближенного числа называется разность между числом x и его приближенным значением а . Погрешность приближенного числа а будем обозначать . Итак,
Точное число x чаще всего бывает неизвестно, поэтому найти истинную и абсолютную погрешности не представляет возможным. С другой стороны, бывает необходимо оценить абсолютную погрешность, т.е. указать число, которого не может превысить абсолютная погрешность. Например, измеряя длину предмета данным инструментом, мы должны быть уверены в том, что погрешность полученного числового значения не превысит некоторого числа, например 0,1 мм. Другими словами, мы должны знать границу абсолютной погрешности. Эту границу будем называть предельной абсолютной погрешностью.
Определение 3 . Предельной абсолютной погрешностью приближенного числа а называется положительное число такое, что , т.е.
Значит, х по недостатку, - по избытку. Применяют также такую запись:
| . | (2.5) |
Ясно, что предельная абсолютная погрешность определяется неоднозначно: если некоторое число есть предельная абсолютная погрешность, то любое большее число тоже есть предельная абсолютная погрешность. На практике стараются выбирать возможно меньшее и простое по записи (с 1-2 значащими цифрами) число , удовлетворяющее неравенству (2.3).
Пример. Определить истинную, абсолютную и предельную абсолютную погрешности числа а = 0,17, взятого в качестве приближенного значения числа .
Истинная погрешность: ![]()
Абсолютная погрешность: ![]()
За предельную абсолютную погрешность можно принять число и любое большее число. В десятичной записи будем иметь: Заменяя это число большим и возможно более простым по записи, примем:
Замечание . Если а есть приближенное значение числа х , причем предельная абсолютная погрешность равна h , то говорят, что а есть приближенное значение числа х с точностью до h.
Знания абсолютной погрешности недостаточно для характеристики качества измерения или вычисления. Пусть, например, получены такие результаты при измерении длины. Расстояние между двумя городами S 1 =500 1 км и расстояние между двумя зданиями в городе S 2 =10 1 км. Хотя абсолютные погрешности обоих результатов одинаковы, однако существенное значение имеет то, что в первом случае абсолютная погрешность в 1 км приходится на 500 км, во втором - на 10 км. Качество измерения в первом случае лучше, чем во втором. Качество результата измерения или вычисления характеризуется относительной погрешностью.
Погрешности принято подразделять на грубые (промахи), систематические и случайные при проведении прямых (непосредственных) измерений какой-либо физической величины.
Грубые погрешности исключены;
Поправки, которые следовало определить (например, смещение нулевого деления шкалы) вычислены и внесены в окончательные результаты;
Систематические погрешности определяются неточностью средства измерения и указаны в его техническом паспорте. Знак этой погрешности заранее неизвестен, поэтому её необходимо учитывать в окончательном результате измерений.
Случайные погрешности уменьшаются при увеличении числа измерений. Пусть проведены n измерений величины x. Тогда за лучшую оценку истинного значения принимается среднее арифметическое отдельных измерений
где: x i - результат i–го измерения.
Для оценки случайной погрешности существует несколько способов. Наиболее распространенная так называемая средняя квадратичная погрешность среднего арифметического
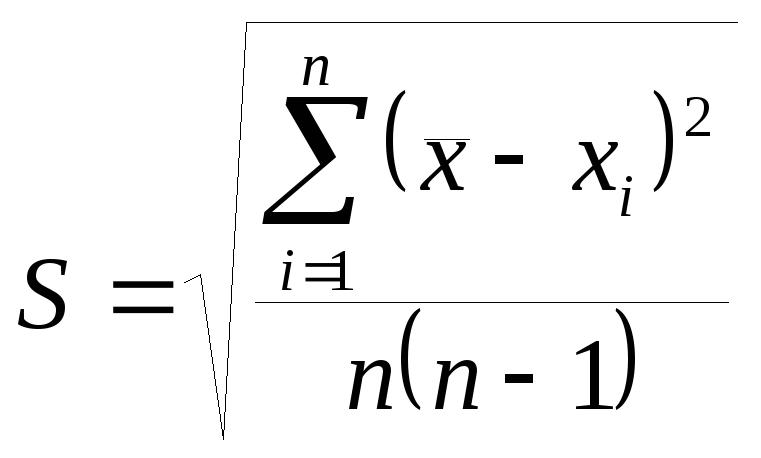 (2)
(2)
Пусть P означает вероятность того, что результат измерений отличается от истинного на величину ∆x , где ∆x - суммарная погрешность измерения данной величины: абсолютная погрешность. Тогда можно записать
где x ист – истинное значение измеряемой величины, которое заранее неизвестно.
Вероятность P
называется доверительной вероятностью,
а интервал от
 до
до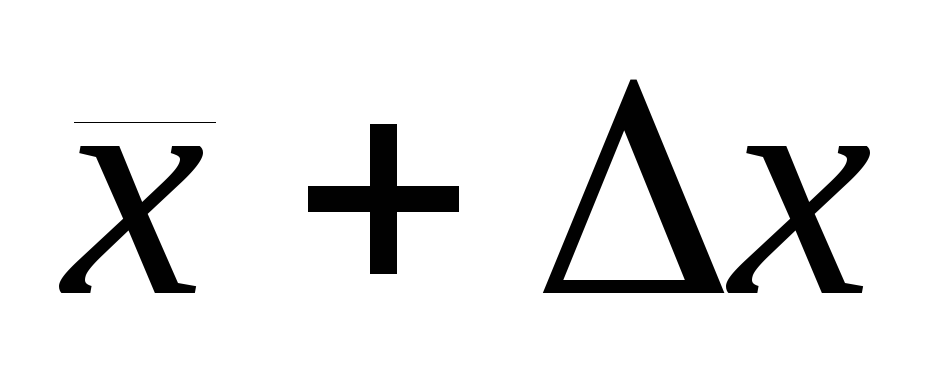 -
доверительным интервалом.
-
доверительным интервалом.
Если ограничиться учётом только случайных погрешностей, то при небольшом числе измерений полуширина доверительного интервала равна
 (3)
(3)
где t P , n – коэффициенты Стьюдента, которые табулированы в зависимости от P и n. В наших работах установим P = 0,95. Тогда при n = 3 t 0,95;4 = 4,3, при n = 4 t 0,95;4 = 3,2, при n = 5 t 0,95;5 = 2,8.
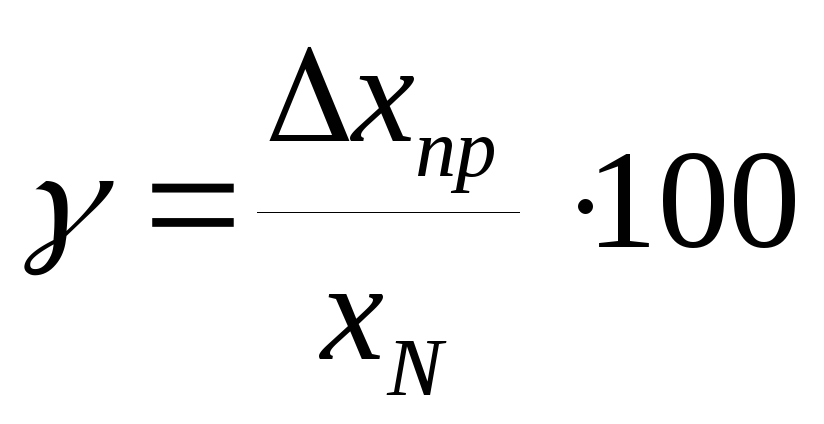 (4)
(4)
где ∆x пр - наибольшая абсолютная погрешность прибора; x N – предельное значение шкалы прибора.
Из (4) следует, что
 (5)
(5)
Погрешности цифровых измерительных приборов даются в паспорте каждого из них.
При многократных измерениях среднеквадратическое значение инструментальной погрешности P = 0,95 определяется по формуле:
 (6)
(6)
Если при нескольких измерениях устойчиво получаются одни и те же результаты, то за ∆x си можно принять половину цены деления шкалы или половину единицы цифры последнего разряда результата.
Относительная погрешность результата находится по формуле
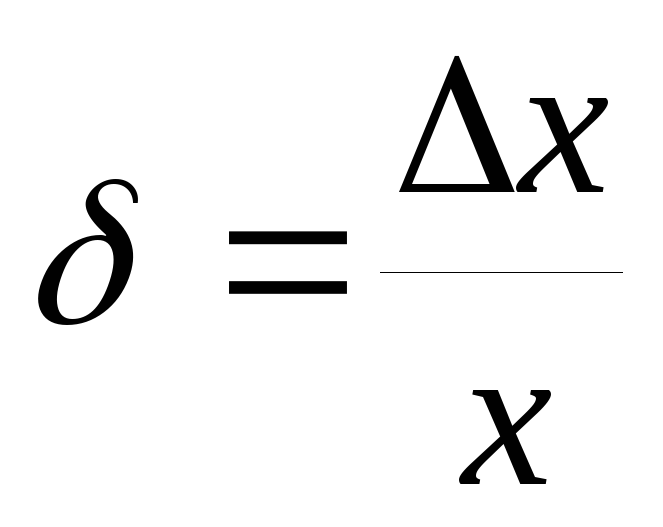 (7)
(7)
или часто в процентах
 (8)
(8)
Таким образом предлагается следующий порядок операций при прямых измерениях.
Вычисляется среднее арифметическое из n измерений:
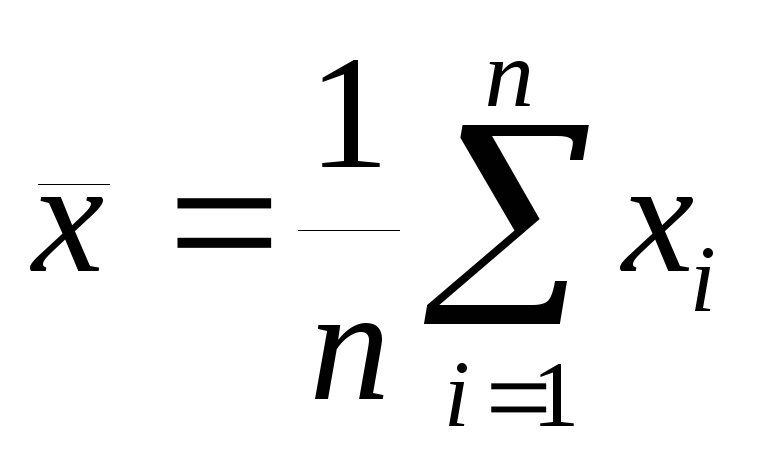
Определяется средняя квадратичная погрешность среднего арифметического:
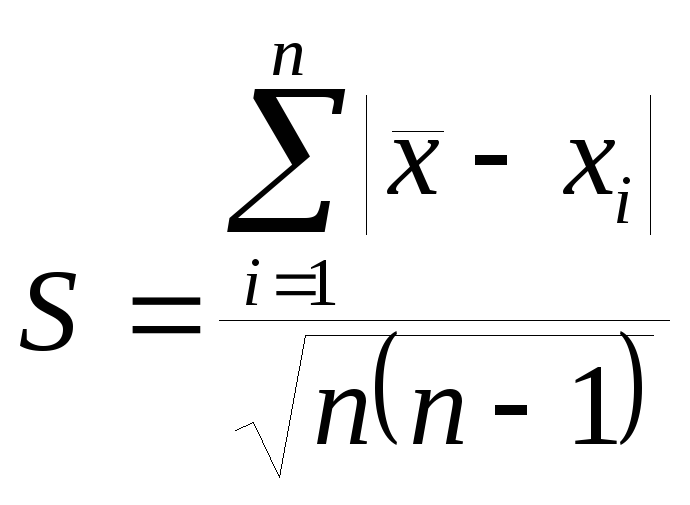
Находится
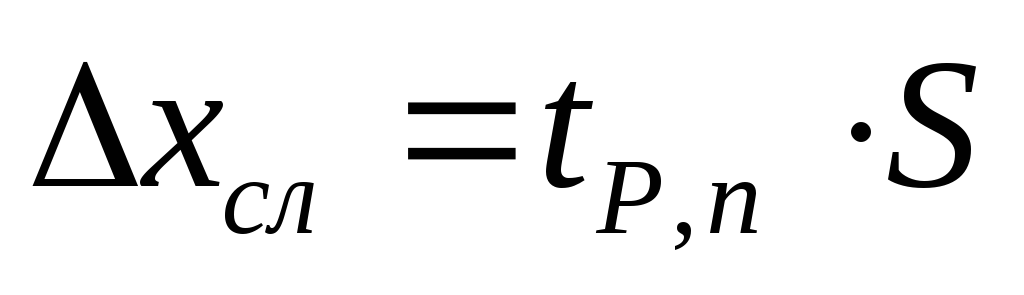
Определяется абсолютная погрешность результата измерений

Оценивается относительная погрешность результата измерений

Окончательный результат записывается в виде
 ;
P
= 0,95, n
= 3÷5.
;
P
= 0,95, n
= 3÷5.
Погрешности косвенных измерений
Пусть измеряемая величина является функцией непосредственно измеряемых величин
 (9)
(9)
Теория погрешностей определяет, что абсолютная погрешность ∆y находится по формуле
 (10)
(10)
где ∂f/∂x i обозначает так называемую частную производную, т. е. производная, которая вычисляется от функции f по аргументу x i , причём все остальные аргументы считаются постоянными.
Если измеряемые величины x i входят в основную формулу в виде произведения, то удобно определить вначале относительную погрешность по формуле
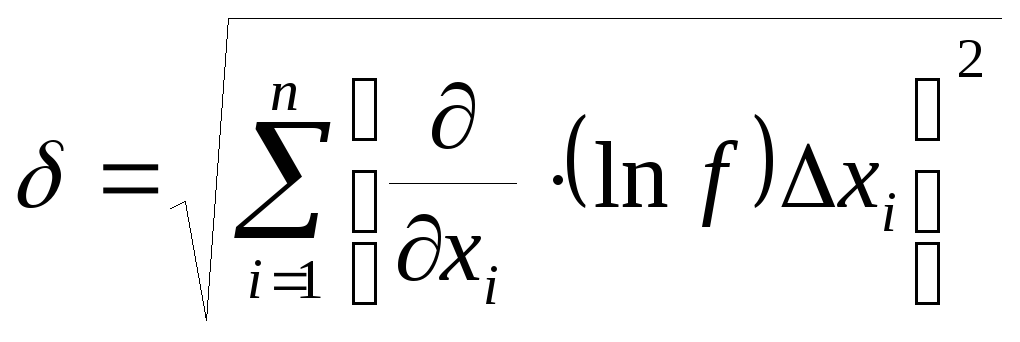 (11)
(11)
а затем найти и

Рассмотрим применение формул (10) и (11) на примерах.
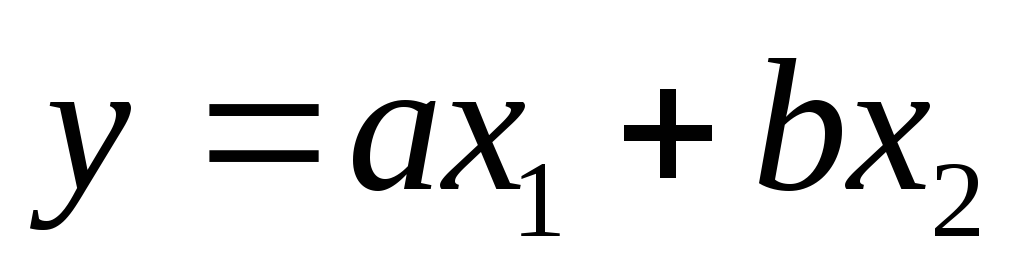 .
.
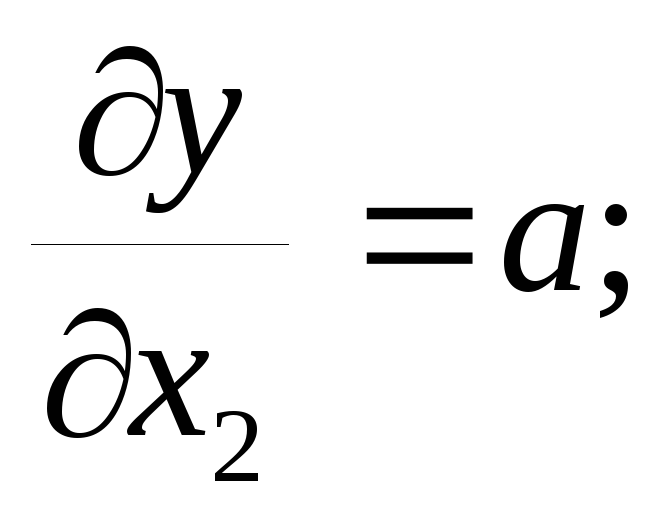
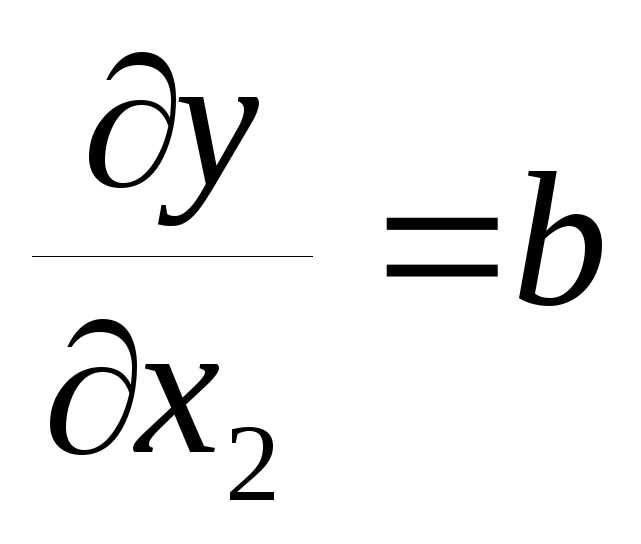
и по формуле (10)
причём ∆x 1 и ∆x 2 определены предварительно по формуле (4).
 .
.
В этом случае сначала найдём натуральный логарифм, а затем – частичные производные:
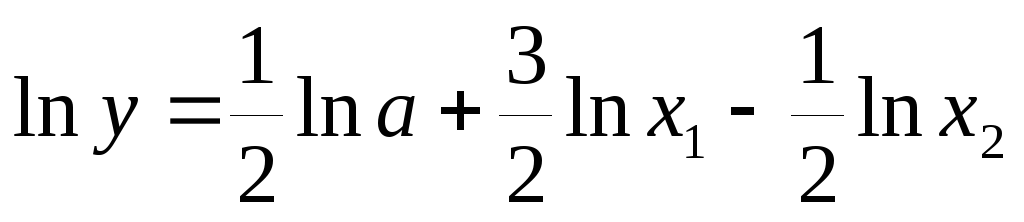
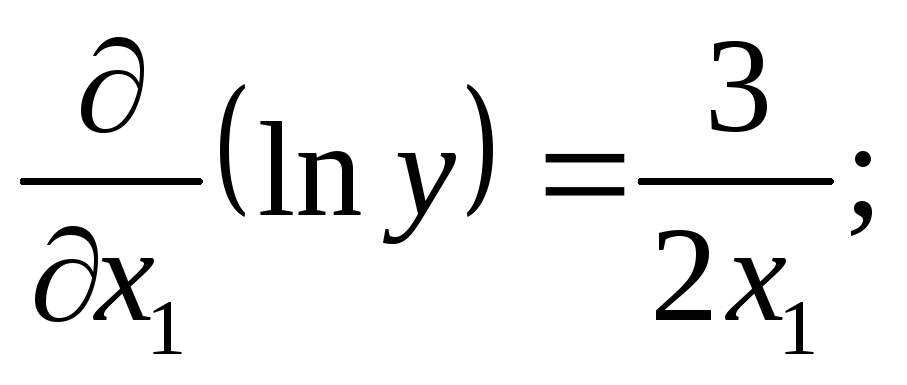

Подставляем в (11), найдём
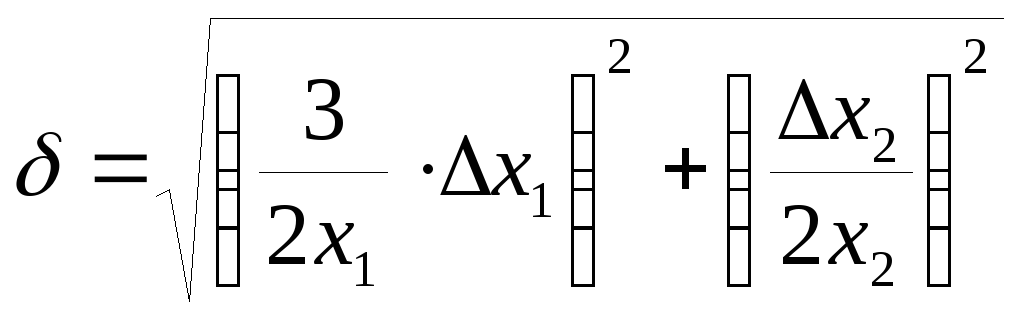
Нетрудно видеть, что предварительное логарифмирование существенно упрощает вид частных производных.
Возможен и другой подход к оценке погрешности результата косвенного измерения. Вместо определения искомой величины через среднее значение
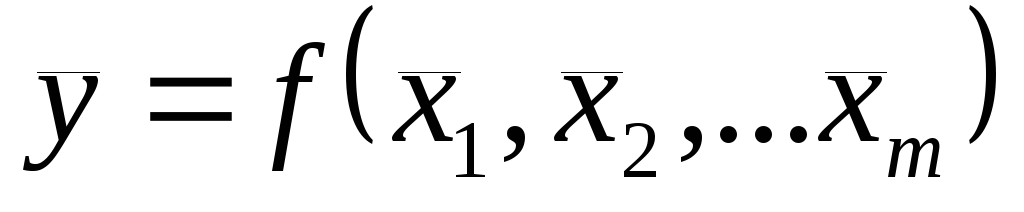
Можно для каждого выполненного опыта вычислить
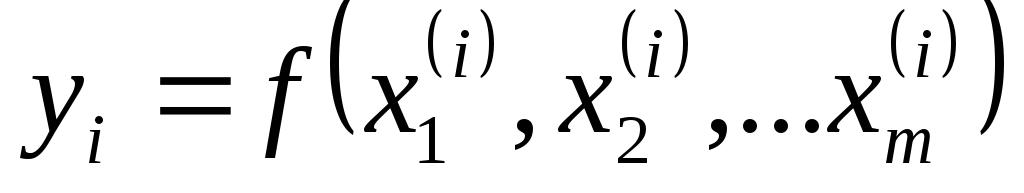
а затем найти
 как среднее арифметическое и далее
абсолютную погрешность по формуле (3).
как среднее арифметическое и далее
абсолютную погрешность по формуле (3).
Оба способа дают близкие результаты.
Пусть, например, находится плотность цилиндрического тела:
ρ = 4 m / πD 2 H ,
причем непосредственно определяется три раза диаметр цилиндра D i и его высота Н i (i = 1, 2, 3). Тогда можно подсчитать
ρ i = 4 m / πD 2 i H i .
для каждого из трех измерений.
Среднее значение плотности можно найти, как обычно, по формуле:
<ρ> =∑ ρ i /3,
а абсолютная погрешность определяется как
Δρ = 4,3√[∑(< ρ > – ρ i ) /6].
Таблица 1.
Коэффициенты Стьюдента.
Округление результата
Результат измерения округляется по следующим правилам:
Абсолютная погрешность берётся с двумя значащими цифрами, если первая из них 1 или 2.
Абсолютная погрешность берётся с одной значащей цифрой, если она больше или равна 3.
Это правило вытекает из законов математической статистики, так как оказывается, что даже при 10 измерениях относительная погрешность самой погрешности превышает 3 % (30% от 2 составляет 0,6; а, например, от 4 – 1,2, что превышает единицу первого разряда).
Числовое значение результата измерений должно оканчиваться цифрой того же порядка, что и числовое значение абсолютной погрешности.
Если первая отбрасываемая цифра больше или равна 5, то последняя сохраняемая цифра увеличивается на единицу.
Если отбрасываемая цифра меньше 5, то последняя сохраняемая цифра остаётся без изменений.
При округлении целых чисел все цифры, отброшенные при округлении, заменяют множителем 10 m , где m – число от брошенных цифр. Например, при округлении до двух значащих цифр число 31127 примет вид 31×10 3 .
