Задача ставится так: пусть искомая величина z определяется через другие величины a, b, c , ..., полученные при прямых измерениях
z = f (a, b, c,...) (1.11)
Необходимо найти среднее значение функции и погрешность ее измерений, т.е. найти доверительный интервал
при надежности a и относительную погрешность .
Что касается , то оно находится путем подстановки в правую часть (11) вместо a, b, c ,... их средних значений
Абсолютная погрешность косвенных измерений является функцией абсолютных погрешностей прямых измерений и вычисляется по формуле
 (1.14)
(1.14)
Здесь частные производные функции f по переменным a, b, …
Если величины a, b, c, ... в функцию Z = f (a, b, c,...) входят в виде сомножителей в той или иной степени, т. е. если
![]() , (1.15)
, (1.15)
то сначала удобно вычислить относительную погрешность
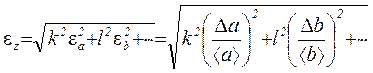 , (1.16)
, (1.16)
а затем абсолютную
Формулы для Dz и e z приводятся в справочной литературе.
Примечания.
1. При косвенных измерениях в расчетные формулы могут входить известные физические константы (ускорение свободного падения g
, скорость света в вакууме с
и т. д.), числа типа дробные множители ... . Эти величины при вычислениях округляются. При этом, естественно, в расчет вносится погрешность ![]() ‒ погрешность округления при вычислениях, которая должна учитываться.
‒ погрешность округления при вычислениях, которая должна учитываться.
Принято считать, что погрешность округления приближенного числа равна половине единицы того разряда, до которого это число было округлено. Например,p = 3,14159... . Если взять p= 3,1, то Dp = 0,05, если p = 3,14, то Dp = 0,005 ... и т.д. Вопрос о том, до какого разряда округлять приближенное число, решается так: относительная ошибка, вносимая округлением, должна быть того же порядка или на порядок меньше, что и максимальная из относительных ошибок других видов. Таким же образом оценивается абсолютная ошибка табличных данных. Например, в таблице указано r = 13,6×10 3 кг/ м 3 , следовательно,Dr = 0,05×10 3 кг/м 3 .
Ошибка значений универсальных постоянных часто указывается вместе с их принятыми за средние значения: (с
= ![]() м/c, где Dс
= 0,3×10 3 м/c.
м/c, где Dс
= 0,3×10 3 м/c.
2. Иногда при косвенных измерениях условия опыта при повторных наблюдениях не совпадают. В этом случае значение функции z вычисляется для каждого отдельного измерения, а доверительный интервал вычисляется через значения z так же, как при прямых измерениях (все погрешности здесь входят в одну случайную погрешность измерения z ). Величины, которые не измеряются, а задаются (если они есть) должны быть указаны при этом с достаточно большой точностью.
Порядок обработки результатов измерений
Прямые измерения
1. Вычислить среднее значение для n измерений
2. Найти погрешности отдельных измерений ![]() .
.
3. Вычислить квадраты погрешностей отдельных измерений и их сумму: 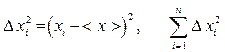 .
.
4. Задать надежностьa (для наших целей принимаем a = 0,95) и по таблице определить коэффициенты Стьюдента t a,n и t a, ¥ .
5. Произвести оценку систематических погрешностей: приборной Dх пр и ошибки округления при измеренияхDх окр = D/2 (D ‒ цена деления прибора) и найти полную погрешность результата измерений (полуширину доверительного интервала):
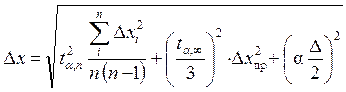 .
.
6. Оценить относительную погрешность
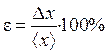 .
.
7. Окончательный результат записать в виде
![]() ε = … % при a = ...
ε = … % при a = ...
Косвенные измерения
1. Для каждой величины, измеренной прямым способом, входящей в формулу для определения искомой величины ![]() , провести обработку, как указано выше. Если среди величин a, b, c
, ... есть табличные константы или числа типа p, е
,..., то при вычислениях округлять их следует так (если это возможно), чтобы вносимая при этом относительная ошибка была на порядок меньше наибольшей относительной ошибки величин, измеренных прямым способом.
, провести обработку, как указано выше. Если среди величин a, b, c
, ... есть табличные константы или числа типа p, е
,..., то при вычислениях округлять их следует так (если это возможно), чтобы вносимая при этом относительная ошибка была на порядок меньше наибольшей относительной ошибки величин, измеренных прямым способом.
Определить среднее значение искомой величины
z = f (,,
3. Оценить полуширину доверительного интервала для результата косвенных измерений
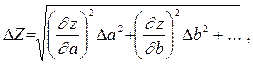 ,
,
где производные ... вычисляются при
4. Определить относительную погрешность результата
![]()
5. Если зависимость z от a, b, c
,... имеет вид ![]() , где k, l, m
‒ любые действительные числа, то сначала следует найти относительную
ошибку
, где k, l, m
‒ любые действительные числа, то сначала следует найти относительную
ошибку
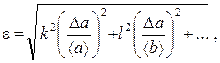
а затем абсолютную .
6. Окончательный результат записать в виде
z =
Примечание:
При обработке результатов прямых измерений нужно следовать следующему правилу: численные значения всех рассчитываемых величин должны содержать на один разряд больше, чем исходные (определенные экспериментально) величины.
При косвенных измерениях вычисления производить по правилам приближенных вычислений :
Правило 1. При сложении и вычитании приближенных чисел необходимо:
а) выделить слагаемое, у которого сомнительная цифра имеет наиболее высокий разряд;
б) все остальные слагаемые округлить до следующего разряда (сохраняется одна запасная цифра);
в) произвести сложение (вычитание);
г) в результате отбросить последнюю цифру путем округления (разряд сомнительной цифры результата при этом совпадает со старшим из разрядов сомнительных цифр слагаемых).
Пример: 5,4382·10 5 – 2,918·10 3 + 35,8 + 0,064.
В этих числах последние значащие цифры сомнительные (неверные уже отброшены). Запишем их в виде 543820 – 2918 + 35,8 + 0,064.
Видно, что у первого слагаемого сомнительная цифра 2 имеет наиболее высокий разряд (десятки). Округлив все другие числа до следующего разряда и сложив, получим
543820 – 2918 + 36 + 0 = 540940 = 5,4094·10 5 .
Правило 2. При умножении (делении) приближенных чисел необходимо:
а) выделить число (числа) с наименьшим количеством значащих цифр (ЗНАЧАЩИЕ – цифры отличные от ноля и ноли стоящие между ними );
б) округлить остальные числа так, чтобы в них было на одну значащую цифру больше (сохраняется одна запасная цифра), чем выделенном по п. а;
в) перемножить (разделить) полученные числа;
г) в результате оставить столько значащих цифр, сколько их было в числе (числах) с наименьшим количеством значащих цифр.
Пример: .
Правило 3. При возведении в степень, при извлечении корня в результате сохраняется столько значащих цифр, сколько их в исходном числе.
Пример:
![]() .
.
Правило 4. При нахождении логарифма числа мантисса логарифма должна иметь столько значащих цифр, сколько их в исходном числе:
Пример:
![]() .
.
В окончательной записиабсолютной погрешности следует оставлять только одну значащую цифру . (Если этой цифрой окажется 1, то после нее сохраняют еще одну цифру).
Среднее значение округляется до того же разряда, что и абсолютная погрешность.
Например: V = (375,21 0,03) см 3 = (3,7521 0,0003) см 3 .
I
= (5,530 0,013) А, A
= ![]() Дж.
Дж.
Порядок выполнения работы
Определение диаметра цилиндра .
1. Штангенциркулем измерить 7 раз (в разных местах и направлениях) диаметр цилиндра. Результаты записать в таблицу.
| № п/п | d i , мм | d i
- | (d i
- | h i , мм
и Похожая информация: |
ЭЛЕМЕНТАРНЫЕ ОЦЕНКИ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЙ
Измерение есть нахождение значения физической величины опытным путем с помощью специальных технических средств - мер, измерительных приборов.
Мера есть средство измерений, воспроизводящее физическую величину заданного размера - единица измерения, ее кратное или дробное значение. Например, гири 1 кг, 5 кг, 10 кг.
Измерительный прибор есть средство измерений, предназначенное для выработки сигнала измерительной информации в форме, доступной для непосредственного восприятия наблюдателем. Измерительный прибор позволяет прямо или косвенно сравнивать измеряемую величину с мерами. Измерения также разделяют на прямые и косвенные.
При прямых измерениях искомое значение величины находят непосредственно из основных (опытных) данных.
При косвенных измерениях искомое значение величины находят на основании известной зависимости между этой величиной и величинами, подвергаемыми прямым измерениям. Принцип измерений есть совокупность физических явлений, на которых основаны измерения.
Метод измерений - совокупность приемов использования принципов и средств измерений. Значение физической величины, которое идеальным образом отражало бы в качественном и количественном отношениях соответствующее свойство данного объекта есть истинное значение физической величины. Значение физической величины, найденное путем ее измерения есть результат измерения.
Отклонение результата измерения от истинного значения измеряемой величины есть погрешность измерения.
Абсолютная погрешность измерения есть погрешность измерения, выраженная в единицах измеряемой величины и равная разности результата и истинного значения измеряемой величины. Отношение абсолютной погрешности к истинному значению измеряемой величины есть относительная погрешность измерения.
Вклад в погрешность измерения вносят погрешности средств измерений (инструментальная или приборная погрешность), несовершенство метода измерений, погрешность отсчитывания по шкале прибора, внешние влияния на средства и объекты измерений, запаздывание реакции человека на световой и звуковой сигналы.
По характеру проявления погрешности делят на систематические и случайные. Случайным называется событие, которое при заданном комплексе факторов может произойти или не произойти.
Случайная погрешность - составляющая погрешности измерения, изменяющаяся случайным образом при повторных измерениях одной и той же величины. Характерным признаком случайных погрешностей является изменение величин и знака погрешности в неизменных условиях измерений.
Систематическая погрешность - составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же величины. Систематические погрешности в принципе могут быть исключены путем поправок, применением более точных приборов и методов (хотя на практике обнаружить систематическую погрешность не всегда легко). Исключить случайные погрешности отдельных измерений невозможно, математическая теория случайных явлений (теория вероятности) позволяет лишь установить обоснованную оценку их величины.
Погрешности прямых измерений
Положим,
что систематические погрешности
исключены и погрешности результатов
измерений являются только случайными.
Обозначим буквами
- результаты измерений физической
величины, истинное значение которого
равно![]() .
Абсолютные погрешности результатов
отдельных измерений обозначены:
.
Абсолютные погрешности результатов
отдельных измерений обозначены:
Суммируя получено левые и правые стороны равенства (1), получим:
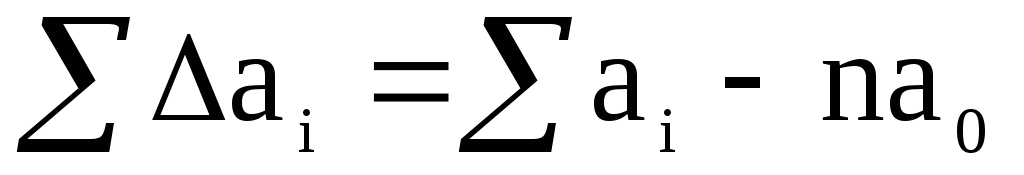 (2)
(2)
В основе теории случайных погрешностей лежат подтверждаемые опытом предположения:
погрешности могут принимать непрерывный ряд значений;
при большом числе измерений случайные погрешности одинаковой величины, но разного знака встречаются одинаково часто;
вероятность появления погрешности уменьшается с ростом ее величины. Необходимо также, чтобы погрешности были малы по сравнению с измеряемой величиной и независимы.
Согласно предположению (1) при числе измерений n получим
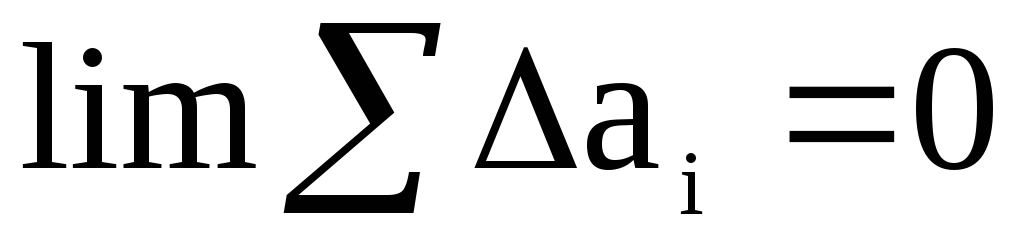
 ,
,
Однако,
всегда число измерений конечно и
![]() остается неизвестным. Но для практических
целей достаточно найти экспериментальным
путем значение физической величины
настолько приближающееся к истинному,
что
остается неизвестным. Но для практических
целей достаточно найти экспериментальным
путем значение физической величины
настолько приближающееся к истинному,
что может быть использована вместо истинного.
Вопрос в том, как оценить степень этого
приближения?
может быть использована вместо истинного.
Вопрос в том, как оценить степень этого
приближения?
По
теории вероятности среднее арифметическое
серии измерений
 достовернее результатов отдельных
измерений, т.к. случайные отклонения от
истинного значения в разные стороны
равновероятны. За вероятность
появления величины a i
в интервале шириной 2a i
понимают относительную частоту появления
значений a i ,
попадающих в интервал 2a i
к числу всех появляющихся значений a i
при числе опытов (измерений), стремящихся
к бесконечности. Очевидно, что вероятность
достоверного события равна единице,
вероятность невозможного события равна
нулю, т.е. 0
100 %.
достовернее результатов отдельных
измерений, т.к. случайные отклонения от
истинного значения в разные стороны
равновероятны. За вероятность
появления величины a i
в интервале шириной 2a i
понимают относительную частоту появления
значений a i ,
попадающих в интервал 2a i
к числу всех появляющихся значений a i
при числе опытов (измерений), стремящихся
к бесконечности. Очевидно, что вероятность
достоверного события равна единице,
вероятность невозможного события равна
нулю, т.е. 0
100 %.
Вероятность того, что искомая величина (истинное значение ее) содержится в интервале (a - a, a + a) назовем доверительной вероятностью (надежностью) , а соответствующий интервал (a - a, a + a) - доверительным интервалом; чем меньше величина погрешности a, тем меньше и вероятность того, что измеряемая величина содержится в интервале, определенной этой погрешностью. Верно и обратное утверждение: чем меньше надежность результата, тем уже доверительный интервал искомой величины.
При большом n (практически при n 100) полуширина доверительного интервала при заданной надежности равна
 ,
(3)
,
(3)
где K() = 1 при = 0,68; K() = 2 при = 0,95; K() = 3 при = 0,997.
При малом числе измерений, что чаще всего и встречается в студенческом лабораторном практикуме, коэффициент K()в (3) зависит не только от , но еще и от числа измерений n. Поэтому мы всегда будем при наличии только случайной погрешности полуширину доверительного интервала находить по формуле
 (4)
(4)
В (4) коэффициент t n называется коэффициентом Стьюдента. Для = 0,95 принятой в студенческом практикуме, значения t n таковы:
Величину называют среднеквадратичной погрешностью среднего арифметического из серии измерений.
Погрешность прибора или меры обычно указывается в паспорте его (ее) или условным знаком на шкале прибора. Обычно под погрешностью прибора понимают полуширину интервала, внутри которого с вероятностью измерений 0,997 может быть заключена измеряемая величина, если погрешность измерений обусловлена только погрешностью прибора. В качестве общей (полной) погрешности результата измерений примем с вероятностью = 0,95
Абсолютная погрешность позволяет установить в каком знаке полученного результата содержится неточность. Относительная погрешность дает информацию о том, какую долю (процент) измеряемой величины составляет погрешность (полуширина доверительного интервала).
Окончательный результат серии прямых измерений величины a 0 запишем в виде
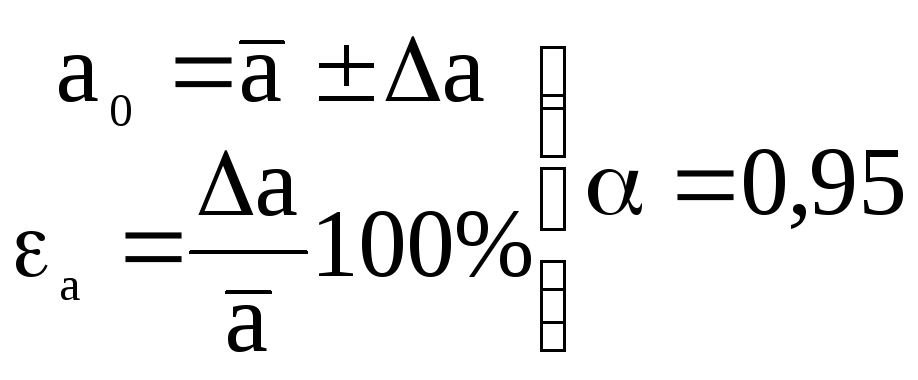 .
.
Например
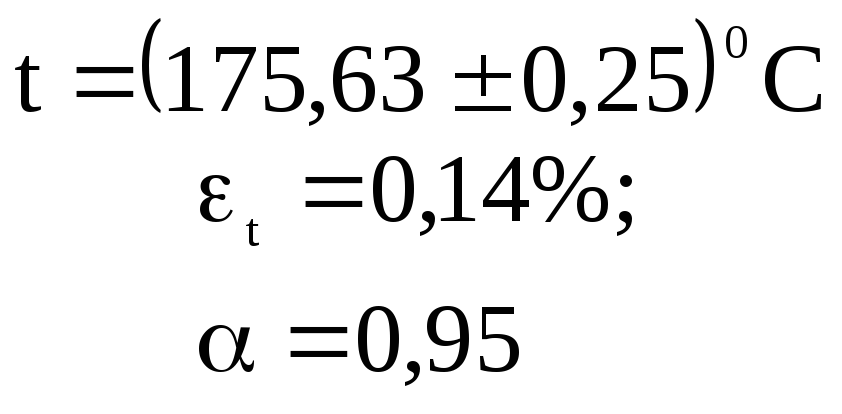 (6)
(6)
Таким образом, любая физическая величина, найденная опытным путем, должна быть представлена:

Погрешности измеряемых и табличных величин обуславливают погрешности DХ ср косвенно определяемой величины, причем наибольший вклад в DХ ср дают наименее точные величины, имеющие максимальную относительную погрешность d . Поэтому, для повышения точности косвенных измерений, необходимо добиваться равноточности прямых измерений
(d А, d В, d С, …).
Правила нахождения погрешностей косвенных измерений:
1. Находят натуральный логарифм от заданной функции
ln{X = f(A,B,C,…)};
2. Находят полный дифференциал (по всем переменным) от найденного натурального логарифма заданной функции;
3. Заменяют знак дифференциала d на знак абсолютной погрешности D;
4. Заменяют все «минусы», стоящими перед абсолютными погрешностями DА, DВ, DС , … на «плюсы».
В результате получается формула наибольшей относительной погрешности d x косвенно измеренной величины Х:
d x = = j (A ср, B ср, C ср, …, DA ср, DB ср, DC ср, …). (18)
По найденной относительной погрешности d x определяют абсолютную погрешность косвенного измерения:
DХ ср = d x . Х ср . (19)
Результат косвенных измерений записывают в стандартном виде и изображают на числовой оси:
X = (X ср ± DХ ср), ед.изм. (20)

Пример :
Найти значения относительной и средней погрешностей физической величины L , определяемой косвенно по формуле:
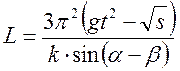 , (21)
, (21)
где π, g, t, k, α, β – величины, значения которых измерены или взяты из справочных таблиц и занесены в таблицу результатов измерений и табличных данных (подобную табл.1).
1. Вычисляют среднее значение L ср , подставляя в (21) средние значения из таблицы – π ср, g ср, t ср, k ср, α ср, β ср.
2. Определяют наибольшую относительную погрешность δ L :
a). Логарифмируют формулу (21):
b). Дифференцируют полученное выражение (22):
c).Заменяют знак дифференциала d на Δ, а «минусы» перед абсолютными погрешностями – на «плюсы», и получают выражение для наибольшей относительной погрешности δ L :
d). Подставляя в полученное выражение средние значения входящих величин и их погрешностей из таблицы результатов измерений, вычисляют δ L .
3. Затем вычисляют абсолютную погрешность ΔL ср :
![]()
Результат записывают в стандартном виде и изображают графически на оси L :
![]() , ед. изм.
, ед. изм.
