Jaotis 1. Ligikaudsed arvud ja tehted nendega
1.1 Ligikaudsete arvutuste vigade tüübid
Mõne matemaatilise ülesande täpset lahendust ei ole võimalik saada klassikaliste meetoditega või saab seda lahendust nii. keeruline vorm, mis on edasiseks praktiliseks kasutamiseks vastuvõetamatu. Lisaks võib probleemi täpne lahendus nõuda väga suur hulk(mitmekümnest mitme miljardini) toimingud. Sellistel juhtudel kasutage lahenduse ligikaudseid ja arvulisi meetodeid.
Arvutite tulek on nende meetodite ulatust oluliselt laiendanud. Praegu on raske ette kujutada inseneri, kellel pole arvutit ja ligikaudsete arvutuste meetodeid.
Pange tähele, et iga arvuti suudab meelde jätta suuri, kuid piiratud arvude massiive ning sooritada nendega aritmeetilisi tehteid ja võrdlusi suure, kuid piiratud kiirusega. See tähendab, et masin on võimeline tegema väga suurt, kuid piiratud arvu toiminguid. Seetõttu saate arvutiga töötades kasutada ainult neid matemaatilisi mudeleid, mida kirjeldab piiratud arvude hulk, ja kasutada ainult aritmeetiliste toimingute lõplikke jadasid.
Erinevate nähtuste matemaatilised mudelid on funktsioonid, tuletised, integraalid, diferentsiaalvõrrandid jne. Arvutiga töötades tuleks need esialgsed mudelid asendada nendega, mida kirjeldavad lõplikud arvud, mis näitavad nende töötlemise lõplikku toimingute jada. Selleks asendatakse funktsioon tabeliga, kindel integraal- summa jne. Lisaks on arvutil piiratud mälu ja see võib töötada piiratud pikkusega arvudega, nii et vahetulemused ümardatakse. Selle tulemusena muutub ligikaudseks isegi täpne meetod, millel on piiratud arv etappe.
Seega on numbrilisel meetodil saadud lahendus ligikaudne.
Vigade põhjused on järgmised:
- Matemaatilise mudeli ebakõla uuritava reaalnähtusega
- Esialgsete andmete viga.
- Lahendusmeetodi viga.
- Ümardamisvead aritmeetikas ja muudes arvudega tehtavates operatsioonides.
Kahe esimese põhjuse põhjustatud otsustusviga nimetatakse Tappev— see ei sõltu matemaatikust.
Meetodi viga tekib seetõttu, et numbriline meetod ei lahenda reeglina mitte algset, vaid lihtsamat probleemi. Lisaks põhineb numbriline meetod tavaliselt lõpmatul protsessil, mis tuleb mingil etapil lõpetada.
Enamik arvulisi meetodeid sõltub ühest või mitmest parameetrist. Meetodi parameetrite valik võimaldab reguleerida meetodi viga.
Ümardamise viga ei tohiks olla märkimisväärne rohkem viga meetod. Ja meetodi viga on soovitav valida 2-5 korda vähem kui saatuslik viga.
1.2 Ligikaudsed arvud
Praktikas tuleb sageli tegeleda arvudega, mis väljendavad tegelikku väärtust mitte täpselt, vaid umbkaudselt. Selliseid numbreid nimetatakse ligikaudne.
Tähistame mõne väärtuse täpset arvulist väärtust a , sama väärtuse ligikaudset arvväärtust a * . Siis a » a * .
Asendades täpse arvu a ligikaudse arvuga a * , teeme vea (vea).
Definitsioon 1.1. Ligikaudse arvu a * absoluutne viga on selle arvu ja selle täpse väärtuse erinevuse absoluutväärtus | a-a* |.
Kuna koguse täpne väärtus on tavaliselt teadmata, on võimatu arvutada ja absoluutne viga. Kuid võite määrata positiivse arvu D(a*), rahuldades ebavõrdsust:
Suvaline number d(a*) , mis rahuldab ebavõrdsust
Pange tähele, et ebavõrdsusi (1.2) ja (1.3) rahuldavaid arve on palju. Seetõttu pole piirvea väärtus päris kindel.
Praktikas võetakse tavaliselt piirvea väikseim võimalik väärtus. Iga ligikaudse arvu jaoks määratakse tingimata kindlaks selle piirviga (absoluutne või suhteline). Piirav absoluutviga võimaldab määrata piirid, mille piires arv a asub, s.t.
Piirav suhteline viga iseloomustab arvutuste või mõõtmiste täpsust.
Näited.
1.2.1 . Ülesannete lahendamisel täpse arvu asemel p = 3,14159265... kasutame selle ligikaudset väärtust 3,14 ja teeme vea:
p - 3,14 > 0,00159265
1.2.2 . Raja pikkuse mõõtmisel saadi 2m täpsusega tulemuseks 25,2 km. Arvutage piiravad absoluutsed ja piiravad suhtelised vead.
Lahendus. Meie puhul on piirav absoluutviga võrdne D = 0,002 km ja piirav suhteline viga
Samamoodi arvutame
tähendab, et * on arvu a ligikaudne väärtus absoluutse veaga D(a*). Kui * on arvu a ligikaudne väärtus suhtelise veaga d(a*), siis nad kirjutavad nii:
1.4 Olulised arvud, tõesed ja kahtlased arvud
Praktikas kasutatakse erinevaid tehnikaid, mis võimaldavad selle viga hinnata ainult kõige ligikaudseima arvu registreerimisega.
Ligikaudsete arvude ja absoluutsete vigade salvestamisel kehtivad teatud reeglid.
Kümnendmärgistuses märkimisväärne näitaja Kutsutakse iga numbrit, mis ei võrdu nulliga. Nulli loetakse oluliseks numbriks, kui see asub tähendusnumbrite vahel või kõigist olulistest numbritest paremal.
Näide 1.3.1. Ligikaudne arv 0, 38 sisaldab 2 tähenduslikku numbrit, 0, 308 - kolm, 0, 3080 - neli, 0.00 308 - kolm. Olulised numbrid on allajoonitud numbrid.
Definitsioon 1.3. Märkimisväärset numbrit nimetatakse tõsi laiemas mõttes kui arvu absoluutviga ei ületa üht ühikut sellele arvule vastavast numbrist.
Märkimisväärset numbrit nimetatakse õige kitsas tähenduses kui arvu absoluutviga ei ületa poolt sellele arvule vastava numbri ühikut.
Vastasel juhul arvestatakse arvuga kahtlane.
Kui ligikaudne arv kirjutatakse ilma selle absoluutset (lõplikku absoluutset) viga täpsustamata, siis kirjutatakse välja ainult selle õiged arvud. Sel juhul ei jäeta arvu paremas otsas olevaid tõelisi nulle kõrvale. Arvud 0,25 ja 0,250 on ligikaudsete näitajatena erinevad. Kui kasutada kirjeid kujul (1.4) või (1.5), siis tuleb nende võrrandite paremal pool olevad numbrid kirjutada sama arvu komakohtadega.
Absoluutne või suhteline viga See on tavaks kirjutada numbrina, mis sisaldab ühte või kahte tähenduslikku numbrit. Sel juhul tehakse ümardamine ülejäägiga.
Võib selguda, et ligikaudne arv selle täisarvulises osas sisaldab rohkem olulisi numbreid kui õigeid märke. Sel juhul kasutatakse tähistust normaliseeritud kujul a * = m 10 n, samas kui arv m ≤ 1 peab sisaldama ainult kehtivaid numbreid. Normaliseeritud tähistuses nimetatakse arvu m mantiss, n — eksponent
Pange tähele, et piirava absoluutvea määrab kümnendkohtade arv pärast koma: mida vähem komakohti pärast koma, seda rohkem D(a*).
Piirav suhteline viga määratakse oluliste numbrite arvu järgi: mida vähem olulisi numbreid, seda rohkem d(a*).
1.5 Ümardamine
Ligikaudsete arvude kirjutamiseks õigete numbritega kasutatakse seda ümardamine.
Täpsed arvud tuleb ümardada ka siis, kui kasutatavate numbrite arv on piiratud.
Ümardamine (täiendi järgi) numbrit nimetatakse selle arvu kirjutamiseks vähemate numbritega vastavalt järgmisele reeglile: kui esimene kõrvalejäetud number on suurem või võrdne 5-ga, siis viimast allesjäänud numbrit suurendatakse ühe võrra. Numbrite ümardamisel tekib viga, millega tuleb samuti arvestada.
Ümardamisviga täiendi järgi ei ületa poolt absoluutväärtuses vähima tähtsusega numbri ühikut. Saadud vea arvutamisel tuleb ümardusviga liita arvu algsele absoluutveale.
Näide 1.3.2. Numbril a * = 413287.51 on suhteline viga d(a*) = 0,01. (1.3) järeldub, et D(a*)=| a * | d(a*).
Seetõttu on selle arvu absoluutviga 4133. See tähendab, et arvu neljas number a * võib juba sisaldada viga. Seetõttu on õiged ainult numbri kaks esimest numbrit. Siis normaliseeritud kujul kirjutatakse see arv järgmiselt: a * = 0,41 ·10 6 .
Sarnaselt argumenteerides on ligikaudne arv b * = 0,0794 at d(b*) = 2% kirjutage normaliseeritud kujul b * = 0,8 10 - 1 .
Pange tähele, et siin pidime arvu ümardama.
Ligikaudsete arvudega aritmeetiliste toimingute tegemisel tekib kaks vastastikku pöördülesannet:
1. Autor teadaolevad vead sisendandmed, et hinnata tulemuse viga.
2. Määrata kindlaks lähteandmete täpsus, mis annab tulemuse määratud täpsuse.
Lisaks tuleb ligikaudsete arvudega töötades ühildada erinevate sisendandmete täpsus, et mitte raisata aega tarbetute ja valede numbrite väljakirjutamisele.
Arvutuste käigus on vaja jälgida ka vahetulemuste täpsust.
Enne aritmeetiliste toimingute alustamist rakendatakse ümardamist, nii et kõik nendes tehtes osalevad numbrid kirjutatakse sama arvu komakohtadega. Järelejäänud kümnendkohtade arv määratakse algandmete väikseima kehtivate numbrite arvu järgi.
Ligikaudsete arvude liitmisel ja lahutamisel, millel on pärast koma sama palju õigeid numbreid, ümardamist ei teostata.
Ligikaudsete arvude liitmisel ja lahutamisel, mille pärast koma on erinev arv õigeid numbreid, ümardatakse tulemus algandmetes väikseima arvu õigete numbriteni pärast koma.
Erineva arvu õigete numbritega ligikaudsete arvude korrutamisel ja jagamisel ümardatakse tulemus algandmete minimaalse õigete numbrite arvu võrra.
1.6 Aritmeetilised vead
Olgu a * ja b * ligikaudsed arvud, siis nende summa c * = a * + b * on samuti ligikaudne arv.
Kui tähistame terminite absoluutseid vigu D(a*) ja D(b*), siis arvu c * absoluutviga määratakse valemiga
|
Seetõttu liidetakse kahe ligikaudse arvu liitmisel nende piiravad absoluutvead.
See reegel kehtib mis tahes piiratud arvu terminite puhul. Lisaks kehtib valem (1.6) ka kahe arvu erinevuse kohta.
Tõepoolest, kahe arvu erinevust saab esitada summana
a * - b * = a * + ( - b *),
ja arvu absoluutne viga ( -b*) on võrdne arvu b * absoluutveaga.
Kommenteeri Kahe sama märgiga arvu lahutamisel võib erinevuse suhteline viga olla palju suurem kui iga liikme suhteline viga. Eriti suur täpsuse kaotus tekib siis, kui lahutada üksteisele lähedased arvud.
Näide 1.4.1. Olgu nõutud erinevuse leidmiseks 61,32 - 61,31 .
Nende arvude absoluutsed vead on vastavalt D1 = 0,01 ja D2 = 0,01. Leiame nüüd nende arvude suhtelised vead:
Lahutamisel saadakse arv 0,01 (märkame, et kadus kolm olulist numbrit). Selle absoluutviga võrdub terminite absoluutsete vigade summaga D1+ D 2 = 0,02. Siis on tulemuse suhteline viga Võrreldes algandmete ja tulemuse vigu, leiame suhtelise vea järsu tõusu. Näitest 1.4.1. Sellest järeldub, et tuleks püüda vältida absoluutväärtuselt lähedaste arvude lahutamist. Mõnikord on seda võimalik saavutada arvutusvalemi teisendamisega. Kui sellist lahutamist pole võimalik vältida, on vaja suurendada vahearvutuste täpsust, võttes arvesse oluliste arvude kadu. Kahe ligikaudse arvu a * ja b * korrutamisel ja jagamisel määratakse vead valemitega: Seega liidetakse ligikaudsete arvude korrutamisel ja jagamisel nende piiravad suhtelised vead. Märkus . Kui ligikaudse arvu Δ (a *) absoluutne viga ei ületa selle numbri kümnendkoha n-nda tähendusliku numbriga väljendatud numbri ühikut, kehtib piirväärtusliku suhtelise vea kohta järgmine ebavõrdsus: δ(a *) ≤ 1 / k 10 n - 1 kus k - numbri esimene oluline number a *. Kui ligikaudse arvu absoluutviga D(a*) ei ületa poolt numbri ühikut, väljendatuna selle arvu kümnendkoha n-nda tähendusega numbriga, kehtib piirväärtusliku suhtelise vea puhul järgmine ebavõrdsus: δ(a *) ≤ 1/2 k 10 n − 1 kus k on a * esimene oluline number. Viimasel juhul kehtib ka vastupidi: kui d (a *) J 1/2 (k + 1) 10 n - 1, siis a * on ligikaudne arv n kehtiva numbriga. Olgu antud domeenis G pidevalt diferentseeruv funktsioon u \u003d f (x 1, x 2, j, x n). Funktsiooni väärtuse ligikaudse arvutamise vea hinnang asendatakse selle hälbe mooduli hinnanguga täpne väärtus põhjustatud argumentide vigadest. Sel juhul asendatakse funktsiooni hälve selle kogudiferentsiaaliga, milles argumentide juurdekasvud asendatakse nende absoluutsete vigadega. Siis määratakse funktsiooni väärtuse absoluutne piirviga seosega
d=
0,02
0,01
= 2.
D(a*b*) = | b * | D(a *) + | a * | D(b*),
d(a*b*) = d(a*) + d(b*),
(1.7)
D(a*/b*) =
| b*|D(a*)+| a*|D(b*)| b * | 2
d(a*/b*) = d(a*) + d(b*).
1.7 Funktsiooniviga
Piirava suhtelise vea jaoks on meil võrdsus
Valemite (1.11) abil saab määrata argumentide täpsuse, mis tagab funktsiooni väärtuse etteantud täpsuse.
Näide 1.5.1. Tuleb täpselt mõõta d=1% tüvikoonuse külgpindala, mille põhiraadiused on r 1 » 2m, r 2" 1m ja generatrix l» 5m.
Millise absoluutveaga on vaja mõõta raadiusi ja generatriksit ning mitme märgiga, laiemas mõttes õige, võtta arv p?
Kui a D(a*) ei ületa ühte numbrit, väljendatuna n-nda olulise numbriga, siis nimetatakse *-ks numbrit, millel on n kehtivat numbrit laiemas mõttes.)
Lahendus. Tüvikoonuse külgpinna pindala arvutatakse järgmise valemi abil:
S = π l(r 1 + r 2).
Seega on meil nelja argumendi funktsioon S = S(p , l, r 1 , r 2).
Leidke osatuletised ja jagage S .
Valemitest (1.11) väljendame argumentide absoluutsed vead:
sellest järeldub, et number lk tuleks võtta märkide arvuga n = 3 .
KONTROLLI END
Antud on ligikaudne arv a * = 1,0754327 ja seda piirav absoluutviga D(a*)=0,0005.
Ümarda see arv õigeteks numbriteks. Võtke arvesse ümardamisviga.
Mõõda rätsepa mõõdulindiga meridiaani, tsaarikahuri kahurikuuli ja tennisepalli ümbermõõt. Milline mõõtmine annab suurima suhtelise vea?
Ringi raadiuse mõõtmisel 0,5 cm täpsusega saadi arv 12 cm. Leidke ringi pindala absoluutsed ja suhtelised vead.
Täielik aritmeetilised tehtedüle ligikaudsete arvude, mille kõik numbrid on õiged:
130,6 + 0,255 + 1,15224 + 41,84 + 11,8216;
35,2 1,748;
Väärtus nimetatakse seda, mida saab väljendada arvuga teatud ühikutes. Näiteks pikkus, pindala, maht on suurused. Koguse väärtust, mille tõesuses me ei kahtle, nimetatakse täpseks. ( edasi x on täpne arv). Kuid praktikas saadakse mingi suuruse väärtust otsides vaid selle ligikaudne väärtus. ( edasi a on ligikaudne arv ). Näiteks mõõtmisel füüsikalised kogused mõõteriistade abil.
Nimetatakse suuruse täpse ja ligikaudse väärtuse erinevuse moodulit absoluutne viga
lähendamine Absoluutse lähenduse vea või veapiiri piiramine või absoluutne
vead
helistas numbrile 
. Sellised hinnangud võivad olla lõpmatu arv. parim hinnang veapiir on väikseim hinnang.
Lühike täpse arvu jaoks:
Nimetatakse lähenduse absoluutvea ja suuruse täpse väärtuse mooduli suhet suhteline viga . Praktikas kasutatakse suhtelise vea piiramiseks (suhtelise vea hindamiseks): . Suhtelist viga väljendatakse tavaliselt protsentides.
Hiljem sõna hinne läheb alla.
NÄIDE. Leia absoluutne ja suhteline lähendusviga a = 3,14 jaoks x=π.
On teada, et 3,14 <π<3,15 .
Siit järeldub, et s.o.
Võttes seda arvesse 3,14 <π<3,142, siis saame parima hinnangu
Koguse ligikaudse väärtuse kümnendmärgistuses olev number X helistas tõsi laiemas mõttes , kui absoluutne lähendusviga ei ületa selle numbri ühtsust r, kuhu see number kuulub (null numbrit loetakse ühikute numbriks, kümnendkohti negatiivseteks numbriteks). On veel üks kontseptsioon tõeline kuju kitsas tähenduses : . Edaspidi kaalume õigeid numbreid laiemas mõttes. Ülejäänud numbrid kutsutakse kahtlane . Sisukas kümnendkujul kirjutatud arvu numbrid on kõik arvu õiged numbrid, alates esimesest vasakul, välja arvatud 0. Kõik nullid vasakul on ebaolulised. Tähendusnumbrite arvu järgi saab hõlpsasti hinnata ligikaudse arvu absoluutset viga. Absoluutvea hinnangu saamiseks võite võtta viimase olulise numbri järel 0,5 numbrit. Piirava suhtelise vea võib võtta võrdseks murdosaga, mille lugeja on 1 ja nimetaja on topelttäisarv, mis on kirjutatud antud arvu kõiki olulisi numbreid kasutades.
NÄIDE. a = 0,065;
ÜLESANNE 1.1. Ruumi maht V määratud suhtelise veaga δ Mitu olulist numbrit sisaldab V ?
ÜLESANNE 1.2. On teada, et ligikaudne väärtus a Sellel on n olulised numbrid. Hinnake absoluutset ja suhtelist viga.
Arvutustega seotud ülesannete lahendamisel saadakse numbrilised tulemused, mis sageli ei ole täpsed, sest. vead esinevad ülesande sõnastamisel ja arvutuste tegemisel.
Vigade allikad on:
1) algandmete vead;
2) vahe- ja lõpptulemuste ümardamisvead;
3) ülesande lahendamise ligikaudse meetodi vead.
Ligikaudsete arvudega toimingute tegemisel peate:
1) teades lähteandmete täpsust, oskama hinnata tulemuse õigsust;
2) võtma lähteandmeid sellise täpsusega, et tagada tulemuse määratud täpsus.
2.1 Ligikaudsete arvude vead
Olgu arv x täpne väärtus ja arv a mingi suuruse ligikaudne väärtus.
Definitsioon. Arvu x ja selle ligikaudse väärtuse a erinevust nimetatakse ligikaudse arvu a veaks: Δ = |x-a |.
Olgu x=10,5, a=10, siis Δ=10,5-10=0,5.
Olgu x=9,5, a=10, siis Δ=9,5-10=-0,5.
Definitsioon. Arvu x ja selle ligikaudse väärtuse a vahelise erinevuse absoluutväärtust nimetatakse ligikaudse arvu a absoluutveaks: Δа = |х-а|
Olgu x=10,5, a=10, siis Δa=|10,5-10|=0,5.
Olgu x=9,5, a=10, siis Δa=|9,5-10|=0,5.
Tihti pole täpne arv x teada. Siis on võimatu leida Δа = |х-а|, seetõttu kasutatakse absoluutvea hinnangut - piiravat absoluutset viga Δа ≥ Δа =x-а|. Sel juhul on arv x ümbritsetud piiridega:
a - Δ a x a + Δ a või lühidalt: x = a ± Δ a.
Nad loevad: x on võrdne a täpsusega Δ a.
Tehtud arvutuste kvaliteedi määramiseks on vaja kindlaks teha, milline osa on mõõdetud väärtuse absoluutne viga. Selleks kasutage suhtelist viga.
Definitsioon. Ligikaudse arvu a suhteline viga δа on absoluutse vea Δа ja arvu x mooduli suhe:
või 
.
Suhtelise vea ba hinnang on suhteline piirviga: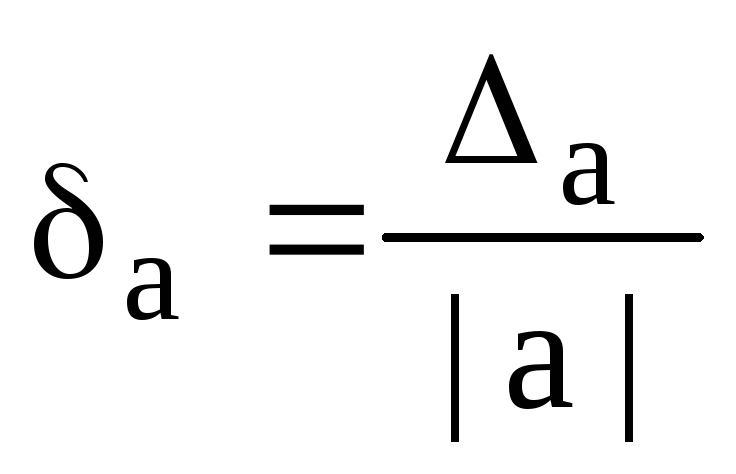 
Näide. Antud arv x=0,4287 ja selle ligikaudne väärtus a=0,4264. Leia arvu a absoluutsed ja suhtelised vead.
Lahendus. Arvutame arvu a absoluutvea:
Δa=|0,4287-0,4264| = 0,0023.
Arvutame arvu a suhtelise vea:
ehk 5,4%.
Märkused. 1. Vea salvestamisel on tavaks jätta 1-2 märgilist numbrit. Vead ümardatakse alati ülespoole. Sel juhul laienevad täpse arvu x piirid.
2. Kui arv x on tundmatu, kasutatakse suhtelise vea leidmiseks arvu a.
3. Suhtelist viga väljendatakse sageli protsendina, korrutades selle 100%.
2.2. Ligikaudse arvu olulised ja tõesed numbrid
Ligikaudse arvu a täpsuse hindamiseks on tavaks kirjutada see kümnendmurruna. Arvutuste täpsust ei määra mitte komakohtade arv (numbrid pärast koma), vaid tulemuse kehtivate tähenduslike numbrite arv.
Definitsioon. Arvu a olulised numbrid on kõik selle numbrid, välja arvatud nullid, mis on kirjutatud enne esimest nullist erinevat numbrit, ja nullid kirje lõpus, kui need aitavad säilitada numbrit või numbri täpsust.
Näide. Leidke tähe a tähenduslikud numbrid.
a = 0,02701 => olulised arvud: 2.7.0.1.
a = 0,0270 => olulised arvud: 2.7.0.
a = 2700 => olulised arvud: 2.7.0.0.
Definitsioon. Ligikaudse arvu a numbrit α i nimetatakse tõeliseks tähendusarvuks laiemas tähenduses (kõiges mõttes), kui arvu a piirav absoluutviga ei ületa ühte (poolt) numbrist, milles number α i kirjutatakse: Δ a 10 i (Δ a 0,5∙10 i).
Näide. Määrake ligikaudse arvu a = 0,7264 õiged arvud, kui absoluutne viga on Δ a = 0,0023.
Lahendus. Absoluutne viga Δ a \u003d 0,0023 0,005 \u003d 0,5 ∙ 10 -2. Seetõttu on numbrid 7 ja 2 õiged kitsas tähenduses, numbrid 6 ja 4 on valed (kahtlased). Kuna Δ a = 0,0023< 0,01 = 10 -2 , то цифры 7 и 2 являются верными в широком смысле.
Märkused. 1. Matemaatilistes tabelites on kõik olulised arvud täpses tähenduses õiged.
2. Lõpptulemuses on tavaks jätta ainult õiged numbrid. Siis määratakse arvu a piirav absoluutviga väikseima numbri ühikuga. Näiteks olgu a = 127,38, siis Δ a = 0,01, kui kõik arvud on õiged kitsamas tähenduses, ja Δ a = 0,5 ∙ 0,01 = 0,005, kui kõik arvud on õiged laiemas tähenduses.
Näide. Määrake, milline võrdus on täpsem 13/19=0,684 või 
=7,21?
Lahendus. Tähistame a = 0,684, b = 7,21. Leiame nende arvude absoluutsed vead. Selleks võta 13/19 ja suure arvu komakohtadega: 13/39=0,68421..., =7,2111...
Siis Δ a =|0,68421...-0,684|< 0,00022, Δ в = |7,2111...-7,21| < 0,0012.
Leiame suhtelised vead:
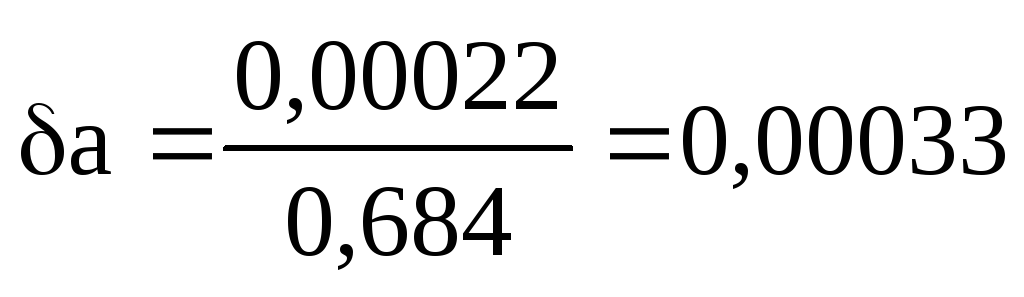ehk 0,033%.
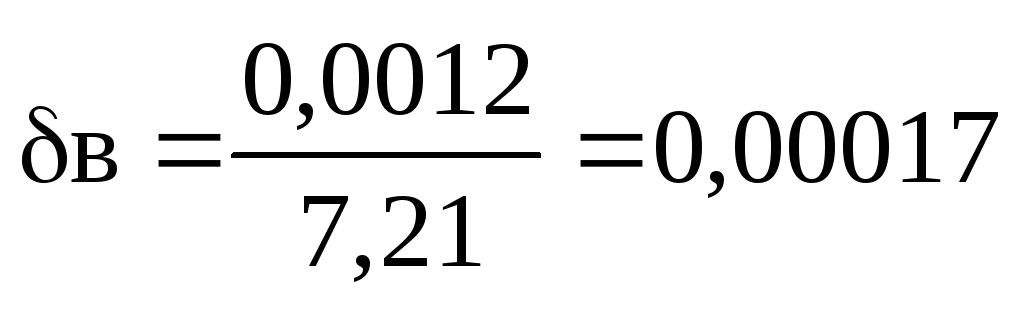ehk 0,017%.
Teine võrrand on täpsem, kuna 
.
2.3. Numbrite ümardamine
Ligikaudsete arvutuste puhul on sageli vaja ümardada nii ligikaudsed kui ka täpsed numbrid, st jätta kõrvale üks või mitu viimast numbrit. Arvu ümardamisel asendame selle ligikaudse arvuga, milles on vähem olulisi numbreid, mille tulemuseks on ümardamisviga. Selleks, et see viga oleks minimaalne, tuleb järgida mõningaid ümardamisreegleid.
reegel I. Kui äravisatud numbritest esimene vasakul on suurem kui 5, siis võimendatakse viimast allesjäänud numbritest, s.t. suureneb ühe võrra. Võimendatakse ka siis, kui äravisatud numbrite esimene vasakpoolne osa on 5, millele järgneb nullist erinev number.
Näide.Ümardades kümnendikku arvust 73,473, saame 73,5. Viimane järelejäänud number on tugevdatud, kuna 7 > 5.
reegel II. Kui esimene äravisatud number on väiksem kui 5, siis viimast ülejäänud numbrit ei suurendata, st see jääb muutumatuks.
Näide.Ümardades arvust 73,473 sajandikku, saame 73,47.
reegelIII. Kui esimene kõrvalejäetud numbritest vasakul on 5 ja sellele ei järgne nullist erinevat numbrit, siis viimast allesjäänud numbrit suurendatakse, kui see on paaritu, ja jäetakse muutmata, kui see on paaris (paarisnumbri reegel).
Näide.Ümardades arvu 5,785 sajandikuteks, saame 5,78. Me võimendusi ei tee, kuna viimane salvestatud number 8 on paaris. Ümardades arvu 5,775 teise kümnendkohani, saame 5,78. Viimast salvestatud numbrit 7 suurendatakse ühe võrra, kuna see on paaritu.
Reegli III rakendamisel üksiku arvu ümardamisel me tegelikult arvutuste täpsust ei suurenda, kuid arvukate ümardamiste korral esineb ülearve umbes sama sageli kui alaarve. Toimub vastastikune vigade kompenseerimine, tulemus on täpsem.
Seega ei ületa ülaltoodud ümardamisreeglite rakendamisel absoluutne ümardamisviga poolt numbriühikut, mis on määratud viimase järelejäänud olulise numbri järgi.
Kui täpne arv x ümardatakse n olulise numbrini, siis on saadud ligikaudse arvu a absoluutne viga, mis on võrdne ümardamisveaga. Sel juhul on ligikaudsel arvul a kitsas tähenduses n õiget tähenduslikku numbrit.
Näide.Ümardades arvu x=26,837 kolmeks tähenduslikuks numbriks, saame a =26,8, kust Δ a = |x-a | = | 26,837-26,8 |=0,037< 0,05, т. е. число а имеет три верные значащие цифры в узком смысле.
Ligikaudse arvu a ümardamisel saame uue ligikaudse arvu a 1 .
Definitsioon. Arvu Δ a1 \u003d Δ a + Δ env nimetatakse ümardamisveaks.
Arvu a 1 absoluutviga on algarvu absoluutvea Δ a ja ümardamisvea Δ env summa, s.o.
Δ a1 = Δ a + Δ env.
Näide.Ümardage arvu x = 34,124 ± 0,021 kahtlased numbrid. Määrake tulemuse absoluutne viga.
Lahendus. Ligikaudsel arvul a=34,124 on kolm õiget arvu kitsamas tähenduses: 3, 4, 1, kuna Δ a = 0,021< 0,05. Применяя правила округления, найдем приближенное значение а 1 , сохранив десятые доли: а 1 = 34,1. Погрешность округления Δ окр =|34,124-34,1|=0,024. Тогда абсолютная погрешность числа а 1 равна Δ а1 =Δ а +Δ окр =0,021+0,024 = 0,045 < 0,05.
Seega on arvu a 2 kõik olulised numbrid õiged (kitsamas tähenduses).
Seega x=34,1±0,045.
Kui aga ümardada ligikaudne arv a, millel on n õiget tähenduslikku numbrit (kitsas tähenduses), n-ks, võib selguda, et ümardatud arvul a 1 on laiemas tähenduses n õiget tähenduslikku numbrit.
Näide. Ligikaudsel arvul a=15,3654 (± 0,0018) on neli õiget tähenduslikku arvu kitsas tähenduses (1, 5, 3, 6), kuna Δ a = 0,0018< 0,005. При округлении до четырех значащих цифр получим а 1 = 15,37 и Δ а1 =Δ а +Δ окр =0,0018+|15,3654-15,37|=0,0064.
Ilmselgelt 0,005< 0,0064 < 0,01. Следовательно, число 15,37 (± 0,0064) on neli õiget numbrit kõige laiemas tähenduses.
Seega x=15,37±0,0064.
Näide.Ümardage arvu a = 26,7245 (± 0,0026) kahtlased arvud, jättes õiged märgid kitsas tähenduses. Määrake tulemuse absoluutne viga.
Lahendus. Tingimuse järgi Δ a = 0,0026< 0,005, следовательно, в числе 26,7245 верными в узком смысле являются цифры 2, 6, 7, 2. Используя правила округления, найдем приближенное значение а 1 , сохранив сотые доли:
Saadud viga on suurem kui 0,005 (0,005< 0,0071), поэтому уменьшим число цифр в приближенном числе до трех; а 2 = 26,7. Leiame Δ a2 = = Δ a + Δ env = 0,0026 + | 26,7245-26,7 | = 0,0271< 0,05. Следовательно, оставшиеся три цифры верны в узком смысле.
Niisiis, x=26,7 ±0,0271 => x=26,7 ±0,03, ümardades vea kahe kümnendkohani.
Näide.Ümardage arvu a = 22,7314 kahtlased numbrid, jättes õiged märgid kitsas tähenduses. Määrake arvu absoluutviga, kui δ a = 0,2%.
Lahendus. Kirjutame δ a kümnendmurru kujul: δа=0,002 ja määrake absoluutne viga . Kuna Δ a \u003d \u003d 0,0455< 0,05, то верными в этом числе будут три цифры: 2, 2, 7. Округлим число 22,7314, сохранив в нем десятые доли: а 1 = 22,73. Siis Δ a1 = = Δ a + Δ env = 0,0455 + | 22,7314-22,73 | = 0,0769> 0,05, seetõttu vähendame ligikaudse arvu numbrite arvu kaheks: a 2 = 23. Leiame Δ a2 = = Δ a + Δ env = 0,0455 + | 22,7314-23 | = 0,3141< 0,05. Следовательно, оставшиеся две цифры верны в узком смысле.
Seega x=23±0,3141 => x=23±0,32.
2.3. Ligikaudsete arvudega tehtavate reeglid
1. reegel Mitme ligikaudse arvu algebralise summa absoluutne viga on võrdne nende arvude absoluutvigade summaga:
Δ a ± b = Δ a + Δ b
2. reegel Mitme ligikaudse arvu korrutise suhteline viga on võrdne nende arvude suhteliste vigade summaga:
δ av \u003d δ a + δ c.
3. reegel Osaliste ligikaudsete arvude suhteline viga on võrdne nende suhteliste arvude summaga: δ a / b \u003d δ a + δ c.
4. reegel Ligikaudse arvu a astme suhteline viga on: δa n = nδ a.
5. reegel Ligikaudse arvu a juure suhteline viga on: 
.
6. reegel Kui vigade ranget arvutust ei tehta, on arvutamisel soovitatav kasutada arvude loendamise reegleid. Need reeglid täpsustavad, kuidas tulemusi ümardada, et tulemus oleks võimalikult täpne ilma ülenumbrite arvutusteta.
Reeglid eeldavad, et opereeritavad numbrid sisaldavad ainult kehtivaid numbreid ja toimingute arv on väike.
I. Ligikaudsete arvude liitmisel ja lahutamisel peab tulemuseks jääma nii palju komakohti, kui on arvus, millel on kõige vähem kümnendkohti.
II. Korrutamisel ja jagamisel peaks tulemuses jääma nii palju tähenduslikke numbreid, kui palju on kõige vähem oluliste numbritega arvus.
III. Ligikaudse arvu tõstmisel astmeni peaks tulemuseks olema nii palju olulisi numbreid, kui on astme baasis.
IV. Ligikaudsest arvust juure eraldamisel peaksite säilitama nii palju olulisi numbreid, kui on juurarvus.
V. Vahetulemustes tuleks jätta 1-2 numbrit rohkem, kui reeglid I-IV soovitavad. Lõpptulemuses jäetakse "varunumbrid" arvu ümardamisel kõrvale.
VI. Kui mõnel lähteandmetel on rohkem komakohti (liitmiseks ja lahutamiseks) või rohkem tähenduslikke numbreid (muude tehete jaoks), siis tuleks need kõigepealt ümardada, jättes alles ainult ühe "turvalise arvu".
VII. N õige numbriga tulemuse saamiseks tuleks lähteandmed võtta sellise arvu numbritega, mis eelnevate reeglite kohaselt annaksid tulemuses N + 1 numbrit.
Näide. Leiame s=2,35+11,8 ilma vigu arvestamata. Rakendades reeglit I, saame s=14,15. Tulemus ümardatakse väikseima kümnendkohtade arvuga arvuni 11,8. Saame: s \u003d 14,2.
Lahendame probleemi, võttes arvesse vigu. Arvu s=14,15 puhul tuleks jätta ainult õiged numbrid. Selleks leiame summa s piirava absoluutvea reegli 1 abil. Arvestades, et kõik arvud arvudes 2,35 ja 11,8 on õiged, saame: Δ 14,15 = Δ 2,35 + Δ 11,8 = 0,01 +0,1=0,11< 0,5. Последняя верная цифра в числе 14,15 находится в разряде единиц. Поэтому число s=14,15 надо округлить: s=14 и найти абсолютную погрешность округленного числа. Погрешность округления равна: |14,15-14|=0,15. Тогда абсолютная погрешность округленного числа Δ 14 =0,11+0,15=0,26 <0,5. Окончательный результат примет вид: s=14 ± 0,26.
Sarnaselt lahendatakse ülesandeid ka muude tehtete sooritamisel ligikaudsete arvudega.
Saada oma head tööd teadmistebaasi on lihtne. Kasutage allolevat vormi
Üliõpilased, magistrandid, noored teadlased, kes kasutavad teadmistebaasi oma õpingutes ja töös, on teile väga tänulikud.
postitatud http://www.allbest.ru/
postitatud http://www.allbest.ru/
Moskva Majandusinstituut,juhtimine ja õigus
abstraktne
distsipliini järgi:
« Kõrgemmmatemaatika»
« Pligikaudsed arvutused javeahinnangumbesjää»
Valmis: üliõpilane
Jantšuk Ljudmila Aleksandrovna
teaduslik nõunik Pitertseva Galina Aleksandrovna
Moskva, 2000
Plaan
Sissejuhatus. Arvutustehnika kaasaegses teaduses ja tehnoloogias
1. Ligikaudsed väärtused ja lähendusvead
2. Numbrite ümardamine. Ümardamise viga
Järeldus. Natuke infot arvutite kohta
Kirjandus
Sissejuhatus. Arvutustehnika kaasaegses teaduses ja tehnoloogias
Mõõtmised ja arvutused on ühiskonnaelus mänginud olulist rolli iidsetest aegadest peale. Vajadus arvutada saaki, mõõta laevade võimsust, maatükkide suurust, teha arvutusi suurte ehitiste ehitamisel, teha mitmesuguseid astronoomilisi arvutusi - see on mittetäielik nimekiri ülesannetest, mida inimesed pidid iidsetel aegadel lahendama.
Viimase aja üheks olulisemaks sündmuseks tuleb pidada inimkonna kosmoseuurimist. Jälgime ärevusega lende Kuule, Veenusele, Marsile, mehitatud orbitaaljaamade teket. Kosmoselaeva start oleks mõeldamatu, kui see poleks laeva liikumise täpseks arvutamiseks ning see nõuab kolossaalset ja keerulist arvutustööd.
Kaasaegsel perioodil, teadusliku ja tehnoloogilise revolutsiooni perioodil, suureneb matemaatiliste meetodite roll. Matemaatilisi meetodeid ei kasutata mitte ainult füüsikas, vaid ka keemias, bioloogias, meditsiinis, majanduses, ajaloos ja keeleteaduses.
Tööstusettevõtete, teadusinstituutide, riigiasutuste, talude ja kolhooside igapäevases ja jooksvas tegevuses tuleb teha palju arvutustööd matemaatikutel ja inseneridel.
Arvutusmeetodeid kasutatakse tänapäeval laialdaselt majandusarvutustes, üksiku ettevõtte, piirkonna ja kogu riigi majanduse töö planeerimisel.
On palju probleeme, mille puhul numbrilise tulemuse saamiseks on vaja arvutusi, mis ületavad ühe inimese võimalusi. Selliste probleemide näideteks on tammi elastsuspingete arvutamine, õhusõiduki lennu ajal kogetava takistuse või mürskude trajektooride arvutamine. Seda keerulist arvutustööd teevad kümned arvutiinsenerid, kasutades erinevaid arvuteid.
Arvuti tulek põhjustas revolutsiooni arvutustehnoloogias. Aga selleks, et viia matemaatikaülesannete lahendamine sellesse etappi, mille järel saab need arvuliste tulemuste saamiseks arvutisse üle kanda, on vajalik ka paljude kalkulaatorite töö. Arvutite loomine stimuleeris matemaatika enda, eriti selle rakendusvaldkondade arengut, arvutused ei mängi nüüd mitte abistavat, vaid peamist rolli paljudes teaduse ja tehnika saavutustes. Kõigil juhtudel, kui on vaja lahendada mõni praktilist laadi matemaatiline ülesanne, on vaja saada numbriline tulemus. Kui algandmed on ligikaudsed, on tulemuse täpsust võimatu saavutada. Tuleb osata hinnata lähteandmete täpsust, samuti teha kindlaks, millise tulemuse täpsust on võimalik saavutada ja millist tulemuse täpsust on vaja saadud arvuliste tulemuste praktilisel kasutamisel. Mõned arvutused nõuavad väga suurt täpsust, teised aga mitte. Sellest on selge, et arvutused on vaja korraldada nii, et minimaalse arvutustöökuluga saadakse nõutava täpsusega tulemused.
Selle eesmärgi saavutamiseks on vaja:
uurida ligikaudsete andmetega arvutamise põhimõtteid ja reegleid;
omandada vajalikke oskusi ratsionaalseks arvutamiseks olemasolevate vahendite abil, mille hulka kuuluvad erinevad suuliste arvutuste meetodid, matemaatilised tabelid, kantseleiarvestused, slaidireeglid, aritmomeetrid, poolautomaatsed ja automaatsed arvutid.
1. Ligikaudsed väärtused ja lähendusvead
Praktilises tegevuses tuleb inimesel mõõta erinevaid koguseid, arvestada materjalide ja töötoodetega ning teha erinevaid arvutusi. Erinevate mõõtmiste, loenduste ja arvutuste tulemused on arvud. Mõõtmise tulemusel saadud numbrid iseloomustavad soovitud väärtusi ainult ligikaudselt, teatud täpsusega. Täpsed mõõtmised on võimatud mõõteriistade ebatäpsuse, meie nägemisorganite ebatäiuslikkuse tõttu ja mõõdetud objektid ise ei võimalda mõnikord nende väärtust täpselt määrata.
Nii näiteks on teada, et Suessi kanali pikkus on 160 km, raudtee vahemaa Moskvast Leningradini on 651 km. Siin on meil kuni kilomeetrise täpsusega tehtud mõõtmiste tulemused. Kui näiteks ristkülikukujulise lõigu pikkus on 29 m, laius 12 m, siis arvatavasti tehti mõõtmised kuni meetrise täpsusega ja meetri murrud jäeti tähelepanuta,
Enne mistahes mõõtmise tegemist tuleb otsustada, millise täpsusega on vaja see sooritada, s.t. milliseid mõõtühiku murdosasid tuleks arvesse võtta ja milliseid tähelepanuta jätta.
Kui on mingi väärtus a, mille tegelik väärtus on teadmata ja selle väärtuse ligikaudne väärtus (ligikaudne väärtus) on võrdne X, nad kirjutavad a X.
Sama koguse erinevate mõõtmiste korral saame erinevad ligikaudsed väärtused. Kõik need ligikaudsed väärtused erinevad mõõdetud väärtuse tegelikust väärtusest, võrdub näiteks a, teatud summa võrra, mida me helistame viga. Definitsioon. Kui arv x on mingi suuruse ligikaudne väärtus (ligikaudne väärtus), mille tegelik väärtus on võrdne arvuga a, siis arvude erinevuse moodul, a ja X helistas absoluutne viga antud ligikaudne ja tähistatud ax: või lihtsalt a. Seega definitsiooni järgi
ax = a- x (1)
Sellest määratlusest järeldub, et
a = x ax (2)
Kui on teada, mis suurusest me räägime, siis tähistuses ax indeks a jäetakse välja ja võrdsus (2) kirjutatakse järgmiselt:
a = x x (3)
Kuna soovitud väärtuse tegelik väärtus on enamasti teadmata, ei ole võimalik selle väärtuse lähenduses absoluutset viga leida. Igal konkreetsel juhul saab näidata ainult positiivset arvu, millest suurem see absoluutviga olla ei saa. Seda arvu nimetatakse koguse lähenduse absoluutvea piiriks a ja tähistatud h a. Seega, kui x on väärtuse a suvaline lähendus antud protseduuri jaoks lähenduste saamiseks, siis
ax = a- x h a (4)
Eelnevast järeldub, et kui h a on suuruse lähenduse absoluutvea piir a, siis suvaline arv, mis on suurem kui h a, on ka suuruse lähenduse absoluutvea piir a.
Praktikas on tavaks absoluutvea piiriks valida väikseim ebavõrdsust (4) rahuldav arv.
Ebavõrdsuse lahendamine a- x h a me saame sellest aru a sisalduvad piirides
x-h a a x+ h a (5)
Absoluutse veapiiri rangema kontseptsiooni saab esitada järgmiselt.
Lase X- palju võimalikke lähendusi X kogused a antud protseduuri jaoks lähenduse saamiseks. Siis suvaline number h, mis vastab tingimusele a- x h a iga X X, nimetatakse hulga lähenduste absoluutvea piiriks X. Tähistage h a väikseim teadaolev arv h. See number h a ja valitakse praktikas absoluutvea piiriks.
Absoluutne lähendusviga ei iseloomusta mõõtmiste kvaliteeti. Tõepoolest, kui me mõõdame mis tahes pikkust 1 cm täpsusega, siis pliiatsi pikkuse määramisel on see halb täpsus. Kui määrate 1 cm täpsusega võrkpalliväljaku pikkuse või laiuse, on see suur täpsus.
Mõõtmistäpsuse iseloomustamiseks võetakse kasutusele suhtelise vea mõiste.
Definitsioon. Kui a ax: on absoluutne lähendusviga X mingi suurus, mille tegelik väärtus on võrdne arvuga a, siis suhe ax arvu moodulile X nimetatakse lähenduse suhteliseks veaks ja seda tähistatakse ax või x.
Seega definitsiooni järgi
Suhtelist viga väljendatakse tavaliselt protsentides.
Erinevalt absoluutsest veast, mis on enamasti mõõtmete suurus, on suhteline viga mõõtmeteta suurus.
Praktikas ei arvestata mitte suhtelist viga, vaid nn suhtelise vea piiri: sellist arvu E a, mis ei saa olla suurem kui soovitud väärtuse lähenduse suhteline viga.
Sellel viisil, ax E a.
Kui a h a-- suuruse ligikaudsete väärtuste absoluutvea piir a, siis ax h a ja seega
Ilmselgelt suvaline number E, mis vastab tingimusele, on suhtelise vea piir. Praktikas on tavaliselt teatud ligikaudne väärtus X kogused a ja absoluutne veapiir. Siis number
2. Numbrite ümardamine. Ümardamise viga
Arvutuste tegemisel tekib sageli vajadus arvude ümardamine, s.t. asendades need arvudega, millel on vähem olulisi numbreid.
Numbrite ümardamiseks on kolm võimalust:
Ümardades alla k märkimisväärne number tähendab, et tühistatakse kõik numbrid, mis algavad tähega (k+1) th.
Üles ümardamine erineb allapoole ümardamisest selle poolest, et viimast salvestatud numbrit suurendatakse ühe võrra.
Väikseima veaga ümardamine erineb ülemääraga ümardamisest selle poolest, et ühe viimase salvestatud numbri võrra suurendatakse ainult siis, kui esimene kõrvalejäetud number on suurem kui 4.
Erand: kui väikseima veaga ümardamisel jäetakse ära ainult üks number 5, siis viimast salvestatud numbrit ei muudeta, kui see on paaris, ja suurendatakse 1 võrra, kui see on paaritu.
Eeltoodud ligikaudsete arvude ümardamise reeglitest tuleneb, et väikseima veaga ümardamisel tekkinud viga ei ületa poolt viimase salvestatud numbri ühikut ning puudujäägi või liiaga ümardamisel võib viga olla suurem kui pool ühik viimasest salvestatud numbrist, kuid mitte rohkem kui terve selle tühjenemise ühik.
Vaatame seda järgmistes näidetes.
1. Summa viga. Lase x a, juures-- mingi ligikaudne väärtus b. Lase X ja juures-- vastavate lähenduste absoluutsed vead X ja juures. Leiame absoluutse vea piiri h a+b summad x+y, mis on summa ligikaudne väärtus a+b.
a = x + X,
b = y + y.
Lisades need kaks võrdsust, saame
a + b = x + y + x + y.
Ilmselgelt lähenduste summa viga x ja juures on võrdne terminite vigade summaga, s.o.
(x + y) = x + y
On teada, et summa moodul on väiksem või võrdne liikmete moodulite summaga. Sellepärast
(x + y) = x + y x + y
See tähendab, et lähenduste summa absoluutne viga ei ületa terminite absoluutsete vigade summat. Seetõttu võib summa absoluutvea piiriks võtta terminite absoluutvigade piiride summa.
Tähistab suuruse absoluutvea piiri a läbi h a, ja b läbi h b saab
h a + b = h a + h b
2. Erinevusviga. Lase X ja juures-- lähendusvead x ja juures vastavalt a ja b.
a = x + X,
b = y + y.
Lahutage esimesest võrdsusest teine, saame
a - b = (x - y) + ( x - y)
Ilmselt on lähenduste erinevuse viga võrdne minuendi ja alamosa vigade vahega, s.o.
(x - y) = x - y) ,
(x - y) = x + (- y)
Ja siis, vaieldes samamoodi nagu liitmise puhul, on meil
(x - y) = x + (- y) x + y
Sellest järeldub, et erinevuse absoluutviga ei ületa minuendi ja alamosa absoluutsete vigade summat.
Erinevuse absoluutvea piiriks võib võtta taandatud ja alamosa absoluutvea piiride summa. Sellel viisil.
h a - b = h a + h b (9)
Valemist (9) järeldub, et erinevuse absoluutvea piir ei saa olla väiksem kui iga lähenduse absoluutvea piir. See eeldab lähenduste lahutamise reeglit, mida mõnikord arvutustes kasutatakse.
Kui lahutada arvud, mis on mõne suuruse ligikaudsed arvud, peaks tulemuseks olema sama palju kohta pärast koma, kui koma järel on kõige väiksema arvu numbritega lähendus.
3. Toote viga. Mõelge arvude korrutisele X ja juures, mis on koguste ligikaudsed väärtused a ja b. Tähistage x lähendusviga X, ja läbi juures-- lähendusviga juures,
a = x + X,
b = y + y.
Korrutades need kaks võrdsust, saame
Absoluutne tooteviga hu on võrdne
Ning seetõttu
Saadud ebavõrdsuse mõlemad pooled jagades hu, saame
Võttes arvesse, et korrutise moodul on võrdne tegurite mooduli korrutisega, saame
Siin on ebavõrdsuse vasak pool korrutise suhteline viga hu, -- suhteline lähendusviga X, ja on suhteline lähendusviga juures. Seetõttu, jättes siin väikese väärtuse kõrvale, saame ebavõrdsuse
Seega ei ületa lähenduste korrutise suhteline viga tegurite suhteliste vigade summat. Sellest järeldub, et tegurite suhteliste vigade piiride summa on toote suhtelise vea piir, s.o.
E ab = E a + E b (10)
Valemist (10) järeldub, et korrutise suhtelise vea piir ei saa olla väiksem kui kõige vähem täpse teguri suhtelise vea piir. Seetõttu pole siin, nagu ka eelmistes etappides, mõtet tegurites hoida liiga palju olulisi numbreid.
Mõnikord on töömahu vähendamiseks kasulik kasutada arvutustes järgmist reeglit: Kui korrutada lähendusi erineva arvu tähenduslike numbritega, peaks tulemuses jääma nii palju olulisi numbreid, kui on kõige väiksema arvu numbritega lähendusel.
4. Jagatise viga. Kui a x-- väärtuse ligikaudne väärtus a, kelle viga x, a juures-- väärtuse ligikaudne väärtus b veaga y, siis
Kõigepealt arvutame jagatise absoluutvea:
ja siis suhteline viga:
Võttes arvesse seda y vähe võrreldes y, võib murdosa absoluutväärtust lugeda võrdseks ühega. Siis
viimasest valemist järeldub, et jagatise suhteline viga ei ületa dividendi ja jagaja suhteliste vigade summat. Seetõttu võime eeldada, et jagatise suhtelise vea piir on võrdne dividendi ja jagaja suhteliste vigade piiride summaga, s.o.
5. Kraadi ja juure viga. 1) Lase u = a n, kus n on naturaalarv ja olgu x. Siis kui E a-- suhtelise lähendusvea piir x kogused a, siis
ning seetõttu
Seega on astme suhtelise vea piir võrdne aluse suhtelise vea piiri korrutisega astendajaga, s.o.
E u = n E a (11)
2) Las kus n on naturaalarv ja olgu a X.
Valemi (11) järgi
ja seega
vea mahaarvamise arvutus
Seega juure suhtelise vea piir n aastal n korda väiksem kui radikaalarvu suhtelise vea piir.
6. Ligikaudsete arvutuste pöördülesanne. Otseses ülesandes on vaja leida funktsiooni ligikaudne väärtus u=f(x, y, ...,n) vastavalt argumentide antud ligikaudsetele väärtustele
ja veapiir h a, mida väljendatakse mõne funktsiooni argumentide vigadena
h u = (h x, h y, …, h z) (12)
Praktikas on sageli vaja lahendada pöördülesanne, mille puhul tuleb välja selgitada, millise täpsusega tuleks argumentide väärtused esitada x, y, …, z funktsioonide vastavate väärtuste arvutamiseks u = f(x, y, ...,z) etteantud täpsusega h u .
Seega pöördülesande lahendamisel otsitakse funktsiooni antud veapiiriga seotud argumentide veapiire h u võrrand (12) ja pöördülesande lahendus taandatakse võrrandi koostamiseks ja lahendamiseks h u = (h x, h y, …, h z) suhteliselt h x, h y, …, h z. Sellisel võrrandil on kas lõpmatu arv lahendeid või pole neid üldse. Ülesanne loetakse lahendatuks, kui sellisest võrrandist leitakse vähemalt üks lahendus.
Pöördülesande, mis on sageli määramatu, lahendamiseks tuleb kehtestada lisatingimused tundmatute vigade suhetele, näiteks lugeda need võrdseks ja taandada seeläbi ülesande võrrandiks ühe tundmatuga.
Järeldus. Veidi infot selle kohtanende arvutamineXnike
Sõltuvalt lähteandmete täpsusest ja arvutuste eesmärgist kasutatakse erinevaid arvutusvahendeid. Paljude massikutsealade töötajad hõlbustavad oluliselt arvutuste tegemist ning säästavad aega ja tööjõudu erinevate arvutuste tegemisel Venemaa aabitsa abil, loendades slaidireegleid, aritmomeetriid ning igasuguseid tasku- ja lauaarvuti elektroonilisi kalkulaatoreid (mikro- ja minikalkulaatoreid).
Praegu meie riigis leiduvasse minikalkulaatorite klassi kuuluvad elektrooniliste lauakalkulaatorite perekond Iskra ja kalkulaatorite perekond Elektronika, kuhu kuuluvad ka mitut tüüpi taskukalkulaatorid. Arusaadavatel põhjustel on need kalkulaatorid vananenud, kuid sellest hoolimata on need ainsad kodumaise tööstuse toodetud mudelid.
Perekondade Elektronika ja Iskra masinad on mõeldud peamiselt lihtsate inseneriarvestuse ja arvestusülesannete lahendamiseks 8-10 märgilise täpsusega. Paljud neist pakuvad elementaarsete funktsioonide väärtuste automaatse arvutamise võimalust ja on programmi juhtimise elemente.
Meie tööstuse ja põllumajanduse tehniliste seadmete kiire kasvuga, teaduse arenguga suureneb vajadus kõikvõimalike arvutuste järele üha enam. Kiirete elektrooniliste arvutite (arvutite) abil saab teadlane nüüd lahendada probleeme, mida varem isegi ei püstitatud, kuna nende lahendamine nõudis liiga palju aega.
Elektroonilisi arvuteid kasutatakse näiteks võrrandite arvuliseks lahendamiseks. Esimesed arvutid olid mõeldud spetsiaalselt selliste arvutuste jaoks.
Praegu kasutatakse arvuteid edukalt tehnoloogiliste protsesside juhtimiseks. Kui kiiresti voolava protsessi juhtimine eeldab selle protsessi käigus saadud andmete põhjal keerulisi arvutusi, siis ilma arvutita oleks selline ülesanne üldjuhul võimatu.
Kirjandus
Algebra ja analüüsi algus. Osa 1. Toim. G.N. Jakovlev. - M.: Nauka, 1981. 336 lk.
Vygotsky M.Ya. Kõrgema matemaatika käsiraamat. M.: 1987.
Sissejuhatus metroloogiasse. Tyurin N.I., M., Publishing House of Standards, 1976, 304 lk.
Majutatud saidil Allbest.ru
...Sarnased dokumendid
Ligikaudsete arvude absoluutsete ja suhteliste vigade määramine. Vigade hindamine tulemuses. Andmete interpoleerimine ja ekstrapoleerimine, Lagrange'i ja Newtoni interpolatsioonipolünoom, nende põhitunnused ja võrdlev kirjeldus.
laboritööd, lisatud 06.08.2013
Absoluutsete ja suhteliste vigade olemus ja matemaatiline tõlgendamine, väärtuse kirjutamise viisid koos nendega. Ligikaudse väärtuse ja lähendusvea mõiste, nende kategooriate analüüsi suund. Kümnendkohtade ümardamise reegel.
abstraktne, lisatud 13.09.2014
Matemaatiliste ja rakendusülesannete numbrilisel lahendamisel tekkivate peamiste vealiikide tunnused ja tunnused: ülesanded, meetodid, ümardamine. Mõõtmisvigade mõiste ja põhjused. Juhuslike vigade, hetkede kirjeldus.
test, lisatud 13.01.2012
Klassikaline mõõtmisteooria füüsikalise suuruse tegeliku väärtuse kohta, selle peamised postulaadid. Vigade klassifikatsioon väljendusmeetodi, selle tüüpide järgi: absoluutne, redutseeritud ja suhteline. Juhuslikud vead, nende jaotumise seadus.
abstraktne, lisatud 07.06.2014
Antud arvu ümardamine kuue, viie, nelja ja kolme kümnendkohani. Vigade arvutamine pärast iga ümardamist. Absoluutse ja suhtelise vea määramine funktsiooni u väärtuste arvutamisel, võttes arvesse asjaolu, et kõik operandid a, b, c ja d märgid on õiged.
test, lisatud 05.02.2012
Vigade määramise meetodite uurimine ja jaotuste statistiline hindamine. Empiirilise funktsiooni konstrueerimine, mis määrab sündmuse eripära juhusliku suuruse iga väärtuse jaoks. Arvutused antud proovi kohta, selle analüüs ja parameetrite määramine.
kursusetöö, lisatud 13.01.2011
Numbriliste meetodite tutvustus, arvutusliku katse konstrueerimise plaan. Arvutuste täpsus, vigade klassifitseerimine. Arvulise integreerimise ja diferentseerimise meetodite ülevaade, tagantjärele vea hindamine. Lineaarvõrrandisüsteemide lahendamine.
koolitusjuhend, lisatud 23.09.2010
Progressi liikmete arvu ja väärtuse määramine lõpmatult kahaneva geomeetrilise progressiooni korral. Koguse suhtelise vea arvutamine. Masina nulli ja lõpmatuse väärtuste määramine. Vigade käitumine olenevalt argumendist.
laboritööd, lisatud 15.11.2014
Lahendusvea sõltuvuse uurimine süsteemi parema poole vigadest. Võrrandi juure määramine etteantud täpsusega. Meetodite täpsushinnangute arvutamine koordinaatide järgi. Splaini interpolatsioon ja diferentsiaalvõrrandi lahendus.
test, lisatud 26.04.2011
Cauchy ülesande lahendus diferentsiaalvõrrandi jaoks. Ligikaudsete lahenduste viga. Funktsioon, mis rakendab selgesõnalist Euleri meetodit. Vea arvutamine Runge reegli järgi. Teist järku diferentsiaalvõrrandite lahendus. Maatriksi stabiilsustingimus.