Mõõtmise all mõistetakse mõõdetud väärtuse võrdlemist mõne muu väärtusega, mida võetakse mõõtühikuna. Mõõtmisel peate tegema kolm järjestikust toimingut:
1) seadmete kontrollimine ja seadistamine;
2) nende ütluste jälgimine ja ülelugemine;
3) mõõtmistulemustest soovitud väärtuse arvutamine ja vea hinnang.
Mõõtmised jagunevad otsesteks ja kaudseteks. Otsemõõtmisel võrreldakse määratavat suurust mõõtühikuga kas otse või vastavates ühikutes kalibreeritud mõõtevahendiga. Sellised mõõtmised hõlmavad pikkuse mõõtmist joonlaua, nihiku, mikromeetriga; kehakaalu, ajavahemike, pinge või voolu mõõtmine vastavalt vastava seadme skaalale.
Kell kaudsed mõõtmised meile huvipakkuv füüsikaline kogus määratakse vastava valemi järgi arvutamisega. Spetsiifiline valem sisaldab mitmeid parameetreid, mis määratakse otseste mõõtmiste abil.
Näiteks helitugevuse määramisel V silinder, peate mõõtma selle läbimõõtu D ja kõrgus H ja seejärel vastavalt valemile V = π HD 2 /4 arvutage helitugevus.
Mõned arvutusvalemis sisalduvad füüsikalised suurused jäävad muutumatuks (mõõtmise seadistusparameetrid, füüsikalised ja matemaatilised konstandid) ja mõned suurused x i mõõdetakse rea katsete käigus. Lisaks on üldiselt igas katses mõõdetud koguse väärtused x 1 , x 2 , …, x n võib olla erinev.
Seda seletatakse asjaoluga, et mis tahes suuruse mõõtmisel saame alati mitte selle suuruse tõelise, vaid ligikaudse väärtuse. Põhjus on seotud nii kasutatavate tööriistade ja seadmete mõõtmistäpsusega kui ka võimatusega võtta arvesse kõiki välised tegurid mis mõjutavad lõplikku mõõtmistulemust.
Isegi sama koguse korduv mõõtmine samadel tingimustel ja samu instrumente kasutades annab veidi erinevaid tulemusi. Seega tehakse kõik mõõtmised alati vigade või vigadega.
Mõõtmisviga (või viga) on antud mõõtetulemuse kõrvalekalle tõeline väärtus mõõdetud füüsikaline suurus.
Töö lõpp -
See teema kuulub:
ÜLDINE INFORMATSIOON
Füüsikaliste suuruste mõõtmisvead Mõõtmise all mõistetakse mõõdetud suuruse võrdlust ... Mõõtmisvigade klassifikatsioon ...
Kui vajate sellel teemal lisamaterjali või te ei leidnud seda, mida otsisite, soovitame kasutada otsingut meie tööde andmebaasis:
Mida teeme saadud materjaliga:
Kui see materjal osutus teile kasulikuks, saate selle sotsiaalvõrgustikes oma lehele salvestada:
| säutsuma |
Kõik selle jaotise teemad:
Töökäsk
1. Teostage kuulide aksiaalse paigalduse reguleerimine. Selleks keerake palli, mis asub ülal, nii, et pallide riskid oleksid samal tasemel. 2. Reguleerimine
Ballistiline pendel on silinder massiga M, alla
Töökäsk
1. Paigaldusel on märgitud kuuli ja pendli mass. 2. Mõõda joonlauaga kaugus l riputuspunktist keerme kinnituspunktini pendli külge. 3. Tooge pendel sisse
Töökäsk
1. Laske laual asuvast püstolist 5 lasku põrandal asuvasse liivakasti või paberilehte. Pärast iga lasku kuuli märgil liivas või linal,
Paigaldus- ja mõõtmismeetodi kirjeldus
Hooratas koosneb massiivsest kettast ja võllile paigaldatud rihmarattast. Võll on kinnitatud laagritesse. Rihmarattale keritakse niit (mõnede paigalduste puhul mängib rihmaratta rolli võll), vabale
Töökäsk
1. Reguleerige niidi pikkust nii, et raskus ei puudutaks statiivi alust. 2. Mõõtke nihikuga rihmaratta läbimõõt, määrake koormuse mass m. Salvestage tulemused
Paigaldus- ja mõõtmismeetodi kirjeldus
Paigaldusseade on näidatud joonisel fig. 1. Alus 1 on varustatud reguleeritavaga
Töökäsk
1. Kinnitage pendli kettale suvaliselt valitud rõngas. 2. Parandage pendli paigaldust, pöörates tähelepanu asjaolule, et selle telg on alusega paralleelne
JA HÕRDEJÕU MOMENTI MÄÄRAMINE
Töö eesmärgid: koostada hoorattale nurkiirenduse b sõltuvuse graafik tõmbejõu Mn momendist ja määrata selle järgi hõõrdejõu moment
Paigaldus- ja mõõtmismeetodi kirjeldus
Hooratas koosneb võllile paigaldatud kettast 1 ja rihmarattast 2 (joonis 1). Võll
Töökäsk
1. Mõõtke nihikuga rihmaratta läbimõõt D. 2. Hooratast keerates tõsta niidil rippuv koorem kõrgusele h. Mõõtke joonlauaga kõrgus (loendage alla vastavalt
Paigaldus- ja mõõtmismeetodi kirjeldus
Oberbecki pendel (joonis 1) on hooratas, mis on kinnitatud
Töökäsk
1. Määrake koormuste mass m1 ja m2 (võta m1 ligikaudu kaks korda rohkem kui m2). Määrake kõrgus h, millest alates
Paigaldus- ja mõõtmismeetodi kirjeldus
Elastsele keermele riputatud jäik keha tekitab väändevõnke, kui seda pööratakse vertikaaltelje suhtes teatud nurga all, mis langeb kokku vedrustuskeermega, ja
Töökäsk
1. Pöörates alumist ketast, viige süsteem võnkuvale liikumisele. Jälgi, et ketta massikese ei liiguks küljele, st liiguks vertikaalselt. Võnkumise amplituud
Paigaldus- ja mõõtmismeetodi kirjeldus
Töökäsk
1. Kinnitage tugiprisma varda otsa. Asetage pendel koos tugiprisma servaga alusele ja seadke see võnkuvale liikumisele nii, et võnkeamplituud ei ületaks ~ 6
Väliste jõudude mõjul kõik tahke deformeerunud, st muudab oma kuju ja mõõtmeid. Elastne deformatsioon on deformatsioon, mis kaob koos jõu lõppemisega. Jah, tihe
Diferentseerides funktsiooni (2) kaks korda aja suhtes, saame
a = − w2Acos(wt + a) = − w2x. (4) Pärast (4) asendamist (3) leiame w =
Töökäsk
ÜLESANNE № 1 Joon. 1 Töö eesmärk: kontrollida Hooke'i seadust. 1. Riputage vedru alumisse otsa erineva massiga m
Lühike teoreetiline teave
Enamik kaudseid meetodeid kiirenduse mõõtmiseks vabalangus g põhineb perioodi valemi kasutamisel harmoonilised vibratsioonid füüsiline pendel &nb
Paigaldus- ja mõõtmismeetodi kirjeldus
Veerg 2 on fikseeritud alusele 1 (joonis 1);
Töökäsk
1. Kinnitage üks raskus varda otsa ja teine varda keskosa lähedale. 2. Kinnitage prismad nii, et need oleksid vastamisi. Asetage üks neist vaba lähedale
Lühike teoreetiline teave
Kui venitate nööri ja ergutate selles vibratsioone, siis jooksevad mööda nööri lained, mis fikseeritud otstest peegeldudes ja üksteisega liites loovad keeruka vibratsioonimustri.
Paigaldamise kirjeldus
Keelte vibratsiooni ergutamiseks kasutatakse töös resonantsmeetodit. Nööri paneb liikuma magnetväljas voolu juhtivale juhile mõjuv jõud. püsimagnet lk
Töökäsk
1. Ühendage seade 220 V võrku Vajutage nuppu "NETWORK". 2. Laske elektroonilisel seadmel 1–2 minuti jooksul režiimi lülituda. 3. Määrake stringi pinge F =
Lühike teoreetiline teave
Vibratsiooni levimise protsessi elastses keskkonnas nimetatakse laineks. Kaugust, mille üle laine levib võnkeperioodiga võrdse aja jooksul, nimetatakse lainepikkuseks. Pikkus
Paigaldamise kirjeldus
Installatsiooni üldvaade on näidatud joonisel fig. 2. Mikrofon 2 on jäigalt kinnitatud metalltoru 1 otsa. Elektrodünaamiline g saab varda 3 abil mööda toru vabalt liikuda.
Töökäsk
1. Ühendage kõlar helisagedusgeneraatoriga ja mikrofon ostsilloskoobiga. Ühendage generaator ja ostsilloskoop võrku. Generaatori sageduskomplekti näide
Töökäsk
Aτ, deg
JUHUSLIKU VERA ARVUTAMINE KALKULAATORIS
Juhuslik viga mõjutab lõplikku mõõtmistulemust, kas hindab seda üle või alahindab. Seetõttu tuleb numbriteljel (vt lk 8) märkida intervall, milles
§ mehaaniliste vibratsioonide põhivalemid
Gaaside molekulaarkineetiline teooria põhivalemid
I. ligikaudsete arvutuste kohta
Põhivalemid
Põhivalemid
§ jõud mehaanikas
§ 10. Statistilise füüsika elemendid
§ 11. Termodünaamika füüsikalised alused
1. MÕÕTMISTE LIIGID. VIGADE KLASSIFIKATSIOON
Füüsiline kogus - See on füüsilise objekti (süsteemi, nähtuse või protsessi) ühe omaduse tunnus. Kvalitatiivselt võib samal füüsikalisel suurusel olla erinev kvantitatiivne väljend. Konkreetsele materiaalsele objektile omase füüsikalise suuruse kvantitatiivset kindlust iseloomustab selle suurus. Füüsikalise suuruse väärtus on selle suuruse hinnang selle jaoks aktsepteeritud teatud arvu ühikute kujul. Füüsikalise suuruse väärtust väljendatakse selle arvväärtuse korrutisena selle suuruse jaoks valitud ühikuga. Arvväärtus on abstraktne arv. Füüsikalise suuruse ühik on füüsikaline suurus, millele on tavapäraselt omistatud arvväärtus, mis võrdub 1-ga.
Prime p: pikkuse väärtust saab väljendada kui L = 0,202 m = 20,2 cm = 202 mm. Järelikult muutub füüsikalise suuruse arvväärtus koos ühiku suuruse muutumisega. Väärtuse suurus ja väärtus on samad.
Eristama tõsi füüsikalise suuruse väärtus, mis ideaalis peegeldab materiaalse objekti omadusi, ja tõeline - katseliselt leitud väärtus.
Füüsikalise suuruse h mõõtmine See seisneb mõõdetud suuruse võrdlemises selle ühikuga, et saada selle suuruse väärtus kasutamiseks kõige mugavamal kujul. Mõõtmine toimub tehniliste vahenditega, mis salvestavad ühikut või reprodutseerivad füüsilise suuruse skaalat.
Seda mõistet ei tohiks samastada mõõtmine kontseptsiooniga vaatlus mõõtmise ajal - aastal teostatud katseoperatsioon protsessi mõõdud. Vaatluse tulemuseks on üks väärtus ( tagasiarvestus) mõõdetud väärtus. Mõõtmistulemus saadakse pärast kõigi näitude matemaatilist töötlemist.
Mõõtmine üksikute vaatlustega nimetatakse mõõtmist, mille käigus iga näit saadakse mõõdetud kogusega seotud füüsikaliste suuruste erinevatel väärtustel.
Näide: erineva massiga kehade kiirenduse mõõtmine neile mõjuva fikseeritud jõu toimel.
Mõõtmine mitme vaatlusega kutsutakse mõõtmine, mille käigus kõik näidud saadakse mõõdetud kogusega seotud füüsikaliste suuruste fikseeritud väärtustel.
Näide: antud massiga keha kiirenduse mõõtmine sama jõu mõjul katse korduval kordamisel.
Mõõtmisi on kahte peamist tüüpi: sirge Ja kaudne.
Otsene mõõtmine nimetatakse füüsikalise suuruse mõõtmiseks, mille puhul selle väärtus leitakse otse katseandmetest.
Näited: pikkuse mõõtmine joonlauaga; oomi takistuse mõõtmine
Kaudse mõõtmise teel nimetatakse füüsikalise suuruse mõõtmiseks, mille puhul selle väärtus leitakse teadaoleva seose põhjal selle suuruse ja suuruste vahel, mille väärtused saadakse otsemõõtmiste teel.
Prime p: takistuse määramine pinge ja voolu järgi, mõõdetuna vastavalt voltmeetri ja ampermeetriga.
liigend nimetatakse selliseid mõõtmisi, mille puhul mõõdetakse samaaegselt kahte või enamat ebahomogeenset suurust, et leida nendevaheline seos või määrata selle seose parameetrid.
Näide: voolu mõõtmine erinevatel pingetel, et kontrollida Ohmi seadust.
Mõõteobjekti mudel nimetatakse reaalse objekti abstraktseks, tavaliselt idealiseeritud kujutiseks.
Näited: materiaalne punkt, absoluutselt jäik keha, ideaalne gaas, homogeenne juht.
Mõõtmismeetod on meetodite kogum mõõdetud suuruse võrdlemiseks selle ühikuga. Mõõtmismeetod viiakse läbi vastavalt mõõteobjekti mudelile ja olemasolevatele tehniliste vahendite komplektile.
Tõeline mõõtmisviga on füüsikalise suuruse (tegeliku väärtuse) mõõtmistulemuse kõrvalekalle selle tegelikust väärtusest. Mõõtmiste tegemisel ei ole reeglina mõõdetud suuruse tegelik väärtus teada. Mõõtmistulemus on hinne tegelik väärtus, mis enamasti sellega ei kattu. Olenemata sellest, kas tegelik väärtus on teada või teadmata, on aktsepteeritud iseloomustada viga nn usaldusvahemik, mis sisaldab tõelist väärtust teatud kindlusega. Selle intervalli keskpunkt langeb kokku tegeliku väärtuse hinnanguga (joonis 1).
Viga väljendatakse järgmiselt absoluutne Ja sugulane vead.
Absoluutne viga võrdne hinnangu ja intervalli piiri erinevuse mooduliga , need. pool laiust usaldusvahemikust.
Suhteline viga on võrdne absoluutvea ja tegeliku väärtuse hinnangu suhtega. Reeglina väljendatakse seda viga protsentides. Nimetatakse suhtelise vea pöördarvu täpsus mõõdud.
Joonis 1. Mõõtmise tulemus x=(±?x). Näiteks F=(53,2±0,3) H.
Sama füüsikalise suuruse mõõtmistulemuste võrdlemisel toimi järgmiselt. Kui usaldusvahemikud kattuvad, ütleme, et erinevused tähtsusetu ja mõõtmistulemused on ühtsed. Vastasel juhul võetakse erinevused arvesse tähendusrikas ja mõõtmistulemused ei ühti.
Näide: lase kell erinevaid meetodeid sama jõu mõõtmisel saadi järgmised tulemused: F=240±8 N, F=250±5 N. Erinevus 10 N on antud juhul ebaoluline ja tulemused on ühtsed. Kui mõlemad tulemused oleksid F=242±2 N, F=249±3 N, siis oleks erinevus 7 N märkimisväärne ja mõõtmistulemused ei ühtiks.
Mõõtmistulemuste mõju järgi võib eristada järgmisi veaklasse:
Süstemaatiline viga - viga, mis jääb konstantseks või muutub mõõtmiste kordamisel regulaarselt.
juhuslik viga on viga, mis muutub mõõtmiste kordamisel juhuslikult.
igatsema (eksimine ) - viga, mis ületab oluliselt
Metoodiline viga - mõõtmismeetodi ebatäiuslikkusest tingitud viga.
Instrumentaalne viga - mõõteriistade (instrumentide) viga.
Täiendav viga - viga, mis on tingitud tegurite mõjust, mida mõõteobjekti mudelis arvesse ei võeta.
Süstemaatilise vea arvestamine ja välistamine (või vähendamine) on üks raskemaid probleeme mõõtmisteoorias. Selle probleemi lahendamise meetodid sõltuvad teatud tüüpi mõõtmistest ja selle lahendamiseks puudub üldine metoodika. Sageli kasutatakse terviklikku lähenemist teoreetiline analüüs mõõtmisprotseduurid ja kasutatavate seadmete omadused. Selline analüüs võib anda hinnangu süstemaatilise vea piiridele. Täpsete mõõtmiste korral hinnatakse süstemaatiline viga soovitud väärtuse mõõtmise tulemuste põhjal erinevate, põhimõtteliselt sõltumatute meetoditega, kasutades erinevaid seadmeid. Palju kaasaegseid viise süstemaatilise vea analüüs aparaadi abil matemaatiline statistika(dispersioon, regressioon, korrelatsioon, spektraalanalüüs), otsustusteooria, mänguteooria jne. Neid küsimusi käsitletakse üksikasjalikumalt metroloogia erikursusel.
Juhuslikku viga saab enamikul juhtudel vähendada mõõtmistulemuste suhteliselt lihtsa statistilise töötlemisega.
Puudused viitavad anomaalsetele mõõtmistulemustele, mis võivad tuleneda mõne segava teguri lühiajalisest mõjust mõõtmisprotsessile, mis domineerib teiste üle. Libisemise põhjuseks võib olla operaatori viga mõõtmisel või mõõteseadme rike. Sellistel juhtudel tuleb ebanormaalne tulemus kõrvale jätta. Anomaalsete andmete tagasilükkamine on aga vastuoluline teema, milles ekspertidel pole üksmeelt. Näiteks ajaloost
Füüsikud teavad, et suurte avastusteni viisid just eksperimendi anomaalsed tulemused. Seetõttu, millal teaduslikud uuringud ja enamiku tehniliste mõõtmiste puhul on vaja hoolikalt analüüsida libisemise põhjust, eelkõige katset korduvalt korrates. Küll aga hästi uuritud olukorras, kui ei leia väline põhjus preili, anomaalse loenduse kõrvalejätmise küsimus tuleks lahendada kõigi katseandmete töötlemise põhjal.
Mõõtmiste ajal füüsilise töökoja laboris korraldatakse katse nii, et:
1. Metoodiline viga võib tähelepanuta jätta või selle väärtust hinnata.
2. Instrumentaalveal on ainult süstemaatiline komponent.
3. Lisaveal on ainult juhuslik komponent.
4. Mõõteseadmete ja instrumentide näitude täpsus on tagatud.
2. OTSETE MÕÕTMISTE TÖÖTLEMINE
2.1. Instrumentaalne viga
Seadme vea tuvastamise meetod on toodud selle passis. Enamiku seadmete iseloomustamiseks kasutatakse sageli seda mõistet. vähendatud viga, võrdne absoluutveaga protsentides mõõteskaala vahemikust. Vastavalt antud veale on seadmed jagatud täpsusklassidesse. Täpsusklass on näidatud armatuurlaual ja võib võtta järgmisi väärtusi:
0.05; 0.1; 0.2; 0.5 - täpsus; 1,0; 1,5; 2,5; 4.0 - tehnilised seadmed.
Suurim absoluutne instrumentaalviga
A=K A/100, (1)
Kus K on täpsusklass, on A kõrgeim väärtus instrumendi skaala.
Valemist (1) järeldub, et suhteline viga on minimaalne, kui mõõdetud väärtus viib indikaatori noole täisskaalale. Seetõttu valitakse instrumendi optimaalseks kasutamiseks selle piirang nii, et mõõdetud väärtuse väärtus langes skaala lõppu.
Metroloogias kasutatakse lisaks valemile (1) muid, keerukamaid instrumentaalvea ja sellega seotud täpsusklassi määratlusi, eriti ebaühtlase mõõtkavaga instrumentide puhul.
Lineaarsete mõõtmete mõõtmise instrumentide instrumentaalne viga on näidatud instrumendil endal absoluutvea või jagamise väärtusena. Kui seadmel pole märgitud ei täpsusklassi ega absoluutset viga, siis võetakse see võrdseks poole väikseima jaotuse hinnast.
Mõõdetud väärtuste digitaalse näiduga seadmete puhul on vea arvutamise meetod antud seadme passiandmetes. Kui need andmed pole saadaval, võetakse absoluutveaks väärtus, mis võrdub poolega indikaatori viimasest digitaalsest numbrist.
Instrumentaalset viga ei saa vähendada
näitude statistiline töötlemine.
Erinevate instrumentide skaalade lugemise näited on näidatud joonisel fig. 2-7.
Vernieri seadme põhimõtet käsitletakse 5. lisas.
2.2. juhuslik viga
Juhuslike vigade olemasolul hajuvad mõõdetud suuruse mitmel mõõtmisel täheldatud väärtused selle tegeliku väärtuse suhtes juhuslikult hajutatud. Sel juhul leitakse tegelik väärtus näitude seeriast kõige tõenäolisemana ja viga iseloomustatakse intervalli laiusega, mis katab tegeliku väärtuse antud tõenäosusega. Järgmiste sätete matemaatiline põhjendus on esitatud punktides 6, 7 ja 8 ning kirjanduses, seoses füüsika praktilise töögakirjanduses.
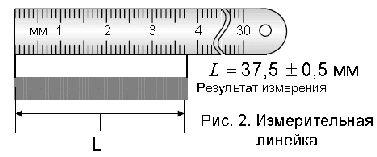
Riis. 3. nihik.
Riis. 7. Digitaalne oommeeter.
Koguse tegeliku väärtuse parim hinnang X on
proovi keskmine
,
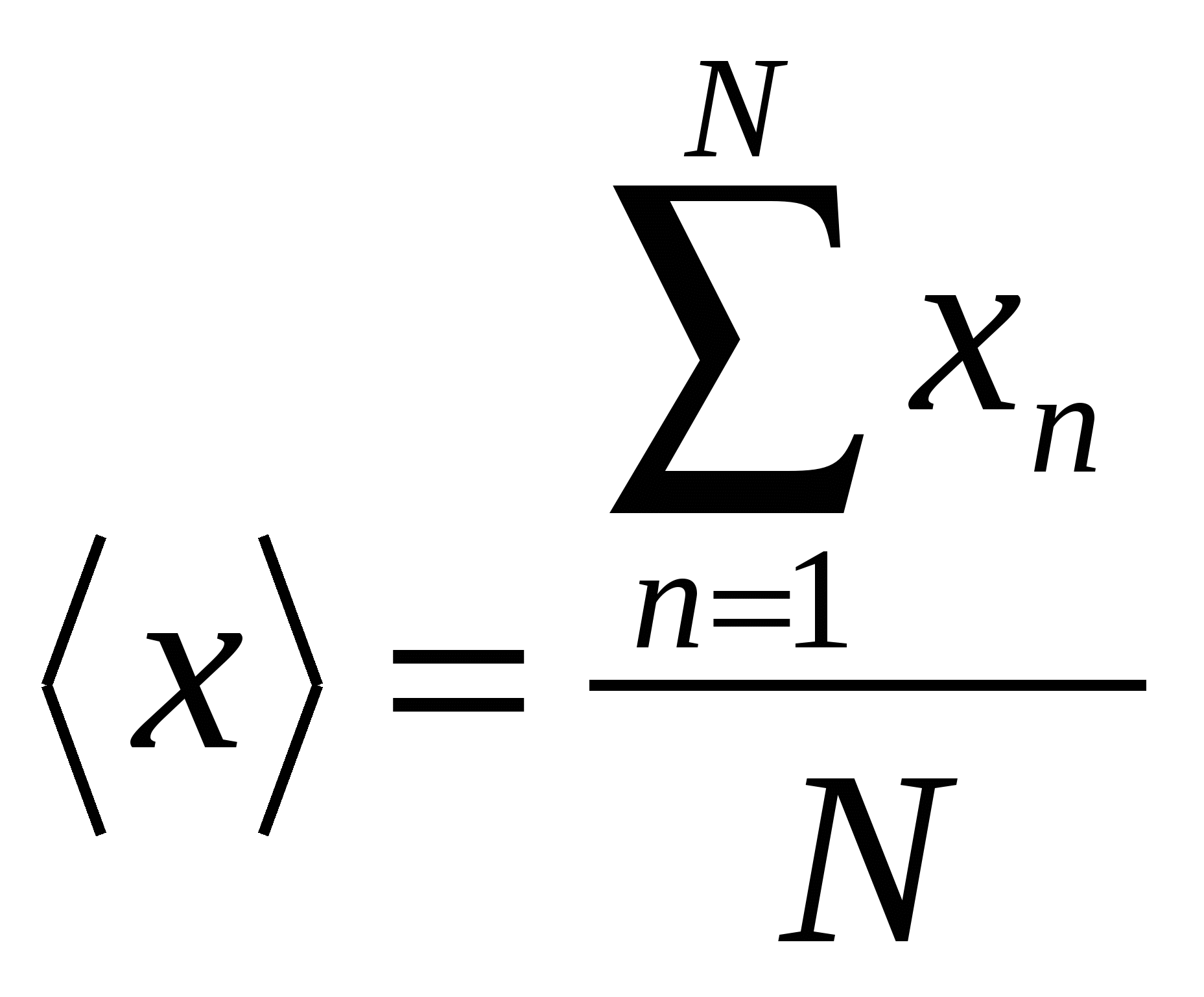(2)
Kus x n- väärtuse näit X, N on näitude arv.
Mõõtmise ajal näitude hajumise hindamiseks kasutame
proovide standardhälve
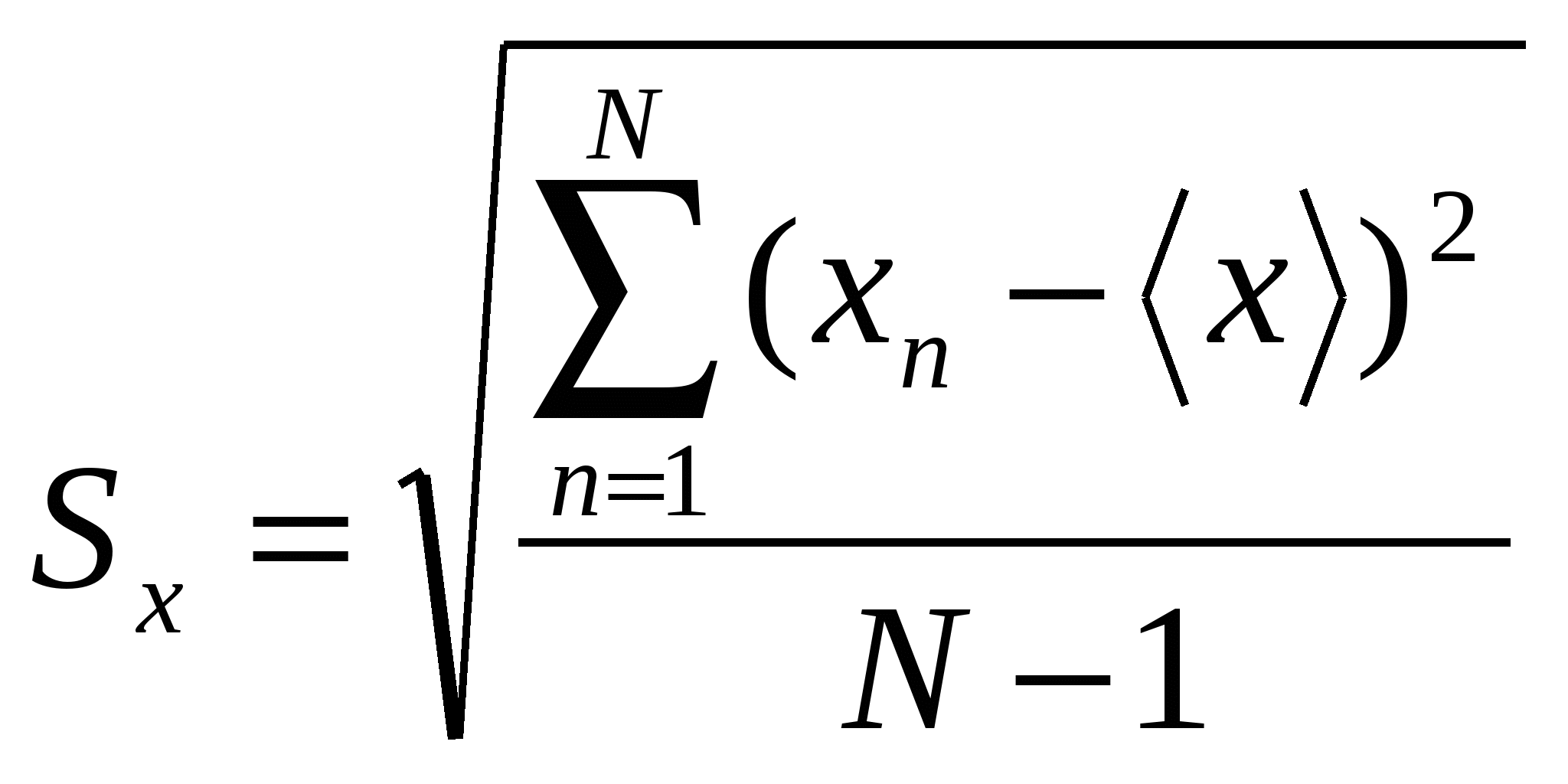, (3)
Valimi keskmine on juhuslik suurus ja selle levikut mõõdetud väärtuse tegeliku väärtuse suhtes hinnatakse
valimi keskmise standardhälve
.
(4)
Keskmise standardhälveNnäidud V 
korda väiksem kui ühe näidu standardhälve
Usaldusvahemik nimetatakse intervalliks
Mis teatud kindlusastmega sisaldab mõõdetud väärtuse tegelikku väärtust (joonis 1).
Usalduse tõenäosus(usaldusväärsus) Vaatluste seeria tulemust nimetatakse tõenäosuseks?, millega usaldusvahemik sisaldab mõõdetud suuruse tegelikku väärtust.
Vea juhuslikku komponenti väljendatakse tavaliselt usaldusvahemiku poollaiuses. Usaldusvahemiku suurus esitatakse tavaliselt kordsena 
väärtused. Siis
mitme mõõtmise vea juhuslik komponent
, (5)
Kus
- mõõtmeteta usalduskoefitsient(õpilaste koefitsient).
Usalduse suhe näitab, mitu korda on vaja suurendada keskmise standardhälvet, et saada nende tulemuse antud usaldusväärsus antud arvu mõõtmistega. Usaldusfaktor sõltub kompleksselt mõõtmiste usaldusväärsusest ja arvust ning selle väärtus määratakse statistilistest tabelitest (lisa 1).
Juhuslike vigade arvutamisel antakse need mõõtmiste usaldusväärsusega, mis (olenevalt mõõtmise eesmärkidest ja neile esitatavatest nõuetest) on 0,9; 0,95; 0,96; 0,98; 0,99; 0,997; 0,999.
Mida kõrgem on usaldustase, seda usaldusväärsem
intervalli hinnang ja samal ajal selle piirist laiem.
totaalne viga 
otsesed mõõtmised on võrdne selle komponentide ruutsummaga: instrumentaalne - 
ja juhuslik -
, (6)
2.3. Preilid
Soovitatav on alustada otseste mõõtmiste töötlemist, kontrollides näitude puudumist. Kriteeriume möödalaskmiste tuvastamiseks ja kõrvaldamiseks on palju, kuid ükski neist pole universaalne. Kriteeriumi valik oleneb mõõtmiste eesmärgist, kuid otsus mõnest andmetest loobuda on lõppkokkuvõttes alati subjektiivne.
Sõnastame nn Chauvenet' kriteerium . Saadud N proovi sisaldavatest seeriatest valitakse anomaalne proov - x k ja selle keskmisest väärtusest kõrvalekalde moodul arvutatakse proovi standardhälbe murdosades:
, (7)
Seejärel arvutatakse selle kõrvalekalde tõenäosus ja eeldatav mõõtmiste arv n, mis annab näidud hälbega Z, mis ei ole väiksem kui katsealusel. Kui kätte saadakse n
Kui M>N, siis valim x k loetakse möödalaskeks. M ja Z seos on toodud lisas 3.
Algoritm otsemõõtmiste töötlemiseks
1. Määrake instrumentaalne viga.
2. Arvutage mõõtmiste seeria keskmine väärtus - valem (2)
3. Arvutage näidu standardhälve - valem (3)
Kui möödalask on parandatud, minge 5. juurde;
muidu kuni 4.
4. Kontrollige näitude puudumist:
vali ebanormaalne näit;
arvutada selle suhteline hälve - valem (7)
määrata eeldatav näitude arv, mille hulgas
see arv on suurem kui loenduste arv,
minge 2 juurde; muidu mine 5. juurde.
5. Arvutage näidise keskmine ruut
keskväärtuse hälve - valem (4)
6. Määrake antud usaldustegur
töökindlus ja saadud näitude arv - Lisa 1
7. Arvuta juhuslik viga - valem (5)
8. Arvuta kogu viga – valem (6)
9. Pärast ümardamist tuleks töötlemismõõtmiste tulemus kirjutada kujul:
; 
; ?
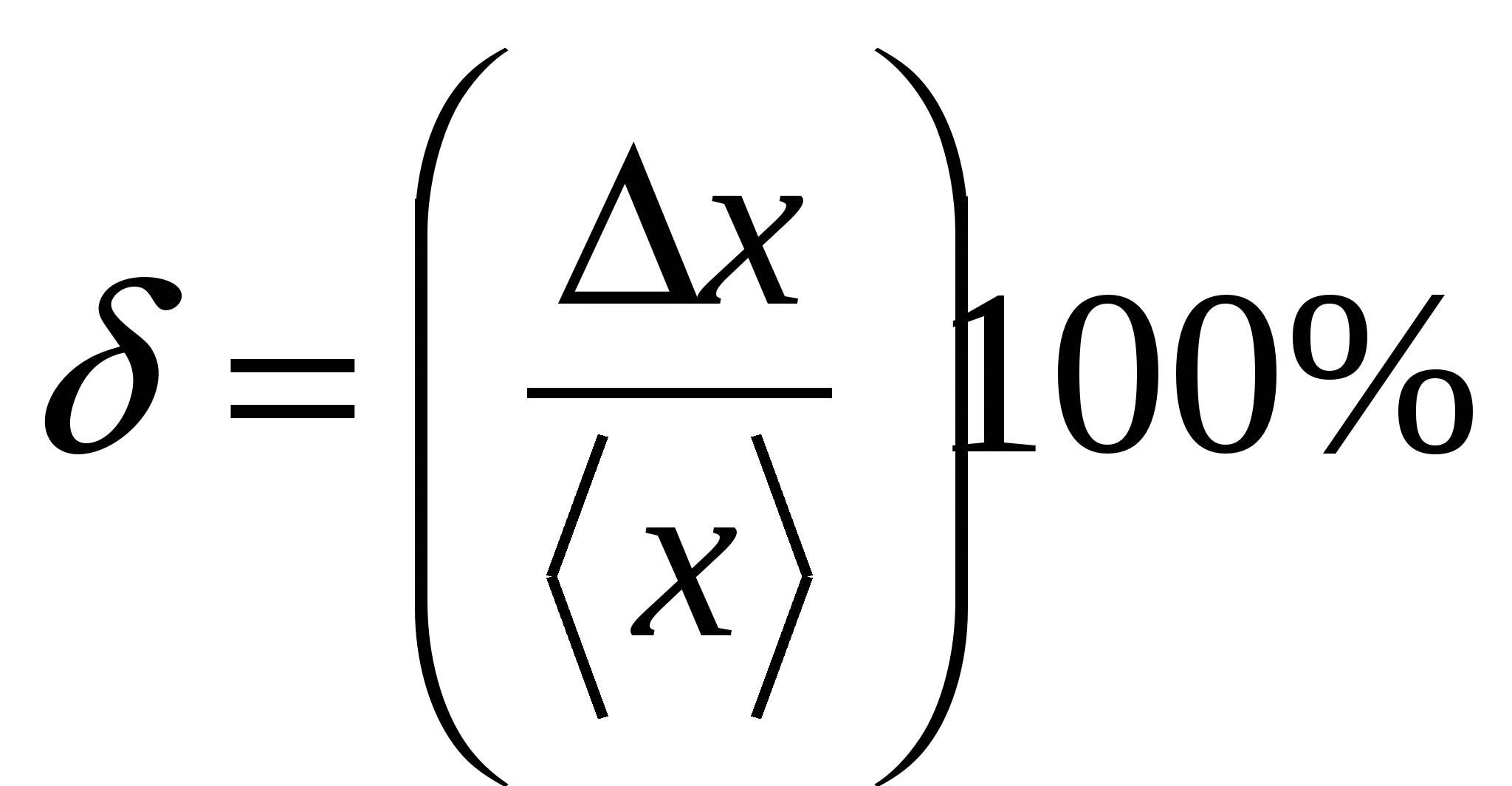Mõnikord on vaja kombineerida sama füüsikalise suuruse mitme otsemõõtmise seeria tulemusi. Seda probleemi saab lahendada järgmisel viisil. Las tulemused M mõõdud on toodud vormil 
, 
, … , 
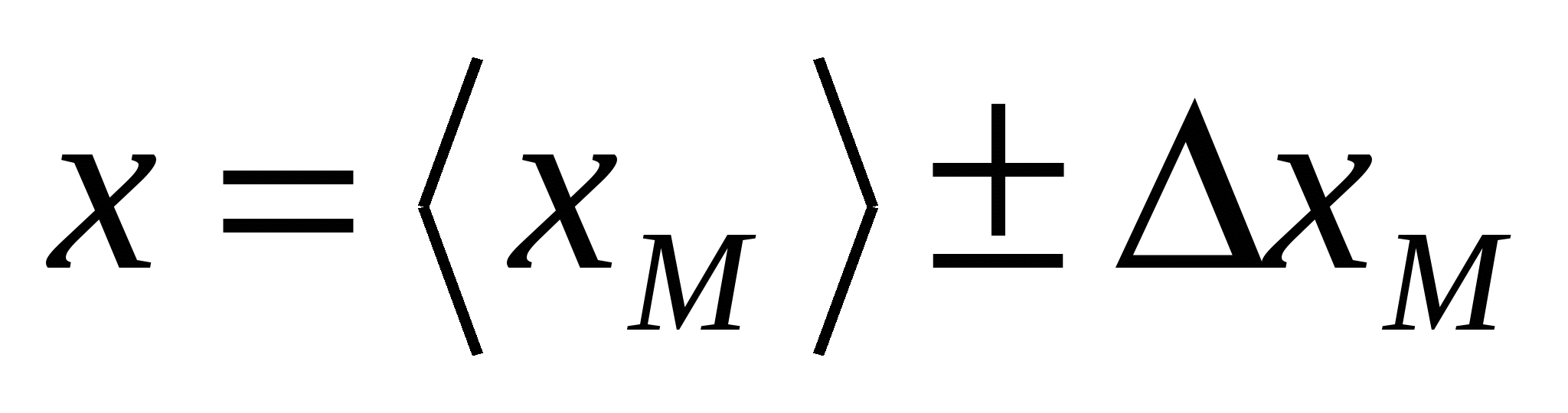. parim hind 
Ja selle viga ∆ x ja selle viga arvutatakse valemitega:
, 
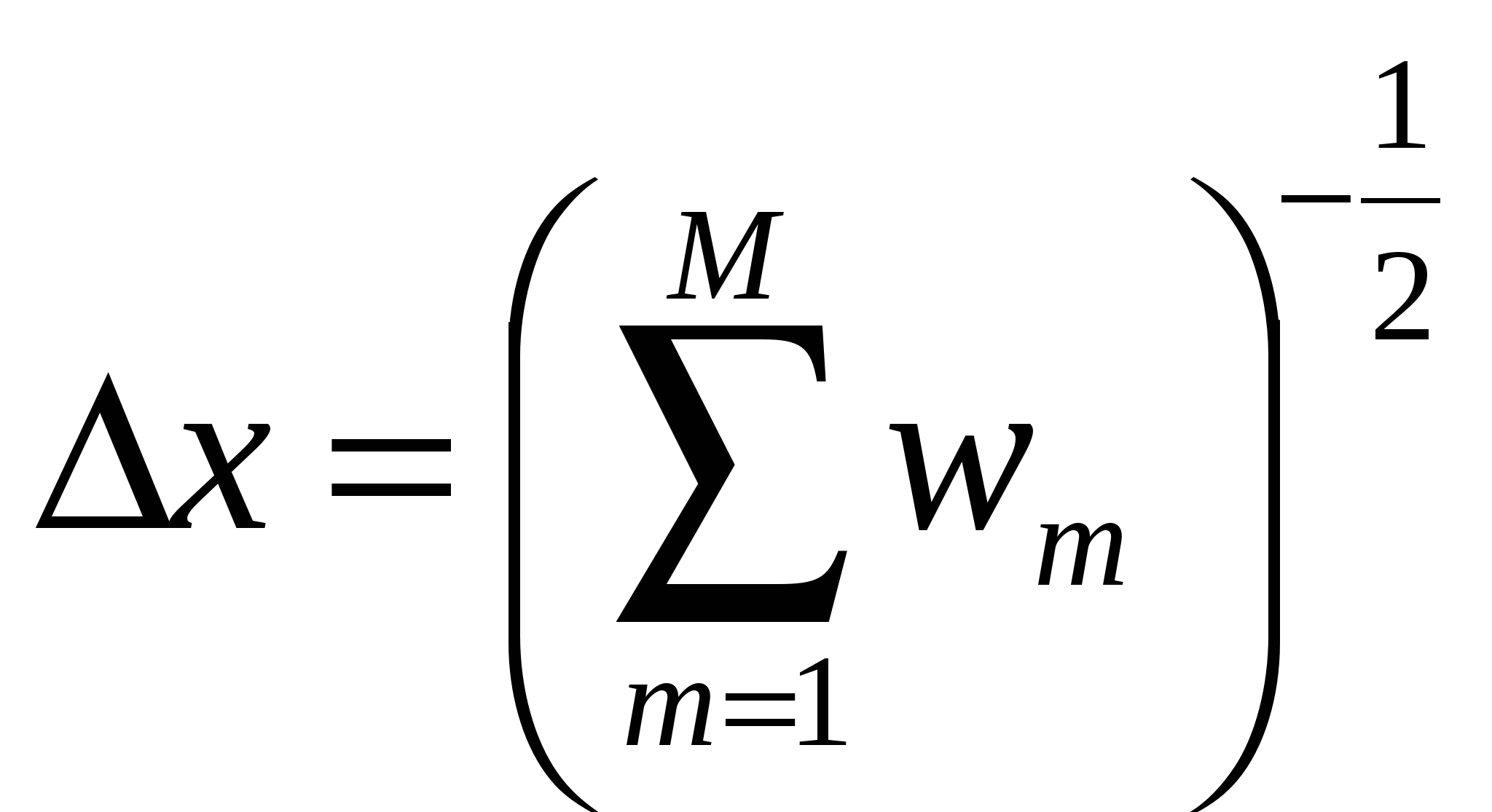, (8)
-
Kus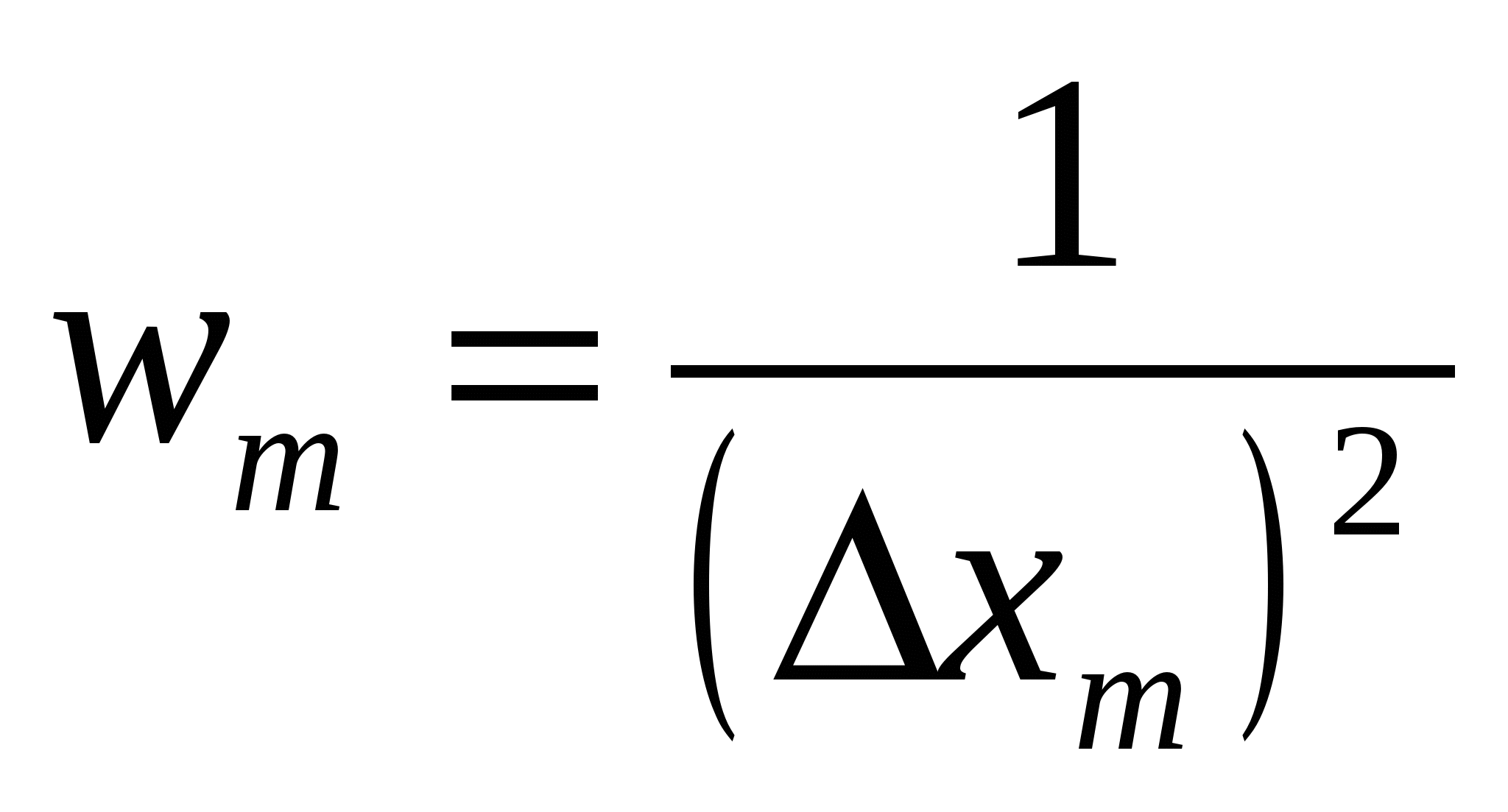 
- iga mõõtmiste seeria statistiline kaal.
3. KAUDSTE MÕÕTMISTE TÖÖTLEMINE
Laske u = f(x, y,…)- funktsionaalne seos mõõdetud väärtuse vahel u ja kogused x, y,... , mille väärtused leitakse otsemõõtmise teel. Tegelik väärtus 
defineeritud kui:
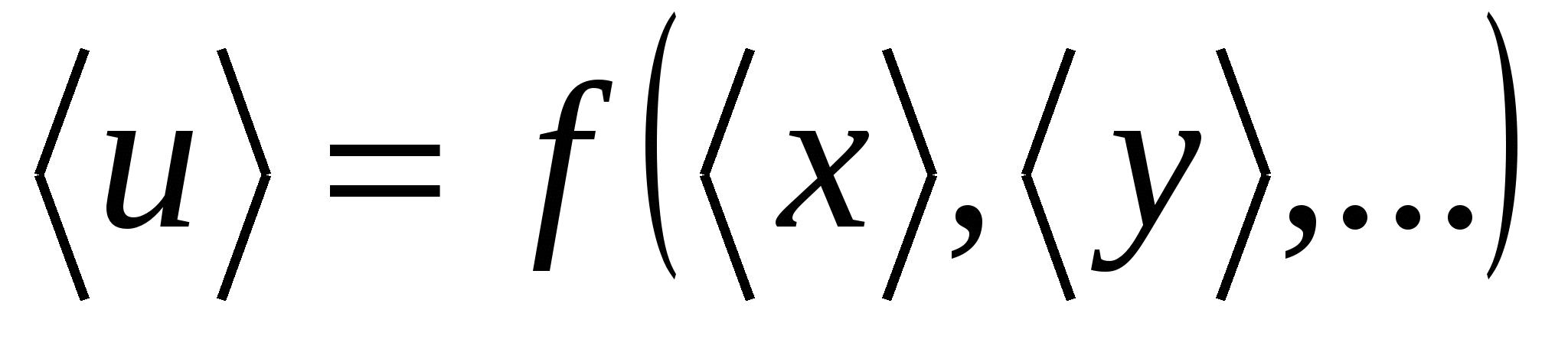. (9)
Saame vea ∆ avaldise u. Kui fikseerite näiteks kõigi argumentide väärtused, välja arvatud ühe x, siis on funktsiooni juurdekasv selle argumendi muutumisel kujul:
Kui ∆ väärtus x väike, siis intervalliga [ 
, 
] funktsiooni u=f(x) võib pidada lineaarseks ja
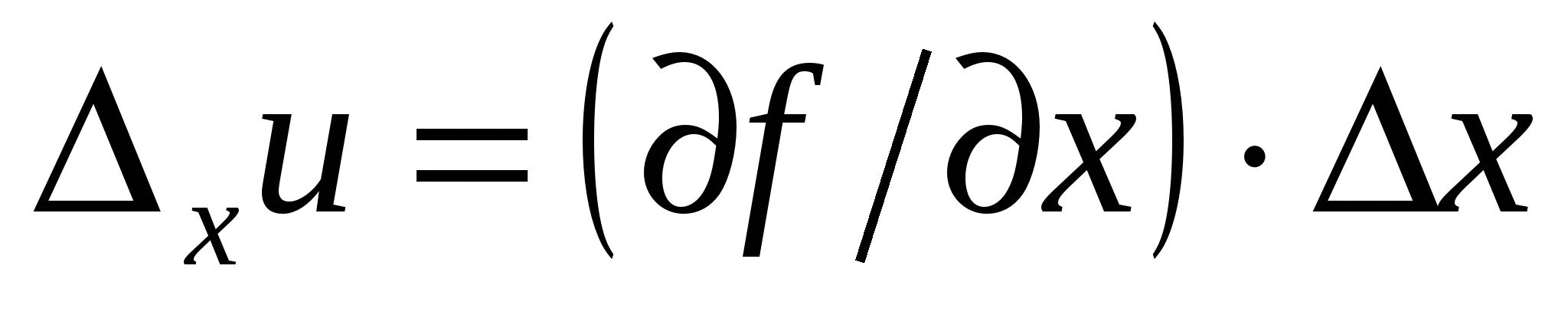. (11)
∆x väärtus u iseloomustab viga ∆ u, vea tõttu ∆ x. Veakomponendid ∆ määratakse sarnaselt u, mis on toodud teiste argumentidega. Kogu viga ∆ u kaudsed mõõtmised u arvutatakse iga argumendi poolt kaasatud komponentide ruutliitmise või moodulliitmise abil:
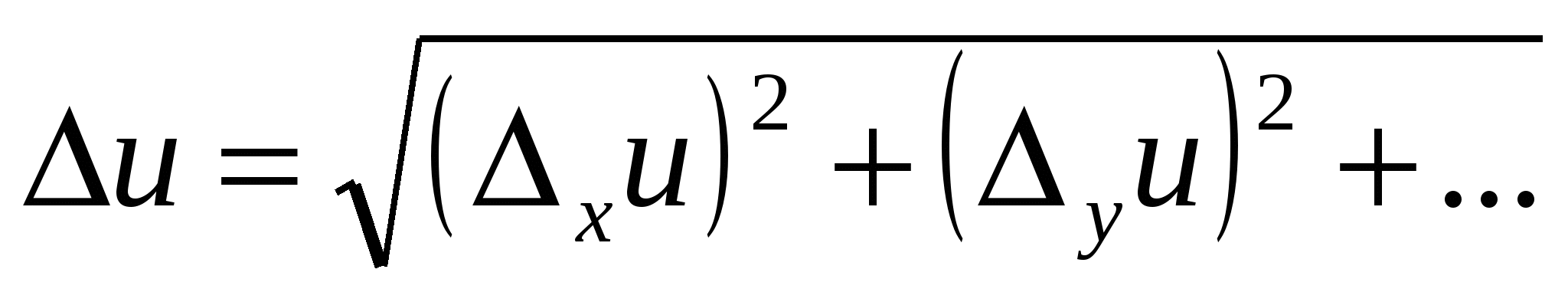. (12)
. (13)
Suhet (12) rakendatakse, kui on täidetud kaks tingimust. Esiteks on argumentide viga tingitud paljude tegurite mõjust, mille hulgas ei ole ühtegi domineerivat tegurit. Teiseks ei ole argumentide vead statistiliselt seotud. Muudel juhtudel kasutatakse seost (13). Summeerimisreegel (13) viib aga sageli kaudsete mõõtmiste vea ülehinnatud väärtuseni. Lisateavet vigade summeerimise kohta leiate jaotisest 8.
Näide. Olgu takistuse väärtus alalisvooluahela sektsioonis määratud selle lõigu voolu ja pinge otsemõõtmiste tulemuste põhjal. Kui voolu ja pinge mõõtmise viga on tingitud paljude tegurite mõjust (temperatuur, ampermeetri ja voltmeetri sisetakistused, elektrimüra, toiteallika ebastabiilsus jne), siis on vigade summeerimisel parem kasutada valemit (12). Kui otsemõõtmiste viga on peamiselt tingitud toiteallika sisetakistuse juhuslikust muutusest, siis on parem rakendada valemit (13).
Seosed (9-12) võimaldavad kasutada kaudsete mõõtmiste töötlemiseks kahte algoritmi. Ühes neist on vaja leida osatuletistele analüütilised avaldised, teises kasutatakse ainult numbrilisi meetodeid. Lisa 3 sisaldab valemeid vea esmaseks arvutamiseks mõnede praktikas sageli esinevate funktsionaalsete seoste jaoks.
Algoritm kaudsete mõõtmiste töötlemiseks
Vastavalt mõõdetava suuruse teadaolevale sõltuvusele
kasutades otsemõõtmisi, arvuta
funktsiooni tegelik väärtus - valem (9)
Arvutage veakomponendid kui
või
leida osatuletised kõigi argumentide suhtes
ja arvutage vea komponendid - valem (11)
Arvutage funktsiooni koguviga - valem (12)
Pärast ümardamist töötlemismõõtmiste tulemus
; 
; ?
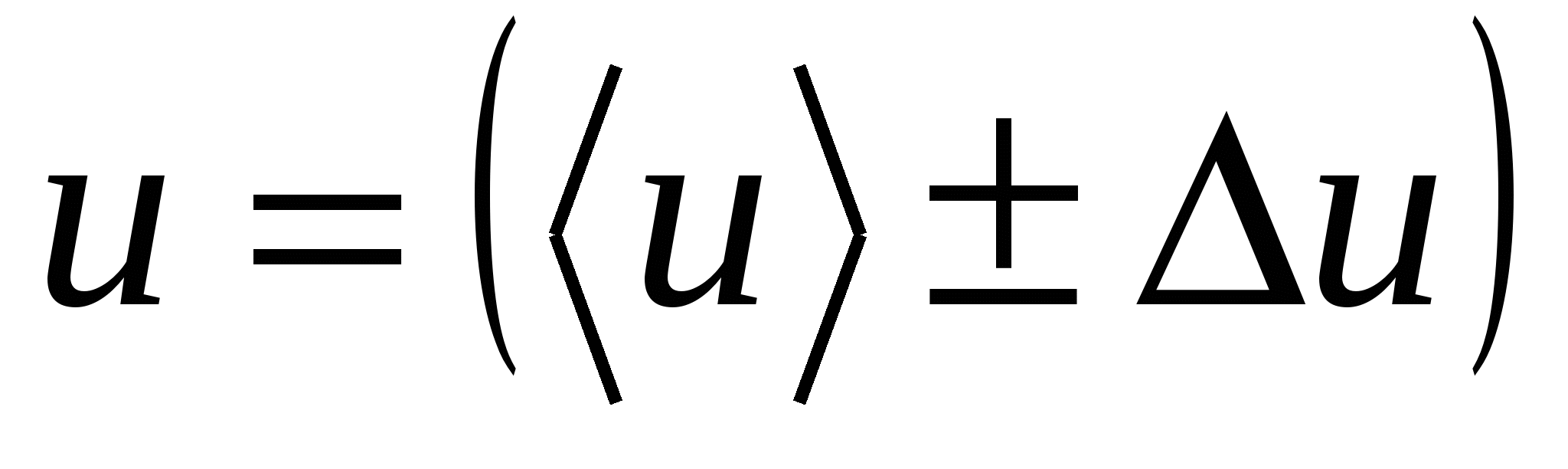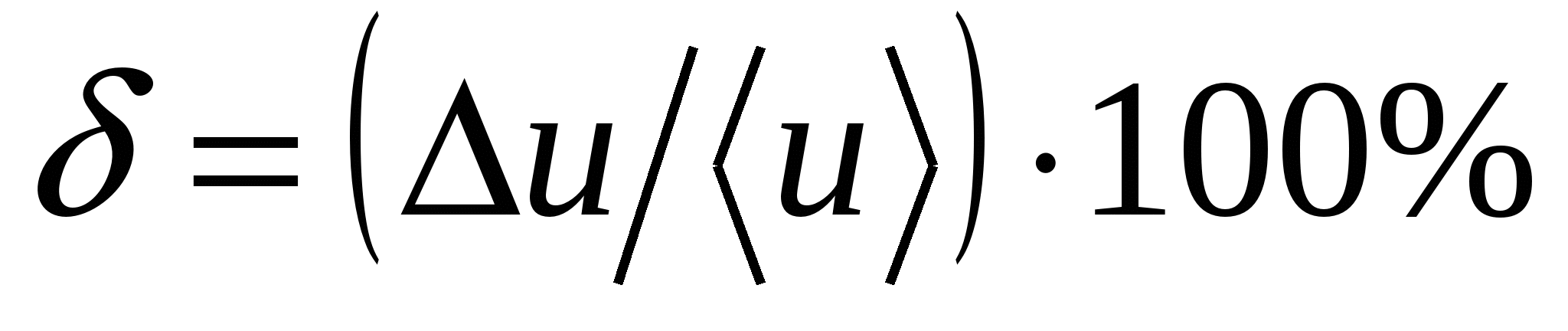Sageli mõõdetav kogus lk on funktsionaalse sõltuvuse parameeter y=f(x,p) kogused x Ja y, mis leitakse üksikute vaatlustega tehtud otsemõõtmiste seeria tulemusena. Sel juhul kaudsete mõõtmiste vea juhuslik komponent 
määratakse töötlemise teel arvutatud väärtused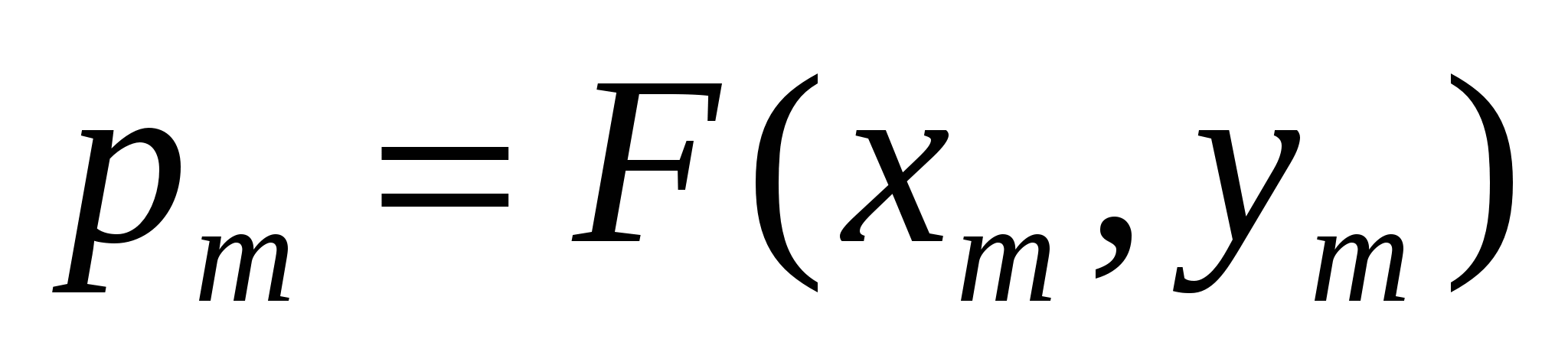 
vastavalt töötlemismeetodile otsesed mõõtmised(Siin m=1..M, kus M on väärtuste üksikute vaatluste arv
x Ja y).
Funktsiooni kaudsete mõõtmiste viga reeglina rohkem viga selle argumentide otsesed mõõtmised. Kuid teatud juhtudel võidakse seda reeglit rikkuda. Vaatleme sellist erijuhtumit võnkeperioodi mõõtmise näitel.
Näide. Laske kl otsene mõõtmine võnkeperiood, kasutades stopperit, sai väärtuseks T=2,0±0,2 s. Sama stopperiga saab perioodi mõõta kaudselt, fikseerides aja t=200±0,2 s, mille jooksul toimus N=100 võnkumist. Siis periood T=t/N, s.o. T=2,000±0,002 s. On vale väita, et sel juhul on kogu mõõtmisviga väiksem kui instrumentaalne viga, kuna me räägime mõõtmisest erinevad suurused, nimelt: aja otsene mõõtmine ja perioodi kaudne mõõtmine. Viimast tüüpi mõõtmine ei ole otseselt seotud instrumentaalveaga.
4. LIIKESE ARVU ÜMARDAMINE.
tähtsusetu eesmised nullid on arvu numbrid kümnendmurrud, väiksem kui 1 ja nullid arvu lõpus, asendades pärast ümardamist kõrvale jäetud numbrid. Ülejäänud numbritele helistatakse tähendusrikas.
Kahtlane näitaja mõõtetulemus on number selles numbris, mis vastab kõige olulisemale numbrile koos veaväärtuse olulise numbriga. Kutsutakse kahtlasest numbrist vasakul olevaid numbreid ustav, ja paremal - truudusetu.
Näited.
Arvud 536±6; 0,00234±0,00002; 1,00±0,03; 2000±30 sisaldab kolme olulist numbrit. Arvu 299793±1 ümardamisel väärtuseni 3·10 5 lubati viga 207, mistõttu on saadud arvus sajad kahtlane arv ja seetõttu on kaks viimast nulli tähtsusetud.
Viga väljendatakse tavaliselt ühes olulises numbris ja ainult eriti kriitilistes mõõtmistes - kahes.
Ümardamisviga ja tegelik väärtus .
Viga ümardatuna ühe olulise numbrini. See näitaja on kaheldav. veaväärtusel pole õigeid numbreid .
Tegelik väärtus ümardatakse lähima numbrini, mille number on võrdne vea olulise numbri numbriga. Tegeliku väärtuse viimane number on kahtlane, ülejäänud numbrid on õiged.
Eriti täpsete mõõtmiste korral ümardatakse viga kahe olulise numbrini, kui esimene neist on väiksem kui 4, ja ühe numbrini, kui esimene number on suurem kui 3. Mõnikord jäetakse teiseks numbriks 0 või 5.
Salvestusnumbrid loetakse instrumendi skaalalt .
Seadme skaalalt loetud mõõdetud väärtuse arvväärtuses on kirjas vaid õiged numbrid ja kahtlane arv, mille numbri määrab seadme instrumentaalvea väärtus.
Numbrite ümardamine.
Täisarvude lisanumbrid asendatakse nullidega ja kümnendmurrud jäetakse kõrvale. Kui kõige olulisem nulliga asendatav või ära jäetav number on väiksem kui 5, siis ülejäänud numbreid ei muudeta. Kui määratud number on suurem kui 5, siis viimast allesjäänud numbrit suurendatakse 1 võrra. Kui nulliga asendatav või ära jäetav number on 5, siis ümardatakse järgmiselt: viimane number jääb ümardatud arvus muutumatuks, kui see on paaris, ja suureneb 1 võrra, kui see on paaritu.
Ümardamine arvutustes.
Vahearvutuste tulemuste salvestamisel salvestatakse üks varunumber - kahtlasest paremal olev number. Ligikaudsete arvude liitmisel ja lahutamisel langeb tulemuse kahtlase numbri number kokku terminite kahtlaste numbrite suurimaga. Korrutamise ja jagamise tulemus sisaldab nii palju tähenduslikke numbreid, kui on algandmetes, kus on kõige vähem olulisi numbreid. Kui tõstetakse võimule
(juure eraldamine) ligikaudsest arvust, peaks tulemuses olema nii palju olulisi numbreid, kui palju on aluses (radikaalavaldis). Logaritmi võtmisel salvestab mantiss nii palju olulisi numbreid, kui on algses numbris. Kui üks operanditest on täpne arv, siis selle numbrite arv ei mõjuta tehte tulemuse ümardamist. Kui arvutustes kasutatakse tabeliandmeid, on kõik nende numbrid õiged.
Ruutsummeerimine
Kui ruutliitmisel on üks arv teisest 3 või enam korda väiksem, võib selle tähelepanuta jätta.
Toome näiteid mõõtmistulemuste ümardamisest.
| Salvestage enne ümardamist | Salvestage pärast ümardamist |
| 123357±678 A/m. | 123400±700 A/m. |
| 123357±678 V. | 123,4±0,7 kV. |
| 237,46±0,13 mm | 237,5±0,1 mm. |
| 0,00283±0,00034 kg. | (2,8±0,3)10-3 kg. |
| 1,045±0,000003 s. | 1,045000±0,000003 s. |
| 359623±307 s. | (359,6±0,3)10 3 s. |
| 0,000000047±0,0000000098 m. | 50±10 nm. |
| 67,8910 -7 ±49,310 -8 A | 6,8±0,5 µA. |
| 589±0,69 N. | 589,0±0,7 N. |
| 589±0,078 N. | 589,00±0,08 H. |
5. MÕÕTMISTULEMUSTE TÖÖTLEMISE NÄITED
Näide 5.1. Otsemõõtmiste töötlemine.
Voltmeeter mõõtis 10 näitu pinget U tolli elektriahel. Voltmeetril, mille täpsusklass on K=2,5, on maksimaalne skaala väärtus A=200 V. Mõõtmistulemused on toodud tabelis. Töötle mõõtmistulemused, tagades pingehinnangu 98% usaldusväärsuse.
| № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| U, V | 145 | 140 | 145 | 105 | 130 | 150 | 150 | 155 | 175 | 160 |
Arvutame instrumentaalse vea
Antud usaldusnivoo?=98% ja näitude arvu N=10 puhul määrame koefitsiendi t 98;10 =2 (lisa 1).
Arvutage keskmine väärtus
Arvutame näitude standardhälbe
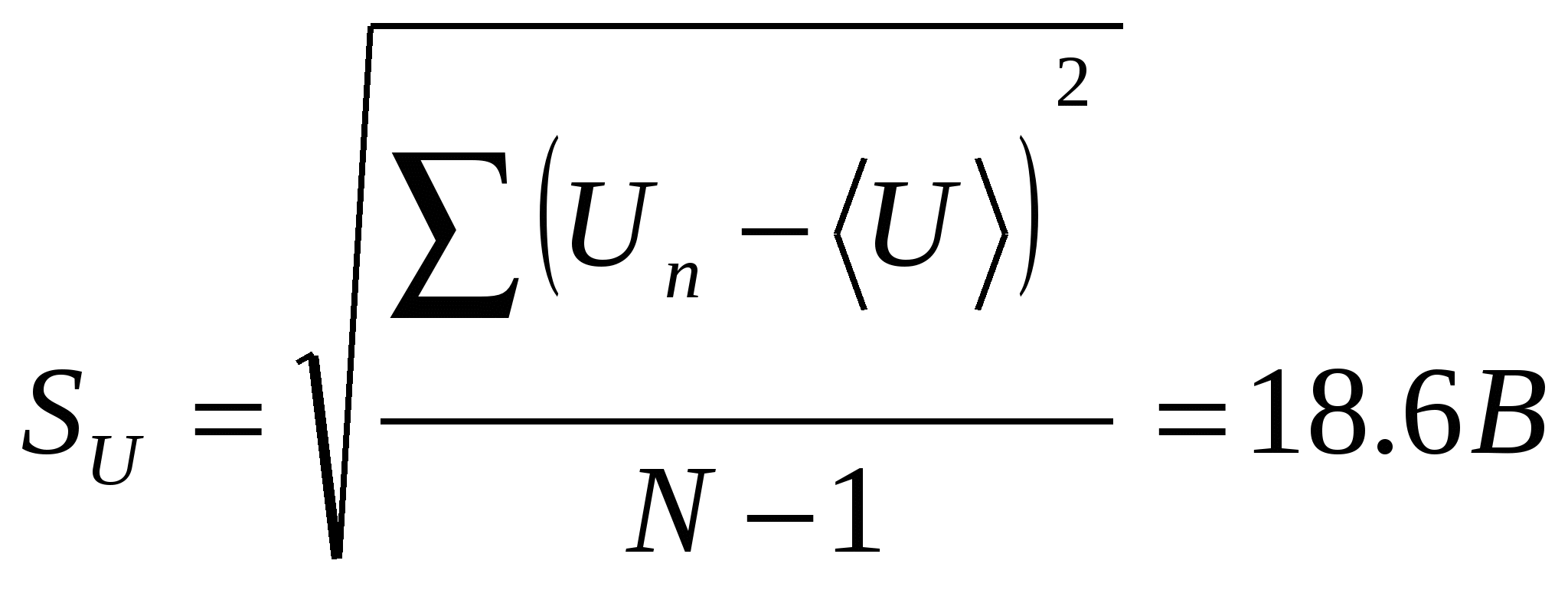
Kontrollige näitude puudumist.
Anomaalne arv on number 4. Arvutame normaliseeritud hälbe U 4 keskmisest väärtusest
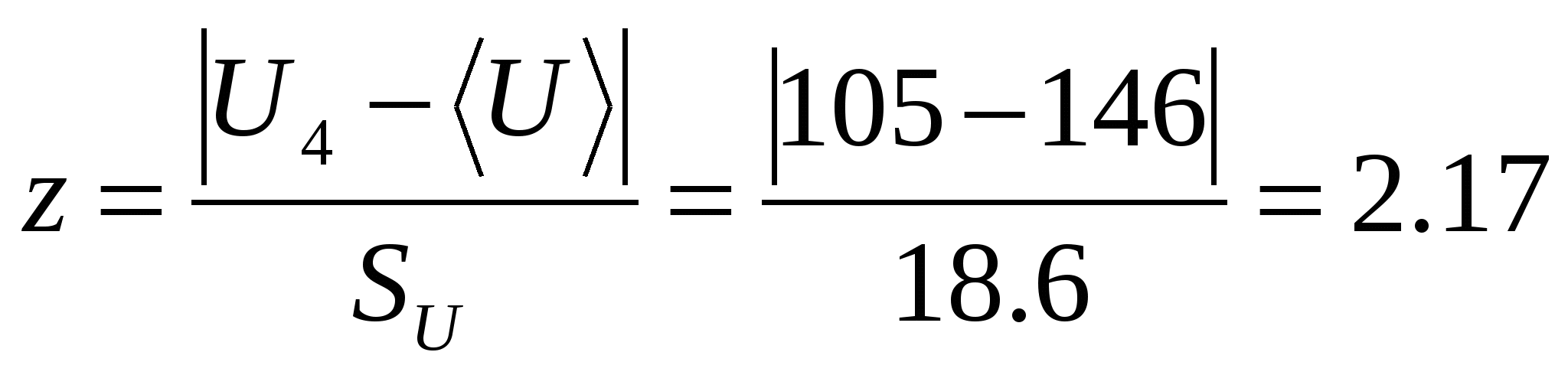
Vastavalt lisale 3 on katsete arv, mille puhul saadud näitu ei saa lugeda möödalaskeks, 17. See arv on suurem kui N=10. Seetõttu on näit U=105 V vale ja see tuleb töödeldud seeriast eemaldada.
Uus pingenäitude seeria (N=9, t 98;9 = 2,9)
| № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| U, V | 145 | 140 | 145 | 130 | 150 | 150 | 155 | 175 | 160 |
Arvutage uus keskmine
Arvutage standardhälve
Arvutame vea juhusliku komponendi
Arvutage kogu viga
Absoluutne
Sugulane
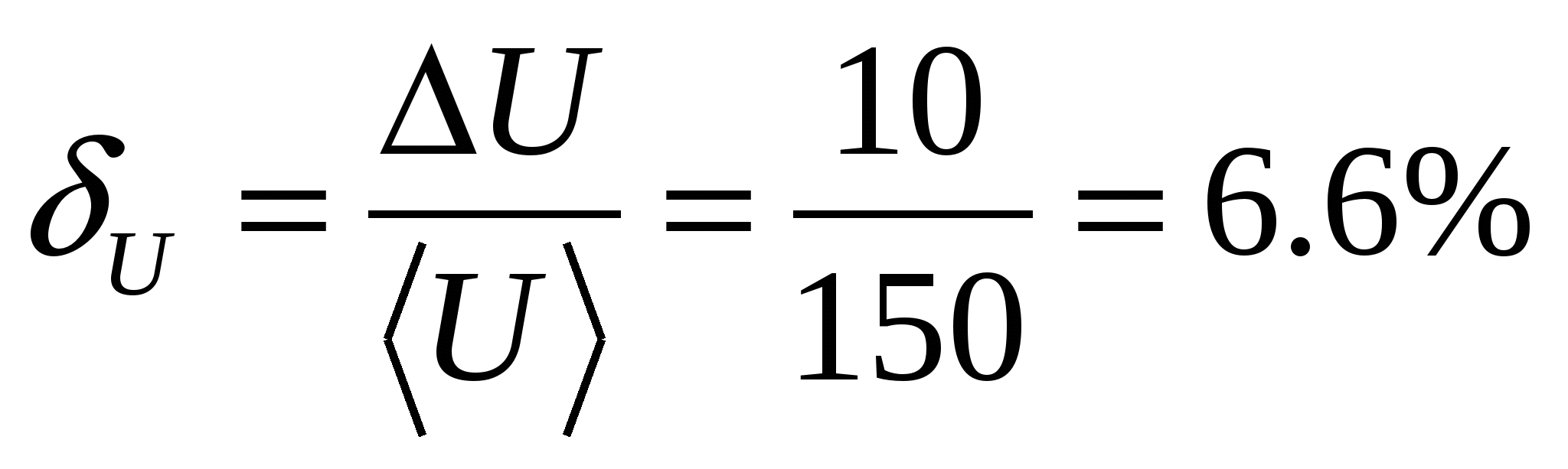
Pärast ümardamist kirjutatakse pinge mõõtmise tulemus järgmiselt:
U=(150±10)B, ?=7%, ?=98%
Näide 5.2. Otsemõõtmiste tulemuste kombineerimine.
Sama juhi takistust mõõdeti kolmel erineval tingimusel. Mõõtmistulemused on esitatud järgmiselt:
R 1 \u003d (11 ± 2) oomi.
R 2 \u003d (12 ± 2) oomi.
R 3 \u003d (10 ± 3) oomi.
Need mõõtmised tuleb kombineerida.
Leidke iga mõõtmise statistiline kaal (panus).
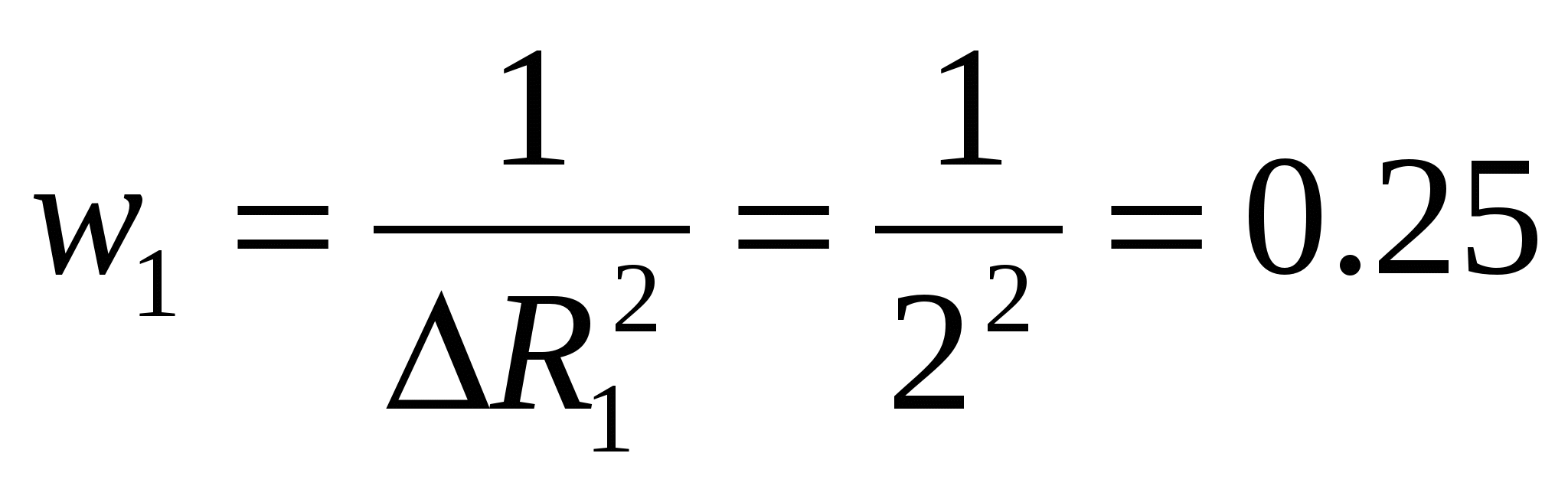1/ohm 2,
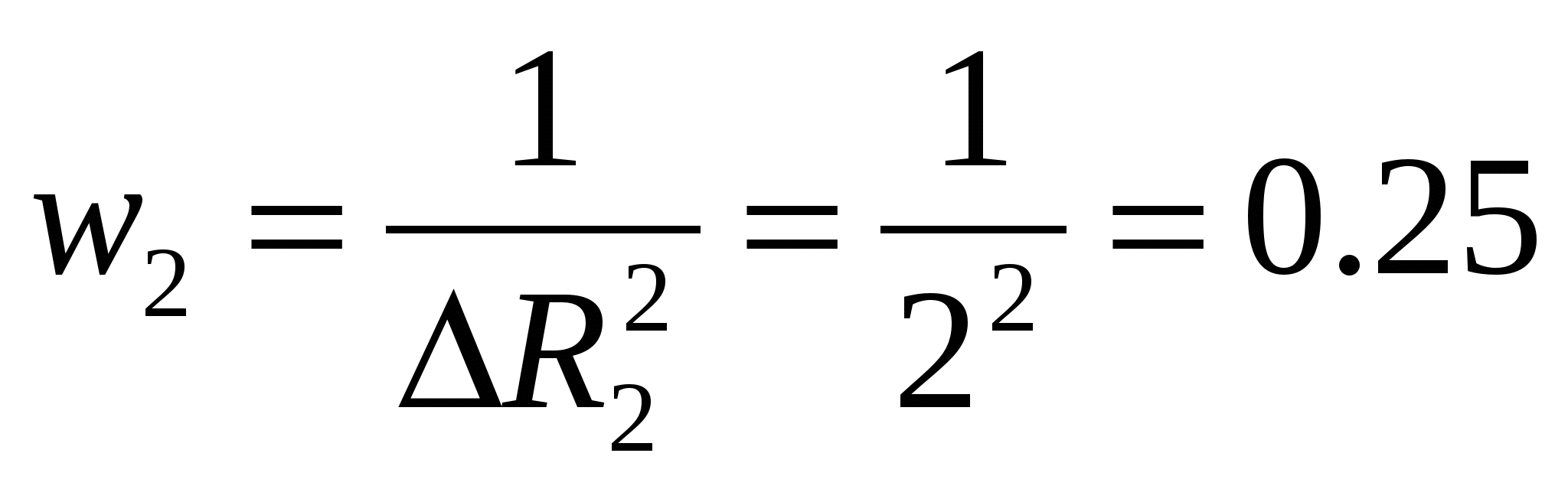1/ohm 2,
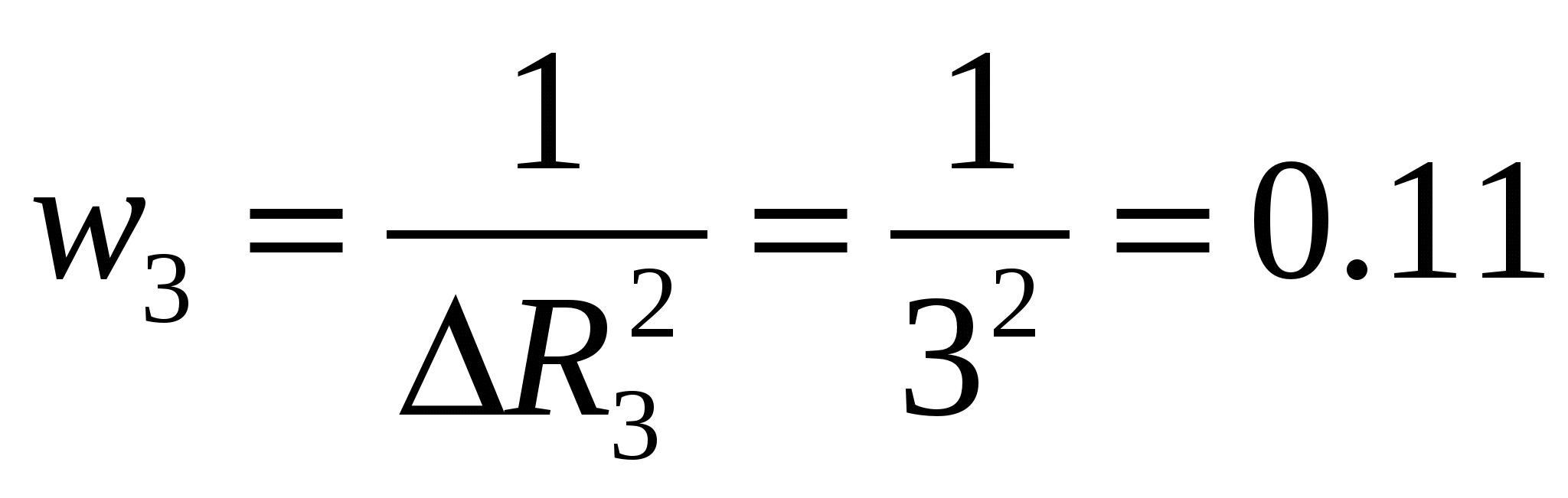1/ohm 2,
Uue takistuse hinnangu leidmine
Uue veahinnangu leidmine
Ühise vastupanu hindamise tulemus
R=(11±1) oomi.
Näide 5.3.
Otsesed mõõtmised on leidnud massi m, raadiuse R ja ühtlase pöörlemise lineaarkiiruse v väärtused ümber materjali punkti ümbermõõdu. On vaja hinnata materiaalsele punktile mõjuva tsentrifugaaljõu F väärtust.
M = (310 ± 6) g, R = (104 ± 5) mm, v = (30 ± 1) m/s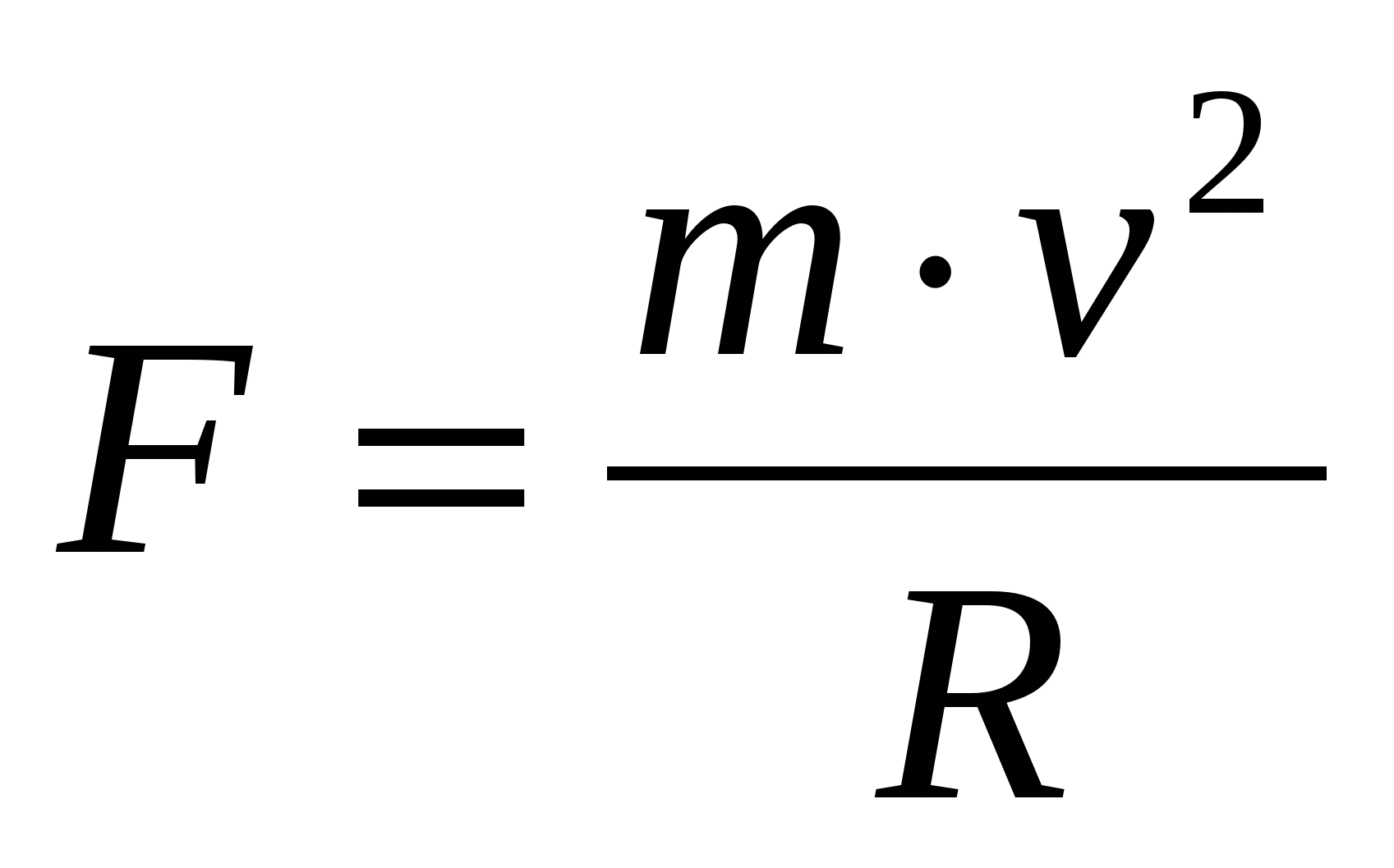 
Mõelge kaudsete mõõtmiste vea arvutamiseks kolmele meetodile
Algoritm, mis kasutab mõõdetud suuruse tuletiste arvutamist oma argumentide suhtes.
kN.
Leiame osalised tuletised ja arvutame nende väärtused argumentide keskmiste väärtuste jaoks
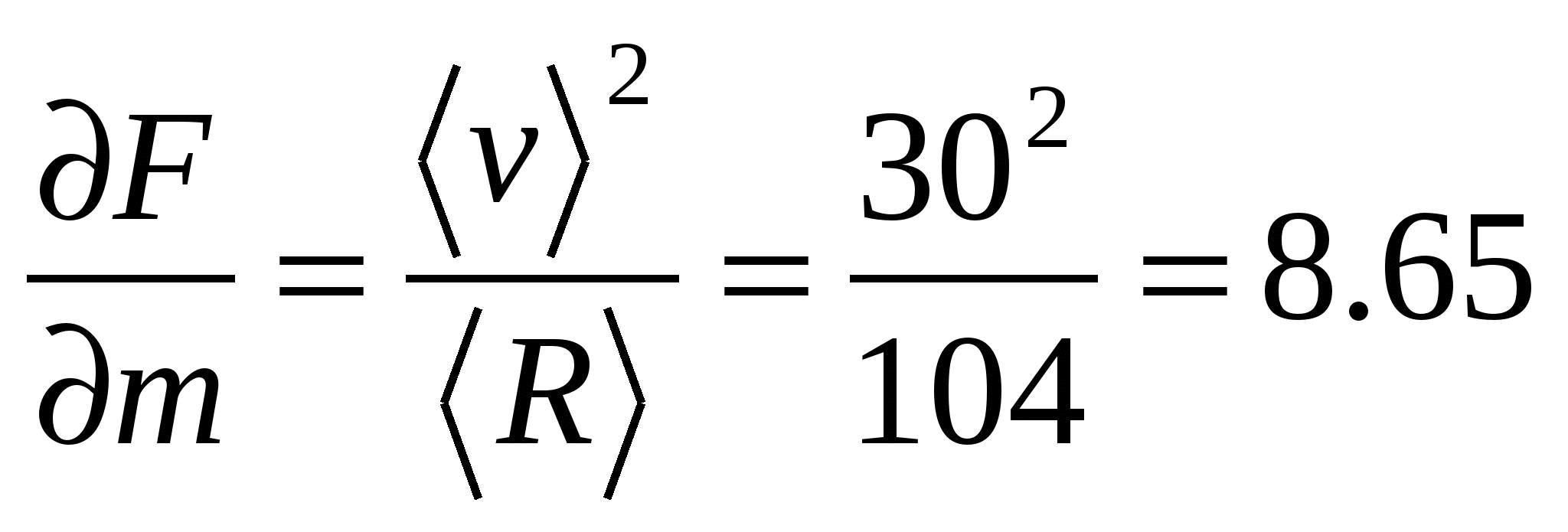
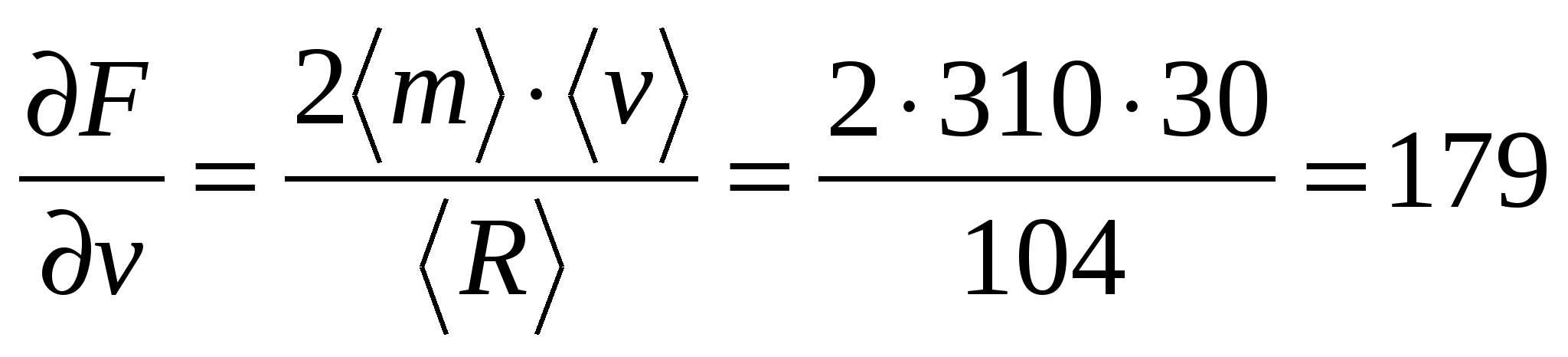
Arvutame vea komponendid iga argumendi põhjal
H 
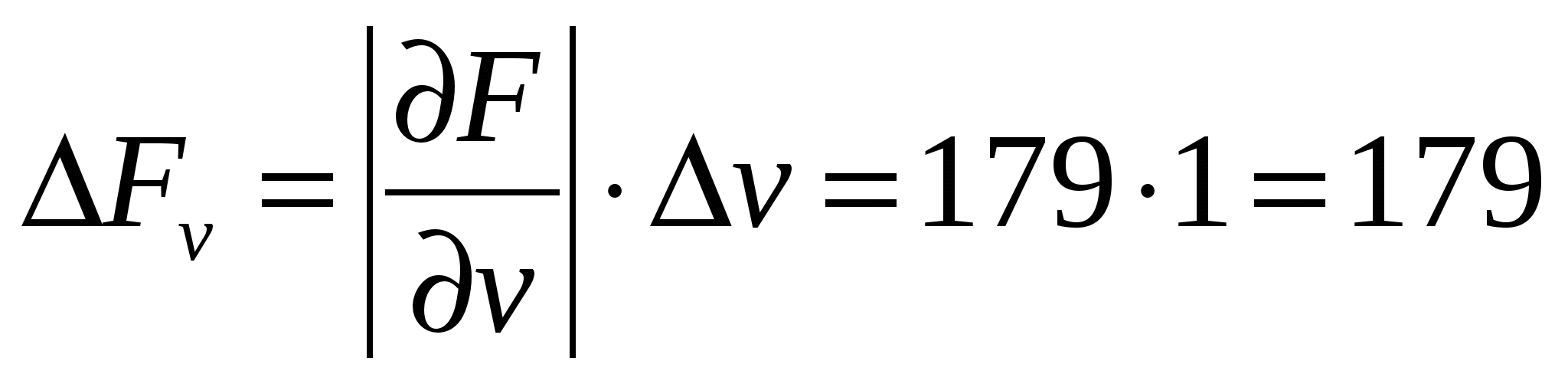H
H
Arvutame kogu vea
Sugulane
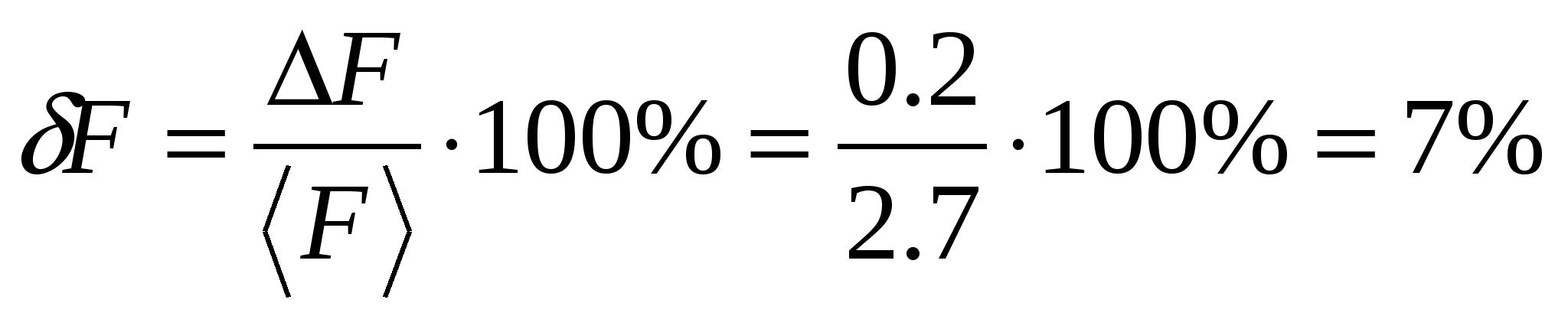
Algoritm, mis kasutab oma argumentide alusel mõõdetud väärtuse juurdekasvu arvutamist.
Arvutame jõu keskmise väärtuse
Arvutame funktsiooni juurdekasvu selle argumentide järgi
Arvutame kogu vea
Sugulane
Peale ümardamist paneme kirja kaudsete mõõtmiste tulemuse
Algoritm, mis kasutab absoluutsete veaväärtuste liitmist
Arvutame jõu keskmise väärtuse
Arvutame argumentide suhtelised vead
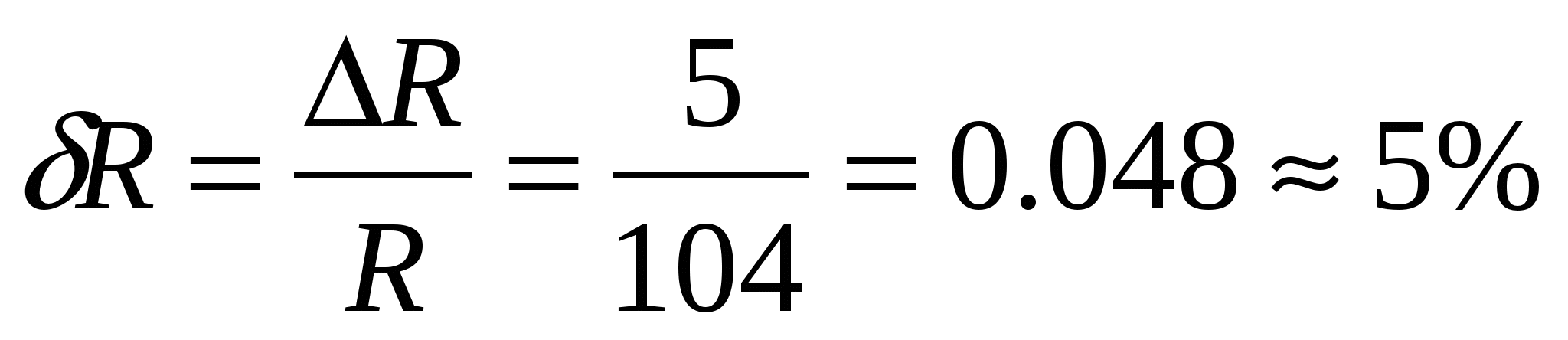
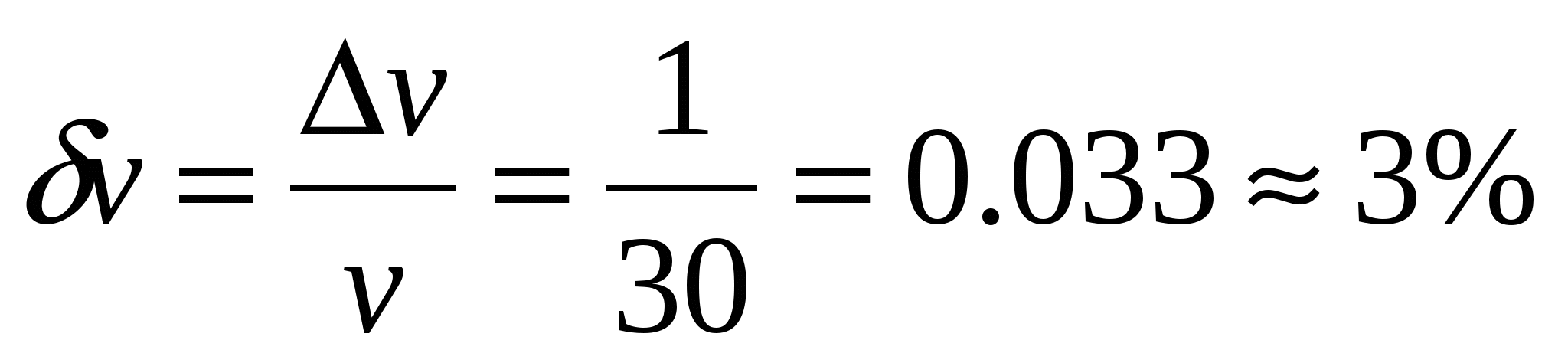
Funktsiooni suhtelise vea arvutame lisa 2 valemite järgi
Arvutame funktsiooni absoluutvea
Peale ümardamist paneme kirja kaudsete mõõtmiste tulemuse
Näide 5.4. Kaudsete mõõtmiste tulemuste töötlemine.
Selles näites võrdleme kahe algoritmi abil kaudsete mõõtmiste vigade arvutamise keerukust. Vaatleme juhtumit, kus mõõdetud suuruse kompleksne funktsionaalne sõltuvus argumentidest.
Olgu järjestikuse võnkeahela elementide väärtused leitud otsemõõtmiste teel. Aktiivne takistus R=(10±1) Ohm. Induktiivsus L=(30,0±1,5) mH. Mahutavused C=(100±2) uF. Sundvõnkumisi ergastatakse ahelas sagedusel?=1000 rad/s. EMF-i allika amplituud? = 10 V. Voolu amplituudi ja vooluahela elementide parameetrite vahelise seose määrab seos:
EMF amplituud? ja sagedus? mõõdetakse suure täpsusega ja neid võib pidada konstantideks.
Algoritm, mis kasutab oma argumentide alusel mõõdetud väärtuse juurdekasvu arvutamist
Funktsiooni sammude arvutamine
Arvutame kogu vea
Sugulane
Peale ümardamist paneme kirja kaudsete mõõtmiste tulemuse
Algoritm, mis kasutab mõõdetud suuruse tuletiste arvutamist oma argumentide suhtes
Arvutame voolu keskmise väärtuse
Arvutame funktsioonide tuletisi
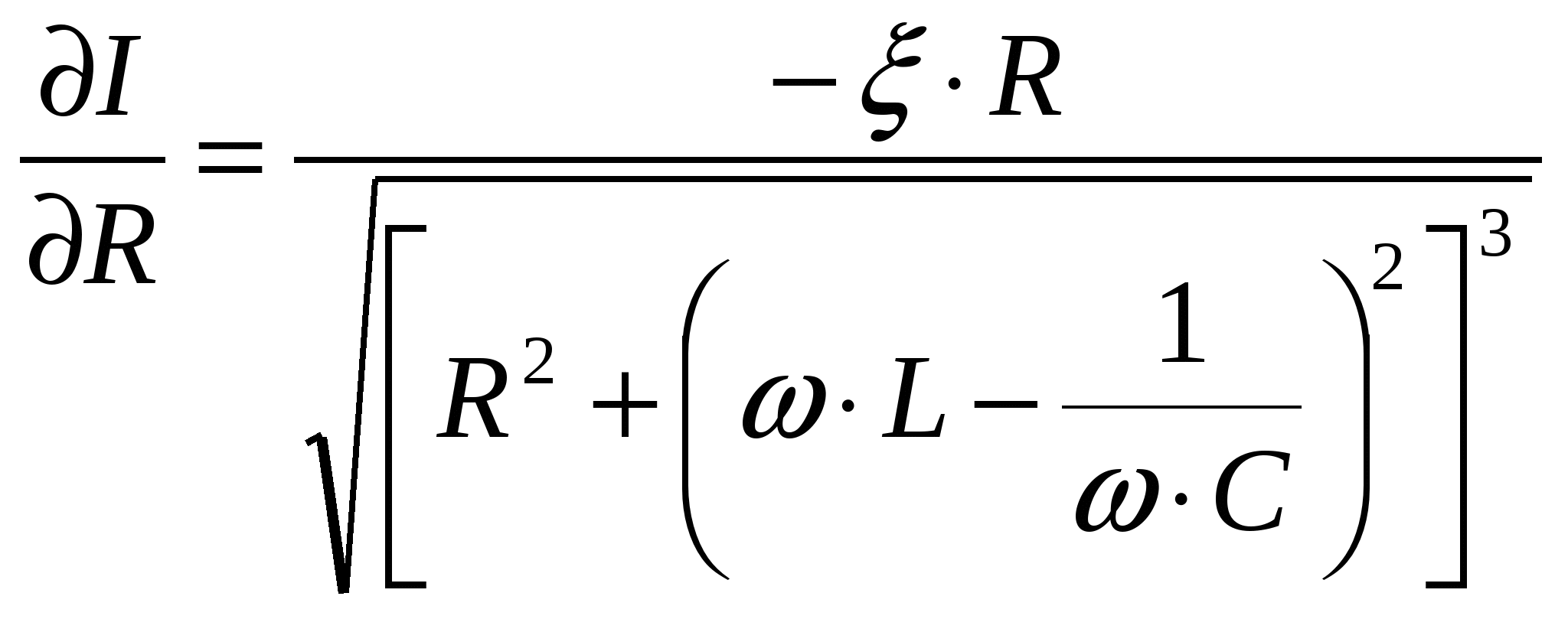
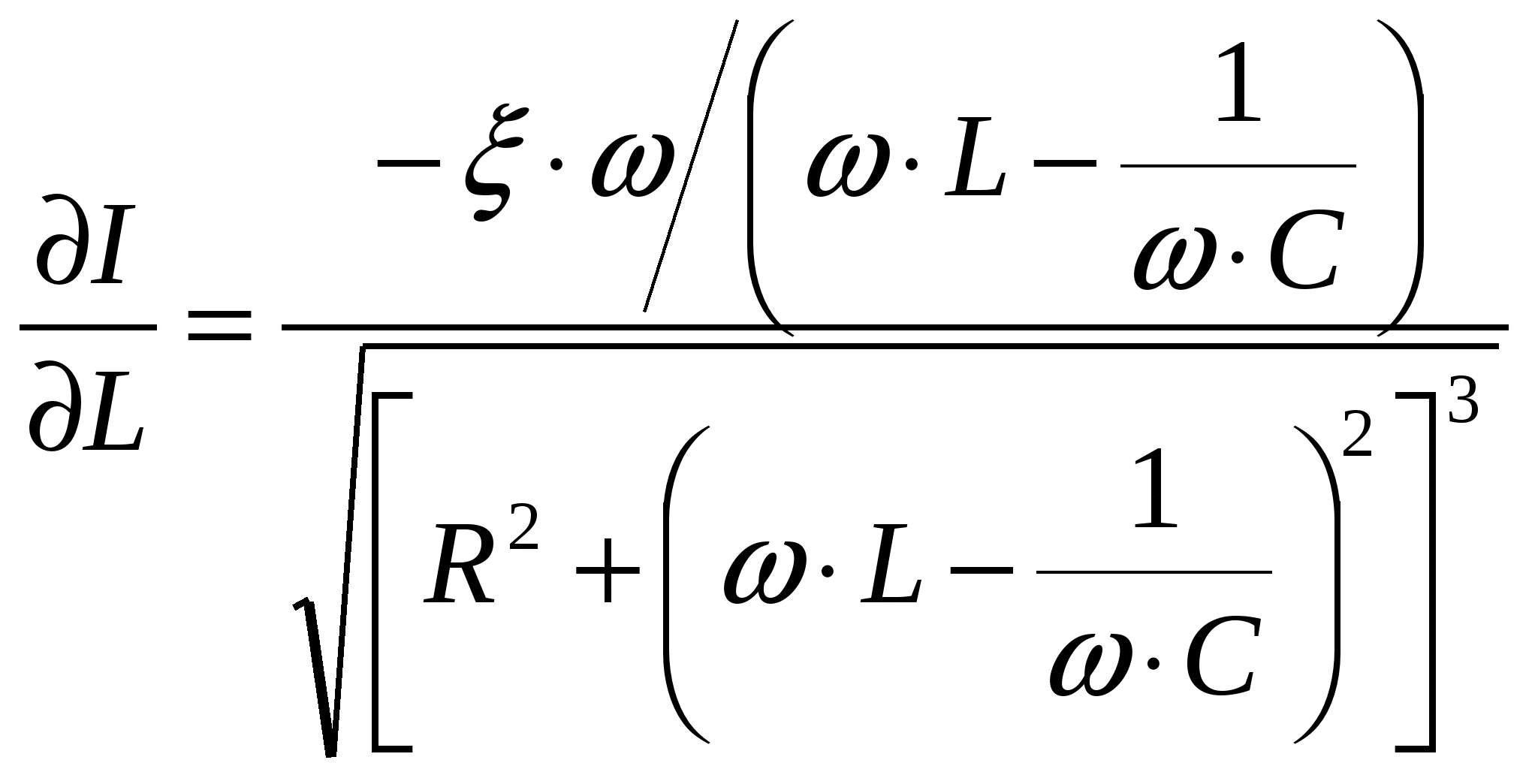
Arvutage tuletiste väärtused argumentide keskmiste väärtuste põhjal
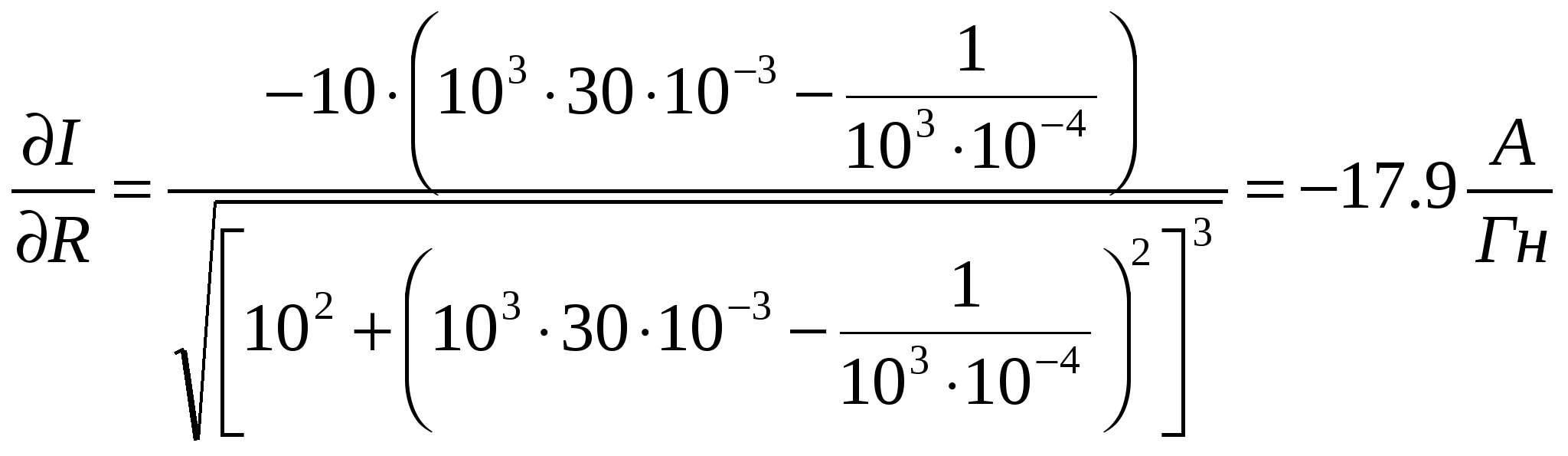
Arvutame funktsioonide veakomponendid
Arvutame kogu vea
Sugulane
Peale ümardamist paneme kirja kaudsete mõõtmiste tulemuse
Näide 5.5. Kaudsete mõõtmiste tulemuste töötlemine.
Selles näites vaatleme argumentide vigade statistilise seose mõju nende funktsiooni kaudsete mõõtmiste tulemusele.
Teatava sisemise takistusega alalisvoolu EMF-i allikas on laaditud sobiva võimsusega aktiivne koormus(Koormust nimetatakse sobitatuks, kui selles vabastatakse maksimaalne võimsus, sel juhul on koormuse takistus võrdne EMF-i allika sisetakistusega).
Otsemõõtmistel leiti koormusel N=10 voolu I ja pinge U väärtust. Voolu ∆I a =0,005 A, pinge instrumentaalne mõõtmisviga ∆U a =0,05 V. Voolu ja pinge hinnangute usaldusväärsus peaks olema 95%. Kaudsete mõõtmiste abil on vaja määrata allikast tarbitav võimsus P. Joule-Lenzi seaduse järgi 
.
On teada, et voolu ja pinge mõõdetud väärtuste hajumise peamine põhjus on allika ebastabiilsus, mis põhjustab selle EMF-i ja sisemise takistuse juhuslikke muutusi. Seetõttu on koormuse voolu ja pinge muutused statistiliselt seotud (korrelatsioonis), kuna need on põhjustatud samadest põhjustest. Sel juhul tuleb voolu ja pinge vigade liitmine läbi viia mitte ruutkeskmiselt, vaid absoluutarvudes.
Mõelge võimsuse arvutamise järjekorda.
| № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Mina, A | 0.265 | 0.255 | 0.225 | 0.245 | 0.235 | 0.210 | 0.260 | 0.240 | 0.210 | 0.215 |
| U, V | 6.55 | 6.40 | 5.60 | 6.20 | 5.95 | 5.20 | 6.55 | 6.00 | 5.30 | 5.40 |
Antud usalduse tõenäosuse? = 95% ja näitude arvu N = 10 korral määrame usaldusteguri t 95; 10 = 2,3 (lisa 1.)
Arvutame voolu ja pinge keskmise väärtuse
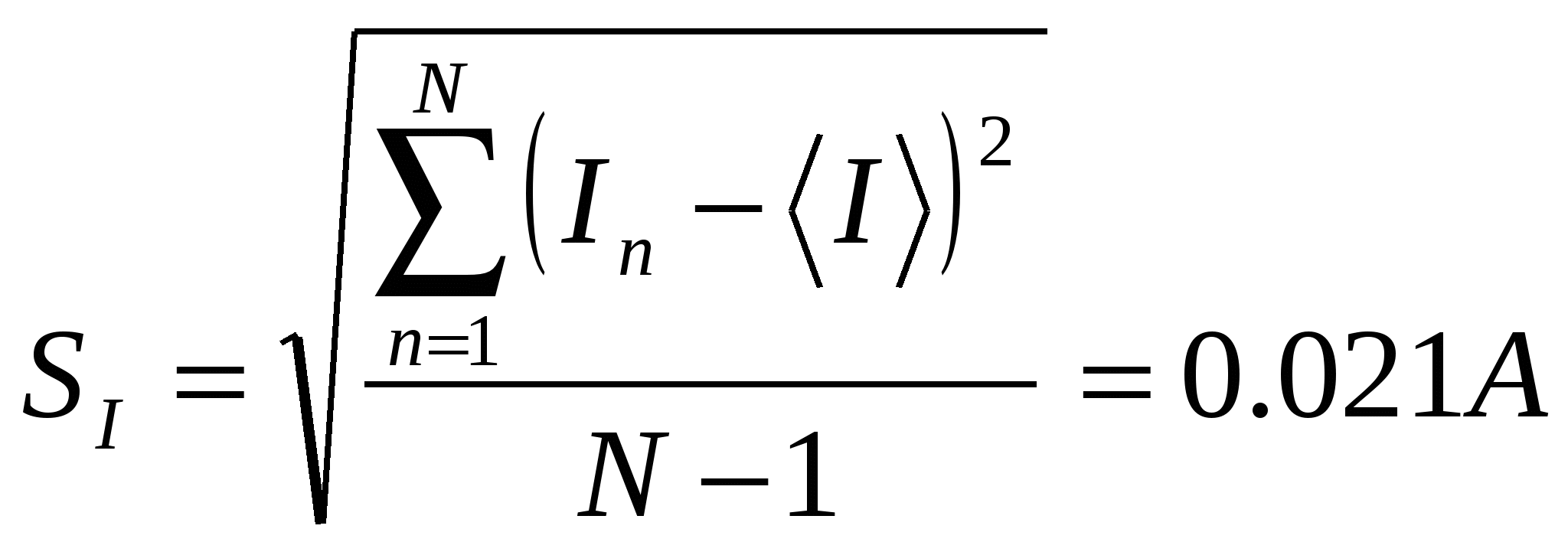
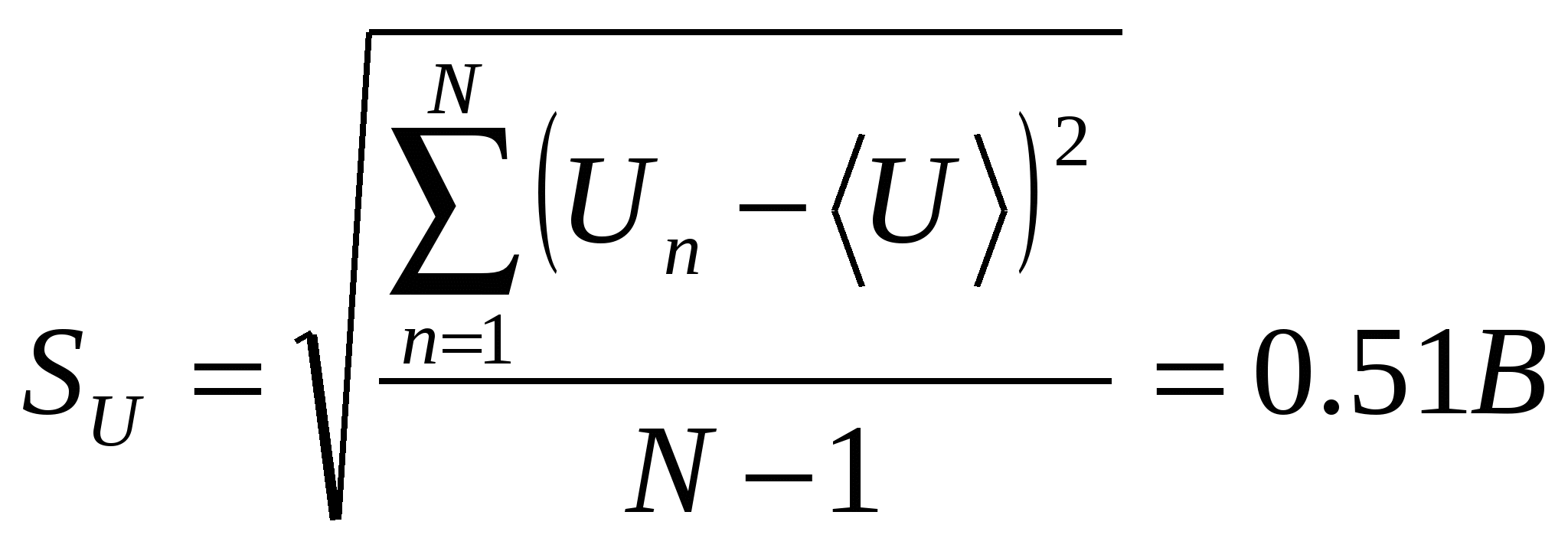
Vastavalt lisale 4 on N=10 korral tõenäosus, et voolu ja pinge koormuse vahel ei ole korrelatsiooni, null. Seetõttu näitavad eksperimentaalsed andmed seost voolu ja pinge vea vahel.
Arvutame voolu- ja pingevigade juhusliku komponendi
,
,
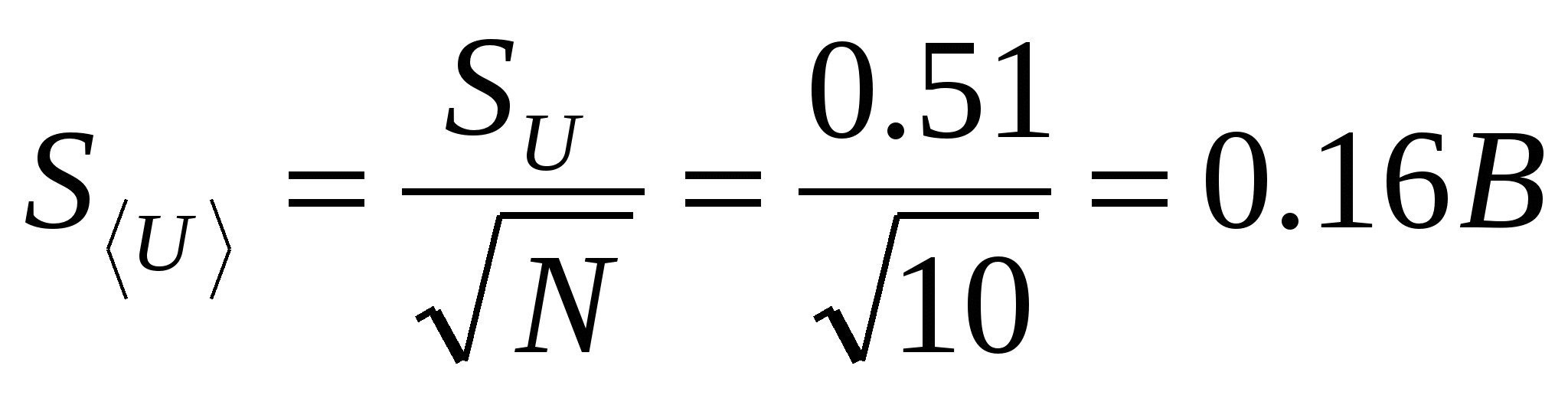Arvutame kogu vea
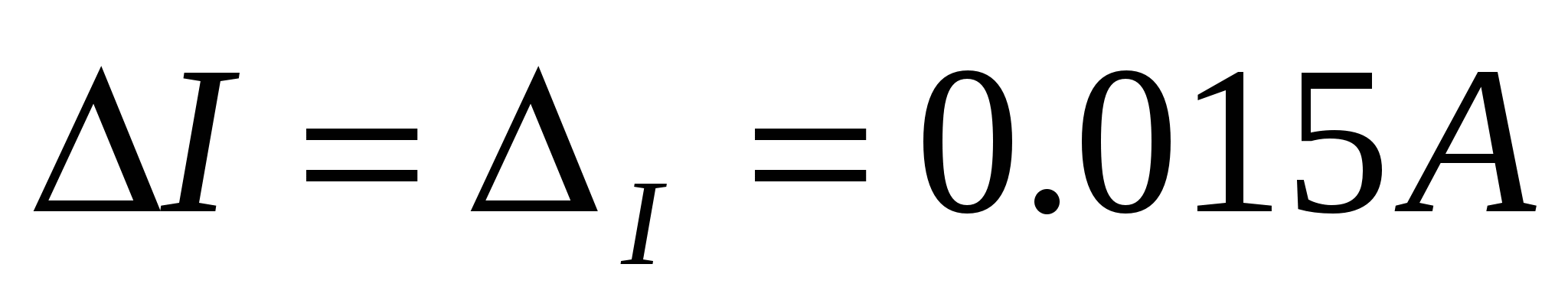
Sugulane
Pärast ümardamist saame voolu ja pinge mõõtmise tulemused
U=(5,9±0,4) B, ? U=6%, ?=95%
Arvutame võimsuse mõõtmise suhtelise vea
Arvutame võimsuse mõõtmise absoluutvea
Vigade ruutliitmisel ei võeta otsemõõtmiste näitude vahelist seost arvesse. See võib kaasa tuua kaudsete mõõtmiste vea alahindamise, mis võrdub kaudsete mõõtmiste usaldusväärsuse vähenemisega. Mõnikord võib vea vähendamine jõuda sellise väärtuseni, et usaldusvahemik ei kata tegelikku väärtust. Sel juhul saame voolu ja pinge mõõtmise vigade ruutliitmisel
P=(1,4±0,1) W, ?P=7%
Vaadeldavas probleemis on võimu tegelik väärtus
Võrdluseks vaatleme sama mõõtmisülesannet, kuid tingimustes, mille korral voolu ja pinge näitude levik on tingitud suurest hulgast mittedomineerivatest teguritest. Sel juhul ei ole voolu ja pinge näidu vead statistiliselt seotud.
| № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Mina, A | 0.290 | 0.285 | 0.285 | 0.275 | 0.190 | 0.245 | 0.220 | 0.275 | 0.230 | 0.210 |
| U, V | 6.55 | 6.40 | 5.60 | 6.20 | 5.95 | 5.20 | 6.55 | 6.00 | 5.30 | 5.30 |
Antud usalduse tõenäosuse?=95% ja näitude arvu N=10 korral määrame usaldusteguri t 95;10 =2,3. Arvutame voolu ja pinge keskmise väärtuse
Arvutame voolu ja pinge standardhälbe
Arvutame voolu ja pinge korrelatsioonikordaja
Lisa 4 kohaselt on etteantud arvu mõõtmiste korral tõenäosus, et voolu ja pinge vead koormusel ei ole omavahel seotud, 78%. Seetõttu näitavad eksperimentaalsed andmed, et voolu ja pinge vigade vahel puudub seos.
Vigade kontrollimine
Katsete arv, mille puhul seda tulemust ei saa lugeda möödalaskvaks, on 14 (lisa 3). See arv on suurem kui N=10. Seetõttu on näit U 9 =8,2 V vale ja see tuleb töödeldud seeriast eemaldada. Uuel real on N=9 loendit ja t 95;9 =2,3.
Arvutage uus keskmine ja standardhälve
Arvutame vea juhusliku komponendi
S U >
=
0,76B ?
U =
0,18B
?mina= 0,03 A ?U= 0,4B
Arvutame absoluutse ja suhtelise vea kokku
? I = 12%, ? U = 7%.
Voolu ja pinge otsemõõtmiste tulemus
U=(5,7±0,4) B, ?=7%, ?=95%
Arvutame keskmise võimsuse väärtuse
= 1,43 W.
Arvutage absoluutse ja suhtelise võimsuse mõõtmise vead voolu ja pinge mõõtmisvigade ruutliitmise teel
Kaudse võimsuse mõõtmise tulemus
Kui argumentide vahel korrelatsiooni ei ole, siis nende vigade absoluutväärtusega liitmine toob kaasa funktsiooni kaudsete mõõtmiste vea ülehindamise ja usaldusvahemiku laienemise, s.t. suurendada mõõtmiste usaldusväärsust. Selline vea ülehindamine on vastuvõetav. Sel juhul
?P=?I+?U= 12+7=19%.
?P=
P = 1,4 0,19 = 0,3 W.
8.1.1 Mõõtmiste tüübid (otsene, kaudne, summaarne, ühine)
Mõõtmise eesmärk on leida mõõdetava suuruse suhe selle ühikuga ja saada selle suuruse väärtus. Vastavalt mõõdetud suuruse väärtuse saamise meetodile jagatakse mõõtmised otsesteks, kaudseteks, kumulatiivseteks ja liitmõõtmisteks.
Otsene mõõtmine on mõõtmine, mille käigus saadakse füüsikalise suuruse soovitud väärtus otse katseandmetest.
Kaudsed mõõtmised on füüsikalise suuruse soovitud väärtuse määramine muude otsitava väärtusega funktsionaalselt seotud füüsikaliste suuruste otseste mõõtmiste tulemuste põhjal.
Koondmõõtmised on mitme samanimelise suuruse samaaegsed mõõtmised, mille käigus määratakse soovitud suuruste väärtused, lahendades võrrandisüsteemi, mis saadakse nende suuruste mõõtmisel erinevates kombinatsioonides.
Ühismõõtmised on kahe või enama erineva suuruse samaaegsed mõõtmised, et määrata nendevaheline seos.
Enne katseandmete mõõtmistulemuste statistilist töötlemist tuleks:
a) teadaolevad süstemaatilised vead on välistatud;
b) jämedad vead ja vead on kontrollitud ja välistatud.
Mõõtmistulemuste statistilise töötlemise üldine protseduur on järgmine:
a) hüpoteesi testimine, et empiiriline jaotus vastab ühe kriteeriumi järgi normaalseadusele;
b) mõõtmistulemuste arvkarakteristikute määramine - keskmine aritmeetiline väärtus, dispersioon või standardhälve;
c) mõõtetulemuse keskmise väärtuse standardhälbe ja mõõtevea juhusliku komponendi usalduspiiride määramine;
*d) välistamata süstemaatiliste vigade (NSP) piiride määramine ja nende mõju mõõtmistulemusele;
e) mõõtmistulemuse usaldusvahemiku arvutamine.
Otsese mõõtmise üksikute punktide arvutuste tegemise korda käsitleti eelmistes peatükkides (3,4,7). Muud tüüpi mõõtmiste tulemuste jaoks on statistilise töötlemise tunnused.
Kaudsete mõõtmiste tulemuste töötlemise algoritmid kehtestatakse sõltuvalt argumentide mõõtmisvigade vastastikusest mõjust (korrelatsioonist) ning funktsionaalse seose tüübist mõõdetud väärtuse ja selle argumentide vahel.
Argumentide mõõtmisvigade vahel on korrelatsioon, kui on täidetud järgmine tingimus:
kus n on iga argumendi dimensioonide arv;
t P - Studenti koefitsient usaldustõenäosuse P ja vabadusastmete arvu jaoks f = n - 2;
r on korrelatsioonikordaja:
,
(8.2)
kus a hi , a ki on i-nda mõõtmise tulemused, vastavalt h-nda ja j-nda argument
*Punkt (d) viiakse läbi eriti täpsetel juhtudel, kui on võimalik määrata NSP piire.
on mõõdetud argumentide keskmised väärtused.
Argumentide mõõtmisvigade korrelatsiooni ja normaaljaotuse tuvastamisel määrab statistilise töötlemise järjekorra mõõdetud väärtuse funktsionaalse sõltuvuse tüüp selle argumentidest.
Vormi lineaarse funktsionaalse sõltuvusega
, (8.3)
kus b j on a j-nda argumendi koefitsient,
Keskmise mõõdetud väärtuse RMS määratakse järgmise valemiga:
, (8.4)
Kus 
– j-nda argumendi keskmise RMSD:
Mittelineaarse funktsionaalse sõltuvusega: keskmise mõõdetud väärtuse RMS määratakse järgmise valemiga:
,
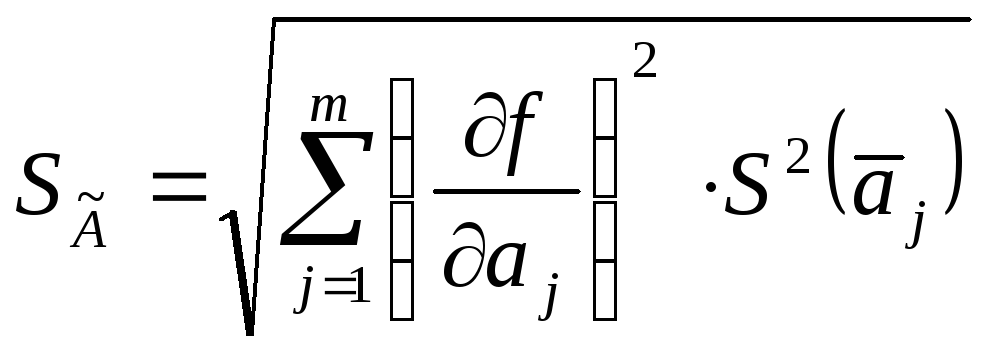(8.6)
Kus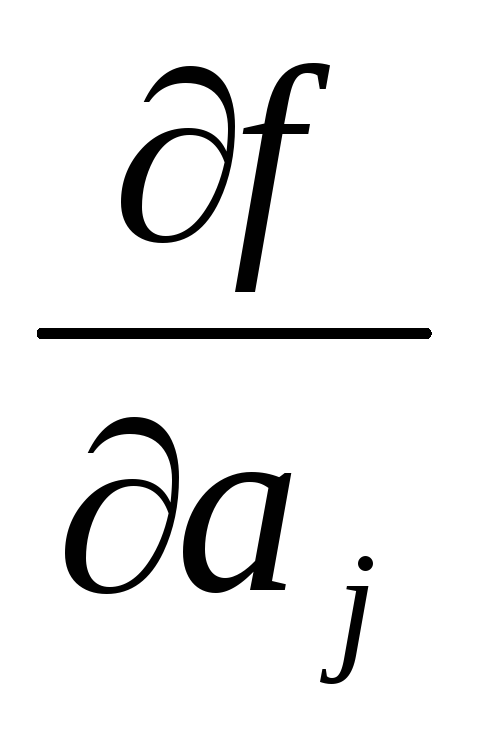 
- funktsionaalse sõltuvuse esimene osatuletis 
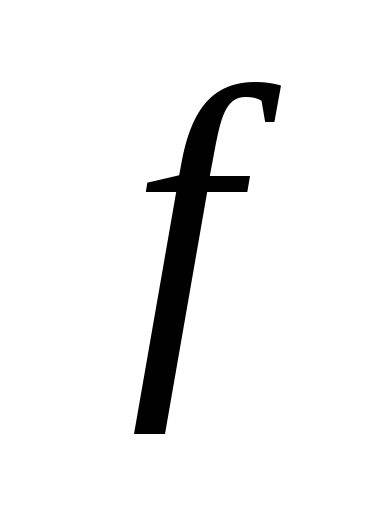mõõdetud suurusest a j -nda argumendi argumentidest.
Mittelineaarse sõltuvuse lineariseerimisel ilmneb Taylori laiendusseeria ümardamisest metoodiline NSP - R:
Kus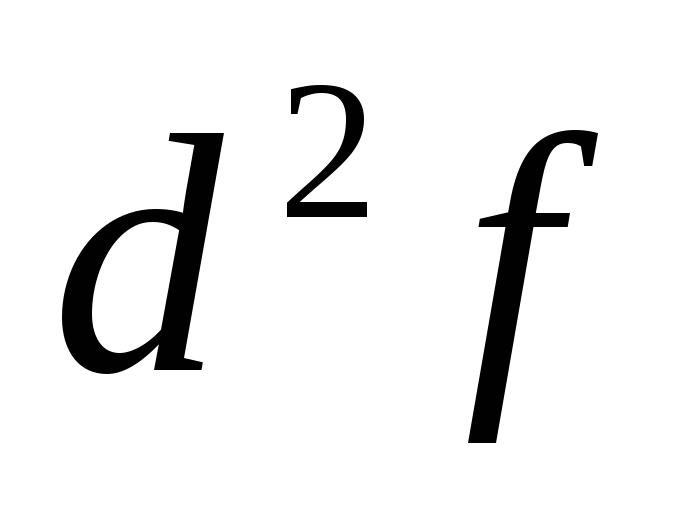 
on funktsionaalse sõltuvuse teist järku diferentsiaal.
Metoodilise vea R võib tähelepanuta jätta, kui
. (8.8)
Vastasel juhul tuleb lõplikus mõõtetulemuses arvestada R-ga.
Korrelatsiooni puudumisel, olenemata katseandmete jaotuse tüübist ja funktsionaalsest sõltuvusest, kasutatakse redutseerimismeetodit:
Arvutatakse mõõdetud koguse praegused väärtused:
(8.9)
Kus 
– j-nda argumendi i-s väärtus.
Arvutatakse keskmise mõõdetud väärtuse hinnang:
Keskmise mõõdetud väärtuse hinnangu standardhälve arvutatakse:
.
(8.11)
Kaudsete mõõtmiste lõpptulemus esitatakse usaldusvahemiku kujul:
Kus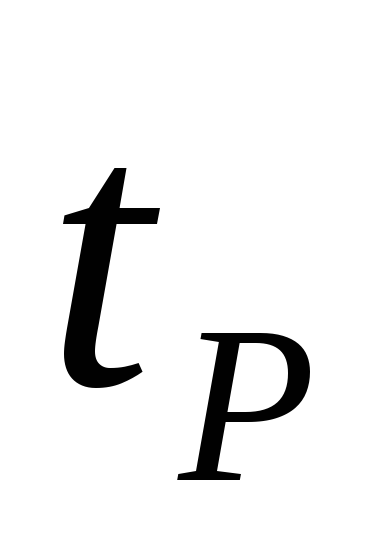 
- Studenti koefitsient antud usalduse tõenäosuse Р jaoks.
Kumulatiivsete ja liitmõõtmiste tulemused saadakse võrrandisüsteemist, mille kuju on:
kus on mõõtmiste käigus saadud väärtused;
on soovitud väärtused.
Mõõtmistulemuste täpsuse parandamiseks peaks süsteemis olema rohkem võrrandeid kui tundmatute arv.
Algne tingimusvõrrandite süsteem taandatakse normaalvõrrandite süsteemiks järgmisel kujul:
* Kus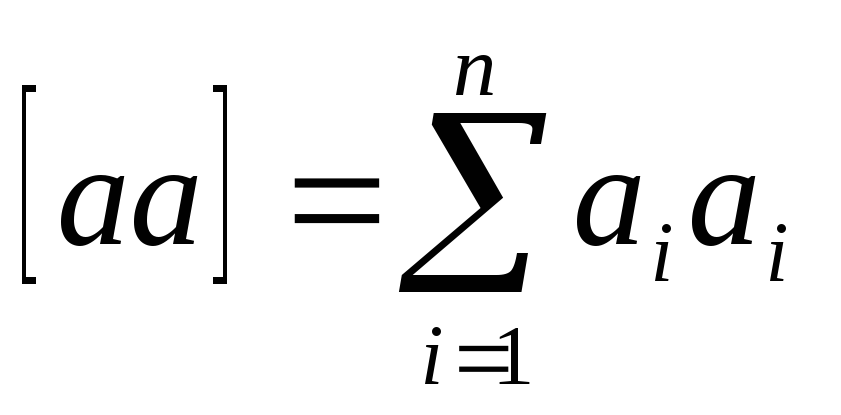 
,
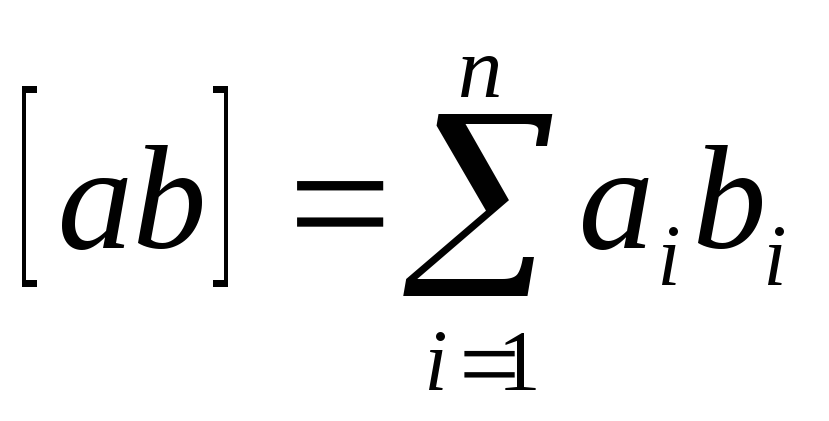ja nii edasi.
Süsteemi (8.14) lahendus on tundmatute suuruste hinnangud 
. Asendades need väärtused tingimusvõrranditesse, määrake jääkvead 
i , nn "jäägid". Jäägid määravad kindlaks vajalike suuruste mõõtmisvead, mille alusel arvutatakse nende suuruste usaldusvahemikud.
*Ühismõõtmiste läbiviimisel on tingimusvõrrandid võrdsed, kumulatiivsete mõõtmiste korral ei ole võrrandid erinevate mõõdetud väärtuste kombinatsioonide tõttu võrdsed ning kasutusele võetakse lisatunnus - kaal:
.
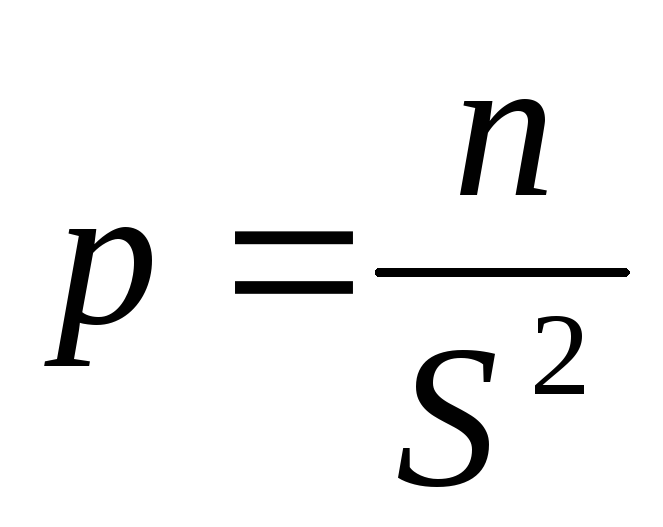(8.15)
Kõik suurused a, b, c, l korrutatakse koefitsiendiga.
Saada oma head tööd teadmistebaasi on lihtne. Kasutage allolevat vormi
Üliõpilased, magistrandid, noored teadlased, kes kasutavad teadmistebaasi oma õpingutes ja töös, on teile väga tänulikud.
Majutatud aadressil http://www.allbest.ru/
KURSUSETÖÖ
teemal: "Füüsikaliste suuruste mõõtmisvead"
1. Mõõtmisvead
2. Otsemõõtmisel otse mõõdetud koguste vigade hindamine
3. Kaudsete mõõtmiste vea hindamine
4. Tulemuse lõpprekord
5. Graafiline esitus mõõtmistulemused
7. Vigade teooria elemendid. RMS-i vead
Kirjandus
1. Mõõtmisvead
Ükski mõõtmine ei saa olla absoluutselt täpne. Mõõtes suvalist väärtust saame alati mingi veaga (veaga) tulemuse. Teisisõnu, suuruse mõõdetud väärtus erineb alati selle tegelikust väärtusest. Eksperimenteerija ülesandeks ei ole mitte ainult väärtuse enda leidmine, vaid ka mõõtmisel tehtud vea hindamine. Olenevalt omadustest ja tekkepõhjustest süstemaatilised ja juhuslikud vead ja igatseb.
Vigu nimetatakse süstemaatilisteks, mis sama meetodiga ja samade mõõteriistadega korduvate mõõtmiste korral jäävad konstantseks.
Süstemaatilised vead on põhjustatud teguritest, mis toimivad samamoodi, kui samu mõõtmisi korratakse mitu korda. Need vastavad mõõdetud väärtuse kõrvalekaldele tegelikust, alati ühes suunas - kas üles või alla.
Süstemaatilised vead võivad olla põhjustatud esiteks kasutatavate instrumentide riketest või valest tööst (näiteks vale nulli seadistus). Teiseks võib nende põhjuseks olla kasutatud mõõtmistehnika ebatäiuslikkus või uuritavat nähtust mõjutavate konstantsete tegurite arvestamata jätmine. Näiteks on võimalik saada kristallide sulamistemperatuuri ülehinnatud väärtusi, kui mõõtmised tehakse kõrgendatud välisrõhul.
Lisaks mõõtmisprotsessi käigus tekkivatele vigadele on süstemaatilised vead seotud ligikaudsete (“lihtsustatud”) valemite kasutamisega ning vead, mis tulenevad tegeliku objekti ja aktsepteeritud mudeli erinevusest. Nii võib näiteks tiheduse määramisel tekkida suur süstemaatiline viga, kui uuritav proov ei ole homogeenne ja sisaldab sees tühimikke.
Pärast põhjuste väljaselgitamist saab süstemaatilise vea kõrvaldada sobiva paranduse sisseviimisega. Süstemaatilist viga ei ole alati lihtne avastada ja selle põhjust välja selgitada ning sageli peab katse läbiviija tegema lisauuringuid. Eeldatakse, et füüsilise töökoja ülesannetes süstemaatilised vead on probleemi seadmisel minimeeritud ja neid saab ignoreerida.
Juhuslikud vead on need, mis korduvate mõõtmiste korral samades tingimustes muutuvad ettearvamatult.
Juhuslikke vigu põhjustavad paljud kontrollimatud põhjused, mille mõju ei ole igas katses sama. Selle tulemusena saadakse sama koguse mitu korda järjest samadel tingimustel mõõtmisel terve rida selle suuruse väärtusi, mis erinevad tegelikust väärtusest juhuslikult nii üles- kui ka allapoole.
Juhuslike vigade olemus võib olla erinev: kõikumised mõõteriista osuti nullasendis; eksperimenteerija meelte ebatäiuslikkus (näiteks võimetus stopperit täpselt õigel hetkel sisse lülitada); juhuslikud kontrollimatud muutused välismõjudes - temperatuur, niiskus, rõhk; pikapid elektriahelas jne, millega on peaaegu võimatu arvestada.
Juhuslikud vead on katses alati olemas.
Juhuslike suuruste käitumist kirjeldavad statistilised seaduspärasused, mis on tõenäosusteooria teemaks. Sündmuse i tõenäosuse w i statistiline määratlus on suhe
Kus n- katsete koguarv, n i– katsete arv, milles sündmus toimus i juhtus. Sel juhul peaks katsete koguarv olema väga suur ( n--®Ґ). Kell suured numbrid mõõtmiste korral järgivad juhuslikud vead normaaljaotust (Gaussi jaotus), mille põhijooned on järgmised:
1. Mida suurem on mõõdetud väärtuse kõrvalekalle tegelikust väärtusest, seda väiksem on sellise tulemuse tõenäosus.
2. Kõrvalekalded tegelikust väärtusest mõlemas suunas on võrdselt tõenäolised.
Allpool toodud juhuslike vigade arvutamise retseptid põhinevad tõenäosusteooria matemaatilisel aparaadil juhuslike suuruste Gaussi jaotusega. Peaksite teadma, et väikese (n = 310) mõõtmiste arvuga töökoja tingimustes on need arvutused alati hinnangulised.
Instrumentaalviga on mis tahes instrumendi näitude ja mõõdetud suuruse tegeliku väärtuse vahe. See võib sisaldada juhuslikke ja süstemaatilisi komponente.
Möödajäämised (või jämedad vead) väljenduvad tavaliselt üksiku mõõtmise tulemuse järsu kõrvalekaldumisena muust. Peamiselt on möödalaskmised tingitud katsetaja ebapiisavast tähelepanust või mõõteriistade talitlushäiretest. Selliste mõõtmiste tulemused jäetakse kõrvale.
2. Otsemõõtmisel otse mõõdetud koguste vigade hindamine
a) Juhuslikud vead. Põhimõisted.
Mõnda juhuslikku suurust a mõõdetakse samadel tingimustel n korda. Mõõtmistulemused andsid hulga n erinevat arvu
Koguse kõige tõenäolisema väärtuse jaoks ja tavaliselt võetakse mõõtmistulemuste aritmeetiline keskmine
Kuidas rohkem numbrit mõõtmised, seda lähemal on keskmine väärtus tegelikule väärtusele.
I-nda mõõtmise absoluutviga on väärtus
Absoluutne viga on mõõtmete väärtus. Absoluutsete vigade n väärtuste hulgas on tingimata nii positiivseid kui ka negatiivseid.
I-nda mõõtmise suhteline viga on väärtus
füüsikalise koguse vea usaldusvahemik
Suhteline viga on mõõtmeteta suurus. Tavaliselt suhtelist viga väljendatakse protsendina e i korrutada 100%. Suhtelise vea väärtus iseloomustab mõõtmise täpsust.
Keskmine absoluutviga määratletakse järgmiselt:
Rõhutame summeerimise vajalikkust absoluutväärtused(moodulite) kogused -- D A i. Vastasel juhul saadakse identne nulltulemus.
Keskmine suhteline viga on väärtus
Suure hulga mõõtmistega.
b) Usaldusvahemik ja usaldusnivoo.
Mõõtmistulemuste töötlemise ülesandeks on määrata mõõdetud väärtuse tegelikku väärtust sisaldava intervalli piirid. See intervall määratakse selle aritmeetilise keskmise suhtes, mis on tõese väärtuse parim hinnang.
Mis tahes suuruse mõõtmistulemuste registreerimiseks on aktsepteeritud järgmine vorm A:
A = (b A Koos -- ± -- D A) ühikut mõõdud ( e%),
kus D a- selle intervalli piir ühel või teisel viisil määratud.
Tõenäosusteooria võimaldab määrata intervalli suurust, milles teadaoleva tõenäosusega w leitakse üksikute mõõtmiste tulemused. Seda tõenäosust nimetatakse usalduse tase, ja vastavat intervalli nimetatakse usaldusvahemikuks.
Kui mõõtmiste arv n on piisavalt suur, siis usaldustõenäosus väljendab nende mõõtmiste koguarvu n osakaalu, mille puhul mõõdetud väärtus jäi usaldusvahemikku. Iga usaldustõenäosus w vastab tema enda usaldusvahemikule.
Näiteks numbriteljel tähistame tulemusi punktidega n= 10 tingimuslikku mõõtmist. Need koonduvad keskmise ümber b A Koos.
Sulgudes tähistame usaldusvahemikku, mille sees on 5 katseväärtust 10-st, s.o. usaldustõenäosus w 1 50%. Ruudusulud vastavad tõenäosuse w 2 80% usaldusvahemikule. Mida laiem on usaldusvahemik, seda tõenäolisem on selle intervalli sees tulemus. Tõenäosusteoorias luuakse kvantitatiivne seos usaldusvahemiku väärtuse, usalduse tõenäosuse ja mõõtmiste arvu vahel.
Kui valime usaldusvahemikuks keskmisele veale vastava intervalli, see tähendab D a = bD A s, siis piisavalt suure arvu mõõtmiste jaoks see vastab usaldustasemele w 60%. Mõõtmiste arvu vähenemisel suureneb sellisele usaldusvahemikule vastav usaldustõenäosus (b A Koos -- ± --bD A c) väheneb.
Seega usaldusvahemiku hindamiseks juhuslik muutuja võite kasutada keskmist viga -- bD A Koos . Usaldusvahemike range teooria on toodud viimases lõigus.
c) Instrumentaalne viga.
Instrumentaalviga on instrumendile iseloomulik pass. See määratakse kogu seda tüüpi seadmete komplekti jaoks, võrreldes uuritava partii seadmete näitu võrdlusseadme näitudega (kalibreerimise teel). Saadud väärtustest suurim võetakse instrumentaalvea väärtuseks.
Eraldi seadmega töötades on instrumentaalvea konkreetne väärtus teadmata, kuid jääb teadaolevatesse piiridesse, mis on märgitud seadme passiandmetes.
Osutitega elektriliste mõõteriistade puhul määrab vea täpsusklass. Enamiku instrumentide täpsusklass on võrdne instrumendi maksimaalse võimaliku suhtelise veaga, väljendatuna protsendina skaala ülemise piiri väärtusest. Sellise seadme täpsusklassi väärtus on märgitud selle skaala kõrvale numbri kujul (mitte ringiga ega tärniga!).
Tähistage täpsusklass e max. Definitsiooni põhjal
kus D x i arr . - maksimaalne võimalik absoluutne instrumentaalviga i mõõde, x max- mõõteseadme skaala ülemise piiri väärtus.
Sellest järeldub
ja i-nda mõõtmise maksimaalne suhteline instrumentaalviga arvutatakse valemiga
Näiteks 0,2 täpsusklassiga voltmeetri puhul, mis on ette nähtud pinge mõõtmiseks kuni V max \u003d 300 V, on maksimaalne suhteline instrumentaalne viga ülemise mõõtepiiri juures 0,2%. Ja pinge V = 50 V mõõtmisel suureneb maksimaalne suhteline viga 1,2% -ni. Seega nullilähedasel mõõtmisel (skaala esimeses pooles) väheneb mõõtmistäpsus oluliselt. Mõõtmised skaala algosas on ebasoovitavad.
Ülaltoodud valemitega määratud instrumentaalvead tähistavad instrumendi maksimaalset võimalikku viga. Konkreetse mõõtmise viga võib olla väiksem.
Kui täpsusklass on määramata, siis instrumentaalveaks võib võtta pool skaala väikseima jaotuse hinnast. Tavaliselt on see väärtus täpsusklassiga kooskõlas.
Digitaalsete elektriliste mõõteriistade viga on tavaliselt märgitud instrumendi passi.
d) Usaldusvahemik, võttes arvesse juhuslikke ja instrumentaalseid vigu.
Teatud väärtuse ühekordse mõõtmisega on juhuslikku viga võimatu määrata ja usaldusvahemiku piiri määrab instrumentaalvea väärtus
Sel juhul nimetatakse viga meetodi veaks.
Mitme mõõtmise korral määratakse usaldusvahemiku piir, võttes arvesse juhuslikku viga ja instrumentide tekitatud viga. Seda viga nimetatakse eksperimentaalseks veaks.
Katsevea hindamiseks võib kasutada valemit
(vt ka lk 22).
Loomulikult, kui üks terminitest on teisest palju suurem, saab see hindamisel määravaks. Kui kell suurel hulgal mõõtmiste korral on instrumentaalviga palju suurem kui juhuslik mõõtmisviga, siis tuleb kasutatav instrument täpsema vastu välja vahetada. Kui instrumentaalviga on palju väiksem kui juhuslik, saab mõõtmiste arvu suurendada, et tulemuse täpsust parandada. Kui instrumentaalviga on võrreldav juhusliku mõõtmisveaga, siis ilmselgelt pole mõtet mõõtmiste arvu suurendada. Seetõttu on enne mõõtmist soovitatav hinnata instrumentaalset viga.
3. Kaudsete mõõtmiste veahinnangJaI
Enamasti ei saa katsetajale huvipakkuvat kogust otse mõõta, vaid see saadakse arvutustega, kasutades mitut otseselt mõõdetavat suurust. Selliseid mõõtmisi nimetatakse kaudseteks. Olgu meile huvipakkuv suurus a arvutatud mingi valemiga, mis eeldab mitmete otseselt mõõdetud suuruste x, y, z, ... tundmist:
a = f(x, y, z, ....).
Siin on f (x, y, z, ....) mingi (veel konkretiseerimata) arvutusvalemiga määratud funktsioon.
Mõõtmisel võib esineda kaks olukorda.
a) Konstantsete parameetritega kaudsed mõõtmised.
Enamiku füüsiliste praktiliste ülesannete puhul mõõdetakse korduvalt suurusi x, y, z, ..., mille tegelikud väärtused jäävad mõõtmisprotsessi ajal konstantseks (konstantsed parameetrid). Näiteks määratakse aine tihedus sama proovi massi ja joonmõõtmete korduva mõõtmise teel.
Sel juhul koguse keskmine väärtus A saadakse keskmiste väärtuste valemiga asendamisel b x Koos , -- b y Koos , -- b z Koos , .... mõõdetud väärtused:
ja suuruse vigade arvutamisel ning alusta absoluutsete või suhteliste vigade arvutamisega, olenevalt funktsiooni f tüübist (x, y, z, ....).
IN üldine vaadeülesanne on järgmine. Olgu koguste hulk teada x±D x, y±D y, z±D z... , Kus -- D x, D y, D z- otseste mõõtmiste vead, mis määratakse kindlaks eelmises lõigus kirjeldatud viisil. Kuidas määrata suuruse absoluutset viga a? Arvestame sellega, et enamasti on otsemõõtmiste vead mõõdetud väärtustest tunduvalt väiksemad, moodustades neist mõne protsendi või vähem. Need. pD x n«n x P , pD y n«n y P , pD z n«n z P ... Seejärel võime formaalselt pidada viga väikeseks mõõdetud väärtuse juurdekasvuks, asendada sümbolid: D x dx, D ydy, D zdz, ... D ada- ja leida väärtus - D a kasutada diferentsiaalarvutuse matemaatilist aparaati -
Siin on osatuletis, mis arvutatakse tavapäraste diferentseerimisreeglite järgi. Kui see on määratletud, siis kõik teised funktsiooni argumendid f(välja arvatud x) tuleks pidada konstantseks ja võrdseks nende keskmiste väärtustega. Kas termin vastab veale, mis sisaldub koguveas? a ainult koguste mõõtmise ebatäpsus x(eeldusel, et kõik muud kogused: y, z, ....- mõõdetud vigadeta). Kõigil teistel terminitel on sarnane tähendus. Seega suuruse absoluutse vea hindamiseks A kaudsete mõõtmiste korral on see võimalik valemiga
Väärtuse suhtelise vea koheseks määramiseks A, jaga D a peal A ja arvestage sellega, et avaldist saab mugavalt teisendada.
Kui arvutusvalem sisaldab koos mõõdetud väärtustega ka tabeliandmeid või võrdluskonstandid, siis väärtuse a vea arvutamisel tuleks arvesse võtta ka nende vigu. Kui nende viga pole konkreetselt märgitud, siis tavaliselt arvestatakse, et see ei ületa viit ühikut esimeses puuduvas numbris. Näiteks vabalangemise kiirendamiseks:
g\u003d 9,8 m/s 2? D g\u003d 0,05 m/s 2,
g\u003d 9,81 m/s 2? D g\u003d 0,005 m/s 2.
Pärast absoluutvea arvutamist määratakse tulemuse suhteline viga.
Siin on tabel mõne arvutustes sageli esineva mõõdetud väärtuste kombinatsiooni vea hindamiseks.
Tabel 1.
Juhime lugeja tähelepanu mõnele olulised punktid laual.
1. Arvestame, et juhuslikud mõõtmisvead võivad olla võrdse tõenäosusega positiivsed ja negatiivsed. Seetõttu mõõdetud väärtuste liitmisel ja lahutamisel absoluutsed vead kokku liitma.
2. Kahe suuruse lahutamisel sisaldab suhteline viga nimetajas kahe suuruse erinevust. Kui need väärtused on lähedased, võib erinevuse suhteline viga oluliselt ületada iga väärtuse suhtelist viga eraldi. Täpsuse kadumise vältimiseks tuleks selliseid mõõtmisi ja arvutusi vältida, kui on vaja lahutada väärtuselt lähedased suurused.
3. Suuruste korrutamisel ja jagamisel liidetakse suhtelised vead.
See tähendab, et kui arvutusvalem on monoom ja kui summad ja erinevused on olemas, siis on eraldi tegurite kujul lihtsam arvutada esmalt mitte väärtuse a absoluutne, vaid suhteline viga. Kui arvutusvalemil on polünoomi kuju, on soovitatav alustada absoluutvea arvutamisega.
4. Astendatuna n, selline, et n n 1, suhteline viga suureneb n pühad
Näiteks kaaluge arvutuse vea arvutamist valemiga
Kõige mugavam on seda teha järgmise skeemi järgi.
Tähistage
ja
kus s 1 , s 2 , v 0 , t, a on mõõdetud väärtuste keskmised väärtused.
Siis
; ;
;
ja lõpuks
.
b) Muudetavate parameetritega kaudsed mõõtmised.
Mõnes ülesandes sama väärtuse määramisel a = f (x, y, z, ....) samade parameetrite x, y, z, .... n-kordse mõõtmise asemel n põhimõtteliselt erinevate väärtuste mõõtmist. (muutuvad parameetrid) x 1 , x 2 , ... , x n x-st ja neile vastavad väärtused y, z, ... . Näiteks määratakse aine tihedus mitme proovi massi ja joonmõõtmete üksikute mõõtmiste abil.
Sel juhul tehakse arvutused järgmiselt. Väärtus a arvutatakse iga katse jaoks eraldi: a 1 \u003d a (x 1, y 1, z 1 ...), a 2 \u003d (x 2, y 2, z 2 ...) ... a n \u003d a ( x n , y n , z n ...) - ja seda töödeldakse nagu otsemõõtmistel. Selle tulemusena määratakse keskmine väärtus a:
ja vastav keskmine juhuslik viga bD A Koos.
Instrumendi viga D a arr arvutatakse lisaks. Selle määramiseks punktis a kirjeldatud meetodil tuletatakse väärtuse absoluutse või suhtelise vea valem a. Selles valemis as D x, D y, D z, .... asendada instrumentaalvead D x arr, D y arr, D z arr, ... , aga x, y, z.... asendusväärtused x i,y i, z i, ... mis tahes katsetest. Et mitte saada instrumentaalvea tugevalt üle- või alahinnatud väärtust, tuleb katse vahepealse (mitte minimaalse) ja mitte maksimaalsed) parameetrite väärtused x i,y i, z i, ....
Katse koguviga määratakse otseste mõõtmiste korral:
.
4. KOHTAlõpptulemuse rekord
Arvutuste täpsus mõõtmiste töötlemisel
Töötlemise mõõtmiste tulemusena saadakse alati mõõdetud suuruse ligikaudne väärtus, mille täpsuse määrab ainult mõõtmisprotsessi käigus tehtud viga ja ükski arvutus seda täpsust parandada ei suuda. Seetõttu peab mõõtetöötluse lõpptulemus tähenduslike numbrite arvu poolest vastama mõõtmisprotsessis saadud täpsusele.
Lõpptulemust numbriliselt kirjutades nõustume kinni pidama järgmistest reeglitest (vt ka lk 21).
1. Veasse on jäänud ainult esimene oluline arv. Kui esimene tähendusnumber on üks, siis on lubatud kirjutada kaks olulist numbrit ja ülejäänud jäetakse ümardades kõrvale.
2. Mõõdetud väärtuse keskmine väärtus ümardatakse vastavalt vea väärtusele. Ümardamise reeglid on normaalsed.
Jah, number c= 4,862452±0,12465 tuleks kirjutada:
c= 4,86±0,12,
ja number d= 242,87546±0,0094265 tuleks kirjutada:
d= 242,875±0,009.
Tulemuse salvestamise näited:
v = (210±8) m/s (e = 4%)
või v = (2,10±0,08). 10 2 m/s (e = 4%) - standardvorm.
R = (49,8±0,3). 10 3 oomi (e = 0,6%)
R = (49,8±0,3) kOhm (e = 0,6%)
R = (4,98 ± 0,03). 10 4 Ohm (e = 0,6%) - standardvorm.
Tuleb meeles pidada, et viimastes numbrites olevad nullid on olulised numbrid. Seega ei ole numbrid 2,86 ja 2,86000 oma täpsuselt samaväärsed.
Pange tähele, et kui arvutustes tehakse kaudseid mõõtmisi, matemaatilised tehtedüle ligikaudsete arvude, mis on määratud erineva täpsusega. Sel juhul järgitakse järgmisi ümardamis- ja arvutusreegleid.
1. Ligikaudsete arvude liitmisel ja lahutamisel salvestatakse nii palju numbreid, kui palju neid on kõige väiksema arvu numbritega arvus.
2. Korrutamisel ja jagamisel jääb tulemuseks alles nii palju tähenduslikke numbreid, kuivõrd need sisalduvad väikseima tähendusnumbriga arvus.
3. Mõne funktsiooni väärtuste arvutamise tulemus
ligikaudne arv x peab sisaldama sama palju olulisi numbreid, kui on x-is.
4. Vahearvutustes on lubatud kasutada ühte või kahte märgilist numbrit rohkem (“varuga”).
5. Mõõtmistulemuste graafiline esitus
Diagrammide koostamisel tuleb järgida järgmisi reegleid.
1. Graafik peab sisaldama pealdist, millest oleks selge esitatava seaduspärasuse füüsiline sisu.
2. Koordinaatide telgede mastaabid ja alguspunktid valitakse nii, et sõltuvuskujutise graafik hõivab suure osa joonistusväljast. Sel juhul ei pea telgede ristumiskohas koguste nullväärtused tingimata olema.
Skaalat valides tuleb meeles pidada, et graafiku täpsus ei tohiks olla väiksem kui mõõtmise täpsus.
3. Koordinaatide telgedele kantakse võrdsed skaalajaotised, et graafikuga oleks mugav töötada. Katse käigus saadud väärtusi ei ole näidatud.
4. Koordinaatide lõpus tuleb märkida teljed konventsioonid ootel olevad väärtused ja komadega eraldatuna nende mõõtühikud.
5. Koguste (punktide) katseväärtused on selgelt joonistatud koos vigadega - usaldusvahemiku pikkusega segmendid, mis asuvad paralleelselt vastava teljega, kujul:
Kui valitud skaalal kõverat joonistades ei ole piki mõlemat koordinaattelge usaldusvahemikud nähtavad, märgitakse katsepunktid väikeste ringidena (kolmnurkadena jne), mille keskpunkt on katseandmetele vastavas punktis.
6. Katsekõver tõmmatakse sujuvalt läbi kõigi või enamiku katsepunktide usaldusvahemike nii, et katsepunktid oleksid kõige lähemal ja paikneksid ühtlaselt kõvera eri külgedel.
7. Kui diagrammil on kuvatud teoreetiline kõver, siis näidatakse valem, mille järgi see arvutatakse.
8. Graafiku ühel väljal mitme kõvera kuvamisel on igaüks neist nummerdatud või muul viisil esile tõstetud. Vastavad selgitused on antud välja vabas osas.
6. Soovitused laboriuuringu protokolli koostamiseksAMõlemad
Laboriaruanne peaks olema järgmise sisuga:
1. Töö nimetus.
2. Kokkuvõte töö eesmärgid.
3. Instrumentide ja seadmete loetelu.
4. Paigaldusskeem.
5. Lühikokkuvõte meetodi teooriast koos töövalemite tuletamisega.
6. Katsetulemuste registreerimine koos mõõtühikute ja instrumentaalvea näitamisega. Järgmiste arvutuste jaoks vajalike paigaldusparameetrite kirje (märkides ka ühikud ja vead).
7. Töödeldud mõõtmistulemused esitatakse tabelite, numbrite, graafikute kujul - vastavalt laboritööde metoodilises arenduses määratletud ülesandele.
8. Vigade arvutamine.
9. Tulemuste analüüs: võrdlus tabeliandmetega, teooriaga, teiste katsete andmetega - arvestades ka vigu.
10. Järeldused.
7. Vigade teooria elemendid. RMS nOpatusus
a) Jaotusfunktsioon. Gaussi jaotus ja selle omadused.
Oletame, et mõne juhusliku suuruse x: x 1 , x 2 , ... x n mõõtmist tehakse n - samal meetodil ja sama hoolikalt. Võib eeldada, et saadud tulemuste arv dn, mis asuvad mõnes üsna kitsas vahemikus x kuni x + dx, peaks olema võrdeline:
- võetud intervalli dx väärtus;
- koguarv mõõdud n.
Seega võib nii kirjutada
dn = f (x) n dx,
kus f (x) on funktsioon, mis iseloomustab juhuslike suuruste väärtuste jaotust erinevatel intervallidel.
Tõenäosus dw(x), et mingi väärtus x jääb x ja x + dx vahele, on määratletud järgmiselt:
(koos mõõtmiste arvuga n--®Ґ).
Funktsiooni f(x) nimetatakse jaotusfunktsiooniks ehk tõenäosustiheduseks.
Vigade teooria postulaadina eeldatakse, et otsemõõtmiste tulemused ja nende juhuslikud vead, kusjuures neid on palju, järgivad normaaljaotuse seadust.
Gaussi leitud pideva juhusliku suuruse x jaotusfunktsioon on järgmisel kujul:
, kus m -- Ja -- s ----- jaotusparameetrid .
Parameeter -- m -- normaaljaotus on võrdne keskmise väärtusega b x juhuslikust muutujast, mis suvalise teadaoleva jaotusfunktsiooni korral on määratud integraaliga
.
Seega väärtus m -- on mõõdetud suuruse kõige tõenäolisem väärtus x, need. tema parim hinnang.
Normaaljaotuse parameeter s 2-- võrdub dispersiooniga D juhuslik suurus, mis on üldiselt määratud järgmise integraaliga
.
Dispersiooni ruutjuurt nimetatakse juhusliku suuruse standardhälbeks.
Juhusliku suuruse - bsc keskmine hälve (viga) määratakse jaotusfunktsiooni abil järgmiselt
Gaussi jaotusfunktsioonist arvutatud keskmine mõõtmisviga -bsc korreleerub standardhälbe väärtusega s-- järgmine tee: < s > = 0,8-- s .
Parameetrid s--ja--m on seotud järgmiselt:
.
See avaldis võimaldab leida standardhälbe s -- kui on olemas normaaljaotuse kõver.
Gaussi funktsiooni graafik on näidatud joonistel. Funktsioon f(x) on punktis tõmmatud ordinaadi suhtes sümmeetriline x= m; läbib punktis maksimumi x= m ja selle pöördepunkt on m--±s. Seega iseloomustab dispersioon jaotusfunktsiooni laiust või näitab, kui laialt on juhusliku suuruse väärtused selle tegeliku väärtuse suhtes hajutatud. Mida täpsemad on mõõtmised, seda lähemal on tegelikule väärtusele üksikute mõõtmiste tulemused, s.o. s väärtus on väiksem. Joonis A näitab funktsiooni f(x) kolme väärtuse jaoks s .
Kõveraga piiratud kujundi pindala f(x) ja punktidest tõmmatud vertikaalsed jooned x 1 ja x 2 (joonis B) , on arvuliselt võrdne tõenäosusega, et mõõtmistulemus langeb intervalli D x = x 1 - x 2 , mida nimetatakse usaldustasemeks. Kogu kõvera alune ala f(x) on võrdne tõenäosusega, et juhuslik suurus langeb vahemikku 0 kuni -Ґ, s.o.
,
kuna teatud sündmuse tõenäosus on võrdne ühega.
Normaaljaotust kasutades püstitab ja lahendab veateooria kaks peamist probleemi. Esimene on mõõtmiste täpsuse hindamine. Teine on mõõtmistulemuste aritmeetilise keskmise väärtuse täpsuse hindamine.
b) Mõõtmistulemuste täpsus.
Mõõtmiste täpsust vigade teoorias iseloomustab usaldusvahemik (x>--±--D x) w, nii, et usalduse tõenäosus on võrdne w, jääb ühe mõõtmise tulemus intervalli sees. See tõenäosus võrdub ka usaldusvahemikku jäävate tulemuste suhtelise osakaaluga (vt lk 4-5).
Seega on juhusliku vea suuruse iseloomustamiseks vaja määrata kaks numbrit, nimelt usaldusvahemiku suurus ja usalduse tõenäosuse suurus . Ainult vea suuruse täpsustamine ilma vastava usaldustõenäosuseta on suures osas mõttetu.
Kui teada keskmine viga bsc mõõtmised, usaldusvahemik on kirjutatud kujul (<x> ±--bsc) w, määratud usalduse tõenäosusega-- w= 0,57.
Kui on teada standardhälve s -- mõõtetulemuste jaotus, näidatud intervall on kujul (x>±-- t w s) w, Kus t w- koefitsient, mis sõltub usalduse tõenäosuse väärtusest ja arvutatakse Gaussi jaotuse järgi.
Kõige sagedamini kasutatavad kogused D x= t w s on toodud tabelis 2.
Tabel 2.
Praktikas läbiviimisel piiratud arv mõõte me ei tea. täpne väärtus dispersioon, kuid me saame ainult hinnata selle väärtust. Standardhälbe s parim hinnang on keskmine ruudu vigan mõõdud nS:
See väärtus statistiliselt kaldub -- s -- juures n--®Ґ .
Seega asendame me paratamatult s--in väärtus usaldusvahemikku oma ligikaudse väärtuseni nS. Samas tuleb meeles pidada, et vähem numbrit mõõtmised, seda halvem on see lähendus. Niisiis näitab teooria, et usaldusvahemiku korrektseks määramiseks usalduse tõenäosusega w= 0,9 nõuab vähemalt 40 mõõtmist.)
c) Mõõtmistulemuste aritmeetilise keskmise täpsus.
Eespool käsitlesime üksiku mõõtmise tulemuse kõrvalekaldumise tõenäosust suuruse tegelikust väärtusest x. Sama oluline on teada, kui palju võib mõõtmistulemuste aritmeetiline keskmine tegelikust väärtusest erineda. Seda kõrvalekallet iseloomustab ka usaldusvahemik (
Rangelt võttes, kui väärtus x on normaaljaotusega matemaatiline ootus m ja dispersioon
s 2, siis selle keskmine väärtus
on normaaljaotus ootusega m
ja dispersioon s 2 / n. Need. juhuslik
aritmeetilise keskmise viga on väiksem kui ühe mõõtmise viga.
Kui hinnanguliselt
s kasutatakse ruutkeskmist viga nS, siis keskmise väärtuse hälbe hindamiseks aritmeetilise keskmise ruutviga nS
:
Väärtus nS
kipub statistiliselt nulli n®Ґ.
Vigade teoorias on tõestatud, et väikese arvu mõõtmiste korral ( n< 30), которое реально имеет место в работах физического практикума, в доверительный интервал необходимо ввести коэффициентt w,n, mida nimetatakse õpilase koefitsiendiks. Seejärel võtab usaldusvahemik kuju (<x> ± t w,n nS
) w.
Mida väiksem on number n mõõtmised, seda rohkem võib keskmine väärtus tegelikust väärtusest erineda. Nii et sama usaldustaseme jaoks wÕpilaste suhtarv peaks vähenedes suurenema n, vaata tabelit 3.
Tabel 3
???n |
||||||||||||||
d) Täielik viga. Kaudsete mõõtmiste viga.
Teooria kohaselt arvutatakse täiesti sõltumatute juhuslike ja instrumentaalsete vigade korral kogu katseviga järgmiselt:
.
Sel juhul peaksid mõlemad vead määrama usaldusvahemikud sama tõenäosusega. Instrumentaalviga määrab oma intervalli usaldusnivooga w = 0,9. Tekkinud katsevea arvessevõtmiseks on ka teisi viise.
Kaudsete mõõtmiste puhul arvutatakse keskmine ruut absoluutviga valemiga
kus D x, D y, D z,.... on katse keskmised ruutvead.
Kaudse väärtuse a suhtelise vea arvutamise valem sisaldab ruute suhtelised vead. Näiteks väärtusele a, mis on antud arvutusvalemiga
,
kus k on arvuline koefitsient, on vigade teooriaga määratud suhteline viga:
,
millest järeldub
Kirjandus
1. A.N. Seidel. Füüsikaliste suuruste mõõtmisvead. L., Nauka, 1985.
2. L.G. Dedenko. V.V. Keržentsev. Matemaatiline töötlemine ja katsetulemuste esitlemine. M., Moskva Riikliku Ülikooli kirjastus, 1977.
3. Füüsiline töötuba. Mehaanika ja molekulaarfüüsika. Toimetanud V.I. Iveronova. M., Nauka, 1967.
4. P.V. Novitsky, I.A. Zograf. Mõõtmistulemuste vigade hindamine. L., Energoatomizdat, 1991.
5. Laboratoorsed tööd Moskva Riikliku Ülikooli loodusteaduskondade füüsika kursusel. Mehaanika. M., Mosk. un-t. 1997. aastal.
6. Metoodiline arendusüldfüüsika praktika. Mõõtmisvead. Comp. D.V. Belov. Moskva, Moskva Riiklik Ülikool, 1993.
Majutatud saidil Allbest.ru
Sarnased dokumendid
Füüsikaliste suuruste mõõtmine ja vigade klassifitseerimine. Otseste ja kaudsete mõõtmiste vigade määramine. Mõõtmistulemuste graafiline töötlemine. Seoste määratlus erisoojusvõimsused gaasid Clementi ja Desormesi meetodil.
koolitusjuhend, lisatud 22.06.2015
Raskete vigade kriteeriumid. Standardhälbe intervallhinnang. Kaudsete ja otseste mõõtmistüüpide tulemuste töötlemine. Mõõtesüsteemi vigade statistiliste karakteristikute arvutamise meetod. Täpsusklassi määramine.
kursusetöö, lisatud 17.05.2015
Füüsikaliste suuruste mõõtmise otsesed ja kaudsed tüübid. Absoluutsed, suhtelised, süstemaatilised, juhuslikud ja aritmeetilised keskmised vead, tulemuse standardhälve. Vea hindamine nihikutega tehtud arvutustes.
test, lisatud 25.12.2010
Füüsikalise suuruse olemus, klassifikatsioon ja selle mõõtmiste omadused. Füüsikaliste suuruste staatilised ja dünaamilised mõõtmised. Otsese, kaudse ja ühismõõtmise tulemuste töötlemine, nende esitusvormi normaliseerimine ja määramatuse hindamine.
kursusetöö, lisatud 12.03.2013
Plaadi materjali tiheduse määramise tunnused, otseste ja kaudsete mõõtmiste vea arvutamise analüüs. Peamised veatüübid: süstemaatilised, juhuslikud, ümardamisvead ja möödalaskmised. Vead otsesel ja kaudsel mõõtmisel.
test, lisatud 14.04.2014
Mõõdetava suuruse punkti- ja intervallhinnang. Otsese ja kaudse mõõtmise absoluutvea arvutamine. Vigade statistiline jaotus, Gaussi jaotus. Mõõtmiste ettevalmistamine ja läbiviimine. Arvtulemuste ümardamise reeglid.
koolitusjuhend, lisatud 26.12.2016
Materiaalse punkti kinemaatika uurimine ja vabalangemise kiirenduse mõõtmise vigade hindamise meetodite valdamine. Vabalangemise mõõtmiseks kasutatava eksperimentaalse seadistuse kirjeldus. Kaudsete mõõtmiste vigade hindamine.
laboritööd, lisatud 21.12.2015
Füüsikaliste suuruste mõiste ja olemus, nende kvalitatiivne ja kvantitatiivne väljendus. Mõõteskaalade põhitüüpide tunnused: nimetused, järjekord, erinevused (intervallid) ja suhted, nende tunnused. Logaritmiliste ja biofüüsikaliste skaalade omadused.
abstraktne, lisatud 13.11.2013
Mõõtühikute, tüüpide ja mõõtevahendite struktuur-klassifikatsioonimudel. Vigade liigid, nende hindamine ja töötlemine Microsoft Excelis. Ruuteri, magnetoelektrilise seadme, infrapuna termomeetri, kaasaskantavate kaalude täpsusklassi määramine.
kursusetöö, lisatud 04.06.2015
Füüsikaliste suuruste süsteemid ja nende ühikud, nende suuruse ja väärtuse roll, klassifitseerimise eripära. Mõõtmiste ühtsuse mõiste. Füüsikaliste suuruste ühikute etalonide karakteristikud. Koguste ühikute suuruste edastamine: süsteemi omadused ja kasutatavad meetodid.