Probleem püstitatakse järgmiselt: lase soovitud väärtus z määratud muude koguste järgi a, b, c, ... saadud otsemõõtmistel
z = f(a,b,c,...) (1.11)
Tuleb leida funktsiooni keskmine väärtus ja selle mõõtmiste viga, s.o. leida usaldusvahemik
usaldusväärsuse a ja suhtelise veaga .
Mis puutub , siis see leitakse, asendades selle asemel (11) paremasse serva a, b, c,... nende keskmised väärtused
Absoluutne viga kaudsed mõõtmised on otseste mõõtmiste absoluutsete vigade funktsioon ja arvutatakse valemiga
 (1.14)
(1.14)
Siin on funktsioonide osatuletised f muutujate järgi a, b, …
Kui kogused a, b, c,... funktsiooniks Z = f(a,b,c,...) sisestada tegurite kujul ühel või teisel määral, st kui
![]() , (1.15)
, (1.15)
siis on kõigepealt mugav arvutada suhteline viga
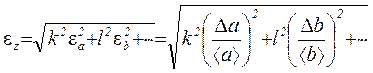 , (1.16)
, (1.16)
ja siis absoluutne
Valemid D jaoks z ja e z on toodud teatmekirjanduses.
Märkmed.
1. Kaudsete mõõtmiste puhul võivad arvutusvalemid sisaldada teadaolevaid füüsikalisi konstante (kiirendus vabalangus g, valguse kiirus vaakumis Koos jne), arvud nagu murdtegurid ... . Need väärtused on arvutustes ümardatud. Sel juhul sisestatakse arvutusse loomulikult viga ![]() - ümardamisviga arvutustes, millega tuleb arvestada.
- ümardamisviga arvutustes, millega tuleb arvestada.
Üldiselt aktsepteeritakse, et ligikaudse arvu ümardamisviga võrdub poolega selle numbri ühikust, milleni see arv ümardati. Näiteks lk = 3,14159... . Kui võtta p=3,1, siis Dp=0,05, kui p=3,14, siis Dp=0,005...jne. Küsimus, millise numbrini ligikaudne arv ümardada, lahendatakse järgmiselt: ümardamisel tekkiv suhteline viga peab olema samas suurusjärgus või suurusjärgu võrra väiksem kui teist tüüpi suhteliste vigade maksimum. Tabeliandmete absoluutset viga hinnatakse samal viisil. Näiteks on tabelis näidatud r = 13,6 × 10 3 kg / m 3, seega Dr = 0,05 × 10 3 kg / m 3.
Universaalsete konstantide väärtuste viga teatatakse sageli koos nende keskmiste väärtustega: ( Koos = ![]() m/s, kus D Koos= 0,3 × 10 3 m/s.
m/s, kus D Koos= 0,3 × 10 3 m/s.
2. Mõnikord ei lange kaudsete mõõtmiste korral katsetingimused kokku korduvate vaatlustega. Sel juhul funktsiooni väärtus z arvutatakse iga üksiku mõõtmise jaoks ja usaldusvahemik arvutatakse väärtuste kaudu z samamoodi nagu otsemõõtmistel (kõik vead siin sisalduvad ühes juhuslikus mõõtmisveas z). Väärtused, mida ei mõõdeta, kuid on antud (kui on), tuleb näidata piisavalt suure täpsusega.
Mõõtmistulemuste töötlemise kord
Otsesed mõõtmised
1. Arvutage keskmine väärtus n mõõdud
2. Leia üksikute mõõtmiste vead ![]() .
.
3. Arvutage üksikute mõõtmiste ruuduvead ja nende summa: 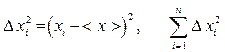 .
.
4. Määrake usaldusväärsus a (oma eesmärkidel võtame a = 0,95) ja määrake tabelist Studenti koefitsiendid t a, n ja ta, ¥ .
5. Andke hinnang süstemaatilised vead: instrument D X pr ja ümardamisvead mõõtmisel D X env \u003d D / 2 (D on seadme skaala jaotus) ja leidke mõõtmistulemuse koguviga (usaldusvahemiku pool laius):
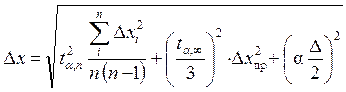 .
.
6. Hinnake suhtelist viga
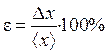 .
.
7. Kirjutage lõpptulemus kujul
![]() ε = … %, kui a = ...
ε = … %, kui a = ...
Kaudsed mõõtmised
1. Iga soovitud väärtuse määramise valemis sisalduva otse mõõdetud koguse kohta ![]() , töötle nagu ülal. Kui koguste hulgas a, b, c, ... on tabelikonstandid või p-tüüpi arvud, e,..., siis tuleks need arvutustes (võimaluse korral) ümardada nii, et antud juhul tekitatav suhteline viga on suurusjärgu võrra väiksem kui vahetult mõõdetud väärtuste suurim suhteline viga.
, töötle nagu ülal. Kui koguste hulgas a, b, c, ... on tabelikonstandid või p-tüüpi arvud, e,..., siis tuleks need arvutustes (võimaluse korral) ümardada nii, et antud juhul tekitatav suhteline viga on suurusjärgu võrra väiksem kui vahetult mõõdetud väärtuste suurim suhteline viga.
Määrake soovitud väärtuse keskmine väärtus
z = f( ,,
3. Hinnake kaudsete mõõtmiste tulemuse usaldusvahemiku poollaiust
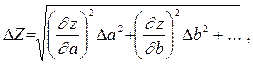 ,
,
kus tuletised ... on arvutatud
4. Määrake tulemuse suhteline viga
![]()
5. Kui z sõltuvus on a, b, c,... omab vormi ![]() , kus k,l,m on reaalarvud, peate esmalt leidma sugulane viga
, kus k,l,m on reaalarvud, peate esmalt leidma sugulane viga
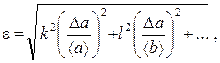
ja siis absoluutne .
6. Kirjutage lõpptulemus kujul
z=
Märge:
Otsemõõtmiste tulemuste töötlemisel tuleb järgida järgmist reeglit: kõigi arvutatud väärtuste arvväärtused peavad sisaldama ühe numbri võrra rohkem esialgseid (katseliselt määratud) väärtusi.
Kaudsete mõõtmiste puhul tuleks arvutused teha vastavalt lähendamise reeglid:
1. reegel Ligikaudsete arvude liitmisel ja lahutamisel peate:
a) tõsta esile termin, milles kahtlasel arvul on kõrgeim number;
b) ümardada kõik ülejäänud terminid järgmise numbrini (üks varunumber jäetakse alles);
c) sooritada liitmist (lahutamist);
d) selle tulemusena ära visata viimane numberümardamise teel (tulemuse kaheldava numbri number ühtib liikmete kahtlaste numbrite suurimaga).
Näide: 5,4382 10 5 - 2,918 10 3 + 35,8 + 0,064.
Nendes numbrites on viimased olulised numbrid kahtlased (valed on juba ära visatud). Kirjutame need kujul 543820 - 2918 + 35,8 + 0,064.
On näha, et esimesel liikmel on kahtlasel arvul 2 kõrgeim number (kümned). Kõik ülejäänud arvud ümardades järgmise numbrini ja liites, saame
543820-2918 + 36 + 0 = 540940 = 5,4094 10 5 .
2. reegel Ligikaudsete arvude korrutamisel (jagamisel) peate:
a) vali number (numbrid), millel on kõige vähem olulisi numbreid ( TÄHTIS – numbrid peale nulli ja nullid nende vahel);
b) ümardage ülejäänud numbrid nii, et neil oleks üks oluline number rohkem (üks varunumber on salvestatud) kui punktis a määratud number;
c) korrutada (jagada) saadud arvud;
d) selle tulemusena jätke nii palju tähenduslikke numbreid, kui palju oli kõige väiksema arvu numbritega arvus (arvudes).
Näide: .
3. reegel Tõstmisel astmeni, juure eraldamisel salvestatakse nii palju olulisi numbreid, kui palju on algses numbris.
Näide: ![]() .
.
4. reegel Arvu logaritmi leidmisel peab logaritmi mantissil olema nii palju olulisi numbreid, kui palju on algarvus:
Näide: ![]() .
.
Viimases sissekandes absoluutne vead tuleks jätta ainult üks oluline number. (Kui see number osutub 1-ks, salvestatakse selle järele veel üks number).
Keskmine väärtus ümardatakse sama numbrini kui absoluutne viga.
Näiteks: V\u003d (375,21 0,03) cm 3 \u003d (3,7521 0,0003) cm 3.
I\u003d (5,530 0,013) A, A = ![]() J.
J.
Töökäsk
Silindri läbimõõdu määramine.
1. Mõõtke nihikuga 7 korda (in erinevad kohad ja suunad) silindri läbimõõt. Kirjutage tulemused tabelisse.
| Nr p / lk | d i , mm | d i- | (d i- | tere, mm ja Seotud Informatsioon: |
MÕÕTMISVIGA ELEMENTAARSED HINNANGUD
Mõõtmine on füüsikalise suuruse väärtuse leidmine empiiriliselt spetsiaalsete tehniliste vahendite – mõõdikute, mõõteriistade – abil.
Mõõt on mõõtmisvahend, mis reprodutseerib etteantud suurusega füüsikalist suurust – mõõtühikut, selle mitmekordset või murdosa väärtust. Näiteks kaalud 1 kg, 5 kg, 10 kg.
Mõõteseade on mõõtevahend, mis on ette nähtud mõõteinformatsiooni signaali genereerimiseks vaatlejale vahetult tajutavas vormis. Mõõteseade võimaldab mõõdetud väärtust mõõtudega otseselt või kaudselt võrrelda. Mõõtmised jagunevad ka otsesteks ja kaudseteks.
Otsemõõtmistega leitakse soovitud koguse väärtus otse põhi(katse)andmetest.
Kaudsete mõõtmiste korral leitakse suuruse soovitud väärtus selle suuruse ja otsemõõdetavate suuruste vahelise teadaoleva seose alusel. Mõõtmispõhimõte on füüsikaliste nähtuste kogum, millel mõõtmised põhinevad.
Mõõtmismeetod - meetodite kogum mõõtmispõhimõtete ja -vahendite kasutamiseks. Tähendus füüsiline kogus, mis ideaalis peegeldaks kvalitatiivses ja kvantitatiivses mõttes antud objekti vastavaks omaduseks on füüsikalise suuruse tegelik väärtus. Selle mõõtmisel leitud füüsikalise suuruse väärtus on mõõtmise tulemus.
Mõõtetulemuse kõrvalekalle mõõdetud suuruse tegelikust väärtusest on mõõtmisviga.
Absoluutne mõõtmisviga on mõõtmisviga, mida väljendatakse mõõdetud suuruse ühikutes ja mis on võrdne tulemuse ja mõõdetud suuruse tegeliku väärtuse vahega. Absoluutvea ja mõõdetud suuruse tegeliku väärtuse suhe on suhteline mõõtmisviga.
Mõõtmisveale aitavad kaasa mõõteriistade vead (instrumentaal- või instrumentaalviga), mõõtmismeetodi ebatäiuslikkus, näiduviga mõõteriista skaalal, välismõjud mõõtevahenditel ja -objektidel, inimese valgus- ja helisignaalidele reageerimise viivitus.
Vigade avaldumise olemuse järgi jaotatakse need süstemaatilisteks ja juhuslikeks. Juhuslik sündmus on sündmus, mis teatud tegurite kogumi tõttu võib toimuda või mitte.
Juhuslik viga - mõõtevea komponent, mis muutub juhuslikult sama väärtusega korduvatel mõõtmistel. iseloomulik tunnus juhuslikud vead on vea suuruse ja märgi muutus konstantsetes mõõtmistingimustes.
Süstemaatiline viga - mõõtmisvea komponent, mis jääb sama väärtusega korduvate mõõtmiste käigus konstantseks või muutub regulaarselt. Süstemaatilisi vigu saab põhimõtteliselt kõrvaldada paranduste abil, kasutades täpsemaid instrumente ja meetodeid (kuigi praktikas pole süsteemset viga alati lihtne avastada). Üksikute mõõtmiste juhuslikke vigu ei saa välistada, juhuslike nähtuste matemaatiline teooria (tõenäosusteooria) võimaldab vaid nende suurust mõistlikult hinnata.
Otseste mõõtmiste vead
Oletame, et süstemaatilised vead on välistatud ja mõõtmistulemuste vead on juhuslikud. Tähistame tähtedega - füüsikalise suuruse mõõtmise tulemusi, tõeline väärtus mis on võrdne ![]() . Näidatud on üksikute mõõtmiste tulemuste absoluutsed vead:
. Näidatud on üksikute mõõtmiste tulemuste absoluutsed vead:
Summeerides saadud võrdsuse (1) vasaku ja parema külje, saame:
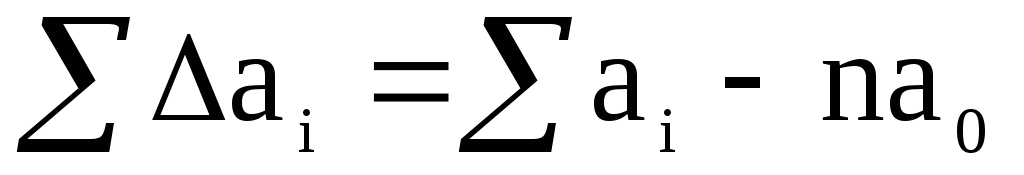 (2)
(2)
Juhuslike vigade teooria põhineb eksperimentaalselt kinnitatud eeldustel:
vead võivad võtta pideva väärtuste jada;
juures suured numbrid mõõtmised juhuslikud vead samas suurusjärgus, kuid erinev märk kohtuda võrdselt sageli;
vea esinemise tõenäosus väheneb selle suuruse kasvades. Samuti on vajalik, et vead oleksid mõõdetud väärtusega võrreldes väikesed ja sõltumatud.
Eelduse (1) kohaselt saame mõõtmiste arvuga n
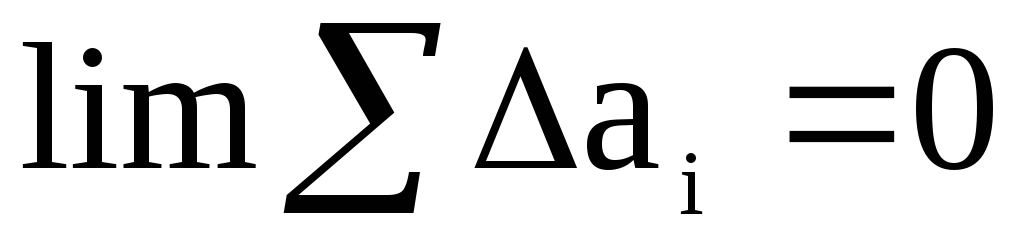
 ,
,
Mõõtmete arv on aga alati lõplik ja ![]() jääb teadmata. Kuid praktilistel eesmärkidel piisab, kui leida katseliselt füüsikalise suuruse väärtus, mis on nii lähedane tegelikule väärtusele, et
jääb teadmata. Kuid praktilistel eesmärkidel piisab, kui leida katseliselt füüsikalise suuruse väärtus, mis on nii lähedane tegelikule väärtusele, et  saab kasutada tõelise asemel. Küsimus on selles, kuidas hinnata selle lähenduse astet?
saab kasutada tõelise asemel. Küsimus on selles, kuidas hinnata selle lähenduse astet?
Tõenäosusteooria järgi mõõtmiste jada aritmeetiline keskmine  usaldusväärsem kui üksikute mõõtmiste tulemused, sest juhuslikud kõrvalekalded tegelikust väärtusest erinevates suundades on võrdselt tõenäolised. Väärtuse a i ilmumise tõenäosuse puhul laiuse vahemikus 2a i mõistame intervalli 2a i langevate väärtuste a i suhtelist esinemissagedust kõigi esinevate väärtuste arvuga a i arvuga. katsetest (mõõtmistest), mis kalduvad lõpmatusse. Ilmselgelt on teatud sündmuse tõenäosus võrdne ühega, võimatu sündmuse tõenäosus on null, s.t. 0 100%.
usaldusväärsem kui üksikute mõõtmiste tulemused, sest juhuslikud kõrvalekalded tegelikust väärtusest erinevates suundades on võrdselt tõenäolised. Väärtuse a i ilmumise tõenäosuse puhul laiuse vahemikus 2a i mõistame intervalli 2a i langevate väärtuste a i suhtelist esinemissagedust kõigi esinevate väärtuste arvuga a i arvuga. katsetest (mõõtmistest), mis kalduvad lõpmatusse. Ilmselgelt on teatud sündmuse tõenäosus võrdne ühega, võimatu sündmuse tõenäosus on null, s.t. 0 100%.
Tõenäosust, et soovitud väärtus (selle tegelik väärtus) sisaldub intervallis (a - a, a + a), nimetatakse usaldustõenäosuseks (usaldusväärsuseks) ja vastavaks intervalliks (a - a, a + a) - usaldusvahemik; mida väiksem on vea väärtus a, seda väiksem on tõenäosus, et mõõdetud väärtus sisaldub selle veaga määratud intervallis. Tõsi on ka vastupidine väide: mida väiksem on tulemuse usaldusväärsus, seda kitsam on soovitud väärtuse usaldusvahemik.
Suure n korral (praktiliselt n 100 puhul) on antud usaldusväärsuse usaldusvahemiku poollaius võrdne
 ,
(3)
,
(3)
kus K() = 1, kui = 0,68; K() = 2 at = 0,95; K() = 3 ja = 0,997.
Väikese mõõtmiste arvu korral, mida kõige sagedamini esineb üliõpilaste laboripraktikas, sõltub (3) koefitsient K() mitte ainult -st, vaid ka mõõtmiste arvust n. Seetõttu sõltume alati ainult saadavusest juhuslik viga usaldusvahemiku poollaius leitakse valemiga
 (4)
(4)
Punktis (4) nimetatakse koefitsienti t n Studenti koefitsiendiks. Üliõpilaspraktikas kasutatava = 0,95 korral on t n väärtused järgmised:
Väärtust nimetatakse mõõtmiste seeria aritmeetilise keskmise ruutkeskmise veaks.
Seadme või mõõdiku viga on tavaliselt näidatud tema passis või seadme skaalal oleva sümboliga. Tavaliselt mõistetakse instrumendi veana poollaiust intervallist, mille sees mõõdetud väärtus mahub mõõtetõenäosusega 0,997, kui mõõtmisviga on tingitud ainult instrumendi veast. Mõõtmistulemuse summaar- (kogu)veana aktsepteerime tõenäosusega = 0,95
Absoluutne viga võimaldab teil määrata, milline tulemuse märk sisaldab ebatäpsust. Suhteline viga annab teavet selle kohta, kui suur osa (protsent) mõõdetud väärtusest on viga (usaldusvahemiku pool laius).
Kirjutame vormile 0 otsemõõtmiste seeria lõpptulemuse
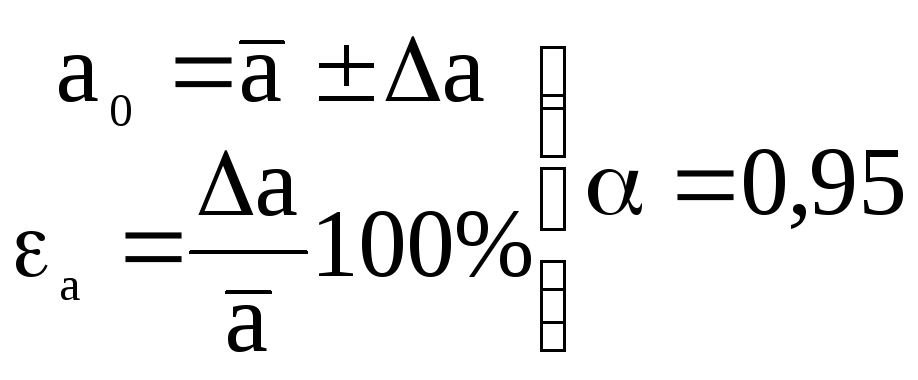 .
.
Näiteks
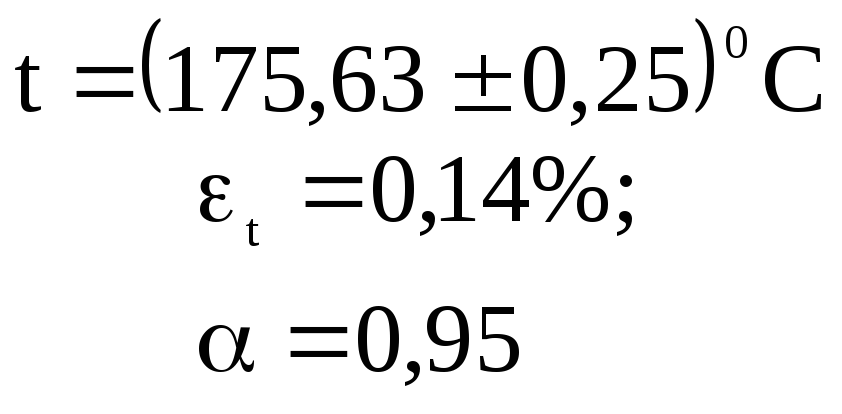 (6)
(6)
Seega peab iga empiiriliselt leitud füüsikaline suurus olema esindatud järgmisega:

Mõõdetud ja tabeliväärtuste vead põhjustavad kaudselt määratud väärtuse DX avg vigu ning suurima panuse DX keskmisse annavad kõige vähem täpsed väärtused maksimaalse suhtelise veaga d. Seetõttu on kaudsete mõõtmiste täpsuse parandamiseks vaja saavutada otseste mõõtmiste võrdne täpsus.
(d A, d B, d C, ...).
Kaudsete mõõtmiste vigade leidmise reeglid:
1. Leia antud funktsiooni naturaallogaritm
log(X = f(A,B,C,…));
2. Leidke leitud kogudiferentsiaal (üle kõigi muutujate). naturaallogaritm antud funktsioon;
3. Asenda diferentsiaali d märk absoluutvea D märgiga;
4. Asendage kõik absoluutsete vigadega "miinused". DA, DB, DC, ... "proffidele".
Tulemuseks on suurima valem suhteline viga d x kaudselt mõõdetud väärtus X:
d x = = j (A av, B av, C av, …, DA av, DB av, DC av, …).(18)
Vastavalt leitud suhtelisele veale d x määrata absoluutne viga kaudne mõõtmine:
DX cf \u003d d x. X vrd . (19)
Kaudsete mõõtmiste tulemus registreeritakse standardsel kujul ja kujutatakse numbriteljel:
X \u003d (X sr ± DX sr),üksus. (kakskümmend)

Näide:
Otsige üles sugulane ja keskmised vead füüsiline kogus L, määratakse kaudselt valemiga:
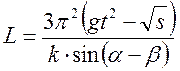 , (21)
, (21)
kus π, g, t, k, α, β- kogused, mille väärtused on mõõdetud või võetud võrdlustabelitest ja kantud mõõtmistulemuste ja tabeliandmete tabelisse (sarnaselt tabeliga 1).
1. Arvutage keskmine väärtus L vrd, asendades punktis (21) tabelis olevad keskmised väärtused - π cf, g cf, t cf, k cf, α cf, β cf.
2. Määrake suurim suhteline viga δ L:
a). Valem (21) on logaritmitud:
b). Saadud avaldis (22) eristatakse:
c) Asendage diferentsiaali d märk Δ-ga ja "miinused" absoluutsete vigade ees - "plussidega" ja hankige suurima suhtelise vea avaldis δ L:
d). Asendades saadud avaldises sisendsuuruste keskmised väärtused ja nende vead mõõtmistulemuste tabelist, arvutage δ L.
3. Seejärel arvutage absoluutviga ΔLav:
![]()
Tulemus salvestatakse standardsel kujul ja joonistatakse graafiliselt teljel L:
![]() , ühikut rev.
, ühikut rev.
