حاصل ضرب الف ب. وکتور برای آدمک. اقدامات با بردارها مختصات برداری ساده ترین مسائل با بردارها

7.1. تعریف محصول متقاطع

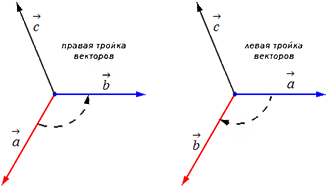
سه بردار غیرهمسطح a، b و c که به ترتیب نشان داده شده گرفته شده اند، یک سه گانه سمت راست را تشکیل می دهند اگر از انتهای بردار سوم c، کوتاه ترین چرخش از بردار اول a به بردار دوم b دیده شود. در خلاف جهت عقربه های ساعت باشد و اگر در جهت عقربه های ساعت باشد یک سه قلو چپ گرد باشد (شکل 16 را ببینید).

حاصلضرب بردار a و بردار b را بردار c می نامند که:

1. عمود بر بردارهای a و b یعنی c ^ a و c ^ ب

2. دارای طول عددی برابر با مساحت متوازی الاضلاع ساخته شده بر روی بردارهای a وبهمانطور که در طرفین (نگاه کنید به شکل 17)، i.e.

3. بردارهای a، b و c یک سه گانه راست را تشکیل می دهند.

اثر هنری وکتوربا x b یا [a,b] نشان داده می شود. روابط زیر بین بردارهای واحد من مستقیماً از تعریف حاصلضرب بردار تبعیت می کند. jو ک(شکل 18 را ببینید):

i x j = k، j x k = i، k x i = j.
مثلاً این را ثابت کنیم i xj = k.

1) k ^ i، k ^ j ;

2) |k |=1، اما | من x j| = |i | |J | sin(90°)=1;

3) بردارهای i، j و کیک سه گانه راست تشکیل دهید (شکل 16 را ببینید).

7.2. خواص یک محصول متقاطع

1. هنگام تنظیم مجدد فاکتورها، محصول برداری علامت تغییر می کند، i.e. و xb =(b xa) (شکل 19 را ببینید).

بردارهای a xb و b xa هم خط هستند، دارای ماژول های یکسان هستند (مساحت متوازی الاضلاع بدون تغییر باقی می ماند)، اما جهت مخالف هستند (سه برابر a، b، a xb و a، b، b x a با جهت مخالف). به این معنا که axb = -(b xa).

2. حاصلضرب برداری نسبت به ضریب اسکالر خاصیت ترکیبی دارد، یعنی l (a xb) = (l a) x b = a x (l b).

اجازه دهید l > 0. بردار l (a xb) بر بردارهای a و b عمود است. بردار ( لتبر بهمچنین بر بردارهای a و عمود است ب(بردارهای a، لاما در همان هواپیما دراز بکشید). این بدان معناست که بردارها ل(axb) و ( لتبر بخطی بدیهی است که جهت آنها منطبق است. طول آنها یکسان است:

از همین رو ل(a xb)= لیک xb به روشی مشابه برای ل<0.

3. دو بردار غیر صفر a و بخطی هستند اگر و فقط اگر حاصلضرب بردار آنها برابر بردار صفر باشد، یعنی a ||b<=>و xb = 0.

به طور خاص، i *i =j *j =k *k =0 .

4. محصول برداری دارای خاصیت توزیع است:

(الف + ب) xc = یک xc + ب xs.

بدون مدرک می پذیریم.

7.3. بیان ضربدر بر حسب مختصات

از جدول حاصل ضرب بردار i استفاده خواهیم کرد، jو ک:

اگر جهت کوتاه ترین مسیر از بردار اول به بردار دوم با جهت فلش منطبق باشد، حاصل ضرب برابر بردار سوم است و اگر منطبق نباشد، بردار سوم با علامت منفی گرفته می شود.

بگذارید دو بردار a =a x i +a y داده شود j+a z کو b =b x من+b y j+b z ک. بیایید حاصل ضرب برداری این بردارها را با ضرب آنها به صورت چند جمله ای (با توجه به ویژگی های حاصلضرب بردار) پیدا کنیم:

فرمول حاصل را می توان حتی به طور خلاصه تر نوشت:

از آنجایی که سمت راست برابری (7.1) با بسط تعیین کننده مرتبه سوم از نظر عناصر ردیف اول مطابقت دارد. برابری (7.2) به راحتی قابل یادآوری است.

7.4. برخی از کاربردهای محصول متقابل

ایجاد هم خطی بردارها

پیدا کردن مساحت متوازی الاضلاع و مثلث

با توجه به تعریف حاصلضرب برداری بردارها آو ب | یک xb | =|a | * |b |sin g، یعنی S جفت = |a x b |. و بنابراین، D S = 1/2|a x b |.

تعیین لحظه نیرو در مورد یک نقطه

بگذارید نیرویی در نقطه A اعمال شود F =ABرهایش کن در باره- نقطه ای در فضا (شکل 20 را ببینید).

از علم فیزیک معلوم است که لحظه نیرو اف نسبت به نقطه در بارهبردار نامیده می شود م،که از نقطه عبور می کند در بارهو:

1) عمود بر صفحه ای که از نقاط عبور می کند O, A, B;

2) عددی برابر حاصل ضرب نیرو در هر بازو

3) یک سه ضلعی راست با بردارهای OA و A B تشکیل می دهد.

بنابراین، M = OA x F.

یافتن سرعت چرخش خطی

سرعت vنقطه M یک جسم صلب که با سرعت زاویه ای می چرخد wحول یک محور ثابت، با فرمول اویلر v =w xr تعیین می شود، جایی که r = OM، جایی که O نقطه ثابت محور است (شکل 21 را ببینید).

Yandex.RTB R-A-339285-1

قبل از ارائه مفهوم حاصلضرب بردار، اجازه دهید به سؤال جهت گیری یک سه گانه مرتب شده از بردارهای a →، b →، c → در فضای سه بعدی بپردازیم.

برای شروع، بردارهای a → , b → , c → را از یک نقطه کنار می گذاریم. جهت سه گانه a → , b → , c → بسته به جهت خود بردار c → می تواند راست یا چپ باشد. نوع سه گانه a → , b → , c → از جهتی که کوتاه ترین چرخش از بردار a → به b → از انتهای بردار c → انجام می شود تعیین می شود.

اگر کوتاه ترین چرخش در خلاف جهت عقربه های ساعت انجام شود، سه بردار a → , b → , c → نامیده می شود. درست، اگر در جهت عقربه های ساعت باشد - ترک کرد.

سپس دو بردار غیر خطی a → و b → را بگیرید. سپس بردارهای A B → = a → و A C → = b → را از نقطه A رسم می کنیم. بیایید یک بردار A D → = c → بسازیم که به طور همزمان بر هر دو A B → و A C → عمود است. بنابراین، هنگام ساختن خود بردار A D → = c →، می‌توانیم دو کار انجام دهیم، که به آن یک جهت یا مخالف بدهیم (به شکل نگاه کنید).

یک سه مرتبه از بردارهای a → , b → , c → می تواند، همانطور که متوجه شدیم، بسته به جهت بردار، راست یا چپ باشد.

از موارد فوق می توان تعریف یک محصول برداری را معرفی کرد. این تعریف برای دو بردار تعریف شده در یک سیستم مختصات مستطیلی از فضای سه بعدی ارائه شده است.

تعریف 1

حاصل ضرب برداری دو بردار a → و b → ما چنین بردار تعریف شده در یک سیستم مختصات مستطیلی فضای سه بعدی را به گونه ای فراخوانی می کنیم که:

اگر بردارهای a → و b → هم خط باشند، صفر خواهد بود.
بر هر دو بردار a → و بردار b → یعنی عمود خواهد بود. ∠ a → c → = ∠ b → c → = π 2 ;
طول آن با فرمول تعیین می شود: c → = a → · b → · sin ∠ a → , b → ;
سه بردار a → , b → , c → جهت گیری یکسانی با سیستم مختصات داده شده دارد.

حاصل ضرب برداری بردارهای a → و b → نماد زیر است: a → × b →.

مختصات حاصلضرب بردار

از آنجایی که هر بردار دارای مختصات خاصی در سیستم مختصات است، می‌توانیم تعریف دومی از حاصلضرب بردار ارائه کنیم که به ما امکان می‌دهد مختصات آن را با استفاده از مختصات داده شده بردارها پیدا کنیم.

تعریف 2

در یک سیستم مختصات مستطیلی از فضای سه بعدی حاصل ضرب برداری دو بردار a → = (a x ; a y ; a z) و b → = (b x ; b y ; b z) بردار c → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k → ، جایی که i → , j → , k → بردارهای مختصاتی هستند.

حاصلضرب برداری را می توان به عنوان تعیین کننده یک ماتریس مربع مرتبه سوم نشان داد، که در آن سطر اول شامل بردارهای i → , j → , k → است، سطر دوم حاوی مختصات بردار a → و سطر سوم است. شامل مختصات بردار b → در یک سیستم مختصات مستطیلی مشخص است، این تعیین کننده ماتریس به نظر می رسد: c → = a → × b → = i → j → k → a x a y a z b x b y b z

با گسترش این تعیین کننده به عناصر ردیف اول، برابری را بدست می آوریم: c → = a → × b → = i → j → k → a x a y a z b x b y b z = a y a z b y b z · i → - a x a z b x b z · j → + a x a y x b → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k →

خواص یک محصول متقاطع

مشخص است که حاصلضرب برداری در مختصات به عنوان تعیین کننده ماتریس c → = a → × b → = i → j → k → a x a y a z b x b y b z نمایش داده می شود، سپس بر اساس خواص تعیین کننده ماتریسموارد زیر نمایش داده می شود خواص یک محصول برداری:

ضد جابجایی a → × b → = - b → × a → ;
توزیع a (1) → + a (2) → × b = a (1) → × b → + a (2) → × b → یا a → × b (1) → + b (2) → = a → × b (1) → + a → × b (2) → ;
ارتباط λ a → × b → = λ a → × b → یا a → × (λ b →) = λ a → × b →، که در آن λ یک عدد واقعی دلخواه است.

این خواص اثبات ساده ای دارند.

به عنوان مثال، ما می توانیم خاصیت ضد جابجایی یک محصول برداری را اثبات کنیم.

اثبات ضد جابجایی

طبق تعریف، a → × b → = i → j → k → a x a y a z b x b y b z و b → × a → = i → j → k → b x b y b z a x a y a z . و اگر دو ردیف از ماتریس تعویض شوند، مقدار تعیین کننده ماتریس باید به عکس تغییر کند، بنابراین، a → × b → = i → j → k → a x a y a z b x b y b z = - i → j → k → b x b y b z a x ay - b → × a → که و ثابت می کند که حاصلضرب بردار ضد جابجایی است.

محصول برداری - مثال ها و راه حل ها

در بیشتر موارد، سه نوع مشکل وجود دارد.

در مسائل نوع اول معمولا طول دو بردار و زاویه بین آنها آورده می شود و باید طول حاصلضرب بردار را پیدا کنید. در این مورد از فرمول زیر c → = a → · b → · sin ∠ a → , b → استفاده کنید.

مثال 1

طول حاصلضرب برداری بردارهای a → و b → را در صورتی که a → = 3، b → = 5، ∠ a →، b → = π 4 می دانید، بیابید.

راه حل

با تعیین طول حاصل ضرب برداری بردارهای a → و b → این مشکل را حل می کنیم: a → × b → = a → · b → · sin ∠ a → , b → = 3 · 5 · sin π 4 = 15 2 2 .

پاسخ: 15 2 2 .

مسائل نوع دوم با مختصات بردارها، در آنها حاصل ضرب برداری، طول آن و غیره ارتباط دارند. از طریق مختصات شناخته شده بردارهای داده شده جستجو می شوند a → = (a x; a y; a z) و b → = (b x؛ b y؛ b z) .

برای این نوع مشکلات، شما می توانید بسیاری از گزینه های کار را حل کنید. به عنوان مثال، مختصات بردارهای a → و b → را نمی توان مشخص کرد، بلکه بسط آن ها را به بردارهای مختصات شکل می توان تعیین کرد. b → = b x · i → + b y · j → + b z · k → و c → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k →، یا بردارهای a → و b → را می توان با مختصات شروع آنها مشخص کرد. و نقاط پایانی

مثال های زیر را در نظر بگیرید.

مثال 2

در یک سیستم مختصات مستطیلی، دو بردار داده می شود: a → = (2؛ 1؛ - 3)، b → = (0؛ - 1؛ 1). محصول متقابل آنها را پیدا کنید.

راه حل

با تعریف دوم، حاصل ضرب برداری دو بردار را در مختصات داده شده پیدا می کنیم: a → × b → = (a y · b z - a z · b y) · i → + (a z · b x - a x · b z) · j → + ( a x · b y - a y · b x) · k → = = (1 · 1 - (- 3) · (- 1)) · i → + ((- 3) · 0 - 2 · 1) · j → + (2) · (- 1) - 1 · 0) · k → = = - 2 i → - 2 j → - 2 k → .

اگر حاصلضرب برداری را از طریق تعیین کننده ماتریس بنویسیم، جواب این مثال به این صورت است: a → × b → = i → j → k → a x a y a z b x b y b z = i → j → k → 2 1 - 3 0 - 1 1 = - 2 i → - 2 j → - 2 k → .

پاسخ: a → × b → = - 2 i → - 2 j → - 2 k → .

مثال 3

طول حاصلضرب برداری بردارهای i → - j → و i → + j → + k → را بیابید که i →، j →، k → بردارهای واحد سیستم مختصات دکارتی مستطیلی هستند.

راه حل

ابتدا، اجازه دهید مختصات یک حاصلضرب برداری معین i → - j → × i → + j → + k → را در یک سیستم مختصات مستطیلی مشخص پیدا کنیم.

مشخص است که بردارهای i → - j → و i → + j → + k → به ترتیب دارای مختصات (1؛ - 1؛ 0) و (1؛ 1؛ 1) هستند. بیایید طول حاصلضرب برداری را با استفاده از تعیین کننده ماتریس پیدا کنیم، سپس i → - j → × i → + j → + k → = i → j → k → 1 - 1 0 1 1 1 = - i → داریم. - j → + 2 k → .

بنابراین، حاصلضرب برداری i → - j → × i → + j → + k → دارای مختصات (- 1 ; - 1 ; 2) در سیستم مختصات داده شده است.

طول حاصلضرب برداری را با استفاده از فرمول پیدا می کنیم (به بخش یافتن طول یک بردار مراجعه کنید): i → - j → × i → + j → + k → = - 1 2 + - 1 2 + 2 2 = 6.

پاسخ: i → - j → × i → + j → + k → = 6. .

مثال 4

در یک سیستم مختصات دکارتی مستطیلی، مختصات سه نقطه A (1، 0، 1)، B (0، 2، 3)، C (1، 4، 2) آورده شده است. چند بردار عمود بر A B → و A C → همزمان پیدا کنید.

راه حل

بردارهای A B → و A C → به ترتیب دارای مختصات زیر هستند (- 1 ; 2 ; 2) و (0 ; 4 ; 1). با یافتن حاصلضرب برداری بردارهای A B → و A C →، بدیهی است که بردار عمود بر هر دو A B → و A C → است، یعنی راه حلی برای مسئله ما است. بیایید آن را A B → × A C → = i → j → k → - 1 2 2 0 4 1 = - 6 i → + j → - 4 k → پیدا کنیم.

پاسخ: - 6 i → + j → - 4 k → . - یکی از بردارهای عمود بر.

مسائل نوع سوم بر استفاده از ویژگی های حاصلضرب برداری بردارها متمرکز است. پس از اعمال آن، راه حلی برای مشکل داده شده به دست خواهیم آورد.

مثال 5

بردارهای a → و b → عمود هستند و طول آنها به ترتیب 3 و 4 است. طول حاصلضرب برداری 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 a → × a → + 3 · a → × - 2 · b → + - b → × a → + - b → × - 2 · b → .

راه حل

با خاصیت توزیعی یک محصول برداری، می توانیم 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 بنویسیم. a → × a → + 3 a → × - 2 b → + - b → × a → + - b → × - 2 b →

با خاصیت تداعی، ضرایب عددی را از علامت محصولات برداری در آخرین عبارت خارج می کنیم: 3 · a → × a → + 3 · a → × - 2 · b → + - b → × a → + - b → × - 2 · b → = = 3 · a → × a → + 3 · (- 2) · a → × b → + (- 1) · b → × a → + (- 1) · (- 2) · b → × b → = = 3 a → × a → - 6 a → × b → - b → × a → + 2 b → × b →

حاصلضرب های برداری a → × a → و b → × b → برابر با 0 هستند، زیرا a → × a → = a → · a → · sin 0 = 0 و b → × b → = b → · b → · sin 0 = 0، سپس 3 · a → × a → - 6 · a → × b → - b → × a → + 2 · b → × b → = - 6 · a → × b → - b → × a → . .

از ضد جابجایی حاصلضرب بردار نتیجه می شود - 6 · a → × b → - b → × a → = - 6 · a → × b → - (- 1) · a → × b → = - 5 · a → × ب → .

با استفاده از ویژگی های حاصلضرب بردار، برابری 3 · a → - b → × a → - 2 · b → = = - 5 · a → × b → را به دست می آوریم.

بر اساس شرط، بردارهای a → و b → عمود هستند، یعنی زاویه بین آنها برابر با π 2 است. اکنون تنها چیزی که باقی می ماند این است که مقادیر یافت شده را با فرمول های مناسب جایگزین کنید: 3 a → - b → × a → - 2 b → = - 5 a → × b → = = 5 a → × b → = 5 a → b → · sin (a → , b →) = 5 · 3 · 4 · sin π 2 = 60 .

پاسخ: 3 a → - b → × a → - 2 b → = 60.

طول حاصلضرب برداری بردارها طبق تعریف برابر است با a → × b → = a → b → · sin ∠ a → , b → . از آنجایی که قبلاً (از دوره مدرسه) مشخص شده است که مساحت یک مثلث برابر است با نصف حاصل ضرب طول دو ضلع آن در سینوس زاویه بین این ضلع ها. در نتیجه، طول حاصلضرب بردار برابر است با مساحت متوازی الاضلاع - یک مثلث دو برابر شده، یعنی حاصل ضرب اضلاع به شکل بردارهای a → و b →، که از یک نقطه، توسط سینوس گذاشته شده است. زاویه بین آنها گناه ∠ a →، b →.

این معنای هندسی یک محصول برداری است.

معنای فیزیکی محصول برداری

در مکانیک، یکی از شاخه های فیزیک، به لطف حاصلضرب بردار، می توانید ممان یک نیرو را نسبت به نقطه ای از فضا تعیین کنید.

تعریف 3

در لحظه اعمال نیروی F ← به نقطه B، نسبت به نقطه A، حاصلضرب برداری زیر A B → × F → را درک خواهیم کرد.

در صورت مشاهده خطایی در متن، لطفاً آن را برجسته کرده و Ctrl+Enter را فشار دهید

تعریف. حاصلضرب برداری بردار a (ضربی) و بردار غیر خطی (چند برابری) سومین بردار c (مضرب) است که به صورت زیر ساخته شده است:

1) ماژول آن از نظر عددی برابر با مساحت متوازی الاضلاع در شکل است. 155)، بر روی بردارها ساخته شده است، یعنی برابر است با جهت عمود بر صفحه متوازی الاضلاع مذکور؛

3) در این حالت، جهت بردار c (از دو مورد ممکن) انتخاب می شود تا بردارهای c یک سیستم سمت راست را تشکیل دهند (§ 110).

نامگذاری: یا

اضافه بر تعریف. اگر بردارها خطی باشند، با در نظر گرفتن شکل متوازی الاضلاع (شرط) طبیعی است که مساحت صفر را اختصاص دهیم. بنابراین حاصل ضرب برداری بردارهای خطی برابر با بردار صفر در نظر گرفته می شود.

از آنجایی که بردار تهی را می توان به هر جهتی اختصاص داد، این توافق با بندهای 2 و 3 تعریف مغایرتی ندارد.

نکته 1. در اصطلاح «ضرب بردار» اولین کلمه نشان می‌دهد که نتیجه عمل یک بردار است (برخلاف حاصلضرب اسکالر؛ رجوع کنید به § 104، تبصره 1).

مثال 1. حاصلضرب برداری را پیدا کنید که بردارهای اصلی سیستم مختصات سمت راست هستند (شکل 156).

1. از آنجایی که طول بردارهای اصلی برابر با یک واحد مقیاس است، مساحت متوازی الاضلاع (مربع) از نظر عددی برابر با یک است. یعنی مدول حاصلضرب بردار برابر با یک است.

2. از آنجایی که عمود بر صفحه یک محور است، حاصلضرب بردار مورد نظر بردار خطی بردار k است. و از آنجایی که هر دوی آنها مدول 1 دارند، حاصل ضرب برداری مورد نظر برابر با k یا -k است.

3. از بین این دو بردار ممکن، اولین بردار باید انتخاب شود، زیرا بردارهای k یک سیستم سمت راست (و بردارها یک سمت چپ) را تشکیل می دهند.

مثال 2. حاصل ضرب متقاطع را پیدا کنید

راه حل. مانند مثال 1، نتیجه می گیریم که بردار برابر با k یا -k است. اما اکنون باید -k را انتخاب کنیم، زیرا بردارها یک سیستم سمت راست را تشکیل می دهند (و بردارها یک سیستم چپ را تشکیل می دهند). بنابراین،

مثال 3. طول بردارها به ترتیب برابر با 80 و 50 سانتی متر است و زاویه 30 درجه را تشکیل می دهند. با در نظر گرفتن متر به عنوان واحد طول، طول حاصلضرب برداری a را پیدا کنید

راه حل. مساحت متوازی الاضلاع ساخته شده بر روی بردارها برابر است با طول حاصلضرب برداری مورد نظر برابر است با

مثال 4. طول حاصل ضرب بردار همان بردارها را با واحد طول سانتیمتر بیابید.

راه حل. از آنجایی که مساحت متوازی الاضلاع ساخته شده روی بردارها برابر است، طول حاصلضرب بردار برابر با 2000 سانتی متر است، یعنی.

از مقایسه مثال های 3 و 4 مشخص می شود که طول بردار نه تنها به طول عوامل بلکه به انتخاب واحد طول نیز بستگی دارد.

معنای فیزیکی یک محصول برداریاز بین مقادیر فیزیکی متعددی که توسط حاصلضرب بردار نشان داده شده است، فقط لحظه نیرو را در نظر خواهیم گرفت.

نقطه اعمال نیرو A باشد. گشتاور نیرو نسبت به نقطه O را حاصلضرب بردار می گویند. از آنجایی که مدول این ضرب برداری از نظر عددی برابر با مساحت متوازی الاضلاع است (شکل 157) پس مدول ممان برابر است با حاصل ضرب پایه و ارتفاع، یعنی نیروی ضرب شده در فاصله نقطه O تا خط مستقیمی که نیرو در امتداد آن وارد می شود.

در مکانیک ثابت شده است که برای اینکه جسم صلب در حالت تعادل باشد، لازم است که نه تنها مجموع بردارهایی که نیروهای وارد شده به جسم را نشان می دهند، برابر با صفر باشد، بلکه مجموع گشتاور نیروها نیز برابر باشد. در موردی که همه نیروها با یک صفحه موازی هستند، جمع بردارهایی که ممان ها را نشان می دهند را می توان با جمع و تفریق قدر آنها جایگزین کرد. اما با جهت گیری دلخواه نیروها، چنین جایگزینی غیرممکن است. مطابق با این، محصول برداری دقیقاً به عنوان یک بردار تعریف می شود و نه به عنوان یک عدد.

در این مقاله نگاهی دقیق‌تر به مفهوم حاصلضرب دو بردار خواهیم داشت. ما تعاریف لازم را ارائه می دهیم، فرمولی برای یافتن مختصات یک محصول برداری می نویسیم، خواص آن را فهرست و توجیه می کنیم. پس از این، به معنای هندسی حاصلضرب بردار دو بردار می پردازیم و راه حل هایی را برای مثال های مختلف در نظر می گیریم.

پیمایش صفحه.

تعریف محصول متقاطع

قبل از تعریف یک محصول برداری، بیایید جهت یک سه بردار مرتب شده در فضای سه بعدی را درک کنیم.

بیایید بردارها را از یک نقطه رسم کنیم. بسته به جهت بردار، این سه می توانند راست یا چپ باشند. بیایید از انتهای بردار به چگونگی کوتاهترین چرخش از بردار به . اگر کوتاه ترین چرخش در خلاف جهت عقربه های ساعت اتفاق بیفتد، سه بردار نامیده می شود درست، در غیر این صورت - ترک کرد.

حال دو بردار غیر خطی و . اجازه دهید بردارها و از نقطه A را رسم کنیم. بیایید چند بردار عمود بر هر دو و و بسازیم. بدیهی است که هنگام ساختن یک بردار، می‌توانیم دو کار انجام دهیم، یا یک جهت یا برعکس بدهیم (به تصویر مراجعه کنید).

بسته به جهت بردار، سه گانه مرتب شده از بردارها می تواند راست دست یا چپ باشد.

این ما را به تعریف یک محصول برداری نزدیک می کند. برای دو بردار تعریف شده در یک سیستم مختصات مستطیلی از فضای سه بعدی داده شده است.

تعریف.

حاصلضرب متقاطع دو بردارو مشخص شده در یک سیستم مختصات مستطیلی فضای سه بعدی، بردار نامیده می شود به طوری که

حاصل ضرب بردارها و به صورت .

مختصات حاصلضرب بردار.

اکنون تعریف دوم یک محصول برداری را ارائه می دهیم که به شما امکان می دهد مختصات آن را از مختصات بردارهای داده شده پیدا کنید و.

تعریف.

در یک سیستم مختصات مستطیلی از فضای سه بعدی حاصل ضرب برداری دو بردار و یک بردار است که بردارهای مختصات در آن قرار دارند.

این تعریف به ما محصول متقاطع را به صورت مختصات می دهد.

به راحتی می توان حاصلضرب برداری را به عنوان تعیین کننده یک ماتریس مربع مرتبه سوم نشان داد، ردیف اول آن بردارها، سطر دوم شامل مختصات بردار و سوم شامل مختصات بردار در یک داده شده است. سیستم مختصات مستطیلی:

اگر این تعیین کننده را به عناصر ردیف اول گسترش دهیم، برابری را از تعریف حاصلضرب بردار در مختصات به دست می آوریم (در صورت لزوم، به مقاله مراجعه کنید):

لازم به ذکر است که فرم مختصات حاصلضرب برداری کاملاً با تعریف ارائه شده در بند اول این مقاله مطابقت دارد. علاوه بر این، این دو تعریف از یک محصول متقاطع معادل هستند. اثبات این حقیقت را می توانید در کتابی که در انتهای مقاله ذکر شده است مشاهده کنید.

ویژگی های یک محصول برداری

از آنجایی که حاصل ضرب برداری در مختصات را می توان به عنوان یک تعیین کننده ماتریس نشان داد، موارد زیر را می توان به راحتی بر اساس توجیه کرد. خواص محصول متقاطع:

به عنوان مثال، اجازه دهید خاصیت ضد جابجایی یک محصول برداری را اثبات کنیم.

الف- مقدماتی و . می دانیم که در صورت تعویض دو ردیف، مقدار تعیین کننده یک ماتریس معکوس می شود، بنابراین، ، که خاصیت ضد جابجایی یک محصول برداری را اثبات می کند.

محصول برداری - مثال ها و راه حل ها.

به طور عمده سه نوع مشکل وجود دارد.

در مسائل نوع اول، طول دو بردار و زاویه بین آنها آورده شده است و باید طول حاصلضرب بردار را پیدا کنید. در این مورد از فرمول استفاده می شود .

مثال.

طول حاصلضرب برداری بردارها و در صورت شناخته شدن را بیابید .

راه حل.

از این تعریف می دانیم که طول حاصلضرب بردارها و برابر است با حاصلضرب طول بردارها و با سینوس زاویه بین آنها، بنابراین، .

پاسخ:

مسائل نوع دوم مربوط به مختصات بردارها است که در آن حاصل ضرب برداری، طول آن یا هر چیز دیگری از طریق مختصات بردارهای داده شده جستجو می شود. و .

در اینجا گزینه های مختلف زیادی وجود دارد. برای مثال، نه مختصات بردارها و قابل تعیین، بلکه بسط آنها به بردارهای مختصات فرم و یا بردارها و می توان با مختصات نقطه شروع و پایان آنها مشخص کرد.

بیایید به نمونه های معمولی نگاه کنیم.

مثال.

دو بردار در یک سیستم مختصات مستطیلی داده شده است . محصول متقابل آنها را پیدا کنید.

راه حل.

طبق تعریف دوم، حاصل ضرب برداری دو بردار در مختصات به صورت زیر نوشته می شود:

اگر حاصلضرب بردار بر حسب دترمینان نوشته می شد به همین نتیجه می رسیدیم

پاسخ:

مثال.

طول حاصلضرب برداری بردارهای و را بیابید، که بردارهای واحد سیستم مختصات دکارتی مستطیل شکل هستند.

راه حل.

ابتدا مختصات حاصلضرب برداری را پیدا می کنیم در یک سیستم مختصات مستطیلی داده شده

از آنجایی که بردارها و مختصات دارند و به ترتیب (در صورت لزوم به مقاله مختصات یک بردار در سیستم مختصات مستطیلی مراجعه کنید)، پس با تعریف دوم حاصلضرب برداری،

یعنی محصول برداری دارای مختصات در یک سیستم مختصات معین است.

طول یک بردار را به عنوان جذر مجموع مجذورات مختصات آن می‌یابیم (این فرمول را برای طول یک بردار در بخش یافتن طول یک بردار به دست آوردیم):

پاسخ:

مثال.

در یک سیستم مختصات دکارتی مستطیلی، مختصات سه نقطه آورده شده است. برداري را پيدا كنيد كه عمود بر هم باشد.

راه حل.

بردارها و دارای مختصات و به ترتیب (به مقاله یافتن مختصات یک بردار از طریق مختصات نقاط مراجعه کنید). اگر حاصل ضرب برداری بردارها و را پیدا کنیم، بنابر تعریف، بردار عمود بر هر دو و بر است، یعنی راه حلی برای مسئله ما است. بیا پیداش کنیم

پاسخ:

- یکی از بردارهای عمود بر.

در مسائل نوع سوم، مهارت استفاده از خواص حاصلضرب بردارها مورد آزمایش قرار می گیرد. پس از اعمال خواص، فرمول های مربوطه اعمال می شود.

مثال.

بردارها و عمود بر هم هستند و طول آنها به ترتیب 3 و 4 است. طول محصول متقاطع را پیدا کنید .

راه حل.

با خاصیت توزیعی یک محصول برداری، می توانیم بنویسیم

به دلیل خاصیت ترکیبی، ضرایب عددی را از علامت حاصلضرب بردار در عبارت آخر خارج می کنیم:

محصولات برداری و برابر با صفر هستند، زیرا و ، سپس .

از آنجایی که محصول برداری ضد جابجایی است، پس .

بنابراین، با استفاده از ویژگی های حاصلضرب بردار، به برابری رسیدیم .

بر اساس شرط، بردارها و عمود هستند، یعنی زاویه بین آنها برابر است. یعنی ما تمام داده ها را برای یافتن طول مورد نیاز داریم

پاسخ:

معنای هندسی یک محصول برداری.

طبق تعریف، طول حاصلضرب برداری بردارها است . و از یک درس هندسه دبیرستان می دانیم که مساحت مثلث برابر است با نصف حاصلضرب طول دو ضلع مثلث و سینوس زاویه بین آنها. در نتیجه، طول حاصلضرب بردار برابر با دو برابر مساحت مثلثی است که اضلاع آن بردار هستند و اگر از یک نقطه رسم شوند. به عبارت دیگر، طول حاصلضرب برداری بردارها برابر است با مساحت متوازی الاضلاع با اضلاع و زاویه بین آنها برابر است. این معنای هندسی محصول برداری است.

تعریف مجموعه مرتب شده ای از (x 1 , x 2 , ... , x n) n عدد واقعی نامیده می شود. بردار n بعدیو اعداد x i (i = ) - اجزاء،یا مختصات،

مثال. اگر مثلاً یک کارخانه خودروسازی خاص باید در هر شیفت 50 خودرو، 100 کامیون، 10 اتوبوس، 50 مجموعه لوازم یدکی خودرو و 150 دستگاه کامیون و اتوبوس تولید کند، برنامه تولید این کارخانه را می توان به صورت برداری نوشت. (50، 100، 10، 50، 150)، دارای پنج جزء.

نشانه گذاری. بردارها با حروف کوچک پررنگ یا حروف با نوار یا فلش در بالا مشخص می شوند، به عنوان مثال. آیا. دو بردار نامیده می شوند برابر، اگر تعداد اجزای آنها یکسان باشد و اجزای متناظر آنها مساوی باشد.

اجزای برداری را نمی توان با هم عوض کرد، به عنوان مثال، (3، 2، 5، 0، 1)و (2، 3، 5، 0، 1) بردارهای مختلف.
عملیات بر روی بردارهاکار ایکس= (x 1 , x 2 , ... ,x n) توسط یک عدد واقعیλ بردار نامیده می شودλ ایکس= (λ x 1، λ x 2، ...، λ x n).

میزانایکس= (x 1 , x 2 , ... ,x n) و y= (y 1 , y 2 , ... ,y n) بردار نامیده می شود x+y= (x 1 + y 1 , x 2 + y 2 , ... , x n + + y n).

فضای بردارین -فضای برداری بعدی آر n به عنوان مجموعه ای از تمام بردارهای n بعدی تعریف می شود که برای آنها عملیات ضرب در اعداد واقعی و جمع تعریف شده است.

تصویر اقتصادی تصویر اقتصادی فضای برداری n بعدی: فضای کالا (کالاها). زیر کالاهاما برخی از کالاها یا خدماتی را که در زمان معینی در یک مکان خاص به فروش می رسد، درک خواهیم کرد. فرض کنید تعداد محدودی از کالاهای موجود n وجود دارد. مقدار هر یک از آنها خریداری شده توسط مصرف کننده با مجموعه ای از کالاها مشخص می شود

ایکس= (x 1، x 2، ...، x n)،

که در آن x i مقدار i-امین کالای خریداری شده توسط مصرف کننده را نشان می دهد. ما فرض می کنیم که همه کالاها دارای خاصیت تقسیم دلخواه هستند، به طوری که هر مقدار غیر منفی از هر یک از آنها قابل خریداری است. سپس تمام مجموعه کالاهای ممکن بردار فضای کالا C = ( ایکس= (x 1 , x 2 , ... , x n) x i ≥ 0، i =).

استقلال خطی سیستم ه 1 , ه 2 , ... , ه m بردارهای n بعدی نامیده می شوند وابسته خطی، اگر چنین اعدادی وجود داشته باشدλ 1، λ 2، ...، λ m ، که حداقل یکی از آنها غیر صفر است، به طوری که برابر استλ 1 ه 1 + λ 2 ه 2 +... + λ m ه m = 0; در غیر این صورت، این سیستم از بردارها نامیده می شود مستقل خطی، یعنی برابری ذکر شده تنها در صورتی امکان پذیر است که همه . معنای هندسی وابستگی خطی بردارها در آر 3 که به عنوان بخش های جهت دار تفسیر می شود، قضایای زیر را توضیح دهید.

قضیه 1. یک سیستم متشکل از یک بردار به صورت خطی وابسته است اگر و فقط اگر این بردار صفر باشد.

قضیه 2. برای اینکه دو بردار به صورت خطی وابسته باشند لازم و کافی است که هم خط (موازی) باشند.

قضیه 3 . برای اینکه سه بردار به صورت خطی وابسته باشند، همسطح بودن (در یک صفحه) لازم و کافی است.

سه گانه چپ و راست بردارها. سه بردار غیرهمسطح الف، ب، جتماس گرفت درست، اگر ناظر از مبدأ مشترک آنها انتهای بردارها را دور بزند الف، ب، جبه ترتیب داده شده به نظر می رسد در جهت عقربه های ساعت رخ می دهد. در غیر این صورت الف، ب، ج -سه سمت چپ. تمام سه گانه راست (یا چپ) بردارها نامیده می شوند همان جهت دار.

مبانی و مختصات. ترویکا ه 1, ه 2 , ه 3 بردار غیر همسطح در آر 3 نامیده می شود اساسو خود بردارها ه 1, ه 2 , ه 3 - پایه ای. هر بردار آرا می توان به طور منحصر به فرد به بردارهای پایه گسترش داد، یعنی به شکل نمایش داده شود

آ= x 1 ه 1+x2 ه 2 + x 3 ه 3, (1.1)

اعداد x 1 , x 2 , x 3 در بسط (1.1) نامیده می شوند مختصاتآدر اساس ه 1, ه 2 , ه 3 و تعیین شده اند آ(x 1، x 2، x 3).

پایه ارتونرمال. اگر بردارها ه 1, ه 2 , ه 3 به صورت جفتی عمود بر هم هستند و طول هر یک از آنها برابر با یک است، سپس پایه نامیده می شود. متعارفو مختصات x 1 , x 2 , x 3 - مستطیل شکل.بردارهای پایه یک پایه متعارف با نشان داده می شوند من، ج، ک.

ما آن را در فضا فرض خواهیم کرد آر 3 سیستم مناسب مختصات مستطیلی دکارتی انتخاب شده است (0، من، ج، ک}.

اثر هنری وکتور. اثر هنری وکتور آبه بردار ببردار نامیده می شود ج، که با سه شرط زیر تعیین می شود:

1. طول برداری جاز نظر عددی برابر با مساحت متوازی الاضلاع ساخته شده بر روی بردارها است آو بیعنی
ج= |الف||ب|گناه ( آ^ب).

2. وکتور جعمود بر هر یک از بردارها آو ب

3. بردارها آ، بو ج، که به ترتیب مشخص شده گرفته شده است، یک سه گانه راست تشکیل دهید.

برای یک محصول متقابل جنامگذاری معرفی شده است c =[ab] یا
c = a × ب

اگر بردارها آو بخطی هستند، سپس گناه ( a^b) = 0 و [ ab] = 0، به ویژه، [ aa] = 0. محصولات برداری بردارهای واحد: [ ij]=ک، [jk] = من, [کی]=j.

اگر بردارها آو بدر اساس مشخص شده است من، ج، کمختصات آ(a 1، a 2، a 3)، ب(ب 1، ب 2، ب 3)، سپس

کار مختلط. اگر حاصل ضرب برداری دو بردار آو ببه صورت اسکالار در بردار سوم ضرب می شود جآنگاه چنین حاصل ضرب سه بردار نامیده می شود کار مختلطو با علامت نشان داده می شود آ قبل از میلاد مسیح.

اگر بردارها الف، بو جدر اساس من، ج، کبا مختصات آنها داده می شود
آ(a 1، a 2، a 3)، ب(ب 1، ب 2، ب 3)، ج(ج 1، ج 2، ج 3)، سپس

محصول مخلوط دارای یک تفسیر هندسی ساده است - این یک عدد اسکالر است که از نظر مقدار مطلق برابر با حجم یک موازی شکل ساخته شده بر روی سه بردار معین است.

اگر بردارها یک سه برابر راست تشکیل دهند، آنگاه حاصلضرب مخلوط آنها یک عدد مثبت برابر با حجم مشخص شده است. اگر سه باشد الف، ب، ج -چپ، پس a b c<0 и V = - a b cبنابراین V =|a b c|.

مختصات بردارهایی که در مسائل فصل اول با آن مواجه می شوند، فرض می شود که نسبت به یک مبنای متعارف درست داده شده اند. بردار واحد هم جهت با بردار آ،با نماد نشان داده شده است آ O. سمبل r=OMبا بردار شعاع نقطه M، نمادهای a، AB یا نشان داده می شود|a|, | AB|ماژول های بردارها مشخص می شوند آو AB

مثال 1.2. زاویه بین بردارها را پیدا کنید آ= 2متر+4nو ب= m-n، جایی که مترو n-بردار واحد و زاویه بین مترو nبرابر با 120 o.

راه حل. ما داریم: cos φ = ab/ab ab =(2متر+4n) (m-n) = 2متر 2 - 4n 2 +2دقیقه=
= 2 - 4+2cos120 o = - 2 + 2(-0.5) = -3; a = ; آ 2 = (2متر+4n) (2متر+4n) =
= 4متر 2 +16دقیقه+16n 2 = 4+16(-0.5)+16=12 که به معنی a = . b = ; ب 2 =
= (m-n)(m-n) = متر 2 -2دقیقه+n 2 = 1-2(-0.5)+1 = 3 که به معنی b = . در نهایت داریم: cosφ = = -1/2، φ = 120 o.

مثال 1.3.شناخت بردارها AB(-3،-2.6) و قبل از میلاد مسیح.(-2،4،4)، طول ارتفاع AD مثلث ABC را محاسبه کنید.

راه حل. با نشان دادن مساحت مثلث ABC با S به دست می آید:
S = 1/2 قبل از میلاد مسیح. سپس AD=2S/BC، BC= = = 6,
S = 1/2| AB ×AC|. AC=AB+BC، که به معنای بردار است A.C.مختصات دارد
. .

مثال 1.4 . دو بردار داده شده است آ(11،10،2) و ب(4،0،3). بردار واحد را پیدا کنید جمتعامد به بردارها آو بو طوری هدایت می شود که بردارهای سه گانه مرتب شده باشند الف، ب، جدرست بود.

راه حل.اجازه دهید مختصات بردار را مشخص کنیم جبا توجه به یک مبنای متعارف راست مفروض بر حسب x، y، z.

از آنجا که ج ⊥ الف، ج ⊥ب، آن حدود= 0، cb= 0. با توجه به شرایط مسئله، لازم است که c = 1 و a b c >0.

ما یک سیستم معادلات برای یافتن x,y,z داریم: 11x +10y + 2z = 0، 4x+3z=0، x 2 + y 2 + z 2 = 0.

از معادلات اول و دوم سیستم z = -4/3 x، y = -5/6 x به دست می آید. با جایگزینی y و z در معادله سوم، داریم: x 2 = 36/125، از این رو
x =± . با استفاده از شرط a b c > 0، نابرابری را دریافت می کنیم

با در نظر گرفتن عبارات z و y، نابرابری حاصل را به این شکل بازنویسی می کنیم: 625/6 x > 0، که به معنای x>0 است. بنابراین، x =، y = -، z =-.