تعریف. حاصلضرب برداری بردار a (ضربی) و بردار غیر خطی (چند برابری) سومین بردار c (مضرب) است که به صورت زیر ساخته شده است:

1) مدول آن عددی است برابر مساحتمتوازی الاضلاع در شکل 155)، بر روی بردارها ساخته شده است، یعنی برابر است با جهت عمود بر صفحه متوازی الاضلاع مذکور؛

3) در این حالت، جهت بردار c (از دو مورد ممکن) انتخاب می شود تا بردارهای c یک سیستم سمت راست را تشکیل دهند (§ 110).

نامگذاری: یا

اضافه بر تعریف. اگر بردارها خطی باشند، با در نظر گرفتن شکل متوازی الاضلاع (شرط) طبیعی است که مساحت صفر را اختصاص دهیم. از همین رو محصول برداریبردارهای خطی برابر با بردار صفر در نظر گرفته می شود.

از آنجایی که بردار تهی را می توان به هر جهتی اختصاص داد، این توافق با بندهای 2 و 3 تعریف مغایرتی ندارد.

نکته 1. در اصطلاح «ضرب بردار» اولین کلمه نشان می‌دهد که نتیجه عمل یک بردار است (برخلاف حاصلضرب اسکالر؛ رجوع کنید به § 104، تبصره 1).

مثال 1. حاصلضرب برداری را پیدا کنید که بردارهای اصلی سیستم مختصات سمت راست هستند (شکل 156).

1. از آنجایی که طول بردارهای اصلی برابر با یک واحد مقیاس است، مساحت متوازی الاضلاع (مربع) از نظر عددی برابر با یک است. این بدان معناست که مدول حاصلضرب بردار برابر با یک.

2. از آنجایی که عمود بر صفحه یک محور است، حاصلضرب بردار مورد نظر بردار خطی بردار k است. و از آنجایی که هر دوی آنها مدول 1 دارند، حاصل ضرب برداری مورد نظر برابر با k یا -k است.

3. از بین این دو بردار ممکن، اولین بردار باید انتخاب شود، زیرا بردارهای k یک سیستم سمت راست (و بردارها یک سمت چپ) را تشکیل می دهند.

مثال 2. حاصل ضرب متقاطع را پیدا کنید

راه حل. مانند مثال 1، نتیجه می گیریم که بردار برابر با k یا -k است. اما اکنون باید -k را انتخاب کنیم، زیرا بردارها یک سیستم سمت راست را تشکیل می دهند (و بردارها یک سیستم چپ را تشکیل می دهند). بنابراین،

مثال 3. طول بردارها به ترتیب برابر با 80 و 50 سانتی متر است و زاویه 30 درجه را تشکیل می دهند. با در نظر گرفتن متر به عنوان واحد طول، طول حاصلضرب برداری a را پیدا کنید

راه حل. مساحت متوازی الاضلاع ساخته شده بر روی بردارها برابر است با طول حاصلضرب برداری مورد نظر برابر است با

مثال 4. طول حاصل ضرب بردار همان بردارها را با واحد طول سانتیمتر بیابید.

راه حل. از آنجایی که مساحت متوازی الاضلاع ساخته شده روی بردارها برابر است، طول حاصلضرب بردار برابر با 2000 سانتی متر است، یعنی.

از مقایسه مثال های 3 و 4 مشخص می شود که طول بردار نه تنها به طول عوامل بلکه به انتخاب واحد طول نیز بستگی دارد.

معنای فیزیکی یک محصول برداریاز تعداد زیادی مقادیر فیزیکی، که با حاصلضرب بردار نشان داده می شود، فقط لحظه نیرو را در نظر می گیریم.

اجازه دهید A نقطه اعمال نیرو باشد، گشتاور نیرو نسبت به نقطه O را حاصلضرب بردار می نامند. مدول ممان برابر است با حاصل ضرب پایه و ارتفاع، یعنی نیروی ضرب شده در فاصله نقطه O تا خط مستقیمی که نیرو در امتداد آن وارد می شود.

در مکانیک ثابت شده است که برای تعادل جامدلازم است که نه تنها مجموع بردارهایی که نیروهای وارد شده به جسم را نشان می دهند برابر با صفر باشد، بلکه مجموع گشتاور نیروها نیز برابر باشد. در موردی که همه نیروها با یک صفحه موازی هستند، جمع بردارهایی که ممان ها را نشان می دهند را می توان با جمع و تفریق قدر آنها جایگزین کرد. اما با جهت گیری دلخواه نیروها، چنین جایگزینی غیرممکن است. مطابق با این، محصول برداری دقیقاً به عنوان یک بردار تعریف می شود و نه به عنوان یک عدد.

بردار واحد- این بردار، قدر مطلق (مدول) آن برابر با وحدت است. برای نشان دادن یک بردار، از زیرنویس e استفاده می کنیم بنابراین، اگر یک بردار داده شود آ، سپس بردار واحد آن بردار خواهد بود آ e این بردار واحد در همان جهت هدایت می شود که خود بردار آو ماژول آن برابر با یک است، یعنی a e = 1.

به طور مشخص، آ= a آ e (الف - ماژول برداری آ). این از قاعده ای که عمل ضرب یک اسکالر در یک بردار را انجام می دهد نتیجه می گیرد.

بردارهای واحداغلب با محورهای مختصات یک سیستم مختصات (به ویژه با محورهای یک سیستم مختصات دکارتی) مرتبط است. جهت اینها بردارهامنطبق با جهت محورهای مربوطه است، و مبدا آنها اغلب با مبدا سیستم مختصات ترکیب می شود.

بگذارید این را به شما یادآوری کنم سیستم مختصات دکارتیدر فضا، به طور سنتی به سه محور عمود بر هم متقاطع در نقطه ای به نام مبدأ مختصات گفته می شود. محورهای مختصات معمولاً با حروف X، Y، Z مشخص می شوند و به ترتیب به آنها محور ابسیسا، محور مختصات و محور اعمال می گویند. خود دکارت فقط از یک محور استفاده کرد که بر روی آن آبسیساها ترسیم شد. شایستگی استفاده سیستم هایتبر متعلق به شاگردانش است. بنابراین عبارت سیستم مختصات دکارتیاشتباه تاریخی صحبت کردن بهتر است مستطیل شکل دستگاه مختصاتیا سیستم مختصات متعامد. با این حال، ما سنت ها را تغییر نخواهیم داد و در آینده فرض خواهیم کرد که سیستم مختصات دکارتی و مستطیلی (متعامد) یکی و یکی هستند.

بردار واحد، در امتداد محور X نشان داده می شود من, بردار واحد، در امتداد محور Y نشان داده می شود j، آ بردار واحد، که در امتداد محور Z هدایت می شود، نشان داده می شود ک. بردارها من, j, کنامیده می شوند orts(شکل 12، سمت چپ)، آنها تک ماژول دارند، یعنی
i = 1، j = 1، k = 1.

تبرها و بردارهای واحد سیستم مختصات مستطیلیدر برخی موارد نام ها و نام های متفاوتی دارند. بنابراین، محور آبسیسا X را می توان محور مماس نامید و بردار واحد آن را نشان داد. τ (حرف كوچك يوناني tau)، محور مختصات، محور معمولي است، بردار واحد آن مشخص شده است. n، محور کاربردی محور باینرمال است که بردار واحد آن مشخص می شود ب. چرا اگر ماهیت یکسان است، نام ها را تغییر دهید؟

واقعیت این است که به عنوان مثال، در مکانیک، هنگام مطالعه حرکت اجسام، اغلب از سیستم مختصات مستطیلی استفاده می شود. بنابراین، اگر خود سیستم مختصات ساکن باشد و تغییر مختصات یک جسم متحرک در این سیستم ثابت ردیابی شود، معمولاً محورها X، Y، Z و آنها تعیین می‌شوند. بردارهای واحدبه ترتیب من, j, ک.

اما اغلب، هنگامی که یک جسم در امتداد نوعی مسیر منحنی (مثلاً در یک دایره) حرکت می کند، در نظر گرفتن فرآیندهای مکانیکی در سیستم مختصات که با این جسم حرکت می کنند راحت تر است. برای چنین سیستم مختصات متحرکی است که از نام های دیگر محورها و بردارهای واحد آنها استفاده می شود. همین طور است. در این حالت، محور X به صورت مماس به مسیری که در آن نقطه است هدایت می شود این لحظهاین شی واقع شده است. و سپس این محور دیگر محور X نامیده نمی شود، بلکه محور مماس نامیده می شود و بردار واحد آن دیگر تعیین نمی شود. من، آ τ . محور Y در امتداد شعاع انحنای مسیر (در مورد حرکت در یک دایره - به مرکز دایره) هدایت می شود. و از آنجایی که شعاع بر مماس عمود است، محور را محور معمولی می گویند (عمود و عادی یکی هستند). بردار واحد این محور دیگر نشان داده نمی شود j، آ n. محور سوم (Z سابق) بر دو محور قبلی عمود است. این یک بی طبیعی با ارث است ب(شکل 12، سمت راست). به هر حال، در این مورد چنین است سیستم مختصات مستطیلیاغلب به عنوان "طبیعی" یا طبیعی شناخته می شود.

Yandex.RTB R-A-339285-1

قبل از ارائه مفهوم حاصلضرب بردار، اجازه دهید به مسئله جهت گیری یک سه گانه مرتب شده از بردارهای a →، b →، c → در فضای سه بعدی بپردازیم.

برای شروع، بردارهای a → , b → , c → را از یک نقطه کنار می گذاریم. جهت سه گانه a → , b → , c → بسته به جهت خود بردار c → می تواند راست یا چپ باشد. نوع سه گانه a → , b → , c → از جهتی که کوتاه ترین چرخش از بردار a → به b → از انتهای بردار c → انجام می شود تعیین می شود.

اگر کوتاه ترین چرخش در خلاف جهت عقربه های ساعت انجام شود، سه بردار a → , b → , c → نامیده می شود. درست، اگر در جهت عقربه های ساعت باشد - ترک کرد.

سپس دو بردار غیر خطی a → و b → را بگیرید. سپس بردارهای A B → = a → و A C → = b → را از نقطه A رسم می کنیم. بیایید یک بردار A D → = c → بسازیم که به طور همزمان بر هر دو A B → و A C → عمود است. بنابراین، هنگام ساختن خود بردار A D → = c →، می‌توانیم دو کار انجام دهیم، که به آن یک جهت یا مخالف بدهیم (به شکل نگاه کنید).

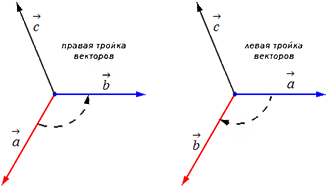
یک سه مرتبه از بردارهای a → , b → , c → می تواند، همانطور که متوجه شدیم، بسته به جهت بردار، راست یا چپ باشد.

از موارد فوق می توان تعریف یک محصول برداری را معرفی کرد. این تعریف برای دو بردار تعریف شده در یک سیستم مختصات مستطیلی از فضای سه بعدی ارائه شده است.

تعریف 1

حاصل ضرب برداری دو بردار a → و b → ما چنین بردار تعریف شده در یک سیستم مختصات مستطیلی فضای سه بعدی را به گونه ای فراخوانی می کنیم که:

• اگر بردارهای a → و b → هم خط باشند، صفر خواهد بود.
• بر هر دو بردار a → و بردار b → یعنی عمود خواهد بود. ∠ a → c → = ∠ b → c → = π 2 ;
• طول آن با فرمول تعیین می شود: c → = a → · b → · sin ∠ a → , b → ;
• سه گانه بردارهای a → , b → , c → دارای جهتی مشابه در این سیستممختصات

ضرب ضربدر بردارهای a → و b → نماد زیر است: a → × b → .

مختصات حاصلضرب بردار

از آنجایی که هر بردار دارای مختصات خاصی در سیستم مختصات است، می‌توانیم تعریف دومی از حاصلضرب بردار ارائه کنیم که به ما امکان می‌دهد مختصات آن را با استفاده از مختصات داده شده بردارها پیدا کنیم.

تعریف 2

در یک سیستم مختصات مستطیلی از فضای سه بعدی حاصل ضرب برداری دو بردار a → = (a x ; a y ; a z) و b → = (b x ; b y ; b z) بردار c → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k → ، جایی که i → , j → , k → بردارهای مختصاتی هستند.

حاصلضرب برداری را می توان به عنوان تعیین کننده یک ماتریس مربع مرتبه سوم نشان داد، که در آن سطر اول شامل بردارهای i → , j → , k → است، سطر دوم حاوی مختصات بردار a → و سطر سوم است. شامل مختصات بردار b → در یک سیستم مختصات مستطیلی مشخص است، این تعیین کننده ماتریس به نظر می رسد: c → = a → × b → = i → j → k → a x a y a z b x b y b z

با گسترش این تعیین کننده به عناصر ردیف اول، برابری را بدست می آوریم: c → = a → × b → = i → j → k → a x a y a z b x b y b z = a y a z b y b z · i → - a x a z b x b z · j → + a x a y x b → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k →

خواص یک محصول متقاطع

مشخص است که حاصلضرب برداری در مختصات به عنوان تعیین کننده ماتریس c → = a → × b → = i → j → k → a x a y a z b x b y b z نمایش داده می شود، سپس بر اساس خواص تعیین کننده ماتریسموارد زیر نمایش داده می شود خواص یک محصول برداری:

1. ضد جابجایی a → × b → = - b → × a → ;
2. توزیع a (1) → + a (2) → × b = a (1) → × b → + a (2) → × b → یا a → × b (1) → + b (2) → = a → × b (1) → + a → × b (2) → ;
3. ارتباط λ a → × b → = λ a → × b → یا a → × (λ b →) = λ a → × b →، که در آن λ یک عدد واقعی دلخواه است.

این خواص اثبات ساده ای دارند.

به عنوان مثال، ما می توانیم خاصیت ضد جابجایی یک محصول برداری را اثبات کنیم.

اثبات ضد جابجایی

طبق تعریف، a → × b → = i → j → k → a x a y a z b x b y b z و b → × a → = i → j → k → b x b y b z a x a y a z . و اگر دو ردیف از ماتریس تعویض شوند، مقدار تعیین کننده ماتریس باید به عکس تغییر کند، بنابراین، a → × b → = i → j → k → a x a y a z b x b y b z = - i → j → k → b x b y b z a x ay - b → × a → که و ثابت می کند که حاصلضرب بردار ضد جابجایی است.

محصول برداری - مثال ها و راه حل ها

در بیشتر موارد، سه نوع مشکل وجود دارد.

در مسائل نوع اول معمولا طول دو بردار و زاویه بین آنها آورده می شود و باید طول حاصلضرب بردار را پیدا کنید. در این مورد از فرمول زیر c → = a → · b → · sin ∠ a → , b → استفاده کنید.

مثال 1

طول حاصلضرب برداری بردارهای a → و b → را در صورتی که a → = 3، b → = 5، ∠ a →، b → = π 4 می دانید، بیابید.

راه حل

با تعیین طول حاصل ضرب برداری بردارهای a → و b → این مشکل را حل می کنیم: a → × b → = a → · b → · sin ∠ a → , b → = 3 · 5 · sin π 4 = 15 2 2 .

پاسخ: 15 2 2 .

مسائل نوع دوم با مختصات بردارها، در آنها حاصل ضرب برداری، طول آن و غیره ارتباط دارند. از طریق مختصات شناخته شده بردارهای داده شده جستجو می شوند a → = (a x; a y; a z) و b → = (b x؛ b y؛ b z) .

برای این نوع مشکلات، شما می توانید بسیاری از گزینه های کار را حل کنید. به عنوان مثال، مختصات بردارهای a → و b → را نمی توان مشخص کرد، بلکه بسط آن ها را به بردارهای مختصات شکل می توان تعیین کرد. b → = b x · i → + b y · j → + b z · k → و c → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k →، یا بردارهای a → و b → را می توان با مختصات شروع آنها مشخص کرد. و نقاط پایانی

به مثال های زیر توجه کنید.

مثال 2

در یک سیستم مختصات مستطیلی، دو بردار داده می شود: a → = (2؛ 1؛ - 3)، b → = (0؛ - 1؛ 1). محصول متقاطع آنها را پیدا کنید.

راه حل

با تعریف دوم، حاصل ضرب برداری دو بردار را در مختصات داده شده پیدا می کنیم: a → × b → = (a y · b z - a z · b y) · i → + (a z · b x - a x · b z) · j → + ( a x · b y - a y · b x) · k → = = (1 · 1 - (- 3) · (- 1)) · i → + ((- 3) · 0 - 2 · 1) · j → + (2) · (- 1) - 1 · 0) · k → = = - 2 i → - 2 j → - 2 k → .

اگر حاصلضرب برداری را از طریق تعیین کننده ماتریس بنویسیم، جواب این مثال به این صورت است: a → × b → = i → j → k → a x a y a z b x b y b z = i → j → k → 2 1 - 3 0 - 1 1 = - 2 i → - 2 j → - 2 k → .

پاسخ: a → × b → = - 2 i → - 2 j → - 2 k → .

مثال 3

طول حاصل ضرب برداری بردارهای i → - j → و i → + j → + k → را بیابید که i →، j →، k → بردارهای واحد سیستم مختصات دکارتی مستطیلی هستند.

راه حل

ابتدا، اجازه دهید مختصات یک حاصلضرب برداری معین i → - j → × i → + j → + k → را در یک سیستم مختصات مستطیلی مشخص پیدا کنیم.

مشخص است که بردارهای i → - j → و i → + j → + k → به ترتیب دارای مختصات (1؛ - 1؛ 0) و (1؛ 1؛ 1) هستند. بیایید طول حاصلضرب برداری را با استفاده از تعیین کننده ماتریس پیدا کنیم، سپس i → - j → × i → + j → + k → = i → j → k → 1 - 1 0 1 1 1 = - i → داریم. - j → + 2 k → .

بنابراین، حاصلضرب برداری i → - j → × i → + j → + k → دارای مختصات (- 1 ; - 1 ; 2) در سیستم مختصات داده شده است.

طول حاصلضرب برداری را با استفاده از فرمول پیدا می کنیم (به بخش یافتن طول یک بردار مراجعه کنید): i → - j → × i → + j → + k → = - 1 2 + - 1 2 + 2 2 = 6.

پاسخ: i → - j → × i → + j → + k → = 6. .

مثال 4

در یک سیستم مختصات دکارتی مستطیلی، مختصات سه نقطه A (1، 0، 1)، B (0، 2، 3)، C (1، 4، 2) آورده شده است. چند بردار عمود بر A B → و A C → همزمان پیدا کنید.

راه حل

بردارهای A B → و A C → به ترتیب دارای مختصات زیر هستند (- 1 ; 2 ; 2) و (0 ; 4 ; 1). با یافتن حاصلضرب برداری بردارهای A B → و A C →، بدیهی است که بردار عمود بر هر دو A B → و A C → است، یعنی راه حلی برای مسئله ما است. بیایید آن را A B → × A C → = i → j → k → - 1 2 2 0 4 1 = - 6 i → + j → - 4 k → پیدا کنیم.

پاسخ: - 6 i → + j → - 4 k → . - یکی از بردارهای عمود بر.

مسائل نوع سوم بر استفاده از ویژگی های حاصلضرب برداری بردارها متمرکز است. پس از اعمال آن، راه حلی برای مشکل داده شده به دست خواهیم آورد.

مثال 5

بردارهای a → و b → عمود هستند و طول آنها به ترتیب 3 و 4 است. طول حاصلضرب برداری 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 a → × a → + 3 · a → × - 2 · b → + - b → × a → + - b → × - 2 · b → .

راه حل

با خاصیت توزیعی یک محصول برداری، می توانیم 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 بنویسیم. a → × a → + 3 a → × - 2 b → + - b → × a → + - b → × - 2 b →

با خاصیت تداعی، ضرایب عددی را از علامت محصولات برداری در آخرین عبارت خارج می کنیم: 3 · a → × a → + 3 · a → × - 2 · b → + - b → × a → + - b → × - 2 · b → = = 3 · a → × a → + 3 · (- 2) · a → × b → + (- 1) · b → × a → + (- 1) · (- 2) · b → × b → = = 3 a → × a → - 6 a → × b → - b → × a → + 2 b → × b →

حاصلضرب های برداری a → × a → و b → × b → برابر با 0 هستند، زیرا a → × a → = a → · a → · sin 0 = 0 و b → × b → = b → · b → · sin 0 = 0، سپس 3 · a → × a → - 6 · a → × b → - b → × a → + 2 · b → × b → = - 6 · a → × b → - b → × a → . .

از ضد جابجایی حاصلضرب بردار نتیجه می شود - 6 · a → × b → - b → × a → = - 6 · a → × b → - (- 1) · a → × b → = - 5 · a → × ب → .

با استفاده از ویژگی های حاصلضرب بردار، برابری 3 · a → - b → × a → - 2 · b → = = - 5 · a → × b → را به دست می آوریم.

بر اساس شرط، بردارهای a → و b → عمود هستند، یعنی زاویه بین آنها برابر با π 2 است. اکنون تنها چیزی که باقی می ماند این است که مقادیر یافت شده را با فرمول های مناسب جایگزین کنید: 3 a → - b → × a → - 2 b → = - 5 a → × b → = = 5 a → × b → = 5 a → b → · sin (a → , b →) = 5 · 3 · 4 · sin π 2 = 60 .

پاسخ: 3 a → - b → × a → - 2 b → = 60.

طول حاصلضرب برداری بردارها طبق تعریف برابر است با a → × b → = a → b → · sin ∠ a → , b → . از آنجایی که قبلاً (از دوره مدرسه) مشخص شده است که مساحت یک مثلث برابر است با نصف حاصل ضرب طول دو ضلع آن در سینوس زاویه بین این ضلع ها. در نتیجه، طول حاصلضرب بردار برابر است با مساحت متوازی الاضلاع - یک مثلث دو برابر شده، یعنی حاصل ضرب اضلاع به شکل بردارهای a → و b →، که از یک نقطه، توسط سینوس گذاشته شده است. زاویه بین آنها گناه ∠ a →، b →.

این معنای هندسی یک محصول برداری است.

معنای فیزیکی محصول برداری

در مکانیک، یکی از شاخه های فیزیک، به لطف حاصلضرب بردار، می توانید ممان یک نیرو را نسبت به یک نقطه از فضا تعیین کنید.

تعریف 3

در لحظه اعمال نیروی F ← به نقطه B، نسبت به نقطه A، حاصلضرب برداری زیر A B → × F → را درک خواهیم کرد.

اگر خطایی در متن مشاهده کردید، لطفاً آن را برجسته کرده و Ctrl+Enter را فشار دهید

در این درس به دو عمل دیگر با بردارها نگاه خواهیم کرد: حاصلضرب برداری بردارهاو حاصلضرب مخلوط بردارها (لینک فوری برای کسانی که به آن نیاز دارند). اشکالی ندارد، گاهی اوقات اتفاق می افتد که برای خوشبختی کامل، علاوه بر حاصل ضرب اسکالر بردارها، بیشتر و بیشتر مورد نیاز است. این اعتیاد بردار است. ممکن است به نظر برسد که ما در حال ورود به جنگل هندسه تحلیلی هستیم. این اشتباه است. در این بخش از ریاضیات عالی به طور کلی چوب کمی وجود دارد، به جز شاید به اندازه کافی برای پینوکیو. در واقع، مواد بسیار رایج و ساده است - به سختی پیچیده تر از همان حاصلضرب عددی، حتی وظایف معمولی کمتری وجود خواهد داشت. نکته اصلی در هندسه تحلیلی، همانطور که بسیاری متقاعد شده اند یا قبلاً متقاعد شده اند، اشتباه نکردن در محاسبات است. مثل یک طلسم تکرار کنید و خوشحال خواهید شد =)

اگر بردارها در جایی دور می درخشند، مانند رعد و برق در افق، مهم نیست، با درس شروع کنید وکتور برای آدمکبرای بازیابی یا کسب مجدد دانش اولیه در مورد بردارها. خوانندگان آماده تر می توانند به طور انتخابی با اطلاعات آشنا شوند کار عملی

چه چیزی شما را بلافاصله خوشحال می کند؟ وقتی کوچک بودم، می‌توانستم با دو یا حتی سه توپ دستکاری کنم. خوب کار کرد. اکنون دیگر نیازی به دستکاری نخواهید داشت، زیرا ما در نظر خواهیم گرفت فقط بردارهای فضایی، و بردارهای مسطح با دو مختصات کنار گذاشته می شوند. چرا؟ به این ترتیب این کنش ها متولد شدند - بردار و حاصلضرب مخلوط بردارها تعریف شده و در فضای سه بعدی کار می کنند. در حال حاضر آسان تر است!

این عملیات، درست مانند محصول اسکالر، شامل دو بردار. بگذار اینها حروف فنا ناپذیر باشند.

خود عمل نشان داده شده بابه روش زیر: . گزینه های دیگری نیز وجود دارد، اما من عادت دارم که حاصل ضرب برداری بردارها را به این شکل، در پرانتز مربع با یک ضربدر نشان دهم.

و بلافاصله سوال: اگر در حاصل ضرب اسکالر بردارهادو بردار درگیر هستند، و در اینجا دو بردار نیز ضرب می شوند، سپس تفاوت در چیست? تفاوت آشکار، اول از همه، در نتیجه است:

حاصل حاصل ضرب اسکالر بردارها NUMBER است:

حاصل ضرب ضربدری بردارها بردار است: یعنی بردارها را ضرب می کنیم و دوباره بردار می گیریم. باشگاه تعطیل شده در واقع، نام عملیات از اینجا آمده است. در ادبیات آموزشی مختلف، نام‌گذاری‌ها نیز ممکن است متفاوت باشد.

تعریف محصول متقاطع

ابتدا یک تعریف با یک تصویر وجود دارد، سپس نظرات.

تعریف: محصول برداری غیر خطیبردارها، به این ترتیب گرفته شده استبه نام VECTOR، طولکه به صورت عددی است برابر با مساحت متوازی الاضلاع است، بر اساس این بردارها ساخته شده است. بردار متعامد به بردارها، و به گونه ای هدایت می شود که اساس جهت گیری درست داشته باشد:

بیایید تعریف را بشکنیم، چیزهای جالب زیادی در اینجا وجود دارد!

بنابراین، می توان به نکات مهم زیر اشاره کرد:

1) بردارهای اصلی که با فلش های قرمز مشخص شده اند، طبق تعریف خطی نیست. مناسب است که کمی بعد مورد بردارهای خطی را در نظر بگیریم.

2) بردارها گرفته می شوند به ترتیب کاملاً تعریف شده: – "الف" در "بودن" ضرب می شود، و نه "بودن" با "الف". حاصل ضرب برداری VECTOR است که با رنگ آبی نشان داده شده است. اگر بردارها به ترتیب معکوس ضرب شوند، بردار برابر طول و مخالف جهت (رنگ تمشک) به دست می آوریم. یعنی برابری درست است .

3) حال با معنای هندسی حاصلضرب بردار آشنا می شویم. این نکته بسیار مهمی است! LENGTH بردار آبی (و بنابراین بردار زرشکی) از نظر عددی برابر با AREA متوازی الاضلاع ساخته شده روی بردارها است. در شکل، این متوازی الاضلاع به رنگ مشکی است.

توجه داشته باشید : رسم شماتیک است و طبیعتاً طول اسمی حاصلضرب بردار با مساحت متوازی الاضلاع برابر نیست.

بیایید یکی از فرمول های هندسی را به یاد بیاوریم: مساحت متوازی الاضلاع برابر است با حاصل ضرب اضلاع مجاور و سینوس زاویه بین آنها.. بنابراین، بر اساس موارد فوق، فرمول محاسبه LENGTH حاصلضرب بردار معتبر است:

تاکید می کنم که فرمول مربوط به LENGTH بردار است و نه در مورد خود بردار. معنای عملی چیست؟ و معنی این است که در مسائل هندسه تحلیلی، مساحت متوازی الاضلاع اغلب از طریق مفهوم یک محصول برداری پیدا می شود:

بیایید فرمول مهم دوم را بدست آوریم. مورب متوازی الاضلاع (خط نقطه چین قرمز) آن را به دو قسمت تقسیم می کند مثلث مساوی. بنابراین، مساحت یک مثلث ساخته شده بر روی بردارها (سایه دهی قرمز) را می توان با استفاده از فرمول پیدا کرد:

4) یک واقعیت به همان اندازه مهم این است که بردار متعامد با بردارها است، یعنی . البته بردار جهت مخالف (فلش تمشک) نیز با بردارهای اصلی متعامد است.

5) بردار به گونه ای جهت داده شده است که اساساین دارد درستگرایش. در درس در مورد انتقال به یک پایه جدیدمن با جزئیات کافی در مورد آن صحبت کردم جهت هواپیما، و اکنون متوجه خواهیم شد که جهت گیری فضا چیست. من روی انگشتان شما توضیح خواهم داد دست راست . ذهنی ترکیب کنید انگشت اشاره با وکتور و انگشت وسطبا وکتور انگشت حلقه و انگشت کوچکآن را در کف دست خود فشار دهید. در نتیجه شست - محصول برداری به بالا نگاه می کند. این یک مبنای راست گرا است (این یکی در شکل است). حالا بردارها را تغییر دهید ( انگشت اشاره و وسط) در بعضی جاها، در نتیجه انگشت شست به اطراف می چرخد ​​و حاصلضرب بردار از قبل به پایین نگاه می کند. این نیز یک مبنای حق مدار است. ممکن است این سوال برای شما پیش بیاید: کدام پایه گرایش چپ دارد؟ "تخصیص" به همان انگشتان دست چپبردارها، و پایه سمت چپ و جهت چپ فضا را بدست آورید (در این حالت انگشت شست در جهت بردار پایینی قرار می گیرد). به بیان تصویری، این پایه ها فضا را در جهات مختلف "پیچان" یا جهت می دهند. و این مفهوم را نباید چیزی دور از ذهن یا انتزاعی در نظر گرفت - به عنوان مثال، جهت گیری فضا توسط معمولی ترین آینه تغییر می کند، و اگر شما "شیء منعکس شده را از شیشه بیرون بکشید"، در حالت کلی ترکیب آن با "اصلی" امکان پذیر نخواهد بود. به هر حال، سه انگشت خود را به سمت آینه بگیرید و انعکاس را تجزیه و تحلیل کنید ;-)

...چقدر خوبه که الان میدونی راست و چپمبانی، زیرا اظهارات برخی از اساتید در مورد تغییر جهت گیری ترسناک است =)

ضرب ضربدر بردارهای خطی

تعریف به تفصیل مورد بحث قرار گرفته است، باید بدانیم وقتی بردارها هم خط هستند چه اتفاقی می افتد. اگر بردارها خطی باشند، می توان آنها را روی یک خط مستقیم قرار داد و متوازی الاضلاع ما نیز در یک خط مستقیم "تا" می شود. حوزه از جمله، همانطور که ریاضیدانان می گویند، منحطمتوازی الاضلاع برابر با صفر است. از فرمول نیز به همین صورت است - سینوس صفر یا 180 درجه برابر با صفر است، یعنی مساحت صفر است.

بنابراین، اگر، پس . به بیان دقیق، خود حاصلضرب بردار برابر با بردار صفر است، اما در عمل اغلب از این موضوع غفلت می شود و می نویسند که به سادگی برابر با صفر است.

یک مورد خاص، حاصل ضرب برداری یک بردار با خودش است:

با استفاده از ضربدر می توانید همخطی بودن بردارهای سه بعدی را بررسی کنید این وظیفهدر میان دیگران، ما نیز تجزیه و تحلیل خواهیم کرد.

برای حل مثال های عملی ممکن است نیاز داشته باشید جدول مثلثاتیبرای یافتن مقادیر سینوس ها از آن.

خوب، بیایید آتش را روشن کنیم:

مثال 1

الف) طول حاصل ضرب برداری بردارها را بیابید اگر

ب) مساحت متوازی الاضلاع ساخته شده بر روی بردارها را بیابید اگر

راه حل: نه، این اشتباه تایپی نیست، من عمداً داده های اولیه را در بندها یکسان کردم. زیرا طراحی راه حل ها متفاوت خواهد بود!

الف) با توجه به شرایط، باید پیدا کنید طولبردار (محصول متقاطع). طبق فرمول مربوطه:

پاسخ:

اگر از شما در مورد طول سؤال شد ، در پاسخ ما بعد - واحدها را نشان می دهیم.

ب) با توجه به شرط، باید پیدا کنید مربعمتوازی الاضلاع بر روی بردارها ساخته شده است. مساحت این متوازی الاضلاع از نظر عددی برابر است با طول حاصلضرب بردار:

پاسخ:

لطفاً توجه داشته باشید که پاسخ اصلاً در مورد محصول برداری صحبت نمی کند مساحت شکلبر این اساس، بعد واحد مربع است.

ما همیشه به آنچه که باید بر اساس شرایط پیدا کنیم نگاه می کنیم و بر این اساس، فرمول بندی می کنیم روشنپاسخ. ممکن است به معنای واقعی کلمه به نظر برسد، اما در بین معلمان تعداد زیادی از لفظ گرایان وجود دارد و این تکلیف شانس خوبی برای بازگرداندن آن برای تجدید نظر دارد. اگر چه این یک سخن گفتن دور از ذهن نیست - اگر پاسخ نادرست باشد، این تصور به وجود می آید که شخص چیزهای ساده را نمی فهمد و/یا اصل کار را درک نکرده است. این نکته همیشه باید در حل هر مسئله ای در ریاضیات عالی و همچنین در دروس دیگر تحت کنترل باشد.

حرف بزرگ "en" کجا رفت؟ در اصل، می‌توانست به راه‌حل اضافه شود، اما برای کوتاه کردن ورودی، این کار را نکردم. امیدوارم همه این را بفهمند و برای همین کار تعیین شوند.

یک مثال محبوب برای راه حل DIY:

مثال 2

مساحت مثلثی که بر روی بردارها ساخته شده است را پیدا کنید اگر

فرمول یافتن مساحت یک مثلث از طریق حاصلضرب برداری در نظرات تعریف شده است. راه حل و پاسخ در پایان درس است.

در عمل، این کار واقعاً بسیار رایج است.

برای حل مشکلات دیگر نیاز داریم:

ویژگی های حاصلضرب برداری بردارها

ما قبلاً برخی از ویژگی های محصول برداری را در نظر گرفته ایم، با این حال، آنها را در این لیست قرار می دهم.

برای بردارهای دلخواه و یک عدد دلخواه، ویژگی های زیر درست است:

1) در سایر منابع اطلاعاتی معمولاً این مورد در خواص برجسته نمی شود، اما از نظر عملی بسیار مهم است. پس بگذارید باشد.

2) - ملک نیز در بالا مورد بحث قرار گرفته است، گاهی اوقات به آن می گویند ضد جابجایی. به عبارت دیگر، ترتیب بردارها مهم است.

3) – انجمنی یا انجمنیقوانین محصول برداری ثابت ها را می توان به راحتی به خارج از محصول برداری منتقل کرد. راستی اونجا باید چیکار کنن؟

4) – توزیع یا توزیعیقوانین محصول برداری باز کردن براکت ها هم مشکلی ندارد.

برای نشان دادن، اجازه دهید به یک مثال کوتاه نگاه کنیم:

مثال 3

پیدا کنید اگر

راه حل:این شرط دوباره مستلزم یافتن طول حاصلضرب بردار است. بیایید مینیاتور خود را نقاشی کنیم:

(1) طبق قوانین انجمنی، ثابت ها را خارج از محدوده حاصلضرب برداری می گیریم.

(2) ثابت را به خارج از ماژول منتقل می کنیم و ماژول علامت منفی را می خورد. طول نمی تواند منفی باشد.

(3) بقیه روشن است.

پاسخ:

وقت آن است که چوب بیشتری به آتش اضافه کنید:

مثال 4

مساحت مثلثی را که بر روی بردارها ساخته شده است محاسبه کنید اگر

راه حل: با استفاده از فرمول مساحت مثلث را پیدا کنید . نکته مهم این است که بردارهای "tse" و "de" خود به عنوان مجموع بردارها ارائه می شوند. الگوریتم در اینجا استاندارد است و تا حدودی یادآور مثال های شماره 3 و 4 درس است. حاصل ضرب نقطه ای بردارها. برای وضوح، ما راه حل را به سه مرحله تقسیم می کنیم:

1) در مرحله اول، حاصلضرب برداری را از طریق حاصلضرب بردار بیان می کنیم، در واقع، بیایید یک بردار را بر اساس یک بردار بیان کنیم. هنوز در مورد طول مدت صحبتی نشده است!

(1) عبارات بردارها را جایگزین کنید.

(2) با استفاده از قوانین توزیعی، براکت ها را طبق قانون ضرب چندجمله ای ها باز می کنیم.

(3) با استفاده از قوانین انجمنی، همه ثابت ها را فراتر از محصولات برداری حرکت می دهیم. با کمی تجربه می توان مراحل 2 و 3 را به طور همزمان انجام داد.

(4) جمله اول و آخر به دلیل خاصیت nice برابر با صفر (بردار صفر) است. در عبارت دوم از خاصیت ضد جابجایی یک محصول برداری استفاده می کنیم:

(5) ما اصطلاحات مشابهی را ارائه می دهیم.

در نتیجه، مشخص شد که بردار از طریق یک بردار بیان می شود، که برای دستیابی به آن نیاز بود:

2) در مرحله دوم طول حاصلضرب برداری مورد نیاز خود را پیدا می کنیم. این اقداممثال 3 را یادآوری می کند:

3) مساحت مثلث مورد نیاز را پیدا کنید:

مراحل 2-3 راه حل می توانست در یک خط نوشته شود.

پاسخ:

مشکل در نظر گرفته شده کاملاً رایج است تست ها، در اینجا یک مثال برای یک راه حل مستقل آورده شده است:

مثال 5

پیدا کنید اگر

یک راه حل و پاسخ کوتاه در پایان درس. بیایید ببینیم هنگام مطالعه نمونه های قبلی چقدر دقت کردید ;-)

ضرب ضربدری بردارها در مختصات

، به صورت متعارف مشخص شده است، با فرمول بیان می شود:

فرمول واقعاً ساده است: در خط بالای تعیین کننده، بردارهای مختصات را می نویسیم، در خط دوم و سوم، مختصات بردارها را "قرار می دهیم" و می گذاریم. به ترتیب دقیق– ابتدا مختصات بردار “ve” سپس مختصات بردار “double-ve”. اگر بردارها باید به ترتیب دیگری ضرب شوند، سطرها باید تعویض شوند:

مثال 10

بررسی کنید که آیا بردارهای فضای زیر خطی هستند یا خیر:
آ)
ب)

راه حل: بررسی بر اساس یکی از عبارات این درس است: اگر بردارها به صورت هم خط باشند، حاصلضرب بردار آنها برابر با صفر (بردار صفر) است: .

الف) حاصلضرب برداری را پیدا کنید:

بنابراین، بردارها خطی نیستند.

ب) حاصلضرب برداری را پیدا کنید:

پاسخ: الف) خطی نیست، ب)

در اینجا، شاید، تمام اطلاعات اولیه در مورد حاصلضرب برداری بردارها وجود دارد.

این بخش خیلی بزرگ نخواهد بود، زیرا مشکلات کمی در استفاده از حاصلضرب مخلوط بردارها وجود دارد. در واقع، همه چیز به تعریف، معنای هندسی و چند فرمول کاری بستگی دارد.

حاصلضرب مخلوط بردارها است محصول سهبردارها:

بنابراین آنها مانند یک قطار در صف ایستادند و نمی توانند منتظر شناسایی شوند.

ابتدا یک تعریف و یک تصویر:

تعریف: کار مختلط غیر همسطحبردارها، به این ترتیب گرفته شده است، تماس گرفت حجم موازی، که بر روی این بردارها ساخته شده است، اگر پایه درست باشد با علامت "+" و اگر پایه سمت چپ باشد علامت "-".

بیایید نقاشی را انجام دهیم. خطوطی که برای ما نامرئی هستند با خطوط نقطه چین ترسیم می شوند:

بیایید به تعریف بپردازیم:

2) بردارها گرفته می شوند به ترتیب خاصی، یعنی همان طور که ممکن است حدس بزنید، بازآرایی بردارها در محصول بدون عواقب اتفاق نمی افتد.

3) قبل از اظهار نظر در مورد معنای هندسی، یک واقعیت آشکار را متذکر می شوم: حاصلضرب مخلوط بردارها یک عدد است: . در ادبیات آموزشی، طراحی ممکن است کمی متفاوت باشد.

الف- مقدماتی محصول مخلوط، حجم موازی است، بر روی بردارها ساخته شده است (شکل با بردارهای قرمز و خطوط سیاه ترسیم شده است). یعنی عدد برابر با حجم یک متوازی الاضلاع معین است.

توجه داشته باشید : نقاشی شماتیک است.

4) دوباره نگران مفهوم جهت گیری مبنا و فضا نباشیم. منظور از قسمت پایانی این است که می توان یک علامت منفی به حجم اضافه کرد. به زبان ساده، محصول مخلوط می تواند منفی باشد: .

به طور مستقیم از تعریف، فرمول محاسبه حجم یک متوازی الاضلاع ساخته شده بر روی بردارها را دنبال می کند.

تعریف مجموعه مرتب شده ای از (x 1 , x 2 , ... , x n) n عدد واقعی نامیده می شود. بردار n بعدیو اعداد x i (i = ) - اجزاء،یا مختصات،

مثال. اگر مثلاً یک کارخانه خودروسازی خاص باید در هر شیفت 50 خودرو، 100 کامیون، 10 اتوبوس، 50 مجموعه لوازم یدکی خودرو و 150 دستگاه کامیون و اتوبوس تولید کند، برنامه تولید این کارخانه را می توان به صورت برداری نوشت. (50، 100، 10، 50، 150)، دارای پنج جزء.

نشانه گذاری. بردارها به صورت پررنگ نشان داده شده اند حروف کوچکیا حروف با نوار یا فلش در بالا، به عنوان مثال، آیا. دو بردار نامیده می شوند برابر، در صورتی که تعداد اجزای آنها یکسان باشد و اجزای مربوطه آنها مساوی باشد.

اجزای برداری را نمی توان با هم عوض کرد، به عنوان مثال، (3، 2، 5، 0، 1)و (2، 3، 5، 0، 1) بردارهای مختلف.
عملیات بر روی بردارهاکار ایکس= (x 1 , x 2 , ... ,x n) توسط یک عدد واقعیλ بردار نامیده می شودλ ایکس= (λ x 1، λ x 2، ...، λ x n).

میزانایکس= (x 1 , x 2 , ... ,x n) و y= (y 1 , y 2 , ... ,y n) بردار نامیده می شود x+y= (x 1 + y 1 , x 2 + y 2 , ... , x n + + y n).

فضای بردارین -فضای برداری بعدی آر n به عنوان مجموعه ای از تمام بردارهای n بعدی تعریف می شود که برای آنها عملیات ضرب در اعداد واقعی و جمع تعریف شده است.

تصویر اقتصادی تصویر اقتصادی فضای برداری n بعدی: فضای کالا (کالاها). زیر کالاهاما برخی از کالاها یا خدماتی را که در زمان معینی در یک مکان خاص فروخته شده است، درک خواهیم کرد. فرض کنید تعداد محدودی از کالاهای موجود n وجود دارد. مقدار هر یک از آنها خریداری شده توسط مصرف کننده با مجموعه ای از کالاها مشخص می شود

ایکس= (x 1، x 2، ...، x n)،

که در آن x i مقدار i-امین کالای خریداری شده توسط مصرف کننده را نشان می دهد. ما فرض می کنیم که همه کالاها دارای خاصیت تقسیم دلخواه هستند، به طوری که هر مقدار غیر منفی از هر یک از آنها قابل خریداری است. سپس تمام مجموعه کالاهای ممکن بردار فضای کالا C = ( ایکس= (x 1 , x 2 , ... , x n) x i ≥ 0، i =).

استقلال خطی سیستم ه 1 , ه 2 , ... , ه m بردارهای n بعدی نامیده می شوند وابسته به خط، اگر چنین اعدادی وجود داشته باشدλ 1، λ 2، ...، λ m ، که حداقل یکی از آنها غیر صفر است، به طوری که برابر استλ 1 ه 1 + λ 2 ه 2 +... + λ m ه m = 0; در غیر این صورت، این سیستم از بردارها نامیده می شود مستقل خطی، یعنی برابری ذکر شده تنها در صورتی امکان پذیر است که همه . معنی هندسیوابستگی خطی بردارها در آر 3 که به عنوان بخش های جهت دار تفسیر می شود، قضایای زیر را توضیح دهید.

قضیه 1. یک سیستم متشکل از یک بردار به صورت خطی وابسته است اگر و فقط اگر این بردار صفر باشد.

قضیه 2. برای اینکه دو بردار به صورت خطی وابسته باشند، لازم و کافی است که آنها هم خط (موازی) باشند.

قضیه 3 . برای اینکه سه بردار به صورت خطی وابسته باشند، همسطح بودن (در یک صفحه) لازم و کافی است.

سه گانه چپ و راست بردارها. سه بردار غیرهمسطح الف، ب، جتماس گرفت درست، اگر ناظر از مبدأ مشترک آنها انتهای بردارها را دور بزند الف، ب، جبه ترتیب داده شده به نظر می رسد در جهت عقربه های ساعت رخ می دهد. در غیر این صورت الف، ب، ج -سه سمت چپ. تمام سه گانه راست (یا چپ) بردارها نامیده می شوند همان جهت دار.

مبانی و مختصات. تروئیکا ه 1, ه 2 , ه 3 بردار غیرهمسطح در آر 3 نامیده می شود اساسو خود بردارها ه 1, ه 2 , ه 3 - پایه ای. هر بردار آرا می توان به طور منحصر به فرد به بردارهای پایه گسترش داد، یعنی به شکل نمایش داده شود

آ= x 1 ه 1+x2 ه 2 + x 3 ه 3, (1.1)

اعداد x 1 , x 2 , x 3 در بسط (1.1) نامیده می شوند مختصاتآدر اساس ه 1, ه 2 , ه 3 و تعیین شده اند آ(x 1، x 2، x 3).

پایه ارتونرمال. اگر بردارها ه 1, ه 2 , ه 3 به صورت جفتی عمود بر هم هستند و طول هر یک از آنها برابر با یک است، سپس پایه نامیده می شود. متعارفو مختصات x 1 , x 2 , x 3 - مستطیل شکل.بردارهای پایه یک پایه متعارف با نشان داده می شوند من، ج، ک.

ما آن را در فضا فرض خواهیم کرد آر 3 سیستم مناسب مختصات مستطیلی دکارتی انتخاب شده است (0، من، ج، ک}.

اثر هنری وکتور. اثر هنری وکتور آبه بردار ببردار نامیده می شود ج، که با سه شرط زیر تعیین می شود:

1. طول برداری جاز نظر عددی برابر با مساحت متوازی الاضلاع ساخته شده بر روی بردارها است آو بیعنی
ج= |الف||ب|گناه ( آ^ب).

2. وکتور جعمود بر هر یک از بردارها آو ب

3. بردارها آ، بو ج، که به ترتیب نشان داده شده گرفته شده است، یک سه گانه راست تشکیل دهید.

برای یک محصول متقابل جنامگذاری معرفی شده است c =[ab] یا
c = a × ب

اگر بردارها آو بخطی هستند، سپس گناه ( a^b) = 0 و [ ab] = 0، به ویژه، [ aa] = 0. محصولات برداری بردارهای واحد: [ ij]=ک، [jk] = من, [کی]=j.

اگر بردارها آو بدر اساس مشخص شده است من، ج، کمختصات آ(a 1، a 2، a 3)، ب(ب 1، ب 2، ب 3)، سپس

کار مختلط. اگر حاصل ضرب برداری دو بردار آو ببه صورت اسکالار در بردار سوم ضرب می شود جآنگاه چنین حاصل ضرب سه بردار نامیده می شود کار مختلطو با علامت نشان داده می شود آ قبل از میلاد مسیح.

اگر بردارها الف، بو جدر اساس من، ج، کبا مختصات آنها داده شده است
آ(a 1، a 2، a 3)، ب(ب 1، ب 2، ب 3)، ج(ج 1، ج 2، ج 3)، سپس

.

محصول مخلوط دارای یک تفسیر هندسی ساده است - این یک عددی است که از نظر مقدار مطلق برابر با حجم یک موازی شکل ساخته شده بر روی سه بردار معین است.

اگر بردارها یک سه برابر راست تشکیل دهند، آنگاه حاصلضرب مخلوط آنها یک عدد مثبت برابر با حجم مشخص شده است. اگر سه باشد الف، ب، ج -چپ، پس a b c<0 и V = - a b cبنابراین V =|a b c|.

مختصات بردارهایی که در مسائل فصل اول با آن مواجه می شوند، نسبت به یک مبنای متعارف درست فرض می شود. بردار واحد هم جهت با بردار آ،با نماد نشان داده شده است آ O. سمبل r=OMبا بردار شعاع نقطه M، نمادهای a، AB یا نشان داده می شود|a|, | AB|ماژول های بردارها مشخص می شوند آو AB

مثال 1.2. زاویه بین بردارها را پیدا کنید آ= 2متر+4nو ب= m-n، جایی که مترو n-بردار واحد و زاویه بین مترو nبرابر با 120 o.

راه حل. ما داریم: cos φ = ab/ab ab =(2متر+4n) (m-n) = 2متر 2 - 4n 2 +2دقیقه=
= 2 - 4+2cos120 o = - 2 + 2(-0.5) = -3; a = ; آ 2 = (2متر+4n) (2متر+4n) =
= 4متر 2 +16دقیقه+16n 2 = 4+16(-0.5)+16=12 که به معنی a = . b = ; ب 2 =
= (m-n)(m-n) = متر 2 -2دقیقه+n 2 = 1-2(-0.5)+1 = 3 که به معنی b = . در نهایت داریم: cosφ = = -1/2، φ = 120 o.

مثال 1.3.شناخت بردارها AB(-3،-2.6) و قبل از میلاد مسیح.(-2،4،4)، طول ارتفاع AD مثلث ABC را محاسبه کنید.

راه حل. با نشان دادن مساحت مثلث ABC با S به دست می آید:
S = 1/2 ق.م. سپس AD=2S/BC، BC= = = 6,
S = 1/2| AB ×AC|. AC=AB+BC، که به معنای بردار است A.C.مختصات دارد
. .

مثال 1.4 . دو بردار داده شده است آ(11،10،2) و ب(4،0،3). بردار واحد را پیدا کنید جمتعامد به بردارها آو بو طوری هدایت می شود که بردارهای سه گانه مرتب شده باشند الف، ب، جدرست بود.

راه حل.اجازه دهید مختصات بردار را مشخص کنیم جبا توجه به یک مبنای متعارف راست مفروض بر حسب x، y، z.

زیرا ج ⊥ الف، ج ⊥ب، آن حدود= 0، cb= 0. با توجه به شرایط مسئله، لازم است که c = 1 و a b c >0.

ما یک سیستم معادلات داریم برای پیدا کردن x,y,z: 11x +10y + 2z = 0، 4x+3z=0، x 2 + y 2 + z 2 = 0.

از معادلات اول و دوم سیستم z = -4/3 x، y = -5/6 x به دست می آید. با جایگزینی y و z در معادله سوم، داریم: x 2 = 36/125، از این رو
x =± . با استفاده از شرط a b c > 0، نابرابری را دریافت می کنیم

با در نظر گرفتن عبارات z و y، نابرابری حاصل را به این شکل بازنویسی می کنیم: 625/6 x > 0، که به معنای x>0 است. بنابراین، x =، y = -، z =-.