7.1. çapraz ürünün tanımı
Belirtilen sırayla alınan üç eş düzlemli olmayan vektör a , b ve c , üçüncü vektör c'nin sonundan birinci vektör a'dan ikinci vektör b'ye en kısa dönüşün saat yönünün tersine olduğu görülüyorsa bir dik üçlü oluşturur ve saat yönünde ise soldaki (bkz. Şekil 16).
Bir vektör a ve vektör b'nin vektör çarpımı vektör c olarak adlandırılır, bu:
1. a ve b vektörlerine dik, yani c ^ a ve c ^ b;
2. A ve vektörleri üzerine inşa edilmiş paralelkenarın alanına sayısal olarak eşit bir uzunluğa sahiptir.b yanlarda olduğu gibi (bkz. şekil 17), yani.
3. a , b ve c vektörleri bir dik üçlü oluşturur.
vektör ürünü a x b veya [a,b] ile gösterilir. Bir vektör çarpımının tanımından, doğrudan takip ettiğim ortlar arasındaki aşağıdaki ilişkiler, j ve k(bkz. şekil 18):
ben x j \u003d k, j x k \u003d ben, k x ben \u003d j.
Örneğin şunu kanıtlayalım ben xj \u003d k.
1) k ^ ben , k ^ j;
2) |k |=1, ancak | ben x j| = |ben | |J| sin(90°)=1;
3) i , j vektörleri ve k bir sağ üçlü oluşturun (bkz. Şekil 16).
7.2. Çapraz ürün özellikleri
1. Faktörler yeniden düzenlendiğinde vektör çarpımı işaret değiştirir, yani ve xb \u003d (b xa) (bkz. Şekil 19).
A xb ve b xa vektörleri doğrusaldır, aynı modüllere sahiptir (paralelkenarın alanı değişmeden kalır), ancak zıt yönlüdür (a, b, a xb ve a, b, b x a üçlüleri zıt yönde). Yani aksb = -(bxa).
2. Vektör ürünü, bir skaler faktöre göre bir kombinasyon özelliğine sahiptir, yani l (a xb) \u003d (l a) x b \u003d a x (l b).
l >0 olsun. l (a xb) vektörü, a ve b vektörlerine diktir. vektör ( ben a)x b a ve vektörlerine de diktir. b(vektörler bir, ben ama aynı düzlemde yat). Yani vektörler ben(bir xb) ve ( ben a)x b doğrusal. Yönlerinin çakıştığı açıktır. Aynı uzunluğa sahipler:
Bu yüzden ben(bir xb)= ben bir xb. için benzer şekilde kanıtlanmıştır. ben<0.
3. Sıfır olmayan iki vektör a ve b eşdoğrusaldır, ancak ve ancak vektör çarpımı sıfır vektörüne eşitse, yani ve ||b<=>ve xb \u003d 0.
Özellikle, i *i =j *j =k *k =0 .
4. Vektör çarpımının bir dağılım özelliği vardır:
(a+b) xs = bir xs + b.
Kanıt olmadan kabul et.
7.3. Koordinatlar cinsinden çapraz çarpım ifadesi
Vektör çapraz çarpım tablosunu kullanacağız i , j ve k:
birinci vektörden ikinciye giden en kısa yolun yönü okun yönü ile çakışıyorsa çarpım üçüncü vektöre eşittir, uyuşmuyorsa üçüncü vektör eksi işareti ile alınır.
İki vektör a =a x i +a y olsun j+az k ve b=bx i+tarafından j+bz k. Bu vektörleri polinom olarak çarparak (vektör çarpımının özelliklerine göre) vektörel çarpımını bulalım:
Ortaya çıkan formül daha da kısa yazılabilir:
eşitliğin (7.1) sağ tarafı üçüncü dereceden determinantın birinci satırın elemanları cinsinden açılımına karşılık geldiğinden, eşitliğin (7.2) hatırlanması kolaydır.
7.4. Çapraz çarpımın bazı uygulamaları
Vektörlerin eşdoğrusallığının oluşturulması
Paralelkenar ve üçgenin alanını bulma
Vektörlerin çapraz çarpımının tanımına göre a ve B |bir xb | =| bir | * |b |sin g , yani S par = |axb |. Ve bu nedenle, D S \u003d 1/2 | a x b |.
Bir noktaya göre kuvvet momentinin belirlenmesi
A noktasına bir kuvvet uygulansın. F = AB bırak gitsin Ö- boşlukta bir nokta (bkz. Şekil 20).
Fizikten biliniyor ki tork F noktaya göre Ö vektör denir M , hangi noktadan geçer Ö ve:
1) noktalardan geçen düzleme dik O, A, B;
2) sayısal olarak kuvvet ve omuz ürününe eşittir
3) OA ve A B vektörleri ile bir dik üçlü oluşturur.
Bu nedenle, M \u003d OA x F.
Doğrusal dönüş hızını bulma
Hız v açısal hızla dönen rijit bir cismin M noktası w sabit bir eksen etrafında, Euler formülü v \u003d w x r ile belirlenir, burada r \u003d OM, burada O, eksenin bazı sabit noktalarıdır (bkz. Şekil 21).
Bir vektör çarpımı kavramını vermeden önce, a → , b → , c → vektörlerinin sıralı üçlüsünün üç boyutlu uzayda yönelimi sorusuna dönelim.
Başlangıç olarak a → , b → , c → vektörlerini bir noktadan ayıralım. a → , b → , c → üçlüsünün yönü, c → vektörünün yönüne bağlı olarak sağ veya soldur. a → vektörünün sonundan b → vektörüne en kısa dönüşün yapıldığı yönden c → , a → , b → , c → üçlüsünün formu belirlenir.
En kısa dönüş saat yönünün tersine ise, a → , b → , c → vektörlerinin üçlüsü denir Sağ saat yönünde ise - ayrıldı.
Ardından, doğrusal olmayan iki vektör a → ve b → alın. O halde A noktasından A B → = a → ve AC → = b → vektörlerini erteleyelim. Hem AB → hem de AC → 'ye aynı anda dik olan bir A D → = c → vektörü oluşturalım. Böylece, AD → = c → vektörünü oluştururken, ona bir yön veya ters yön vererek iki şey yapabiliriz (şekle bakın).
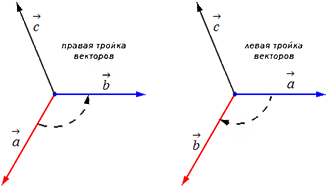
a → , b → , c → vektörlerinin sıralı üçlüsü, öğrendiğimiz gibi, vektörün yönüne bağlı olarak sağ veya sol olabilir.
Yukarıdan, bir vektör çarpımının tanımını sunabiliriz. Bu tanım, üç boyutlu uzayın dikdörtgen koordinat sisteminde tanımlanan iki vektör için verilmiştir.
tanım 1
İki vektörün vektör ürünü a → ve b → üç boyutlu uzayın dikdörtgen koordinat sisteminde verilen böyle bir vektöre şöyle diyeceğiz:
- a → ve b → vektörleri eşdoğrusal ise, sıfır olacaktır;
- hem a → vektörüne hem de b → vektörüne dik olacaktır, yani ∠ bir → c → = ∠ b → c → = π 2 ;
- uzunluğu şu formülle belirlenir: c → = a → b → sin ∠ a → , b → ;
- a → , b → , c → vektörlerinin üçlüsü, verilen koordinat sistemiyle aynı oryantasyona sahiptir.
a → ve b → vektörlerinin çapraz çarpımı aşağıdaki gösterime sahiptir: a → × b → .
Çapraz ürün koordinatları
Herhangi bir vektörün koordinat sisteminde belirli koordinatları olduğundan, vektör çarpımının ikinci bir tanımını yapmak mümkündür; bu, vektörlerin verilen koordinatlarından koordinatlarını bulmanızı sağlar.
Tanım 2
Üç boyutlu uzayın dikdörtgen koordinat sisteminde iki vektörün vektör çarpımı a → = (a x ; a y ; a z) ve b → = (b x ; b y ; bz) c → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k → , burada i → , j → , k → koordinat vektörleridir.
Vektör çarpımı, üçüncü dereceden bir kare matrisin determinantı olarak temsil edilebilir; burada birinci sıra orta vektörler i → , j → , k → , ikinci sıra vektörün koordinatlarını içerir a → , ve üçüncü sıra belirli bir dikdörtgen koordinat sisteminde b → vektörünün koordinatlarıdır, bu matris determinantı şuna benzer: c → = a → × b → = i → j → k → a x a y a z b x b y b z
Bu determinantı ilk satırın elemanları üzerine genişleterek eşitliği elde ederiz: c → = a → × b → = i → j → k → a x a y a z b x b y b z = a y a z by y b z ben → - a x a z b x b z j → + a x a y b x b y k → = = a → × b → = ( a y b z - a z b y) ben → + (a z b x - a x b z) j → + (a x b y - a y b x) k →
Çapraz ürün özellikleri
Koordinatlardaki vektör ürününün, c → = a → × b → = i → j → k → a x a y a z b x b y bz matrisinin determinantı olarak temsil edildiği bilinmektedir. matris belirleyici özellikler aşağıdaki vektörel ürün özellikleri:
- değişmelilik a → × b → = - b → × a → ;
- dağılım a (1) → + a (2) → × b = a (1) → × b → + a (2) → × b → veya a → × b (1) → + b (2) → = a → × b (1) → + a → × b (2) → ;
- ilişkilendirme λ a → × b → = λ a → × b → veya a → × (λ b →) = λ a → × b → , burada λ keyfi bir gerçek sayıdır.
Bu özelliklerin karmaşık kanıtları yoktur.
Örneğin, bir vektör çarpımının değişme karşıtı özelliğini ispatlayabiliriz.
Karşıt değişmeliliğin kanıtı
Tanım olarak, a → × b → = i → j → k → a x a y a z b x b y b z ve b → × a → = i → j → k → b x b y b z a x a y a z . Ve matrisin iki satırı değiştirilirse, matrisin determinantının değeri tersine değişmelidir, bu nedenle a → × b → = i → j → k → a x a y a z b x b y b z = - i → j → k → b x b y b z a x a y a z = - b → × a → , bu vektör çarpımının ters değişmeliliğini kanıtlar.
Vektör Çarpımı - Örnekler ve Çözümler
Çoğu durumda, üç tür görev vardır.
Birinci tür problemlerde, genellikle iki vektörün uzunlukları ve aralarındaki açı verilir, ancak çapraz çarpımın uzunluğunu bulmanız gerekir. Bu durumda, aşağıdaki formülü kullanın c → = a → b → sin ∠ a → , b → .
örnek 1
a → = 3 , b → = 5 , ∠ a → , b → = π 4 biliniyorsa a → ve b → vektörlerinin çapraz çarpımının uzunluğunu bulun.
Çözüm
a → ve b → vektörlerinin vektörel çarpımının uzunluğunun tanımını kullanarak şu sorunu çözüyoruz: a → × b → = a → b → sin ∠ a → , b → = 3 5 sin π 4 = 15 2 2 .
Cevap: 15 2 2 .
İkinci tür görevler, vektörlerin koordinatlarıyla bağlantılıdır, bir vektör ürünü, uzunluğu vb. içerirler. verilen vektörlerin bilinen koordinatları üzerinden aranır bir → = (bir x ; bir y ; bir z) ve b → = (b x ; b y ; b z) .
Bu tür görevler için, görevler için birçok seçeneği çözebilirsiniz. Örneğin, a → ve b → vektörlerinin koordinatları değil, ancak formun koordinat vektörlerindeki açılımları b → = b x ben → + b y j → + b z k → ve c → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x by y - a y b x) k → , veya a → ve b → vektörleri koordinatlarıyla verilebilir. başlangıç ve bitiş noktaları.
Aşağıdaki örnekleri göz önünde bulundurun.
Örnek 2
İki vektör dikdörtgen bir koordinat sisteminde ayarlanır a → = (2 ; 1 ; - 3) , b → = (0 ; - 1 ; 1) . Vektörel çarpımlarını bulun.
Çözüm
İkinci tanıma göre, verilen koordinatlarda iki vektörün vektör çarpımını buluyoruz: a → × b → = (a y bz - a z b y) i → + (a z bx - a x bz) j → + (a x b y - a y bx) k → = = (1 1 - (- 3) (- 1)) ben → + ((- 3) 0 - 2 1) j → + (2 (- 1) - 1 0) k → = = - 2 ben → - 2 j → - 2 k → .
Vektör çarpımını matris determinantı üzerinden yazarsak, bu örneğin çözümü şu şekildedir: a → × b → = i → j → k → a x a y a z b x b y b z = i → j → k → 2 1 - 3 0 - 1 1 = - 2 ben → - 2 j → - 2 k → .
Cevap: a → × b → = - 2 ben → - 2 j → - 2 k → .
Örnek 3
Dikdörtgen bir Kartezyen koordinat sisteminin i → - j → ve i → + j → + k → vektörlerinin çapraz çarpımının uzunluğunu bulun; burada i → , j → , k → - orts.
Çözüm
İlk olarak, verilen vektörel çarpımın i → - j → × i → + j → + k → koordinatlarını verilen dikdörtgen koordinat sisteminde bulalım.
i → - j → ve i → + j → + k → vektörlerinin sırasıyla (1 ; - 1 ; 0) ve (1 ; 1 ; 1) koordinatlarına sahip olduğu bilinmektedir. Matris determinantını kullanarak vektör çarpımının uzunluğunu bulun, sonra i → - j → × i → + j → + k → = i → j → k → 1 - 1 0 1 1 1 = - i → - j → + 2 k → .
Bu nedenle, i → - j → × i → + j → + k → vektör çarpımı verilen koordinat sisteminde (- 1 ; - 1 ; 2) koordinatlara sahiptir.
Vektör çarpımının uzunluğunu formülle buluruz (vektörün uzunluğunu bulma bölümüne bakın): i → - j → × i → + j → + k → = - 1 2 + - 1 2 + 2 2 = 6.
Cevap: ben → - j → × ben → + j → + k → = 6 . .
Örnek 4
A (1 , 0 , 1) , B (0 , 2 , 3) , C (1 , 4 , 2) üç noktasının koordinatları dikdörtgen bir Kartezyen koordinat sisteminde verilmiştir. Aynı anda A B → ve AC →'ye dik bir vektör bulun.
Çözüm
A B → ve AC → vektörleri sırasıyla (- 1 ; 2 ; 2) ve (0 ; 4 ; 1) aşağıdaki koordinatlara sahiptir. A B → ve A C → vektörlerinin vektör çarpımını bulduktan sonra, bunun hem AB → hem de A C → vektörlerine tanım gereği dik bir vektör olduğu, yani problemimizin çözümü olduğu açıktır. Bul A B → × A C → = i → j → k → - 1 2 2 0 4 1 = - 6 ben → + j → - 4 k → .
Cevap: - 6 ben → + j → - 4 k → . dikey vektörlerden biridir.
Üçüncü tip problemler, vektörlerin vektör çarpımının özelliklerini kullanmaya odaklanır. Hangisini uyguladıktan sonra, verilen soruna bir çözüm elde edeceğiz.
Örnek 5
a → ve b → vektörleri diktir ve uzunlukları sırasıyla 3 ve 4'tür. 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 a → × a → çapraz çarpımının uzunluğunu bulun + 3 bir → × - 2 b → + - b → × bir → + - b → × - 2 b → .
Çözüm
Vektörel çarpımın dağılım özelliği ile 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 yazabiliriz. a → × a → + 3 a → × - 2 b → + - b → × a → + - b → × - 2 b →
İlişkilendirilebilirlik özelliği ile, son ifadedeki vektör çarpımlarının işaretinin ötesindeki sayısal katsayıları çıkarıyoruz: 3 a → × a → + 3 a → × - 2 b → + - b → × a → + - b → × - 2 b → = = 3 a → × a → + 3 (- 2) a → × b → + (- 1) b → × a → + (- 1) (- 2) b → × b → = = 3 a → × a → - 6 a → × b → - b → × a → + 2 b → × b →
a → × a → ve b → × b → vektör ürünleri 0'a eşittir, çünkü a → × a → = a → a → sin 0 = 0 ve b → × b → = b → b → sin 0 = 0 , o zaman 3 a → × a → - 6 a → × b → - b → × a → + 2 b → × b → = - 6 a → × b → - b → × a → . .
Vektör çarpımının ters değişmeliliğinden şu sonuç çıkar - 6 a → × b → - b → × a → = - 6 a → × b → - (- 1) a → × b → = - 5 a → × b → . .
Vektör çarpımının özelliklerini kullanarak, 3 · a → - b → × a → - 2 · b → = = - 5 · a → × b → eşitliğini elde ederiz.
Koşullu olarak, a → ve b → vektörleri diktir, yani aralarındaki açı eşittir π 2 . Şimdi geriye kalan tek şey, bulunan değerleri karşılık gelen formüllerle değiştirmektir: 3 a → - b → × a → - 2 b → = - 5 a → × b → = = 5 a → × b → = 5 a → b → günah (a →, b →) = 5 3 4 sin π 2 = 60.
Cevap: 3 bir → - b → × bir → - 2 b → = 60 .
Tanım gereği vektörlerin çapraz çarpımının uzunluğu şu şekildedir: a → × b → = a → · b → · sin ∠ a → , b → . Zaten bilindiği için (okul kursundan), bir üçgenin alanı, iki kenarının uzunluklarının çarpımının yarısına ve bu taraflar arasındaki açının sinüsüne eşittir. Bu nedenle, vektör ürününün uzunluğu bir paralelkenarın alanına eşittir - iki katına çıkmış bir üçgen, yani a → ve b → vektörleri biçimindeki kenarların çarpımı , bir noktadan sinüs tarafından atılır sin ∠ a → , b → .
Bu vektör çarpımının geometrik anlamıdır.
Vektör ürününün fiziksel anlamı
Fiziğin dallarından biri olan mekanikte vektörel çarpım sayesinde uzayda bir noktaya göre kuvvet momentini belirleyebilirsiniz.
Tanım 3
A noktasına göre B noktasına uygulanan F → kuvveti momenti altında, aşağıdaki A B → × F → vektör ürününü anlayacağız.
Metinde bir hata fark ederseniz, lütfen onu vurgulayın ve Ctrl+Enter tuşlarına basın.
Tanım. Bir a vektörünün (çarpan) kendisine eşdoğrusal olmayan bir vektör (çarpan) ile vektörel çarpımı, aşağıdaki gibi oluşturulan üçüncü vektör c'dir (çarpım):
1) modülü, Şekil l'deki paralelkenarın alanına sayısal olarak eşittir. 155), vektörler üzerine inşa edilmiştir, yani bahsedilen paralelkenarın düzlemine dik olan yöne eşittir;
3) bu durumda, c vektörünün yönü (iki olası yön arasından) c vektörlerinin sağ elli bir sistem oluşturacağı şekilde seçilir (§ 110).
atama: veya
Tanıma ek. Vektörler eşdoğrusal ise, şekli (şartlı olarak) bir paralelkenar olarak düşünürsek, sıfır alan atamak doğaldır. Bu nedenle, eşdoğrusal vektörlerin vektör çarpımı boş vektöre eşit kabul edilir.
Sıfır vektörü herhangi bir yöne atanabileceğinden, bu kural tanımın 2. ve 3. maddeleriyle çelişmez.
Açıklama 1. "Vektör çarpımı" terimindeki ilk kelime, bir eylemin sonucunun bir vektör olduğunu belirtir (skaler çarpımın aksine; bkz. § 104, açıklama 1).
Örnek 1. Doğru koordinat sisteminin ana vektörlerinin bulunduğu vektör çarpımını bulun (Şek. 156).
1. Ana vektörlerin uzunlukları ölçek birimine eşit olduğu için paralelkenarın (karenin) alanı sayısal olarak bire eşittir. Bu nedenle, vektör çarpımının modülü bire eşittir.
2. Düzleme dik eksen eksen olduğu için, istenen vektör çarpımı k vektörüne doğrusal bir vektördür; ve her ikisinin de modülü 1 olduğundan, gerekli çapraz çarpım ya k ya da -k'dir.
3. Bu iki olası vektörden ilki seçilmelidir, çünkü k vektörleri bir sağ sistem oluşturur (ve vektörler bir sol sistem oluşturur).
Örnek 2. Çapraz çarpımı bulun
Çözüm. Örnek 1'de olduğu gibi, vektörün k veya -k olduğu sonucuna varıyoruz. Ama şimdi -k'yi seçmemiz gerekiyor, çünkü vektörler doğru sistemi oluşturuyor (ve vektörler solu oluşturuyor). Yani,
Örnek 3 Vektörlerin uzunlukları sırasıyla 80 ve 50 cm'dir ve 30°'lik bir açı oluştururlar. Uzunluk birimi olarak bir metre alarak, vektör çarpımının uzunluğunu bulun a
Çözüm. Vektörler üzerine inşa edilmiş bir paralelkenarın alanı eşittir İstenen vektör çarpımının uzunluğu eşittir
Örnek 4. Uzunluk birimi olarak bir santimetre alarak aynı vektörlerin çapraz çarpımının uzunluğunu bulun.
Çözüm. Vektörler üzerine inşa edilen paralelkenarın alanı, vektör çarpımının uzunluğuna eşit olduğundan 2000 cm'dir, yani
Örnek 3 ve 4'ün karşılaştırılması, vektörün uzunluğunun sadece faktörlerin uzunluklarına değil, aynı zamanda uzunluk birimi seçimine de bağlı olduğunu göstermektedir.
Vektör çarpımının fiziksel anlamı. Vektör çarpımı tarafından temsil edilen birçok fiziksel nicelikten yalnızca kuvvet momentini dikkate alacağız.
A, kuvvetin uygulama noktası olsun O noktasına göre kuvvet momentine vektör ürünü denir.Bu vektör ürününün modülü sayısal olarak paralelkenarın alanına eşittir (Şekil 157), momentin modülü, taban ile yüksekliğin çarpımına eşittir, yani kuvvet ile O noktasından kuvvetin etki ettiği düz çizgiye olan mesafenin çarpımıdır.
Mekanikte, rijit bir cismin dengesi için sadece cisme uygulanan kuvvetleri temsil eden vektörlerin toplamının değil, aynı zamanda kuvvetlerin momentlerinin toplamının da sıfıra eşit olması gerektiği kanıtlanmıştır. Tüm kuvvetlerin aynı düzleme paralel olması durumunda, momentleri temsil eden vektörlerin toplamı, modüllerinin toplanması ve çıkarılması ile değiştirilebilir. Ancak keyfi güç yönleri için böyle bir değiştirme imkansızdır. Buna göre, çapraz çarpım bir sayı olarak değil, tam olarak bir vektör olarak tanımlanır.
Bu yazıda, iki vektörün çapraz çarpımı kavramı üzerinde duracağız. Gerekli tanımları vereceğiz, bir vektör ürününün koordinatlarını bulmak için bir formül yazacağız, özelliklerini listeleyip gerekçelendireceğiz. Bundan sonra, iki vektörün çapraz çarpımının geometrik anlamı üzerinde duracağız ve çeşitli tipik örneklerin çözümlerini ele alacağız.
Sayfa gezintisi.
Bir vektör çarpımının tanımı.
Bir çapraz çarpımın tanımını vermeden önce, üç boyutlu uzayda sıralı bir üçlü vektörün yönelimini ele alalım.
Vektörleri bir noktadan erteleyelim. Vektörün yönüne göre üçlü sağ veya sol olabilir. Vektörün sonundan en kısa dönüşün vektörden nasıl olduğuna bakalım. En kısa dönüş saat yönünün tersine ise, o zaman vektörlerin üçlüsü denir Sağ, aksi halde - ayrıldı.
Şimdi doğrusal olmayan iki vektör alalım ve . Vektörleri ve A noktasından ayırın. Aynı anda ve ve'ye dik olan bir vektör oluşturalım. Açıkçası, bir vektör oluştururken, ona bir yön veya ters yön vererek iki şey yapabiliriz (resme bakın).
Vektörün yönüne bağlı olarak, vektörlerin sıralı üçlüsü sağ veya sol olabilir.
Böylece bir vektör çarpımının tanımına yaklaştık. Üç boyutlu uzayın dikdörtgen koordinat sisteminde verilen iki vektör için verilmiştir.
Tanım.
İki vektörün vektör ürünü ve , üç boyutlu uzayın dikdörtgen bir koordinat sisteminde verilen bir vektör olarak adlandırılır, öyle ki
Vektörlerin çapraz çarpımı ve olarak gösterilir.
Vektör ürün koordinatları.
Şimdi, verilen vektörlerin koordinatlarından koordinatlarını bulmamızı sağlayan bir vektör çarpımının ikinci tanımını veriyoruz ve.
Tanım.
Üç boyutlu uzayın dikdörtgen koordinat sisteminde iki vektörün çapraz çarpımı 
ve 
bir vektördür, burada koordinat vektörleri vardır.
Bu tanım bize çapraz çarpımı koordinat biçiminde verir.
Vektör çarpımını, birinci satırı ortlar, ikinci satırı vektörün koordinatlarını ve üçüncü satırı vektörün koordinatlarını içeren üçüncü dereceden bir kare matrisin determinantı olarak temsil etmek uygundur. belirli bir dikdörtgen koordinat sistemi: 
Bu determinantı ilk satırın elemanlarına göre genişletirsek, koordinatlarda vektör çarpımının tanımından eşitlik elde ederiz (gerekirse makaleye bakın): 
Çapraz çarpımın koordinat formunun, bu maddenin ilk paragrafında verilen tanımla tamamen tutarlı olduğuna dikkat edilmelidir. Ayrıca, bir çapraz çarpımın bu iki tanımı eşdeğerdir. Bu gerçeğin kanıtı, makalenin sonunda belirtilen kitapta bulunabilir.
Vektör ürün özellikleri.
Koordinatlardaki vektör çarpımı, matrisin determinantı olarak temsil edilebildiğinden, aşağıdakiler temel alınarak kolayca doğrulanabilir. vektörel ürün özellikleri:
Örnek olarak, bir vektör çarpımının değişme karşıtı özelliğini kanıtlayalım.
Tanım olarak 
ve 
. Bir matrisin determinantının değerinin, iki satır yer değiştirdiğinde tersine çevrildiğini biliyoruz, yani, 
, bu vektör çarpımının değişme karşıtı özelliğini kanıtlar.
Vektör ürünü - örnekler ve çözümler.
Temel olarak üç tür görev vardır.
Birinci tip problemlerde iki vektörün uzunlukları ve aralarındaki açı verilir ve çarpım uzunluğunun bulunması istenir. Bu durumda formül kullanılır. 
.
Örnek.
Vektörlerin çapraz çarpımının uzunluğunu bulun ve biliniyorsa 
.
Çözüm.
Tanımdan, ve vektörlerinin çapraz çarpımının uzunluğunun, vektörlerin uzunluklarının çarpımına ve aralarındaki açının sinüsüne eşit olduğunu biliyoruz, bu nedenle, 
.
Cevap:
.
İkinci tür görevler, verilen vektörlerin koordinatları aracılığıyla vektör ürününün, uzunluğunun veya başka bir şeyin arandığı vektörlerin koordinatlarıyla ilişkilendirilir. ve .
Burada birçok farklı seçenek mevcuttur. Örneğin, ve vektörlerinin koordinatları değil, ancak formun koordinat vektörlerindeki açılımları 
ve , veya vektörler ve başlangıç ve bitiş noktalarının koordinatlarıyla belirtilebilir.
Tipik örnekleri ele alalım.
Örnek.
Dikdörtgen koordinat sisteminde iki vektör verilmiştir. 
. Vektörel çarpımlarını bulun.
Çözüm.
İkinci tanıma göre, koordinatlarda iki vektörün çapraz çarpımı şu şekilde yazılır: 
Vektörel çarpımı determinant üzerinden yazsaydık aynı sonuca varırdık. 
Cevap:
.
Örnek.
Dikdörtgen Kartezyen koordinat sisteminin ortları nerede ve vektörlerinin çapraz çarpımının uzunluğunu bulun.
Çözüm.
İlk olarak, vektör çarpımının koordinatlarını bulun 
belirli bir dikdörtgen koordinat sisteminde.
Vektörler ve sırasıyla koordinatlara sahip olduğundan (gerekirse, dikdörtgen koordinat sistemindeki bir vektörün makale koordinatlarına bakın), o zaman bir çapraz çarpımın ikinci tanımına göre, elimizde 
Yani, vektör çarpımı verilen koordinat sisteminde koordinatlara sahiptir.
Bir vektör ürününün uzunluğunu, koordinatlarının karelerinin toplamının karekökü olarak buluyoruz (bir vektörün uzunluğu için bu formülü, bir vektörün uzunluğunu bulma bölümünde elde ettik):
Cevap:
.
Örnek.
Üç noktanın koordinatları, dikdörtgen bir Kartezyen koordinat sisteminde verilmiştir. Aynı anda ona dik olan bir vektör bulun.
Çözüm.
Vektörler ve sırasıyla koordinatlara sahiptir ve (noktaların koordinatları aracılığıyla bir vektörün koordinatlarını bulma makalesine bakın). Eğer ve vektörlerinin çapraz çarpımını bulursak, o zaman tanımı gereği hem 'ye hem de 'ye dik bir vektördür, yani problemimizin çözümü budur. hadi onu bulalım 
Cevap:
dikey vektörlerden biridir.
Üçüncü tip görevlerde, vektörlerin vektör çarpımının özelliklerini kullanma becerisi kontrol edilir. Özellikler uygulandıktan sonra ilgili formüller uygulanır.
Örnek.
ve vektörleri diktir ve uzunlukları sırasıyla 3 ve 4'tür. Vektör çarpımının uzunluğunu bulun 
.
Çözüm.
Vektör çarpımının dağılma özelliğine göre şunu yazabiliriz: 
İlişkisel özellik sayesinde, son ifadedeki vektör çarpımlarının işareti için sayısal katsayıları çıkarıyoruz: 
Vektör ürünleri ve sıfıra eşittir, çünkü 
ve 
, sonra .
Vektör çarpımı ters değişmeli olduğundan, o zaman .
Böylece, vektör çarpımının özelliklerini kullanarak eşitliğe geldik. 
.
Koşullu olarak, ve vektörleri diktir, yani aralarındaki açı eşittir . Yani, gerekli uzunluğu bulmak için tüm verilere sahibiz. 
Cevap:
.
Vektör çarpımının geometrik anlamı.
Tanım olarak, vektörlerin çapraz çarpımının uzunluğu 
. Ve lise geometri dersinden, bir üçgenin alanının, üçgenin iki kenarının uzunluklarının ve aralarındaki açının sinüsünün çarpımının yarısına eşit olduğunu biliyoruz. Bu nedenle, çapraz çarpımın uzunluğu, vektörlerin kenarları olan bir üçgenin alanının iki katına eşittir ve , eğer bir noktadan ertelenirlerse. Başka bir deyişle, vektörlerin çapraz çarpımının uzunluğu ve kenarları olan bir paralelkenarın alanına ve aralarındaki açıya eşittir. Bu vektör çarpımının geometrik anlamıdır.
Tanım Gerçek sayıların (x 1 , x 2 , ... , x n) sıralı bir koleksiyonuna denir n boyutlu vektör, ve sayılar x ben (i = ) - bileşenler veya koordinatlar,
Örnek. Örneğin, bir otomobil fabrikasının vardiya başına 50 araba, 100 kamyon, 10 otobüs, 50 takım otomobil yedek parçası ve 150 takım kamyon ve otobüs üretmesi gerekiyorsa, bu fabrikanın üretim programı şu şekilde yazılabilir: beş bileşene sahip vektör (50, 100 , 10, 50, 150).
Gösterim. Vektörler, kalın küçük harflerle veya üstte bir çubuk veya ok bulunan harflerle gösterilir; örneğin, a veya. İki vektör denir eşit eğer aynı sayıda bileşene sahiplerse ve bunlara karşılık gelen bileşenler eşitse.
Vektör bileşenleri değiştirilemez, örneğin (3, 2, 5, 0, 1) ve (2, 3, 5, 0, 1) farklı vektörler.
Vektörler üzerinde işlemler. iş
x= (x 1 , x 2 , ... ,x n)'den gerçek bir sayıyaλ vektör denirλ x= (λ x 1 , λ x 2 , ... , λ x n).
toplamx= (x 1 , x 2 , ... ,x n) ve y= (y 1 , y 2 , ... ,y n) vektör olarak adlandırılır x+y= (x 1 + y 1 , x 2 + y 2 , ... , x n + + y n).
Vektörlerin uzayı. N -boyutlu vektör uzayı R n, gerçek sayılarla çarpma ve toplama işlemlerinin tanımlandığı tüm n-boyutlu vektörlerin kümesi olarak tanımlanır.
Ekonomik illüstrasyon. n-boyutlu bir vektör uzayının ekonomik bir gösterimi: mal alanı (mal). Altında emtia belli bir zamanda belli bir yerde satışa çıkmış bazı mal veya hizmetleri anlayacağız. Mevcut n sınırlı sayıda mal olduğunu varsayalım; tüketici tarafından satın alınan her birinin miktarı, bir dizi mal ile karakterize edilir.
x= (x 1 , x 2 , ..., x n),
burada x i, tüketici tarafından satın alınan i. malın miktarını ifade eder. Tüm malların keyfi bölünebilirlik özelliğine sahip olduğunu varsayacağız, böylece her birinin negatif olmayan herhangi bir miktarı satın alınabilir. O zaman tüm olası mal kümeleri, mal uzayının vektörleridir C = ( x= (x 1 , x 2 , ... , x n) x ben ≥ 0, ben = ).
Doğrusal bağımsızlık.
sistem e 1 , e 2 , ... , e m n boyutlu vektörler denir lineer bağımlı böyle sayılar varsaλ 1 , λ 2 , ... , λ m en az biri sıfır olmayan, eşitliği sağlayanλ1 e 1 + λ2 e 2+...+λm e m = 0; aksi takdirde, bu vektörler sistemine denir Doğrusal bağımsız yani bu eşitlik ancak tüm 
. Vektörlerin doğrusal bağımlılığının geometrik anlamı R 3 , yönlü segmentler olarak yorumlanarak aşağıdaki teoremleri açıklayınız.
teorem 1. Tek bir vektörden oluşan bir sistem, ancak ve ancak bu vektör sıfırsa doğrusal olarak bağımlıdır.
Teorem 2. İki vektörün lineer olarak bağımlı olması için bunların eşdoğrusal (paralel) olmaları gerekli ve yeterlidir.
teorem 3 . Üç vektörün doğrusal olarak bağımlı olması için eş düzlemli (aynı düzlemde uzanan) olmaları gerekli ve yeterlidir.
Vektörlerin sol ve sağ üçlüleri. Eş düzlemli olmayan vektörlerin üçlüsü bir, b, c aranan Sağ, eğer gözlemci ortak kökenlerinden vektörlerin uçlarını atlarsa bir, b, c bu sırada saat yönünde ilerliyor gibi görünüyor. Aksi halde bir, b, c -sol üçlü. Tüm sağ (veya sol) vektörlerin üçlüleri denir eşit olarak odaklı.
Temel ve koordinatlar. Troyka e 1, e 2 , e 3 eş düzlemli olmayan vektör R 3 aradı temel ve vektörlerin kendileri e 1, e 2 , e 3 - temel. herhangi bir vektör a temel vektörler açısından benzersiz bir şekilde genişletilebilir, yani şu şekilde temsil edilebilir:
a= x 1 e 1 + x2 e 2 + x 3 e 3, (1.1)
genişletmedeki (1.1) x 1 , x 2 , x 3 sayıları çağrılır koordinatlara temelde e 1, e 2 , e 3 ve gösterilir a(x 1 , x 2 , x 3).
Ortonormal taban. eğer vektörler e 1, e 2 , e 3 çiftler halinde diktir ve her birinin uzunluğu bire eşittir, o zaman tabana denir ortonormal ve x 1 , x 2 , x 3 - koordinatları dikdörtgen. Bir ortonormal bazın temel vektörleri gösterilecektir ben, j, k.
Uzayda olduğunu varsayacağız R 3 doğru Kartezyen dikdörtgen koordinat sistemi (0, ben, j, k}.
Vektör ürünü. vektör sanatı a vektör başına b vektör denir c, aşağıdaki üç koşul tarafından belirlenir:
1. Vektör uzunluğu c vektörler üzerine inşa edilmiş paralelkenarın alanına sayısal olarak eşittir a ve b, yani
c=
|a||b| günah( a^b).
2. Vektör c vektörlerin her birine dik a ve b.
3. Vektörler a, b ve c, bu sırayla alındığında, bir sağ üçlü oluşturur.
Vektör ürünü için c atama tanıtıldı c=[ab] veya
c = bir
× b.
eğer vektörler a ve b eşdoğrusaldır, o zaman sin( a^b) = 0 ve [ ab] = 0, özellikle, [ aa] = 0. Ortların vektör çarpımı: [ ben]=k, [jk] = i, [ki]=j.
eğer vektörler a ve b temelde verilen ben, j, k koordinatlar a(bir 1 , bir 2 , bir 3), b(b 1 , b 2 , b 3), sonra
Karışık iş. İki vektörün çapraz çarpımı ise a ve b skaler çarpı üçüncü vektör c, o zaman üç vektörün böyle bir ürününe denir karışık ürün ve sembolü ile gösterilir a M.Ö.
eğer vektörler bir, b ve c temelde ben, j, k koordinatlarına göre belirlenir
a(bir 1 , bir 2 , bir 3), b(b 1 , b 2 , b 3), c(c 1 , c 2 , c 3), sonra
.
Karışık çarpımın basit bir geometrik yorumu vardır - verilen üç vektör üzerine inşa edilmiş bir paralelyüzün hacmine eşit mutlak değerde bir skalerdir.
Vektörler bir sağ üçlü oluşturuyorsa, bunların karışık çarpımı, belirtilen hacme eşit pozitif bir sayıdır; eğer üç a, b, c - sola, sonra bir b c<0 и V = - bir b c, dolayısıyla V =|a bc|.
Birinci bölümdeki problemlerde karşılaşılan vektörlerin koordinatlarının sağ ortonormal tabana göre verildiği varsayılmıştır. Vektöre eş yönlü birim vektörü a, sembolü ile gösterilir a hakkında. Sembol r=om M noktasının yarıçap vektörü ile gösterilir, a, AB veya|a|, | AB |vektörlerin modülleri gösterilir a ve AB.
Örnek 1.2. Vektörler arasındaki açıyı bulun a= 2m+4n ve b= m-n, nerede m ve n- birim vektörler ve arasındaki açı m ve n 120 o'ya eşittir.
Çözüm. Elimizde: çünkü φ = ab/ab, ab=(2m+4n) (m-n) = 2m 2 - 4n 2 +2mn=
= 2 - 4+2cos120 o = - 2 + 2(-0,5) = -3; bir = ; a 2 = (2m+4n) (2m+4n) =
= 4m 2 +16mn+16n 2 = 4+16(-0,5)+16=12, yani a = . b= ; b 2 =
= (m-n)(m-n) = m 2 -2mn+n 2 =
1-2(-0,5)+1 = 3, yani b = . Sonunda elimizde: çünküφ \u003d -1/2, φ \u003d 120 o.
Örnek 1.3.vektörleri bilmek AB(-3,-2.6) ve M.Ö(-2,4,4), ABC üçgeninin AD yüksekliğini hesaplayınız.
Çözüm. ABC üçgeninin alanını S ile göstererek, şunu elde ederiz:
S = 1/2 M.Ö. O zamanlar AD=2S/BC, BC== 
= 6,
S = 1/2| AB ×AC|.
AC=AB+BC, böylece vektör AC koordinatları var
.
.
Örnek 1.4 . Verilen iki vektör a(11,10,2) ve b(4,0,3). birim vektörü bulun c, vektörlere ortogonal a ve b ve vektörlerin sıralı üçlüsü olacak şekilde yönlendirildi bir, b, c haklıydı.
Çözüm.Vektörün koordinatlarını gösterelim c x, y, z cinsinden verilen dik ortonormal tabana göre.
Çünkü c ⊥ AC ⊥b, sonra CA= 0, cb= 0. Problemin durumuna göre c = 1 ve bir b c >0.
x,y,z'yi bulmak için bir denklem sistemimiz var: 11x +10y + 2z = 0, 4x+3z=0, x 2 + y 2 + z 2 = 0.
Sistemin birinci ve ikinci denklemlerinden z = -4/3x, y = -5/6x elde ederiz. Üçüncü denklemde y ve z'yi yerine koyarsak, şunu elde ederiz: x 2 = 36/125, buradan
x=±
. Kullanım koşulu a bc > 0, eşitsizliği elde ederiz
z ve y için ifadeleri dikkate alarak, ortaya çıkan eşitsizliği şu şekilde yeniden yazarız: 625/6 x > 0, buradan x>0 olur. Yani x = , y = - , z = - .