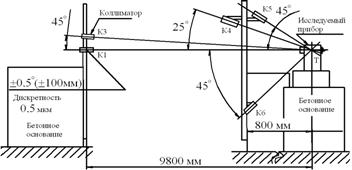
3.2 Классификация погрешностей геодезических измерений. Средняя квадратическая погрешность. Формы Гаусса и Бесселя для её вычисления
Геодезические измерения, выполняемые даже в очень хороших условиях, сопровождаются погрешностями, т.е. отклонение результата измерений L от истинного значения Х нумеруемой величины:
Истинное – такое значение измеряемой величины, которое идеальным образом отражало бы количественные свойства объекта. Недостижимое условие – истинное значение – понятие гипотетическое. Это величина, к которой можно приближаться бесконечно близко, оно не достижимо.
Точность измерений – степень приближения его результата к истинному значению. Чем ниже погрешность, тем выше точность.
Абсолютная погрешность выражается разностью значения, полученного в результате измерения и истинного измерения величины. Например, истинное значение l = 100 м, однако, при измерении этой же линии получен результат 100,05 м, тогда абсолютная погрешность:
E = X изм – X
E = 100,05 – 100 = 0,05 (м)
Чтобы получить значение достаточно произвести одно измерение. Его называют необходимым, но чаще одним измерением не ограничиваются, а повторяют не менее двух раз. Измерения, которые делают сверх необходимого, называют избыточными (добавочными), они являются весьма важным средством контроля результата измерения.
Абсолютная погрешность не даёт представления о точности полученного результата. Например, погрешность в 0,06 м может быть получена при измерении l = 100 м или l = 1000 м. Поэтому вычисляют относительную погрешность:
C = 0,06 / 100 = 1/1667, т.е на 1667 м измеряемой l допущена погрешность в 1 метр.
Относительная погрешность – отношение абсолютной погрешности к истинному или измеренному значению. Выражают дробью. По инструкции линия местности должна быть измерена не грубее 1/1000.
Погрешности, происходящие от отдельных факторов, называются элементарными. Погрешность обобщенная – это сумма элементарных.
Возникают:
· грубые (Q),
· систематические (O),
· случайные (∆).
Грубые погрешности измерений возникают в результате грубых промахов, просчётов исполнителя, его невнимательности, незамеченных неисправностях технических средств. Грубые погрешности совершенно недопустимы и должны быть полностью исключены из результатов измерений путем проведения повторных, дополнительных измерений.
Систематические погрешности измерений – постоянная составляющая, связанная с дефектами: зрение, неисправность технических средств, температура. Систематические погрешности могут быть как одностороннего действия, так и переменного (периодические погрешности). Их стремятся по возможности учесть или исключить из результатов измерений при организации и проведении работ.
Случайные погрешности измерений неизбежно сопутствуют всем измерениям. Погрешности случайные исключить нельзя, но можно ослабить их влияние на искомый результат за счет проведения дополнительных измерений. Это самые коварные погрешности, сопутствующие всем измерениям. Могут быть разные как по величине, так и по знаку.
Если грубые и систематические погрешности могут быть изучены и исключены из результата измерений, то случайные могут быть учтены на основе глубокого измерения. Изучение на основе теории вероятностей.
На практике сложность заключается в том, что измерения проводятся какое-то ограниченное количество раз и поэтому для оценки точности измерений используют приближённую оценку среднего квадратического отклонения, которую называют среднеквадратической погрешностью (СКП).
Гауссом была предложена формула среднеквадратической погрешности:
∆ 2 ср = (∆ 2 1 + ∆ 2 2 +… +∆ 2 n) / n,
∆ 2 = m 2 = (∆ 2 1 + ∆ 2 2 +… +∆ 2 n) / n,
∆ ср = m = √(∑∆ 2 i / n)
Формула применяется, когда погрешности вычислены по истинным значениям.
Формула Бесселя:
m = √(∑V 2 i / (n-1))
Средняя квадратическая погрешность арифметической середины в Ön раз меньше средней квадратической погрешности отдельного измерения
При оценке в качестве единицы меры точности используют среднеквадратическую погрешность с весом равным единице. Её называют средней квадратической погрешностью единицы веса.
µ 2 = P×m 2 – µ = m√P, m = µ / √P, т.е. средняя квадратическая погрешность любого результата измерения равна погрешности измерения с весом 1 (µ) и делённая на корень квадратный из веса этого результата (P).
При достаточно большом числе измерений можно записать ∑m 2 P=∑∆ 2 P (так как ∆ = m):
µ = √(∑(∆ 2 ×P)/n), т.е. средняя квадратическая погрешность измерения с весом, равным 1 равна корню квадратному из дроби в числителе которого сумма произведений квадратов абсолютных погрешностей неравноточных измерений на их веса, а в знаменателе – число неравноточных измерений.
Средняя квадратическая погрешность общей арифметической середины по формуле:
M 0 = µ / √∑P
Подставив вместо µ её значение получим:
M 0 = √(∑∆ 2 ×P/n) / (√∑P) = √[(∑∆ 2 ×P) / n×(∑P)]
M 0 = √[ (∆ 1 2 P 1 + ∆ 2 2 P 2 +… + ∆ n 2 P n) / n×(P 1 + P 2 + … + P n) ] – формула Гаусса, средняя квадратическая погрешность общей арифметической середины равна корню квадратному из дроби, в числителе которой сумма произведений квадратов погрешностей неравноточных измерений на их веса, а знаменатель – произведение количества измерений на сумму их весов.
µ = √ [∑(V 2 ×P) / (n-1)] Это формула Бесселя для вычисления средней арифметической погрешности с измерением веса, равным 1 для ряда неравноточных измерений по их вероятнейшим погрешностям. Она справедлива для большого ряда измерений, а для ограниченного (часто на практике) содержит погрешности: m µ = µ / – это надёжность оценки µ.
Контрольная задача 1
Для исследования теодолита им был многократно измерен один и тот же угол. Результаты оказались следующими: 39˚17.4"; 39˚16.8"; 39˚16.6"; 39˚16.2"; 39˚15.5"; 39˚15.8"; 39˚16.3"; 39˚16.2". Тот же угол был измерен высокоточным угломерным прибором, что дало результат 39˚16"42". Приняв это значение за точное, вычислить среднюю квадратическую погрешность, определить надёжность СКП, найти предельную погрешность.
| № измерения | Результаты измерений, l | Погрешности | ∆2 |
| 1 | 39˚17.4" | +0.7" | 0.49 |
| 2 | 16.8 | +0.1 | 0.01 |
| 3 | 16.6 | -0.1 | 0.01 |
| 4 | 16.2 | -0.5 | 0.25 |
| 5 | 15.5 | -1.2 | 1.44 |
| 6 | 15.8 | -0.9 | 0.81 |
| 7 | 16.3 | -0.4 | 0.16 |
| 8 | 16.2 | -0.5 | 0.25 |
| Сумма | 3.42 |
39˚16"42" = 39˚16.7"
Средняя квадратическая погрешность: m = √([∆ 2 ]/n),
m = √(3.42/8) = 0.65".
Оценка надёжности СКП: m m = m / √2n,
m m = 0.65 / √16=0.1625≈0.16".
Предельная погрешность: ∆ пр = 3×m,
∆ пр = 3×0.65" = 1.96"
Контрольная задача 2
Дана совокупность невязок треугольников триангуляции объёмом 50 единиц. Считая невязки истинными погрешностями, вычислить среднюю квадратическую погрешность и произвести надёжность СКП, вычислить предельную погрешность. На данной совокупности проверить свойство случайных погрешностей:
Lim[∆] / n =0, для чего вычислить W = [W] / n.
| N | W | N | W | N | W | N | W | N | W |
| 1 | +1,02 | 11 | -1,72 | 21 | -0,90 | 31 | +2,80 | 41 | -0,44 |
| 2 | +0,41 | 12 | +1,29 | 22 | +1,22 | 32 | -0,81 | 42 | -0,28 |
| 3 | +0,02 | 13 | -1,81 | 23 | -1,84 | 33 | +1,04 | 43 | -0,75 |
| 4 | -1,88 | 14 | -0,08 | 24 | -0,44 | 34 | +0,42 | 44 | -0,80 |
| 5 | -1,44 | 15 | -0,50 | 25 | +0,18 | 35 | +0,68 | 45 | -0,95 |
| 6 | -0,25 | 16 | -1,89 | 26 | -0,08 | 36 | +0,55 | 46 | -0,58 |
| 7 | +0,12 | 17 | +0,72 | 27 | -1,11 | 37 | +0,22 | 47 | +1,60 |
| 8 | +0,22 | 18 | +0,24 | 28 | +2,51 | 38 | +1,67 | 48 | +1,85 |
| 9 | -1,05 | 19 | -0,13 | 29 | -1,16 | 39 | +0,11 | 49 | +2,22 |
| 10 | +0,56 | 20 | +0,59 | 30 | +1,65 | 40 | +2,08 | 50 | -2,59 |
W = [W] / n, W = +2,51 / 50 = 0,05
Среднюю квадратическую погрешность в данном случае целесообразно вычислять по формуле: m = √( – [W] 2 /n) ÷ (n-1),
m = √(76,5703 – (2,51 2)/50) ÷ 49 = 1,249
Оценку надёжности СКП по формуле: m m = m / √2(n-1),
m m = 1,249/ √(2×49) = 0,13.
Предельная погрешность по формуле: ∆ пр = 3×m,
∆ пр = 3×1,249= 3,747.
Контрольная задача 5 Определить СКП расстояния вычисленного по формуле
S = √(x 2 – x 1) 2 + (y 2 – y 1) 2
если x 2 = 6 068 740 м; y 2 = 431 295 м;
x 1 = 6 068 500 м; y 2 = 431 248 м;
m х = m y = 0,1 м.
S =√(6 068 740 - 6 068 500) 2 + (431 295 - 431 248) 2 =235,36
m m = 0,1/ √4 = 0,05
Контрольная задача 6
Один и тот же угол измерен 5 раз с результатами: 60˚41"; 60˚40"; 60˚40"; 60˚42"; 60˚41". Произвести математическую обработку этого ряда результатов измерений.
| Nп/п | l, ˚ | ε, " | v, " | v2, " |
| 1 | 60˚41" | 1 | -0,2 | 0,04 |
| 2 | 60˚40" | 0 | +0,8 | 0,64 |
| 3 | 60˚40" | 0 | +0,8 | 0,64 |
| 4 | 60˚42" | 2 | -1,2 | 1,44 |
| 5 | 60˚41" | 1 | -0,2 | 0,04 |
| Сумма | 4 | 0 | 2,8 |
l 0 – минимальное значение измеряемой величины, l 0 = 60˚40" ; ε – остаток, полученный как ε = l 1 - l 0 ; L – наилучшее значение измеряемой величины,
L = [l]/n; m = √([ v 2 ]/(n – 1), где v-уклонение от арифметического среднего. М – оценка точности среднего арифметического значения, М = m/√n.
L = 60˚40" + 4/5 = 60˚40,8"
m = √2,8 / 4 = 0,7"
М = 0,7"/√5 = 0,313"
Контрольная задача 7
Произвести математическую обработку результатов измерения планиметром площади одного и того же контура: 26,31; 26,28; 26,32; 26,26; 26,31 га.
| Nп/п | l, га | ε, га | v, га | v2, га |
| 1 | 26,31 | 0,05 | -0,014 | 0,000196 |
| 2 | 26,28 | 0,02 | +0,016 | 0,000256 |
| 3 | 26,32 | 0,06 | -0,024 | 0,000576 |
| 4 | 26,26 | 0 | 0,036 | 0,001296 |
| 5 | 26,31 | 0,05 | -0,014 | 0,000576 |
| Сумма | 0,18 | 0 | 0,0029 |
L = 26,26 + 0,18/5 = 26,296 га
m = √0,0029/ 4 = 0,0269 га
М = 0,0269/√5 = 0,01204 га
Контрольная задача 8
При исследовании сантиметровых делений нивелирной рейки с помощью женевской линейки определялась температура в момент взятия отчета. Для пяти сантиметровых отрезков получены значения: 20,3˚; 19,9˚; 20,1˚; 20,2˚; 20,3˚. Провести математическую обработку результатов измерения.
| Nп/п | l, ˚ | ε, ˚ | v, ˚ | v2, ˚ |
| 1 | 20,3 | 0,4 | -0,14 | 0,0196 |
| 2 | 19,9 | 0 | -0,26 | 0,0676 |
| 3 | 20,1 | 0,2 | -0,06 | 0,0036 |
| 4 | 20,2 | 0,3 | 0,04 | 0,0024 |
| 5
Них не окажется нужной, то тогда средство необходимо разработать вручную, если это оправдано с точки зрения затраченного времени и материальных ресурсов. 2. Обработка геодезических измерений с использованием электронных таблиц Для первоначальной обработки информации, полученной в результате комплекса топографо-геодезических работ, мною использовалась программа “ТОГИ”, являющаяся пакетом...
На стройплощадке необходимо соблюдение требований норм и правил по технике безопасности, изложенных в главе СНиП Ш-4-80 "Техника безопасности в строительстве" и ведомственных инструкциях. К выполнению геодезических работ допускаются лица, прошедшие инструктаж, оформленный приказом по строительному управлению. Опасность получения травмы или увечья определяется в зависимости от условий рабочего...
Электронных приборов при непосредственном участии автора. Вторая глава. Во второй главе рассмотрены разработанные методы проведения исследований метрологических установок и стендов для поверки и калибровки геодезических приборов для измерения превышений. Метод исследования короткопериодической погрешности измерения вертикальных углов геодезических приборов. Важной задачей при исследовании... |
Вот и еще одна средняя, которая связана с погрешностями.
Средняя квадратическая погрешность (СКП) является мерой точности результатов измерений либо функций измеренных величин и является вероятностной характеристикой.
Рис. 3.1. Нормальный закон распределения
случайных погрешностей.
Предположим, что нам известно значение средней квадратической погрешности m . В соответствии с нормальным законом распределения график распределения истинных погрешностей по виду будет подобен графику рис. 3.1. Параметр r характеризует частоту (или частость) появления случайных погрешностей той или иной величины и знака. При этом вероятность появления погрешностей в заданном наперёд диапазоне, например, ±m , определяется площадью фигуры, ограниченной кривой распределения и отрезками ординат на значениях +m и -m . Для нормального закона распределения вероятность появления погрешностей в установленных диапазонах равна следующим значениям:
Для диапазона ±m ® Р = 68,3% (» 68%);
Для диапазона ±2m ® Р = 95,5% (» 95%);
Для диапазона ±3m ® Р = 99,7% (практически 100%).
Таким образом, только в 3-х случаях из 1000 может появиться погрешность, превышающая значение 3m . Погрешности, по абсолютной величине превышающие 3m (предельную погрешность), принято считать грубыми, и результаты измерений, содержащие эту грубую погрешность, исключают из дальнейшей обработки. В некоторых случаях, для ужесточения требований к точности измерений, устанавливают предельную погрешность в диапазоне от 2m до 3m .
Таблица 3.1
Значения коэффициента Стьюдента (t ) для различных вероятностей (Р )
| t | P % | t | P % | t | P % |
| 0,1 | 8,0 | 1,1 | 72,9 | 2,1 | 96,4 |
| 0,2 | 15,9 | 1,2 | 77,0 | 2,2 | 97,2 |
| 0,3 | 23,6 | 1,3 | 80,6 | 2,3 | 97,9 |
| 0,4 | 31,1 | 1,4 | 83,8 | 2,4 | 98,4 |
| 0,5 | 38,3 | 1,5 | 86,6 | 2,5 | 98,8 |
| 0,6 | 45,1 | 1,6 | 89,0 | 2,6 | 99,1 |
| 0,7 | 51,6 | 1,7 | 91,1 | 2,7 | 99,3 |
| 0,8 | 57,6 | 1,8 | 92,8 | 2,8 | 99,5 |
| 0,9 | 63,2 | 1,9 | 94,3 | 2,9 | 99,6 |
| 1,0 | 68,3 | 2,0 | 95,5 | 3,0 | 99,7 |
Часто значение СКП указывают с коэффициентом t (коэффициент Стьюдента ), который и определяет доверительный вероятностный интервал (х ± tm ) результата измерений при установленном уровне вероятности Р . Для этого удобно пользоваться табл. 3.1.
Например, необходимо определить доверительный интервал для величины Х с вероятностью 90%. По таблице интерполированием находим, что для Р 1 = 89,0% t 1 = 1,6, для Р 2 = 91,1% t 2 = 1,7: t х = 1,6476 » 1,65.
Это значит, что результат измерений с вероятностью 90% находится в пределах (Х ± 1,65 m ).
Если измеряемая величина Х известна, то значение СКП определяется по формуле Гаусса :
где Δ - истинные погрешности измерений.
Напомним, что знак [...] – это знак гауссовой суммы.
Для случаев, когда измеряемая величина неизвестна, используется формула Бесселя :
где v - уклонения результатов измерений от среднего арифметического.
Как видно из формул (3.9) и (3.10), в случае, когда измеряемая величина известна, для оценки точности достаточно уже одного измерения (оно и является необходимым). Как уже указывалось выше, чаще всего формулу Гаусса используют при оценках точности эталонируемых приборов при измерении известных величин (эталонов). Для оценки точности по формуле Бесселя необходимыми являются как минимум два измерения. Формула Бесселя используется при оценках точности результатов массовых (многократных) измерений одной величины, заранее неизвестной.
При возрастании числа измерений значения СКП, полученные по формулам Гаусса и Бесселя, становятся практически одинаковыми (примерно с n ³ 20). При этом значение СКП одного измерения стремится к пределу m пред , который определяется точностью прибора, точностью метода или программы измерений. Очевидно, выше об этом уже было сказано, что на практике невозможно, да и нецелесообразно по ряду причин, обеспечивать весьма большое число измерений одной величины. При этом практическое число измерений должно обеспечивать получение результата измерения с заданной точностью при установленном уровне доверительной вероятности.
Поскольку число измерений является ограниченным, то сама СКП содержит погрешность, определяемую по приближенной формуле:
Она так и называется – средняя квадратическая погрешность средней квадратической погрешности (СКП СКП).
Здесь уместно возвратиться к классификации погрешностей. Не все виды погрешностей рассмотрены нами выше.
Часто при исследованиях рядов погрешностей измерений используют т.н. вероятную погрешность , которую обозначают буквой r . Величина вероятной погрешности может быть оценена по приближенной формуле
в предположении, конечно, что распределение погрешностей подчиняется нормальному закону.
Вероятную погрешность называют еще срединной погрешностью . Если не хочется делать вычисления по формуле (3.12), потому что в неё входит значение m , которое необходимо получить по формуле Бесселя, то можно определить вероятную или срединную погрешность, расположив ряд погрешностей по их возрастанию по абсолютным величинам. В середине полученного ряда и будет находиться значение этой погрешности. Это если число погрешностей нечётное. А если оно чётное, то срединной погрешностью будет среднее значение соседних погрешностей в середине ряда.
Не надо путать срединную погрешность со средней погрешностью v o , которую можно получить тоже по простой формуле:
Здесь также требуется условие подчинения ряда измерений (погрешностей) нормальному закону.
Средняя погрешность является математическим ожиданием абсолютных значений отклонений результатов измерений какой-либо величины от математического ожидания для этих результатов. Приближенно значение средней погрешности можно оценить по формуле:
где v i – уклонения результатов измерений от их среднего арифметического.
Часто формулу (3.13) используют для предварительной оценки средней квадратической погрешности.
Случайными погрешностями называют такие погрешности, размер и характер влияния которых на каждый отдельный результат измерения остается неизвестным. Величину и знак случайных погрешностей заранее установить нельзя. Они неизбежны и сопровождают каждое измерение, так как измерение мы проводим только с такой точностью, которую можно достичь применяемыми при этом приборами. Избавить результаты измерений от случайных погрешностей полностью нельзя. Но на основании изучения их свойств можно вывести правила, как из ряда измерений получить наиболее надежные результаты и оценивать их точность. Этими вопросами занимается теория погрешностей измерений.
В теории погрешностей различают равноточные и неравноточные измерения. Равноточными называют измерения, выполненные в одинаковых условиях, приборами одинаковой точности, одинаковое число раз, наблюдателями одинаковой квалификации. Если одно из этих условий не соблюдается, то такие измерения будут неравноточными.
Свойства случайных погрешностей. Случайные погрешности можно определить как разность между измеренными и истинными значениями одной и той же величины. На основании теоретического и практического изучения многих рядов случайных погрешностей выведены их общие свойства:
1 При данных условиях случайные погрешности не могут превышать определенного предела.
2 Одинаковые по абсолютной величине положительные и отрицательные погрешности равновозможны.
3 Меньшие по абсолютной величине погрешности встречаются чаще, чем большие.
4 Среднее арифметическое из случайных погрешностей равноточных измерений одной и той же величины имеет тенденцию стремится к нулю при неограниченном увеличении числа измерений.
4.2 Принцип арифметической середины
Пусть произведены равноточные измерения l 1 , l 2 , … , l n одной и той же величины, истинное значение которой Х. Тогда можно вычислить n значений случайных погрешностей:
Δ 1 = l 1 – X;
Δ 2 = l 2 – X; (4.1)
Δ n = l n – X.
Складывая левые и правые части этих равенств, получим
Δ 1 + Δ 2 +…+ Δ n = l 1 + l 2 +…+ l n – nX. (4.2)
В теории погрешности принято обозначать сумму величин через квадратные скобки, например:
Δ 1 + Δ 2 + … + Δ n = [Δ]; l 1 + l 2 + … + l n = [l] и т. д.
При этих обозначениях равенство (4.2) примет вид
[Δ] = [l] – nX , откуда X = [l] / n – [Δ] / n. (4.3)
Согласно четвертому свойству случайных погрешностей величина [Δ] / n в равенстве (4.3) при неограниченном возрастании числа измерений стремится к нулю. Следовательно, величина [l] / n при этих условиях будет приближаться к истинному значению Х. На основании этого арифметическую середину (среднее арифметическое из результатов измерений) принято считать наиболее надежным или вероятнейшим результатом из равноточных измерений одной и той же величины при любом числе измерений.
L = [l] / n = (l 1 + l 2 + l 3 + … + l n) / n. (4.4)
4.3 Средняя квадратическая погрешность одного измерения.
Формулы Гаусса и Бесселя
В теории погрешностей точность измерений характеризуется средней квадратической погрешностью, которая была введена знаменитым немецким математиком и геодезистом К. Ф. Гауссом (1777–1855 гг.) и обозначается через m:
______________________ ______
m = ± √ (Δ 1 2 + Δ 2 2 + .. + Δ n 2) / n = ± √ [Δ 2 ] / n, (4.5)
где Δ 1 , Δ 2 , …, Δ n – случайные погрешности;
n – число измерений.
Средняя квадратическая погрешность является надежным критерием для оценки точности измерений. Она даже при небольшом числе измерений достаточно устойчива и хорошо отражает наличие крупных случайных ошибок, которые по существу и определяют качество измерений.
Формула (4.5) применена для вычисления средней квадратической погрешности, когда известно истинное значение измеряемой величины. Эти случаи в практике весьма редки. Как правило, истинное значение измеряемой величины неизвестно, но из измерений можно получить наиболее надежный результат – арифметическую середину. Получим формулу для вычисления средней квадратической погрешности при помощи уклонения отдельных результатов от арифметической середины по так называемым вероятнейшим погрешностям V.
Пусть l 1 , l 2 , …, l n – результаты равноточных измерений одной и той же величины, истинное значение которой Х, а арифметическая середина – L. Тогда можно вычислить n случайных или истинных погрешностей
Δ i = l i – X (4.6)
и n вероятнейших погрешностей
V i = l i – L. (4.7)
Сумма n равенству (4.7)
[V] = [l] – nL. (4.8)
Но, согласно равенству (4.4) nL = [l], поэтому
т. е. сумма вероятнейших погрешностей всегда должна быть равна нулю.
Вычитая из равенства (4.6) равенство (4.7), получим
Δ i – V i = L – X. (4.10)
В правой части равенству (4.10) мы имеем случайную погрешность арифметической середины. Обозначим ее через ε. Тогда
Δi = V i + ε. (4.11)
Возведем в квадрат равенство (4.11), возьмем их сумму и разделим ее на n:
[Δ 2 ] / n = / n + nε 2 / n + 2ε[V] / n. (4.12)
Левая часть этого равенства есть не что иное как m 2 . Последнее слагаемое правой части ввиду равенства (4.9) равно нулю.
m 2 = / n + ε 2 . (4.13)
Случайную погрешность ε заменим ее средним значением, т. е. средней квадратической погрешностью арифметической середины. Ниже будет доказано, что средняя квадратическая погрешность арифметической середины
М 2 = ε 2 = m 2 / n. (4.14)
m 2 – m 2 / n = / n или m 2 (n – 1) / n = / n,
откуда ___________
m 2 = / (n – 1), или m = √ / (n – 1). (4.15)
Формула (4.15) называется формулой Бесселя и имеет большое практическое значение. Она позволяет вычислять среднюю квадратическую погрешность по вероятнейшим уклонениям результатов измерений от арифметической средины.
Кроме средней квадратической погрешности различают еще среднюю, вероятную и относительную погрешности.
Средней погрешностью (Θ) называют среднее арифметическое из абсолютных значений случайных погрешностей т. е.
Θ = (|Δ 1 | + |Δ 2 | + … + |Δ n |) / n = [|Δ|] / n. (4.16)
В теории погрешности доказывается, что при n → ∞ Θ = 0,8 m, или m = 1,25Θ.
Иногда в прикладных вопросах пользуются вероятной погрешностью r. Вероятной погрешностью называют такое значение случайной погрешности в одном ряду равноточных измерений, по отношению к которой одинаково возможна погрешность как больше, так и меньше этого значения, по абсолютной величине. Для нахождения r все погрешности данного ряда располагают в порядке возрастания по абсолютной величине и выбирают то значение, которое занимает среднее положение, т. е. погрешностей меньше его столько же, сколько и больше. Вероятная погрешность связана со средней квадратической погрешностью соотношением r = 2/3 m = 0,67 m или m = 1,5 r.
Как видно, m > Θ и m > r, что показывает, что средняя квадратическая погрешность лучше характеризует точность измерений, чем средняя и вероятная погрешности.
Оценку точности таких измеренных величин, как линии, площади и объемы часто производят с помощью относительной погрешности . Относительной погрешностью называют отношение абсолютной погрешности к значению измеренной величины. Относительная погрешность записывается в виде дроби, в числителе которой стоит единица, а в знаменателе – число, показывающее какую долю измеряемой величины должна составлять допустимая погрешность. Например, длина стороны D = 150 м измерена с абсолютной погрешностью m d = 0,05 м. Тогда относительная погрешность результата измерения составит m d / D = 0,05 м / 150 м = 1 / 3000.
Величина 1 / 3000 означает, что на 3000 м расстояния может быть допущена погрешность в 1 м. Чем больше знаменатель относительной погрешности, тем выше точность измерений. Точность всех линейных измерений в геодезии всегда задается относительной погрешностью, которая приводится в соответствующих инструкциях и наставлениях по производству данного вида геодезических работ.
4.4 Закон нормального распределения погрешностей.
Предельная погрешность
Из предыдущего рассмотрения свойств случайных погрешностей следует, что о появлении отдельной погрешности заранее что–либо определенное сказать невозможно. Однако, когда число этих погрешностей возрастает, можно установить определенные закономерности для всей совокупности погрешностей данного ряда измерений. Эти закономерности можно выразить уравнением, полученным К. Ф. Гауссом. Оно имеет вид
y = (1 / σ √2π) e – (l i – a) / 2 σ = (1 /σ √2π) e – Δ c / 2 σ , (4.17)
где y – плотность распределения погрешностей;
σ – параметр уравнения, называемый стандартом, связан со средней
квадратической погрешностью соотношением
a – параметр уравнения, называемый математическим ожиданием,
связан с арифметической срединой соотношением
e – основание натуральных логарифмов;
Δ i = l i – a – случайная погрешность.
Это уравнение называется законом нормального распределения погрешностей.
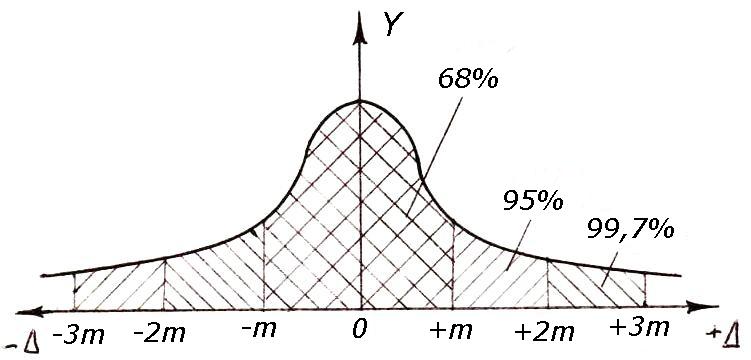
Уравнению (4.17) соответствует колоколообразная кривая, называемая кривой нормального распределения (кривая Гаусса) (рисунок 4.1)
Рисунок 4.1 – Кривая Гаусса
Площадь под кривой, ограниченная кривой и осью абсцисс, принимают равной единице. Часть этой площади, соответствующая какому-либо отрезку оси абсцисс, дает, вероятность попадания случайной погрешности в данный интервал. При l i = a или Δ = 0 получаем максимальное значение ординаты кривой __
Y = 1 / σ √2π.
Из рисунка 4.1 видно, что основная масса погрешностей группируется около наиболее вероятного значения погрешности Δ i = 0 (согласно четвертому свойству случайных погрешностей, среднее арифметическое из случайных погрешностей стремится к нулю). Это положение обосновывает третье свойство случайных погрешностей (малые погрешности встречаются чаще, чем большие). Второе свойство случайных погрешностей о равном появлении положительных и отрицательных ошибок характеризуется симметричностью кривой нормального распределения относительно оси OY.
Теоретические исследования и практика геодезических измерений показывают, что в промежутках от –m до +m попадает 68 % всех случайных погрешностей (см. рисунок 4.1), в промежуток вдвое больший (от –2m до +2m) попадает 95 % погрешностей, а в промежуток втрое больший (от –3m до +3m) попадает 99,73 % погрешностей. Это означает, что из 100 погрешностей измерений только 32 по абсолютной величине превзойдут среднюю квадратическую погрешность m, 3 из 1000 погрешностей будет превышать величину утроенной средней квадратической погрешности ±3m. Таким образом, за пределы ±3m выходит лишь 0,27 % погрешностей измерений. Поэтому в качестве предельной погрешности Δ пред принимается утроенная средняя квадратическая погрешность, т. е.
Δ пред = 3m. (4.18)
Рассмотрим теперь сущность параметров a и σ в уравнении (4.17). Параметр a называемый математическим ожиданием и характеризует центр группирования на кривой Гаусса, т. е. смещение центра группирования вдоль оси абсцисс (рисунок 4.2, а) при сохранении формы кривой. Если при постоянном значении параметра a будем изменять другой параметр σ (называемый стандартом), характеризующий точность измерений, а это возможно, если мы меняем метод измерений или выполняем их другими приборами. Тогда центр группирования остается неизменным, а форма кривой изменится. Она станет более пологой, если точность измерений уменьшается, и станет более крутой при увеличении точности (рисунок 4.2, б).
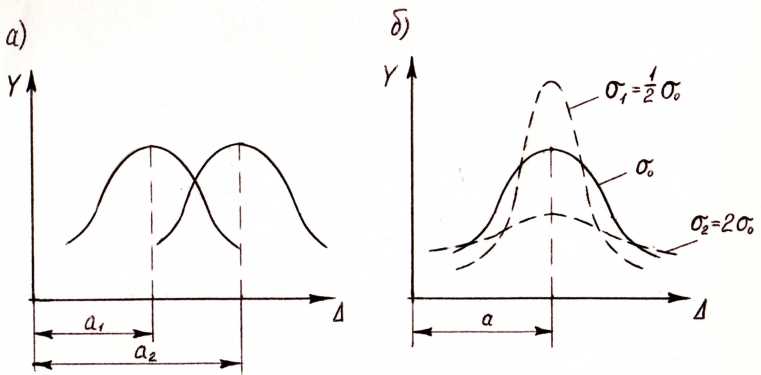
Рисунок 4.2 – Смещение и изменение формы нормальной кривой
Параметры a и σ заранее, до измерений, неизвестны. Они получаются как результат большого числа измерений. На практике вместо параметров a и σ мы получаем приближенные их значения: арифметическую средину L, вычисляемую по формуле (4.4), и среднюю квадратическую погрешность m, вычисляемую по формулам (4.5) или (4.15).
4.5 Средняя квадратическая погрешность функции
измерения величин
В геодезии часто нужно определить точность не только самих измеренных величин, но и их функций. Например, горизонтальное проложение линии является функцией наклонности расстояния и угла наклона, площадь определяемая планиметром является функцией отсчетов по планиметру и т. д. Поэтому важно уметь вычислять средние квадратические погрешности функций. Рассмотрим некоторые виды функций.
m = nm 2 или m φ = m√ n, (4.27)
т. е. средняя квадратическая погрешность суммы равноточно измеренных величин в √n раз больше средней квадратической погрешности отдельного измерения.
П р и м е р. Найти среднюю квадратическую погрешность суммы измеренных углов в четырехугольнике, если средняя квадратическая погрешность одного угла равна ±30 "" . По формуле (4.27) находим
m φ = ± 30 "" √ 4 = ±60 "" = 1 " .
2 Функция линейного вида
где К – постоянное число;
Х – аргумент, полученный из измерений.
Если Х будет измерен со случайной погрешностью Δ Х, то функция будет иметь случайную погрешность
Δ φ = К Δ X . (4.29)
Измерив аргумент n раз, можно составить n уравнений (4.29), взять сумму их квадратов и разделить на n. После чего получим
[Δ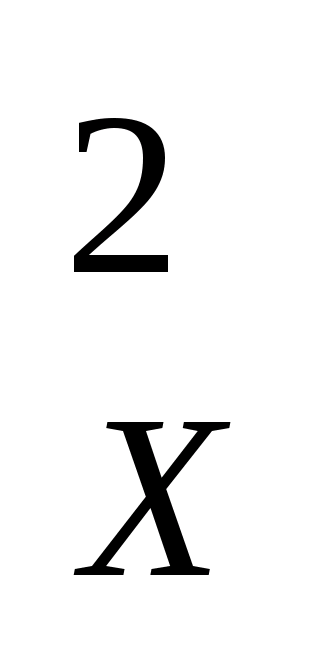
] / n = K 2 [Δ] / n или m = K 2 m, (4.30)
m φ = K m X . (4.31)
Аналогично предыдущему можно показать, что для функции
φ = ± K 1 X ± K 2 Y ± … ± K n U (4.32)
Δ φ = K 1 Δ X ± K 2 Δ Y ± … ± K n Δ U (4.33)
m= (K 1 m X) 2 + (K 2 m Y) 2 + … + (K n m U) 2 . (4.34)
П р и м е р. Определить среднюю квадратическую погрешность M арифметической середины L, если средняя квадратическая погрешность отдельного измерения равна m. Напишем формулу (4.4) арифметической середины в следующем виде:
L = l 1 / n + l 2 / n + … + l n / n. (4.35)
Как видно, здесь можно применить формулу (4.34) для функции (4.35):
m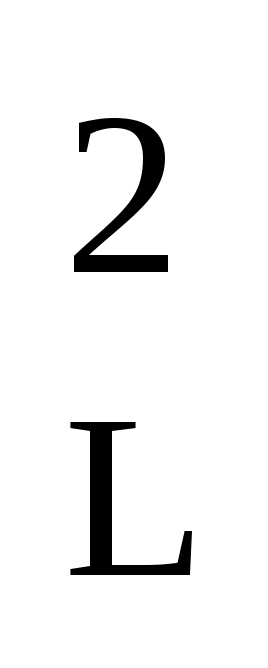
= M 2 = (m 1 / n) 2 + (m 2 / n) 2 + … + (m n / n) 2 .
Учитывая, что измерения l 1 , l 2 ,…, l n равноточные, т. е. m 1 = m 2 = … = m n , получим
M 2 = n(m / n) 2 = m 2 / n,
M = m / √n , (4.36)
т. е. средняя квадратическая погрешность арифметической средины в √n раз меньше средней квадратической погрешности отдельного измерения.
3 Функция общего вида
φ = f (X, Y, Z, … ,U), (4.37)
где X, Y, Z, … ,U – независимо измеренные величины.
С учетом случайных погрешностей функция (4.37) примет вид
φ + Δ φ = f (X + Δ X ; Y + Δ Y ; Z + Δ Z ; …; U + Δ U). (4.38)
Разложив функцию (4.38) в ряд Тейлора и ограничившись только первыми степенями случайных погрешностей, получим функцию
Δ φ = (∂f/∂x) Δ X + (∂f/∂y) Δ Y + (∂f/∂z) Δ Z + … + (∂f/∂u) Δ U , (4.39)
где (∂f/∂x), (∂f/∂y), …, (∂f/∂u) – частные производные, которые для функции
(4.39) являются постоянными величинами.
Как видно, функция (4.39) аналогична функции (4.33). Следовательно, квадрат ее средней квадратической погрешности
= (∂f/∂x ∙ m X) 2 + (∂f/∂y ∙ m Y) 2 + (∂f/∂z ∙ m Z) 2 + … + (∂f/∂u ∙ m U) 2 . (4.40)
П р и м е р. В прямоугольнике измерены две стороны – Х = 200 м и Y = 100 м со средними квадратическими погрешностями m X = +0,20 м и m Y = +0,10 м.
Определить площадь прямоугольника Р и ее среднюю квадратическую погрешность m P .
.m = √ / 2n. (4.43)
Формула (4.43) дает выражение средней квадратической погрешности отдельного измерения из n двойных измерений.
4.7 Неравноточные измерения
В предыдущих разделах были рассмотрены равноточные измерения. Однако на практике часто производятся и неравноточные измерения, которые выполнены в различных условиях или приборами различной точности, различным числом приемов. В этом случае уже нельзя ограничиваться простым арифметическим средним, здесь надо учитывать степень надежности каждого результата измерений.
Степень надежности результата измерения, выраженная числом, называется весом этого измерения. Чем надежнее результат, тем больше его вес. Пусть имеем ряд средних значений: L 1 , L 2 , …, L n – одной величины, полученных из Р 1 , Р 2 , …, Р n отдельных измерений.
Согласно формуле (4.4) произведение L i P i будет равно сумме отдельных измерений l i в данном ряду, а сумма всех измерений во всех рядах будет равна L 1 P 1 + L 2 P 2 + … + L n P n . Число всех измерений будет равно P 1 + P 2 +…+ P n .
Отсюда по правилу арифметической средины получим среднее значение из всех рядов измерений:
L o = (L 1 P 1 + L 2 P 2 + … + L n P n) / (P 1 + P 2 + … +P n) = / [P]. (4.44)
Выражение (4.44) называется формулой весового среднего или общей арифметической середины . Здесь число измерений Р 1 , Р 2, …, Р n в каждом ряду является весом средних результатов L 1 , L 2 , …, L n , а сумма весов является весом общей арифметической средины L o . Во всех случаях, когда известны результаты измерений и их веса, вероятнейшее значение измеренной величины вычисляют по формуле (4.44).
Обозначим среднюю квадратическую погрешность одного измерения через μ, а средние квадратические погрешности величин L 1 ,L 2 ….L n соответственно через m 1 , m 2 , …, m n . Тогда, согласно равенству (4.36), можем написать, что ___ __ __
m 1 = μ / √ P 1 ; m 2 = μ / √ P 2 ; …; m n = μ / √ P n . (4.45)
Если в формуле (4.45) принять P i = 1, то μ = m i . Отсюда следует, что μ является средней квадратической погрешностью измерения, вес которого равен единице или так называемой средней квадратической погрешности единицы веса.
КурсоваяВиды погрешностей. Практически всегда погрешность включает в себя две составляющие ее части: систематическую и случайную.
Δa= Δaсист + Δaслуч.
Систематической называется погрешность, которая в данных условиях сохраняет постоянное значение (или изменяется, но по известному закону).
Такие погрешности вызваны постоянно действующими причинами, в результате чего при измерении мы каждый раз «ошибаемся» на одну и ту же величину. Очень часто такие погрешности вызваны неточным изготовлением прибора (инструментальные погрешности), или постоянным внешним фактором. Например, собственное магнитное поле самолета вызывает погрешность измерения магнитного курса (девиацию), которая на каждом курсе имеет вполне определенное значение.
Систематические погрешности, поскольку они одинаковы при каждом измерении, можно один раз определить с помощью более точных приборов, а затем исключать их из результатов измерений путем ввода поправок.
Систематические погрешности не доставляют особых хлопот при навигации, поскольку после их устранения они уже отсутствуют. Поэтому далее будем считать, что систематические погрешности отсутствуют (уже учтены).
Случайная погрешность при каждом измерении принимает разное значение, причем заранее неизвестно какое именно.
А вот случайные погрешности в принципе устранить нельзя, поскольку они при каждом измерении различны. И они всегда остаются неизвестными.
Определить численные значения случайных погрешностей невозможно, однако пилот постоянно должен иметь в виду, что эти погрешности существуют и иметь представление об их возможных значениях. Наличие неопределенности в результатах измерений является одним из основных факторов, усложняющих навигацию и делающих ее не только наукой, и искусством.
Случайным событием называют событие, которое при данных условиях может произойти или не произойти. Степень возможности наступления такого события численно характеризуют величиной вероятности. Вероятность Р – это число, которое может лежать в пределах от 0 до 1. Если при данных условиях событие никогда не происходит, его называют невозможным событием и его вероятность равна нулю. Если же оно при данных условиях происходит всегда, то его называют достоверным и приписывают ему вероятность равную единице. Если, например, Р=0,3, то это означает, что в среднем в 30 случаях из 100 событие произойдет. Именно в среднем, поскольку событие является случайным. Если создать необходимые для наступления события условия и провести серию из 100 опытов, то событие может произойти, например, 23 раза, или 32 раза… Если провести несколько серий таких опытов, или одну серию из тысячи, десяти тысяч, миллиона опытов, то, чем большее количество опытов проведено, тем ближе среднее количество наступлений события будет ближе к 30% от общего количества опытов (если Р=0,3).
Каким же образом можно описать случайные погрешности, если они не имеют какого-либо определенного значения? Часто их характеризуют величиной средней квадратической погрешности (СКП), которая обозначается буквой σ (сигма). Так, например, СКП измерения величины a будем обозначать σa.
СКП является характеристикой степени рассеяния измеренного значения величины вокруг фактического ее значения. Чем больше σa, тем больше рассеяны (разбросаны) измеренные в разных опытах значения вокруг фактического значения величины.
На рис. 2.19 геометрически представлены в виде числовой оси возможные значения измеряемой величины a и отмечено фактическое ее значение. Крестиками на шкале обозначены полученные в результате нескольких опытов измеренные значения. В первом случае разброс измеренных значений вокруг фактического больше, чем во втором случае, следовательно «сигма», которая и характеризует степень разброса, во втором случае меньше.
Рис. 2.19. Средняя квадратическая погрешность
По величине СКП можно судить о вероятностях того, что измеренное значение примет то или иное значение. Но для этого недостаточно знать СКП, нужно также знать, какому закону распределения подчиняется данная случайная погрешность. Многие случайные величины подчиняются нормальному (гауссовскому) закону распределения. Для этого закона полезно запомнить следующие значения.
Если систематическая погрешность отсутствует и в результате измерения получено значение aизм, то фактическое значение величины лежит в пределах (рис. 2.20):
aизм ± σa с вероятностью Р=0,68;
aизм ± 2σa с вероятностью Р=0,95;
aизм ± 3σa с вероятностью Р=0,997.
Рис. 2.20. Некоторые вероятности для нормального закона распределения
Например, с помощью компаса измерен курс γ=100º, а точность компаса характеризуется СКП σγ =2º . Это означает, что фактический курс (который так и останется нам неизвестным) в среднем :
в 68 случаях из 100 лежит в пределах 100º ±2º, то есть в интервале 98º…102 º;
в 95 случаях из 100 лежит в пределах 100º ±4º, то есть в интервале 96º…104º;
в 997 случаях из 1000 лежит в пределах 100º ±6º, то есть в интервале 94º …106º.
Значение вероятности Р =0,997 настолько близко к единице, что соответствующее ей значение погрешности в «три сигмы» часто называют максимальной погрешностью. На самом деле погрешность может его и превысить. Правда, редко – в среднем в трех случаях из тысячи.
В технических описаниях приборов и оборудования их точность может быть указана непосредственно в виде СКП и тогда все понятно. Но иногда ее указывают, например, так: «погрешность измерения пеленга ±1,5º». Разумеется, это не означает, что такой пеленгатор «ошибается» каждый раз на 1,5º . Это также не означает, что он не может ошибиться более , чем на 1,5º. Как правило, указанное таким образом значение погрешности соответствует вероятности Р =0,95. То есть в среднем в 95 случаях из 100 погрешность не превысит (в большую или меньшую сторону) значения в 1,5º.
Соответственно, в пяти случаях из ста погрешность может быть и больше. Для нормального закона распределения погрешности вероятность 0,95 соответствует удвоенной СКП. Следовательно, СКП измерения пеленга в данном примере составит 0,75º.