Dikdörtgen?
Çözüm. 2,88 dm2 \u003d 288 cm2 ve 0,8 dm \u003d 8 cm olduğundan dikdörtgenin uzunluğu 288: 8 yani 36 cm \u003d 3,6 dm'dir. 3,6 × 0,8 = 2,88 olacak şekilde bir 3,6 sayısı bulduk. 2,88'in 0,8'e bölümüdür.
Şöyle yazıyorlar: 2,88: 0,8 = 3,6.
Cevap 3.6, desimetreyi santimetreye çevirmeden elde edilebilir. Bunu yapmak için, 0,8 bölenini ve 2,88 bölenini 10 ile çarpın (yani, virgülün bir hanesini sağa kaydırın) ve 28,8'i 8'e bölün. Yine şunu elde ederiz: 28,8: 8 = 3,6.
Bir sayıyı ondalık kesre bölmek için şunlara ihtiyacınız vardır:
1) bölünen ve bölende, virgülü, bölendeki ondalık noktadan sonraki basamak sayısı kadar sağa hareket ettirin;
2) Bundan sonra doğal sayıya göre bölme işlemini gerçekleştirin.
örnek 1 12.096'yı 2.24'e bölün. Bölen ve bölen kısmında virgülü 2 basamak sağa kaydırın. 1209,6 ve 224 sayılarını alıyoruz. 1209,6: 224 = 5,4 olduğundan 12,096: 2,24 = 5,4.
Örnek 2 4,5'u 0,125'e bölün. Burada bölen ve bölen kısmında virgülün 3 hanesini sağa kaydırmak gerekiyor. Bölünmede virgülden sonra tek rakam olduğu için sağ tarafa iki sıfır ekleyeceğiz. Virgülün yerini değiştirdikten sonra şunu elde ederiz: sayılar 4500 ve 125. 4500'den beri: 125 = 36, o zaman 4,5: 0,125 = 36.
Örnek 1 ve 2'den, bir sayının bileşik kesirle bölünmesi durumunda bu sayının azaldığı veya değişmediği, normal sayıya bölündüğünde ise bu sayının azaldığı veya değişmediği görülmektedir. ondalık artar: 12,096 > 5,4 ve 4,5< 36.
2,467'yi 0,01'e bölün. Bölen ve bölendeki virgülü 2 basamak sağa kaydırdıktan sonra bölümün 246,7:1 yani 246,7 olduğunu elde ederiz.
Dolayısıyla ve 2,467: 0,01 = 246,7. Buradan kuralı anlıyoruz:
Bir ondalık sayıyı 0,1'e bölmek için; 0,01; 0,001, bölendeki birimin önündeki sıfırlar kadar (yani 10, 100, 1000 ile çarpmak) içindeki virgülü sağa kaydırmak gerekir.
Yeterli sayı yoksa, önce sonda nitelik belirtmeniz gerekir kesirler birkaç sıfır.
Örneğin, 56,87: 0,0001 = 56,8700: 0,0001 = 568,700.
Ondalık kesiri bölme kuralını formüle edin: ondalık kesirle; 0,1 oranında; 0,01; 0.001.
Bölmeyi 0,01 ile değiştirmek için hangi sayı çarpılabilir?
1443. Bölümü bulun ve çarpma işlemiyle test edin:
a) 0,8: 0,5; b) 3,51: 2,7; c) 14,335: 0,61.
1444. Bölümü bulun ve bölmeye göre test edin:
a) 0,096: 0,12; b) 0,126: 0,9; c) 42.105: 3.5.
a) 7,56: 0,6; g) 6.944: 3.2; m) 14,976: 0,72;
b) 0,161: 0,7; h) 0,0456: 3,8; o) 168.392: 5,6;
c) 0,468: 0,09; i) 0,182: 1,3; n) 24.576: 4.8;
d) 0,00261: 0,03; j) 131.67: 5.7; p) 16.51: 1.27;
e) 0,824: 0,8; k) 189,54: 0,78; c) 46,08: 0,384;
e) 10,5: 3,5; m) 636: 0,12; t) 22.256: 20.8.
1446. Şu ifadeleri yazın:
a) 10 - 2,4x = 3,16; e) 4,2p - p = 5,12;
b) (y + 26,1) 2,3 = 70,84; f) 8,2t - 4,4t = 38,38;
c) (z - 1,2): 0,6 = 21,1; g) (10,49 - s): 4,02 = 0,805;
d) 3,5 m + m = 9,9; h) 9k - 8,67k = 0,6699.
1460. İki depoda 119,88 ton benzin vardı. İlk tankta ikinciye göre 1,7 kat daha fazla benzin vardı. Her depoda ne kadar benzin vardı?
1461. Üç parselden 87,36 ton lahana hasadı yapıldı. Aynı zamanda birinci bölümden 1,4 kat, ikinci bölümden ise üçüncü bölüme göre 1,8 kat daha fazla toplandı. Her parselden kaç ton lahana hasat edildi?
1462. Kanguru zürafadan 2,4 kat daha alçaktır ve zürafa kangurudan 2,52 m daha yüksektir.Zürafanın boyu ne kadardır ve kangurunun boyu ne kadardır?
1463. İki yaya birbirinden 4,6 km uzaklıktaydı. Birbirlerine doğru gittiler ve 0,8 saatte buluştular.Bir yayanın hızı diğerinin hızının 1,3 katı ise her yayanın hızını bulunuz.
1464. Aşağıdakileri yapın:
a) (130,2 - 30,8): 2,8 - 21,84:
b) 8,16: (1,32 + 3,48) - 0,345;
c) 3,712: (7 - 3,8) + 1,3 (2,74 + 0,66);
d) (3,4: 1,7 + 0,57: 1,9) 4,9 + 0,0825: 2,75;
e) (4,44: 3,7 - 0,56: 2,8): 0,25 - 0,8;
f) 10,79: 8,3 0,7 - 0,46 3,15: 6,9.
1465. Hayal et ortak kesir ondalık sayı olarak ve değeri bulun ifade:

1466. Sözlü olarak hesaplayın:
a) 25,5:5; b) 9 0,2; c) 0,3:2; d) 6,7 - 2,3;
1,5: 3; 1 0,1; 2:5; 6- 0,02;
4,7: 10; 16 0,01; 17,17: 17; 3,08 + 0,2;
0,48: 4; 24 0,3; 25,5: 25; 2,54 + 0,06;
0,9:100; 0,5 26; 0,8:16; 8,2-2,2.
1467. İşi bulun:
a) 0,1 0,1; d) 0,4 0,4; g) 0,7 0,001;
b) 1,3 1,4; e) 0,06 0,8; h) 100 0,09;
c) 0,3 0,4; f) 0,01 100; i) 0,3 0,3 0,3.
1468. Bulunan: 30 sayısının 0,4'ü; 0,5 sayı 18; 0,1 sayı 6,5; 2,5 sayı 40; 0,12 sayı 100; 1000 üzerinden 0,01.
1469. a=10 olan 5683.25a ifadesinin anlamı nedir? 0,1; 0,01; 100; 0,001; 1000; 0.00001?
1470. Hangi sayıların kesin, hangilerinin yaklaşık olabileceğini düşünün:
a) Sınıfta 32 öğrenci var;
b) Moskova'dan Kiev'e olan mesafe 900 km'dir;
c) paralel yüzlünün 12 kenarı vardır;
d) masa uzunluğu 1,3 m;
e) Moskova'nın nüfusu 8 milyon kişidir;
f) Bir torbada 0,5 kg un;
g) Küba adasının alanı 105.000 km2'dir;
h) Okul kütüphanesinde 10.000 kitap bulunmaktadır;
i) bir açıklık 4 vershok'a eşittir ve bir vershok 4,45 cm'ye eşittir (vershok)
falanks uzunluğu işaret parmağı).
1471. Eşitsizliğin üç çözümünü bulun:
a) 1.2< х < 1,6; в) 0,001 < х < 0,002;
b) 2.1< х< 2,3; г) 0,01 <х< 0,011.
1472. İfadelerin değerlerini hesaplamadan karşılaştırın:
a) 24 0,15 ve (24 - 15): 100;
b) 0,084 0,5 ve (84 5): 10.000.
Cevabını açıkla.
1473. Sayıları yuvarlama:

1474. Bölmeyi gerçekleştir:
a) 22.7:10; 23.3:10; 3.14:10; 9.6:10;
b) 304: 100; 42.5:100; 2,5:100; 0,9:100; 0,03:100;
c) 143.4:12; 1.488:124; 0,3417: 34; 159.9:235; 65.32:568.
1475. Bir bisikletçi saatte 12 km hızla köyden ayrıldı. 2 saat sonra başka bir bisikletli aynı köyden ters istikamette ayrıldı.
ve ikincinin hızı birincinin hızının 1,25 katıdır. İkinci bisikletçi yola çıktıktan 3,3 saat sonra aralarındaki mesafe ne kadardır?
1476. Teknenin kendi hızı 8,5 km/saat, akıntının hızı ise 1,3 km/saattir. Tekne akıntıyla 3,5 saatte ne kadar yol kat edecek? Tekne 5,6 saatte akıntıya karşı ne kadar yol kat edecek?
1477. Fabrika 3,75 bin parça üreterek 950 ruble fiyata sattı. bir parça. Tesisin bir parçanın üretimi için maliyeti 637,5 ruble olarak gerçekleşti. Fabrikanın bu parçaların satışından elde ettiği karı bulunuz.
1478. Dikdörtgen bir paralel yüzün genişliği 7,2 cm'dir. ![]() Bu kutunun hacmini bulun ve cevabınızı en yakın tam sayıya yuvarlayın.
Bu kutunun hacmini bulun ve cevabınızı en yakın tam sayıya yuvarlayın.
1479. Papa Carlo, Piero'ya her gün 4 asker, Pinokyo'ya ise ilk gün 1 asker ve eğer iyi davranırsa ertesi gün 1 asker daha vereceğine söz verdi. Pinokyo gücenmişti: Ne kadar uğraşırsa uğraşsın, toplamda asla Pierrot kadar katı elde edemeyeceğine karar verdi. Pinokyo'nun haklı olup olmadığını düşünün.
1480. 231 m pano 3 dolap ve 9 kitaplığa gitti, dolaba rafa göre 4 kat daha fazla malzeme gitti. Dolaba kaç metre tahta, rafa kaç metre gidiyor?
1481. Sorunu çözün:
1) Birinci sayı 6,3 olup ikinci sayıdır. Üçüncü sayı ikincidir. İkinci ve üçüncü sayıları bulun.
2) İlk sayı 8.1'dir. İkinci sayı birinci sayıdan ve üçüncü sayıdandır. İkinci ve üçüncü sayıları bulun.
1482. İfadenin değerini bulun:
1) (7 - 5,38) 2,5;
2) (8 - 6,46) 1,5.
1483. Özelin değerini bulun:
a) 17.01: 6.3; d) 1,4245: 3,5; g) 0,02976: 0,024;
b) 1.598: 4.7; e) 193.2: 8.4; h) 11.59: 3.05;
c) 39.156: 7.8; e) 0,045: 0,18; i) 74.256: 18.2.
1484. Evden okula giden yol 1,1 km'dir. Kız bu yolu 0.25 saatte kat ediyor.Kız ne kadar hızlı yürüyor?
1485. İki odalı bir dairede bir odanın alanı 20,64 m 2, diğer odanın alanı 2,4 kat daha azdır. Bu iki odanın alanını birlikte bulun.
1486. Motor 7,5 saatte 111 litre yakıt tüketiyor. Motor 1,8 saatte kaç litre yakıt tüketir?
1487. Hacmi 3,5 dm3 olan metal bir parçanın kütlesi 27,3 kg'dır. Aynı metalden yapılmış başka bir parçanın kütlesi 10,92 kg'dır. İkinci bölümün hacmi nedir?
1488. İki boru aracılığıyla tanka 2,28 ton benzin döküldü. Birinci borudan saatte 3,6 ton benzin geldi ve 0,4 saat açık kaldı, ikinci borudan saatte birinci borudan 0,8 ton daha az benzin geldi. İkinci boru ne kadar süre açık kaldı?
1489. Denklemi çözün:
a) 2,136: (1,9 - x) = 7,12; c) 0,2t + 1,7t - 0,54 = 0,22;
b) 4,2 (0,8 + y) = 8,82; d) 5,6g - 2z - 0,7z + 2,65 = 7.
1490. 13,3 ton ağırlığındaki mallar üç araca dağıtıldı. İlk araba 1,3 kat, ikincisi ise üçüncü arabadan 1,5 kat daha fazla yüklendi. Her bir araca kaç ton eşya yüklendi?
1491. İki yaya aynı anda, zıt yönlerde aynı yerden ayrıldı. 0,8 saat sonra aralarındaki mesafe 6,8 km'ye eşitlendi. Bir yayanın hızı diğerinin hızının 1,5 katıydı. Her yayanın hızını bulun.
1492. Aşağıdakileri yapın:
a) (21.2544: 0,9 + 1,02 3,2): 5,6;
b) 4,36: (3,15 + 2,3) + (0,792 - 0,78) 350;
c) (3.91: 2.3 5.4 - 4.03) 2.4;
d) 6,93: (0,028 + 0,36 4,2) - 3,5.
1493. Okula bir doktor geldi ve aşı için 0,25 kg serum getirdi. Her enjeksiyon için 0,002 kg serum gerekiyorsa kaç kişiye enjeksiyon yapılabilir?
1494. Mağazaya 2,8 ton zencefilli kurabiye getirildi. Öğle yemeğinden önce bu zencefilli kurabiyeler satıldı. Satılacak kaç ton zencefilli kurabiye kaldı?
1495. Bir kumaş parçasından 5,6 m kesildi, bu parça kesildiğinde parçanın içinde kaç metre kumaş vardı?
N.Ya. VILENKIN, V. I. ZHOKHOV, A. S. CHESNOKOV, S. I. SHVARTSBURD, Matematik 5. Sınıf, Eğitim kurumları için ders kitabı
§ 107. Ondalık kesirlerin eklenmesi.Ondalık sayıların eklenmesi, tam sayıların eklenmesiyle aynı şekilde yapılır. Bunu örneklerle görelim.
1) 0,132 + 2,354. Şartları alt alta imzalayalım.
Burada 2 binde 4 binde birliklerin toplanmasından 6 binde birlik elde edilmiş;
3 yüzde birlik ile 5 yüzdeliklerin toplanmasından 8 yüzde birlik çıktı;
onda 1 ile 3 onda -4 onda birini eklemekten ve
2 tam sayı ile 0 tam sayının toplanmasından - 2 tam sayıya.
2) 5,065 + 7,83.
İkinci dönemde binde biri olmadığından şartları alt alta imzalarken hata yapmamak önemlidir.
3) 1,2357 + 0,469 + 2,08 + 3,90701.
Burada binde birleri topladığımızda 21 binde bir elde ediyoruz; binde birlerin altına 1 yazdık ve yüzde birlerin altına 2 ekledik, böylece yüzüncü sırada şu terimleri elde ettik: 2 + 3 + 6 + 8 + 0; toplamda 19 yüzde bir veriyorlar, yüzde 9'un altına imza attık, 1 de onda sayıldı vs.
Bu nedenle, ondalık kesirleri eklerken aşağıdaki sıraya uyulmalıdır: kesirler birbiri altında imzalanır, böylece tüm terimlerde aynı rakamlar birbirinin altında olur ve tüm virgüller aynı dikey sütunda olur; Bazı terimlerin ondalık basamaklarının sağına, en azından zihinsel olarak öyle sayıda sıfır atfederler ki, virgülden sonraki tüm terimler aynı sayıda rakama sahip olur. Daha sonra sağ taraftan başlayarak rakamlarla toplama yapılır ve elde edilen miktarda bu terimlerde olduğu gibi aynı dikey sütuna virgül konur.
§ 108. Ondalık kesirlerin çıkarılması.
Ondalık sayıların çıkarılması, tam sayıların çıkarılmasıyla aynı şekilde yapılır. Bunu örneklerle gösterelim.
1) 9,87 - 7,32. Aynı rakamın birimleri birbirinin altında olacak şekilde eksilen kısmın altındaki çıkanı imzalayalım:
2) 16,29 - 4,75. İlk örnekte olduğu gibi eksilen kısmın altındaki çıkanı imzalayalım:
Onda birini çıkarmak için, 6'dan bir birimin tamamını alıp onda birine bölmek gerekiyordu.
3) 14.0213-5.350712. Eksilenin altındaki çıkanı imzalayalım:
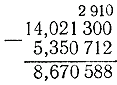
Çıkarma işlemi şu şekilde yapıldı: 0'dan 2 milyonuncu rakamı çıkaramadığımız için sola en yakın rakamı yani yüzbinde bir rakamını kullanmamız gerekiyor ama yüzbinde bir yerine sıfır da var, dolayısıyla 1 alıyoruz. 3 onbinde birden onbinde bir ve bunu yüzbinde birlere bölersek 10 yüzbinde bir elde ederiz, bunun 9 yüzbinde biri yüzbinde bir kategorisinde kalır ve 1 yüzbinde bir milyonda bire bölünür, 10 milyonuncuyu alıyoruz. Böylece, son üç rakamda şunu elde ettik: milyonda bir 10, yüz binde 9, on binde 2. Daha fazla netlik ve kolaylık sağlamak için (unutmadan), bu sayılar azaltılmış sayının karşılık gelen kesirli rakamının üzerine yazılır. Artık çıkarma işlemine başlayabiliriz. 10 milyonuncudan 2 milyonuncuyu çıkarırsak 8 milyonuncu çıkar; 9 yüz binde 1 yüz binde birini çıkarırsak 8 yüz binde bir elde ederiz, vb.
Böylece, ondalık kesirleri çıkarırken aşağıdaki sıra gözlenir: Çıkarılan, azaltılmışın altında imzalanır, böylece aynı rakamlar birbirinin altında olur ve tüm virgüller aynı dikey sütunda olur; sağda, en azından zihinsel olarak aynı sayıda rakama sahip olacak şekilde azaltılmış veya çıkarılmış sıfırlara atfederler, sonra sağ taraftan başlayarak rakamlarla çıkarırlar ve ortaya çıkan farka virgül koyarlar. azaltıldığı ve çıkarıldığı aynı dikey sütun.
§ 109. Ondalık kesirlerin çarpımı.
Ondalık kesirlerin çarpılmasıyla ilgili birkaç örneği düşünün.
Bu sayıların çarpımını bulmak için şu şekilde akıl yürütebiliriz: Eğer çarpan 10 kat arttırılırsa, o zaman her iki faktör de tam sayı olacaktır ve daha sonra bunları tam sayılarla çarpma kurallarına göre çarpabiliriz. Ancak faktörlerden biri birkaç kez artırıldığında ürünün aynı miktarda arttığını biliyoruz. Bu, tamsayı çarpanların yani 28 ile 23'ün çarpılmasından elde edilen sayının gerçek çarpımdan 10 kat daha büyük olduğu anlamına gelir ve doğru çarpımı elde etmek için bulunan çarpımı 10 kat azaltmanız gerekir. Dolayısıyla burada bir kez 10'la çarpma, bir kez de 10'a bölme işlemi yapmanız gerekiyor ama çarpma ve 10'a bölme işlemi virgülün birer işaret sağa ve sola hareket ettirilmesiyle yapılıyor. Bu nedenle, bunu yapmanız gerekir: çarpanda virgülü bir işaret sağa hareket ettirin, bundan 23'e eşit olacaktır, sonra ortaya çıkan tam sayıları çarpmanız gerekir:
Bu ürün gerçek olandan 10 kat daha büyüktür. Bu nedenle 10 kat azaltılması gerekiyor, bunun için virgülünü bir karakter sola kaydırıyoruz. Böylece elde ederiz
28 2,3 = 64,4.
Doğrulama amacıyla, paydayla bir ondalık kesir yazabilir ve sıradan kesirleri çarpma kuralına göre bir işlem gerçekleştirebilirsiniz;
2) 12,27 0,021.
Bu örnek ile önceki örnek arasındaki fark, burada her iki faktörün de ondalık kesirlerle temsil edilmesidir. Ancak burada çarpma işleminde virgüllere dikkat etmeyeceğiz yani geçici olarak çarpanı 100 kat, çarpanı 1.000 kat artıracağız, bu da çarpımı 100.000 kat artıracaktır. Böylece 1227'yi 21 ile çarparak şunu elde ederiz:
1 227 21 = 25 767.
Ortaya çıkan ürünün gerçek üründen 100.000 kat daha büyük olduğunu hesaba katarsak, şimdi içine virgül koyarak onu 100.000 kat azaltmalıyız, o zaman şunu elde ederiz:
32,27 0,021 = 0,25767.
Hadi kontrol edelim:
Böylece iki ondalık kesri çarpmak için virgüllere dikkat etmeden tamsayı olarak çarpmak ve çarpımda çarpımdaki ve çarpımdaki ondalık basamak sayısı kadar sağ tarafta virgülle ayırmak yeterlidir. faktör bir arada.
Son örnekte sonuç, beş ondalık basamağa sahip bir çarpımdır. Bu kadar büyük bir doğruluk gerekmiyorsa, ondalık kesrin yuvarlanması yapılır. Yuvarlarken tamsayılar için belirtilen kuralın aynısını kullanmalısınız.
§ 110. Tabloları kullanarak çarpma.
Ondalık sayıların çarpılması bazen tablolar kullanılarak yapılabilir. Bu amaçla, örneğin daha önce açıklaması verilen iki basamaklı sayıların çarpım tablosunu kullanabilirsiniz.
1) 53'ü 1,5 ile çarpın.
53'ü 15 ile çarpacağız. Tabloda bu çarpım 795'e eşit. 53'ün çarpımını 15 bulduk ama ikinci çarpanımız 10 kat azdı, bu da çarpımın 10 kat azaltılması gerektiği anlamına geliyor yani.
53 1,5 = 79,5.
2) 5,3'ü 4,7 ile çarpın.
Öncelikle tabloda 53 ile 47'nin çarpımını bulalım, 2491 olacak. Ama çarpanı ve çarpanı toplam 100 kat arttırdığımız için ortaya çıkan çarpım olması gerekenden 100 kat daha büyük; yani bu çarpımı 100 kat azaltmamız gerekiyor:
5,3 4,7 = 24,91.
3) 0,53'ü 7,4 ile çarpın.
Öncelikle tabloda 53'ün 74'e çarpımını buluyoruz; 3.922 olacak ama çarpanı 100 kat, çarpanı da 10 kat artırdığımız için çarpım 1.000 kat artmış; yani şimdi bunu 1000 kat azaltmamız gerekiyor:
0,53 7,4 = 3,922.
§ 111. Ondalık sayıların bölünmesi.
Ondalık bölme işlemine şu sırayla bakacağız:
1. Ondalık kesrin bir tam sayıya bölünmesi,
1. Ondalık kesrin bir tam sayıya bölünmesi.
1) 2,46'yı 2'ye bölün.
Önce 2 tam sayıya, sonra onda birliğe ve son olarak da yüzde birliğe böldük.
2) 32,46'yı 3'e bölün.
32,46: 3 = 10,82.
3 onluğu 3'e böldük, sonra 2 birimi 3'e bölmeye başladık; Bölenin (2) birim sayısı bölenden (3) küçük olduğundan bölüme 0 koymak zorunda kaldık; ayrıca geri kalanın onda dördünü yıkıp onda 24'ünü 3'e böldük; onda biri özel olarak alındı ve sonunda yüzde biri 6'ya bölündü.
3) 1,2345'i 5'e bölün.
1,2345: 5 = 0,2469.
Burada ilk etapta bölümde, bir tam sayı 5'e bölünemediği için sıfır tamsayı ortaya çıktı.
4) 13,58'i 4'e bölün.

Bu örneğin özelliği şu ki özelde yüzde 9'u elde ettiğimizde, daha sonra yüzde 2'ye eşit bir kalan bulununca, bu kalanı binde birlere böldük, binde 20'yi elde ettik ve bölmeyi sona getirdik.
Kural. Ondalık kesirin bir tam sayıya bölünmesi, tam sayıların bölünmesiyle aynı şekilde gerçekleştirilir ve elde edilen kalanlar, giderek daha küçük olan ondalık kesirlere dönüştürülür; kalan sıfır oluncaya kadar bölme işlemine devam edilir.
2. Ondalık kesirin ondalık kesirle bölünmesi.
1) 2,46'yı 0,2'ye bölün.
Ondalık kesri bir tam sayıya nasıl böleceğimizi zaten biliyoruz. Bakalım bu yeni bölünme durumu da bir öncekine indirgenebilir mi? Bir zamanlar, bölümün dikkat çekici bir özelliği olduğunu düşündük; bu, bölünen ve böleni aynı sayıda artırırken veya azaltırken değişmeden kalması gerçeğinden oluşur. Eğer bölen tam sayı olsaydı, bize sunulan sayıların bölme işlemini kolaylıkla yapardık. Bunu yapmak için 10 kat artırmak yeterlidir ve doğru oranı elde etmek için temettüyü aynı sayıda yani 10 kat artırmak gerekir. Daha sonra bu sayıların bölünmesi, bu sayıların bölünmesiyle değiştirilecektir:
ve özel olarak herhangi bir değişiklik yapmanıza gerek yoktur.
Bu bölmeyi yapalım:
Yani 2,46: 0,2 = 12,3.
2) 1,25'i 1,6'ya bölün.

Böleni (1,6) 10 kat arttırıyoruz; bölümün değişmemesi için temettüyü 10 kat arttırıyoruz; 12 tam sayı 16'ya bölünemediği için 0 bölümüne yazıp 125'in onda birini 16'ya bölüyoruz, bölümden onda biri 7 çıkıyor ve kalan 13 oluyor. 13 onda birini sıfır atayarak yüzde birlere bölüyoruz ve 130 yüzde birini 16'ya bölüyoruz vs. Aşağıdakilere dikkat edin:
a) Bölümde tamsayı elde edilemediğinde yerine sıfır tamsayı yazılır;
b) kalana bölünen rakamın rakamı alındıktan sonra bölene bölünemeyen bir sayı elde edilirse bölüme sıfır yazılır;
c) Kâr payının son rakamı çıkarıldıktan sonra bölme işlemi bitmediği takdirde kalanlara sıfır verilerek bölme işlemine devam edilir.
d) temettü bir tam sayı ise, o zaman ondalık kesre bölünürken, ona sıfır atanarak artış gerçekleştirilir.
Bu nedenle, bir sayıyı ondalık kesire bölmek için, bölendeki virgülü atmanız ve ardından virgül bırakıldığında bölen arttıkça bölen sayısını artırmanız ve ardından bölmeyi şu şekilde yapmanız gerekir: ondalık kesri bir tam sayıya bölme kuralı.
§ 112. Yaklaşık bölüm.
Önceki paragrafta ondalık kesirlerin bölünmesini ele aldık ve çözdüğümüz tüm örneklerde bölme sonuna getirildi, yani tam bir bölüm elde edildi. Ancak çoğu durumda bölmeyi ne kadar genişletirsek yapalım kesin oran elde edilemez. İşte böyle bir durum: 53'ü 101'e bölün.

Bölümde zaten beş rakamı aldık, ancak bölme henüz bitmedi ve biteceğine dair bir umut da yok, çünkü daha önce karşılaştığımız sayılar kalanlarda görünmeye başlıyor. Bölümde sayılar da tekrarlanacaktır: Açıkçası, 7 sayısından sonra 5 sayısı, ardından 2 sayısı görünecek ve bu şekilde sonsuza kadar devam edecektir. Bu gibi durumlarda bölme işlemi kesintiye uğrar ve bölümün ilk birkaç rakamıyla sınırlıdır. Bu özele denir yaklaşık. Bu durumda bölme işlemi nasıl yapılır örneklerle göstereceğiz.
25'i 3'e bölmek gereksin. Böyle bir bölme işleminden tam sayı veya ondalık kesir olarak ifade edilen tam bölümün elde edilemeyeceği açıktır. Bu nedenle yaklaşık bir bölüm arayacağız:
25: 3 = 8 ve kalan 1
Yaklaşık bölüm 8'dir; elbette tam bölümden küçüktür, çünkü 1'den kalan vardır. Kesin bölümü elde etmek için, bulunan yaklaşık bölüme, yani 8'e, kalanın bölünmesiyle elde edilen kesri eklemeniz gerekir. , 1'e eşit, 3'e; 1/3'lük bir kesir olacak. Bu, tam bölümün 8 1/3 karışık sayısı olarak ifade edileceği anlamına gelir. 1/3 uygun kesir yani kesir olduğundan, birden az, sonra onu atarak varsayıyoruz hata, Hangi birden az. Özel 8 irade yaklaşık bölüm bir dezavantajla bire kadar. 8 yerine 9 alırsak, bir birimin tamamını değil 2/3'ü ekleyeceğimiz için birden küçük bir hataya da izin vermiş oluruz. Böyle özel bir vasiyet fazlalığı olan bire kadar yaklaşık bölüm.
Şimdi başka bir örnek verelim. 27'yi 8'e bölmemiz gereksin. Burada tam sayı olarak ifade edilen tam bir bölüm elde edemeyeceğimiz için yaklaşık bir bölüm arayacağız:
27: 8 = 3 ve kalan 3.
Burada hata 3/8'dir, birden küçüktür, yani yaklaşık bölüm (3) bire kadar bir dezavantajla bulunur. Bölmeye devam ediyoruz: 3'ün geri kalanını onda birine bölüyoruz, 30'u elde ediyoruz; Bunları 8'e bölelim.
Onda üçü ve geri kalan onda b'yi özel olarak aldık. Özellikle 3,3 sayısıyla yetinip geri kalan 6'yı atarsak, onda birinden daha az bir hataya izin vermiş oluruz. Neden? Çünkü 3,3'e 6'nın 8'e bölünmesi sonucunu eklediğimizde tam oran elde edilecektir; bu bölümden 6/80 elde edilir, bu da onda birinden azdır. (Kontrol edin!) Dolayısıyla, bölümde kendimizi onda birlerle sınırlandırırsak bölümü bulduğumuzu söyleyebiliriz. onda birine kadar doğru(dezavantajlı).
Bir ondalık basamak daha bulmak için bölme işlemine devam edelim. Bunu yapmak için onda biri 6'yı yüzlüğe bölüyoruz ve 60 yüzde biri elde ediyoruz; Bunları 8'e bölelim.

Özelde üçüncü sırada 7, geri kalanda ise 4 yüzde birlik çıktı; bunları atarsak yüzde birden daha az bir hataya izin veririz, çünkü yüzde 4'ün 8'e bölümü yüzde birden küçüktür. Bu gibi durumlarda bölümün bulunduğu söylenir. yüzde birine kadar doğru(dezavantajlı).
Şu anda ele aldığımız örnekte, ondalık kesir olarak ifade edilen tam bölümü elde edebilirsiniz. Bunun için son kalan yüzde 4'ü binde birlere bölüp 8'e bölmek yeterlidir.
Ancak çoğu durumda kesin bir oran elde etmek mümkün değildir ve kişinin kendisini yaklaşık değerlerle sınırlaması gerekir. Şimdi böyle bir örneği ele alacağız:
40: 7 = 5,71428571...
Sayının sonundaki noktalar bölmenin tamamlanmadığını yani eşitliğin yaklaşık olduğunu gösterir. Genellikle yaklaşık eşitlik şu şekilde yazılır:
40: 7 = 5,71428571.
Sekiz ondalık basamaklı bölümü aldık. Ancak bu kadar büyük bir kesinlik gerekmiyorsa, bölümün tamamıyla, yani 5 sayısıyla (daha kesin olarak 6) sınırlandırılabilir; daha fazla doğruluk için ondalıklar dikkate alınabilir ve bölüm 5,7'ye eşit olarak alınabilir; herhangi bir nedenle bu doğruluk yetersizse, yüzde birlerde durup 5,71 vb. Alabiliriz. Bireysel bölümleri yazalım ve isimlendirelim.
Bire kadar ilk yaklaşık bölüm 6.
İkinci » » » onda bire kadar 5.7.
Üçüncü » » » yüzde bire kadar 5,71.
Dördüncü » » » 5.714'ün binde birine kadar.
Böylece yaklaşık bir bölümün örneğin 3. basamağa kadar (yani binde bire kadar) bulunması için bu işaret bulunduğu anda bölme işlemi durdurulur. Bu durumda § 40'ta belirtilen kuralı hatırlamak gerekir.
§ 113. İlgi için en basit problemler.
Ondalık kesirleri inceledikten sonra birkaç yüzde problemini daha çözeceğiz.
Bu problemler sıradan kesirler bölümünde çözdüğümüz problemlere benzer; ama şimdi yüzde birleri ondalık kesirler biçiminde, yani açıkça belirlenmiş bir payda olmadan yazacağız.
Öncelikle sıradan bir kesirden paydası 100 olan ondalık kesire kolayca geçiş yapabilmeniz gerekir. Bunu yapmak için payı paydaya bölmeniz gerekir:

Aşağıdaki tablo, % (yüzde) sembolüne sahip bir sayının, paydası 100 olan bir ondalık sayı ile nasıl değiştirildiğini göstermektedir:

Şimdi birkaç sorunu ele alalım.
1. Belirli bir sayının yüzdelerini bulma.
Görev 1. Bir köyde sadece 1.600 kişi yaşıyor. Okul çağındaki çocukların sayısı toplam nüfusun %25'ini oluşturmaktadır. Bu köyde okul çağında kaç çocuk var?
Bu problemde 1.600'ün %25'ini yani 0,25'ini bulmanız gerekiyor. Sorun çarpılarak çözülür:
1.600 0,25 = 400 (çocuklar).
Bu nedenle 1.600'ün %25'i 400'dür.
Bu görevin net olarak anlaşılabilmesi için her yüz nüfusa karşılık 25 okul çağındaki çocuğun bulunduğunu hatırlamakta fayda var. Dolayısıyla okul çağındaki tüm çocukların sayısını bulmak için önce 1600 sayısında kaç yüz olduğunu bulabilir (16), daha sonra 25'i yüzler sayısıyla çarpabilirsiniz (25 x 16 = 400). Bu şekilde çözümün geçerliliğini kontrol edebilirsiniz.
Görev 2. Tasarruf bankaları mevduat sahiplerine yıllık gelirin %2'sini verir. Aşağıdakileri yatıran mevduat sahibi yılda ne kadar gelir elde edecek: a) 200 ruble? b) 500 ruble? c) 750 ruble? d) 1000 ruble?
Dört durumda da sorunu çözmek için belirtilen miktarların 0,02'sini hesaplamak gerekecektir, yani bu sayıların her birinin 0,02 ile çarpılması gerekecektir. Hadi yapalım:
a) 200 0,02 = 4 (ruble),
b) 500 0,02 = 10 (ruble),
c) 750 0,02 = 15 (ruble),
d) 1.000 0,02 = 20 (ruble).
Bu durumların her biri aşağıdaki hususlarla doğrulanabilir. Tasarruf bankaları mevduat sahiplerine gelirin %2'sini, yani tasarruflara yatırılan miktarın 0,02'sini verir. Miktar 100 ruble olsaydı, bunun 0,02'si 2 ruble olurdu. Bu, her yüzün mevduat sahibine 2 ruble getireceği anlamına gelir. gelir. Bu nedenle, ele alınan durumların her birinde, belirli bir sayıda kaç yüz olduğunu bulmak ve 2 rubleyi bu yüz sayısıyla çarpmak yeterlidir. Örnek a) yüzlerce 2, yani
2 2 \u003d 4 (ruble).
Örnek d) yüzler 10'dur, yani
2 10 \u003d 20 (ruble).
2. Bir sayıyı yüzdesine göre bulma.
Görev 1. Bahar döneminde okuldan 54 öğrenci mezun edildi, bu da toplam öğrenci sayısının %6'sına tekabül ediyor. Geçtiğimiz eğitim-öğretim yılında okulda kaç öğrenci vardı?
Öncelikle bu sorunun anlamını açıklayalım. Okul 54 öğrenci mezun etmiştir; bu da toplam öğrenci sayısının %6'sına, yani okuldaki tüm öğrencilerin yüzde 6'sına (0,06) denk gelmektedir. Bu, öğrencilerin sayı (54) ve kesir (0,06) ile ifade edilen kısmını bildiğimiz ve bu kesirden tam sayıyı bulmamız gerektiği anlamına gelir. Dolayısıyla önümüzde bir sayıyı kesirlerine göre bulmanın sıradan bir sorunu var (§ 90 s. 6). Bu tür problemler bölme yoluyla çözülür:
Bu da okulda 900 öğrencinin olduğu anlamına geliyor.
Bu tür problemleri ters problemi çözerek kontrol etmek faydalıdır, yani. problemi çözdükten sonra, en azından aklınızda, ilk türdeki problemi çözmelisiniz (belirli bir sayının yüzdesini bulma): bulunan sayıyı alın ( 900) verildiği gibi ve çözülen problemde belirtilen yüzdeyi ondan bulun, yani:
900 0,06 = 54.
Görev 2. Aile ay içinde yemeğe 780 ruble harcıyor, bu da babanın aylık gelirinin %65'ine tekabül ediyor. Aylık gelirini belirleyin.
Bu görev öncekiyle aynı anlama sahiptir. Aylık kazancın ruble (780 ruble) cinsinden ifade edilen bir kısmını verir ve bu kısmın toplam kazancın %65'i yani 0,65'i olduğunu belirtir. Ve istenen kazancın tamamıdır:
780: 0,65 = 1 200.
Bu nedenle istenen kazanç 1200 ruble.
3. Sayıların yüzdesini bulma.
Görev 1. Okul kütüphanesinde toplam 6.000 kitap bulunmaktadır. Bunların arasında matematikle ilgili 1.200 kitap var. Kütüphanedeki toplam kitap sayısının yüzde kaçı matematik kitaplarından oluşuyor?
Bu tür problemleri zaten ele aldık (§97) ve iki sayının yüzdesini hesaplamak için bu sayıların oranını bulup 100 ile çarpmanız gerektiği sonucuna vardık.
Görevimizde 1.200 ve 6.000 sayılarının yüzdesini bulmamız gerekiyor.
Önce oranlarını buluyoruz, sonra 100 ile çarpıyoruz:
![]()
Böylece 1.200 ve 6.000 sayılarının yüzdesi 20 olur. Yani matematik kitapları tüm kitapların toplam sayısının %20'sini oluşturur.
Kontrol etmek için ters problemi çözüyoruz: 6.000'in %20'sini buluyoruz:
6 000 0,2 = 1 200.
Görev 2. Tesisin 200 ton kömür alması gerekiyor. 80 ton teslim edildi, tesise kömürün yüzde kaçı teslim edildi?
Bu problem, bir sayının (80) diğerinin (200) yüzde kaçı olduğunu sorar. Bu sayıların oranı 80/200 olacaktır. Bunu 100 ile çarpalım:
![]()
Bu da kömürün yüzde 40'ının teslim edildiği anlamına geliyor.
Okulda bu eylemler basitten karmaşığa doğru incelenir. Bu nedenle yukarıdaki işlemleri basit örneklerle gerçekleştirmek için algoritmaya hakim olmak kesinlikle gereklidir. Böylece daha sonra ondalık kesirleri bir sütuna bölmede herhangi bir zorluk yaşanmayacaktır. Sonuçta bu, bu tür görevlerin en zor versiyonudur.
Bu konu tutarlı bir çalışma gerektirir. Bilgideki boşluklar burada kabul edilemez. Bu prensip birinci sınıfta olan her öğrenci tarafından öğrenilmelidir. Bu nedenle, arka arkaya birkaç dersi atlarsanız, materyale kendiniz hakim olmanız gerekecektir. Aksi takdirde daha sonra sadece matematikte değil, matematikle ilgili diğer konularda da sorunlar yaşanacaktır.
Başarılı bir matematik çalışmasının ikinci ön koşulu, toplama, çıkarma ve çarpma işlemlerini iyice öğrendikten sonra sütundaki bölme örneklerine geçmektir.
Bir çocuğun çarpım tablosunu öğrenmemesi durumunda bölme işlemi yapması zor olacaktır. Bu arada, bunu Pisagor tablosundan öğrenmek daha iyidir. Gereksiz hiçbir şey yoktur ve bu durumda çarpmanın sindirimi daha kolaydır.
Bir sütunda doğal sayılar nasıl çarpılır?
Bölme ve çarpma işlemine ilişkin sütundaki örneklerin çözümünde zorluk yaşanıyorsa o zaman sorunun çözümüne çarpma işlemiyle başlamak gerekir. Çünkü bölme çarpmanın tersidir:
- İki sayıyı çarpmadan önce onlara dikkatlice bakmanız gerekir. Rakamları daha fazla olan (daha uzun) olanı seçin ve önce onu yazın. İkincisini altına yerleştirin. Ayrıca ilgili kategoriye ait numaraların da aynı kategori altında olması gerekmektedir. Yani, ilk sayının en sağdaki rakamı, ikinci sayının en sağdaki rakamının üzerinde olmalıdır.
- Sağdan başlayarak alttaki sayının en sağdaki basamağını üstteki sayının her basamağıyla çarpın. Cevabı, son rakamı çarpıldığı rakamın altında olacak şekilde satırın altına yazın.
- Aynı işlemi alttaki sayının diğer rakamı ile tekrarlayın. Ancak çarpma sonucunun bir basamak sola kaydırılması gerekir. Bu durumda son rakamı çarpıldığı rakamın altında olacaktır.
İkinci çarpandaki sayılar bitene kadar bu çarpma işlemine bir sütunda devam edin. Şimdi katlanmaları gerekiyor. Bu istenen cevap olacaktır.

Ondalık kesirlerden oluşan bir sütuna çarpma algoritması
Öncelikle ondalık kesirlerin değil doğal kesirlerin verildiğini hayal etmek gerekiyor. Yani, onlardan virgülleri kaldırın ve ardından önceki durumda anlatıldığı gibi devam edin.
Fark cevap yazıldığında başlar. Bu noktada her iki kesirde de virgülden sonra gelen tüm sayıları saymak gerekir. Cevabın sonundan itibaren kaç tanesini saymanız ve oraya virgül koymanız gerekir.
Bu algoritmayı bir örnekle göstermek uygundur: 0,25 x 0,33:

Bölmeyi öğrenmeye nasıl başlanır?
Sütuna bölme örneklerini çözmeden önce bölme örneğinde yer alan sayıların adlarının hatırlanması gerekmektedir. Bunlardan ilki (bölen) bölünebilendir. İkincisi (ona bölünen) bir bölendir. Cevap özeldir.
Bundan sonra, basit bir günlük örnek kullanarak bu matematiksel işlemin özünü açıklayacağız. Örneğin, 10 şeker alırsanız, bunları anne ve baba arasında eşit olarak bölmek kolaydır. Peki ya bunları anne babanıza ve erkek kardeşinize dağıtmanız gerekirse?
Bundan sonra bölme kurallarını öğrenebilir ve belirli örneklerle bunlara hakim olabilirsiniz. İlk başta basit olanlar, daha sonra giderek daha karmaşık olanlara geçiliyor.
Sayıları bir sütuna bölmek için algoritma

İlk olarak, tek basamaklı bir sayıya bölünebilen doğal sayılara ilişkin prosedürü sunuyoruz. Bunlar aynı zamanda çok basamaklı bölenlerin veya ondalık kesirlerin de temelini oluşturacaktır. Ancak o zaman küçük değişiklikler yapması gerekiyor, ancak daha sonra bunun hakkında daha fazla bilgi:
- Bir sütunda bölme işlemi yapmadan önce bölünenin ve bölenin nerede olduğunu bulmanız gerekir.
- Temettüyü yazın. Sağında bir bölücü var.
- Solda ve altta son köşeye yakın bir köşe çizin.
- Eksik temettüyü, yani bölünme için minimum olacak sayıyı belirleyin. Genellikle bir rakamdan, en fazla iki rakamdan oluşur.
- Cevapta ilk yazılacak sayıyı seçin. Bölenin temettüye sığma sayısı olmalıdır.
- Bu sayıyı bir bölenle çarpmanın sonucunu yazın.
- Tamamlanmamış bir bölenin altına yazın. Çıkarma işlemini gerçekleştirin.
- Bölünen kısımdan sonraki ilk rakamı kalana taşıyın.
- Cevabı tekrar al.
- Çarpma ve çıkarma işlemini tekrarlayın. Kalan sıfırsa ve bölüştürme bittiyse örnek yapılır. Aksi takdirde adımları tekrarlayın: sayıyı yıkın, sayıyı alın, çarpın, çıkarın.
Bölende birden fazla rakam varsa uzun bölme işlemi nasıl yapılır?
Algoritmanın kendisi yukarıda anlatılanlarla tamamen örtüşmektedir. Fark, tamamlanmamış temettüdeki basamak sayısı olacaktır. Şimdi en az iki tane olmalı, ancak bölenden küçük çıkarsa ilk üç rakamla çalışması gerekiyor.
Bu bölümde başka bir nüans daha var. Gerçek şu ki, kalan ve ona taşınan rakam bazen bir bölene bölünemez. Daha sonra sırayla bir rakam daha atfetmek gerekiyor. Ancak aynı zamanda cevap sıfır olmalıdır. Üç basamaklı sayılar bir sütuna bölünürse iki basamaktan fazlasının yıkılması gerekebilir. Daha sonra kural getirilir: Cevaptaki sıfırlar, alınan rakam sayısından bir eksik olmalıdır.
- 12082: 863 örneğini kullanarak böyle bir bölümü düşünebilirsiniz.
- Eksik bölünebilen 1208 sayısıdır. 863 sayısı yalnızca bir kez yer alır. Bu nedenle cevaben 1 yazılması ve 1208'in altına 863 yazılması gerekiyor.
- Çıkarma işleminden sonra kalan 345'tir.
- Ona göre 2 numarayı yıkmanız gerekiyor.
- 3452 sayısının 4 katı 863'tür.
- Cevap olarak dört yazılmalıdır. Üstelik 4 ile çarpıldığında bu sayı elde edilir.
- Çıkarma işleminden sonra kalan sıfırdır. Yani bölme işlemi tamamlandı.
Örnekteki cevap 14'tür.
Ya temettü sıfırla biterse?
Yoksa birkaç sıfır mı? Bu durumda sıfır kalan elde edilir ve temettüde hala sıfırlar vardır. Umutsuzluğa kapılmayın, her şey göründüğünden daha kolaydır. Bölünmemiş kalan tüm sıfırları cevaba atfetmek yeterlidir.
Örneğin 400'ü 5'e bölmeniz gerekiyor. Eksik temettü 40'tır. Beş, 8 kez yerleştirilir. Yani cevabın 8 yazılması gerekiyor. Çıkarma işleminde kalan kalmıyor. Yani bölüşme bitti ama payda sıfır kaldı. Cevaba eklenmesi gerekecek. Böylece 400'ü 5'e bölersek 80 elde ederiz.

Peki ya bir ondalık sayıyı bölmeniz gerekiyorsa?
Bu sayı da tamsayı kısmını kesirli kısımdan ayıran virgül olmasa yine bir doğal sayıya benziyor. Bu, ondalık kesirlerin bir sütuna bölünmesinin yukarıda açıklanana benzer olduğunu göstermektedir.
Tek fark noktalı virgül olacaktır. Kesirli kısmın ilk rakamı alınır alınmaz hemen cevaplanması gerekiyor. Başka bir deyişle şu şekilde söylenebilir: Tamsayı bölümünün bölünmesi sona erdi - virgül koyun ve çözüme devam edin.
Ondalık kesirli bir sütuna bölme örneklerini çözerken, ondalık noktadan sonraki kısma herhangi bir sayıda sıfır atanabileceğini hatırlamanız gerekir. Bazen sayıları sonuna kadar tamamlamak için bu gereklidir.

İki ondalık sayının bölünmesi
Karmaşık görünebilir. Ama sadece başlangıçta. Sonuçta, bir kesir sütununda doğal bir sayıya göre bölmenin nasıl gerçekleştirileceği zaten açıktır. Dolayısıyla bu örneği zaten tanıdık olan forma indirgememiz gerekiyor.
Kolaylaştır. Her iki kesri de 10, 100, 1.000 veya 10.000 veya görev gerektiriyorsa belki bir milyonla çarpmanız gerekir. Çarpan, bölenin ondalık kısmında kaç sıfır olduğuna göre seçilmelidir. Yani sonuç olarak, bir kesri doğal sayıya bölmeniz gerekeceği ortaya çıkıyor.
Ve en kötü durumda olacak. Sonuçta, bu işlemden elde edilen temettünün bir tam sayı haline geldiği ortaya çıkabilir. Daha sonra örneğin bir kesir sütununa bölünmesiyle çözümü en basit seçeneğe indirgenecektir: doğal sayılarla işlemler.
Örnek olarak: 28,4 bölü 3,2:
- İlk olarak, 10 ile çarpılmalıdır, çünkü ikinci sayıda virgülden sonra yalnızca bir rakam vardır. Çarpmak 284 ve 32'yi verecektir.
- Bölünmeleri gerekiyor. Ve bir kerede tam sayı 284'e 32'dir.
- Cevapta eşleşen ilk sayı 8'dir. Bu sayının çarpılması 256'yı verir. Geriye kalan 28'dir.
- Tamsayı kısmının bölünmesi bitti ve cevaba virgül konulması gerekiyor.
- Kalan 0'a kadar yıkın.
- Tekrar 8'i al.
- Kalan: 24. Buna bir 0 daha ekleyin.
- Şimdi 7'yi almanız gerekiyor.
- Çarpma sonucu 224, kalan 16 olur.
- Bir 0 daha yıkın. 5 alın ve tam olarak 160 alın. Geri kalan 0.
Bölüm tamamlandı. 28.4:3.2 örneğinin sonucu 8.875'tir.
Ya bölen 10, 100, 0,1 veya 0,01 ise?

Çarpma işleminde olduğu gibi burada da uzun bölme işlemine gerek yoktur. Belirli sayıda basamak için virgülü doğru yönde hareket ettirmeniz yeterlidir. Üstelik bu prensibe göre hem tamsayılı hem de ondalık kesirli örnekleri çözebilirsiniz.
Yani 10, 100 veya 1000'e bölmeniz gerekiyorsa, bölendeki sıfır sayısı kadar virgül sola kaydırılır. Yani bir sayı 100'e bölünüyorsa virgül iki basamak sola kaydırılmalıdır. Bölünen doğal sayı ise sonunda virgül olduğu varsayılır.
Bu eylem, sayının 0,1, 0,01 veya 0,001 ile çarpılmasıyla aynı sonucu üretir. Bu örneklerde virgül de kesirli kısmın uzunluğuna eşit sayıda basamak kadar sola kaydırılır.
0,1'e (vb.) bölme veya 10 (vb.) ile çarpma sırasında virgül bir rakam (veya sıfır sayısına veya kesirli kısmın uzunluğuna bağlı olarak iki, üç) sağa doğru hareket etmelidir.
Kâr payında verilen rakam sayısının yeterli olmayabileceğini belirtmekte fayda var. Daha sonra eksik sıfırlar sola (tamsayı kısmında) veya sağa (ondalık noktadan sonra) atanabilir.

Periyodik kesirlerin bölünmesi
Bu durumda sütuna bölme işleminde kesin cevaba ulaşamazsınız. Noktalı bir kesirle karşılaşılırsa bir örnek nasıl çözülür? Burada sıradan kesirlere geçmek gerekiyor. Daha sonra daha önce çalışılan kurallara göre bölünmelerini gerçekleştirin.
Örneğin 0'ı (3) 0,6'ya bölmeniz gerekir. İlk fraksiyon periyodiktir. İndirgeme sonrasında 1/3 verecek olan 3/9 oranına dönüştürülür. İkinci kesir son ondalık sayıdır. Sıradan bir tane yazmak daha da kolaydır: 6/10, yani 3/5'e eşittir. Sıradan kesirleri bölme kuralı, bölmeyi çarpmayla ve böleni bir sayının tersiyle değiştirmeyi öngörür. Yani örnek 1/3'ü 5/3 ile çarpmaktan ibarettir. Cevap 5/9.
Örnekte farklı kesirler varsa...
O zaman birkaç olası çözüm var. Öncelikle sıradan bir kesri ondalık sayıya dönüştürmeyi deneyebilirsiniz. Daha sonra yukarıdaki algoritmaya göre zaten iki ondalık sayıyı bölün.
İkinci olarak, her son ondalık kesir ortak bir kesir olarak yazılabilir. Her zaman uygun değil. Çoğu zaman, bu tür kesirler çok büyük olur. Evet ve cevaplar hantal. Bu nedenle ilk yaklaşımın daha çok tercih edildiği düşünülmektedir.
Bu açıdan ondalık sayıları bölme örneklerini düşünün.
Örnek.
Ondalık sayıyı 1,2'yi ondalık sayıyı 0,48'e bölün.
Çözüm.
Cevap:
1,2:0,48=2,5 .
Örnek.
Periyodik ondalık sayıyı 0.(504) ondalık sayı 0,56'ya bölün.
Çözüm.
Periyodik ondalık kesri sıradan bir sayıya çevirelim:. Ayrıca son ondalık kesir olan 0,56'yı sıradan bir kesre çeviriyoruz, 0,56 \u003d 56/100 elde ediyoruz. Artık orijinal ondalık sayıları bölmekten sıradan kesirleri bölmeye geçebilir ve hesaplamaları tamamlayabiliriz: .
Ortaya çıkan sıradan kesri, bir sütundaki payı paydaya bölerek ondalık kesire çevirelim:
Cevap:
0,(504):0,56=0,(900) .
Sonsuz periyodik olmayan ondalık kesirleri bölme ilkesi tekrarlanmayan ondalık kesirler sıradan kesirlere dönüştürülemediği için sonlu ve periyodik ondalık kesirleri bölme ilkesinden farklıdır. Sonsuz periyodik olmayan ondalık kesirlerin bölünmesi, gerçekleştirildiği sonlu ondalık kesirlerin bölünmesine indirgenir. sayıları yuvarlama belli bir seviyeye kadar. Ayrıca, bölmenin yapıldığı sayılardan biri sonlu veya periyodik bir ondalık kesir ise, o zaman periyodik olmayan ondalık kesirle aynı rakama yuvarlanır.
Örnek.
Sonsuz, yinelenmeyen ondalık sayıyı 0,779... son ondalık sayı olan 1,5602'ye bölün.
Çözüm.
Öncelikle, sonsuz, tekrarlanmayan bir ondalık kesiri bölmekten sonlu ondalık kesirleri bölmeye geçmek için ondalık kesirleri yuvarlamanız gerekir. Yüzde birlere yuvarlayabiliriz: 0,779…≈0,78 ve 1,5602≈1,56. Böylece, 0,779…:1,5602≈0,78:1,56= 78/100:156/100=78/100 100/156= 78/156=1/2=0,5 .
Cevap:
0,779…:1,5602≈0,5 .
Doğal bir sayıyı ondalık kesre bölmek (ve bunun tersi)
Bir doğal sayıyı ondalık kesre bölme ve ondalık kesri bir doğal sayıya bölme yaklaşımının özü, ondalık kesirleri bölmenin özünden farklı değildir. Yani, sonlu ve periyodik kesirler sıradan kesirler ile değiştirilir ve sonsuz periyodik olmayan kesirler yuvarlanır.
Örneklemek için, ondalık bir kesirin doğal bir sayıya bölünmesi örneğini düşünün.
Örnek.
Ondalık kesir 25,5'i doğal sayı 45'e bölün.
Çözüm.
25,5 ondalık kesirini sıradan bir kesir olan 255/10=51/2 ile değiştirirsek, bölme işlemi sıradan bir kesri bir doğal sayıya bölmeye indirgenir: . Ondalık gösterimde elde edilen kesir 0,5(6)'dır.
Cevap:
25,5:45=0,5(6) .
Ondalık kesrin bir doğal sayıya bir sütunla bölünmesi
Son ondalık kesirlerin doğal sayılara bölünmesi, doğal sayılar sütununa bölme işlemine benzetilerek uygun bir şekilde bir sütunla gerçekleştirilir. İşte bölme kuralı.
İle bir ondalık sayıyı bir doğal sayıya bir sütuna bölmek, gerekli:
- 0'ın bölünebilir ondalık kesirinde sağa birkaç rakam ekleyin (bölme sırasında gerekirse istediğiniz sayıda sıfır ekleyebilirsiniz, ancak bu sıfırlara gerek olmayabilir);
- doğal sayılar sütununa bölmek için tüm kurallara göre ondalık kesirin bir sütununu doğal bir sayıya göre bölmeyi gerçekleştirin, ancak ondalık kesrin tam sayı kısmının bölünmesi tamamlandığında, o zaman özelde yapmanız gerekir virgül koyup bölmeye devam edin.
Hemen söyleyelim ki, sonlu bir ondalık kesirin bir doğal sayıya bölünmesi sonucunda ya son bir ondalık kesir ya da sonsuz bir periyodik ondalık kesir elde edilebilir. Aslında, bölünebilir kesirin 0 dışındaki tüm ondalık basamaklarını böldükten sonra, ya 0 kalanını alabiliriz ve son bir ondalık kesir elde ederiz, ya da geri kalan periyodik olarak tekrarlanmaya başlar ve periyodik bir ondalık sayı elde ederiz. kesir.
Örnekleri çözerken ondalık kesirleri doğal sayılara bir sütunla bölmenin tüm inceliklerini ele alalım.
Örnek.
Ondalık sayıyı 65,14'ü 4'e bölün.
Çözüm.
Ondalık kesrin bir doğal sayıya bir sütunla bölünmesini gerçekleştirelim. 65.14 kesirinin kaydında sağa bir çift sıfır ekleyelim, bu arada 65.1400'e eşit ondalık kesir elde edelim (bkz. eşit ve eşit olmayan ondalık kesirler). Artık 65.1400 ondalık kesirinin tam sayı kısmını bir doğal sayı olan 4'e bir sütunla bölmeye başlayabilirsiniz: 
Bu, ondalık kesrin tam sayı kısmının bölünmesini tamamlar. Burada özel olarak bir ondalık nokta koymanız ve bölmeye devam etmeniz gerekir: 
0 kalanına geldik, bu aşamada sütuna bölme işlemi sona eriyor. Sonuç olarak 65.14:4=16.285 elde ederiz.
Cevap:
65,14:4=16,285 .
Örnek.
164,5'i 27'ye bölün.
Çözüm.
Ondalık kesri bir doğal sayıya bir sütunla bölelim. Tam sayı kısmını böldükten sonra aşağıdaki resmi elde ederiz: 
Şimdi özele virgül koyup bölmeye bir sütunla devam ediyoruz: 
Artık bölümde 9, 2 ve 5 rakamlarının tekrarlandığı, 25, 7 ve 16 rakamlarının da tekrarlanmaya başladığı açıkça görülüyor. Yani 164,5'i 27'ye bölmek bize periyodik ondalık sayıyı 6,0(925) verir.
Cevap:
164,5:27=6,0(925) .
Ondalık kesirlerin bir sütuna bölünmesi
Ondalık kesirin ondalık kesirle bölünmesi, ondalık kesirin bir doğal sayıya bir sütunla bölünmesine indirgenebilir. Bunu yapmak için, bölenin doğal bir sayı haline gelmesi için, bölünen ve bölenin 10, 100 veya 1000 vb. bir sayı ile çarpılması ve ardından bir doğal sayıya bir sütunla bölünmesi gerekir. Bunu bölme ve çarpma özelliklerinden dolayı yapabiliriz, çünkü a:b=(a 10):(b 10) , a:b=(a 100):(b 100) vb.
Başka bir deyişle, son ondalık sayıyı son ondalık sayıya bölmek, şunları yapmanız gerekir:
- bölen ve bölende, virgülü bölendeki ondalık noktadan sonraki karakter sayısı kadar sağa hareket ettirin, eğer aynı zamanda payda virgülü hareket ettirmek için yeterli karakter yoksa, o zaman eklemeniz gerekir sağa doğru gerekli sayıda sıfır;
- bundan sonra, ondalık kesrin bir sütunu ile doğal bir sayıya bölme işlemini gerçekleştirin.
Bir örneği çözerken, bu kuralın ondalık kesirlere bölmek için uygulanmasını düşünün.
Örnek.
7.287 sütununu 2.1'e bölün.
Çözüm.
Bu ondalık kesirlerde virgülü bir basamak sağa kaydıralım; bu, ondalık kesir 7,287'yi ondalık kesir 2,1'e bölmekten, ondalık kesir 72,87'yi doğal sayı 21'e bölmemize olanak tanır. Bir sütuna bölelim: 
Cevap:
7,287:2,1=3,47 .
Örnek.
Ondalık sayıyı 16,3'ü ondalık sayı 0,021'e bölün.
Çözüm.
Bölen ve bölendeki virgülü 3 basamak sağa taşıyın. Açıkçası, bölende virgülün taşınması için yeterli rakam yok, bu yüzden gerekli sayıda sıfırı sağa ekleyelim. Şimdi 16300.0 kesirinin sütununu 21 doğal sayısına bölelim: 
Bu andan itibaren 4, 19, 1, 10, 16 ve 13 numaralı kalanlar tekrar etmeye başlar, bu da bölümdeki 1, 9, 0, 4, 7 ve 6 rakamlarının da tekrarlanacağı anlamına gelir. Sonuç olarak, periyodik bir ondalık kesir 776,(190476) elde ederiz.
Cevap:
16,3:0,021=776,(190476) .
Sesli kuralın, doğal bir sayıyı son ondalık kesirle bir sütuna bölmenize izin verdiğini unutmayın.
Örnek.
Doğal sayı 3'ü ondalık kesir 5.4'e bölün.
Çözüm.
Virgül 1 hanesini sağa kaydırdıktan sonra 30,0 sayısını 54'e bölmeye geliyoruz. Bir sütuna bölelim:  .
.
Bu kural sonsuz ondalık kesirleri 10, 100, ...'e bölerken de uygulanabilir. Örneğin, 3,(56):1000=0,003(56) ve 593,374…:100=5,93374… .
Ondalık sayıları 0,1, 0,01, 0,001 vb.'ye bölme.
0,1 \u003d 1/10, 0,01 \u003d 1/100 vb. olduğundan, ondalık kesirin 0,1, 0,01, 0,001 vb. ile bölünmesi sıradan bir kesirle bölme kuralından kaynaklanır. verilen ondalık sayıyı 10 , 100 , 1000 vb. ile çarpmak gibidir. sırasıyla.
Başka bir deyişle, ondalık kesri 0,1, 0,01, ...'e bölmek için virgülü 1, 2, 3, ... basamak sağa kaydırmanız gerekir ve ondalık kesirde yeterli basamak yoksa virgülü hareket ettirin, ardından gerekli sayıyı sağdaki sıfırlara eklemeniz gerekir.
Örneğin, 5,739:0,1=57,39 ve 0,21:0,00001=21,000 .
Sonsuz ondalık sayıları 0,1, 0,01, 0,001 vb.'ye bölerken de aynı kural uygulanabilir. Bu durumda, bölme sonucu elde edilen kesrin periyoduyla karıştırılmamak için periyodik kesirlerin bölünmesine çok dikkat etmelisiniz. Örneğin, 7.5(716):0.01=757,(167) , çünkü ondalık kesir kaydındaki virgülün taşınmasından sonra 7.5716716716 ... iki basamak sağa doğru 757.167167 ... kaydına sahibiz. Sonsuz periyodik olmayan ondalık sayılarla her şey daha basittir: 394,38283…:0,001=394382,83… .
Bir kesri veya karışık sayıyı ondalık sayıya bölmek veya tam tersi
Sıradan bir kesirin veya karışık bir sayının sonlu veya periyodik bir ondalık kesir ile bölünmesinin yanı sıra sonlu veya periyodik bir ondalık kesirin sıradan bir kesir veya karışık bir sayı ile bölünmesi, sıradan kesirlerin bölünmesine indirgenir. Bunu yapmak için, ondalık kesirlerin yerini karşılık gelen sıradan kesirler alır ve karışık sayı, uygunsuz bir kesir olarak temsil edilir.
Sonsuz periyodik olmayan bir ondalık kesiri sıradan bir kesirle veya karışık bir sayıyla bölerken ve bunun tersi durumda, normal kesir veya karışık sayıyı karşılık gelen ondalık kesirle değiştirerek ondalık kesirleri bölmeye devam edilmelidir.
Kaynakça.
- Matematik: çalışmalar. 5 hücre için. Genel Eğitim kurumlar / N. Ya.Vilenkin, V. I. Zhokhov, A. S. Chesnokov, S. I. Shvartsburd. - 21. baskı, silindi. - M.: Mnemosyne, 2007. - 280 s.: hasta. ISBN 5-346-00699-0.
- Matematik. 6. Sınıf: ders kitabı. genel eğitim için kurumlar / [N. Ya Vilenkin ve diğerleri]. - 22. baskı, Rev. - M.: Mnemosyne, 2008. - 288 s.: hasta. ISBN 978-5-346-00897-2.
- Cebir: ders kitabı 8 hücre için. Genel Eğitim kurumlar / [Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova]; ed. S. A. Telyakovsky. - 16. baskı. - M. : Eğitim, 2008. - 271 s. : hasta. - ISBN 978-5-09-019243-9.
- Gusev V.A., Mordkovich A.G. Matematik (teknik okullara başvuran adaylar için bir kılavuz): Proc. ödenek.- M.; Daha yüksek okul, 1984.-351 s., hasta.
Son derste ondalık kesirlerin nasıl toplanıp çıkarılacağını öğrendik (" Ondalık kesirlerin eklenmesi ve çıkarılması" dersine bakın). Aynı zamanda, hesaplamaların olağan "iki katlı" kesirlere kıyasla ne kadar basitleştirildiğini de tahmin ettiler.
Ne yazık ki ondalık kesirlerin çarpılması ve bölünmesi sırasında bu etki oluşmaz. Bazı durumlarda ondalık gösterim bu işlemleri bile karmaşık hale getirir.
Öncelikle yeni bir tanım verelim. Onunla sadece bu derste değil, sık sık buluşacağız.
Bir sayının önemli kısmı, römorklar da dahil olmak üzere sıfırdan farklı ilk ve son rakam arasındaki her şeydir. Sadece rakamlardan bahsediyoruz, virgül dikkate alınmıyor.
Sayının anlamlı kısmında yer alan rakamlara anlamlı rakamlar denir. Tekrarlanabilirler ve hatta sıfıra eşit olabilirler.
Örneğin, birkaç ondalık kesri düşünün ve bunlara karşılık gelen önemli kısımları yazın:
- 91,25 → 9125 (önemli rakamlar: 9; 1; 2; 5);
- 0,008241 → 8241 (önemli rakamlar: 8; 2; 4; 1);
- 15,0075 → 150075 (önemli rakamlar: 1; 5; 0; 0; 7; 5);
- 0,0304 → 304 (anlamlı rakamlar: 3; 0; 4);
- 3000 → 3 (yalnızca tek bir anlamlı rakam vardır: 3).
Lütfen dikkat: sayının önemli kısmının içindeki sıfırlar hiçbir yere gitmez. Ondalık kesirleri sıradan kesirlere dönüştürmeyi öğrendiğimizde zaten benzer bir şeyle karşılaştık (“Ondalık Kesirler” dersine bakın).
Bu nokta o kadar önemli ve burada o kadar sık hata yapılıyor ki yakın gelecekte bu konuyla ilgili bir test yayınlayacağım. Mutlaka pratik yapın! Ve biz, önemli bir kısım kavramıyla donanmış olarak, aslında dersin konusuna geçeceğiz.
Ondalık çarpma
Çarpma işlemi ardışık üç adımdan oluşur:
- Her kesir için önemli kısmı yazın. Herhangi bir payda ve ondalık nokta olmadan iki sıradan tamsayı elde edeceksiniz;
- Bu sayıları uygun bir şekilde çarpın. Sayılar küçükse veya bir sütun halindeyse doğrudan. İstenilen fraksiyonun önemli bir kısmını alıyoruz;
- İlgili anlamlı kısmı elde etmek için orijinal kesirlerde virgülün nereye ve kaç basamak kaydırıldığını öğrenin. Önceki adımda elde edilen önemli parça üzerinde ters kaydırmalar yapın.
Önemli kısmın kenarlarındaki sıfırların asla dikkate alınmadığını bir kez daha hatırlatayım. Bu kuralın göz ardı edilmesi hatalara yol açar.
- 0,28 12,5;
- 6,3 1,08;
- 132,5 0,0034;
- 0,0108 1600,5;
- 5,25 10.000.
İlk ifadeyle çalışıyoruz: 0,28 12,5.
- Bu ifadedeki sayıların anlamlı kısımlarını yazalım: 28 ve 125;
- Çarpımları: 28 125 = 3500;
- İlk çarpanda, ondalık nokta 2 basamak sağa (0,28 → 28) ve ikincisinde ise 1 basamak daha kaydırılır. Toplamda üç haneli sola kaymaya ihtiyaç var: 3500 → 3,500 = 3,5.
Şimdi 6.3 1.08 ifadesiyle ilgilenelim.
- Önemli kısımları yazalım: 63 ve 108;
- Çarpımları: 63 108 = 6804;
- Yine sağa iki kayma: sırasıyla 2 ve 1 basamak. Toplamda - yine sağa 3 hane, yani ters kaydırma 3 hane sola olacaktır: 6804 → 6,804. Bu sefer sonunda sıfır yok.
Üçüncü ifadeye ulaştık: 132,5 0,0034.
- Önemli parçalar: 1325 ve 34;
- Çarpımları: 1325 34 = 45.050;
- İlk kesirde, ondalık nokta 1 basamak sağa, ikincisinde ise 4'e kadar gider. Toplam: 5 sağa. Sola 5 kaydırma yapıyoruz: 45050 → .45050 = 0,4505. Sıfır sondan çıkarıldı ve “çıplak” bir ondalık nokta bırakmayacak şekilde öne eklendi.
Aşağıdaki ifade: 0,0108 1600,5.
- Önemli kısımları yazıyoruz: 108 ve 16 005;
- Bunları çarpıyoruz: 108 16 005 = 1 728 540;
- Ondalık noktadan sonraki sayıları sayıyoruz: ilk sayıda 4, ikincisinde - 1. Toplamda - yine 5. Elimizde: 1.728.540 → 17.28540 = 17.2854. Sonunda “ekstra” sıfır kaldırıldı.
Son olarak son ifade: 5,25 10.000.
- Önemli parçalar: 525 ve 1;
- Bunları çarpıyoruz: 525 1 = 525;
- İlk kesir 2 basamak sağa, ikinci kesir ise 4 basamak sola kaydırılır (10.000 → 1.0000 = 1). Toplam 4 − 2 = sola doğru 2 basamak. Sağa 2 basamak ters kaydırma yapıyoruz: 525, → 52 500 (sıfır eklemek zorunda kaldık).
Son örneğe dikkat edin: virgül farklı yönlerde hareket ettiğinden toplam kayma fark üzerinden olur. Bu çok önemli bir konu! İşte başka bir örnek:
1,5 ve 12.500 sayılarını ele alalım: 1,5 → 15 (sağa 1 kaydırma); 12 500 → 125 (2'yi sola kaydırın). 1 hane sağa, ardından 2 hane sola “adım atıyoruz”. Sonuç olarak 2 − 1 = 1 basamak sola adım attık.
Ondalık bölme
Bölünme belki de en zor operasyondur. Elbette burada çarpma işlemine benzeterek hareket edebilirsiniz: önemli kısımları bölün ve ardından ondalık noktayı "hareket ettirin". Ancak bu durumda potansiyel tasarrufları boşa çıkaran pek çok incelik var.
Şimdi biraz daha uzun ama çok daha güvenilir olan genel bir algoritmaya bakalım:
- Tüm ondalık sayıları ortak kesirlere dönüştürün. Biraz pratik yaparsanız bu adım birkaç saniyenizi alacaktır;
- Ortaya çıkan kesirleri klasik şekilde bölün. Başka bir deyişle, ilk kesiri "tersine çevrilmiş" ikinciyle çarpın (" Sayısal kesirlerin çarpması ve bölünmesi" dersine bakın);
- Mümkünse sonucu ondalık sayı olarak döndürün. Bu adım aynı zamanda hızlıdır çünkü çoğu zaman paydanın zaten onluk bir kuvveti vardır.
Görev. İfadenin değerini bulun:
- 3,51: 3,9;
- 1,47: 2,1;
- 6,4: 25,6:
- 0,0425: 2,5;
- 0,25: 0,002.
İlk ifadeyi ele alıyoruz. Öncelikle obi kesirlerini ondalık sayılara dönüştürelim:
Aynısını ikinci ifadeyle de yapıyoruz. İlk kesrin payı yine faktörlere ayrıştırılır:

Üçüncü ve dördüncü örneklerde önemli bir nokta var: ondalık gösterimden kurtulduktan sonra iptal edilebilir kesirler ortaya çıkıyor. Ancak bu indirimi yapmayacağız.

Son örnek ilginçtir çünkü ikinci kesrin payı asal bir sayıdır. Burada çarpanlara ayıracak hiçbir şey yok, bu yüzden bunu "boş" olarak değerlendiriyoruz:

Bazen bölme işlemi tam sayıyla sonuçlanır (son örnekten bahsediyorum). Bu durumda üçüncü adım hiç gerçekleştirilmez.
Ek olarak, bölerken genellikle ondalık sayılara dönüştürülemeyen "çirkin" kesirler ortaya çıkar. Bölmenin çarpmadan farklı olduğu nokta burasıdır; burada sonuçlar her zaman ondalık biçimde ifade edilir. Elbette bu durumda son adım yine gerçekleştirilmez.
3. ve 4. örneklere de dikkat edin. Ondalık sayılardan elde edilen sıradan kesirleri bilinçli olarak azaltmıyoruz. Aksi takdirde, son cevabı tekrar ondalık biçimde temsil eden ters problemi karmaşıklaştıracaktır.
Unutmayın: Bir kesrin temel özelliği (matematiğin diğer kuralları gibi) kendi başına onun her yerde, her zaman, her fırsatta uygulanması gerektiği anlamına gelmez.
