معادلة المماس للرسم البياني للدالة

رومانوف ، ت.رومانوفا ،
ماغنيتوغورسك ،
منطقة تشيليابينسك

معادلة المماس للرسم البياني للدالة

نُشر المقال بدعم من ITAKA + Hotel Complex. البقاء في مدينة بناة السفن سيفيرودفينسك ، لن تواجه مشكلة العثور على سكن مؤقت. ، على الموقع الإلكتروني للمجمع الفندقي "ITAKA +" http://itakaplus.ru ، يمكنك بسهولة وبسرعة استئجار شقة في المدينة ، لأي فترة ، مع الدفع اليومي.

على المرحلة الحاليةتطوير التعليم كأحد مهامه الرئيسية هو تكوين شخصية تفكير إبداعي. لا يمكن تطوير القدرة على الإبداع لدى الطلاب إلا إذا شاركوا بشكل منهجي في أساسيات الأنشطة البحثية. يتم تشكيل المعرفة والمهارات الكاملة للطلاب لاستخدام قواهم الإبداعية وقدراتهم ومواهبهم. في هذا الصدد ، فإن مشكلة تكوين نظام للمعرفة والمهارات الأساسية لكل موضوع من مقرر الرياضيات المدرسية ليست ذات أهمية كبيرة. في الوقت نفسه ، يجب أن تكون المهارات الكاملة الهدف التعليمي ليس للمهام الفردية ، ولكن لنظامهم المدروس بعناية. بالمعنى الأوسع ، يُفهم النظام على أنه مجموعة من العناصر المتفاعلة المترابطة التي تتمتع بالسلامة والبنية المستقرة.

ضع في اعتبارك منهجية لتعليم الطلاب كيفية رسم معادلة ظل الرسم البياني للوظيفة. من حيث الجوهر ، يتم تقليل جميع المهام الخاصة بإيجاد معادلة الظل إلى الحاجة إلى الاختيار من مجموعة (حزمة ، عائلة) من الخطوط التي تفي بمتطلبات معينة - فهي مماسة للرسم البياني لوظيفة معينة. في هذه الحالة ، يمكن تحديد مجموعة السطور التي يتم الاختيار منها بطريقتين:

أ) نقطة ملقاة على مستوى xOy (قلم رصاص مركزي للخطوط) ؛
ب) معامل الزاوي (حزمة متوازية من الخطوط).

في هذا الصدد ، عند دراسة موضوع "الظل للرسم البياني للدالة" من أجل عزل عناصر النظام ، حددنا نوعين من المهام:

1) المهام على الظل المعطاة من النقطة التي يمر من خلالها ؛
2) المهام على الظل المعطاة من خلال ميلها.

تم تنفيذ تعلم حل المشكلات على الظل باستخدام الخوارزمية التي اقترحها A.G. مردكوفيتش. اختلافها الأساسي عن تلك المعروفة بالفعل هو أن الحد الأقصى لنقطة الظل يُشار إليه بالحرف أ (بدلاً من x0) ، فيما يتعلق بمعادلة الظل التي تأخذ الشكل

ص \ u003d و (أ) + و "(أ) (س - أ)

(قارن مع y \ u003d f (x 0) + f "(x 0) (x - x 0)). تسمح هذه التقنية المنهجية ، في رأينا ، للطلاب بإدراك مكان كتابة إحداثيات النقطة الحالية بسرعة وسهولة في معادلة الظل العامة ، وأين توجد نقاط الاتصال.

خوارزمية لتجميع معادلة الظل للرسم البياني للدالة y = f (x)

1. عيّن بالحرف حدودًا لنقطة الاتصال.
2. أوجد f (a).
3. أوجد f "(x) و f" (a).
4. استبدل الأرقام التي تم العثور عليها a ، f (a) ، f "(a) في المعادلة العامة للماس y \ u003d f (a) \ u003d f" (a) (x - a).

يمكن تجميع هذه الخوارزمية على أساس اختيار الطلاب المستقل للعمليات وتسلسل تنفيذها.

أظهرت الممارسة أن الحل المتسق لكل مهمة من المهام الأساسية باستخدام الخوارزمية يسمح لك بتكوين القدرة على كتابة معادلة الظل إلى الرسم البياني للوظيفة على مراحل ، وأن خطوات الخوارزمية تعمل كنقاط قوية للإجراءات . يتوافق هذا النهج مع نظرية التكوين التدريجي للأفعال العقلية التي طورها P.Ya. جالبرين ون. Talyzina.

في النوع الأول من المهام ، تم تحديد مهمتين رئيسيتين:

• المماس يمر عبر نقطة تقع على المنحنى (المشكلة 1) ؛
• الظل يمر عبر نقطة لا تقع على المنحنى (المشكلة 2).

المهمة 1. مساواة الظل بالرسم البياني للوظيفة عند النقطة م (3 ؛ - 2).

حل. النقطة M (3 ؛ - 2) هي نقطة الاتصال ، منذ ذلك الحين

1. a = 3 - حدود نقطة اللمس.
2. و (3) = - 2.
3. f "(x) \ u003d x 2-4، f" (3) \ u003d 5.
y \ u003d - 2 + 5 (x - 3) ، y \ u003d 5x - 17 هي معادلة الظل.

المهمة 2. اكتب معادلات جميع المماسات على الرسم البياني للدالة y = - x 2 - 4x + 2 ، مروراً بالنقطة M (- 3 ؛ 6).

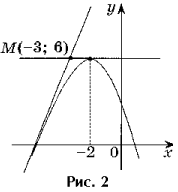حل. النقطة M (- 3 ؛ 6) ليست نقطة الظل ، حيث أن f (- 3) 6 (الشكل 2).

2. و (أ) = - أ 2 - 4 أ + 2.
3. f "(x) \ u003d - 2x - 4، f" (a) \ u003d - 2a - 4.
4. y \ u003d - a 2-4a + 2-2 (a + 2) (x - a) - معادلة الظل.

المماس يمر عبر النقطة M (- 3 ؛ 6) ، لذلك فإن إحداثياته ​​تفي بمعادلة الظل.

6 = - أ 2 - 4 أ + 2 - 2 (أ + 2) (- 3 - أ) ،
أ 2 + 6 أ + 8 = 0^ أ 1 = - 4 ، 2 = - 2.

إذا كانت a = - 4 ، فإن معادلة الظل هي y = 4x + 18.

إذا كانت a \ u003d - 2 ، فإن معادلة الظل لها الشكل y \ u003d 6.

في النوع الثاني تكون المهام الرئيسية كما يلي:

• الظل يوازي بعض الخطوط المستقيمة (المشكلة 3) ؛
• المماس يمر بزاوية ما للخط المعطى (المشكلة 4).

المهمة 3. اكتب معادلات جميع الظلال على الرسم البياني للوظيفة y \ u003d x 3 - 3x 2 + 3 ، بالتوازي مع الخط y \ u003d 9x + 1.

حل.

1. أ - حدود نقطة اللمس.
2. و (أ) = أ 3 - 3 أ 2 + 3.
3. f "(x) \ u003d 3x 2-6x، f" (a) \ u003d 3a 2 - 6a.

لكن ، من ناحية أخرى ، f "(a) \ u003d 9 (حالة التوازي). لذلك ، نحتاج إلى حل المعادلة 3a 2 - 6a \ u003d 9. جذورها a \ u003d - 1 ، a \ u003d 3 (الشكل . 3).

4. 1) أ = - 1 ؛
2) و (- 1) = - 1 ؛
3) و "(- 1) = 9 ؛
4) ص = - 1 + 9 (س + 1) ؛

y = 9x + 8 هي معادلة الظل ؛

1) أ = 3 ؛
2) و (3) = 3 ؛
3) و "(3) = 9 ؛
4) ص = 3 + 9 (س - 3) ؛

y = 9x - 24 هي معادلة الظل.

المهمة 4. اكتب معادلة المماس للرسم البياني للدالة y = 0.5x 2 - 3x + 1 ، مروراً بزاوية 45 درجة للخط المستقيم y = 0 (الشكل 4).

حل. من الشرط f "(a) \ u003d tg 45 ° نجد: a - 3 \ u003d 1^ أ = 4.

1. a = 4 - حدود نقطة اللمس.
2. و (4) = 8-12 + 1 = - 3.
3. f "(4) \ u003d 4 - 3 \ u003d 1.
4. ص \ u003d - 3 + 1 (س - 4).

ص \ u003d س - 7 - معادلة الظل.

من السهل إظهار أن حل أي مشكلة أخرى يقتصر على حل مشكلة رئيسية واحدة أو عدة مشاكل رئيسية. ضع في اعتبارك المشكلتين التاليتين كمثال.

1. اكتب معادلات المماس للقطع المكافئ y = 2x 2 - 5x - 2 ، إذا تقاطعت المماسات بزاوية قائمة وكان أحدها يلمس القطع المكافئ عند النقطة مع الإحداثيات 3 (الشكل 5).

حل. نظرًا لإعطاء الإحداثي السيني لنقطة الاتصال ، يتم تقليل الجزء الأول من الحل إلى المشكلة الرئيسية 1.

1. a \ u003d 3 - حدود نقطة التلامس لأحد جانبي الزاوية اليمنى.
2. و (3) = 1.
3. f "(x) \ u003d 4x - 5، f" (3) \ u003d 7.
4. y \ u003d 1 + 7 (x - 3) ، y \ u003d 7x - 20 - معادلة الظل الأول.

دع أ هي زاوية ميل الظل الأول. بما أن المماس متعامد ، إذن هي زاوية ميل الظل الثاني. من المعادلة y = 7x - 20 من الظل الأول لدينا tgأ = 7. بحث

هذا يعني أن ميل المماس الثاني هو.

يتم تقليل الحل الإضافي إلى المهمة الرئيسية 3.

دع B (c ؛ f (c)) هي نقطة الظل للخط الثاني ، إذن

1. - حدود نقطة الاتصال الثانية.
2.
3.
4.
هي معادلة الظل الثاني.

ملحوظة. يمكن إيجاد المعامل الزاوي للماس أسهل إذا عرف الطلاب نسبة معاملات الخطوط العمودية k 1 k 2 = - 1.

2. اكتب معادلات جميع المماسات الشائعة للرسوم البيانية للوظيفة

حل. يتم تقليل المهمة إلى إيجاد حدود نقاط التلامس للظل المشترك ، أي حل المشكلة الرئيسية 1 بشكل عام ، وتجميع نظام المعادلات ثم حلها (الشكل 6).

1. لنفترض أن a هو حدود نقطة اللمس الواقعة على الرسم البياني للدالة y = x 2 + x + 1.
2. و (أ) = أ 2 + أ + 1.
3. f "(أ) = 2 أ + 1.
4. y \ u003d a 2 + a + 1 + (2a + 1) (x - a) \ u003d (2a + 1) x + 1 - a 2.

1. لنفترض أن c هي حدود نقطة الظل الموجودة على الرسم البياني للوظيفة
2.
3. f "(c) = c.
4.

بما أن الظلال شائعة ، إذن

إذن ، y = x + 1 و y = - 3x - 3 هي مماسات شائعة.

الهدف الرئيسي من المهام التي يتم النظر فيها هو إعداد الطلاب للاعتراف الذاتي بنوع المهمة الرئيسية عند حل المهام الأكثر تعقيدًا التي تتطلب مهارات بحثية معينة (القدرة على التحليل والمقارنة والتعميم وطرح فرضية ، وما إلى ذلك). تتضمن هذه المهام أي مهمة يتم تضمين المهمة الرئيسية فيها كمكون. دعونا نعتبر كمثال مشكلة (معكوس المشكلة 1) لإيجاد دالة من عائلة ظلها.

3. ما هو b و c الخطوط y \ u003d x و y \ u003d - 2x مماس للرسم البياني للوظيفة y \ u003d x 2 + bx + c؟

حل.

لنفترض أن t هي الحد الفاصل لنقطة اتصال الخط y = x مع القطع المكافئ y = x 2 + bx + c ؛ p هي حدود نقطة التلامس للخط y = - 2x مع القطع المكافئ y = x 2 + bx + c. بعد ذلك ، ستأخذ معادلة الظل y = x الصيغة y = (2t + b) x + c - t 2 ، وستأخذ معادلة الظل y = - 2x الصيغة y = (2p + b) x + c - p 2 .

يؤلف ويحل نظام المعادلات

إجابة:

مهام الحل المستقل

1. اكتب معادلات المماس المرسومة على الرسم البياني للدالة y = 2x 2 - 4x + 3 عند نقاط تقاطع الرسم البياني مع الخط y = x + 3.

الجواب: y \ u003d - 4x + 3، y \ u003d 6x - 9.5.

2. ما هي قيم المماس المرسوم على الرسم البياني للوظيفة y \ u003d x 2 - الفأس عند نقطة الرسم البياني مع الحد الفاصل x 0 \ u003d 1 يمر عبر النقطة M (2 ؛ 3) ؟

الجواب: أ = 0.5.

3. ما هي قيم p التي يلمسها الخط y = px - 5 المنحنى y = 3x 2 - 4x - 2؟

الجواب: ص 1 \ u003d - 10 ، ص 2 \ u003d 2.

4. أوجد جميع النقاط المشتركة في الرسم البياني للدالة y = 3x - x 3 والماس المرسوم على هذا الرسم البياني من خلال النقطة P (0 ؛ 16).

الجواب: أ (2 ؛ - 2) ، ب (- 4 ؛ 52).

5. أوجد أقصر مسافة بين القطع المكافئ y = x 2 + 6x + 10 والخط

إجابة:

6. على المنحنى y \ u003d x 2 - x + 1 ، أوجد النقطة التي يكون عندها ظل الرسم البياني موازيًا للخط y - 3x + 1 \ u003d 0.

الجواب: م (2 ؛ 3).

7. اكتب معادلة المماس للرسم البياني للدالة y = x 2 + 2x - | 4x | التي تلامسها عند نقطتين. جعل الرسم.

الجواب: ص = 2 س - 4.

8. أثبت أن الخط y = 2x - 1 لا يتقاطع مع المنحنى y = x 4 + 3x 2 + 2x. أوجد المسافة بين أقرب نقاطهم.

إجابة:

9. على القطع المكافئ y \ u003d x 2 ، يتم أخذ نقطتين مع abscissas x 1 \ u003d 1 ، x 2 \ u003d 3. يتم رسم قاطع من خلال هذه النقاط. في أي نقطة من القطع المكافئ سيكون مماسها موازٍ للقطع المرسوم؟ اكتب معادلات القاطع والظل.

الجواب: ص \ u003d 4x - 3 - معادلة قاطعة ؛ y = 4x - 4 هي معادلة الظل.

10. أوجد الزاوية q بين مماسات الرسم البياني للوظيفة y \ u003d x 3 - 4x 2 + 3x + 1 ، مرسومة عند نقاط مع abscissas 0 و 1.

الجواب: q = 45 درجة.

11. في أي نقطة يكون مماس الرسم البياني للوظيفة زاوية مقدارها 135 درجة مع محور الثور؟

الجواب: أ (0 ؛ - 1) ، ب (4 ؛ 3).

12. عند النقطة أ (1 ؛ 8) إلى المنحنى يتم رسم الظل. أوجد طول الجزء المماس المحصور بين محوري الإحداثيات.

إجابة:

13. اكتب معادلة جميع الظلال الشائعة للرسوم البيانية للوظائف y \ u003d x 2 - x + 1 و y \ u003d 2x 2 - x + 0.5.

الجواب: ص = - 3 س وص = س.

14. أوجد المسافة بين مماسات الرسم البياني للوظيفة الموازية للمحور x.

إجابة:

15. حدد الزوايا التي يقطعها القطع المكافئ y \ u003d x 2 + 2x - 8 مع المحور x.

الجواب: q 1 \ u003d arctan 6 ، q 2 \ u003d arctan (- 6).

16. على الرسم البياني للدالة أوجد جميع النقاط ، حيث يتقاطع المماس عند كل منها مع هذا الرسم البياني مع أنصاف المحاور الموجبة للإحداثيات ، مما يؤدي إلى قطع أجزاء متساوية منها.

الجواب: أ (-3 ؛ 11).

17. يتقاطع الخط y = 2x + 7 والقطع المكافئ y = x 2-1 عند النقطتين M و N. أوجد نقطة التقاطع K للخطين المماس للقطع المكافئ عند النقطتين M و N.

الجواب: ك (1 ؛ - 9).

18. ما قيم b هو الخط y \ u003d 9x + b مماس للرسم البياني للدالة y \ u003d x 3 - 3x + 15؟

الجواب: - 1 ؛ 31.

19. ما قيم k التي يمتلكها الخط y = kx - 10 نقطة مشتركة واحدة فقط مع التمثيل البياني للدالة y = 2x 2 + 3x - 2؟ لقيم ك التي تم العثور عليها ، حدد إحداثيات النقطة.

الجواب: ك 1 = - 5 ، أ (- 2 ؛ 0) ؛ ل 2 = 11 ، ب (2 ؛ 12).

20. ما هي قيم b التي يمر بها الظل المرسوم على الرسم البياني للدالة y = bx 3 - 2x 2 - 4 عند النقطة التي بها الحد الأقصى x 0 = 2 يمر بالنقطة M (1 ؛ 8)؟

الجواب: ب = - 3.

21. القطع المكافئ الذي رأسه على المحور x هو مماس لخط يمر بالنقطتين A (1 ؛ 2) و B (2 ؛ 4) عند النقطة B. أوجد معادلة القطع المكافئ.

إجابة:

22. ما هي قيمة المعامل k هل يلمس القطع المكافئ y \ u003d x 2 + kx + 1 محور الثور؟

الجواب: ك = س 2.

23. أوجد الزوايا الواقعة بين الخط y = x + 2 والمنحنى y = 2x 2 + 4x - 3.

29. أوجد المسافة بين مماسات الرسم البياني لمولدات الدالة مع الاتجاه الموجب لمحور Ox بزاوية 45 درجة.

إجابة:

30. أوجد موضع رءوس كل القطع المكافئ بالشكل y = x 2 + ax + b التي تلامس الخط y = 4x - 1.

الجواب: الخط المستقيم y = 4x + 3.

الأدب

1. Zvavich L.I.، Shlyapochnik L.Ya.، Chinkina M.V. الجبر وبدايات التحليل: 3600 مشكلة لتلاميذ المدارس والمتقدمين للجامعة. - م ، بوستارد ، 1999.
2. مردكوفيتش أ. الندوة الرابعة للمعلمين الشباب. الموضوع هو "تطبيقات مشتقة". - م. "رياضيات" رقم 21/94.
3. تكوين المعرفة والمهارات على أساس نظرية الاستيعاب التدريجي للأفعال العقلية. / إد. ص. جالبيرين ، ن. Talyzina. - ماجستير ، جامعة موسكو الحكومية ، 1968.

دعنا نعطي الدالة f ، والتي عند نقطة ما x 0 لها مشتق محدود f (x 0). ثم الخط المار بالنقطة (x 0 ؛ f (x 0)) ، الذي له ميل f '(x 0) ، يسمى المماس.

ولكن ماذا يحدث إذا كانت المشتقة عند النقطة x 0 غير موجودة؟ هناك خياران:

1. ظل الرسم البياني غير موجود أيضًا. المثال الكلاسيكي هو الوظيفة y = | x | عند النقطة (0 ؛ 0).
2. يصبح الظل عموديًا. هذا صحيح ، على سبيل المثال ، بالنسبة للدالة y = arcsin x عند النقطة (1 ؛ π / 2).

معادلة الظل

يتم الحصول على أي خط مستقيم غير عمودي بواسطة معادلة بالصيغة y = kx + b ، حيث k هو الميل. الظل ليس استثناءً ، ومن أجل تكوين معادلته عند نقطة ما × 0 ، يكفي معرفة قيمة الوظيفة والمشتق في هذه المرحلة.

لذلك ، دع الدالة تُعطى y \ u003d f (x) ، والتي لها مشتق y \ u003d f '(x) على المقطع. ثم في أي نقطة × 0 ∈ (أ ؛ ب) يمكن رسم الظل للرسم البياني لهذه الوظيفة ، والتي تعطى بالمعادلة:

y \ u003d f '(x 0) (x - x 0) + f (x 0)

هنا f '(x 0) هي قيمة المشتق عند النقطة x 0 ، و f (x 0) هي قيمة الوظيفة نفسها.

مهمة. بالنظر إلى الدالة y = x 3. اكتب معادلة لمماس الرسم البياني لهذه الدالة عند النقطة x 0 = 2.

معادلة الظل: y \ u003d f '(x 0) (x - x 0) + f (x 0). النقطة x 0 = 2 معطاة لنا ، لكن القيم f (x 0) و f '(x 0) يجب أن تحسب.

أولًا ، لنجد قيمة الدالة. كل شيء سهل هنا: f (x 0) = f (2) = 2 3 = 8 ؛
الآن دعنا نجد المشتق: f '(x) \ u003d (x 3)' \ u003d 3x 2 ؛
عوّض في المشتق x 0 = 2: f '(x 0) = f' (2) = 3 2 2 = 12؛
فنحصل على: y = 12 (x - 2) + 8 = 12x - 24 + 8 = 12x - 16.
هذه هي معادلة الظل.

مهمة. قم بتكوين معادلة الظل للرسم البياني للوظيفة f (x) \ u003d 2sin x + 5 عند النقطة x 0 \ u003d π / 2.

هذه المرة لن نصف بالتفصيل كل إجراء - سنشير فقط إلى الخطوات الرئيسية. لدينا:

و (س 0) \ u003d و (/ 2) \ u003d 2 ثانية (π / 2) + 5 \ u003d 2 + 5 \ u003d 7 ؛
و '(x) \ u003d (2sin x + 5)' \ u003d 2cos x ؛
f '(x 0) \ u003d f' (π / 2) \ u003d 2cos (π / 2) \ u003d 0 ؛

معادلة الظل:

ص = 0 (س - π / 2) + 7 ص = 7

في الحالة الأخيرة ، كان الخط أفقيًا ، لأن منحدره k = 0. لا حرج في ذلك - لقد عثرنا على نقطة قصوى.

Y \ u003d f (x) وإذا كان من الممكن في هذه المرحلة رسم الظل إلى الرسم البياني للوظيفة غير العمودي على المحور x ، فإن ميل المماس هو f "(a). لقد استخدمنا هذا بالفعل عدة مرات. على سبيل المثال ، في الفقرة 33 ، تم التأكيد على أن الرسم البياني للوظيفة y \ u003d sin x (sinusoid) في الأصل يشكل زاوية 45 درجة مع محور الإحداثي (بتعبير أدق ، المماس للرسم البياني عند الأصل يصنع زاوية 45 درجة مع الاتجاه الإيجابي للمحور x) ، وفي المثال ، تم العثور على 5 من § 33 نقطة في جدول معين المهام، حيث يكون المماس موازيًا لمحور x. في المثال 2 § 33 ، تم وضع معادلة للماس للرسم البياني للوظيفة y \ u003d x 2 عند النقطة x \ u003d 1 (بتعبير أدق ، عند النقطة (1 ؛ 1) ، ولكن في كثير من الأحيان فقط يشار إلى قيمة الإحداثي ، بافتراض أنه إذا كانت قيمة الإحداثي معروفة ، فيمكن العثور على قيمة الإحداثي من المعادلة y = f (x)). في هذا القسم ، سنطور خوارزمية لتجميع معادلة المماس للرسم البياني لأي دالة.

دع الدالة y \ u003d f (x) والنقطة M (a ؛ f ​​(a)) تُعطى ، ومن المعروف أيضًا أن f "(a) موجود. دعونا نؤلف معادلة الظل للرسم البياني لـ الدالة المعطاة عند نقطة معينة. هذه المعادلة تشبه معادلة أي خط مستقيم ، وليس موازيًا للمحور y ، على شكل y = kx + m ، لذا تكمن المشكلة في إيجاد قيم المعاملات k وم.

لا توجد مشاكل مع المنحدر k: نحن نعلم أن k \ u003d f "(a). لحساب قيمة m ، نستخدم حقيقة أن الخط المطلوب يمر عبر النقطة M (a ؛ f ​​(a)). هذا يعني أننا إذا استبدلنا نقاط الإحداثيات M في معادلة الخط المستقيم ، فسنحصل على المساواة الصحيحة: f (a) \ u003d ka + m ، حيث نجد ذلك m \ u003d f (a) - ka.
يبقى استبدال القيم الموجودة لمعاملات الحوت في المعادلةمستقيم:

لقد حصلنا على معادلة الظل للرسم البياني للوظيفة y \ u003d f (x) عند النقطة x \ u003d a.
إذا قل
الاستبدال في المعادلة (1) القيم الموجودة أ \ u003d 1 ، f (a) \ u003d 1 f "(a) \ u003d 2 ، نحصل على: y \ u003d 1 + 2 (x-f) ، أي y \ u003d 2x -1.
قارن هذه النتيجة بالنتيجة التي تم الحصول عليها في المثال 2 من الفقرة 33. وبطبيعة الحال ، حدث نفس الشيء.
دعونا نؤلف معادلة الظل للرسم البياني للوظيفة y \ u003d tg x في الأصل. لدينا: ومن ثم cos x f "(0) = 1. استبدال القيم الموجودة a \ u003d 0، f (a) \ u003d 0، f" (a) \ u003d 1 في المعادلة (1) ، نحصل على: y \ u003d x .
هذا هو السبب في أننا رسمنا المماس في الفقرة 15 (انظر الشكل 62) من خلال أصل الإحداثيات بزاوية 45 درجة بالنسبة لمحور الإحداثي.
لحل هذه الأمثلة البسيطة نوعًا ما ، استخدمنا بالفعل خوارزمية معينة مضمنة في الصيغة (1). لنجعل هذه الخوارزمية صريحة.

الخوارزمية لتكوين معادلة دالة الظل إلى الرسم البياني y \ u003d f (x)

1) عيّن حدود نقطة الاتصال بالحرف أ.
2) احسب 1 (أ).
3) أوجد f "(x) واحسب f" (a).
4) استبدل الأرقام الموجودة أ ، و (أ) ، (أ) في الصيغة (1).

مثال 1اكتب معادلة لمماس الرسم البياني للدالة عند النقطة x = 1.
دعنا نستخدم الخوارزمية ، مع الأخذ في الاعتبار ذلك في هذا المثال

على التين. 126 يُظهر القطع الزائد ، الخط المستقيم y \ u003d 2x مبني.
يؤكد الرسم الحسابات المذكورة أعلاه: في الواقع ، يلامس الخط y \ u003d 2-x القطع الزائد عند النقطة (1 ؛ 1).

إجابة:ص \ u003d 2-س.
مثال 2ارسم ظلًا للرسم البياني للدالة بحيث يكون موازيًا للخط المستقيم y \ u003d 4x - 5.
دعونا نحسن صياغة المشكلة. عادة ما يعني مطلب "رسم الظل" "عمل معادلة للماس". هذا أمر منطقي ، لأنه إذا كان الشخص قادرًا على تكوين معادلة للماس ، فمن غير المرجح أن يواجه صعوبات في بناء خط مستقيم على المستوى الإحداثي وفقًا لمعادلته.
دعنا نستخدم الخوارزمية لتجميع معادلة الظل ، مع الأخذ في الاعتبار أنه في هذا المثال ، ولكن ، على عكس المثال السابق ، هناك غموض هنا: لم يتم الإشارة صراحة إلى حدودي نقطة الظل.
لنبدأ الحديث هكذا. يجب أن يكون الظل المطلوب موازٍ للخط المستقيم y \ u003d 4x-5. خطان متوازيان إذا وفقط إذا كان ميلهما متساويًا. هذا يعني أن ميل المماس يجب أن يكون مساويًا لميل الخط المستقيم المحدد: وبالتالي ، يمكننا إيجاد قيمة a من المعادلة f "(a) \ u003d 4.
لدينا:
من المعادلة إذن ، يوجد ظلان يفيان بشروط المشكلة: أحدهما عند النقطة التي بها السداسية 2 ، والآخر عند النقطة مع الإحداثيات -2.
الآن يمكنك التصرف وفقًا للخوارزمية.

مثال 3من النقطة (0 ؛ 1) ارسم ظلًا للرسم البياني للدالة
دعنا نستخدم الخوارزمية لتجميع معادلة الظل ، بالنظر إلى أنه في هذا المثال ، لاحظ أنه هنا ، كما في المثال 2 ، لا تتم الإشارة صراحة إلى حدودي نقطة الظل. ومع ذلك ، فإننا نتصرف وفقًا للخوارزمية.

حسب الشرط ، يمر الظل عبر النقطة (0 ؛ 1). بالتعويض في المعادلة (2) القيم س = 0 ، ص = 1 ، نحصل على:
كما ترون ، في هذا المثال ، فقط في الخطوة الرابعة من الخوارزمية تمكنا من العثور على حدود نقطة اللمس. استبدال القيمة a \ u003d 4 في المعادلة (2) ، نحصل على:

على التين. يُظهر 127 توضيحًا هندسيًا للمثال المدروس: رسم بياني للوظيفة

في الفقرة 32 ، لاحظنا أنه بالنسبة للدالة y = f (x) ، التي لها مشتق عند نقطة ثابتة x ، فإن المساواة التقريبية تحمل:

لتسهيل المزيد من التفكير ، نغير الترميز: بدلاً من x سنكتب a ، بدلاً من ذلك سنكتب x ، وبناءً عليه سنكتب x-a بدلاً من ذلك. ثم تأخذ المساواة التقريبية المكتوبة أعلاه الشكل:

الآن نلقي نظرة على التين. 128. يتم رسم الظل على الرسم البياني للوظيفة y \ u003d f (x) عند النقطة M (a ؛ f ​​(a)). تم وضع علامة x على المحور x بالقرب من a. من الواضح أن f (x) هو إحداثيات الرسم البياني للوظيفة عند النقطة المحددة x. وما هو f (a) + f "(a) (x-a)؟ هذا هو إحداثيات الظل المقابل للنقطة نفسها x - انظر الصيغة (1). ما معنى المساواة التقريبية (3)؟ احسب القيمة التقريبية للدالة ، يتم أخذ قيمة إحداثيات الظل.

مثال 4أوجد القيمة التقريبية للتعبير العددي 1.02 7.
نحن نتحدث عن إيجاد قيمة الدالة y \ u003d x 7 عند النقطة x \ u003d 1.02. نستخدم الصيغة (3) مع مراعاة ذلك في هذا المثال
نتيجة لذلك ، نحصل على:

إذا استخدمنا آلة حاسبة ، فسنحصل على: 1.02 7 = 1.148685667 ...
كما ترى ، دقة التقريب مقبولة تمامًا.
إجابة: 1,02 7 =1,14.

اي جي. Mordkovich الجبر الصف 10

التقويم المواضيعي التخطيط في الرياضيات ، فيديوفي الرياضيات عبر الإنترنت ، تنزيل الرياضيات في المدرسة

محتوى الدرس ملخص الدرسدعم إطار عرض الدرس بأساليب متسارعة تقنيات تفاعلية يمارس مهام وتمارين امتحان ذاتي ورش عمل ، تدريبات ، حالات ، أسئلة ، واجبات منزلية ، أسئلة مناقشة أسئلة بلاغية من الطلاب الرسوم التوضيحية مقاطع الصوت والفيديو والوسائط المتعددةصور فوتوغرافية ، صور رسومات ، جداول ، مخططات فكاهة ، نوادر ، نكت ، أمثال كاريكاتورية ، أقوال ، ألغاز كلمات متقاطعة ، اقتباسات الإضافات الملخصاترقائق المقالات لأوراق الغش الفضولي والكتب المدرسية الأساسية والإضافية معجم مصطلحات أخرى تحسين الكتب المدرسية والدروستصحيح الأخطاء في الكتاب المدرسيتحديث جزء في الكتاب المدرسي من عناصر الابتكار في الدرس واستبدال المعرفة القديمة بأخرى جديدة فقط للمعلمين دروس مثالية خطة التقويملسنة القواعد الارشاديةبرامج المناقشة دروس متكاملة

تقدم المقالة شرحًا مفصلاً للتعريفات والمعنى الهندسي للمشتق مع تدوين بياني. سيتم النظر في معادلة خط الظل مع أمثلة ، وسيتم العثور على معادلات مماس منحنيات الترتيب الثاني.

Yandex.RTB R-A-339285-1 التعريف 1

زاوية ميل الخط المستقيم y \ u003d k x + b تسمى الزاوية α ، والتي يتم قياسها من الاتجاه الإيجابي للمحور x إلى الخط المستقيم y \ u003d k x + b في الاتجاه الموجب.

في الشكل ، يُشار إلى اتجاه الثور بسهم أخضر وقوس أخضر ، وزاوية الميل بقوس أحمر. يشير الخط الأزرق إلى خط مستقيم.

التعريف 2

يُطلق على منحدر الخط المستقيم y \ u003d k x + b المعامل العددي k.

الميل يساوي ميل الخط المستقيم ، بمعنى آخر k = t g α.

• ميل الخط المستقيم يساوي 0 فقط عندما يكون o x متوازيًا والميل يساوي صفرًا ، لأن مماس الصفر يساوي 0. إذن ، ستكون صيغة المعادلة y = b.
• إذا كانت زاوية ميل الخط المستقيم y = k x + b حادة ، فإن الشروط 0< α < π 2 или 0 ° < α < 90 ° . Отсюда имеем, что значение углового коэффициента k считается رقم موجب، عدد إيجابي، لأن قيمة الظل تفي بالشرط t g α> 0 ، وهناك زيادة في الرسم البياني.
• إذا كانت α \ u003d π 2 ، فإن موقع الخط عمودي على x. يتم تحديد المساواة من خلال المساواة س = ج مع كون القيمة ج عددًا حقيقيًا.
• إذا كانت زاوية ميل الخط المستقيم y = k x + b منفرجة ، فإنها تتوافق مع الشروط π 2< α < π или 90 ° < α < 180 ° , значение углового коэффициента k принимает معنى سلبي، والرسم البياني يتناقص.

التعريف 3

القاطع هو خط مستقيم يمر عبر نقطتين من الدالة f (x). بعبارة أخرى ، القاطع هو خط مستقيم يمر عبر أي نقطتين على الرسم البياني لوظيفة معينة.

يوضح الشكل أن A B قاطع ، و f (x) منحنى أسود ، و α قوس أحمر يشير إلى زاوية ميل القاطع.

عندما يكون ميل الخط المستقيم مساويًا لمماس زاوية الميل ، فمن الواضح أن المماس من المثلث القائم أ ب ج يمكن إيجاده بالنسبة إلى الضلع المقابلة للزاوية المجاورة.

التعريف 4

نحصل على صيغة إيجاد قاطع النموذج:

k = t g α = B C A C = f (x B) - f x A x B - x A ، حيث تكون عبارات النقطتين A و B هي القيم x A و x B و f (x A) و f (x ب) هي وظائف القيم في هذه النقاط.

من الواضح أن ميل القاطع محدد باستخدام المساواة k \ u003d f (x B) - f (x A) x B - x A أو k \ u003d f (x A) - f (x B) x A - x ب ، ويجب كتابة المعادلة كـ y = f (x B) - f (x A) x B - x A x - x A + f (x A) أو
y = f (x A) - f (x B) x A - x B x - x B + f (x B).

يقسم القاطع الرسم البياني بصريًا إلى 3 أجزاء: على يسار النقطة أ ، من أ إلى ب ، إلى يمين ب. يوضح الشكل أدناه أن هناك ثلاثة قاطعات تعتبر متشابهة ، أي أنها مجموعة باستخدام معادلة مماثلة.

بحكم التعريف ، من الواضح أن الخط وقاطعته يتطابقان في هذه الحالة.

يمكن أن يتقاطع القاطع مع الرسم البياني لوظيفة معينة عدة مرات. إذا كانت هناك معادلة بالصيغة y \ u003d 0 للقاطع ، فإن عدد نقاط التقاطع مع الجيب الجيبي لا نهائي.

التعريف 5

ظل للرسم البياني للدالة f (x) عند النقطة x 0 ؛ تسمى f (x 0) بالخط المستقيم الذي يمر عبر نقطة معينة x 0 ؛ f (x 0) ، مع وجود مقطع به العديد من قيم x قريبة من x 0.

مثال 1

دعنا نلقي نظرة فاحصة على المثال أدناه. ثم يمكن ملاحظة أن الخط المعطى بواسطة الدالة y = x + 1 يعتبر مماسًا لـ y = 2 x عند النقطة ذات الإحداثيات (1 ؛ 2). من أجل الوضوح ، من الضروري النظر في الرسوم البيانية ذات القيم القريبة من (1 ؛ 2). الدالة y = 2 x مميزة باللون الأسود ، والخط الأزرق هو الظل ، والنقطة الحمراء هي نقطة التقاطع.

من الواضح أن y \ u003d 2 x تندمج مع السطر y \ u003d x + 1.

لتحديد المماس ، يجب على المرء أن يأخذ في الاعتبار سلوك المماس A B عندما تقترب النقطة B من النقطة A بلا حدود ، وللتوضيح ، نقدم شكلاً.

القاطع A B ، المشار إليه بالخط الأزرق ، يميل إلى موضع الظل نفسه ، وستبدأ زاوية ميل القاطع α في الاقتراب من زاوية ميل الظل نفسه α x.

التعريف 6

الظل للرسم البياني للوظيفة y \ u003d f (x) عند النقطة A هو الموضع المحدد للقاطع A B عند B يميل إلى A ، أي B → A.

ننتقل الآن إلى النظر في المعنى الهندسي لمشتقة دالة عند نقطة ما.

دعنا ننتقل إلى اعتبار القاطع A B للوظيفة f (x) ، حيث A و B بإحداثيات x 0 و f (x 0) و x 0 + ∆ x و f (x 0 + x) و يُشار إلى x على أنه زيادة في الوسيطة. الآن ستأخذ الدالة الشكل ∆ y = ∆ f (x) = f (x 0 + ∆ x) - f (∆ x). من أجل الوضوح ، دعنا نأخذ صورة كمثال.

ضع في اعتبارك النتيجة مثلث قائمأ ب ج. نستخدم تعريف المماس للحل ، أي نحصل على النسبة ∆ y ∆ x = t g α. ويترتب على تعريف المماس أن lim ∆ x → 0 ∆ y ∆ x = t g α x. وفقًا لقاعدة الاشتقاق عند نقطة ما ، لدينا أن المشتق f (x) عند النقطة x 0 يسمى حد نسبة زيادة الدالة إلى زيادة السعة ، حيث ∆ x → 0 ، إذن يُشار إليه على أنه f (x 0) = lim ∆ x → 0 ∆ y ∆ x.

ويترتب على ذلك أن f "(x 0) = lim ∆ x → 0 ∆ y ∆ x = t g α x = k x ، حيث يُشار إلى k x على أنه ميل المماس.

أي أننا نحصل على أن f '(x) يمكن أن توجد عند النقطة x 0 ، وكذلك الظل للرسم البياني المعطى للوظيفة عند نقطة الاتصال التي تساوي x 0 ، f 0 (x 0) ، حيث تساوي قيمة ميل المماس عند النقطة المشتق عند النقطة x 0. ثم نحصل على k x = f "(x 0).

المعنى الهندسي لمشتق دالة عند نقطة ما هو أن مفهوم وجود مماس للرسم البياني في نفس النقطة معطى.

لكتابة معادلة أي خط مستقيم في المستوى ، من الضروري أن يكون لديك ميل بالنقطة التي يمر بها. يتم تعيينه على أنه x 0 عند التقاطع.

معادلة الظل للرسم البياني للوظيفة y \ u003d f (x) عند النقطة x 0 ، f 0 (x 0) تأخذ الشكل y \ u003d f "(x 0) x - x 0 + f (x 0).

وهذا يعني أن القيمة النهائية للمشتق f "(x 0) يمكن أن تحدد موضع الظل ، أي عموديًا تحت الشرط lim x → x 0 + 0 f" (x) = ∞ و lim x → x 0 - 0 f "(x) = ∞ أو الغياب على الإطلاق في ظل الشرط lim x → x 0 + 0 f" (x) ≠ lim x → x 0 - 0 f "(x).

يعتمد موقع الظل على قيمة ميله k x \ u003d f "(x 0). عند موازاة المحور x ، نحصل على k k \ u003d 0 ، عندما يكون بالتوازي مع حوالي y - k x \ u003d ∞ ، و شكل معادلة الظل x \ u003d x 0 يزيد مع k x> 0 ، يتناقص مثل k x< 0 .

مثال 2

قم بتجميع معادلة الظل للرسم البياني للوظيفة y \ u003d e x + 1 + x 3 3-6-3 3 x - 17-3 3 عند نقطة ذات إحداثيات (1 ؛ 3) مع تعريف زاوية ميل.

حل

من خلال الافتراض ، لدينا أن الوظيفة محددة لجميع الأرقام الحقيقية. لقد حصلنا على أن النقطة ذات الإحداثيات المحددة بالشرط (1 ؛ 3) هي نقطة الاتصال ، ثم x 0 = - 1 ، f (x 0) = - 3.

من الضروري إيجاد المشتق عند النقطة ذات القيمة - 1. لقد حصلنا على ذلك

y "= e x + 1 + x 3 3-6-3 3 x - 17-3 3" = = e x + 1 "+ x 3 3" - 6-3 3 x "- 17-3 3" = e x + 1 + x 2-6-3 3 y "(x 0) = y" (- 1) = e - 1 + 1 + - 1 2-6-3 3 = 3 3

قيمة f '(x) عند نقطة الاتصال هي ميل الظل ، والذي يساوي ظل المنحدر.

ثم k x = t g α x = y "(x 0) = 3 3

ويترتب على ذلك أن α x = a r c t g 3 3 = π 6

إجابة:تأخذ معادلة الظل الشكل

y \ u003d f "(x 0) x - x 0 + f (x 0) y \ u003d 3 3 (x + 1) - 3 y \ u003d 3 3 x - 9-3 3

من أجل الوضوح ، نقدم مثالاً في رسم توضيحي بياني.

يستخدم اللون الأسود لمؤامرة الوظيفة الأصلية ، لون ازرق- صورة الظل ، النقطة الحمراء - نقطة الاتصال. يوضح الشكل الموجود على اليمين منظرًا مكبّرًا.

مثال 3

اكتشف وجود مماس للرسم البياني لدالة معينة
y = 3 x - 1 5 + 1 عند النقطة ذات الإحداثيات (1 ؛ 1). اكتب معادلة وحدد زاوية الميل.

حل

من خلال الافتراض ، لدينا أن مجال الوظيفة المعينة هو مجموعة جميع الأرقام الحقيقية.

دعنا ننتقل إلى إيجاد المشتقة

ص "= 3 س - 1 5 + 1" = 3 1 5 (س - 1) 1 5-1 = 3 5 1 (س - 1) 4 5

إذا كانت x 0 = 1 ، فإن f '(x) لم يتم تعريفها ، ولكن تتم كتابة الحدود على أنها lim x → 1 + 0 3 5 1 (x - 1) 4 5 = 3 5 1 (+ 0) 4 5 = 3 5 1 + 0 = + و lim x → 1-0 3 5 1 (x - 1) 4 5 = 3 5 1 (- 0) 4 5 = 3 5 1 + 0 = + ∞ ، مما يعني وجود الظل الرأسي عند نقطة (1 ؛ 1).

إجابة:ستأخذ المعادلة الشكل x \ u003d 1 ، حيث ستكون زاوية الميل مساوية لـ π 2.

دعونا نرسمها من أجل الوضوح.

مثال 4

أوجد نقاط منحنى الدالة y = 1 15 x + 2 3-4 5 x 2-16 5 x - 26 5 + 3 x + 2 حيث

1. الظل غير موجود.
2. الظل يوازي x ؛
3. الظل يوازي الخط y = 8 5 x + 4.

حل

من الضروري الانتباه إلى مجال التعريف. من خلال الافتراض ، لدينا أن الوظيفة محددة في مجموعة جميع الأرقام الحقيقية. قم بتوسيع الوحدة وحل النظام بفواصل زمنية x ∈ - ∞ ؛ 2 و [- 2 ؛ + ∞). لقد حصلنا على ذلك

ص = - 1 15 × 3 + 18 × 2 + 105 × + 176 ، س ∈ - ∞ ؛ - 2 1 15 × 3 - 6 × 2 + 9 × + 12 ، × ∈ [- 2 ؛ + ∞)

يجب التمييز بين الوظيفة. لدينا هذا

ص "= - 1 15 × 3 + 18 × 2 + 105 × + 176" ، × ∈ - ∞ ؛ - 2 1 15 x 3-6 x 2 + 9 x + 12 "، x ∈ [- 2 ؛ + ∞) ⇔ y" = - 1 5 (x 2 + 12 x + 35)، x ∈ - ∞ ؛ - 2 1 5 × 2-4 × + 3 ، × ∈ [- 2 ؛ + ∞)

عندما x = - 2 ، فإن المشتق غير موجود لأن الحدود أحادية الجانب غير متساوية في تلك النقطة:

ليم س → - 2 - 0 ص "(س) = ليم س → - 2 - 0 - 1 5 (س 2 + 12 س + 35 = - 1 5 (- 2) 2 + 12 (- 2) + 35 = - 3 ليم س → - 2 + 0 ص "(س) = ليم س → - 2 + 0 1 5 (س 2-4 س + 3) = 1 5 - 2 2 - 4 - 2 + 3 = 3

نحسب قيمة الوظيفة عند النقطة x \ u003d - 2 ، حيث نحصل على ذلك

1. ص (- 2) \ u003d 1 15 - 2 + 2 3 - 4 5 (- 2) 2 - 16 5 (- 2) - 26 5 + 3 - 2 + 2 \ u003d - 2 ، أي الظل عند النقطة (- 2 ؛ - 2) لن تكون موجودة.
2. الظل يوازي x عندما يكون الميل صفرًا. ثم k x \ u003d t g α x \ u003d f "(x 0). أي أنه من الضروري إيجاد قيم x عندما يحولها مشتق الوظيفة إلى الصفر. أي القيم \ u200b \ u200b of f '(x) وستكون نقاط اتصال ، حيث يكون الظل موازيًا حول x.

عندما س ∈ - ∞ ؛ - 2 ، ثم - 1 5 (x 2 + 12 x + 35) = 0 ، وبالنسبة إلى x ∈ (- 2 ؛ + ∞) نحصل على 1 5 (x 2-4 x + 3) = 0.

1 5 (x 2 + 12 x + 35) = 0 D = 12 2-4 35 = 144-140 = 4 x 1 = - 12 + 4 2 = - 5 ∈ - ∞ ؛ - 2 × 2 = - 12 - 4 2 = - 7 ∈ - ∞ ؛ - 2 1 5 (× 2-4 × + 3) = 0 د = 4 2 - 4 3 = 4 × 3 = 4 - 4 2 = 1 - 2 ؛ + ∞ × 4 = 4 + 4 2 = 3 - 2 ؛ + ∞

نحسب القيم المقابلة للدالة

ص 1 = ص - 5 = 1 15-5 + 2 3 - 4 5 - 5 2 - 16 5 - 5 - 26 5 + 3 - 5 + 2 = 8 5 ص 2 = ص (- 7) = 1 15-7 + 2 3 - 4 5 (- 7) 2 - 16 5 - 7 - 26 5 + 3 - 7 + 2 = 4 3 ص 3 = ص (1) = 1 15 1 + 2 3 - 4 5 1 2 - 16 5 1-26 5 + 3 1 + 2 = 8 5 y 4 = y (3) = 1 15 3 + 2 3 - 4 5 3 2-16 5 3-26 5 + 3 3 + 2 = 4 3

ومن ثم - 5 ؛ 8 5 ، - 4 ؛ 4 3 ، 1 ؛ 85 ، 3 ؛ 4 3 تعتبر النقاط المرغوبة في الرسم البياني للوظيفة.

يعتبر صورة بيانيةحلول.

الخط الأسود هو الرسم البياني للوظيفة ، والنقاط الحمراء هي نقاط اللمس.

1. عندما تكون الخطوط متوازية ، تكون المنحدرات متساوية. ثم من الضروري البحث عن نقاط الرسم البياني للوظيفة ، حيث سيكون الميل مساويًا للقيمة 8 5. للقيام بذلك ، تحتاج إلى حل معادلة بالصيغة y "(x) = 8 5. ثم ، إذا كانت x ∈ - ∞ ؛ - 2 ، نحصل على ذلك - 1 5 (x 2 + 12 x + 35) = 8 5 ، وإذا كانت x ∈ (- 2 ؛ +) ، إذن 5 1 (× 2-4 × + 3) = 8 5.

المعادلة الأولى ليس لها جذور لأن المميز أقل من الصفر. دعنا نكتب ذلك

1 5 × 2 + 12 × + 35 = 8 5 × 2 + 12 × + 43 = 0 د = 12 2 - 4 43 = - 28< 0

إذن ، هناك معادلة أخرى لها جذرين حقيقيين

1 5 (× 2-4 × + 3) = 8 5 × 2-4 × - 5 = 0 د = 4 2-4 (- 5) = 36 × 1 = 4 - 36 2 = - 1 - 2 ؛ + ∞ × 2 = 4 + 36 2 = 5 - 2 ؛ + ∞

دعنا ننتقل إلى إيجاد قيم الوظيفة. لقد حصلنا على ذلك

ص 1 = ص (- 1) = 1 15 - 1 + 2 3 - 4 5 (- 1) 2 - 16 5 (- 1) - 26 5 + 3 - 1 + 2 = 4 15 ص 2 = ص (5) = 1 15 5 + 2 3 - 4 5 5 2 - 16 5 5-26 5 + 3 5 + 2 = 8 3

النقاط ذات القيم - 1 ؛ 4 15 ، 5 ؛ 8 3 هي النقاط التي يكون فيها المماس موازيين للخط y = 8 5 x + 4.

إجابة:الخط الأسود - الرسم البياني للوظيفة ، الخط الأحمر - الرسم البياني y \ u003d 8 5 x + 4 ، الخط الأزرق - الظلال عند النقاط - 1 ؛ 4 15 ، 5 ؛ 8 3.

من الممكن وجود عدد لا حصر له من الظلال لوظائف معينة.

مثال 5

اكتب معادلات جميع المماسات المتاحة للدالة y = 3 cos 3 2 x - π 4-1 3 ، المتعامدة على الخط y = - 2 x + 1 2.

حل

لصياغة معادلة الظل ، من الضروري إيجاد معامل وإحداثيات نقطة الاتصال ، بناءً على حالة عمودي الخطوط. يبدو التعريف كالتالي: حاصل ضرب المنحدرات المتعامدة على الخطوط المستقيمة يساوي - 1 ، أي أنه مكتوب بالصيغة k x · k ⊥ = - 1. من شرط أن يكون الميل عموديًا على الخط المستقيم ويساوي k ⊥ = - 2 ، ثم k x = - 1 k ⊥ = - 1 - 2 = 1 2.

نحتاج الآن إلى إيجاد إحداثيات نقاط اللمس. تحتاج إلى إيجاد x ، وبعد ذلك قيمتها لدالة معينة. لاحظ ذلك من المعنى الهندسي للمشتق عند النقطة
x 0 نحصل على k x \ u003d y "(x 0). من هذه المساواة ، نجد قيم x لنقاط اللمس.

لقد حصلنا على ذلك

y "(x 0) = 3 cos 3 2 x 0 - π 4-1 3" = 3 - sin 3 2 x 0 - π 4 3 2 x 0 - π 4 "= - 3 sin 3 2 x 0 - 4 3 2 \ u003d - 9 2 sin 3 2 x 0 - π 4 ⇒ k x \ u003d y "(x 0) ⇔ - 9 2 sin 3 2 x 0 - π 4 \ u003d 1 2 ⇒ sin 3 2 x 0 - π 4 = - 1 9

هذا المعادلة المثلثيةسيُستخدم لحساب إحداثيات نقاط اللمس.

3 2 x 0 - π 4 = a r c sin - 1 9 + 2 πk أو 3 2 x 0 - π 4 = π - a r c sin - 1 9 + 2 πk

3 2 x 0 - π 4 = - a r c sin 1 9 + 2 πk أو 3 2 x 0 - π 4 = π + a r c sin 1 9 + 2 πk

x 0 = 2 3 π 4 - a r c sin 1 9 + 2 k أو x 0 = 2 3 5 π 4 + a r c sin 1 9 + 2 πk، k ∈ Z

Z هي مجموعة الأعداد الصحيحة.

تم العثور على نقاط اتصال س. أنت الآن بحاجة للذهاب إلى البحث عن قيم y:

y 0 = 3 cos 3 2 x 0 - π 4-1 3

y 0 = 3 1 - sin 2 3 2 x 0 - π 4-1 3 أو y 0 = 3-1 - sin 2 3 2 x 0 - π 4-1 3

ص 0 = 3 1 - - 1 9 2-1 3 أو ص 0 = 3-1 - - 1 9 2-1 3

ص 0 = 4 5-1 3 أو ص 0 = - 4 5 + 1 3

من هنا نحصل على 2 3 π 4 - a r c sin 1 9 + 2 πk ؛ 4 5 - 1 3، 2 3 5 π 4 + a r c sin 1 9 + 2 πk؛ - 4 5 + 1 3 هي نقاط اتصال.

إجابة:ستتم كتابة المعادلات الضرورية على شكل

y = 1 2 x - 2 3 π 4 - a r c sin 1 9 + 2 πk + 4 5 - 1 3، y = 1 2 x - 2 3 5 π 4 + a r c sin 1 9 + 2 πk - 4 5 + 1 3 ، ك ∈ Z

للتمثيل المرئي ، ضع في اعتبارك الوظيفة والظل على خط الإحداثيات.

يوضح الشكل أن موقع الوظيفة يقع على الفاصل الزمني [- 10 ؛ 10] ، حيث يكون الخط الأسود هو الرسم البياني للدالة ، فإن الخطوط الزرقاء هي مماسات متعامدة مع الخط المعطى بالصيغة y = - 2 x + 1 2. النقاط الحمراء هي نقاط اتصال.

المعادلات الأساسية للمنحنيات من الدرجة الثانية ليست دوال ذات قيمة واحدة. يتم تجميع معادلات الظل الخاصة بهم وفقًا لمخططات معروفة.

الظل للدائرة

لوضع دائرة متمركزة عند نقطة x c e n t e r ؛ y c e n t e r ونصف القطر R ، الصيغة x - x c e n t e r 2 + y - y c e n t e r 2 = R 2 مستخدمة.

يمكن كتابة هذه المساواة على أنها اتحاد وظيفتين:

y = R 2 - x - x c e n t e r 2 + y c e n t e r y = - R 2 - x - x c e n t e r 2 + y c e n t e r

الوظيفة الأولى في الأعلى والثانية في الأسفل ، كما هو موضح في الشكل.

لرسم معادلة دائرة عند نقطة × 0 ؛ y 0 ، الموجود في نصف الدائرة العلوي أو السفلي ، يجب أن تجد معادلة الرسم البياني للوظيفة بالشكل y \ u003d R 2 - x - x c e n t e r 2 + y c e n t e r أو y \ u003d - R 2 - x - x c e n t e r 2 + y c e n t e r عند النقطة المحددة.

عندما تكون عند النقاط x c e n t e r ؛ y c e n t e r + R و x c e n t e r ؛ y c e n t e r - يمكن إعطاء الظل R بواسطة المعادلات y = y c e n t e r + R و y = y c e n t e r - R ، وعند النقاط x c e n t e r + R ؛ y c e n t e r و
x c e n t e r - R ؛ سيكون y c e n t e r متوازيًا حول y ، ثم نحصل على معادلات بالصيغة x = x c e n t e r + R و x = x c e n t e r - R.

الظل إلى قطع ناقص

عندما يتم توسيط القطع الناقص عند x c e n t e r ؛ y c e n t e r بنصفي a و b ، ثم يمكن إعطاؤها باستخدام المعادلة x - x c e n t e r 2 a 2 + y - y c e n t e r 2 b 2 = 1.

يمكن الإشارة إلى القطع الناقص والدائرة من خلال الجمع بين وظيفتين ، وهما الجزء العلوي والسفلي شبه الناقص. ثم نحصل على ذلك

y = b a a 2 - (x - x c e n t e r) 2 + y c e n t e r y = - b a a 2 - (x - x c e n t e r) 2 + y c e n t e r

إذا كانت الظل تقع عند رؤوس القطع الناقص ، فهي متوازية حول x أو حوالي y. من أجل الوضوح ، ضع في اعتبارك الشكل أدناه.

مثال 6

اكتب معادلة المماس للقطع الناقص x - 3 2 4 + y - 5 2 25 = 1 عند النقاط ذات قيم x تساوي x = 2.

حل

من الضروري إيجاد نقاط اتصال تتوافق مع القيمة x = 2. نجري تعويضًا في المعادلة الحالية للقطع الناقص ونحصل على ذلك

س - 3 2 4 س = 2 + ص - 5 2 25 = 1 1 4 + ص - 5 2 25 = 1 ص ص - 5 2 = 3 4 25 ص = ± 5 3 2 + 5

ثم 2 5 3 2 + 5 و 2 ؛ - 5 3 2 + 5 هي نقاط الظل التي تنتمي إلى شبه القطع الناقص العلوي والسفلي.

دعنا ننتقل إلى إيجاد وحل معادلة القطع الناقص بالنسبة إلى y. لقد حصلنا على ذلك

س - 3 2 4 + ص - 5 2 25 = 1 ص - 5 2 25 = 1 - س - 3 2 4 (ص - 5) 2 = 25 1 - س - 3 2 4 ص - 5 = ± 5 1 - س - ٣ ٢ ٤ ص = ٥ ± ٥ ٢ ٤ - س - ٣ ٢

من الواضح أن النصف العلوي من القطع الناقص محدد باستخدام دالة بالصيغة y = 5 + 5 2 4 - x - 3 2 ، والصيغة السفلية y = 5 - 5 2 4 - x - 3 2.

نطبق الخوارزمية القياسية من أجل صياغة معادلة المماس للرسم البياني للدالة عند نقطة ما. نكتب أن معادلة المماس الأول عند النقطة 2 ؛ سيبدو الشكل 5 3 2 + 5

ص "= 5 + 5 2 4 - س - 3 2" = 5 2 1 2 4 - (س - 3) 2 4 - (س - 3) 2 "= - 5 2 × - 3 4 - (س - 3 ) 2 ⇒ y "(x 0) = y" (2) = - 5 2 2 - 3 4 - (2 - 3) 2 = 5 2 3 ⇒ y = y "(x 0) x - x 0 + y 0 ⇔ ص = 5 2 3 (س - 2) + 5 3 2 + 5

نحصل على معادلة المماس الثاني بالقيمة عند النقطة
2 ؛ - 5 3 2 + 5 يصبح

ص "= 5-5 2 4 - (س - 3) 2" = - 5 2 1 2 4 - (س - 3) 2 4 - (س - 3) 2 "= = 5 2 × - 3 4 - (س - 3) 2 ⇒ y "(x 0) = y" (2) = 5 2 2 - 3 4 - (2-3) 2 = - 5 2 3 ⇒ y = y "(x 0) x - x 0 + ص 0 ⇔ ص = - 5 2 3 (س - 2) - 5 3 2 + 5

بيانيا ، يتم الإشارة إلى الظلال على النحو التالي:

الظل للمبالغة

عندما يكون للقطع الزائد مركز عند النقطة x c e n t e r؛ y c e n t e r والرؤوس x c e n t e r + α ؛ y c e n t e r و x c e n t e r - α ؛ y c e n t e r ، المتباينة x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = 1 معطاة بالرؤوس x c e n t e r؛ y c e n t e r + b و x c e n t e r ؛ ثم تُعطى y c e n t e r - b من خلال المتباينة x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = - 1.

يمكن تمثيل القطع الزائد كوظيفتين مدمجتين للنموذج

y = b a (x - x c e n t e r) 2 - a 2 + y c e n t e r y = - b a (x - x c e n t e r) 2 - a 2 + y c e n t e r أو y = b a (x - x c e n t e r) 2 + a 2 + y c e n t e r y = - b a (x - x c e n t e r y = - b a (x - x c e n t e r y = - b a (x - x c e n t e r y = - b a (x - x c e n t) ) 2 + a 2 + y c e n t e r

في الحالة الأولى ، لدينا أن المماسات موازية لـ y ، وفي الحالة الثانية ، فهي موازية لـ x.

ويترتب على ذلك أنه من أجل إيجاد معادلة المماس للقطع الزائد ، من الضروري معرفة الوظيفة التي تنتمي إليها نقطة الظل. لتحديد ذلك ، من الضروري إجراء استبدال في المعادلات والتحقق من الهوية.

مثال 7

اكتب معادلة المماس للقطع الزائد x - 3 2 4 - y + 3 2 9 = 1 عند النقطة 7 ؛ - 3 3 - 3.

حل

من الضروري تحويل سجل الحل لإيجاد القطع الزائد باستخدام وظيفتين. لقد حصلنا على ذلك

س - 3 2 4 - ص + 3 2 9 = 1 ص + 3 2 9 = س - 3 2 4 - 1 ص + 3 2 = 9 س - 3 2 4 - 1 ص ص + 3 = 3 2 س - 3 2-4 أو y + 3 = - 3 2 x - 3 2-4 ⇒ y = 3 2 x - 3 2-4-3 y = - 3 2 x - 3 2-4-3

من الضروري معرفة الوظيفة التي تنتمي إليها النقطة المعينة ذات الإحداثيات 7 ؛ - 3 3 - 3.

من الواضح ، للتحقق من الوظيفة الأولى ، فأنت بحاجة إلى y (7) = 3 2 (7 - 3) 2 - 4 - 3 = 3 3 - 3 ≠ - 3 3 - 3 ، فإن النقطة لا تنتمي إلى الرسم البياني ، حيث لم يتم استيفاء المساواة.

بالنسبة للدالة الثانية ، لدينا y (7) = - 3 2 (7 - 3) 2 - 4 - 3 = - 3 3 - 3 ≠ - 3 3 - 3 ، مما يعني أن النقطة تنتمي إلى الرسم البياني المعطى. من هنا يجب أن تجد معامل الميل.

لقد حصلنا على ذلك

ص "= - 3 2 (س - 3) 2 - 4 - 3" = - 3 2 × - 3 (س - 3) 2-4 ⇒ ك س = ص "(× 0) = - 3 2 × 0 - 3 س 0-3 2-4 × 0 = 7 = - 3 2 7-3 7-3 2-4 = - 3

إجابة:يمكن تمثيل معادلة الظل على النحو التالي

ص = - 3 س - 7 - 3 3 - 3 = - 3 س + 4 3 - 3

يتم تصورها على النحو التالي:

الظل للقطع المكافئ

لتكوين معادلة الظل للقطع المكافئ y \ u003d a x 2 + b x + c عند النقطة x 0، y (x 0) ، يجب عليك استخدام الخوارزمية القياسية ، ثم ستأخذ المعادلة الشكل y \ u003d y " (x 0) x - x 0 + y (x 0) مثل هذا المماس عند الرأس يوازي x.

يجب تعريف القطع المكافئ x = a y 2 + b y + c على أنه اتحاد وظيفتين. لذلك ، علينا حل معادلة y. لقد حصلنا على ذلك

س = أ ص 2 + ب ص + ج ⇔ أ ص 2 + ب ص + ج - س = 0 د = ب 2-4 أ (ج - س) ص = - ب + ب 2-4 أ (ج - س) 2 أ ص = - ب - ب 2-4 أ (ج - س) 2 أ

دعنا نرسمها على النحو التالي:

لمعرفة ما إذا كانت النقطة x 0 ، y (x 0) تنتمي إلى دالة ، اتبع الخوارزمية القياسية برفق. سيكون هذا الظل موازيًا لـ y بالنسبة إلى القطع المكافئ.

المثال 8

اكتب معادلة المماس للرسم البياني x - 2 y 2-5 y + 3 عندما يكون لدينا ميل مماس 150 °.

حل

نبدأ الحل بتمثيل القطع المكافئ كدالتين. لقد حصلنا على ذلك

2 ص 2-5 ص + 3 - س = 0 د = (- 5) 2 - 4 (- 2) (3 - س) = 49-8 س ص = 5 + 49 - 8 س - 4 ص = 5-49 - 8 × - 4

قيمة المنحدر تساوي قيمة المشتق عند النقطة x 0 لهذه الدالة وتساوي ظل المنحدر.

نحن نحصل:

ك x \ u003d y "(x 0) \ u003d t g α x \ u003d t g 150 ° \ u003d - 1 3

من هنا نحدد قيمة x لنقاط اللمس.

ستتم كتابة الوظيفة الأولى كـ

y "= 5 + 49-8 x - 4" = 1 49-8 x ⇒ y "(x 0) = 1 49-8 x 0 = - 1 3 ⇔ 49-8 x 0 = - 3

من الواضح أنه لا توجد جذور حقيقية ، لأن لدينا قيمة سالبة. نستنتج أنه لا يوجد ظل بزاوية 150 درجة لمثل هذه الوظيفة.

ستتم كتابة الوظيفة الثانية كـ

y "= 5 - 49 - 8 x - 4" = - 1 49-8 x ⇒ y "(x 0) = - 1 49-8 x 0 = - 1 3 ⇔ 49-8 x 0 = - 3 x 0 = 23 4 ص (س 0) = 5 - 49 - 8 23 4 - 4 = - 5 + 3 4

لدينا أن نقاط الاتصال - 23 4 ؛ - 5 + 3 4.

إجابة:تأخذ معادلة الظل الشكل

ص = - ١ ٣ س - ٢٣ ٤ + - ٥ + ٣ ٤

دعنا نرسمها على النحو التالي:

إذا لاحظت وجود خطأ في النص ، فيرجى تمييزه والضغط على Ctrl + Enter