セクション 1. おおよその数とその操作
1.1 近似計算における誤差の種類
一部の数学的問題の正確な解は、古典的な方法では取得できません。または、この解はそのような方法で取得できます。 複雑な形、これ以上の実用的な使用は受け入れられません。 さらに、問題を正確に解決するには、 多数（数百から数十億）アクション。 このような場合は、近似解法と数値解法に頼ってください。
コンピュータの出現により、これらの方法の範囲が大幅に拡大されました。 現在、コンピュータや近似計算の方法を所有していない技術者は想像しがたいです。
どのコンピュータも、大きいが有限の数の配列を記憶し、大きいが有限の速度でそれらの算術演算と比較を実行できることに注意してください。 つまり、マシンは非常に多くの有限数の操作を実行できます。 したがって、コンピューターで作業する場合は、有限の数のセットによって記述される数学モデルのみを使用でき、算術演算の有限のシーケンスのみを使用できます。
さまざまな現象の数学的モデルは、関数、導関数、積分、 微分方程式等々。 コンピューターで作業する場合、これらの初期モデルは、処理のアクションの最終的なシーケンスを示す有限の数値セットによって記述されるモデルに置き換える必要があります。 これを行うには、関数をテーブルに置き換えます。 定積分・金額等 さらに、コンピューターのメモリは有限であり、有限の長さの数値を操作できるため、中間結果は四捨五入されます。 その結果、ステップ数が有限の正確な方法でも近似値になります。
したがって、数値法によって得られる解は近似値です。
エラーの理由は次のとおりです。
- 研究された実際の現象と数学モデルの不一致
- 初期データエラー。
- 解決方法の誤り。
- 数値の算術およびその他の演算における丸め誤差。
最初の 2 つの理由によって引き起こされた決定エラーは、 致命的— 数学者には依存しません。
メソッドエラー数値法は、原則として、元の問題ではなく、より単純な問題を解決するために発生します。 さらに、通常、数値法は、あるステップで終了する必要がある無限プロセスに基づいています。
ほとんどの数値メソッドは、1 つまたは複数のパラメーターに依存します。 メソッド パラメータの選択により、メソッドの誤差を調整できます。
丸め誤差重要であってはならない より多くのエラー方法。 また、メソッドのエラーを致命的なエラーの2〜5倍少なく選択することをお勧めします。
1.2 おおよその数
実際には、真の値を正確ではなく近似的に表す数値を扱わなければならないことがよくあります。 そのような番号は呼ばれます 近似.
ある値 a の正確な数値、同じ値 a * のおおよその数値を示しましょう。 次に a » a * .
正確な数 a をおおよその数 a * に置き換えると、間違い (エラー) になります。
意味 1.1. 近似数 a * の絶対誤差は、この数とその正確な値との差の絶対値です。 | | あ～あ* |.
量の正確な値は通常不明であるため、計算することは不可能です。 絶対誤差. ただし、正の数を指定できます D(a*)、不等式を満たす：
いずれかの番号 d(a*) 、不等式を満たす
不等式 (1.2) と (1.3) を満たす多くの数があることに注意してください。 したがって、限界誤差の値は正確ではありません。
実際には、通常、限界誤差の最小値が使用されます。 おおよその数ごとに、その限界誤差 (絶対または相対) が必ず決定されます。 制限絶対誤差を使用すると、数値 a が存在する制限を設定できます。
限界相対誤差は、計算または測定の精度を特徴付けます。
例。
1.2.1 . 問題を解くとき、正確な数ではなく p = 3.14159265...おおよその値 3.14 を使用して、間違いを犯します。
p - 3.14 > 0.00159265
1.2.2 . 経路の長さを測定すると、2mの精度で25.2kmという結果が得られました。 限界絶対誤差と限界相対誤差を計算します。
解決. この場合、限界絶対誤差は次のようになります。 D = 0.002 km、限界相対誤差
同様に、計算します。
a * は、絶対誤差のある数 a の近似値であることを意味します D(a*). a * が相対誤差のある数 a の近似値である場合 d(a*)、次に、彼らは次のように書きます。
1.4 有効数字、真数字と疑わしい数字
実際には、最も近い数を記録するだけでエラーを判断できるようにするさまざまな手法が使用されます。
おおよその数と絶対誤差の記録には、特定の規則が適用されます。
10 進表記で 有効数字ゼロ以外の任意の数字が呼び出されます。 ゼロが有効数字の間にある場合、またはすべての有効数字の右側にある場合、ゼロは有効数字と見なされます。
例 1.3.1。おおよその数 0、 38 有効数字2桁、0、 308 - 3、0、 3080 - 4、0.00 308 - 三つ。 有効数字は下線付きの数字です。
定義 1.3.有効数字は 広い意味で正しい数値の絶対誤差が、この数値に対応する桁の 1 単位を超えない場合。
有効数字は 狭義で正しい数値の絶対誤差が、この数値に対応する桁の単位の半分を超えない場合。
それ以外の場合、数値が考慮されます 疑わしい.
絶対（究極の絶対）誤差を指定せずに概数を書き込むと、正しい数値だけが書き出されます。 この場合、数値の右端の真のゼロは破棄されません。 0.25 と 0.250 という数値は近似値として異なります。 (1.4) または (1.5) の形式のレコードを使用する場合、これらの等式の右側の数値は、同じ小数点以下の桁数で書き込まれる必要があります。
絶対または 相対誤差 1 桁または 2 桁の有効数字を含む数値として表記するのが通例です。 この場合、丸めは余分に実行されます。
整数部分のおおよその数は、正しい符号よりも有効桁数が多いことが判明する場合があります。 この場合、表記は正規化された形式 a * = m 10 n で使用されますが、数値 m ≤ 1 には有効な数字のみを含める必要があります。 正規化された表記法では、数 m は次のように呼ばれます 仮数、 n — 指数
制限絶対誤差は、小数点以下の桁数によって決定されることに注意してください。 小数点以下の桁数が少ないほど D(a*).
限界相対誤差は、有効桁数によって決まります。 有効桁数が少ないほど、 d(a*).
1.5 丸め
正しい数字でおおよその数字を書くには、 丸め.
使用する桁数が限られている場合は、正確な数値も切り上げる必要があります。
丸め (補数による) number は、次の規則に従って少ない桁数でこの数値を書き込むことで呼び出されます: 最初に破棄された桁が 5 以上の場合、最後の残りの桁が 1 増加します。 数値を四捨五入するとエラーが発生するため、これも考慮する必要があります。
補数による丸め誤差絶対値で最下位桁の単位の半分を超えない。 結果の誤差を計算するときは、数値の元の絶対誤差に丸め誤差を追加する必要があります。
例 1.3.2。数値 a * = 413287.51 には相対誤差があります d(*) = 0.01. (1.3) から、 D(a*)=| * | d(a*).
したがって、この数値の絶対誤差は 4133 です。これは、数値 a * の 4 桁目に既に誤差が含まれている可能性があることを意味します。 したがって、番号の最初の 2 桁のみが正しいです。 次に、正規化された形式では、この数値は次のように記述されます: a * = 0.41 ·10 6 .
同様に、おおよその数 b * = 0.0794 で d(b*) = 2%正規化された形式で書く b * = 0.8 10 - 1 .
ここでは、数値を丸める必要があることに注意してください。
近似数で算術演算を実行すると、2 つの相互に逆の問題が発生します。
1. によって 既知のエラー結果の誤差を推定するための入力データ。
2. 指定された精度の結果を提供する初期データの精度を決定します。
また、おおよその数値を扱う場合は、不要な数値や間違った数値を書き出す時間を無駄にしないように、さまざまな入力データの精度を調整する必要があります。
計算の過程で、中間結果の精度を監視することも必要です。
算術演算を開始する前に、これらの演算に含まれるすべての数値が同じ小数点以下の桁数で書き込まれるように丸めが適用されます。 残りの小数点以下の桁数は、元のデータの有効桁数の最小値によって決まります。
小数点以下の正しい桁数が同じ近似値を加算および減算する場合、四捨五入は行われません。
小数点以下の正しい桁数が異なる概数同士を加減算すると、元のデータの小数点以下の正しい桁数が最小になるように四捨五入されます。
正解桁数の異なる概数を乗除算すると、元データの最小正解桁数で四捨五入されます。
1.6 算術エラー
a * と b * を概数とすると、それらの和 c * = a * + b * も概数になります。
項の絶対誤差を表すと D(a*)と D(b*)、それぞれ、数値 c * の絶対誤差は次の式によって決定されます。
|
したがって、2 つの近似数を加算すると、それらの極限絶対誤差が加算されます。
この規則は、任意の有限数の項に当てはまります。 また、式 (1.6) は 2 つの数の差にも有効です。
実際、2 つの数値の差は合計として表すことができます。
a * - b * = a * + ( - b *)、
および数値の絶対誤差 ( -b*)は、数値 b * の絶対誤差に等しくなります。
コメント同じ符号の 2 つの数値を減算する場合、差の相対誤差は各項の相対誤差よりもはるかに大きくなる可能性があります。 互いに近い数値を減算すると、特に大きな精度の損失が発生します。
例 1.4.1. 違い 61.32 を見つける必要があるとしましょう - 61,31 .
これらの数値の絶対誤差は、それぞれ次のとおりです。 D1 = 0.01と D2 = 0.01。これらの数値の相対誤差を見つけてみましょう。
減算すると、数値 0.01 が得られます (有効数字 3 桁が失われていることがわかります)。 その絶対誤差は、項の絶対誤差の合計に等しい D1+ D 2 \u003d 0.02。 次に、結果の相対誤差は 初期データと結果の誤差を比較すると、相対誤差が急激に増加していることがわかります。 例 1.4.1 から。 したがって、絶対値が近い数値を減算することは避ける必要があります。 計算式を変換することで実現できる場合もあります。 このような減算を回避できない場合は、有効数字の損失を考慮して、中間計算の精度を上げる必要があります。 2 つの近似値 a * と b * を乗算および除算すると、誤差は次の式によって決定されます。 したがって、近似数を乗算および除算すると、それらの極限相対誤差が追加されます。 述べる 。近似数 Δ (a *) の絶対誤差が、この数値の 10 進数表記の有効桁数 n で表される桁の単位を超えない場合、極限相対誤差について次の不等式が成り立ちます。 δ(a *) ≤ 1 / k 10 n - 1 ここで - 数値の最初の有効数字* . おおよその数の絶対誤差の場合 D(a*)この数値の 10 進数表記の n 番目の有効数字で表される数字の単位の半分を超えない場合、次の不等式が限界相対誤差に当てはまります。 δ(a *) ≤ 1 / 2 k 10 n − 1 ここで、k は a * の最初の有効数字です。 後者の場合、逆も真です。 d (a *) J 1/2 (k + 1)10 n - 1 , その場合、* は n 桁の有効数字を持つ概数です。 定義域 G で連続的に微分可能な関数を与える u \u003d f（x 1、x 2、j、x n）。 関数の値の近似計算における誤差の推定値は、からの偏差の係数の推定値に置き換えられます。 正確な値引数エラーが原因です。 この場合、関数の偏差は総微分に置き換えられ、引数の増分は絶対誤差に置き換えられます。 次に、関数の値の限界絶対誤差は、次の関係によって決定されます。
d=
0,02
0,01
= 2.
D(a*b*) = | b * | D(a *) + | * | D(b*)、
d(a*b*) = d(a*) + d(b*)、
(1.7)
D(a*/b*) =
| | b*|D(a*)+| a*|D(b*)| b * | 2
d(a*/b*) = d(a*) + d(b*)。
1.7 関数エラー
限界相対誤差については、等式があります。
式 (1.11) を使用して、関数値の特定の精度を保証する引数の精度を決定できます。
例 1.5.1。正確に測定する必要がある d=1%底面半径が である円錐台の側面積 r 1 » 2メートル、 r 2" 1m、母線 l» 5m.
半径と母線を測定するには、どのくらいの絶対誤差が必要ですか?また、広い意味で正しい符号をいくつ使用して、数 p を取得する必要がありますか?
もしも D(a*) が n 番目の有効桁数で表される 1 桁を超えない場合、* は有効な n 桁の数字と呼ばれます 広い意味で.)
解決. 円錐台の側面の面積は、次の式で計算されます。
S = π l(r 1 + r 2).
したがって、4つの引数の関数があります S = S(p 、 l, r 1、r 2).
偏導関数を求め、 S で割ります。
式 (1.11) から、引数の絶対誤差を表します。
したがって、その数 p文字数 n = 3 で取得する必要があります。
自分自身で調べて
おおよその数 a * = 1.0754327 とその限界絶対誤差を考えると D(a*)=0.0005.
この数値を正しい数値に丸めます。 丸め誤差を考慮してください。
テーラーの巻尺で、子午線の円周、皇帝キャノンの砲弾、テニス ボールを測定します。 最大の相対誤差を与える測定値はどれですか?
円の半径を0.5cmの精度で測ると、12cmという数字が得られました。 円の面積の絶対誤差と相対誤差を見つけます。
完了 算術演算ほぼすべての数字が正しい：
130,6 + 0,255 + 1,15224 + 41,84 + 11,8216;
35.2 1.748;
価値ある単位の数で表現できるものを呼びます。 たとえば、長さ、面積、体積は量です。 私たちがその真実性を疑っていない量の値は、正確であると呼ばれます。 （さらに遠く x は正確な数です). しかし実際には、通常、量の値を探すとき、その近似値しか得られません。 （さらに遠く a はおおよその数です ）。 例えば、測定時 物理量測定器を使用しています。
量の正確な値と近似値の差の係数は呼ばれます 絶対誤差
近似 絶対近似誤差または誤差範囲を制限する、または 絶対
エラー
番号と呼ばれる 
. このような評価は 無限の数. 最良の見積もり誤差範囲は最小の見積もりです。
正確な数の省略形:
量の正確な値のモジュラスに対する近似の絶対誤差の比率は、 相対誤差 . 実際には、相対誤差の制限 (相対誤差の推定) に使用されます。 相対誤差は通常 % で表されます。
その後の言葉 学年低下する。
例。 絶対および相対近似誤差を見つける a=3.14ために x=π.
と知られている 3,14 <π<3,15 .
ここから、つまり
それを考えると 3,14 <π<3,142, 次に、最良の見積もりを取得します
量の概算値の10進表記の桁 バツと呼ばれる 真実 広い意味で 、絶対近似誤差がその桁の単位を超えない場合 r、この数字が属する (ゼロの数字は単位の数字と見なされ、10 進数の数字は負の数字と見なされます)。 別の概念があります 狭義の真の姿 : . 今後は、広い意味での正しい数値を考えていきます。 残りの数字は呼ばれます 疑わしい . 有意義 10 進数形式で書かれた数値の桁は、0 を除いて、左側の最初の桁から始まるすべての数値の正しい桁です。左側のすべてのゼロは重要ではありません。 有効桁数によって、近似数の絶対誤差を簡単に見積もることができます。 絶対誤差を推定するには、最後の有効数字に続く 0.5 桁を取ることができます。 限界相対誤差は、分子が 1 である分数に等しいと見なすことができ、分母は、指定された数値のすべての有効数字を使用して記述された倍精度整数です。
例。 a=0.065;
タスク 1.1. 部屋の容積 Ⅴ 相対誤差を制限して決定 δ 有効桁数は何桁ですか Ⅴ ?
タスク 1.2. 近似値であることが知られている. あ それは持っています n 有効数字。 絶対誤差と相対誤差を推定します。
計算に関連する問題を解くと、数値結果が得られますが、これはしばしば正確ではありません。 エラーは、問題の定式化と計算の過程で発生します。
エラーの原因は次のとおりです。
1) 初期データのエラー。
2) 中間結果と最終結果の丸め誤差。
3) 問題を解く近似法の誤り。
おおよその数値で演算を実行するときは、次のことを行う必要があります。
1) 初期データの精度を知り、結果の精度を評価できる。
2) 結果の指定された精度を確保するために、そのような精度で初期データを取得します。
2.1 概数の誤差
数値 x を正確な値とし、数値 a をある量の近似値とします。
意味。数 x とその近似値 a の差は、近似数 a の誤差 Δ = |x-a | と呼ばれます。
x=10.5、a=10 とすると、Δ=10.5-10=0.5 となります。
x=9.5、a=10 とすると、Δ=9.5-10=-0.5 となります。
意味。数 x とその近似値 a との差の絶対値は、近似数 a の絶対誤差と呼ばれます。
x=10.5、a=10 とすると、Δa=|10.5-10|=0.5 となります。
x=9.5、a=10 とすると、Δa=|9.5-10|=0.5 となります。
多くの場合、正確な数 x は不明です。 その場合、Δа = |х-а| を見つけることは不可能であるため、絶対誤差の推定値 (限界絶対誤差 Δа ≥ Δа =x-а|) が使用されます。 この場合、数値 x は境界で囲まれています。
a - Δ a x a + Δ a または簡潔に: x = a ± Δ a.
彼らは次のように読みます: x は a に等しく、正確さは Δ a です。
実行された計算の品質を判断するには、測定値の絶対誤差の割合を判断する必要があります。 これを行うには、相対誤差を使用します。
意味。近似数 a の相対誤差 δа は、絶対誤差 Δа と数 x の法との比です。
また 
.
相対誤差 ba の推定値は、限界相対誤差です。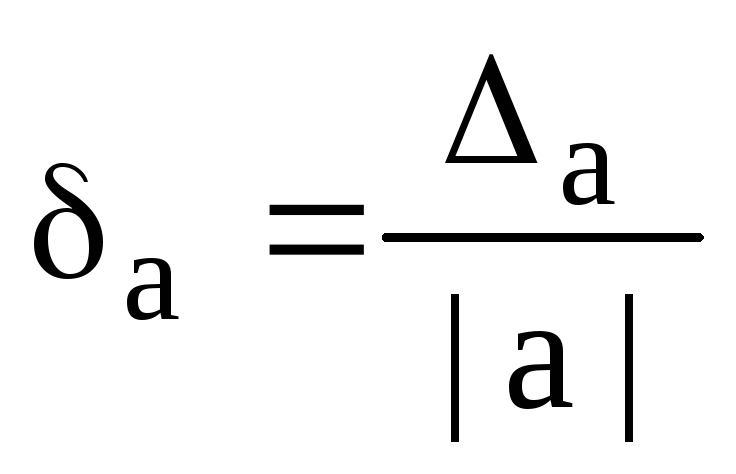 
例。数値 x=0.4287 とその近似値 a=0.4264 が与えられます。 数値 a の絶対誤差と相対誤差を求めます。
解決。数値 a の絶対誤差を計算してみましょう。
Δa=|0.4287-0.4264| = 0.0023。
数値 a の相対誤差を計算してみましょう。
または5.4％。
備考。 1.エラーを記録するときは、1〜2の有効数字を残すのが通例です。 エラーは常に切り上げられます。 この場合、正確な数 x の境界が拡張されます。
2. 数値 x が不明な場合は、数値 a を使用して相対誤差を求めます。
3. 相対誤差は、多くの場合、100% を掛けたパーセンテージで表されます。
2.2. 近似数の有効数字と真の数字
おおよその数 a の精度を評価するには、それを小数として書くのが通例です。 計算の精度は、小数点以下の桁数 (小数点以下の桁数) ではなく、結果の有効な有効桁数によって決まります。
意味。数値 a の有効桁数は、最初の非ゼロ桁の前に書かれたゼロと、数値の桁または精度を保持するために使用される場合はエントリの末尾にあるゼロを除いて、そのすべての桁です。
例。 a の有効数字を求めます。
a = 0.02701 => 有効数字: 2.7.0.1.
a = 0.0270 => 有効数字: 2.7.0.
a = 2700 => 有効数字: 2.7.0.0.
意味。近似数 a の数字 α i は、数字 a の極限絶対誤差が数字 α が含まれる数字の 1 (半分) を超えない場合、広義 (厳密な意味) で真の有効数字と呼ばれます。 i は Δ a 10 i (Δ a 0.5∙10 i) と書きます。
例。絶対誤差が Δ a = 0.0023 の場合、近似数 a = 0.7264 の正しい数値を決定します。
解決。絶対誤差 Δ a \u003d 0.0023 0.005 \u003d 0.5 ∙ 10 -2。 したがって、数字の 7 と 2 は厳密な意味で正しく、数字の 6 と 4 は正しくありません (疑わしい)。 Δ a = 0.0023 なので< 0,01 = 10 -2 , то цифры 7 и 2 являются верными в широком смысле.
備考。 1. 数学の表では、すべての有効数字は厳密な意味で正しいです。
2. 最終結果では、正しい数字だけを残すのが通例です。 次に、数値aの限界絶対誤差は、最下位桁の単位によって決定されます。 たとえば、a = 127.38 とすると、厳密な意味ですべての数値が正しい場合は Δ a = 0.01 となり、広義ですべての数値が正しい場合は Δ a = 0.5 ∙ 0.01 = 0.005 となります。
例。 13/19=0.684 または 
=7,21?
解決。 a = 0.684、b = 7.21 とします。 これらの数値の絶対誤差を見つけてみましょう。 これを行うには、13/19 を取り、 小数点以下の桁数が多い: 13/39=0.68421..., =7,2111...
Δ a =|0.68421...-0.684|< 0,00022, Δ в = |7,2111...-7,21| < 0,0012.
相対誤差を見つけてみましょう。
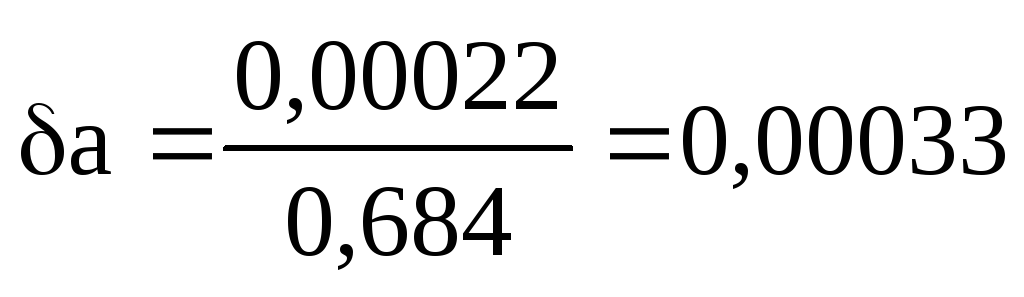または0.033％。
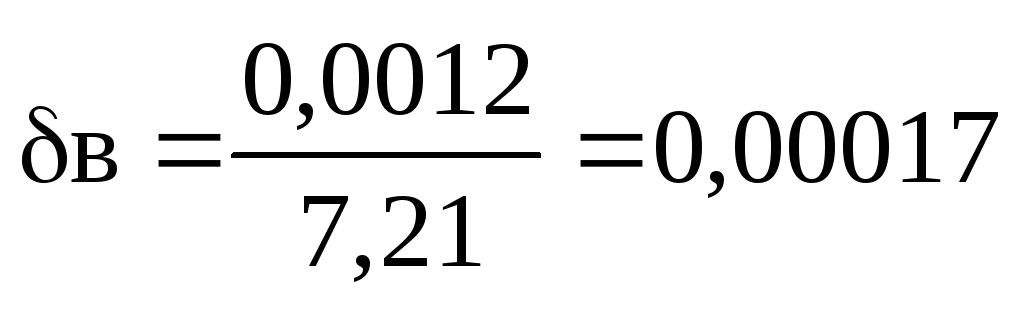または0.017％。
2 番目の式はより正確です。 
.
2.3. 丸め数
近似計算では、概算と正確の両方の数値を丸める必要があることがよくあります。つまり、最後の桁の 1 つ以上を破棄する必要があります。 数値を丸める場合、有効桁数の少ないおおよその数値に置き換えるため、丸め誤差が生じます。 このエラーを最小限に抑えるには、いくつかの丸め規則に従う必要があります。
ルール 私. 破棄された数字の左側の最初の数字が 5 より大きい場合、保持された数字の最後の数字が増幅されます。 1つ増えます。 増幅は、破棄された数字の最初の左が 5 で、その後にゼロ以外の数字が続く場合にも実行されます。
例。 73.473 の 10 分の 1 に丸めると、73.5 になります。 7 > 5 であるため、最後の残りの桁が強化されます。
ルール Ⅱ. 破棄された最初の数字が 5 未満の場合、残りの最後の数字は拡張されません。つまり、変更されません。
例。 73.473 の 100 分の 1 に切り上げると、73.47 になります。
ルールⅢ. 破棄された数字の最初の左が 5 で、その後にゼロ以外の数字が続かない場合、最後に残った数字が奇数の場合はブーストされ、偶数の場合は変更されません (偶数のルール)。
例。 5.785 を 100 分の 1 に丸めると、5.78 になります。 最後に保存された数字 8 は偶数であるため、増幅は行いません。 5.775 を小数点第 2 位に四捨五入すると、5.78 になります。 最後に格納された数字 7 は、奇数であるため 1 増加します。
ルール III を 1 つの数値の丸めに適用しても、実際には計算の精度が向上するわけではありませんが、多数の丸めを行うと、過小数値と同じくらいの頻度で過大数値が発生します。 エラーの相互補償があり、結果はより正確になります。
したがって、上記の丸めルールを適用する場合、絶対丸め誤差は、残りの最後の有効桁数によって決定される桁単位の半分を超えません。
正確な数値 x が有効桁数 n に丸められる場合、結果の近似数値 a には、丸め誤差に等しい絶対誤差があります。 この場合、近似数 a は、狭義の正しい有効桁数が n 桁になります。
例。数値 x=26.837 を有効数字 3 桁に丸めると、a =26.8 が得られます。 = | 26.837-26.8 |=0.037< 0,05, т. е. число а имеет три верные значащие цифры в узком смысле.
おおよその数 a を丸めると、新しいおおよその数 a 1 が得られます。
意味。数 Δ a1 \u003d Δ a + Δ env は丸め誤差と呼ばれます。
数値 a 1 の絶対誤差は、元の数値 Δ a の絶対誤差と丸め誤差 Δ env の合計です。
Δ a1 = Δ a + Δ env.
例。数値 x = 34.124 ± 0.021 の疑わしい桁を四捨五入します。 結果の絶対誤差を決定します。
解決。おおよその数 a=34.124 には、狭義の 3 つの正しい数があります: 3、4、1、Δ a = 0.021 から< 0,05. Применяя правила округления, найдем приближенное значение а 1 , сохранив десятые доли: а 1 = 34,1. Погрешность округления Δ окр =|34,124-34,1|=0,024. Тогда абсолютная погрешность числа а 1 равна Δ а1 =Δ а +Δ окр =0,021+0,024 = 0,045 < 0,05.
したがって、数値 a 2 のすべての有効数字は (狭義で) 正しいです。
したがって、x=34.1±0.045 です。
しかし、（狭義の）正しい有効桁数が n 桁の近似数値 a を有効桁数 n 桁に丸めると、丸められた数値 a 1 は広義の正しい有効桁数が n 桁になる場合があります。
例。おおよその数 a=15.3654 (± 0.0018) は、狭義の 4 つの正しい有効数字 (1、5、3、6) を持ちます。これは、Δ a = 0.0018 であるためです。< 0,005. При округлении до четырех значащих цифр получим а 1 = 15,37 и Δ а1 =Δ а +Δ окр =0,0018+|15,3654-15,37|=0,0064.
明らかに、0.005< 0,0064 < 0,01. Следовательно, число 15,37 (± 0.0064) は、広い意味で 4 桁の正しい数字です。
したがって、x=15.37±0.0064 です。
例。 a = 26.7245 (± 0.0026) の疑わしい数字を四捨五入し、狭義の正しい符号を残します。 結果の絶対誤差を決定します。
解決。条件により Δ a = 0.0026< 0,005, следовательно, в числе 26,7245 верными в узком смысле являются цифры 2, 6, 7, 2. Используя правила округления, найдем приближенное значение а 1 , сохранив сотые доли:
結果の誤差は 0.005 (0.005< 0,0071), поэтому уменьшим число цифр в приближенном числе до трех; а 2 = 26.7。 Δ a2 = = Δ a + Δ env = 0.0026 + | 26.7245-26.7 | = 0.0271 が見つかります。< 0,05. Следовательно, оставшиеся три цифры верны в узком смысле.
したがって、x=26.7 ±0.0271 => x=26.7 ±0.03 となり、誤差を小数点以下 2 桁に丸めます。
例。数 a = 22.7314 の疑わしい桁を四捨五入し、狭義の正しい符号を残します。 δ a = 0.2% の場合、数値の絶対誤差を決定します。
解決。δ a と書く 小数の形式で: δа=0.002 絶対誤差を決定します。 Δa \u003d \u003d 0.0455以来< 0,05, то верными в этом числе будут три цифры: 2, 2, 7. Округлим число 22,7314, сохранив в нем десятые доли: а 1 = 22.73。 次に、Δ a1 = = Δ a + Δ env = 0.0455 + | 22.7314-22.73 | = 0.0769> 0.05 なので、近似数の桁数を 2 に減らします: a 2 = 23. Δ a2 = = Δ a + Δ env = 0.0455 + | 22.7314-23 | = 0.3141 が見つかります。< 0,05. Следовательно, оставшиеся две цифры верны в узком смысле.
したがって、x=23±0.3141 => x=23±0.32 です。
2.3. 概数演算の規則
ルール 1いくつかの近似数の代数和の絶対誤差は、これらの数の絶対誤差の和に等しくなります。
Δ a ± b = Δ a + Δ b
ルール 2いくつかの近似数の積の相対誤差は、これらの数の相対誤差の合計に等しくなります。
δ av \u003d δ a + δ c。
ルール 3部分近似数の相対誤差は、これらの相対数の合計に等しくなります: δ a / b \u003d δ a + δ c.
ルール 4近似数 a の次数の相対誤差は、δa n = nδ a です。
ルール 5近似数 a の根の相対誤差は次のとおりです。 
.
ルール6計算するとき、誤差の厳密な計算が行われない場合は、数を数える規則を使用することをお勧めします。 これらのルールは、桁を超えた計算を行わずに結果が可能な限り正確になるように、結果を丸める方法を指定します。
ルールは、演算対象の数値に有効な数字のみが含まれており、演算の数が少ないことを前提としています。
I. おおよその数値を加算および減算する場合、結果は、小数点以下の桁数が最も小さい数値の小数点以下の桁数を保持する必要があります。
Ⅱ． 乗算と除算を行う場合、結果は、有効桁数が最も少ない数値と同じ数の有効桁数を保持する必要があります。
III. おおよその数を累乗すると、累乗の基数と同じ数の有効桁数が保持されるはずです。
IV. 近似数からルートを抽出するときは、ルート数と同じ数の有効数字を保持する必要があります。
V. 中間結果では、ルール I ～ IV で推奨されているよりも 1 ～ 2 桁多い数字を維持する必要があります。 最終結果では、数値の丸めにより「予備の桁」が破棄されます。
Ⅵ． 一部のソース データの小数点以下の桁数 (加算と減算の場合) または有効桁数 (その他の演算の場合) が他よりも多い場合は、最初に切り上げて、「安全な数値」を 1 つだけ保持する必要があります。
VII. N 桁の正しい結果を取得するには、前の規則に従って結果に N + 1 桁を提供するような桁数でソース データを取得する必要があります。
例。エラーを考慮せずに s=2.35+11.8 を見つけてみましょう。 ルール I を適用すると、s=14.15 が得られます。 結果は、小数点以下の桁数が最も少ない 11.8 に丸められます。 s \u003d 14.2.
エラーを考慮して問題を解いてみましょう。 数 s=14.15 では、正しい数のみを残してください。 これを行うには、ルール 1 を使用して合計 s の極限絶対誤差を見つけます。数値 2.35 と 11.8 のすべての数値が正しいとすると、次のようになります。Δ 14.15 = Δ 2.35 + Δ 11.8 = 0.01 +0.1=0.11< 0,5. Последняя верная цифра в числе 14,15 находится в разряде единиц. Поэтому число s=14,15 надо округлить: s=14 и найти абсолютную погрешность округленного числа. Погрешность округления равна: |14,15-14|=0,15. Тогда абсолютная погрешность округленного числа Δ 14 =0,11+0,15=0,26 <0,5. Окончательный результат примет вид: s=14 ± 0,26.
近似数に対して他の操作を実行する場合も同様に問題が解決されます。
知識ベースであなたの良い仕事を送信するのは簡単です。 以下のフォームを使用してください
研究や仕事で知識ベースを使用する学生、大学院生、若い科学者は、あなたに非常に感謝しています。
ポストする http://www.allbest.ru/
ポストする http://www.allbest.ru/
モスクワ経済大学、経営と法律
エッセイ
規律によって:
« より高いメートル数学»
« Pおおよその計算と誤差推定〇止まる»
完了: 学生
ヤンチュク・リュドミラ・アレクサンドロヴナ
科学ディレクター ピテルツェワ・ガリーナ・アレクサンドロヴナ
モスクワ、2000年
プラン
序章。 現代科学技術におけるコンピューティング
1.近似値と近似誤差
2. 数値の丸め。 丸め誤差
結論。 コンピューティングに関する情報
文学
序章。 現代科学技術におけるコンピューティング
測定と計算は、古くから社会生活において重要な役割を果たしてきました。 収穫を計算し、船の容量を測定し、土地区画のサイズを測定し、大きな構造物の建設中に計算を行い、さまざまな天文学的な計算を実行する必要があります-これは、人々が古代に解決しなければならなかったタスクの不完全なリストです.
最近の最も重要な出来事の 1 つは、人類による宇宙探査です。 私たちは、月、金星、火星への飛行、有人軌道ステーションの作成を不安に思っています。 宇宙船の打ち上げは、船の動きの正確な計算がなければ考えられないでしょう。これには、膨大で複雑な計算作業が必要です。
科学技術革命の時代である近代において、数学的手法の役割はますます大きくなっています。 数学的方法は、物理学だけでなく、化学、生物学、医学、経済学、歴史、言語学でも使用されています。
産業企業、科学研究機関、政府機関、農場、集団農場の日々の現在の活動において、数学者やエンジニアは多くの計算作業を行う必要があります。
計算手法は現在、経済計算、個々の企業、地域、および国の経済全体の作業を計画する際に広く使用されています。
数値的な結果を得るためには、一人の能力を超える計算が必要となる問題が数多くあります。 ダムの弾性応力の計算、飛行中に航空機が受ける抵抗の計算、または発射体の軌道は、このような問題の例です。 何十人ものコンピューター エンジニアが、さまざまなコンピューターを使用して、この複雑な計算作業を実行しています。
コンピュータの出現は、コンピューティング技術に革命をもたらしました。 しかし、数学的問題の解決をコンピュータに転送して数値結果を得ることができる段階にするためには、多くの計算機の作業も必要です。 コンピュータの作成は、数学自体、特にその応用分野の発展を刺激し、現在では計算は補助的なものではなく、多くの科学的および技術的成果において主要な役割を果たしています。 実用的な性質の数学的問題の解決を完了する必要がある場合は常に、数値結果を取得する必要があります。 初期データが近似値である場合、結果の精度を達成することは不可能です。 初期データの精度を評価し、達成できる結果の精度と、得られた数値結果の実際の使用に必要な結果の精度を決定できなければなりません。 非常に高い精度が必要な計算もあれば、そうでない計算もあります。 このことから、最小限の計算労力で必要な精度の結果が得られるように計算を整理する必要があることは明らかです。
この目標を達成するには、次のことが必要です。
おおよそのデータを使用して計算の原則と規則を研究します。
口頭計算、数学表、事務会計、計算尺、アリスモメーター、半自動および自動コンピューターのさまざまな方法を含む、利用可能な手段の助けを借りて、合理的な計算に必要なスキルを習得すること。
1.近似値と近似誤差
実際の活動では、人はさまざまな量を測定し、材料と労働生産物を考慮し、さまざまな計算を実行する必要があります。 さまざまな測定、カウント、計算の結果は数字です。 測定の結果として得られた数値は、ある程度の精度で近似的にのみ、目的の値を特徴付けます。 測定器の不正確さ、視覚器官の不完全さのために正確な測定は不可能であり、測定対象自体が正確にそれらの値を決定できない場合があります。
たとえば、スエズ運河の長さは 160 km、モスクワからレニングラードまでの鉄道距離は 651 km であることがわかっています。 ここに、最大 1 キロメートルの精度で行われた測定結果があります。 たとえば、長方形のセクションの長さが29 m、幅が12 mの場合、おそらく、測定は最大1メートルの精度で行われ、メートルの端数は無視されました。
測定を行う前に、実行する必要がある精度を決定する必要があります。 測定単位のどの分数を考慮する必要があり、どれを無視する必要があるか。
ある程度の価値があれば あ、その真の値は不明であり、この値の近似値 (近似値) は次のようになります。 バツ、あの人たちは書く あ バツ.
同じ量の測定値が異なると、異なる近似が得られます。 これらの近似のそれぞれは、測定値の真の値とは異なります。たとえば、次のようになります。 あ、ある量で、私たちはそれを呼び出します エラー。意味。 数値 x がある量の近似値 (近似値) である場合、その真の値は数値に等しい あ、次に、数の差のモジュラス、 あと バツと呼ばれる 絶対誤差与えられた近似と表示 aバツ: または単に a. したがって、定義により、
aバツ = a- バツ (1)
この定義から、
a = バツ aバツ (2)
私たちが話している量がわかっている場合は、表記法で aバツ索引 あを省略し、等式 (2) は次のように記述されます。
a = バツ バツ (3)
ほとんどの場合、目的の値の真の値は不明であるため、この値の近似で絶対誤差を見つけることは不可能です。 それぞれの特定のケースで正の数のみを示すことができ、この絶対誤差を超えることはできません。 この数は、量の近似の絶対誤差の限界と呼ばれます aと表記 時間 a. したがって、 バツは、近似を取得するための特定の手順に対する値 a の任意の近似です。
aバツ = a- バツ 時間 a (4)
以上のことから、 時間 a量の近似の絶対誤差の境界です あ、次により大きい任意の数 時間 a、量の近似の絶対誤差の境界にもなります あ.
実際には、不等式 (4) を満たす最小の数値を絶対誤差の限界として選択するのが通例です。
不等式を解く a- バツ 時間 a私たちはそれを得る あ境界内に含まれる
バツ-h a a バツ+h a (5)
絶対誤差境界のより厳密な概念は、次のように与えられます。
させて バツ- 多くの可能な近似 バツ量 あ近似値を取得するための特定の手順について。 その後、任意の数 時間、条件を満たす a- バツ 時間 a任意の バツ バツ、セットからの近似の絶対誤差の境界と呼ばれます バツ. で表す 時間 a既知の最小数 時間. この番号 時間 a実際には、絶対誤差の境界として選択されます。
絶対近似誤差は、測定の品質を特徴付けるものではありません。 実際、1cmの精度で長さを測定すると、鉛筆の長さを決定する場合、これは精度が低くなります. 1cmの精度でバレーボールコートの長さまたは幅を決定すると、これは高精度になります。
測定精度を特徴付けるために、相対誤差の概念が導入されています。
意味。 もしも aバツ：絶対近似誤差あり バツある量、その真の値は数に等しい あ、次に比率 aバツ数値のモジュラスに バツは近似の相対誤差と呼ばれ、次のように表されます。 aバツまた バツ.
したがって、定義により、
相対誤差は通常、パーセンテージで表されます。
ほとんどの場合、次元量である絶対誤差とは異なり、相対誤差は無次元量です。
実際には、考慮されるのは相対誤差ではなく、いわゆる相対誤差限界です: そのような数 え a、これは目的の値の近似の相対誤差を超えることはできません。
したがって、 aバツ え a.
もしも 時間 a-- 量の近似値の絶対誤差の限界 あ、 それか aバツ 時間 aそれゆえ
明らかに、任意の数 え、条件を満たす、相対誤差の境界になります。 実際には、ある程度の近似は通常知られています バツ量 あそして絶対誤差限界。 次に、番号
2. 数値の丸め。 丸め誤差
計算を実行するとき、数値を四捨五入することが必要になることがよくあります。 有効桁数の少ない数字に置き換えます。
数値を四捨五入するには、次の 3 つの方法があります。
切り捨て k番目の有効数字は、で始まるすべての数字を破棄することです (k+1) 番目。
切り上げは、格納された最後の桁が 1 増加するという点で、切り捨てとは異なります。
最小誤差での丸めは、破棄された最初の数字が 4 より大きい場合にのみ、格納された最後の数字の 1 による増加が実行されるという点で、超過での丸めとは異なります。
例外: 誤差が最小の丸めで 1 桁の 5 のみを破棄する場合、格納された最後の桁が偶数の場合は変更されず、奇数の場合は 1 増加します。
上記の近似値の丸め規則から、誤差が最小の丸めによって発生する誤差は、最後に格納された桁の単位の半分を超えず、不足または過剰で丸めた場合、誤差は半分以上になる可能性があります。最後に保存された数字の単位ですが、この放電の単位全体を超えてはなりません。
次の例でこれを見てみましょう。
1.金額の誤差。させて バツ あ, で-- 値の概算 b. させて バツと で-- 対応する近似値の絶対誤差 バツと で. 絶対誤差限界を求めよう 時間 a+b金額 x+y、これは合計の近似値です a+b.
a = バツ + バツ、
b = y + y.
これら 2 つの等式を追加すると、次のようになります。
a + b = バツ + y + ×＋ y.
明らかに、近似値の和の誤差 バツと で項の誤差の合計に等しい、つまり
(バツ + y) = バツ + y
和のモジュラスは、項のモジュライの和以下であることが知られています。 それが理由です
(バツ + y) = バツ + y バツ + y
これは、近似値の合計の絶対誤差が項の絶対誤差の合計を超えないことを意味します。 したがって、項の絶対誤差の限界の合計は、合計の絶対誤差の限界と見なすことができます。
量の絶対誤差の境界を示す あ終えた 時間 a、および b を介して 時間 b持つでしょう
時間 a + b = 時間 a + 時間 b
2. 差分エラー。させて バツと で-- 近似誤差 バツ と でそれぞれ aと b.
a = バツ + バツ、
b = y + y.
最初の等号から 2 番目を引くと、次のようになります。
a - b = (バツ - y) + ( バツ - y)
明らかに、近似の差の誤差は、被減数と減数の誤差の差に等しくなります。
(バツ - y) = バツ - y) ,
(バツ - y) = バツ + (- y)
そして、足し算の場合と同じように議論すると、
(バツ - y) = バツ + (- y) バツ + y
したがって、差の絶対誤差は被減数と減数の絶対誤差の合計を超えません。
差の絶対誤差の境界については、被減数と減数の絶対誤差の境界の合計を取ることができます。 したがって。
時間 a - b = 時間 a + 時間 b (9)
式 (9) から、差の絶対誤差の限界は、各近似の絶対誤差の限界より小さくなり得ないということになります。 これは、計算で時々使用される近似値を減算するためのルールを意味します。
いくつかの量の近似値である数値を減算する場合、結果は、小数点以下の桁数が最も小さい近似値と同じ小数点以下の桁数になるはずです。
3.製品エラー。数の積を考える バツと で、これは量の近似値です a と b. で表す バツ近似誤差 バツ、そして で-- 近似誤差 で,
a = バツ + バツ、
b = y + y.
これら 2 つの等式を乗算すると、次のようになります。
絶対積誤差 フに等しい
したがって
得られた不等式の両辺を フ、 我々が得る
積の係数が係数の係数の積に等しいことを考慮すると、次のようになります。
ここで不等式の左辺は積の相対誤差です フ, -- 相対近似誤差 バツ、相対近似誤差 で. したがって、ここで小さな値を捨てると、不等式が得られます。
したがって、近似の積の相対誤差は、因子の相対誤差の合計を超えません。 したがって、因子の相対誤差の限界の合計は、積の相対誤差の限界になります。
え ab = え a + え b (10)
式 (10) から、積の相対誤差の限界は、最も精度の低い要因の相対誤差の限界より小さくなり得ないということになります。 したがって、ここでは、前の手順と同様に、因数に過剰な有効桁数を保持することは意味がありません。
作業量を減らすために、計算で次の規則を使用すると便利な場合があります。有効桁数が異なる近似値を乗算する場合、結果は、有効桁数が最小の近似値と同じ数の有効桁数を保持する必要があります。
4.商の誤差。もしも バツ-- 値の概算 あ、そのエラー バツ、あ で-- 値の概算 bエラーあり y、 それか
まず、商の絶対誤差を計算しましょう。
そして相対誤差：
それを考慮して yに比べて少し y、分数の絶対値は1に等しいと見なすことができます。 それから
最後の式から、商の相対誤差は被除数と除数の相対誤差の合計を超えないことがわかります。 したがって、商の相対誤差の限界は、被除数と除数の相対誤差の限界の合計に等しいと仮定できます。
5. 次数と根の誤差。 1) しましょう あなた = a n、 どこ nは自然数であり、x とする。 もし え a-- 相対近似誤差の境界 バツ量 a、 それか
したがって
したがって、次数の相対誤差の限界は、底の相対誤差の限界と指数の積に等しくなります。
え あなた = n え a (11)
2)どこにしよう nは自然数とし、 あ バツ.
式（11）より
それゆえ
誤差控除の計算
したがって、根の相対誤差の境界 n学位 n根数の相対誤差の限界の 1 倍未満。
6. 近似計算の逆問題。直接問題では、関数の近似値を見つける必要があります あなた=へ(x, y, ...,n) 与えられた引数の近似値によると
と誤差範囲 時間 a、ある関数の引数の誤差で表される
時間 あなた = (時間 バツ, 時間 y, …, 時間 z) (12)
実際には、多くの場合、逆問題を解く必要があります。この問題では、引数の値をどの程度の精度で指定する必要があるかを調べる必要があります。 x、y、…、z対応する関数値を計算する あなた = へ(x, y, ...,z) 所定の精度 h u で。
したがって、逆問題を解くときに求められるのは、関数の指定された誤差限界に関連付けられた引数の誤差限界です。 時間 あなた式（12）、および逆問題の解決策は、式をコンパイルして解くことに還元されます 時間 あなた = (時間 バツ, 時間 y, …, 時間 z) 比較的 時間 バツ, 時間 y, …, 時間 z. このような方程式には、無限の数の解があるか、まったく解がありません。 そのような方程式の解が少なくとも 1 つ見つかった場合、問題は解決されたと見なされます。
多くの場合不定である逆問題を解くには、未知の誤差の比率に追加の条件を導入する必要があります。
結論。 についてのいくつかの情報それらを計算するバツナイキ
初期データの精度と計算の目的に応じて、さまざまな計算ツールが使用されます。 多くの大衆専門職の労働者は、ロシアのそろばん、算数計算尺、アリスモメーター、あらゆる種類のポケットおよびデスクトップ電子計算機（マイクロおよびミニ計算機）を数えることで、計算を大幅に容易にし、時間と労力を節約します。
現在わが国で使用されているミニ電卓のクラスには、電子デスクトップ電卓の Iskra ファミリと、数種類のポケット電卓も含まれる Elektronika ファミリの電卓が含まれます。 明らかな理由から、これらの計算機は時代遅れですが、それでも、これらは国内産業によって製造された唯一のモデルです。
Elektronika および Iskra ファミリのマシンは、主に単純な工学会計および会計問題を有効数字 8 ～ 10 桁の精度で解決することを目的としています。 それらの多くは、初等関数の値の自動計算の可能性を提供し、プログラム制御の要素があります。
私たちの産業と農業の技術機器の急速な成長、科学の発展に伴い、あらゆる種類の計算の必要性がますます高まっています。 高速電子計算機 (コンピューター) を使用すると、研究者は、解決に時間がかかりすぎたため、以前は提起されなかった問題を解決できるようになりました。
電子計算機は、方程式の数値解法などに使用されます。 最初のコンピューターは、この種の計算専用に設計されました。
現在、コンピューターは技術プロセスを制御するためにうまく使用されています。 流れの速いプロセスを制御するために、そのプロセスで得られたデータに基づく複雑な計算が必要な場合、そのようなタスクはコンピュータなしでは一般的に不可能です。
文学
代数と分析の始まり。 パート1。編。 おやすみなさい。 ヤコブレフ。 - M.:ナウカ、1981年、336ページ。
ヴィゴツキー M.Ya. 高等数学のハンドブック。 M.: 1987.
計測学の紹介。 Tyurin N.I., M., Publishing House of Standards, 1976, 304 p.
Allbest.ruでホスト
...類似文書
おおよその数の絶対および相対誤差の決定。 結果の誤差の推定。 データの内挿と外挿、ラグランジュとニュートンの内挿多項式、それらの主な特徴と比較説明。
研究室での作業、2013 年 8 月 6 日追加
絶対誤差と相対誤差の本質と数学的解釈、それらに沿った値の書き方。 近似値と近似誤差の概念、これらのカテゴリの分析の方向性。 小数の丸めのルール。
要約、2014 年 9 月 13 日追加
数学的および応用問題の数値解法で発生する主なタイプのエラーの特性と特徴：問題、方法、丸め。 測定誤差の概念と原因。 ランダムエラー、モーメントの説明。
テスト、2012 年 1 月 13 日追加
物理量の真の値に関する古典的な測定理論、その主な仮定。 表現方法、そのタイプによるエラーの分類：絶対、縮小、および相対。 ランダムエラー、その分布の法則。
要約、2014 年 7 月 6 日追加
指定された数値を小数点以下 6 桁、5 桁、4 桁、および 3 桁に丸めます。 各丸め後の誤差の計算。 オペランドa、b、c、およびdのすべての符号が正しいという事実を考慮して、関数uの値を計算する際の絶対および相対誤差の決定。
テスト、2012 年 5 月 2 日追加
エラーを決定する方法の調査と分布の統計的評価。 確率変数の各値に対するイベントの特殊性を決定する経験的関数の構築。 特定のサンプルの計算、その分析、およびパラメーターの決定。
タームペーパー、2011 年 1 月 13 日追加
数値計算手法の紹介、計算実験の構築計画。 計算の精度、エラーの分類。 数値積分法と微分法の復習、事後誤差の推定。 線形方程式系を解く。
トレーニング マニュアル、2010 年 9 月 23 日追加
無限に減少する等比数列の数と値の決定。 量の相対誤差の計算。 マシンのゼロと無限の値を決定します。 引数に応じたエラーの動作。
研究室での作業、2014 年 11 月 15 日に追加
系の右側の誤差に対する解の誤差の依存性の調査。 与えられた精度で方程式の根を決定します。 座標によるメソッドの精度推定値の計算。 スプライン補間と微分方程式の解。
テスト、2011 年 4 月 26 日追加
微分方程式のコーシー問題の解。 近似解の誤差。 明示的なオイラー法を実装する関数。 ルンゲの法則による誤差の計算。 二次微分方程式の解。 マトリックスの安定条件。