絶対誤差近似的な数値は、この数値とその正確な値の差の係数と呼ばれます。 。 または の中に何が含まれているかということになります。
例1.同社には 1,284 人の労働者と従業員がいます。 この数値を 1300 に四捨五入すると、絶対誤差は |1300 - 1284|=16 になります。 1280 に四捨五入すると、絶対誤差は |1280 - 1284| になります。 = 4.
相対誤差近似数の絶対誤差と近似数の絶対値の比です。 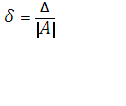 .
.
例 2
。 この学校には 197 人の生徒がいます。 この数値を 200 に丸めます。絶対誤差は |200 - 197| です。 = 3。相対誤差は 3/|197| です。 または1.5%。
ほとんどの場合、それを知ることは不可能です 正確な値おおよその数値、つまり誤差の正確な大きさ。 ただし、ほとんどの場合、誤差 (絶対または相対) が特定の数値を超えないことを確認できます。
例 3.売り手は秤でスイカの重さを量ります。 セットの最小重量は 50 g です。計量すると 3600 g になりました。この数値はおおよその値です。 スイカの正確な重さは不明です。 ただし、絶対誤差は 50 g を超えず、相対誤差は 50/3600 ≈1.4% を超えません。
例 3 では、最大絶対誤差は 50 g、最大相対誤差は 1.4% とみなすことができます。
絶対誤差はギリシャ文字の Δ (「デルタ」) または D で表されます。 ある; 相対誤差 - ギリシャ文字の δ (「小さなデルタ」)。 近似数が文字 A で示される場合、δ = Δ/|A| となります。
有効数字近似数 A は 0 以外の 10 進表現の任意の数字であり、それが有効数字の間に含まれる場合、または格納された小数点以下の桁を表す場合は 0 になります。
例。 A= 0.002080。 ここでは、最初の 3 つのゼロのみが重要ではありません。
n近似数 A の最初の有効数字は次のとおりです。 忠実な、この数値の絶対誤差が表現された桁の半分を超えない場合 n– 左から右に数えて th 番目の有効数字。 正しくない番号が呼び出されます 疑わしい。
例。数なら ある= 0.03450 すべての数値が正しい場合、 。
近似的な数値を含むアクションの結果も近似的な数値になります。 同時に、これらの数値の正確な桁を演算して得られる数値も不正確であることが判明する可能性があります。
例5。近似値 60.2 と 80.1 を掛け合わせます。 書かれた数値はすべて正しいことが知られているため、実際の値はおおよその値と 100 分の 1、1000 分の 1 などの部分だけ異なる場合があります。 製品では 4822.02 が得られます。 ここでは、100 分の 1 と 10 の位の数だけでなく、単位の数も間違っている可能性があります。 たとえば、正確な数値 60.25 と 80.14 を四捨五入して係数を取得するとします。 この場合、正確な積は 4828.435 となるため、近似積 (2) の単位桁は正確な積 (8) と 6 単位異なります。
近似計算の理論により、次のことが可能になります。
1) データの正確性の程度を知っているため、アクションを実行する前でも結果の正確性の程度を評価します。
2) 必要な結果の精度を確保するには十分であるが、計算機が無駄な計算を行わないようにするほど高すぎない、適切な精度のデータを取得します。
3) 計算プロセス自体を合理化し、結果の正確な数値に影響を与えない計算から解放します。
絶対測定誤差は測定結果の差によって決まる量です バツそして測定量の真の値 バツ 0:
Δ バツ = |バツ – バツ 0 |.
値 δ は、絶対測定誤差と測定結果の比に等しく、相対誤差と呼ばれます。
例2.1。π の近似値は 3.14 です。 その場合、その誤差は 0.00159... になります。 絶対誤差は 0.0016、相対誤差は 0.0016 / 3.14 = 0.00051 = 0.051% とみなすことができます。
重要な数字。 値aの絶対誤差が1桁単位を超えない場合 最後の桁数字が a の場合、その数字にはすべて正しい符号があると言われます。 正しい符号のみを残して、おおよその数値を書き留める必要があります。 たとえば、数値 52,400 の絶対誤差が 100 の場合、この数値は、たとえば 524 · 10 2 または 0.524 · 10 5 のように記述する必要があります。 おおよその数値に含まれる正しい有効桁数を示すことで、その数値の誤差を推定できます。 有効数字を数えるとき、数値の左側のゼロはカウントされません。
たとえば、数値 0.0283 には有効な有効数字が 3 つあり、2.5400 には有効な有効数字が 5 つあります。
数値の四捨五入のルール。 おおよその数値に余分な (または間違った) 桁が含まれている場合は、四捨五入する必要があります。 丸めが発生する場合 追加のエラー、最後の有効数字の単位桁の半分を超えない ( d) 四捨五入された数値。 四捨五入する場合、正しい数字のみが保持されます。 余分な文字は破棄され、最初に破棄される数字が次の値以上である場合、 d/2 の場合、保存されている最後の桁が 1 つ増加します。
整数内の余分な桁はゼロに置き換えられ、 小数(余分なゼロも同様に) 破棄されます。 たとえば、測定誤差が 0.001 mm の場合、結果 1.07005 は 1.070 に丸められます。 ゼロで変更されて破棄された最初の桁が 5 未満の場合、残りの桁は変更されません。 たとえば、測定精度 50 の数値 148,935 の丸め値は 148,900 です。ゼロに置き換えられるか破棄される最初の数字が 5 で、その後に数字またはゼロがない場合、最も近い値に丸められます。偶数。 たとえば、数値 123.50 は 124 に四捨五入されます。最初のゼロまたは小数桁が 5 より大きいか 5 に等しいが、その後に有効数字が続く場合、最後に残った桁は 1 ずつ増分されます。 たとえば、数値 6783.6 は 6784 に丸められます。
例2.2。 1284 を 1300 に丸める場合、絶対誤差は 1300 – 1284 = 16 になり、1280 に丸める場合、絶対誤差は 1280 – 1284 = 4 になります。
例2.3。 数値 197 を 200 に四捨五入すると、絶対誤差は 200 – 197 = 3 になります。相対誤差は 3/197 ≈ 0.01523、つまり約 3/200 ≈ 1.5% になります。
例2.4。 売り手は秤でスイカの重さを量ります。 セットの最小重量は 50 g です。計量すると 3600 g になりました。この数値はおおよその値です。 スイカの正確な重さは不明です。 ただし、絶対誤差は 50 g を超えず、相対誤差は 50/3600 = 1.4% を超えません。
問題を解決する際のエラー パソコン
通常、エラーの主な原因として 3 つのタイプのエラーが考えられます。 これらは、切り捨て誤差、丸め誤差、伝播誤差と呼ばれます。 たとえば、非線形方程式の根を探索するために反復法を使用する場合、正確な解が得られる直接法とは対照的に、結果は近似値になります。
切り捨てエラー
このタイプのエラーは、タスク自体に固有のエラーに関連しています。 ソース データの決定が不正確であることが原因である可能性があります。 たとえば、問題ステートメントで何らかの寸法が指定されている場合、実際のオブジェクトでは、これらの寸法は常にある程度の精度でわかっています。 他の物理パラメータにも同じことが当てはまります。 これには、計算式やそれに含まれる数値係数の不正確さも含まれます。
伝播エラー
このタイプのエラーは、問題を解決するための 1 つまたは別の方法の使用に関連しています。 計算中に、誤差の蓄積、つまり伝播が必然的に発生します。 元のデータ自体が正確ではないことに加え、乗算や加算などを行うと新たな誤差が発生します。誤差の蓄積は性質と量によって異なります。 算術演算、計算に使用されます。
丸め誤差
このタイプのエラーは、次のような理由により発生します。 本当の意味数値はコンピュータによって常に正確に保存されるわけではありません。 実数がコンピュータのメモリに保存される場合、実数は電卓で数値が表示されるのとほぼ同じ方法で仮数と指数として書き込まれます。
本当の意味 物理量完全に正確に判断することはほぼ不可能です。 あらゆる測定操作には多くのエラー、言い換えれば不正確さが伴います。 エラーの理由は非常に異なる場合があります。 それらの発生は、測定装置の製造および調整における不正確さに関連している可能性があります。 物理的特徴研究対象の物体(たとえば、厚さが不均一なワイヤの直径を測定する場合、結果は測定領域の選択によってランダムに異なります)、ランダムな理由など。
実験者の仕事は、結果への影響を軽減し、得られた結果がどれだけ真の結果に近いかを示すことです。
絶対誤差と相対誤差の概念があります。
下 絶対誤差 測定により、測定結果と測定量の真の値との違いがわかります。
Δx i =x i -x および (2)
ここで、Δx i は i 番目の測定の絶対誤差、x i _ は i 番目の測定の結果、x は測定値の真の値です。
どれかの結果 物理的次元次の形式で記述するのが一般的です。
平均はどこですか 算術値測定値のうち、真の値に最も近い値 (x と ≈ の妥当性は以下に示されます) が絶対測定誤差です。
式 (3) は、測定量の真の値が [ - , + ] の範囲内にあると理解される必要があります。
絶対誤差は次元量であり、測定量と同じ次元を持ちます。
絶対誤差は、測定の精度を完全に特徴付けるものではありません。 実際、長さ 1 m と 5 mm のセグメントを同じ絶対誤差 ± 1 mm で測定すると、測定の精度は比類のないものになります。 したがって、絶対測定誤差とともに相対誤差も計算されます。
相対誤差測定値は、測定値自体に対する絶対誤差の比率です。
相対誤差は無次元量です。 それはパーセンテージで表されます。
上の例では、相対誤差は 0.1% と 20% です。 それらは互いに著しく異なりますが、 絶対値同じだ。 相対誤差は精度に関する情報を提供します
測定誤差
エラーの発現の性質と発生の理由に応じて、エラーは次のクラスに分類できます: 手段的、系統的、ランダム、およびミス (重大なエラー)。
エラーは、デバイスの誤動作、方法論や実験条件の違反、または主観的な性質のいずれかによって引き起こされます。 実際には、それらは他とは大きく異なる結果として定義されます。 それらの発生を排除するには、デバイスを扱うときに慎重かつ徹底的に行う必要があります。 エラーを含む結果は考慮から除外 (破棄) する必要があります。
機器のエラー。 測定装置が正常に動作し、調整されている場合は、装置の種類によって決まる制限された精度で測定を行うことができます。 ポインター計器の計器誤差は、そのスケールの最小目盛の半分に等しいと考えるのが通例です。 デジタル読み取り機能を備えた機器の場合、機器誤差は機器のスケールの最小 1 桁の値に相当します。
系統的誤差- これらは誤差であり、その大きさと符号は、同じ方法および同じ測定器を使用して実行された一連の測定全体で一定です。
測定を実行するときは、系統誤差を考慮するだけでなく、系統誤差を確実に除去することも重要です。
系統的誤差は通常、次の 4 つのグループに分類されます。
1) エラー。その性質は既知であり、その大きさは非常に正確に決定できます。 このような誤差は、たとえば、温度、湿度、気圧などに依存する空気中の測定質量の変化です。
2) エラー。その性質はわかっていますが、エラー自体の大きさは不明です。 このような誤差には、測定装置自体の故障、ゼロ値に対応しないスケール、または装置の精度クラスなど、測定装置によって引き起こされる誤差が含まれます。
3) エラー。その存在は疑わしいものではありませんが、その規模は重大であることがよくあります。 このような誤差は、複雑な測定で最もよく発生します。 このような誤差の簡単な例は、内部に空洞を含むサンプルの密度の測定です。
