測定は、測定値と別の値を測定単位として比較することとして理解されます。 測定時には、次の 3 つの連続した操作を実行する必要があります。
1) デバイスのチェックとセットアップ。
2) 彼らの証言を観察し、集計する。
3) 測定結果から目標値を計算し、誤差を推定します。
測定は直接測定と間接測定に分けられます。 直接測定では、決定される量が測定単位と直接比較されるか、適切な単位で校正された測定器を使用して比較されます。 このような測定には、定規、ノギス、マイクロメーターを使用した長さの測定が含まれます。 対応するデバイスのスケールに応じた体重、時間間隔、電圧または電流の測定。
で 間接測定私たちにとって関心のある物理量は、対応する公式に従った計算によって決定されます。 特定の式には、直接測定によって決定された多数のパラメーターが含まれています。
たとえば、音量を決めるとき、 Vシリンダー、直径を測定する必要があります Dそして高さ H、そして次の式に従って V = π HD 2 /4 体積を計算します。
計算式に含まれる一部の物理量(測定設定パラメータ、物理定数および数学定数)は変更されません。 x i一連の実験中に測定されます。 さらに、一般的な場合、それぞれの実験で測定された量の値は バツ 1 , バツ 2 , …, ×n異なる場合があります。
これは、何らかの量を測定するとき、常にその量の真の値ではなく近似値が得られるという事実によって説明されます。 その理由は、使用されるツールや装置の測定精度と、すべてを考慮することの不可能性の両方に関係しています。 外部要因最終的な測定結果に影響します。
同じ条件下で同じ機器を使用して同じ量を繰り返し測定した場合でも、結果はわずかに異なります。 したがって、いかなる測定も常に誤差を伴って実行されます。
測定誤差 (またはエラー) は、特定の測定結果の偏差です。 本当の価値測定された物理量。
仕事の終わり -
このトピックは以下に属します:
一般情報
物理量の測定誤差 測定は、測定された量と... 測定誤差の分類 ...
必要な場合は 追加の材料このトピックに関して、または探しているものが見つからなかった場合は、作品データベースの検索を使用することをお勧めします。
受け取った資料をどうするか:
この資料が役に立った場合は、ソーシャル ネットワーク上の自分のページに保存できます。
| つぶやき |
このセクションのすべてのトピック:
作業命令
1. ボールの軸方向の取り付け調整を行います。 これを行うには、ボールのリスクが同じレベルになるように、上にあるボールを回転させます。 2. 調整する
弾道振り子は質量 M の円柱です。
作業命令
1. 弾丸と振り子の質量は設置物に表示されます。 2. 吊り下げ点から振り子への糸の取り付け点までの距離 l を定規で測定します。 3. 振り子を持ち込む
作業命令
1. テーブルの上のピストルから砂箱または床の紙に 5 発撃ちます。 銃を撃つたびに、砂やシートについた弾丸の跡に、
設置方法と測定方法の説明
フライホイールは、巨大なディスクとシャフトに取り付けられたプーリーで構成されています。 シャフトはベアリングで固定されています。 プーリーに糸が巻かれており(一部の設置ではプーリーの役割をシャフトが担っています)、自由に動くようになります。
作業命令
1. 重りが三脚台座に触れないように糸の長さを調整します。 2. プーリーの直径をノギスで測定し、負荷の質量 m を決定します。 結果を次の場所に記録します
設置方法と測定方法の説明
設置装置を図に示します。 1.ベース1には調整可能な機能が装備されています
作業命令
1. 振り子のディスク上に、任意に選択したリングを固定します。 2. 振り子の軸がベースと平行であることに注意して、振り子の取り付けを修正します。
と摩擦力モーメントの決定
研究の目的: フライホイールの角加速度 b の引張力 Mn のモーメントへの依存性のグラフを作成し、そこから摩擦力のモーメントを決定すること
設置方法と測定方法の説明
フライホイールは、シャフトに取り付けられたディスク 1 とプーリー 2 で構成されます (図 1)。 軸
作業命令
1. プーリーの直径 D をノギスで測定します。 2. フライホイールを回して、糸に掛かった荷を高さ h まで持ち上げます。 定規で高さを測ります(基準に従ってカウントダウン)
設置方法と測定方法の説明
オーバーベックの振り子 (図 1) はフライホイールであり、取り付けられています。
作業命令
1. 負荷 m1 と m2 の質量を決定します (m1 は m2 の約 2 倍とします)。 からの高さ h を決定します。
設置方法と測定方法の説明
弾性糸で吊り下げられた剛体は、吊り下げ糸と一致する垂直軸に対して特定の角度だけ回転するとねじり振動を発生します。
作業命令
1. 下部のディスクを回転させて、システムを振動運動させます。 ディスクの質量中心が横に移動しないように、つまり垂直に移動しないようにしてください。 発振振幅
設置方法と測定方法の説明
作業命令
1. サポートプリズムをロッドの端に取り付けます。 サポートプリズムの端を備えた振り子をスタンドに置き、振動振幅が~6を超えないように振動運動をさせます。
外力の影響下では、あらゆるものが 個体変形、つまり形状と寸法が変化します。 弾性変形とは、力がなくなると消える変形のことです。 はい、きついです
関数(2)を時間で2回微分すると、
a = − w2Acos(wt + a) = − w2x。 (4) (4) を (3) に代入すると、w = が得られます。
作業命令
タスク 1 図 1 作業の目的: フックの法則を確認すること。 1. 質量 m の異なる重りをバネの下端に吊り下げます。
簡単な理論的情報
加速度を測定する最も間接的な方法 フリーフォール g は周期式の使用に基づいています 調和振動物理的な振り子&nb
設置方法と測定方法の説明
柱 2 はベース 1 に固定されています (図 1)。
作業命令
1. 1 つの重りをロッドの端近くに、もう 1 つをロッドの中央近くに取り付けます。 2. プリズムを向かい合うように取り付けます。 そのうちの 1 つを空きの近くに配置します
簡単な理論的情報
弦を張って振動を励起すると、波が弦に沿って伝わり、固定端で反射し、互いに加算されて複雑な振動パターンを作り出します。
インストールの説明
弦振動を励起させるために、作品内では共鳴法が用いられている。 弦は、磁場中で電流が流れる導体に作用する力によって動き始めます。 永久磁石p
作業命令
1. 本機を220Vネットワークに接続し、「NETWORK」ボタンを押します。 2. 電子ユニットが 1 ~ 2 分以内にモードに入るようにします。 3. 弦の張力 F = を設定します。
簡単な理論的情報
弾性媒体中での振動の伝播過程を波と呼びます。 振動の周期に等しい時間内に波が伝播する距離を波長といいます。 長さ
インストールの説明
設置の全体図を図に示します。 2. マイク 2 は金属パイプ 1 の端にしっかりと固定されています。電気力学的 g はロッド 3 の助けを借りてパイプに沿って自由に移動できます。
作業命令
1. スピーカーをオーディオ周波数発生器に接続し、マイクをオシロスコープに接続します。 ジェネレーターとオシロスコープをネットワークに接続します。 発電機周波数設定例
作業命令
度、度
電卓によるランダム誤差の計算
ランダム誤差は最終的な測定結果に影響を与え、過大評価または過小評価します。 したがって、数値軸上で間隔を示す必要があります(p. 8 を参照)。
§ 機械振動の基本公式
気体の分子動力学理論の基本式
I. 近似計算について
基本的な公式
基本的な公式
§ 力学における力
§ 10. 統計物理学の要素
§ 11. 熱力学の物理的基礎
1. 測定の種類。 エラーの分類
物理量 -これは、物理オブジェクト (システム、現象、またはプロセス) のプロパティの 1 つの特性です。 定性的には、同じ物理量が異なる量的表現を持つことができます。 特定の物体に固有の物理量の定量的確実性は、そのサイズによって特徴付けられます。 物理量の値は、その量に対して許容される特定の単位数の形でのこの量のサイズの推定値です。 物理量の値は、その量に選択された単位と数値の積として表されます。 数値は抽象的な数値です。 物理量の単位は、従来から 1 に等しい数値が割り当てられている物理量です。
プライム p: 長さの値は、L = 0.202 m = 20.2 cm = 202 mm として表すことができます。 したがって、ユニットの大きさが変わると物理量の数値も変化します。 値のサイズとその値は同じになります。
区別 真実物質の特性を理想的に反映する物理量の値、および 本物 -実験的に見つかった値。
物理量hの測定これは、使用に最も便利な形式でこの量の値を取得するために、測定された量をその単位と比較することにあります。 測定は以下を使用して行われます 技術的手段、単位を保存したり、物理量のスケールを再現したりします。
コンセプトを同一視すべきではない 寸法コンセプトとともに 測定中の観察 -で行われた実験操作 プロセス測定。 観察の結果は単一の値です ( 秒読み)測定値。 測定結果は、すべての測定値を数学的に処理した後に得られます。
単一の観測による測定測定が呼び出され、測定された量に関連付けられた物理量の異なる値で各読み取り値が取得されます。
例:さまざまな質量の物体に一定の力が作用したときの加速度の測定。
複数の観測による測定測定が呼び出され、測定された量に関連付けられた物理量の固定値ですべての読み取り値が取得されます。
例: 実験を繰り返して同じ力が作用したときの、所定の質量の物体の加速度の測定。
測定には主に 2 つのタイプがあります。 真っ直ぐと 間接的な.
直接測定これは物理量の測定と呼ばれ、その値は実験データから直接求められます。
例: 定規で長さを測定します。 オーム抵抗測定
間接測定による物理量の測定と呼ばれ、その値は、この量と直接測定によって値が得られる量との間の既知の関係に基づいて求められます。
プライム p: 電圧計と電流計でそれぞれ測定した電圧と電流による抵抗の決定。
ジョイントこのような測定は、2 つ以上の不均一な量を同時に測定して、それらの間の関係を見つけたり、この関係のパラメータを決定したりするものと呼ばれます。
例:オームの法則をテストするために、さまざまな電圧での電流を測定します。
測定対象モデル抽象的な、通常は現実のオブジェクトの理想化されたイメージと呼ばれます。
例: 物質点、絶対剛体、理想気体、均質導体。
測定方法測定された量をその単位と比較するための一連の方法です。 測定方法は測定対象の機種や利用可能な技術手段に応じて実施されます。
真の測定誤差とは、物理量の測定結果(実際の値)の真の値からのずれのことです。 測定を実行する場合、原則として、測定量の真の値は不明です。 測定結果は、 学年真の値は、ほとんどの場合一致しません。 真の値が既知であるか未知であるかに関係なく、誤差をいわゆる次の方法で特徴付けることが受け入れられています。 信頼区間、ある程度の確実性を持って真の値が含まれています。 この間隔の中央は、真の値の推定値と一致します (図 1)。
誤差は次のように表されます。 絶対と 相対的エラー。
絶対誤差推定値と区間の境界の差の係数に等しい , それらの。 信頼区間の半値幅。
相対誤差は、絶対誤差と真の値の推定値の比に等しくなります。 原則として、この誤差はパーセンテージで表されます。 相対誤差の逆数は次のように呼ばれます。 精度測定。
図1。 測定結果 x=(±?x)。たとえば、F=(53.2±0.3) H。
同じ物理量の測定結果を比較する場合は、次のようにしてください。 もしも 信頼区間重なり合うことを違いと言います 取るに足らない測定結果は一貫しています。 それ以外の場合は、差異が考慮されます 意味のあると測定結果が一致しません。
例: させてください さまざまな方法同じ力の測定では、次の結果が得られました: F=240±8 N、F=250±5 N。この場合の 10 N の差はわずかで、結果は一貫しています。 両方の結果が F=242±2 N、F=249±3 N である場合、7 N の差が大きくなり、測定結果は一致しません。
測定結果への影響に応じて、次のエラー クラスを区別できます。
系統的誤差 - 測定が繰り返されたときに一定のままであるか、定期的に変化する誤差。
ランダムエラー 測定を繰り返すとランダムに変化する誤差です。
逃す (失策 ) - 大幅に超える誤差
方法論上の誤り - 測定方法の不完全性による誤差。
器差 ・測定器(計器)の誤差。
追加のエラー - 測定対象のモデルで考慮されていない要因の影響による誤差。
系統誤差を考慮して除外 (または削減) することは、測定理論において最も困難な問題の 1 つです。 この問題を解決する方法は特定の種類の測定に依存し、それを解決するための一般的な方法論はありません。 包括的なアプローチがよく使用されます 理論的分析測定手順と使用される機器の特性。 このような分析により、系統誤差の限界を推定できます。 正確な測定では、系統誤差は、異なる機器を使用したさまざまな基本的に独立した方法で目的の値を測定した結果に基づいて推定されます。 多くの 現代的な方法装置を用いた系統誤差の解析 数学的統計(分散、回帰、相関、スペクトル分析)、決定理論、ゲーム理論など。これらの問題は、特別な計測コースでさらに詳しく検討されます。
ほとんどの場合、ランダム誤差は、測定結果の比較的単純な統計処理によって削減できます。
ミスとは、異常な測定結果を指します。これは、他の干渉要因よりも優勢な、測定プロセスに対する短期的な影響の結果である可能性があります。 スリップは、測定を行うオペレーターのミス、または測定機器の故障によって発生する可能性があります。 このような場合、異常な結果は破棄されなければなりません。 ただし、異常なデータを破棄するのは困難です。 物議を醸す問題それについては専門家の間で意見の一致がありません。 たとえば、歴史から
物理学者は、実験の異常な結果が偉大な発見につながったことを知っています。 したがって、いつ 科学研究そして、ほとんどの技術的な測定では、特に実験を何度も繰り返すことによって、滑りの原因を注意深く分析する必要があります。 ただし、十分に研究された状況で、それが見つからない場合は、 外的原因間違いです。異常なカウントを破棄するという問題は、すべての実験データを処理することに基づいて解決する必要があります。
物理的なワークショップの実験室での測定中、実験は次のような方法で組織されます。
1. 系統的エラー無視することも、その値を推定することもできます。
2. 器差には系統的成分のみが含まれます。
3. 追加誤差にはランダムな成分のみが含まれます。
4. 測定器や計器の読み取り値の精度は保証されています。
2. 直接測定の処理
2.1. 器差
デバイスのエラーを判断する方法は、デバイスのパスポートに記載されています。 ほとんどのデバイスを特徴付けるために、この概念がよく使用されます。 エラーの減少、測定スケールの範囲のパーセントで表した絶対誤差に等しい。 与えられた誤差に応じて、デバイスは精度クラスに分類されます。 精度等級は計器パネルに表示され、次の範囲の値を取ることができます。
0.05; 0.1; 0.2; 0.5 - 精度; 1.0; 1.5; 2.5; 4.0 - 技術的なデバイス.
最大絶対器差
A=K・A/100、(1)
ここで、K は精度クラス、A は 最高値楽器のスケール。
式 (1) から、測定値がインジケーターの矢印をフルスケールに向けた場合、相対誤差が最小になることがわかります。 したがって、機器を最適に使用するには、次のような制限が選択されます。 測定値が目盛の端まで下がった.
計測学では、式 (1) に加えて、特に不均一なスケールを持つ機器の場合、機器誤差と関連する精度クラスの他のより複雑な定義が使用されます。
直線寸法を測定する機器の器差は、絶対誤差または除算値で機器本体に表示されます。 精度クラスも絶対誤差もデバイスに示されていない場合は、最小の区分の価格の半分に等しいとみなされます。
測定値をデジタルで読み取る装置の場合、誤差の計算方法は装置のパスポート データに記載されています。 これらのデータが利用できない場合は、インジケーターの最後のデジタル桁の半分に等しい値が絶対誤差とみなされます。
器差が軽減できない
測定値の統計処理。
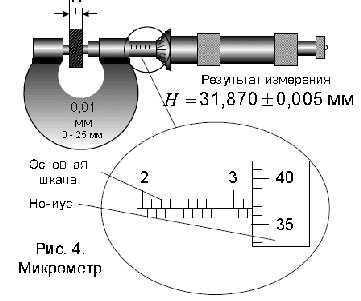
さまざまな楽器のスケールからの読み取りの例を図に示します。 2~7。
バーニア装置の原理については付録 5 で説明します。
2.2. ランダムエラー
ランダム誤差が存在する場合、複数の測定における測定量の観測値は、その真の値に対してランダムにばらつきます。 この場合、実際の値は一連の読み取り値の中で最も可能性の高い値として検出され、誤差は特定の確率で真の値をカバーする間隔の幅によって特徴付けられます。 以下の規定の数学的実証は、物理学における実際の研究に関連して、セクション 6、7、および 8 および文献に記載されています。
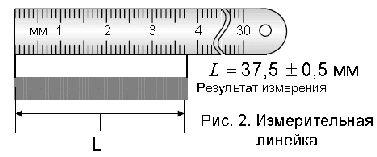

米。 3. キャリパー。

![]()

米。 7. デジタル抵抗計。
量の真の値の最良の推定値 バツは
標本平均
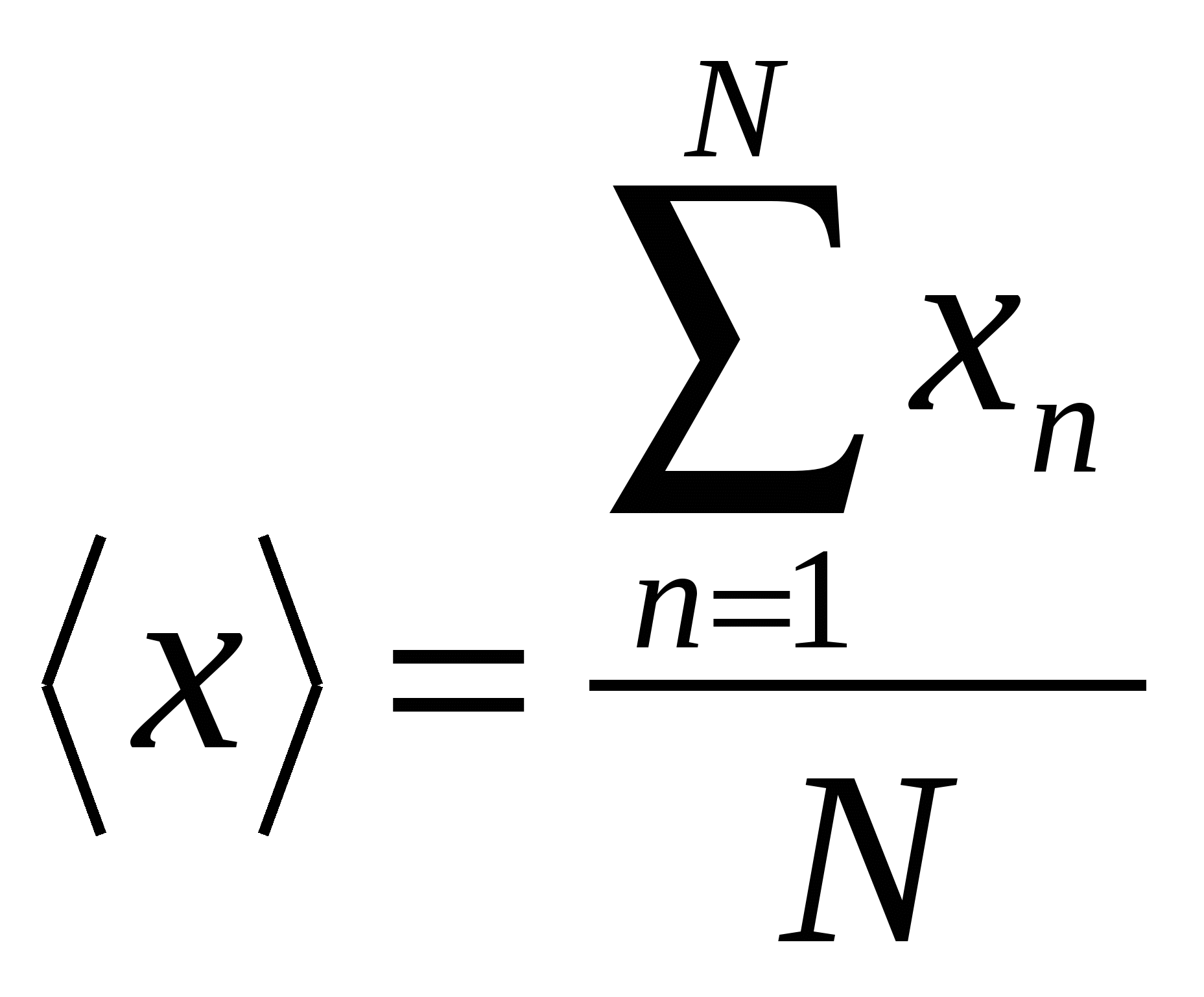 ,
(2)
,
(2)
どこ バツ n- 値の読み出し バツ, N読み取り回数です。
測定中の読み取り値のばらつきを推定するには、次を使用します。
サンプルのサンプル標準偏差
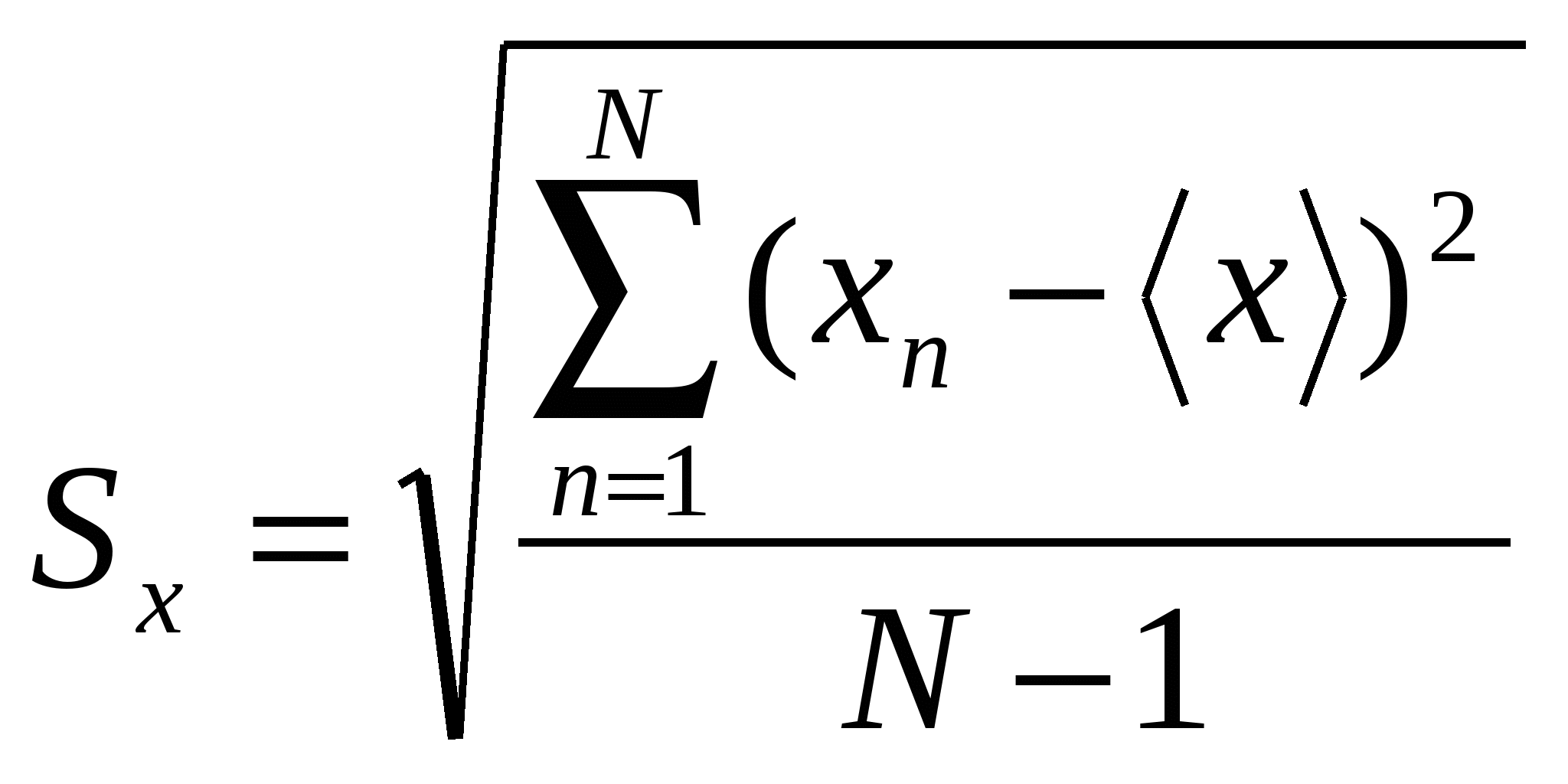 , (3)
, (3)
サンプル平均は確率変数であり、測定値の真の値に対するその広がりが推定されます。
平均値のサンプル標準偏差
 .
(4)
.
(4)
平均値の標準偏差N測定値 V 
1 回の測定値の標準偏差の 1 倍未満
信頼区間 間隔と呼ばれます

これには、一定の確実性で測定値の真の値が含まれます (図 1)。
信頼確率(信頼性) 一連の観測結果は、信頼区間に測定量の真の値が含まれる確率と呼ばれます。
誤差のランダム成分は通常、信頼区間の半値幅として表されます。 信頼区間のサイズは通常、次の倍数として与えられます。  価値観。 それから
価値観。 それから
複数の測定の誤差のランダム成分
 , (5)
, (5)
どこ
![]() - 無次元信頼係数(学生係数)。
- 無次元信頼係数(学生係数)。
信頼比 は、所定の測定回数で結果の所定の信頼性を得るために、平均の標準偏差を何回増やす必要があるかを示しています。 信頼係数は信頼性と測定数に複雑に依存し、その値は統計表 (付録 1) から決定されます。
ランダム誤差を計算する場合、それらは測定の信頼性によって与えられ、(測定の目的とその要件に応じて) 0.9 に等しくなります。 0.95; 0.96; 0.98; 0.99; 0.997; 0.999。
信頼レベルが高いほど信頼性が高くなります
間隔の推定値であると同時に、その境界よりも広い値です。
合計誤差  直接測定値は、その成分の二次和に等しい: 機器 -
直接測定値は、その成分の二次和に等しい: 機器 -  そしてランダム -
そしてランダム -
 , (6)
, (6)
2.3. ミス
測定値のミスをチェックして、直接測定の処理を開始することをお勧めします。 ミスを特定して破棄するための基準は数多くありますが、どれも普遍的なものではありません。 基準の選択は測定の目的によって異なりますが、一部のデータを破棄する決定は最終的には常に主観的です。
いわゆる式を定式化してみましょう ショーヴネ基準 。 N 個のサンプルを含む結果の系列から、異常なサンプルが選択されます - x k で、平均値からの偏差のモジュールがサンプル標準偏差の分数で計算されます。
 , (7)
, (7)
次に、この偏差の確率と、被験者の偏差 Z 以上の測定値が得られる予想される測定数 n が計算されます。 受け取った場合はn
M>N の場合、サンプル x k はミスとみなされます。 M と Z の関係は付録 3 に示されています。
直接測定値を処理するためのアルゴリズム
1. 器差を決定します。
2. 一連の測定の平均値を計算します - 式(2)
3. 読み取り値の標準偏差を計算します - 式(3)
ミスが修正された場合は 5 に進みます。
さもないと 4まで。
4. 読み取り値にミスがないか確認します。
異常な読み取り値を選択します。
その相対偏差を計算する - 式(7)
予想される測定値の数を決定します。
この数値はカウント数より大きく、
2 に進み、それ以外の場合 5に進みます。
5. サンプルの二乗平均の計算
平均値の偏差 - 式(4)
6. 特定の信頼係数を決定する
信頼性と取得された測定値の数 - 付録 1
7. ランダム誤差の計算 - 式(5)
8. 合計誤差の計算 - 式(6)
9. 四捨五入後、測定値の処理結果は次の形式で記述されます。
 ;
; 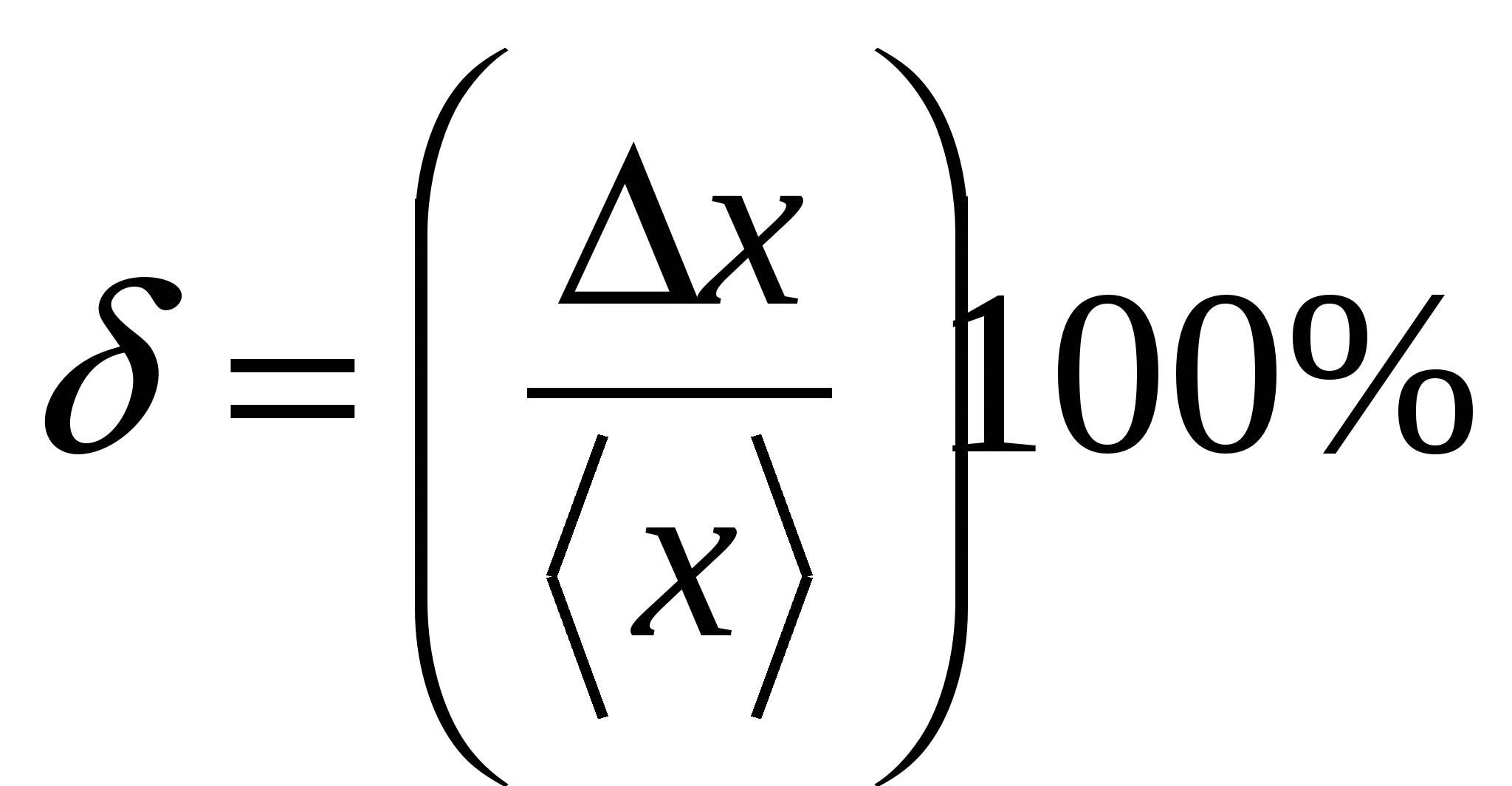 ; ?
; ?
場合によっては、同じ物理量のいくつかの一連の直接測定の結果を組み合わせることが必要になることがあります。 この問題は次の方法で解決できます。 結果を出しましょう M測定値は形式で表示されます  ,
,  , … ,
, … , 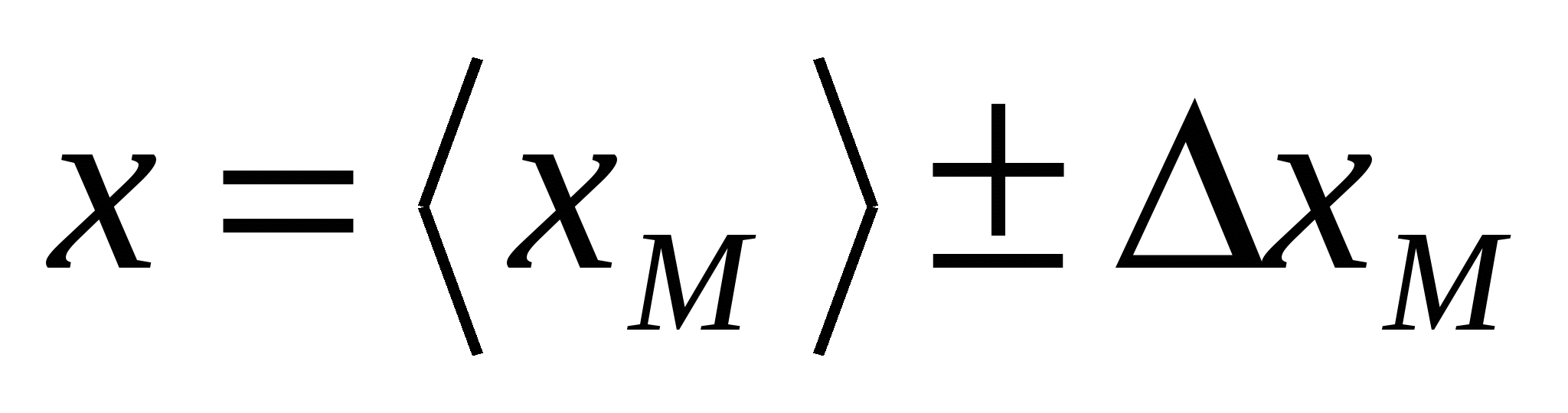 . お買い得
. お買い得 ![]()
そしてその誤差∆ バツとその誤差は次の式で計算されます。
 ,
, 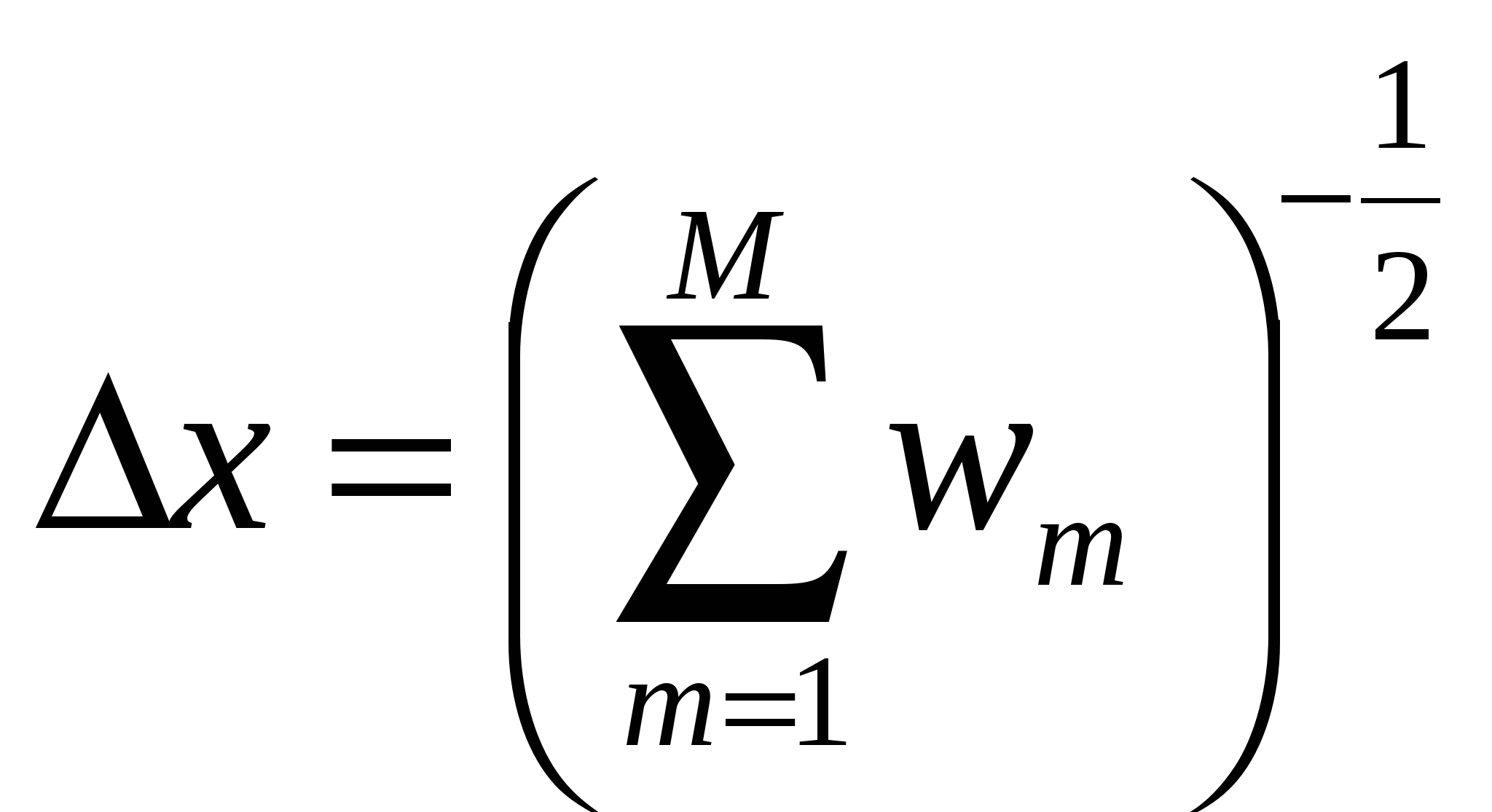 , (8)
, (8)
-
どこ 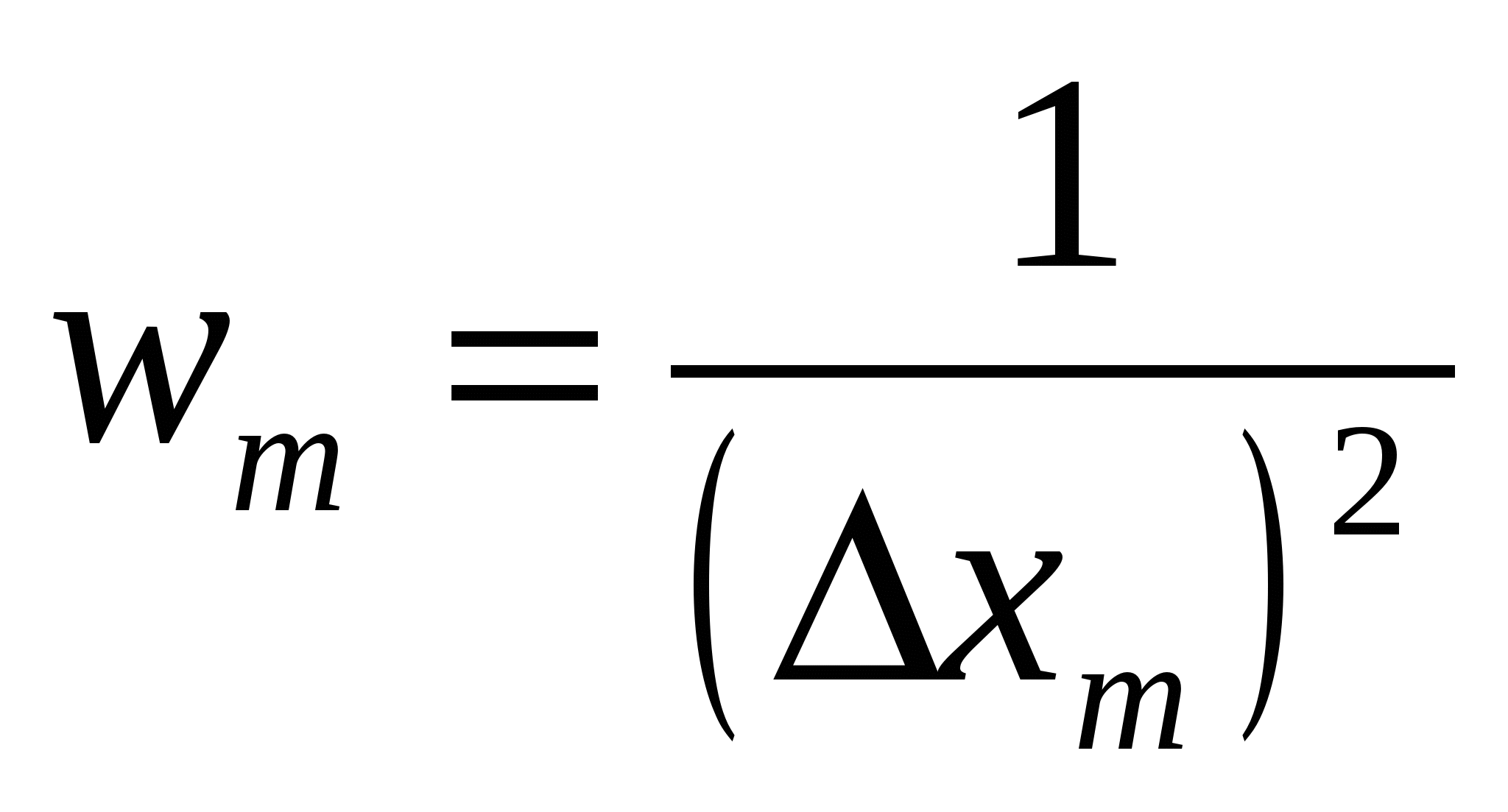 - 各一連の測定値の統計的重み。
- 各一連の測定値の統計的重み。
3. 間接測定の処理
しましょう u= f(x, y,…)- 測定値間の関数関係 あなたと数量 x、y,... 、その値は直接測定によって求められます。 実価  次のように定義されます。
次のように定義されます。
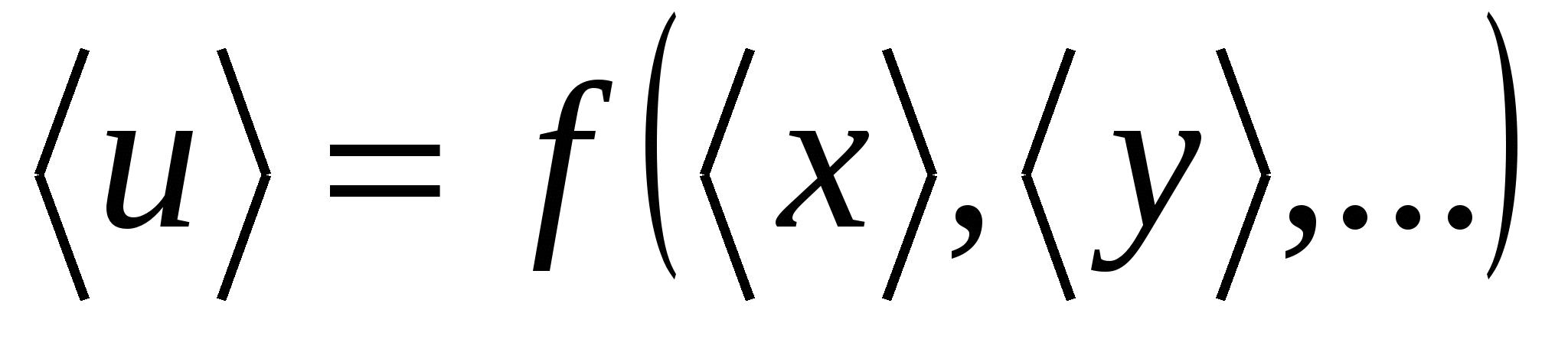 . (9)
. (9)
誤差 ∆ の式が得られます。 あなた。 たとえば、1 つを除くすべての引数の値を固定する場合、 バツの場合、引数が変更されたときの関数の増分は次の形式になります。
Δの値が バツ小さく、その後間隔 [  ,
,  ] 関数 u=f(x)線形と考えることができ、
] 関数 u=f(x)線形と考えることができ、
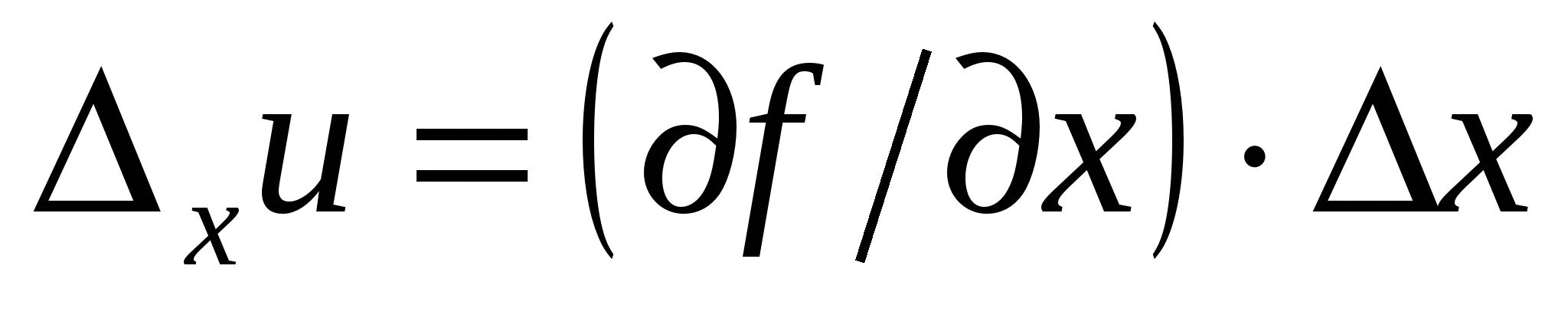 . (11)
. (11)
Δx値 あなた誤差 ∆ の特徴 あなた、誤差 ∆ のため バツ。 誤差成分Δも同様に求めます あなた、他の議論によって導入されました。 合計誤差 Δ あなた間接測定 あなたは、各引数によって提供されるコンポーネントの二次合計またはモジュロ合計を使用して計算されます。
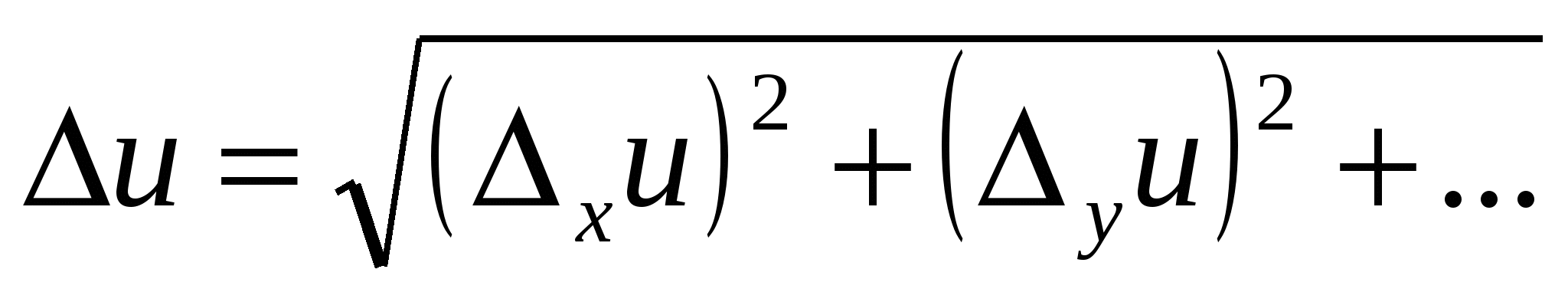 . (12)
. (12)
 . (13)
. (13)
関係式 (12) は、2 つの条件が満たされる場合に適用されます。 第一に、引数の誤りは多くの要因の影響によるものであり、その中で最も有力な要因はありません。 第二に、引数の誤差には統計的な関連性がありません。 それ以外の場合には、関係式(13)が使用される。 ただし、加算規則 (13) は、間接測定の誤差の値を過大評価することがよくあります。 誤差の合計の詳細については、セクション 8 で説明します。
例。 直流回路のあるセクションの抵抗値を、このセクションの電流と電圧の直接測定の結果から決定するとします。 電流と電圧の測定誤差が多くの要因(温度、電流計と電圧計の内部抵抗、電気的干渉、電源の不安定性など)の影響によるものである場合、誤差を合計するときに次のことを行う方がよいでしょう。式(12)を使用します。 直接測定の誤差が主に電源の内部抵抗のランダムな変化によるものである場合は、式 (13) を適用する方がよいでしょう。
関係式 (9-12) により、間接測定の処理に 2 つのアルゴリズムを使用できます。 そのうちの 1 つは偏導関数の解析式を見つける必要があり、もう 1 つは数値的手法のみが使用されます。 付録 3 には、実際によく遭遇するいくつかの関数関係について、最初の方法で誤差を計算する式が含まれています。
間接測定を処理するためのアルゴリズム
測定量の既知の依存性によると
直接測定を使用して計算する
関数の実際の値 - 式(9)
誤差成分を次のように計算します。
また
すべての引数に関して偏導関数を求めます。
そして誤差の成分を計算します - 式(11)
関数の合計誤差を計算する - 式(12)
四捨五入後、測定値を処理した結果
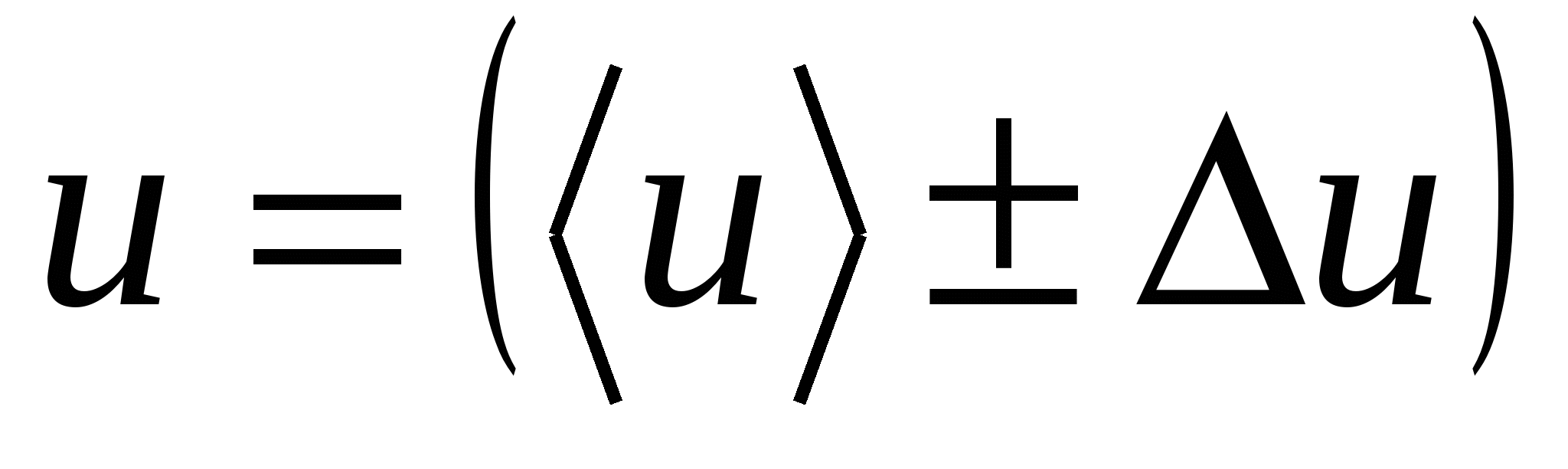 ;
; 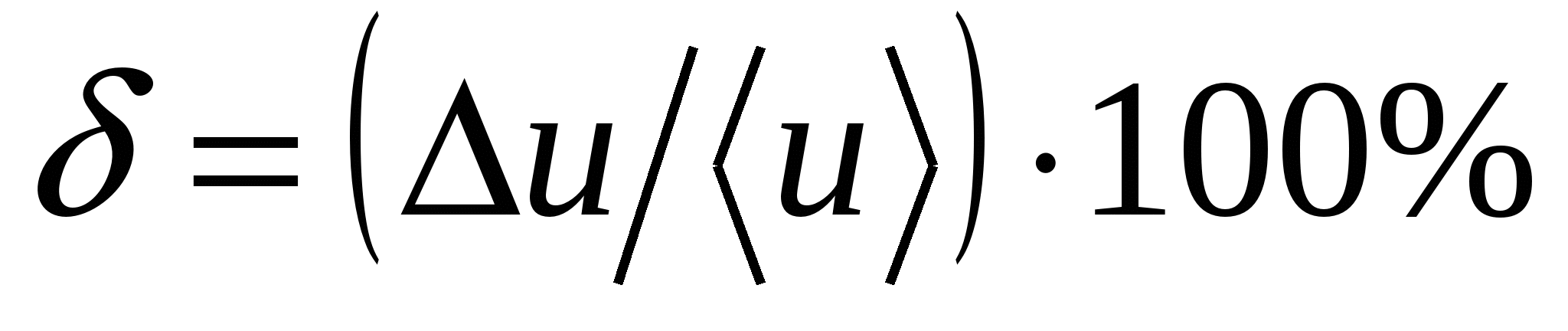 ; ?
; ?
よく測定される値 p関数の依存関係パラメータです y=f(x,p)量 バツと y、これらは単一の観測による一連の直接測定の結果として見つかります。 この場合、間接測定の誤差のランダム成分は  処理によって決定される 計算された価値観
処理によって決定される 計算された価値観 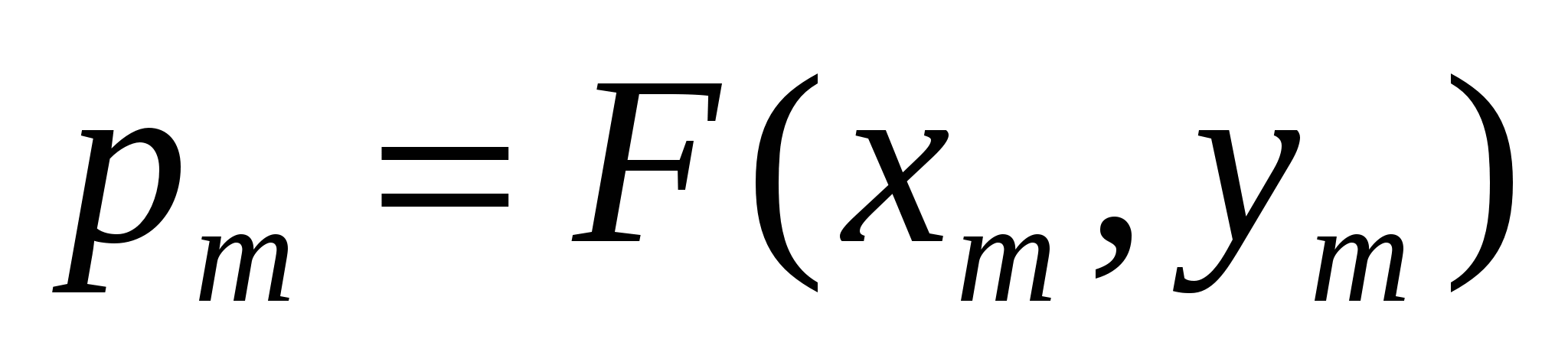 加工方法に応じて 直接測定(ここ メートル=1..M、M は値の単一観測値の数です。
加工方法に応じて 直接測定(ここ メートル=1..M、M は値の単一観測値の数です。
バツと y).
関数の間接測定の誤差は、原則として、 さらにエラーが発生その引数の直接測定。 ただし、特定の場合には、このルールに違反する可能性があります。 このような特殊な場合を、発振周期の測定を例にして考えてみましょう。
例。しましょう 直接測定ストップウォッチを使用した振動周期は、T=2.0±0.2 秒の値を受け取りました。 同じストップウォッチを使用して、N=100 回の振動が発生する時間を t=200±0.2 秒に固定することで、周期を間接的に測定できます。 この場合、周期 T=t/N、つまり、 T=2.000±0.002秒。 この場合、測定値について話しているので、合計の測定誤差が機器誤差よりも小さいというのは誤りです。 異なるサイズつまり、時間の直接的な測定と周期の間接的な測定です。 後者のタイプの測定は、器差に直接関係しません。
4. 四捨五入 近似値の四捨五入。
取るに足らない先頭のゼロは数値の桁です 小数部、1 未満、および数値の末尾にゼロがあり、四捨五入後に破棄された数字が置き換えられます。 残りの数字は次のように呼ばれます 意味のある。
怪しい人物測定結果は、誤差値の有効数字を含む最上位桁に対応する桁の桁です。 疑わしい数字の左側にある数字は次のように呼ばれます。 忠実な、右側に - 不貞な.
例。
数字は536±6。 0.00234±0.00002; 1.00±0.03; 2000±30 には有効数字 3 桁が含まれます。 数値 299793±1 を値 3・10 5 に四捨五入する場合、207 の誤差が許容されるため、結果の数値では百という数字は疑わしいため、最後の 2 つのゼロは重要ではありません。
誤差は通常 1 つの有効数字で表され、特に重要な測定値の場合にのみ 2 桁で表されます。
丸め誤差と実際の値 .
エラー 有効数字 1 桁に四捨五入されます。 この数字には疑問があります。 エラー値に正しい数値がありません .
実価 最も近い桁に四捨五入され、その桁は誤差の有効数字の桁に等しくなります。 実際の値の最後の桁は 疑わしいですが、残りの数値は正しいです。
特に正確な測定の場合、誤差は最初の桁が 4 未満の場合は有効数字 2 桁に丸められ、最初の桁が 3 を超える場合は 1 桁に丸められます。 2 桁目に 0 または 5 が残る場合があります。
計器スケールから読み取った記録番号 .
装置の目盛りから読み取った測定値の数値には、正しい数字と怪しい数字だけが記録されており、その桁は装置の器差の値によって決まります。
丸め数値。
整数の余分な桁はゼロに置き換えられ、小数部は切り捨てられます。 ゼロに置き換えられるか破棄される最上位桁が 5 未満の場合、残りの桁は変更されません。 指定した桁が 5 より大きい場合、最後に残った桁が 1 つ増えます。ゼロに置き換えられるか、または破棄される桁が 5 の場合、丸めは次のように実行されます。 最後の桁四捨五入した数値が偶数の場合は変化せず、奇数の場合は 1 増加します。
計算の四捨五入。
中間計算の結果を記録するとき、予備の桁、つまり疑わしい桁の右側の桁が 1 つ保存されます。 近似的な数値を加算および減算した場合、結果の疑わしい桁の桁は、項の疑わしい桁の最大桁と一致します。 乗算と除算の結果には、有効桁数が最も少ない元のデータと同数の有効桁が含まれます。 べき乗すると
近似数の(根を抽出する)場合、結果には底(根元式)にあるのと同じ数の有効桁数が含まれる必要があります。 対数を計算する場合、仮数には元の数値と同じ数の有効数字が格納されます。 オペランドの 1 つが正確な数値の場合、その桁数は演算結果の丸めに影響しません。 表形式のデータが計算に使用される場合、その数値はすべて正しいです。
二次和
二次和では、一方の数値が他方の数値より 3 倍以上小さい場合、その数値は無視できます。
測定結果を四捨五入する例を示します。
| 丸める前に記録する | 四捨五入後の記録 |
| 123357±678A/m。 | 123400±700A/m。 |
| 123357±678V。 | 123.4±0.7kV。 |
| 237.46±0.13mm | 237.5±0.1mm。 |
| 0.00283±0.00034kg。 | (2.8±0.3)10-3kg。 |
| 1.045±0.000003秒。 | 1.045000±0.000003秒。 |
| 359623±307秒。 | (359.6±0.3)10 3 秒。 |
| 0.000000047±0.0000000098メートル。 | 50±10nm。 |
| 67.89×10 -7 ±49.3×10 -8 A | 6.8±0.5μA。 |
| 589±0.69N | 589.0±0.7N |
| 589±0.078N | 589.00±0.08H. |
5. 測定結果の処理例
例5.1。直接測定の処理。
電圧計は電圧 U を 10 回測定しました 電子回路。 電圧計の精度クラスは K=2.5 で、最大スケール値は A=200 V です。測定結果を表に示します。 測定結果を処理して、98% の信頼性の電圧推定値を提供します。
| № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| U、V | 145 | 140 | 145 | 105 | 130 | 150 | 150 | 155 | 175 | 160 |
器差を計算します

与えられた信頼水準?=98% および読み取り数 N=10 の場合、係数 t 98;10 =2 を決定します (付録 1)。
平均値を計算する
![]()
測定値の標準偏差を計算します
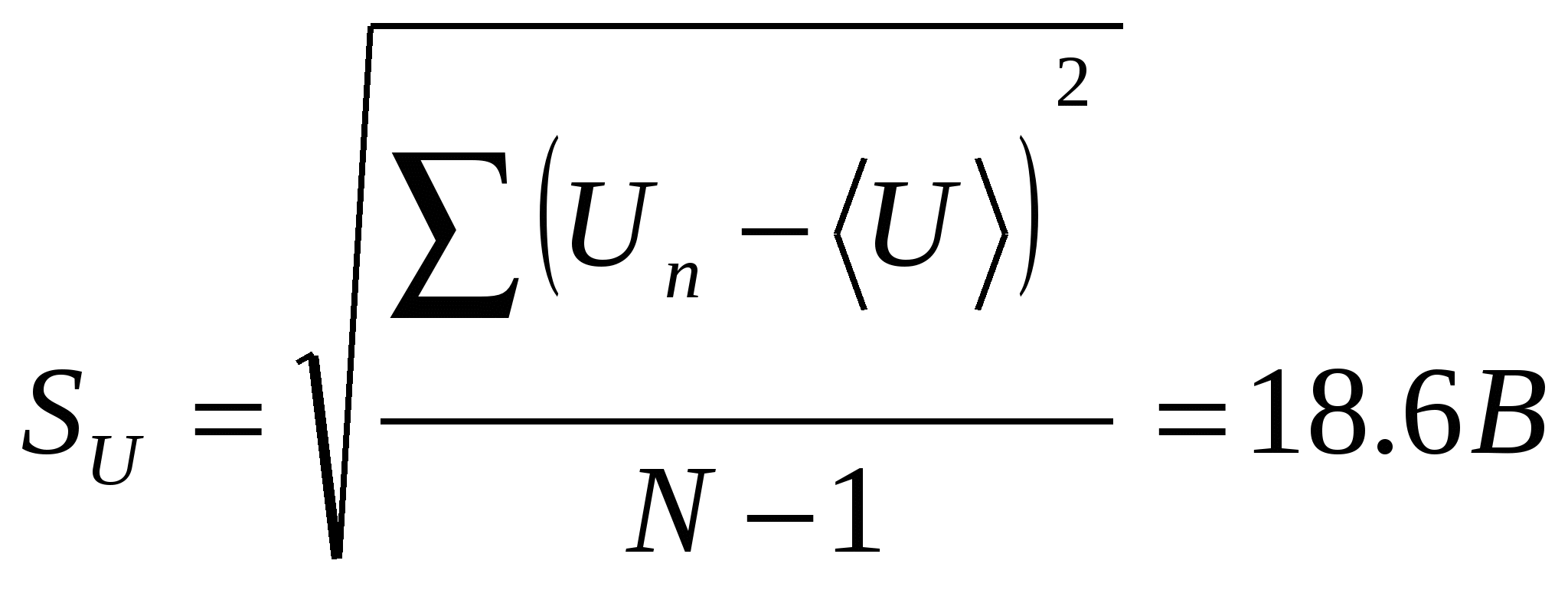
測定値にミスがないか確認します。
異常なカウントはカウント #4 です。 平均値から正規化された偏差 U 4 を計算します。
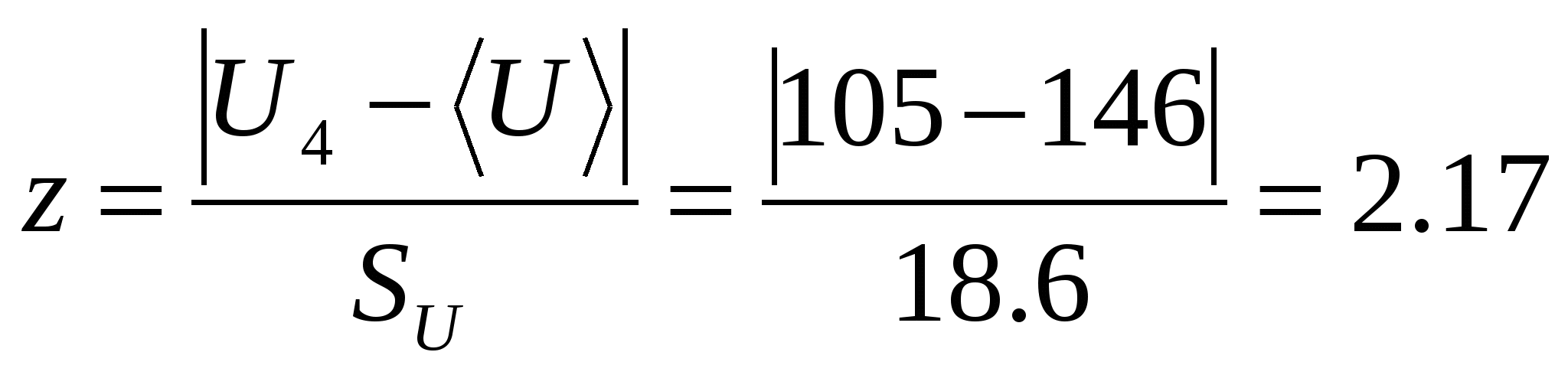
付録 3 によると、受信した読み取り値がミスであるとみなせない実験の数は 17 です。この数は N=10 よりも大きくなります。 したがって、読み取り値 U=105 V はミスであり、処理された一連のデータから削除する必要があります。
新しい一連の電圧測定値 (N=9、t 98;9 = 2.9)
| № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| U、V | 145 | 140 | 145 | 130 | 150 | 150 | 155 | 175 | 160 |
新しい平均を計算する

標準偏差を計算する

誤差のランダム成分を計算します

合計誤差を計算する
絶対
相対的
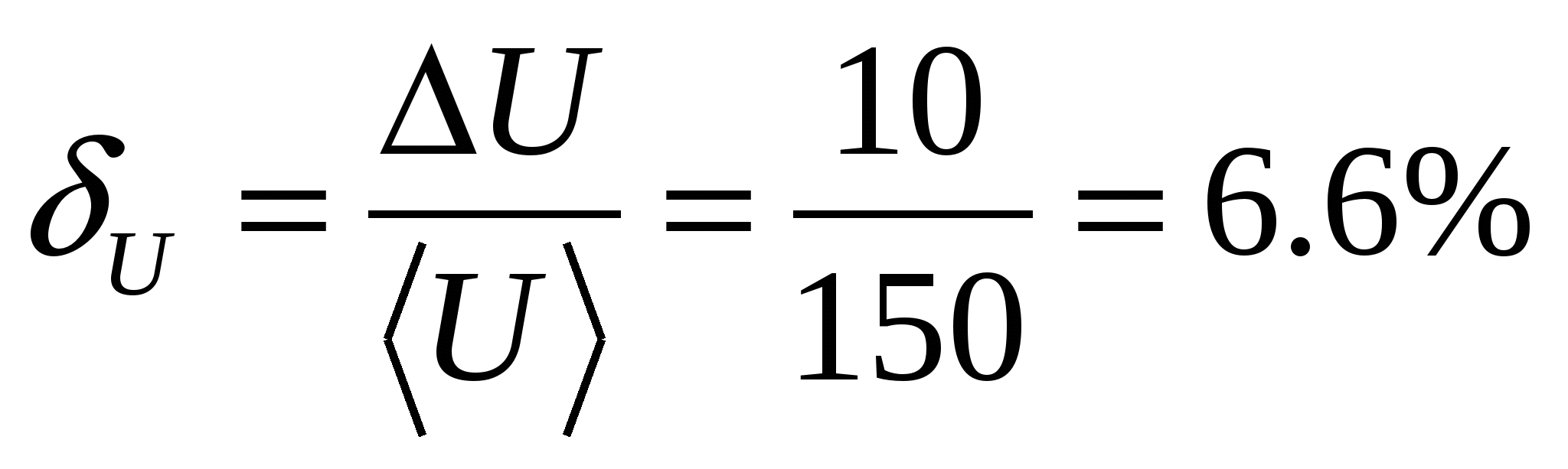
四捨五入後の電圧測定結果は次のように記述されます。
U=(150±10)B、?=7%、?=98%
例5.2。直接測定の結果を組み合わせる。
同じ導体の抵抗を 3 つの異なる条件下で測定しました。 測定結果は次のように表示されます。
R 1 \u003d (11 ± 2) オーム。
R 2 \u003d (12 ± 2) オーム。
R 3 \u003d (10 ± 3) オーム。
これらの測定値を組み合わせる必要があります。
各測定値の統計的重み (寄与度) を見つける
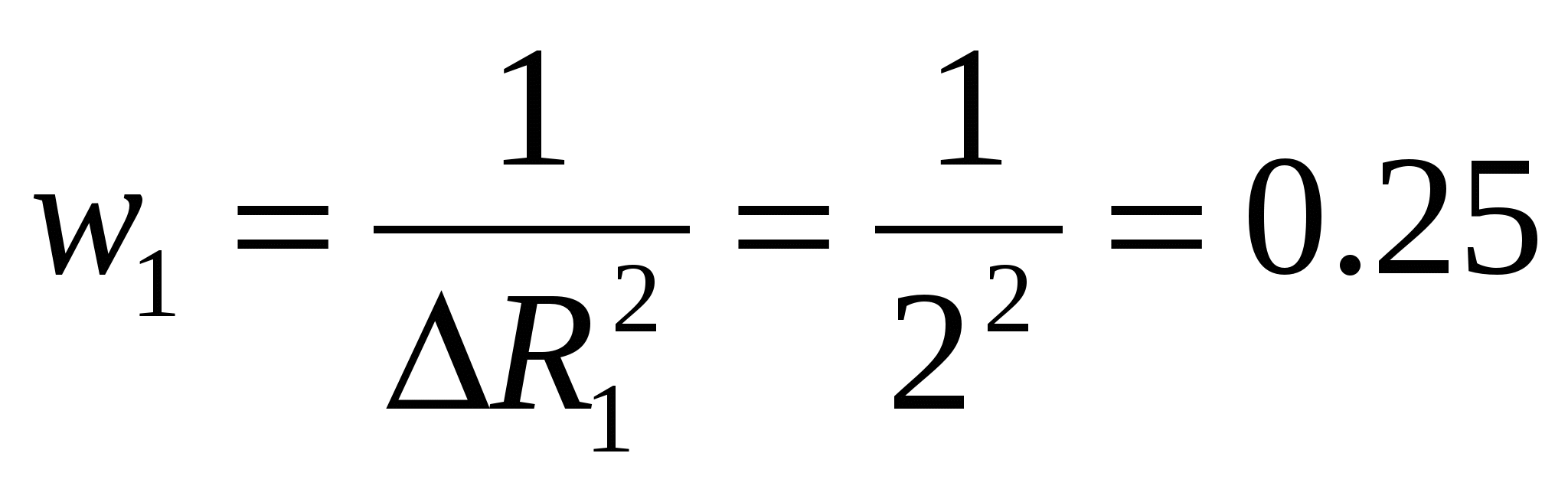 1/オーム2、
1/オーム2、
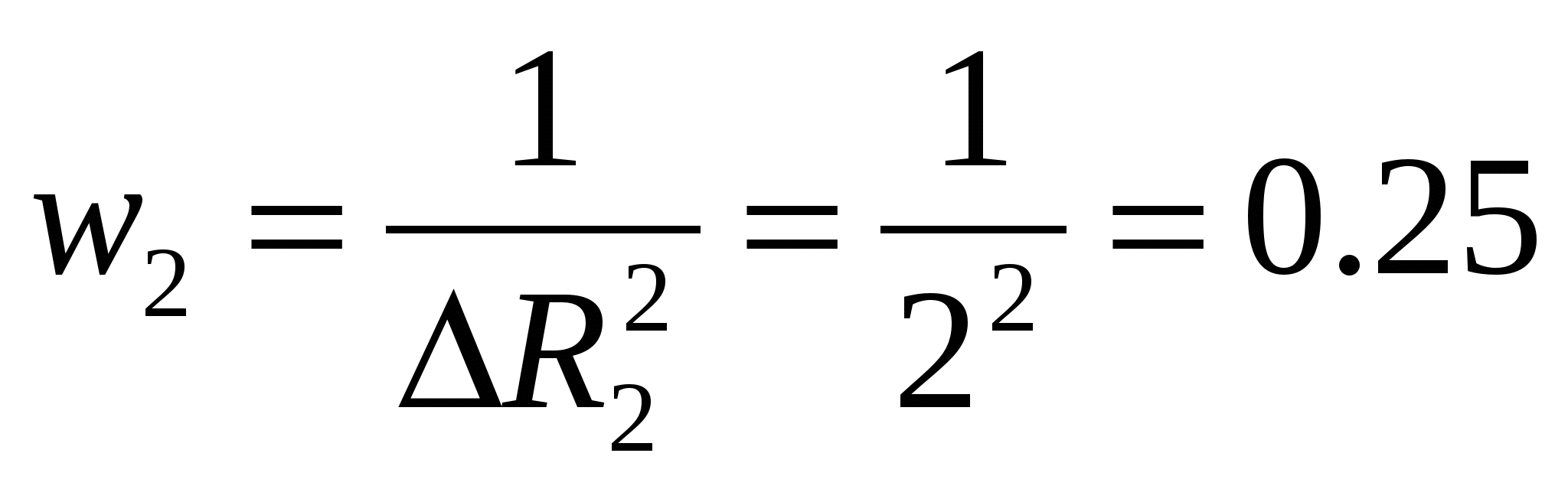 1/オーム2、
1/オーム2、
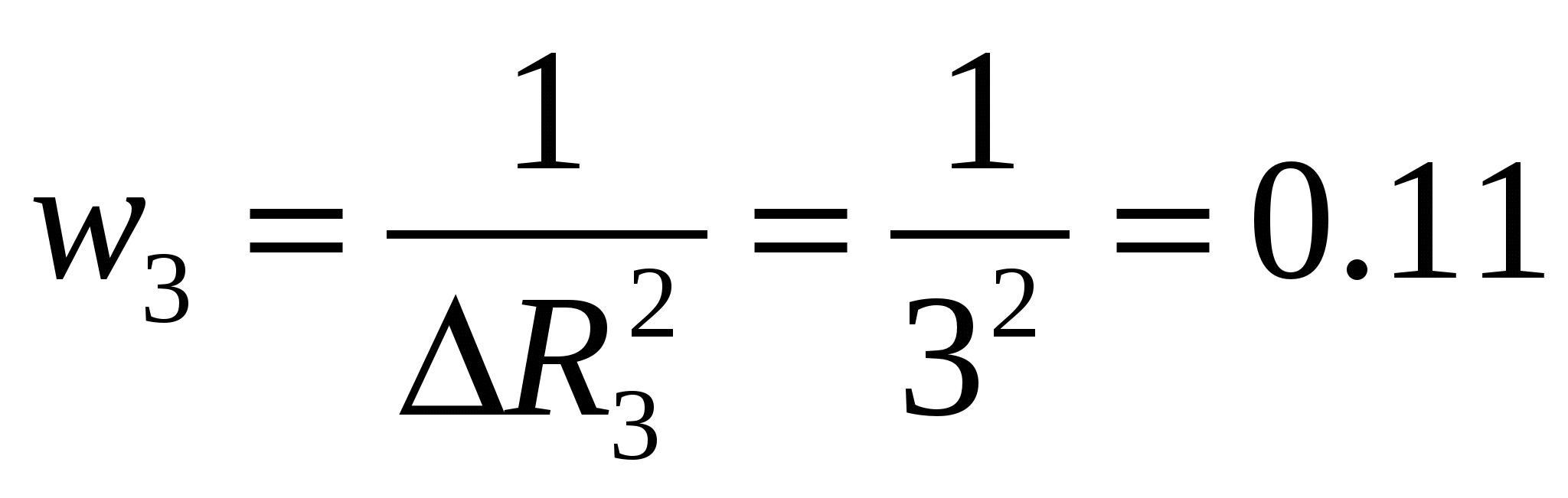 1/オーム2、
1/オーム2、
新しい抵抗推定値を見つける
新しい誤差推定値を見つける
関節抵抗評価結果
R=(11±1)オーム。
例5.3.
直接測定により、物質点の周囲の均一回転の質量 m、半径 R、線速度 v の値が判明しました。 質点に作用する遠心力Fの値を推定する必要があります。
M=(310±6)g、R=(104±5)mm、v=(30±1)m/s 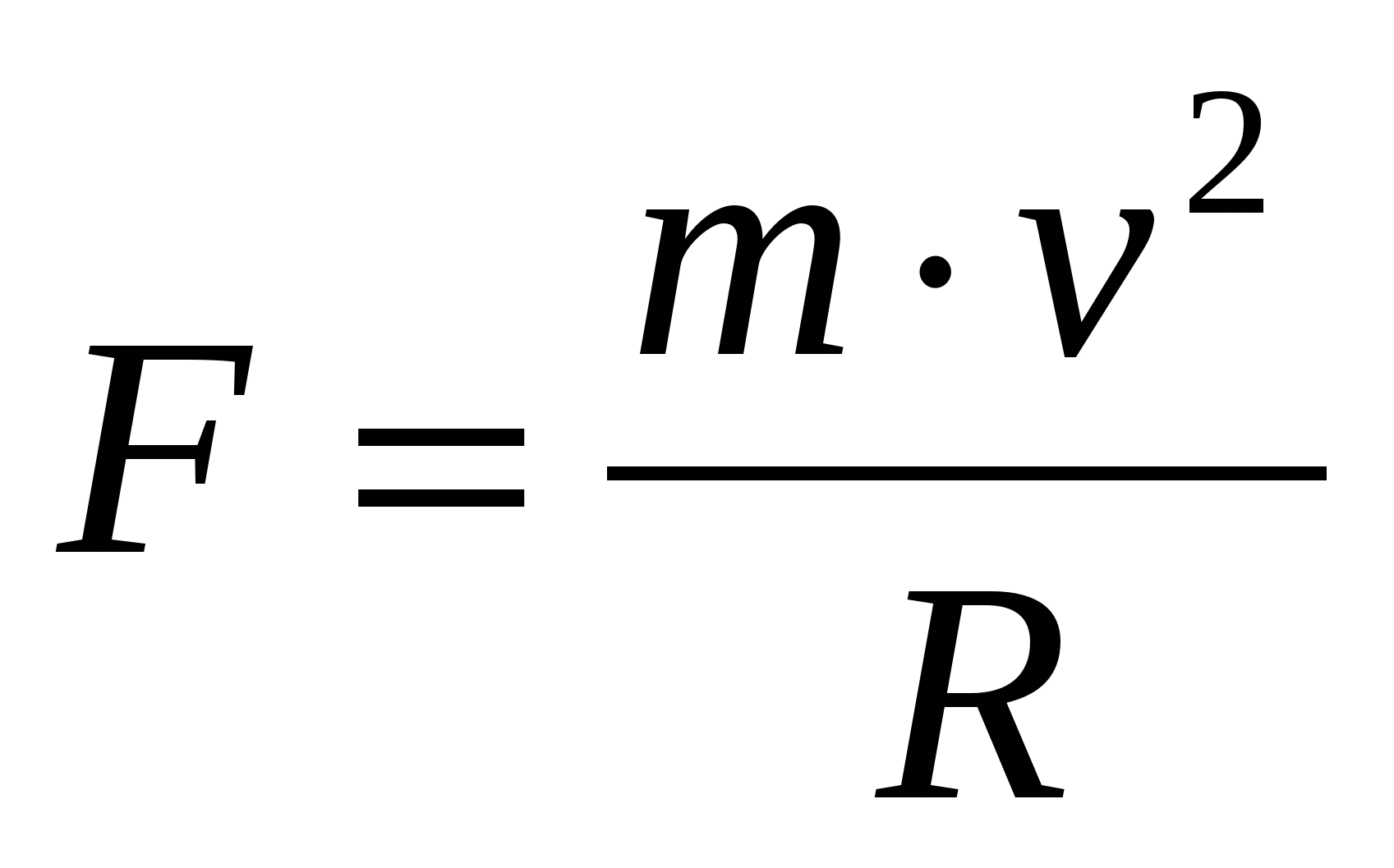
間接測定の誤差を計算するための 3 つの方法を検討します。
引数に関する測定量の導関数の計算を使用するアルゴリズム。
 kN。
kN。
偏導関数を見つけて、引数の平均値に対するその値を計算します
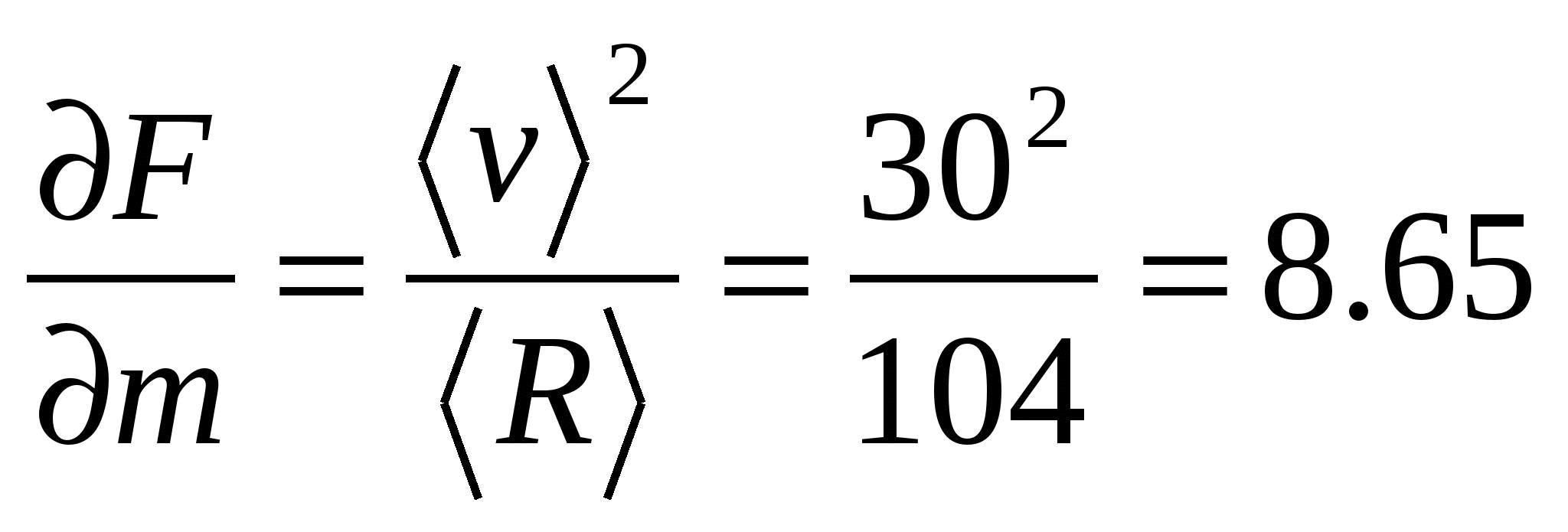

![]()
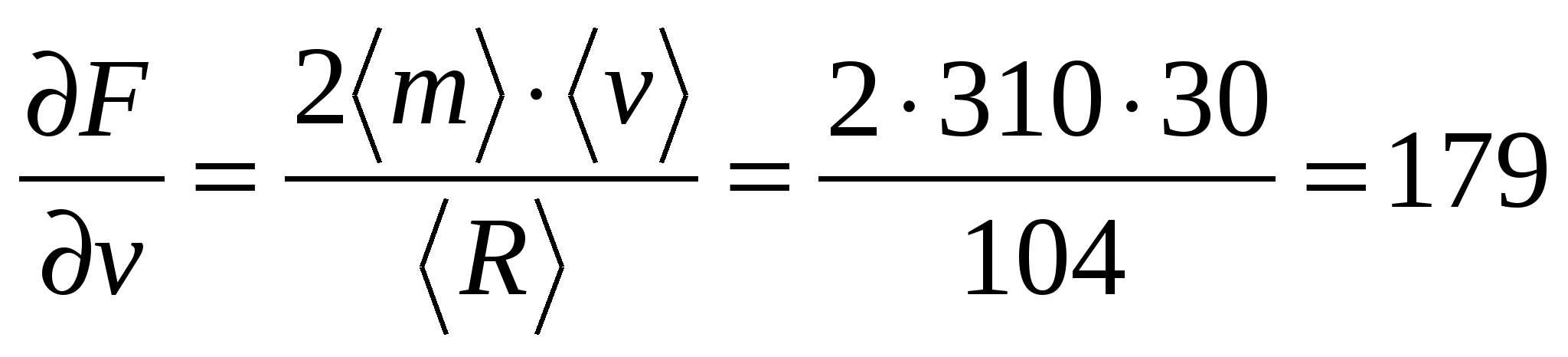
各引数から誤差の成分を計算します
 H
H  H
H
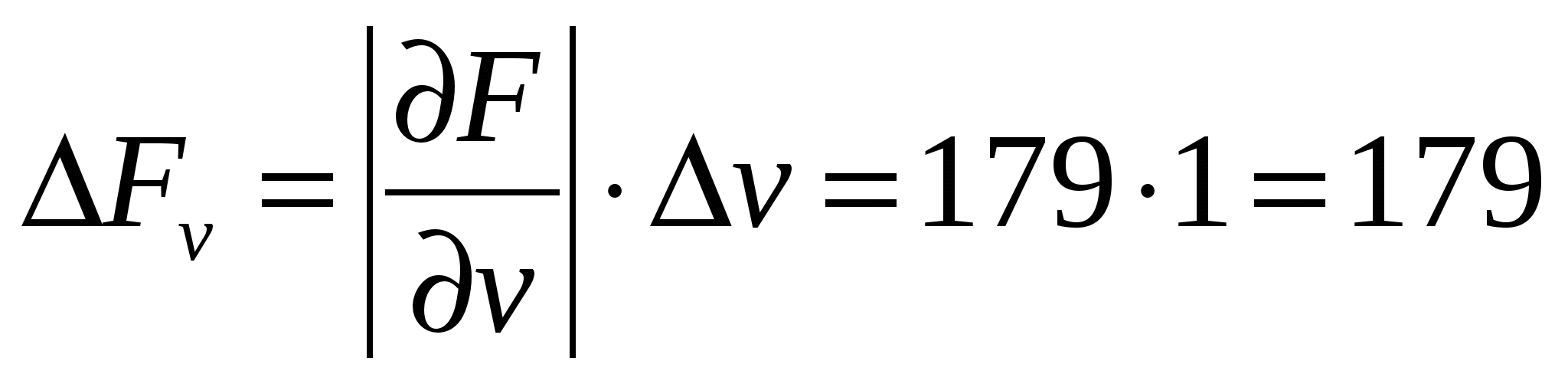 H
H
合計誤差を計算します
相対的
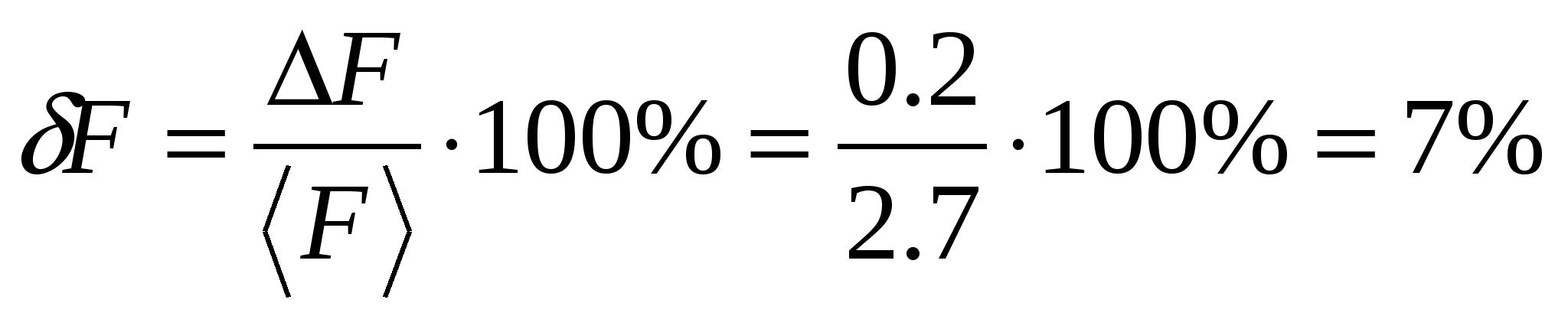
引数による測定値の増分の計算を使用するアルゴリズム。
力の平均値を計算します
引数によって関数の増分を計算します
合計誤差を計算します
相対的

四捨五入後、間接測定の結果を書き留めます。
絶対誤差値の加算を使用するアルゴリズム
力の平均値を計算します
引数の相対誤差を計算します

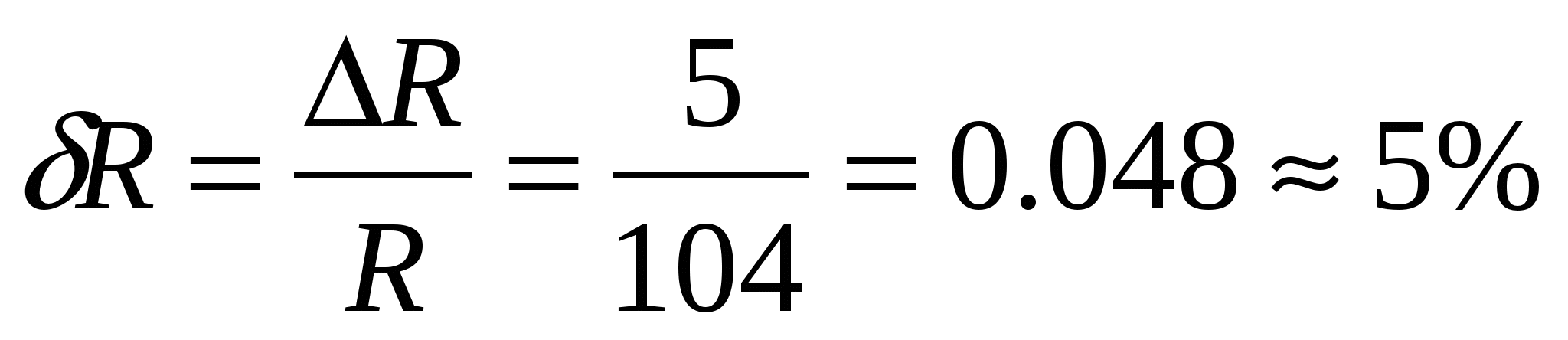
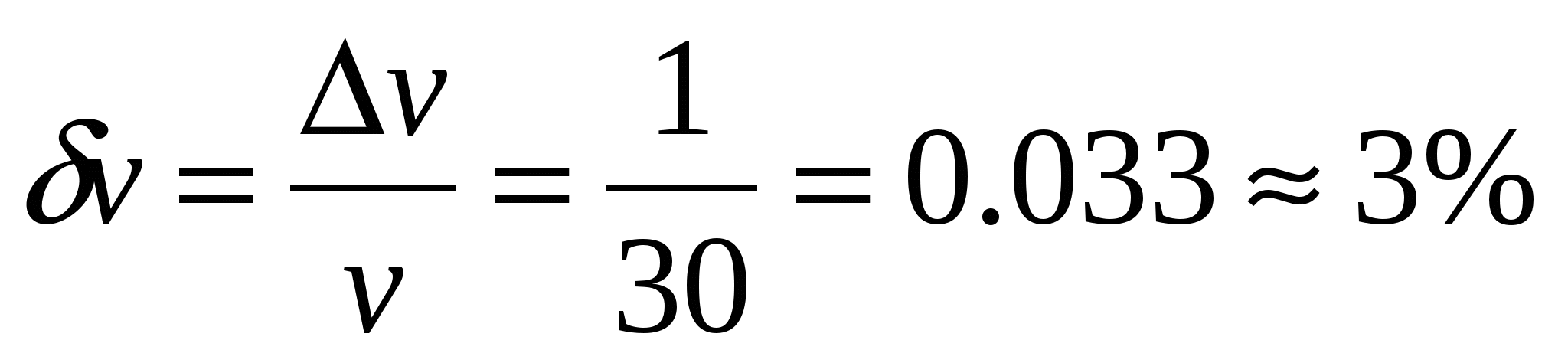
付録 2 の式に従って関数の相対誤差を計算します。
関数の絶対誤差を計算します
四捨五入後、間接測定の結果を書き留めます。
例5.4. 間接測定の結果を処理します。
この例では、2 つのアルゴリズムを使用して間接測定の誤差を計算する複雑さを比較します。 引数に対する測定量の複雑な関数依存の場合を考えてみましょう。
直列発振回路の要素の値を直接測定して求めます。 アクティブ抵抗 R=(10±1) オーム。 インダクタンスL=(30.0±1.5)mH。 静電容量 C=(100±2) uF。 強制振動が回路内で周波数?=1000 rad/s で励起されます。 EMF 源の振幅? = 10 V。電流振幅と回路要素のパラメータの関係は、次の関係によって決まります。

EMF振幅? そして頻度は? 非常に正確に測定され、定数として考慮できます。
引数による測定値の増分計算を使用するアルゴリズム
関数の増分を計算する



合計誤差を計算します
相対的

四捨五入後、間接測定の結果を書き留めます。
引数に関する測定量の導関数の計算を使用するアルゴリズム
電流の平均値を計算します。
関数の導関数を計算します
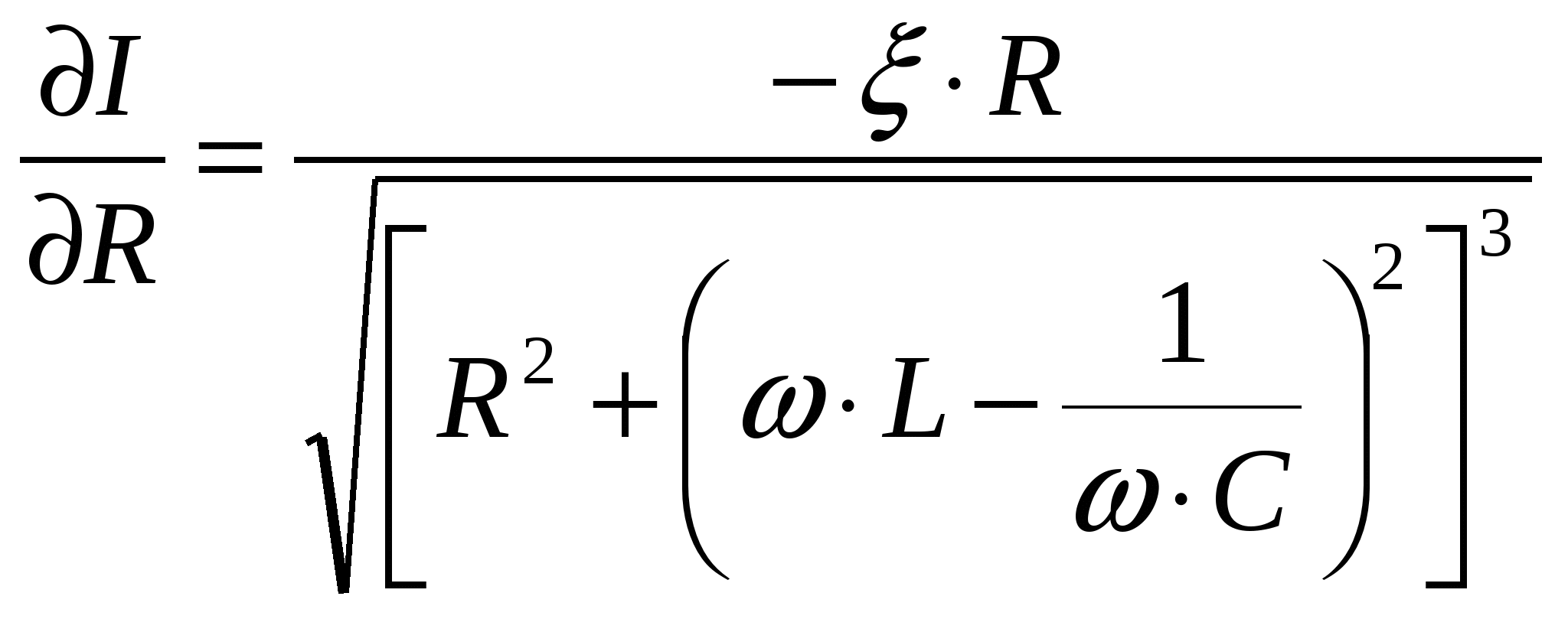
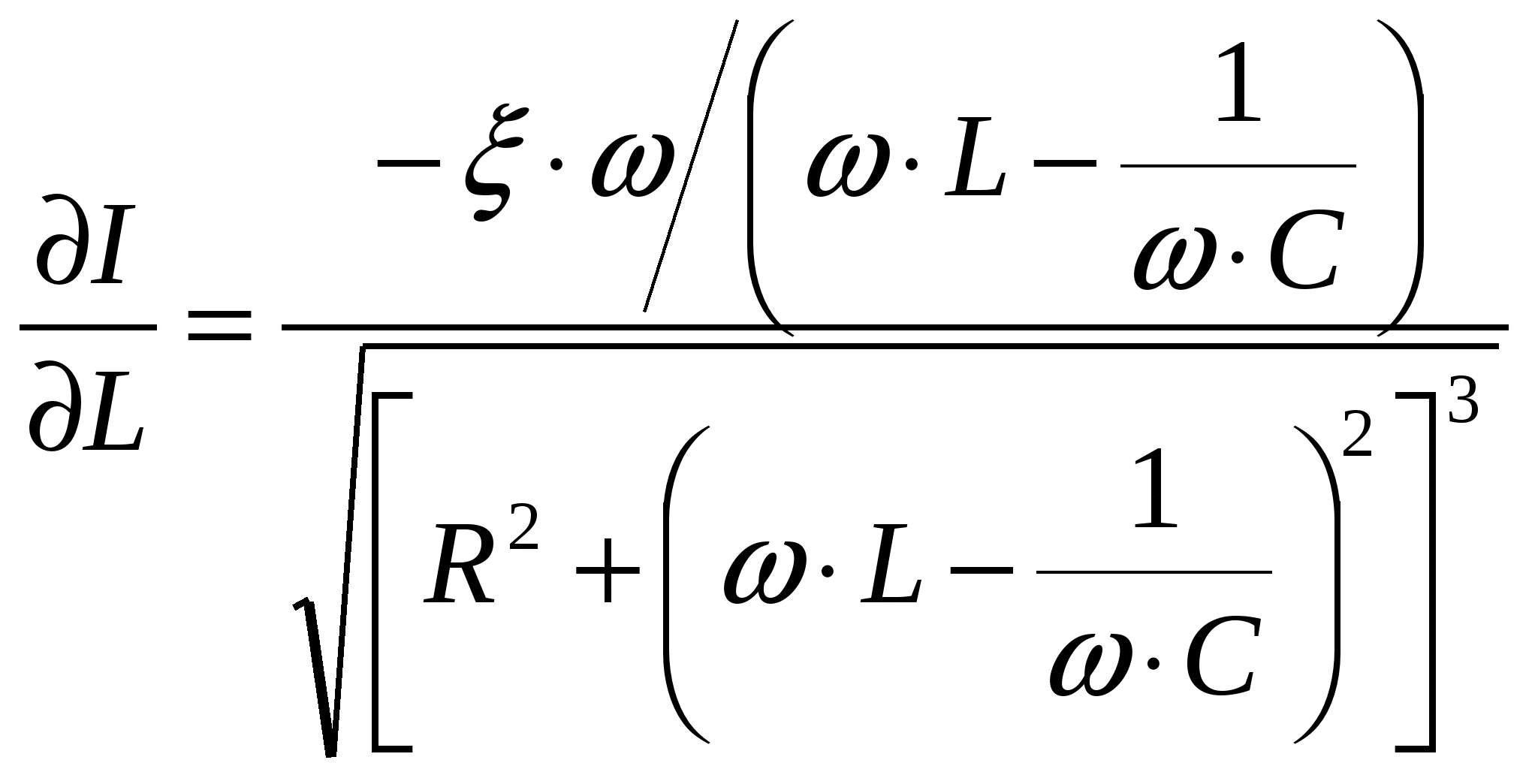

引数の平均値から導関数の値を計算します

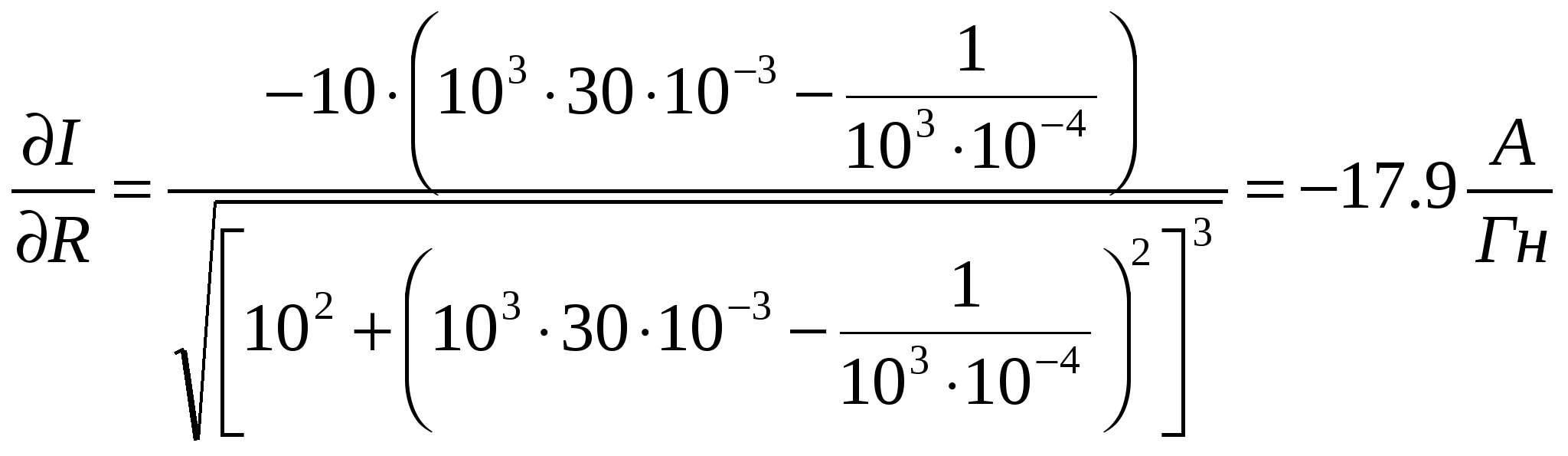

関数の誤差成分を計算します
合計誤差を計算します
相対的
四捨五入後、間接測定の結果を書き留めます。
例5.5。間接測定の結果を処理します。
この例では、引数の関数の間接的な測定の結果に対する引数の誤差の統計的関係の影響を検討します。
ある程度の内部抵抗を持つ DC EMF 源には、整合した電力が負荷されます。 有効負荷(負荷内で最大電力が放出される場合、その負荷は整合していると呼ばれます。この場合、負荷抵抗はEMF源の内部抵抗に等しいです)。
直接測定により、負荷における電流 I と電圧 U の N=10 個の値が見つかりました。 電流の機器測定誤差 ΔI a =0.005 A、電圧 - ΔU a =0.05 V。電流および電圧の推定値の信頼性は 95% である必要があります。 間接測定を使用して、電源から消費される電力 P を決定する必要があります。 ジュール・レンツの法則によると  .
.
電流と電圧の測定値のばらつきの主な理由は、電源の不安定性であり、そのEMFと内部抵抗のランダムな変化につながることが知られています。 したがって、負荷における電流と電圧の変化は、同じ原因によって発生するため、統計的に関連 (相関) します。 この場合、電流誤差と電圧誤差の合計は二次関数ではなく、絶対値で実行する必要があります。
電力計算の順序を考慮してください。
| № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 私、A | 0.265 | 0.255 | 0.225 | 0.245 | 0.235 | 0.210 | 0.260 | 0.240 | 0.210 | 0.215 |
| U、V | 6.55 | 6.40 | 5.60 | 6.20 | 5.95 | 5.20 | 6.55 | 6.00 | 5.30 | 5.40 |
与えられた信頼確率? = 95% および読み取り数 N = 10 の場合、信頼係数 t 95; 10 = 2.3 を決定します (付録 1.)。
電流と電圧の平均値を計算します

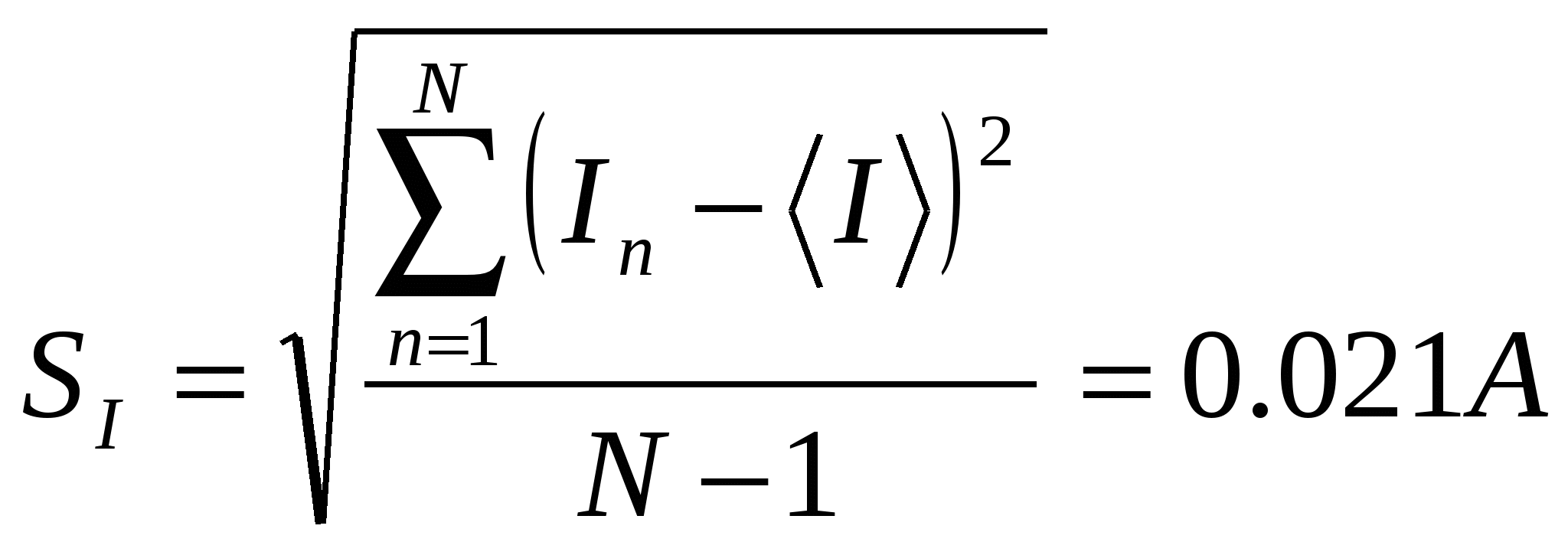
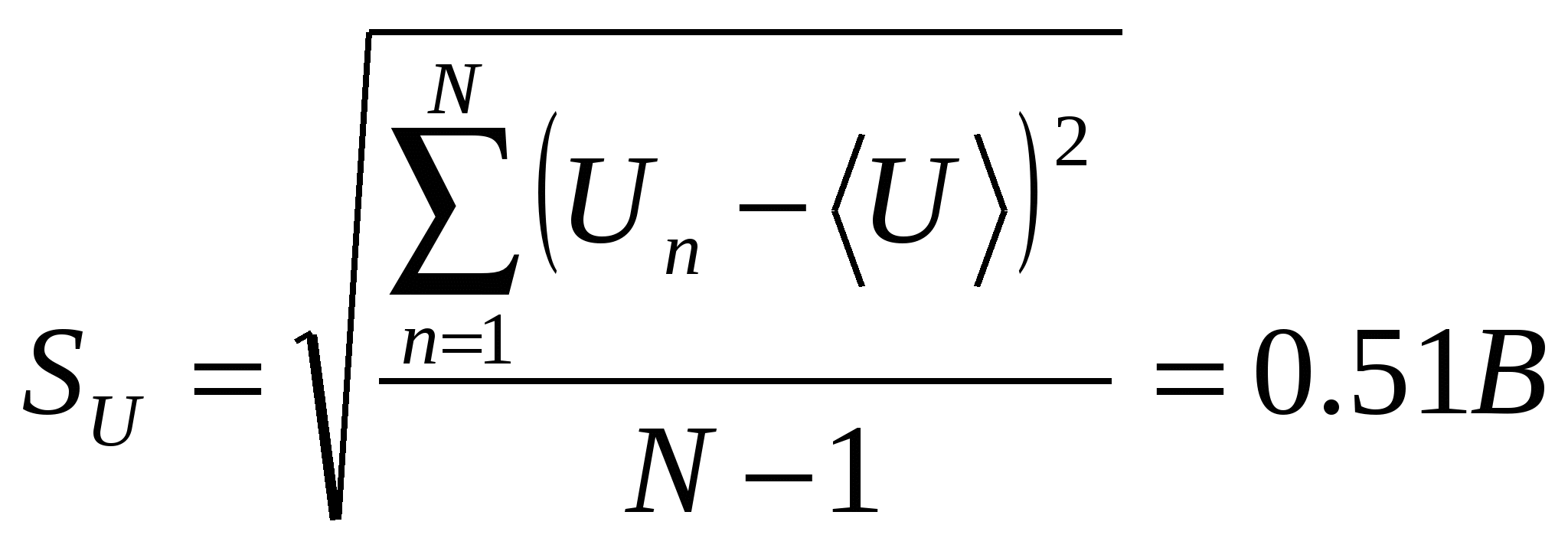

付録 4 によると、N=10 の場合、負荷にかかる電流と電圧に相関がない確率はゼロです。 したがって、実験データは電流と電圧誤差の関係を示しています。
電流誤差と電圧誤差のランダム成分を計算します。
 ,
,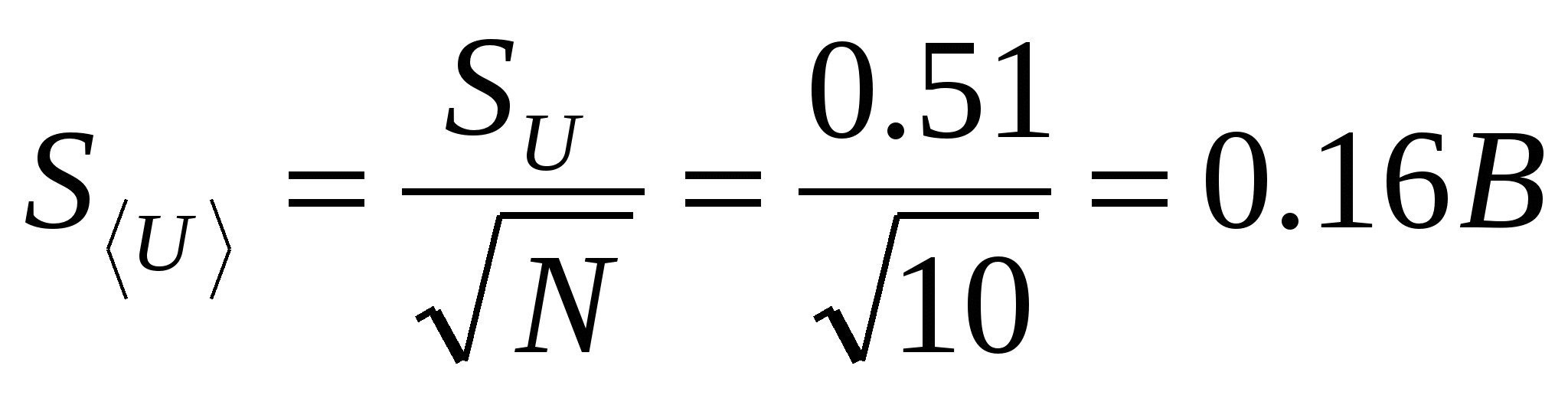 ,
,
合計誤差を計算します
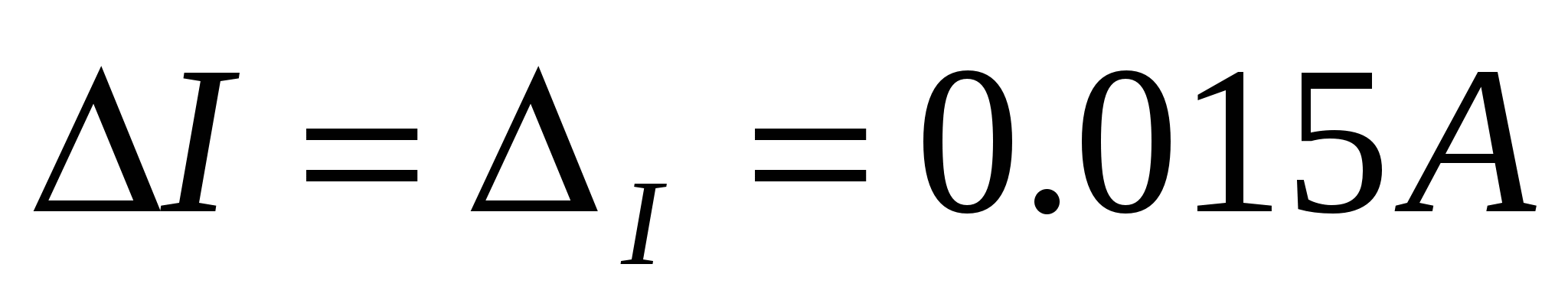

相対的


四捨五入後、電流と電圧の測定結果が得られます。
U=(5.9±0.4)B、? U=6%、?=95%
電力測定の相対誤差を計算します
電力測定の絶対誤差を計算します
誤差の二次和では、直接測定値間の相関は考慮されません。 これは、間接測定の信頼性の低下に相当する、間接測定の誤差の過小評価につながる可能性があります。 場合によっては、誤差の低減が信頼区間が真の値をカバーしないような値に達することがあります。 この場合、電流と電圧の測定誤差の二次和を使用すると、次のようになります。
P=(1.4±0.1)W、?P=7%
考えられた問題における力の真の値
比較のために、同じ測定タスクを考えてみましょう。ただし、電流と電圧の測定値の広がりが多数の非支配的要因によるものである条件下で考えてみましょう。 この場合、電流と電圧の読み取り値の誤差は統計的に関連しません。
| № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 私、A | 0.290 | 0.285 | 0.285 | 0.275 | 0.190 | 0.245 | 0.220 | 0.275 | 0.230 | 0.210 |
| U、V | 6.55 | 6.40 | 5.60 | 6.20 | 5.95 | 5.20 | 6.55 | 6.00 | 5.30 | 5.30 |
与えられた信頼確率?=95% および読み取り数 N=10 の場合、信頼係数 t 95;10 =2.3 を決定します。 電流と電圧の平均値を計算します
電流と電圧の標準偏差を計算します
電流と電圧の相関係数を計算します
付録 4 によると、一定の測定回数で、負荷の電流誤差と電圧誤差が相互に関連しない確率は 78% です。 したがって、実験データは、電流誤差と電圧誤差の間には関連性がないことを示しています。
エラーのチェック
この結果が失敗とみなされない実験の数は 14 です (付録 3)。 この数は N=10 より大きくなります。 したがって、読み取り値U 9 =8.2Vはミスであり、処理された一連のデータから除去する必要がある。 新しい行のカウントは N=9 で、t 95;9 =2.3 です。
新しい平均と標準偏差を計算します
誤差のランダム成分を計算します
S U >
=
0.76B ?
U =
0.18B
?I= 0.03A ?U= 0.4B
絶対誤差と相対誤差の合計を計算します
? 私 = 12%, ? U = 7%.
電流と電圧を直接測定した結果
U=(5.7±0.4) B、?=7%、?=95%
平均電力値を計算します
= 1.43W
電流および電圧測定誤差の二次和を使用して、絶対および相対電力測定誤差を計算します。
間接電力測定の結果
引数間に相関関係がない場合、それらの誤差を絶対値で合計すると、関数の間接測定の誤差が過大評価され、信頼区間が拡大します。 測定の信頼性を高めるため。 このような誤差の過大評価は許容されます。 この場合
?P=?I+?U= 12+7=19%.
?P=
P=1.4 0.19=0.3 W。
8.1.1 測定の種類 (直接、間接、合計、結合)
測定の目的は、測定された量とその単位の比率を求め、その量の値を取得することです。 測定量の値を取得する方法に従って、測定は直接、間接、累積、および結合に分類されます。
直接測定は、物理量の目標値を実験データから直接取得する測定です。
間接測定は、所望の量に関数的に関連する他の物理量の直接測定の結果に基づいて、物理量の所望の値を決定することです。
集合測定は、同じ名前の複数の量を同時に測定することであり、これらの量をさまざまな組み合わせで測定することによって得られる連立方程式を解くことによって、量の望ましい値が決定されます。
同時測定は、2 つ以上の異なる量を同時に測定して、それらの間の関係を決定することです。
実験データからの測定結果を統計処理する前に、次のことを行う必要があります。
a) 既知の系統誤差は除外されます。
b) 重大な間違いや間違いがチェックされ、除外されます。
測定結果の統計処理の一般的な手順は次のとおりです。
a) 経験的分布が基準の 1 つに従って正規法則に対応するという仮説をテストする。
b) 測定結果の数値特性の決定 - 平均 算術値、分散または標準偏差。
c) 測定結果の平均値の標準偏差と測定誤差のランダム成分の信頼限界の決定。
*d) 除外されない系統誤差 (NSP) の境界とその測定結果への影響の決定。
e) 測定結果の信頼区間の計算。
直接測定のための個々の点の計算を実行する手順については、前の章 (3、4、7) で検討しました。 他の種類の測定結果については、統計処理の機能があります。
間接測定の結果を処理するアルゴリズムは、引数の測定誤差の相互影響(相関関係)と、測定値とその引数の間の関数関係の種類に応じて確立されます。
次の条件が満たされる場合、引数の測定誤差間に相関関係があります。
ここで、n は各引数の次元数です。
t P - 信頼確率 P および自由度 f = n - 2 のスチューデント係数。
r は相関係数です。
 ,
(8.2)
,
(8.2)
ここで、 a hi 、 a ki は i 番目の測定結果であり、それぞれ h 番目と j 番目の測定結果です。 口論
*ポイント (d) は、NSP の境界を決定できる場合に特に正確な場合に実行されます。
 は測定された引数の平均値です。
は測定された引数の平均値です。
引数の測定誤差の相関と正規分布を確立する場合、統計処理の順序は、引数に対する測定値の関数依存のタイプによって決まります。
形式の線形関数依存性がある場合
, (8.3)
ここで、 b j は a j 番目の引数の係数です。
平均測定値の RMS は次の式で求められます。
, (8.4)
どこ  – j 番目の引数の平均の RMSD:
– j 番目の引数の平均の RMSD:
非線形関数依存性の場合: 平均測定値の RMS は次の式で求められます。
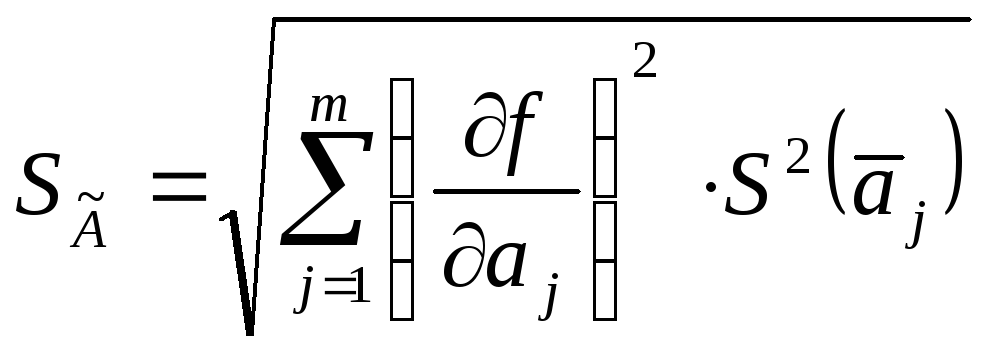 ,
(8.6)
,
(8.6)
どこ 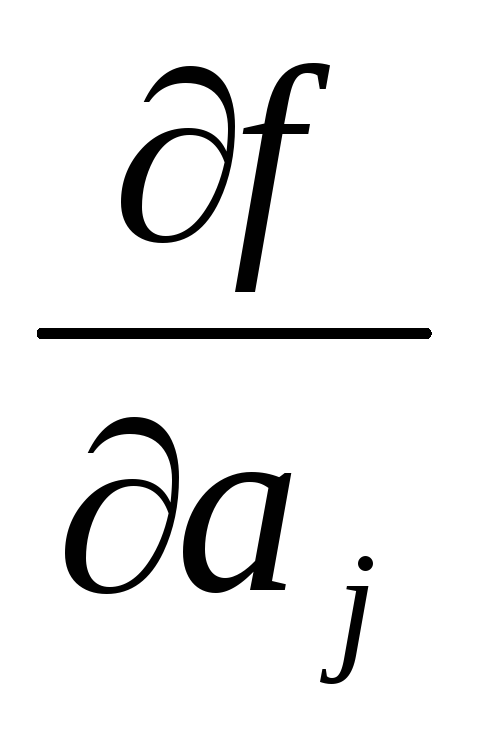 - 関数依存性の最初の偏導関数
- 関数依存性の最初の偏導関数 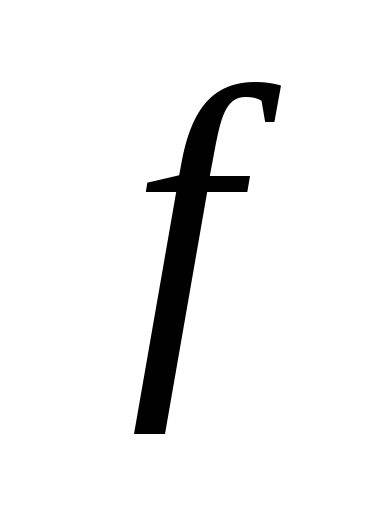 j 番目の引数の引数から測定された量の値。
j 番目の引数の引数から測定された量の値。
非線形依存を線形化すると、テイラー展開級数の丸めから系統的 NSP が現れます - R:
どこ 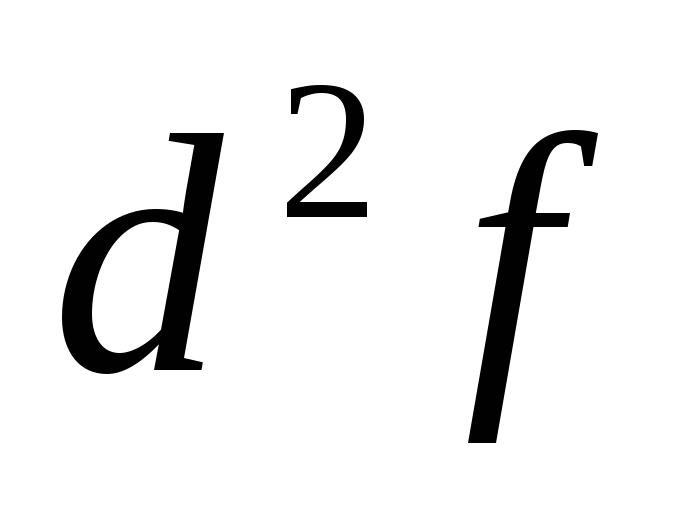 関数依存性の合計 2 階微分です。
関数依存性の合計 2 階微分です。
方法論的誤差 R は次の場合に無視できます。
 . (8.8)
. (8.8)
それ以外の場合は、最終測定結果で R を考慮する必要があります。
相関がない場合は、実験データの分布の種類や関数の依存性に関係なく、リダクション法が使用されます。
測定量の現在値は次のように計算されます。
 (8.9)
(8.9)
どこ  –j 番目の引数の i 番目の値。
–j 番目の引数の i 番目の値。
平均測定値の推定値は次のように計算されます。
平均測定値の推定値の標準偏差は次のように計算されます。
 .
(8.11)
.
(8.11)
間接測定の最終結果は、信頼区間の形式で表示されます。
どこ 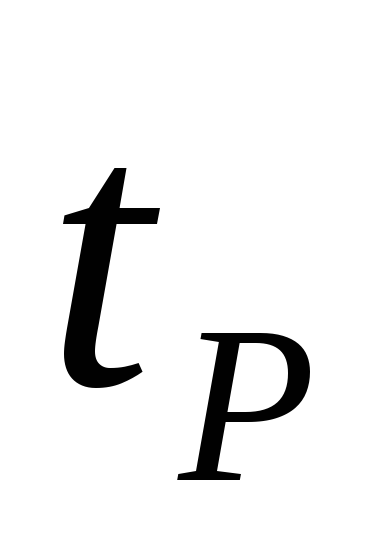 - 特定の信頼確率 Р に対するスチューデントの係数。
- 特定の信頼確率 Р に対するスチューデントの係数。
累積測定と共同測定の結果は、次の形式の方程式系から取得されます。
測定中に得られた値はどこにありますか。
 は希望の値です。
は希望の値です。
測定結果の精度を向上させるには、システムには未知数の数よりも多くの方程式が必要です。
初期の条件方程式系は、次の形式の正規方程式系に変換されます。
*どこ 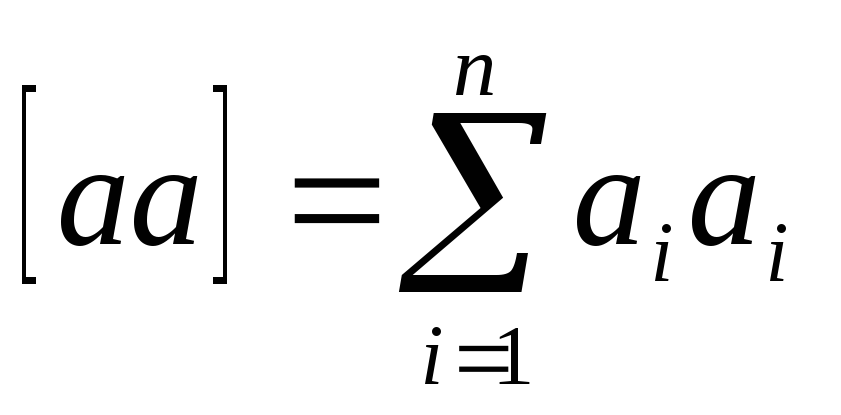 ,
,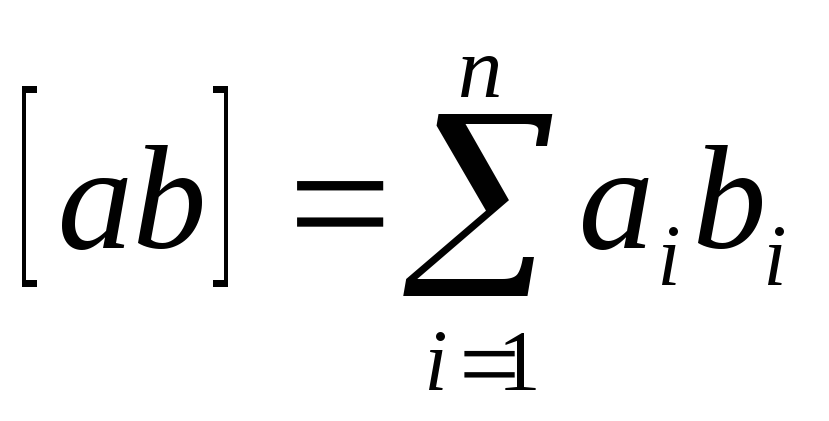 等々。
等々。
システム (8.14) の解は未知の量の推定値です。  。 これらの値を条件式に代入して、残差を決定します
。 これらの値を条件式に代入して、残差を決定します  i 、いわゆる「残差」。 残差は必要な量の測定誤差を決定し、それに基づいてこれらの量の信頼区間が計算されます。
i 、いわゆる「残差」。 残差は必要な量の測定誤差を決定し、それに基づいてこれらの量の信頼区間が計算されます。
*共同測定を実行する場合、条件式は同等ですが、累積測定の場合、測定値のさまざまな組み合わせにより式は等しくなくなり、追加の特性が導入されます - 重量:
 .
(8.15)
.
(8.15)
すべての量 a、b、c、l に係数が掛けられます。
あなたの優れた成果をナレッジベースに送信するのは簡単です。 以下のフォームをご利用ください
研究や仕事でナレッジベースを使用している学生、大学院生、若い科学者の皆様には、大変感謝していることでしょう。
http://www.allbest.ru/ でホストされています。
コースワーク
テーマは「物理量の測定誤差」
1. 測定誤差
2. 直接測定における直接測定量の誤差の推定
3. 間接測定における誤差の評価
4. 結果の最終記録
5. グラフ表示測定結果
7. 誤差理論の要素。 RMSエラー
文学
1. 測定誤差
絶対的に正確な測定はありません。 あらゆる値を測定すると、必ず何らかの誤差(誤差)を伴う結果が得られます。 言い換えれば、量の測定値は常にその真の値とは異なります。 実験者の仕事は、値自体を見つけることだけでなく、測定で生じた誤差を評価することでもあります。 発生の性質と原因に応じて、体系的かつ ランダムエラーそして逃す。
誤差は系統的と呼ばれ、同じ測定器を使用して同じ方法で繰り返し測定を行っても一定になります。
系統誤差は、同じ測定が何度も繰り返された場合に同じように作用する要因によって引き起こされます。 それらは、常に一方向、つまり上または下における、真の値からの測定値の偏差に対応します。
系統的エラーは、まず、使用する機器の誤動作または誤った操作 (たとえば、誤った「ゼロ」設定) によって引き起こされる可能性があります。 第二に、それらの原因は、使用された測定技術が不完全であること、または研究対象の現象に影響を与える一定の要因を考慮に入れていないことである可能性があります。 たとえば、外部圧力が上昇した状態で測定を行うと、結晶融解温度の過大評価値が得られる可能性があります。
測定プロセス中に発生する誤差に加えて、近似 (「簡略化」) 式の使用に伴う系統誤差や、実際の物体と受け入れられたモデルの違いに起因する誤差が発生します。 したがって、たとえば密度を決定する場合、研究対象のサンプルが均質でなく、内部に空隙が含まれている場合、大きな系統誤差が発生する可能性があります。
原因を特定した後、適切な修正を導入することで系統誤差を除去できます。 系統的エラーを検出してその原因を特定することは必ずしも簡単ではなく、実験者は追加の研究を実行する必要があることがよくあります。 物理的なワークショップのタスクでは、 系統的エラー問題を設定するときに最小化されるため、無視できます。
ランダム誤差は、同じ条件下で繰り返し測定を行うと、予測できない形で変化する誤差です。
ランダムなエラーはさまざまな原因で発生します 制御不能な原因、その効果は各実験で同じではありません。 その結果、同じ条件下で同じ量を連続して数回測定すると、この量の一連の値全体が得られますが、それらは真の値とは上下にランダムに異なります。
ランダム誤差の性質はさまざまです。測定器の指針のゼロ位置の変動。 実験者の感覚の不完全さ(たとえば、正しい瞬間にストップウォッチを正確にオンにできないなど)。 外部の影響による制御されていないランダムな変化 - 温度、湿度、圧力。 電気回路内のピックアップなど、これを考慮することはほとんど不可能です。
実験にはランダムな誤差が常に存在します。
確率変数の動作は、確率論の主題である統計的規則性によって記述されます。 イベント i の確率 w i の統計的定義は、比率です。
どこ n- 実験の総数、 n 私- イベントが発生した実験の数 私起こりました。 この場合、実験の総数は非常に多くなるはずです ( n--®̐)。 で 多数測定では、ランダム誤差は正規分布 (ガウス分布) に従います。その主な特徴は次のとおりです。
1. 測定値の真の値からの偏差が大きければ大きいほど、そのような結果が生じる可能性は低くなります。
2. 真の値からの両方向の偏差は同じ確率で発生します。
以下に示すランダム誤差を計算するためのレシピは、確率変数のガウス分布を使用した確率論の数学的装置に基づいています。 測定数が少ない (n = 310) ワークショップの条件では、これらの計算は常に推定されることに注意してください。
機器誤差は、機器の読み取り値と測定量の真の値との差です。 ランダムなコンポーネントと体系的なコンポーネントが含まれる場合があります。
ミス (または重大なエラー) は、通常、個々の測定結果が他の測定結果から大きく逸脱する形で現れます。 ミスの主な原因は、実験者の注意不足や測定器の故障です。 このような測定の結果は破棄されます。
2. 直接測定における直接測定量の誤差の推定
a) ランダムエラー。 基本概念。
ある確率変数 a を同じ条件下で n 回測定するとします。 測定結果は n 個の異なる数値のセットを示しました
量の最も可能性の高い値の場合、通常は測定結果の算術平均を取ります。
どうやって さらに多くの数測定値が大きいほど、平均値は真の値に近づきます。
i 番目の測定の絶対誤差は次の値です。
絶対誤差は寸法値です。 絶対誤差の n 値の中には、必ず正と負の両方が発生します。
i 番目の測定値の相対誤差は次の値です。
物理量誤差信頼区間
相対誤差は無次元量です。 いつもの 相対誤差はパーセンテージで表されます。 e 私 100% を掛けます。 相対誤差の値は、測定精度を特徴づけます。
平均絶対誤差は次のように定義されます。
合計の必要性を強調しましょう 絶対値(モジュール) 数量 -- D あ 私. それ以外の場合は、同じゼロの結果が得られます。
平均相対誤差は次の値です
多数の測定結果が得られます。
b) 信頼区間と信頼水準。
測定結果を処理するタスクは、測定値の真の値が含まれる間隔の境界を決定することです。 この間隔は、真の最良推定値として考慮される算術平均に対して相対的に決定されます。
あらゆる数量の測定結果を記録する次の形式が受け入れられます。 あ:
あ = (b あと -- ± -- D あ)単位 測定値 ( e%),
ここで、D ある- 何らかの方法で決定されたこの間隔の境界。
確率理論により、既知の確率 w を使用して、個々の測定結果が見つかる間隔のサイズを決定することができます。 この確率は信頼確率と呼ばれ、対応する区間は信頼区間と呼ばれます。
測定値の数 n が十分に大きい場合、信頼確率は、測定値が信頼区間内にあった測定値の総数 n の割合を表します。 各信頼確率 w は、それ自体の信頼区間に対応します。
たとえば、数値軸では、結果をポイントで示します。 n= 10 個の条件付き測定。 それらは平均の周りに集まっています b あと。
括弧で、10 個中 5 個の実験値が存在する信頼区間を示します。 信頼確率 w 1 50%。 角括弧は、確率 w 2 80% の信頼区間に対応します。 信頼区間が広いほど、その区間内で結果が得られる可能性が高くなります。 確率理論では、信頼区間の値、信頼確率、および測定数の間に定量的な関係が確立されます。
平均誤差に対応する区間を信頼区間として選択すると、D a = bD あ s、十分な数の測定の場合 それは信頼水準に相当します w 60%。 測定数が減少すると、そのような信頼区間に対応する信頼確率 (b あと -- ± --bD あ c) 減少します。
したがって、信頼区間を推定するには 確率変数平均誤差を使用できます -- bD あと . 信頼区間の厳密な理論は最後の段落で説明されています。
c) 器差。
器差は、器械のパスポート特性です。 このタイプのデバイスのセット全体については、調査対象のバッチのデバイスの読み取り値と基準デバイスの読み取り値 (キャリブレーションによる) を比較することによって決定されます。 得られた値のうち最大のものを器差の値とする。
別のデバイスを使用する場合、器差の具体的な値は不明ですが、デバイスのパスポート データに示されている既知の制限内に収まります。
ポインター式電気測定器の場合、誤差は精度等級によって決まります。 ほとんどの機器の精度クラスは、機器の最大許容相対誤差に等しく、スケールの上限値のパーセンテージとして表されます。 このようなデバイスの精度クラスの値は、目盛りの横に数字の形でマークされています (丸やアスタリスクは付いていません)。
精度クラス e を示します 最大。 定義に基づいて、
ここで、D バツ 私 到着しました . - 考えられる最大絶対器差 私次元、 バツ 最大- 測定器の目盛の上限値。
したがって、次のことがわかります
i 番目の測定の最大相対機器誤差は次の式で計算されます。
したがって、たとえば、V max \u003d 300 Vまでの電圧を測定するように設計された精度クラス0.2の電圧計の場合、測定上限における最大相対機器誤差は0.2%です。 また、電圧 V = 50 V を測定すると、最大相対誤差は 1.2% に増加します。 したがって、ゼロ付近(スケールの前半)を測定すると、測定精度が大幅に低下します。 スケールの最初の部分の測定は望ましくありません。
上記の式で求められる機器誤差は、機器の最大可能誤差を表します。 特定の測定値の誤差はより小さい場合があります。
精度クラスが指定されていない場合は、スケールの最小目盛りの価格の半分を器差として考慮することができます。 通常、この値は精度クラスと一致します。
デジタル電気測定器のエラーは通常、測定器のパスポートに記載されています。
d) ランダム誤差と機器誤差を考慮した信頼区間。
特定の値を 1 回測定しただけでは、ランダム誤差を決定することは不可能であり、信頼区間の境界は機器誤差の値によって決まります。
この場合のエラーをメソッドのエラーと呼びます。
複数の測定では、ランダム誤差と機器によって導入される誤差を考慮して信頼区間の限界が決定されます。 この誤差を実験誤差といいます。
実験誤差を推定するには、次の式を使用できます。
(22ページも参照)。
当然のことながら、一方の項が他方よりもはるかに大きい場合、それが評価において決定的になります。 もし、 大量に測定を行うと、機器誤差がランダム測定誤差よりもはるかに大きくなるため、使用する機器をより正確なものに交換する必要があります。 器差がかなり小さい場合 ランダムエラー、測定の数を増やすと、結果の精度が向上します。 機器誤差がランダムな測定誤差に匹敵する場合、明らかに測定数を増やすのは意味がありません。 したがって、測定を行う前に器差を評価することをお勧めします。
3. 間接測定の誤差推定と私
ほとんどの場合、実験者が関心のある量は直接測定することはできませんが、いくつかの直接測定可能な量を使用した計算によって取得されます。 このような測定は間接的と呼ばれます。 私たちにとって関心のある量 a が、直接測定された多数の量 x、y、z、... の知識を必要とする何らかの式によって計算されるとします。
a = f(x, y, z, ....)。
ここで、f (x, y, z, ....) は、計算式によって決定される何らかの (まだ具体化されていない) 関数です。
測定では 2 つの状況が発生する可能性があります。
a) 一定パラメータによる間接測定。
物理的な実際のタスクの大部分では、量 x、y、z、... が繰り返し測定され、その真の値は測定プロセス中一定のままです (一定パラメータ)。 たとえば、物質の密度は、同じサンプルの質量と長さの寸法を繰り返し測定することによって決定されます。
この場合、数量の平均値は あ平均値bの式に代入して求めます。 バツと , -- b yと , -- b zと , .... 測定値:
量の誤差を計算する場合は、関数 f (x、y、z、...) の種類に応じて、絶対誤差または相対誤差の計算から始めます。
の 一般的な見解タスクは次のとおりです。 一連の量を既知にしましょう バツ±D x、y±D そう、 z±D z... 、 どこ -- D バツ、 D そう、 D z-前の段落で説明したように決定される、直接測定の誤差。 量の絶対誤差を決定する方法 ある? ほとんどの場合、直接測定の誤差は測定値よりはるかに小さく、数パーセント以下にとどまることを考慮しています。 それらの。 PD バツん バツ P , PD yん y P , PD zん z P ... 次に、形式的には誤差を測定値の小さな増分とみなして、記号を置き換えることができます。 D バツ DX、 D yダイ、 D zズ、... D あるだ- そして値を見つけるには --D ある微分積分の数学的装置を使用します--
ここで、 は偏導関数であり、通常の微分の規則に従って計算されます。 これが定義されると、関数の他のすべての引数が f(を除外する バツ) は一定であり、その平均値と等しいと見なす必要があります。 この用語は、合計誤差に含まれる誤差に対応しますか? ある量だけを測定することの不正確さ バツ(他のすべての量を仮定すると: y、z、...- 誤差なく測定されました)。 他のすべての用語も同様の意味を持ちます。 したがって、量の絶対誤差を推定するには あ間接測定では、次の式で可能です。
値の相対誤差をすぐに判断するには あ、D を割る あるの上 あ式が便利に変換できることを考慮してください。
計算式に測定値のほかに表データや基準定数が含まれる場合、値の誤差 a を計算する際にはそれらの誤差も考慮する必要があります。 誤差が特に示されていない場合、通常、最初の欠落桁が 5 単位を超えないと考えられます。 たとえば、自由落下を加速するには:
g\u003d 9.8 m / s 2?D g\u003d 0.05 m / s 2、
g\u003d 9.81 m / s 2?D g\u003d 0.005 m / s 2.
絶対誤差を計算した後、結果の相対誤差が求められます。
以下は、計算でよく発生する測定値のいくつかの組み合わせの誤差を推定するための表です。
表1。
いくつかの点に読者の注意を引いてみましょう 重要な点テーブルの中に。
1. ランダムな測定誤差は等しい確率で正と負の可能性があることを考慮します。 したがって、測定値を加算および減算する場合、 絶対誤差合計します。
2. 2 つの量を減算する場合、相対誤差には分母にある 2 つの量の差が含まれます。 これらの値が近い場合、差の相対誤差が各値の相対誤差を個別に大幅に超える可能性があります。 精度の低下を避けるため、値が近い数量を減算する必要がある場合には、このような測定や計算を避けてください。
3. 数量を乗算および除算する場合、相対誤差が加算されます。
つまり、計算式が単項式で、和と差が存在する場合、別個の係数の形で、値 a の絶対誤差ではなく相対誤差を最初に計算する方が簡単です。 計算式が多項式の場合は、絶対誤差の計算から始めることをお勧めします。
4.べき乗した場合 n、 そのような n n 1、相対誤差は増加します。 n休日
たとえば、次の式による計算における誤差の計算を考えてみましょう。
次のスキームに従って実行するのが最も便利です。
示す
と、
ここで、s 1 、s 2 、v 0 、t、a は測定値の平均値です。
それから
; ;
;
そして最後に
.
b) 可変パラメータによる間接測定。
一部の問題では、同じ値 a = f (x, y, z, ....) を決定するときに、同じパラメータ x、y、z、.... を n 回測定する代わりに、根本的に異なる値を n 回測定します。 (可変パラメータ) x 1 、 x 2 、 ... 、 x の x n 、およびそれらに対応する y 、 z 、 ... の値。 たとえば、物質の密度は、いくつかのサンプルの質量と長さの寸法を 1 回測定することによって決定されます。
この場合、計算は次のように行われます。 値 a は実験ごとに個別に計算されます: a 1 \u003d a (x 1, y 1, z 1 ...)、a 2 \u003d (x 2, y 2, z 2 ...) ... a n \u003d a ( x n , y n , z n ...) - 直接測定と同様に処理されます。 その結果、平均値 a が次のように求められます。
および対応する平均ランダム誤差 bD あと。
器差D ある 到着しました追加で計算します。 段落 a) で検討した方法でそれを決定するには、値の絶対誤差または相対誤差の公式を導き出します。 a.この式では次のようになります D バツ、 D そう、 D z、....器差を代用する D バツ 到着しました, D y 到着しました, D z 到着しました, ... , しかし、として x、y、z.... 置換値 バツ 私、y 私、z 私, .... 実験のいずれか。 器差の過大評価または過小評価を避けるために、最小値ではなく中間値を使用して実験を行います。 最大値ではありません) パラメータ値 バツ 私、y 私、z 私, ....
実験の合計誤差は、直接測定の場合のように定義されます。
.
4. だいたい最終成績記録
測定値を処理する際の計算の精度
測定を処理した結果、測定量の近似値が常に得られますが、その精度は測定プロセス中に発生する誤差によってのみ決定され、計算によってこの精度を向上させることはできません。 したがって、測定処理の最終結果は、有効桁数の観点から、測定プロセスで得られた精度に一致する必要があります。
最終結果を数値で記述する場合は、以下の規則に従うことに同意します(21 ページも参照)。
1. 最初の有効数字のみがエラーに残ります。 最初の有効数字が 1 桁の場合、有効数字 2 桁までの書き込みが許可され、残りは切り上げられて破棄されます。
2. 測定値の平均値は誤差値に応じて四捨五入しています。 丸めルールは正常です。
はい、その番号です c= 4.862452±0.12465 と書く必要があります。
c= 4.86±0.12、
そしてその番号 d= 242.87546±0.0094265 と書く必要があります。
d= 242.875±0.009。
結果の記録の例:
v = (210±8) m/s (e = 4%)
または v = (2.10±0.08) 。 10 2 m/s (e = 4%) - 標準形式。
R = (49.8±0.3) 。 10 3 オーム (e = 0.6%)
R = (49.8±0.3) kΩ (e = 0.6%)
R = (4.98±0.03) 。 10 4 オーム (e = 0.6%) - 標準形式。
最後の桁のゼロは有効数字であることに注意してください。 したがって、2.86 と 2.86000 という数値は精度において同等ではありません。
計算で間接測定が実行される場合、 数学的演算異なる精度で決定されたおおよその数値を超えています。 この場合、次の四捨五入と計算規則に従います。
1. 近似的な数値を加算および減算する場合、結果として、桁数が最も少ない数値に含まれる桁数が保存されます。
2. 乗算および除算を行う場合、結果には、有効桁数が最も少ない数値に含まれる有効桁数が保持されます。
3. いくつかの関数の値を計算した結果
近似数値 x には、x と同じ数の有効数字が含まれている必要があります。
4. 中間計算では、さらに 1 桁または 2 桁の有効数字を使用することができます(「余裕を持たせて」)。
5. 測定結果のグラフ表示
グラフを作成するときは、次のルールに従う必要があります。
1. グラフには、提示された規則性の物理的内容が明らかになる碑文が含まれていなければなりません。
2. 座標軸に沿ったスケールと原点は、依存関係イメージのプロットが描画フィールドの大部分を占めるように選択されます。 この場合、軸の交点では、数量の値が必ずしもゼロである必要はありません。
スケールを選択するときは、プロットの精度が測定の精度より低くてはいけないことに留意する必要があります。
3. グラフを操作しやすいように、等距離のスケール分割が座標軸上にプロットされます。 実験で得られた数値は記載しておりません。
4. 座標軸の最後には を指定する必要があります 慣例保留中の値と、カンマで区切られたその測定単位。
5. 量(点)の実験値は、誤差とともに明確にプロットされます。対応する軸に平行に配置された信頼区間の長さのセグメントが次の形式で表示されます。
選択したスケールで曲線をプロットするときに、両方の座標軸に沿って信頼区間が表示されない場合、実験点は、実験データに対応する点を中心とする小さな円 (三角形など) としてマークされます。
6. 実験曲線は、実験点が曲線の異なる側に最も近く、均等に配置されるように、すべてまたはほとんどの実験点の信頼区間を通して滑らかに描かれます。
7. チャート上に理論曲線が表示されている場合は、その計算式が示されています。
8. グラフの 1 つのフィールドに複数の曲線を表示する場合、それぞれの曲線に番号が付けられるか、他の方法で強調表示されます。 無料のフィールドでは適切な説明が行われます。
6. 臨床検査の報告書作成に関する推奨事項あボテ
ラボレポートには次の内容が含まれている必要があります。
1. 作品のタイトル。
2. まとめ仕事の目標。
3. 機器および装置のリスト。
4. 設置図。
5. 実際の公式の導出を伴う方法の理論の簡単な要約。
6. 測定単位および器差を示す実験結果の記録。 後続の計算に必要な設置パラメータの記録 (単位と誤差も示す)。
7. 実験室作業のための方法論開発で定義されたタスクに従って、表、数値、グラフの形式で表示される処理された測定結果。
8. 誤差の計算。
9. 結果の分析: 表データ、理論、他の実験データとの比較 - 誤差も考慮します。
10. 結論。
7. 誤差理論の要素。 RMS n○罪深さ
a) 分配関数。 ガウス分布とその特徴
ある確率変数 x の n 回の測定値 x 1 、 x 2 、... x n が、同じ方法と同じ注意で行われたと仮定しましょう。 x から x + dx までのかなり狭い範囲にある、得られた結果の数 dn は、次の値に比例することが予想されます。
- 取得された間隔 dx の値。
- 総数測定値n.
したがって、次のように書くことができます
dn = f (x) n dx、
ここで、f (x) は、さまざまな間隔にわたる確率変数の値の分布を特徴付ける関数です。
ある値 x が x と x + dx の間にある確率 dw(x) は次のように定義されます。
(測定回数あり) n--®Ґ).
関数 f(x) は、分布関数または確率密度と呼ばれます。
誤差理論の仮定として、直接測定の結果とそのランダムな誤差(多数の誤差が含まれる)は正規分布の法則に従うと仮定されます。
ガウスによって発見された連続確率変数 x の分布関数は次の形式になります。
ここで、m -- と -- s ----- 分布パラメータ .
パラメータ -- メートル -- 正規分布は平均値 b に等しい バツ任意の既知の分布関数の場合、積分によって決定される確率変数から
.
したがって、値 m -- 測定量の最も可能性の高い値です バツ、それらの。 彼女の最善の見積もり。
正規分布のパラメータ s 2-- は分散に等しい D確率変数。通常は次の積分によって決定されます。
.
分散の平方根は、確率変数の標準偏差と呼ばれます。
確率変数の平均偏差 (誤差) - bsc は、次のように分布関数を使用して決定されます。
ガウス分布関数から計算された平均測定誤差 -bsc は、標準偏差の値と相関します。 さあ、次へ道: < s > = 0,8-- s 。
s-および--m-パラメータは次のように関係します。
.
この式を使用すると、正規分布曲線がある場合に標準偏差 s を見つけることができます。
ガウス関数のグラフを図に示します。 関数 f(バツ) は、点に描かれた縦軸に対して対称です。 x=メートル; 点での最大値を通過します x=mであり、変曲点m−±sを有する。 したがって、分散は分布関数の幅を特徴付けるか、または確率変数の値がその真の値に対してどの程度広く分散しているかを示します。 測定が正確であればあるほど、個々の測定結果は真の値に近づきます。 s の値は小さくなります。 図 A は関数を示しています f(バツ) 3 つの値の場合 .
曲線で囲まれた図形の面積 f(バツ) と点から引かれた垂直線 バツ 1と バツ 2 (図B) , 数値的には、測定結果が区間 D 内に収まる確率に等しい x = x 1 -バツ 2 、これは信頼水準と呼ばれます。 曲線全体の下の領域 f(バツ) は、確率変数が 0 から -ɐ までの範囲に入る確率に等しい、つまり
,
なぜなら、ある出来事が起こる確率は1に等しいからです。
正規分布を使用すると、誤差理論は 2 つの主要な問題を提起し、解決します。 1 つ目は、測定の精度の評価です。 2 つ目は、測定結果の算術平均値の精度の評価です。
b) 測定結果の精度。
誤差理論における測定の精度は信頼区間によって特徴付けられます。 (x>--±--D バツ) w, 信頼確率が次のようになります。 w、単一の測定の結果は間隔内にあります。 この確率は、信頼区間内に収まる結果の相対的な割合にも等しくなります (4 ~ 5 ページを参照)。
したがって、ランダム誤差の大きさを特徴付けるには、信頼区間の大きさと信頼確率の大きさという 2 つの数値を設定する必要があります。 . 対応する信頼確率を指定せずに誤差の大きさだけを指定することは、ほとんど意味がありません。
もし知ってたら 平均誤差 bsc 測定値、信頼区間は (<バツ> ±--bsc) w、信頼できる確率で決定されます -- w= 0,57.
標準偏差 s がわかっている場合 -- 測定結果の分布の場合、指定された間隔は (x>±--) の形式になります。 t w s) w、 どこ t w- 信頼確率の値に依存し、ガウス分布に従って計算される係数。
最も一般的に使用される量 D バツ= t wを表 2 に示します。
表 2.
実際に実施する際には、 数量限定私たちは測定値を知りません。 正確な値分散ですが、その値を推定することしかできません。 標準偏差 s の最良の推定値は平均値です。 二乗誤差n測定値 nS:
この値は統計的に次の傾向があります。 -- s -- で n--®Ґ .
したがって、必然的に置き換えられます s--inの値信頼区間をその近似値まで nS。 同時に忘れてはいけないのは、 少ない数測定値が大きいほど、この近似値は悪くなります。 したがって、理論は、信頼確率を使用して信頼区間を正しく決定するには、次のことを示しています。 w= 0.9 には少なくとも 40 回の測定が必要です。)
c) 測定結果の算術平均の精度。
上記では、個々の測定結果が量の真の値から逸脱する確率を検討しました。 バツ。 測定結果の算術平均が真の値からどの程度乖離する可能性があるかを知ることも同様に重要です。 この偏差は信頼区間 (
厳密に言えば、値が バツは正規分布します 数学的期待 mと分散
s 2 、次にその平均値
期待値 m の正規分布を持ちます
と分散s 2 / n。 それらの。 ランダム
算術平均の誤差は 1 回の測定の誤差よりも小さいです。
目安としてであれば
s 二乗平均平方根誤差が使用されます nS、次に、平均値の偏差、つまり算術平均の二乗平均平方根誤差を推定します。 nS
:
価値 nS
統計的にはゼロになる傾向があります n®Ґ.
誤差の理論では、少数の測定では次のことが証明されています ( n< 30), которое реально имеет место в работах физического практикума, в доверительный интервал необходимо ввести коэффициентt わ、ん、スチューデント係数と呼ばれます。 この場合、信頼区間は次の形式になります (<バツ> ± t わ、ん nS
) w.
数字が小さいほど n測定値が大きいほど、平均値が真の値から乖離する可能性があります。 したがって、同じ信頼レベルに対して、 w学生の割合は減少するにつれて増加するはずです ん、表 3 を参照してください。
表3
???n |
||||||||||||||
d) 合計エラー。 間接測定の誤差。
理論によれば、完全に独立したランダム誤差と機器誤差を使用して、総実験誤差は次のように計算されます。
.
この場合、両方の誤差が同じ信頼確率で信頼区間を設定する必要があります。 器差は、信頼水準 w = 0.9 で独自の区間を設定します。 結果として生じる実験誤差を考慮する方法は他にもあります。
間接測定では、平均二乗絶対誤差は次の式で計算されます。
ここで、D バツ、 D そう、 D z、.... は実験の合計平均二乗誤差です。
間接値 a の相対誤差を計算する式には二乗が含まれます。 相対誤差。 たとえば、計算式で与えられる値 a の場合、
,
ここで、k は数値係数であり、誤差理論によって決定される相対誤差は次のようになります。
,
そこから何が続くのか
文学
1.A.N. ザイデル。 物理量の測定誤差。 L.、ナウカ、1985 年。
2.LG デデンコ。 V.V. ケルジェンツェフ。 数学的処理そして実験結果の発表。 M.、モスクワ州立大学出版社、1977年。
3. 物理的なワークショップ。 力学と分子物理学。 編集者:V.I. イベロノワ。 M.、ナウカ、1967 年。
4.PV ノヴィツキー、I.A. ゾグラフ。 測定結果の誤差の推定。 L.、エネルギーアトミズダット、1991 年。
5. 実験室での作業モスクワ州立大学の自然学部で物理学の課程を修了。 力学。 M、モスク。 ウント。 1997年。
6. 系統的な開発一般的な物理実習。 測定誤差。 コンプ。 DV ベロフ。 モスクワ、モスクワ州立大学、1993年。
Allbest.ru でホストされています
類似の文書
物理量の測定と誤差の分類。 直接および間接測定における誤差の決定。 測定結果のグラフィカル処理。 関係の定義 比熱容量 Clement と Desormes の方法によるガス。
トレーニングマニュアル、2015/06/22 追加
重大なエラーの基準。 標準偏差の区間推定。 間接および直接タイプの測定の結果を処理します。 測定システム誤差の統計的特性を計算する方法。 精度クラスの決定。
学期末レポート、2015/05/17 追加
物理量の直接的および間接的な測定。 絶対的、相対的、系統的、ランダム、平均 算術エラー、結果の標準偏差。 ノギスによる計算誤差の評価。
テスト、2010 年 12 月 25 日追加
物理量の本質、その測定の分類と特性。 物理量の静的および動的測定。 直接的、間接的、および共同測定の結果を処理し、その表示形式を正規化し、不確実性を評価します。
学期末レポート、2013 年 3 月 12 日追加
プレートの材料の密度を決定する機能、直接および間接測定の誤差の計算の分析。 エラーの主な種類: 系統的、ランダム、丸め誤差、およびミス。 直接的および間接的な測定における誤差。
テスト、2014 年 4 月 14 日追加
測定量の点と間隔の推定。 直接測定と間接測定の絶対誤差の計算。 誤差の統計分布、ガウス分布。 測定の準備と実行。 数値結果を四捨五入するためのルール。
トレーニングマニュアル、2016 年 12 月 26 日追加
素材点の運動学を研究し、自由落下の加速度を測定する際の誤差を推定する方法を習得します。 自由落下測定に使用される実験装置の説明。 間接測定の誤差の推定。
研究室での作業、2015 年 12 月 21 日追加
物理量の概念と本質、その定性的および定量的表現。 測定スケールの主な種類の特徴:名前、順序、差(間隔)と比率、その特徴。 対数スケールと生物物理スケールの特徴。
要約、2013 年 11 月 13 日追加
ユニット、種類、測定器の構造分類モデル。 エラーの種類、Microsoft Excel でのその評価および処理。 ルーター、磁電装置、赤外線温度計、ポータブルスケールの精度クラスの決定。
学期末レポート、2015/04/06 追加
物理量の体系とその単位、そのサイズと値の役割、分類の詳細。 測定値の統一の概念。 物理量の単位の規格の特徴。 量の単位の大きさの伝達:システムの特徴と使用される方法。
