☰

ランダム絶対誤差式。 ランダム誤差と系統誤差

ランダムエラーの影響を減らすには、この値を数回測定する必要があります。 ある値 x を測定しているとします。 測定の結果、次の値が得られました。

x 1 、 x 2 、 x 3 、 ... x n 。 (1.4)

この一連の x 値をサンプルと呼びます。 このようなサンプルがあれば、測定結果を評価できます。 そのような推定値となる値を とします。 しかし、この測定結果の評価値は測定量の真の値を表すものではないため、その誤差を見積もる必要があります。 エラー推定値 Δx を決定できると仮定しましょう。 この場合、測定結果を次の形式で記述できます。

x = ± Δx。 (1.5)

測定結果の推定値と誤差 Δx は正確ではないため、測定結果の記録には、その信頼性 P の表示を伴う必要があります。信頼性または信頼確率は、次の確率として理解されます。 本当の価値測定値の範囲は、レコード (3) で示される区間に含まれます。 この区間自体を信頼区間と呼びます。

たとえば、特定のセグメントの長さを測定するとき、最終結果を次のように書きました。

l= (8.34 ± 0.02) んん、(P = 0.95)。 (1.6)

これは、セグメントの長さの真の値が 8.32 から 8.36 までの範囲にある可能性が 100 のうち - 95 であることを意味します。 んん.

したがって、タスクは、測定のサンプルを取得して、測定結果の推定値を見つけることです 、その誤差Δx、および信頼性 P.

この問題は、確率論を使用して解決でき、 数学的統計.

ほとんどの場合、ランダム エラーは、ガウスによって確立された正規分布の法則に従います。 エラーの正規分布は次の式で表されます。

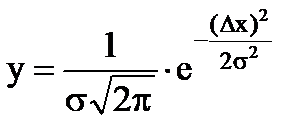, (1.7)

ここで、Δx は真の値からの偏差です。

σ は真の平均二乗誤差です。

σ 2 - 分散。その値は確率変数の広がりを特徴付けます。

式からわかるように、関数 y(x) は 最大値 x=0 の場合、さらに偶数です。

y
バツ
Δx 1
Δx2
-Δx 1
-Δx2

図1.4。 ガウス正規分布の曲線。

図 1.4 にこの関数のグラフを示します。 曲線、Δx 軸、および点 Δx 1 と Δx 2 からの 2 つの縦座標 (影付きの領域) で囲まれた図の領域は、任意のサンプルが間隔 (Δx 1 、Δx 2 ）。

曲線は y 軸に対して対称的に分布しているため、大きさが同じで符号が反対のエラーも同様に発生する可能性が高いと言えます。 これにより、すべてのサンプル要素の平均値を測定結果の推定値として取得できます。

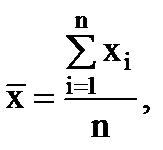(1.8)

ここで – n は測定回数です。

同じ条件で n 回測定すると、ほとんどの 確率値測定値はその平均値（算術）になります。 値は、x の真の値と n → ∞ として測定値に傾向があります。

1 回の測定結果の平均二乗誤差が値です。

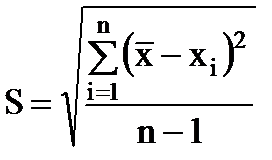(1.9)

個々の測定値の誤差を特徴付けます。 n → ∞ として、S は一定の極限 σ になる傾向があります。

σ = limS。
n → ∞ (1.10)

σ が増加すると、読み取り値のばらつきが増加します。つまり、 測定精度が低下します。

算術平均の二乗平均平方根誤差は値です。


(1.11)

これは、測定回数が増えるにつれて精度が向上するという基本法則です。

誤差は、測定値の平均値が得られる精度を特徴付けます。 結果は次のように書かれています。

x = ± Δx。 (1.12)

このエラー計算手法により、 素晴らしい結果(信頼度 0.68) 同じ値が少なくとも 30 ～ 50 回測定された場合のみ。

1908 年、著名な統計学者でスチューデントというペンネームでよく知られているウィリアム シーリー ゴセットは、統計的アプローチが少数の測定値に対しても有効であることを示しました。 測定数 n → ∞ のスチューデント分布はガウス分布になり、少数の場合はガウス分布とは異なります。

少数の測定値の絶対誤差を計算するために、スチューデント係数 t と呼ばれる、信頼性 P と測定数 n に依存する特別な係数が導入されます。 この係数の導入により

その導入の理論的正当化を省略すると、次のことに注意してください。

Δx t = t、(1.13)

ここで、Δx t は特定の信頼レベルの絶対誤差です。 算術平均の二乗平均平方根誤差です。

スチューデント係数は付録 1 に記載されています。

言われていることから次のようになります。

1.二乗平均平方根誤差の値により、測定値の真の値が算術平均に近い任意の間隔に入る確率を計算できます。

2. n → ∞ → 0 として、つまり、 x の真の値が特定の確率で配置される間隔は、測定数の増加に伴いゼロになる傾向があります。 n を大きくすることで、任意の精度で結果を得ることができるように思われます。 ただし、ランダム誤差が系統誤差と同等になるまで、精度は大幅に向上します。 これ以上の測定数の増加は不都合です。 結果の最終的な精度は、系統誤差のみに依存します。 系統誤差の値がわかれば、ランダム誤差の許容値を設定するのは簡単です。たとえば、系統誤差の 10% に等しくなります。 そうして選んだものを求めることで 信頼区間 P の特定の値 (たとえば、P = 0.95) の場合、必要な測定数を見つけることは難しくありません。これにより、結果の精度に対するランダム エラーの影響が小さくなります。

これを行うには、付録 2 の表を使用する方が便利です。この表では、ランダム エラーに関するこの実験の精度の尺度である値 σ の分数で間隔が示されています。

表 1.6 に、信頼性 P=95% の強調表示された列を含むスチューデント係数の一部を示します。

スチューデント係数 表 1.6

n R 0,9 0,95 0,999
6,31 2,92 2,35 2,13 2,02 1,94 1,89 1,86 1,83 12,7 4,30 3,18 2,78 2,57 2,45 2,36 2,31 2,26 636,6 31,6 12,9 8,61 6,37 5,96 5,41 5,04 4,78
∞ 1,96

複数の直接測定の結果を処理する場合、次の順序で操作します。

1. 各測定結果を表に記録します。

2. n 回の測定値の平均を計算する

(1.14)

3. 1 回の測定の誤差を見つける

(1.15)

4. 個々の測定値の二乗誤差を計算します

(Δx 1) 2 、(Δx 2) 2 、...、(Δx n) 2 。 (1.16)

5.算術平均の標準誤差を決定する

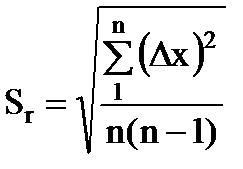. (1.17)

6. 信頼性の値を設定します (通常は P = 0.95 を取ります)。

7. 特定の信頼性 P と測定回数 n に対するスチューデント係数 t を決定します。

8.信頼区間（測定誤差）を見つける

Δx t = t。 (1.18)

測定結果の誤差 Δx が機器の誤差 Δx p と同等であることが判明した場合、信頼区間の境界として次のようにします。

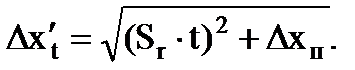(1.19)

エラーの 1 つが他のエラーの 3 倍以上小さい場合は、小さい方のエラーを破棄します。

9. 最終結果を次のように書きます。

. (1.20)

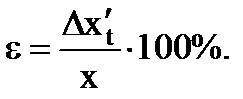(1.21)

数値例を使用して、上記の式を適用することを検討してください。

例。ロッドの直径 d はマイクロメーターで測定されました (系統測定誤差は 0.005 んん）。 測定結果は表の2番目の列に入力され、この表の3番目の列に差を書き、4番目の列に差の2乗を書きます（表1.7）。

表 1.7

n d、 んん
4.02 + 0.01 0.0001
3.98 - 0.03 0.0009
3.97 - 0.04 0.0016
4.01 + 0 .00 0.0000
4.05 + 0.04 0.0016
4.03 + 0.02 0.0004
Σ 24.06 – 0.0046

(1.22)

P = 0.95 の信頼性を考えると、6 つの測定値のスチューデント係数の表から t = 2.57 が見つかります。 絶対誤差は式(10)で求めることができます。

Δd = 0.01238 2.57 = 0.04 んん. (1.24)

ランダム誤差と系統誤差を比較してみましょう。

したがって、δ = 0.005 んん捨てることができます。

最終結果を次のように書きます。

d = (4.01 ± 0.04) んんР = 0.95 で。 (1.26)

測定値 しかしはいくつかの変数の関数です: あ= ふ(バツ, y,..., t), それから 絶対誤差結果 間接測定


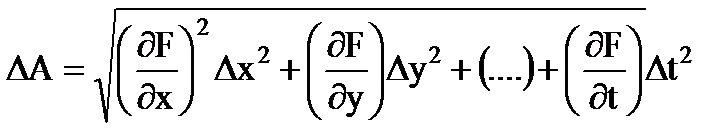(1.29)

間接測定の部分相対誤差は、式によって決定されます

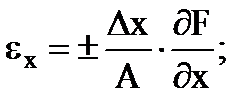
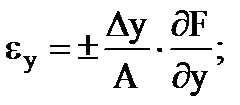…。 等々。 (1.30)

相対誤差測定結果


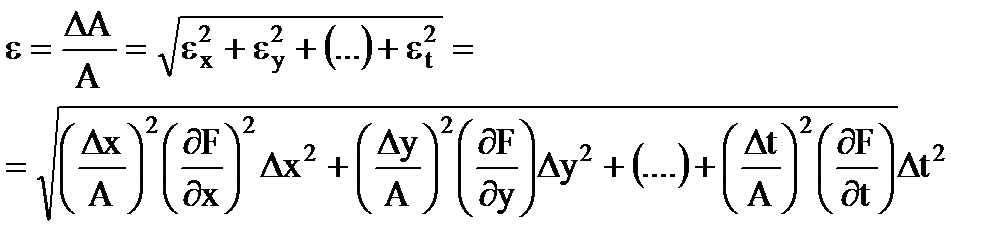(1.31)

グロス エラー (ミス)は、一連の測定に含まれる単一の観測結果のランダム誤差であり、特定の条件で、このシリーズの残りの結果とは大きく異なります。 それらは、原則として、オペレーターのエラーまたは不適切な行動が原因で発生します（心理生理学的状態、誤った読み取り、デバイスの隣接スケールからの読み取り、記録または計算のエラー、デバイスの不適切なスイッチオンまたは誤動作）。それらの操作など）。 考えられる原因ミスの発生は、測定条件の短期間の急激な変化でもあります。 測定プロセス中にミスが検出された場合、それらを含む結果は破棄されます。 ただし、ほとんどの場合、ミスは、特別な統計基準を使用した測定結果の最終処理中にのみ検出されます。

発生の原因に応じて、器械的、方法論的、および主観的なエラーが区別されます。

器差測定器自体に固有のエラーです。 測定が実行されるデバイスまたはトランスデューサ。 器差の原因は、測定器の設計の不完全性、測定器の影響である可能性があります。 環境その特性上、機器の部品の変形や摩耗など。

方法論的エラー測定方法の不完全性が原因で表示されます。 測定された量と測定器の開発に採用されたそのモデルとの間の不一致; 測定対象物およびその中で発生するプロセスに対する測定器の影響。 特徴的な機能 方法論的エラーそれらは測定器に依存しないため、測定器の規制および技術文書で指定することはできませんが、特定のケースごとにオペレーターが決定する必要があります。

主観的（個人的）エラー測定値は、測定器の目盛り、記録器のチャートでのオペレーターの読み取り誤差によるものです。 それらは、オペレーターの状態、作業中の位置、感覚器官の不完全さ、および測定器の人間工学的特性によって引き起こされます。 主観的誤差の特性は、測定器（または記録器のチャート紙）の目盛り分割の正規化された公称値に基づいて決定されます。スケール分割。 これらのエラーは、機器が改善されるにつれて減少します。たとえば、アナログ機器でライトポインターを使用すると、視差によるエラーが解消されます ( 視差（ギリシャの視差から - 偏差）、観察者の目の動きによるオブジェクトの相対位置の目に見える変化）デジタル基準の使用により、主観的なエラーが排除されます。

客観的な測定誤差- 測定者の個人的な資質に依存しない誤差。

外部条件の影響に応じて、測定器の主な誤差と追加の誤差が区別されます。

主なものは測定器の誤差と呼ばれますで定義 通常の状態そのアプリケーション。 各測定器について、規制および技術文書は動作条件を指定します - 一連の影響量 (周囲温度、湿度、圧力、電圧、主電源周波数など)、その下で誤差が正規化されます (影響量は 物理量、この測定器では測定されませんが、その結果に影響を与えます）。

追加と呼ばれる影響する量のいずれかの偏差から生じる測定器の誤差。 追加エラーは、デバイスが通常以外の条件で動作する場合に発生し、デバイスの全体的なエラーを増加させます。

測定値を変更したときの誤差の大きさの変化の性質に応じて、誤差は分割されます 加法と乗法に分けます。

加算誤差デバイスの静的特性の上下（右または左）のシフト、たとえば、計器スケールの変位（ゼロドリフト）、サポートの摩擦などによる。 加法誤差は、測定量 x の値に依存しません。つまり、 楽器のスケール全体で一定です。

ほとんどのアナログ計測器では​​加法的誤差が支配的です。

乗法誤差静特性 y = kx の伝達係数 k の設定誤差により発生します。 乗法誤差は、測定された量の値に依存し、計器の目盛の終わりに向かって増加します。

乗法誤差 (絶対誤差として表される場合) は、測定量の値に比例します。

スケーリング コンバータに関連するデバイス (シャント、追加抵抗、アンプ、分圧器、変圧器など) では、乗算誤差が優勢です。

加法誤差と乗法誤差が同等のデバイスがあります。 このクラスのデバイスには、デジタル デバイスが含まれます。

ランダムな測定誤差は、いくつかの独立した量が測定対象に同時に影響を与え、その変化が本質的に変動するために発生します。 ランダム測定誤差への一定の寄与は、測定器のランダム誤差によっても行われます。

測定誤差の系統的成分は除外され、確率変数としてのランダム誤差は完全に

確率分布密度 (つまり、確率密度) によって特徴付けられます。ここで、 は分布関数です。 したがって、数値は確定しません。 ランダムエラー、ただし、それが特定の間隔内にあるか、特定の値を超えない確率のみ。 分布法則が知られている場合、 と が知られています. から までの与えられた間隔でランダムエラーを見つける確率は、次の式で求められます.

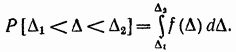
ランダムエラーの変化のパターンは、その値の複数の観測と観測結果の統計処理によって確立できます。

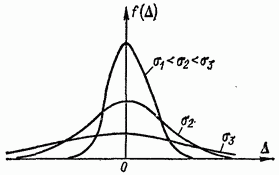
米。 2-1. 正規分布則に基づくランダムエラーの確率密度

この時間のかかる骨の折れる作業は、正確な測定で実行され、取得されたデータが何らかの基準に従って予想される分布に準拠しているかどうかを確認することから成ります。

影響量の変動もランダムであり、分布法則 (一様、三角、正規など) によって特徴付けられます。 しかし、それらの分散の通約性により、すでに 4 ～ 5 の影響量で、結果として得られるランダム測定誤差の分布法則は通常の分布法則と十分に一致します (図 2-1)。

正規分布関数

と確率密度

ここで、 は分布中心に対するランダム エラーの分散を特徴付ける分散とその標準偏差です。

分散と標準偏差は、測定の精度を特徴付けます。分散が大きいほど、精度は低くなります。 測定の実践では、測定値と同じ単位で表されるため、標準偏差 c が主に使用されます。


米。 2-2. 確率積分

式による ～ の範囲のランダムエラーの発生確率

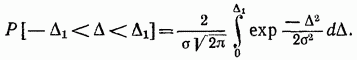
正規化された確率変数を導入すると、等式の右辺は、しばしば確率積分と呼ばれるラプラス関数に変換されます

この関数は表にまとめられており、その値は表に示されています。 グラフは図 1 のようになります。 2-2.

特定の確率 a が与えられた場合、それを見つけたら、正規分布の法則に基づいて、最大誤差 Dmax が次の値に等しいと見なされます。確率が 0.9973 の観測では、誤差は間隔 ± 3a にあり、1 つの観測でのみそれを超える可能性があります。

米。 2-3. 一様分布則によるランダムエラーの確率密度

一様分布の法則は、測定でも発生します。 特に、離散計数法による連続量の測定に適しています。 から までの範囲のエラー確率密度 (図 2-3) は、次の形式で記述されます。

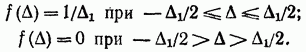
したがって、分散

と標準偏差

たとえば、通常は最下位桁 (-1/2 から 1/2) の範囲内にある量子化誤差は、標準偏差によって特徴付けられます。

正規分布の法則に戻りましょう。 この法則は、数学的パラメーター (数学的期待値と分散) によって特徴付けられます。 正確な定義これらのパラメーターはほとんど不可能です。これには、無限に多くの値が必要になるためです。 確率変数、つまり で観測を実行します。 測定の実践では、常に有限であるため、実験の結果として計算された値が呼び出されます

見積り 数学的期待値および標準偏差。

特定の量の統計的測定の手順を考えてみましょう。その真の値は単一の観測によって作成され、その結果、測定された量の一連のランダム値が得られます。 最初の観測の各絶対誤差では、この誤差の値が不明であるため、この誤差の値を決定することは不可能です。

算術平均は、数学的期待値 (真の値) の推定値として取得されます。

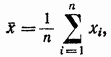
これは、測定された量の実際の値 A と呼ばれます。

これで、平均値に対する各観測結果の絶対偏差を計算できます: 明らかに、で 計算の正確さを制御するために、算術平均からの観測結果の偏差のプロパティを使用できます: 偏差の合計はゼロであり、それらの二乗和は最小です。

単一観測値のそれぞれの絶対偏差の標準偏差の推定値は、式によって決定されます。

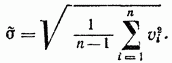
測定結果の精度が高くなります。 これは、算術平均 (実数) 値の標準偏差の推定によって特徴付けられます。

測定数が増えると (独立した結果で)、精度は比例して増加します。増加することで、精度が向上するように思われます。 ただし、測定量自体は測定中に変化する可能性があるため、常識と測定の実践では、ほとんど役に立たないことが示唆されています。

信頼区間と信頼確率。測定値の観察の結果として、式 (2-11) に従って、算術平均 X に等しい実際の値 A の推定値を取得します。 この推定値も確率変数です。 その標準偏差 a - は式 (2-13) によって決定されます。つまり、測定結果には不確実性が含まれます。 同じ条件下での（統計的）量の繰り返し測定中に A の実際の値がどの範囲内で変化するかを調べる必要があります。つまり、の真の値を「カバーする」値の間隔を見つける必要があります。与えられた確率で測定された量。 このような間隔は信頼区間と呼ばれ、特定の (確立された) 確率は信頼区間と呼ばれます。 信頼区間と信頼水準は、測定結果の不確実性を特徴付けます。 分析的には、これは次のように書かれています。

式 (2-14) は次のようになります。測定値の真の値は、信頼区間 から までの範囲内にあり、信頼確率は a です。

ランダムエラーも同様

ランダム測定誤差は から までの信頼区間内にあり、信頼確率は a です。

測定の目的に応じて、信頼水準は に等しく設定されます。 式 (2-14) と (2-15) では、信頼区間は対称です。 信頼区間の半分は、信頼確率 a の制限 (最大、許容) エラーと呼ばれます。 信頼区間が非対称で、次の形式を持つ場合があります。

限界誤差と信頼区間は、標準偏差で表されます。 正規分布の法則の場合、特定の信頼確率 (およびその逆) の信頼区間は、確率積分表 (表 A4) を使用して決定されます。 これらは、0.95 などの信頼レベルで設定されます。 表によると、この場合は 2 に等しい値も見つかります。これは信頼区間であるため、

明らかに、信頼区間と信頼レベルの両方が観測数に関連しています。これは、大きくなるほど区間が狭くなるためです。 ただし、前述のように、実際の測定ではまれです。 観測数の場合、信頼区間は、観測数と信頼確率 a に依存する特定の係数ではなく、観測数によって決定されます。 係数変化の法則は、正規分布で計算された正規化確率変数のスチューデント分布によって決定されます。 係数は、次の式を使用して決定されます。

これらはミスではありません。つまり、オペレーターによる明らかなエラーではありません。その場合、それらが重大なエラーであるかどうかを確認する必要があり、これらもミスのように処理から除外する必要があります。 十分な根拠のない重大なエラーの除外は、測定結果の不合理な改善につながります。 一方、特に観測数が少ない場合、総誤差を除外しないと、測定値の実際の値と信頼区間の境界の両方が歪められます。 したがって、重大なエラーを検出して排除する必要があります。

正規分布の下で総誤差を検出する最も簡単な方法は、「疑わしい」観察の絶対誤差を最大誤差と比較することです.その場合、この結果を破棄して値を再計算する必要があります.この方法はに基づいています.値が算術平均から逸脱する確率は、わずか 0.003 以上です。

ただし、次の場合は覚えておく必要があります。 多数低い確率ではありますが、破棄された数は全体的なエラーではなく、この値の自然な統計的偏差である可能性があります。 したがって、重大なケースでは、確率論に基づいて総誤差の決定が行われます。 所与の確率で何回の測定で、所与の数または所与の限界を超える観測結果を破棄することができるかが確立される。

測定誤差は次の種類に分類されます。

絶対的で相対的。

ポジティブとネガティブ。

定数と比例。

ラフで、ランダムで、体系的。

絶対誤差単一の測定結果 (A y) は、次の量の差として定義されます。

あ y = y私- yです。 » y私-` y.

相対誤差単一の測定結果 (B y) は、次の量の比率として計算されます。

この式から、相対誤差の大きさは絶対誤差の大きさだけでなく、測定量の値にも依存することがわかります。 測定値が変わらない場合（ y) 相対測定誤差は、絶対誤差 (A y）。 絶対測定誤差が一定の場合、相対測定誤差を小さくするには、測定量の値を大きくする方法を使用できます。

例。店舗の商品秤の絶対質量測定誤差が一定であると仮定しましょう: A m = 10 g. このような秤で 100 g のお菓子 (m 1) を計量すると、お菓子の質量を測定する際の相対誤差は次のようになります。 :

.

同じはかりで 500 g のお菓子 (m 2) を計量すると、相対誤差は 5 分の 1 になります。

.

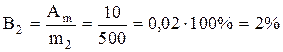したがって、100 g のお菓子を 5 回秤量すると、質量測定誤差により、500 g のうち合計 50 g の製品を受け取ることはありません。 より大きな質量 (500 g) を 1 回計量すると、10 g のお菓子しか減りません。 5倍少ない。

上記を考えると、まず第一に、相対測定誤差を減らすように努力する必要があることに注意することができます。 絶対誤差と相対誤差は、平均を決定した後にのみ計算できます 算術値測定結果。

エラーの符号 (正または負) は、単一の測定結果と実際の測定結果の差によって決まります。

y私-` y > 0 (エラーは正です);

y私-` y < 0 (エラーは負です).

絶対測定誤差が測定量の値に依存しない場合、そのような誤差は呼び出されます 絶え間ない. そうしないと、エラーが発生します 比例. 測定誤差の性質（定数または比例）は、特別な調査の後に決定されます。

重大な間違い測定（ミス）は、測定手順に違反した場合に通常発生する、他の測定結果と大きく異なる測定結果です。 サンプルにおける全体的な測定誤差の存在は、数学的統計の方法によってのみ確立されます (n>2 の場合)。 自分で重大なエラーを検出する方法を理解してください。

エラーのランダムとシステマティックへの分割は、かなり条件付きです。

に ランダムエラー定数値と符号を持たないエラーを含めます。 このようなエラーは、次の要因の影響下で発生します。研究者には不明です。 知られているが規制されていない。 常に変わっている。

ランダム誤差は、測定が行われた後にのみ推定できます。

定量化ランダム測定誤差の大きさのモジュラスは、次のパラメータになる可能性があります。

ランダムな測定誤差を排除することはできず、減らすことしかできません。 ランダム測定誤差の大きさを減らす主な方法の 1 つは、単一測定の数を増やす (n の値を増やす) ことです。 これは、ランダム エラーの大きさが n の値に反比例するという事実によって説明されます。たとえば、次のようになります。

系統誤差大きさと符号が一定の誤差、または既知の法則に従って変化する誤差です。 これらのエラーは、一定の要因によって発生します。 系統誤差は、定量化、削減、さらには排除することができます。

系統誤差は、タイプ I、II、および III のエラーに分類されます。

システマティックに タイプ I エラー既知の原因による誤差を参照してください。これは、測定前に計算によって推定できます。 これらの誤差は、補正の形で測定結果に導入することで排除できます。 この種のエラーの例としては、滴定液がある温度で調製され、濃度が別の温度で測定された場合の、溶液の体積濃度の滴定測定におけるエラーがあります。 滴定液の密度の温度依存性を知っていれば、測定前に温度の変化に伴う滴定液の体積濃度の変化を計算し、この差を次の結果としての補正として考慮することができます。測定。

系統的 タイプ II エラー- これらは既知の原因によるエラーであり、実験中または特別な研究の結果としてのみ評価できます。 このタイプのエラーには、インストルメンタル (instrumental) エラー、リアクティブ エラー、リファレンス エラー、およびその他のエラーが含まれます。 そのようなエラーの特徴を自分で理解してください。

どのデバイスも、測定手順で使用されると、測定結果にその機器誤差が導入されます。 同時に、これらのエラーの一部はランダムであり、残りの部分は体系的です。 ランダム計器誤差は個別に評価されず、他のすべてのランダム測定誤差と一緒に評価されます。

楽器の各インスタンスには、独自の個人的な系統誤差があります。 このエラーを評価するには、特別な調査を行う必要があります。

多くの 信頼できる方法タイプIIの機器の系統誤差の評価 - これは、標準に対する機器の動作の調整です。 測定器具（ピペット、ビュレット、シリンダーなど）の場合、特別な手順が実行されます-キャリブレーション。

実際には、ほとんどの場合、推定するのではなく、タイプ II 系統誤差を削減または排除する必要があります。 系統誤差を減らすための最も一般的な方法は次のとおりです。 相対化とランダム化の方法.でこれらのメソッドを自分でチェックしてください。

に 間違い Ⅲ型 原因不明のエラーが含まれます。 これらのエラーは、すべてのタイプ I および II の系統的エラーが除去された後にのみ検出できます。

に その他の間違い上記で考慮されていない他のすべてのタイプのエラー (許容される可能性のあるわずかなエラーなど) が含まれます。 可能な限界誤差の概念は、測定機器を使用する場合に使用され、可能な最大の機器測定誤差を想定しています (誤差の実際の値は、可能な限界誤差の値よりも小さい場合があります)。

測定器を使用する場合、可能な絶対限界を計算することができます (P` yなど) または相対 (E` yなど）測定誤差。 したがって、たとえば、可能な制限絶対測定誤差は、可能な制限ランダム (x ` y、ランダムなど) および除外されていない体系的 (d` yなど) エラー:

P` y、例 = x ` y、ランダム、pr. + d` yなど

小さなサンプル (n ≤ 20) の場合、未知数 人口、正規分布の法則に従うと、ランダムな可能性のある制限測定誤差は次のように推定できます。

x` y、ランダム、pr. = D` y=S' y½t P、n ½、
ここで、t P,n は、確率 P およびサンプル サイズ n のスチューデント分布 (検定) の分位数です。 この場合の絶対的な限界測定誤差は次のようになります。

P` y,ex.= S ` y½t P, n ½+ d` yなど

測定結果が正規分布の法則に従わない場合、誤差は他の式を使用して推定されます。

d `の値を決定する y、等。 測定器に精度クラスがあるかどうかによって異なります。 測定器に精度クラスがない場合、値 d ` y、等。 受け入れることができます スケール分割の最小値採寸。 値dの既知の精度クラスを持つ測定器の場合 ` y、たとえば、測定器の絶対許容系統誤差を受け入れることができます (d y、 追加。）：

d` y、等。" .

d値 y、 追加。 は、表 5 に示す式に基づいて計算されます。

多くの測定器では、精度クラスは数値 a × 10 n の形式で示されます。ここで、a は 1 です。 1.5; 2; 2.5; 四; 5; 6 で、n は 1 です。 0; -1; -2 など、可能な最大許容系統誤差の値を示します (E y、追加）およびそのタイプを示す特殊記号（相対、縮小、定数、比例）。

表 5

測定器の精度等級の指定例

表 5 の続き

表 5 の終わり

不等式の場合、系統誤差は無視できます。

この場合、次のことが想定されます。

P` yなど」 x` y、 場合 など » D` y»S` y½t P、n ½。

ランダムエラーは無視できます

この場合 P` yなど」 d` y、等。 .

単一測定の数を増やすことは、ランダム エラーを減らすための最も一般的な方法です (測定のコストも増加します)。 総測定誤差が系統誤差のみによって決定されるまで n を増やすことをお勧めします。 これに必要な並列測定の最小数 (n min) は、 既知の値式に従った単一結果の一般母集団

.

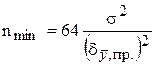測定結果 () の算術平均の絶対系統誤差の成分 (m - 成分の数) がわかっている場合、次の式で推定できます。

,

ここで、k は確率 P と数 m によって決まる係数です。

測定誤差の推定は、測定手段とサンプル サイズだけでなく、測定の種類 (直接測定または間接測定) にも依存します。

測定値を直接的および間接的に分割することは、むしろ条件付きです。 後で、 直接測定測定結果がデバイスの目盛りから読み取られるなど、直接得られる場合は、そのようなことがわかります。 に 間接測定測定結果が 計算された(j) 1 つまたは複数の直接測定の結果 ( バツ 1 , バツ 2 , …, バツ j、。 …、 バツ k）。

間接測定の誤差は、個々の直接測定の誤差よりも常に大きいことを知っておく必要があります。 間接測定の誤差は、関連する法律に従って推定されます。

ランダムエラーは、繰り返し測定中の測定量の観測値がその真の値に対してランダムに散乱するという事実につながります。 次に、実際の値が一連の実験の最も可能性の高いものとして検出され、誤差は間隔の幅によって特徴付けられます。これには、所定の確率で真の値が含まれます。 これらの規定の数学的実証は確率論で与えられ、測定結果を処理するためのその適用は文献で与えられ、作品への直接適用は 物理的なワークショップ文学で。

非常に多くの場合、学生や学童は次の式を使用して測定誤差を見つけます。

, (6.2)

ここで、 は測定プロセス中に得られた量の平均値であり、参考書から取得した値、または理論的概念から計算された値です。 実験の目的は、上に示したように、理論的概念をテストし、表形式のデータを改良することであるため、このような誤差の定義は重大な誤りです。

さらに、多くの場合、エラーは、式を使用して、平均値からの個々の測定結果の偏差の平均値として計算されます。

. (6.3)

このアプローチによれば、エラー値は同じ頻度で表示されます。 異なる大きさのエラーは、同じ確率であると見なされます。 このメソッドは、 研究室の仕事少数の測定で。

ただし、ランダム エラーの確率は同じではありません。 それらを定義するには、測定結果の統計処理が必要です。 そのため、測定結果の統計処理の内容を考慮する必要があると思われる。 エラーの統計理論は、次の規定に基づいています。

1) 多数の測定では、同じ大きさのランダム誤差が観察されますが、 別の記号、つまり、エラーは、減少方向と増加方向の両方で、同じ頻度で発生します。

2) 大きな (絶対値の) エラーは、小さなエラーよりも一般的ではありません。 エラーの大きさが大きくなるにつれて、エラーが発生する確率が低下します。

3) 測定誤差は、連続した一連の値を取ることができます。

リストされたプロパティに従う確率変数の分布は、正規分布と呼ばれます。 スプレッドを推定するには 個人正規分布の確率変数の値または正規分布の理論における個々のサンプルが選択されます 測定値のサンプル標準偏差、これは次の式で計算されます。

. (6.4)

式 (6.4) によって決定される、1 回の測定の誤差値の推定は非常に重要です。 ただし、測定では、測定値の平均値がどの程度の精度で目的の値に対応するかを判断することが重要な作業です。 この問題は、平均値が 異次元. たとえば、平均値は、異なる数の測定値から取得できます。 したがって、経験的平均も確率変数であり、分布関数によっても記述できます。 この関数に対応する標準偏差の値は、確率論で示されているように、次の式によって決定されます。



(6.5)

この値は 平均の標本標準偏差また 標準誤差。

標準誤差の式 (6.5) からわかるように、測定回数が増えると減少し、結果の精度が向上します。これは、前の推論に対応しています。

測定誤差を決定するための上記の式は、確率変数の正規分布の特性を使用しています。 しかし、測定結果がどのような法則で分布しているのかはわかりません。 したがって、これらの見積もりは概算です。 この点で、測定誤差を決定するためにこのアプローチを分析する必要があります。 このような分析では、確率論における信頼区間のよく知られた概念を使用できます。 この値を、測定結果 (平均値) が真の値から より大きくない値だけ異なる確率に等しいとします。 確率論では、このフレーズは次のように記述されます。

値は呼び出されます 信頼度（信頼度）一連の観察の結果。 信頼区間に測定量の真の値が含まれる確率を示します。

信頼区間値の間隔と呼ばれ、一定の確実性で測定値の真の値が含まれます。 この間隔の幾何学的表現を図 1 に示します。

したがって、ランダムエラーを決定するには、ランダムエラー自体の値または信頼区間と信頼確率の値の2つの数値を見つけるか設定する必要があります。

信頼区間の任意の値について、信頼確率を計算できます。 これには、確率積分とも呼ばれるラプラス関数が使用されます。 ラプラス関数の形式は次のとおりです。

,

どこ 。 ほとんどの場合、問題を解決するとき、ラプラス関数の表形式の値が使用されます。 これらの値を表 1 に示します。

この表の結果は、rms エラーの信頼確率が 0.68、2x rms エラーの信頼確率が 0.95、3x rms エラーの信頼確率が 0.997 であることを示しています。

表1

信頼確率 平均二乗誤差の分数で表される信頼区間 . ラプラス関数

1,2 0,77 2,6 0,990
0,05 0,04 1,3 0,80 2,7 0,993
0,1 0,08 1,4 0,84 2,8 0,995
0.15 0,12 1,5 0,87 2,9 0,996
0,2 0,16 1,6 0,89 3,0 0,997
0,3 0,24 1,7 0,91 3,1 0,9981
0,4 0,31 1,8 0,93 3,2 0,9986
0,5 0,38 1,9 0,94 3,3 0,9990
0,6 0,45 2,0 0,95 3,4 0,9993
0,7 0,51 2,1 0,964 3,5 0,9995
0,8 0,57 2,2 0,972 3,6 0,9997
0,9 0,63 2,3 0,978 3,7 0,9998
1,0 0,68 2,4 0,984 3,8 0,99986
1.1 0,73 2,5 0,988 3,9 0,99990
4,0 0,99993

ランダムエラー信頼区間の半値幅として定義するのが通例です。 信頼区間のサイズは、平均のサンプル標準偏差の倍数として与えられます 、式（6.5）によって決定されます。それで 複数の測定のランダム誤差式で決まります。