Časť 1. Približné čísla a operácie s nimi
1.1 Typy chýb v približných výpočtoch
Presné riešenie niektorých matematických úloh nie je možné získať klasickými metódami, alebo je možné toto riešenie získať takýmto spôsobom. komplexná forma, čo je pre ďalšie praktické využitie neprijateľné. Okrem toho presné riešenie problému môže vyžadovať veľmi Vysoké číslo(od niekoľkých desiatok do mnohých miliárd) akcií. V takýchto prípadoch sa uchýlite k približným a numerickým metódam riešenia.
Príchod počítačov značne rozšíril rozsah týchto metód. V súčasnosti je ťažké predstaviť si inžiniera, ktorý nevlastní počítač a metódy približných výpočtov.
Všimnite si, že každý počítač je schopný zapamätať si veľké, ale konečné polia čísel a vykonávať na nich aritmetické operácie a porovnania veľkou, ale konečnou rýchlosťou. To znamená, že stroj je schopný vykonávať veľmi veľký, ale konečný počet operácií. Preto pri práci na počítači môžete používať iba tie matematické modely, ktoré sú opísané konečnou množinou čísel, a používať iba konečné postupnosti aritmetických operácií.
Matematické modely rôznych javov sú funkcie, derivácie, integrály, diferenciálne rovnice atď. Pri práci na počítači by sa tieto počiatočné modely mali nahradiť modelmi, ktoré sú popísané konečnými množinami čísel označujúcich konečnú postupnosť akcií na ich spracovanie. Na tento účel je funkcia nahradená tabuľkou, určitý integrál- množstvo atď. Okrem toho má počítač konečnú pamäť a môže pracovať s číslami konečnej dĺžky, takže medzivýsledky sú zaokrúhlené. Výsledkom je, že aj presná metóda s konečným počtom krokov sa stáva približnou.
Riešenie získané numerickou metódou je teda približné.
Dôvody chýb sú:
- Nekonzistentnosť matematického modelu so skúmaným skutočným javom
- Počiatočná chyba údajov.
- Chyba metódy riešenia.
- Chyby zaokrúhľovania v aritmetických a iných operáciách s číslami.
Chyba rozhodnutia spôsobená prvými dvoma dôvodmi sa nazýva tzv smrteľné— to nezávisí od matematika.
Chyba metódy vzniká, pretože numerická metóda spravidla nerieši pôvodný problém, ale jednoduchší problém. Okrem toho je numerická metóda zvyčajne založená na nekonečnom procese, ktorý musí byť v určitom kroku ukončený.
Väčšina numerických metód závisí od jedného alebo viacerých parametrov. Voľba parametrov metódy umožňuje upraviť chybu metódy.
Chyba zaokrúhľovania by nemalo byť významné viac chýb metóda. A je vhodné zvoliť chybu metódy 2-5 krát menšiu ako fatálnu chybu.
1.2 Približné čísla
V praxi sa často musíme zaoberať číslami, ktoré vyjadrujú skutočnú hodnotu nie presne, ale približne. Takéto čísla sa nazývajú približné.
Označme presnú číselnú hodnotu nejakej hodnoty a , približnú číselnú hodnotu tej istej hodnoty a * . Potom » a * .
Nahradením presného čísla a približným číslom a * urobíme chybu (chybu).
Definícia 1.1. Absolútna chyba približného čísla a * je absolútna hodnota rozdielu medzi týmto číslom a jeho presnou hodnotou | a-a* |.
Keďže presná hodnota množstva je zvyčajne neznáma, nie je možné vypočítať a absolútna chyba. Môžete však zadať kladné číslo D(a*), vyhovujúce nerovnosti:
Akékoľvek číslo d(a*) , uspokojujúce nerovnosť
Všimnite si, že existuje veľa čísel, ktoré spĺňajú nerovnosti (1.2) a (1.3). Preto hodnota hraničnej chyby nie je celkom istá.
V praxi sa zvyčajne berie najmenšia možná hodnota hraničnej chyby. Pre každé približné číslo je nevyhnutne určená jeho hraničná chyba (absolútna alebo relatívna). Limitujúca absolútna chyba umožňuje nastaviť hranice, v ktorých leží číslo a, t.j.
Limitná relatívna chyba charakterizuje presnosť výpočtov alebo meraní.
Príklady.
1.2.1 . Pri riešení problémov namiesto presného čísla p = 3,14159265... používame jeho približnú hodnotu 3,14 a robíme chybu:
p - 3,14 > 0,00159265
1.2.2 . Pri meraní dĺžky cesty bol získaný výsledok 25,2 km s presnosťou na 2m. Vypočítajte obmedzujúce absolútne a obmedzujúce relatívne chyby.
Riešenie. V našom prípade je limitná absolútna chyba rovná D = 0,002 km a hraničná relatívna chyba
Podobne vypočítame
znamená, že a * je približná hodnota čísla a s absolútnou chybou D(a*). Ak * je približná hodnota čísla a s relatívnou chybou d(a*), potom píšu takto:
1.4 Významné čísla, pravdivé a pochybné čísla
V praxi sa používajú rôzne techniky, ktoré umožňujú posúdiť jeho chybu iba zaznamenaním čo najpribližnejšieho čísla.
Zaznamenávanie približných čísel a absolútnych chýb podlieha určitým pravidlám.
V desiatkovom zápise významná postava Volá sa každá číslica, ktorá sa nerovná nule. Nula sa považuje za platnú číslicu, ak sa nachádza medzi platnými číslicami alebo je napravo od všetkých platných číslic.
Príklad 1.3.1. Približné číslo 0, 38 má 2 platné číslice, 0, 308 - tri, 0, 3080 - štyri, 0,00 308 - tri. Významné číslice sú podčiarknuté číslice.
Definícia 1.3. Významná číslica je tzv pravda v širokom zmysle ak absolútna chyba čísla nepresahuje jednu jednotku číslice zodpovedajúcej tomuto obrázku.
Významná číslica je tzv správne v užšom zmysle ak absolútna chyba čísla nepresahuje polovicu jednotky číslice zodpovedajúcej tomuto obrázku.
V opačnom prípade sa berie do úvahy číslo pochybný.
Ak sa zapíše približné číslo bez určenia jeho absolútnej (úplnej absolútnej) chyby, vypíšu sa iba jeho správne čísla. V tomto prípade sa skutočné nuly na pravom konci čísla nevyhadzujú. Čísla 0,25 a 0,250 sa líšia ako aproximácie. Ak použijeme záznamy v tvare (1.4) alebo (1.5), potom čísla na pravej strane týchto rovnosti musia byť zapísané s rovnakým počtom desatinných miest.
Absolútna resp relatívna chyba Je zvykom písať ho ako číslo obsahujúce jednu alebo dve platné číslice. V tomto prípade sa zaokrúhľovanie vykonáva s prebytkom.
Môže sa ukázať, že približné číslo vo svojej celočíselnej časti má viac platných číslic ako správne znamienka. V tomto prípade sa používa zápis v normalizovanom tvare a * = m 10 n , pričom číslo m ≤ 1 musí obsahovať iba platné číslice. V normalizovanom zápise sa číslo m nazýva mantisa, n — exponent
Všimnite si, že limitná absolútna chyba je určená počtom desatinných miest za desatinnou čiarkou: čím menej desatinných miest za desatinnou čiarkou, tým viac D(a*).
Limitná relatívna chyba je určená počtom platných číslic: čím menej platných číslic, tým viac d(a*).
1.5 Zaokrúhľovanie
Používa sa na písanie približných čísel so správnymi číslami zaokrúhľovanie.
Presné čísla je tiež potrebné zaokrúhliť nahor, ak je počet použitých číslic obmedzený.
Zaokrúhľovanie (doplnkom)číslo sa nazýva zápis tohto čísla s menším počtom číslic podľa nasledujúceho pravidla: ak je prvá vyradená číslica väčšia alebo rovná 5, posledná zostávajúca číslica sa zvýši o jednu. Pri zaokrúhľovaní čísel nastáva chyba, s ktorou treba tiež počítať.
Chyba zaokrúhľovania podľa doplnku nepresahuje polovicu jednotky najmenšej významnej číslice v absolútnej hodnote. Pri výpočte výslednej chyby treba k pôvodnej absolútnej chybe čísla pripočítať aj chybu zaokrúhľovania.
Príklad 1.3.2.Číslo a * = 413287,51 má relatívnu chybu d(a*) = 0,01. Z (1.3) vyplýva, že D(a*)=| a * | d(a*).
Absolútna chyba tohto čísla je teda 4133. To znamená, že štvrtá číslica čísla a * už môže obsahovať chybu. Správne sú teda iba prvé dve číslice čísla. Potom sa v normalizovanom tvare toto číslo zapíše takto: a * = 0,41 ·10 6 .
Argumentujúc podobne, približné číslo b * = 0,0794 at d(b*) = 2 % napíšte v normalizovanom tvare b * = 0,8 10 - 1 .
Všimnite si, že tu musíme číslo zaokrúhliť.
Pri vykonávaní aritmetických operácií s približnými číslami vznikajú dva vzájomne inverzné problémy:
1. Podľa známe chyby vstupné údaje na odhad chyby výsledku.
2. Určite presnosť počiatočných údajov, ktoré poskytujú špecifikovanú presnosť výsledku.
Pri práci s približnými číslami je navyše potrebné zladiť presnosť rôznych vstupných údajov, aby sa nestrácal čas vypisovaním zbytočných a nesprávnych čísel.
V procese výpočtov je tiež potrebné sledovať presnosť medzivýsledkov.
Pred začatím aritmetických operácií sa použije zaokrúhľovanie tak, aby všetky čísla zahrnuté v týchto operáciách boli zapísané s rovnakým počtom desatinných miest. Počet zostávajúcich desatinných miest je určený najmenším počtom platných číslic v pôvodných údajoch.
Pri sčítaní a odčítaní približných čísel, ktoré majú za desatinnou čiarkou rovnaký počet správnych číslic, sa zaokrúhľovanie nevykonáva.
Pri sčítaní a odčítaní približných čísel s rôznym počtom správnych číslic za desatinnou čiarkou sa výsledok v pôvodných údajoch zaokrúhli na najmenší počet správnych číslic za desatinnou čiarkou.
Pri násobení a delení približných čísel s rôznym počtom správnych číslic sa výsledok zaokrúhli na minimálny počet správnych číslic v pôvodných údajoch.
1.6 Aritmetické chyby
Nech a * a b * sú približné čísla, potom ich súčet c * = a * + b * je tiež približné číslo.
Ak označíme absolútne chyby pojmov D(a*) a D(b*), respektíve, potom absolútna chyba čísla c * je určená vzorcom
|
Preto sa pri sčítaní dvoch približných čísel sčítajú ich limitujúce absolútne chyby.
Toto pravidlo platí pre ľubovoľný konečný počet výrazov. Okrem toho platí vzorec (1.6) aj pre rozdiel dvoch čísel.
Rozdiel dvoch čísel môže byť skutočne reprezentovaný ako súčet
a * - b * = a * + ( - b *),
a absolútna chyba čísla ( -b*) sa rovná absolútnej chybe čísla b * .
Komentujte Pri odčítaní dvoch čísel rovnakého znamienka môže byť relatívna chyba rozdielu oveľa väčšia ako relatívna chyba každého člena. Obzvlášť veľká strata presnosti nastáva pri odčítaní čísel, ktoré sú blízko seba.
Príklad 1.4.1. Nech je potrebné nájsť rozdiel 61,32 - 61,31 .
Absolútne chyby týchto čísel sú, resp D1 = 0,01 a D2 = 0,01. Poďme teraz nájsť relatívne chyby týchto čísel:
Pri odčítaní dostaneme číslo 0,01 (všimneme si, že došlo k strate troch platných číslic). Jeho absolútna chyba sa rovná súčtu absolútnych chýb členov D1+ D 2 \u003d 0,02. Potom je relatívna chyba výsledku Porovnaním chýb počiatočných údajov a výsledku zistíme prudký nárast relatívnej chyby. Z príkladu 1.4.1. Z toho vyplýva, že by sme sa mali snažiť vyhnúť odčítaniu čísel, ktoré sú si v absolútnej hodnote blízke. Niekedy sa to dá dosiahnuť konverziou výpočtového vzorca. Ak sa takémuto odpočítaniu nedá vyhnúť, je potrebné zvýšiť presnosť medzivýpočtov, berúc do úvahy stratu významných čísel. Pri násobení a delení dvoch približných čísel a * a b * sa chyby určujú podľa vzorcov: Pri násobení a delení približných čísel sa teda sčítavajú ich obmedzujúce relatívne chyby. Poznámka . Ak absolútna chyba približného čísla Δ (a *) nepresiahne jednotku číslice vyjadrenú n-tou platnou číslicou v desiatkovom zápise tohto čísla, platí pre hraničnú relatívnu chybu nasledujúca nerovnosť: 5(a*) ≤ 1/k10n-1 kde k - prvá platná číslica čísla a * . Ak je absolútna chyba približného čísla D(a*) nepresahuje polovicu jednotky číslice vyjadrenej n-tou platnou číslicou v desiatkovom zápise tohto čísla, pre hraničnú relatívnu chybu platí nasledujúca nerovnosť: δ(a *) ≤ 1 / 2 k 10 n − 1 kde k je prvá platná číslica znaku * . V druhom prípade to platí aj naopak: ak d (a *) J 1/ 2 (k + 1) 10 n - 1, potom a * je približné číslo s n platnými číslicami. Nech je daná funkcia spojito diferencovateľná v oblasti G u \u003d f (x 1, x 2, j, x n). Odhad chyby v približnom výpočte hodnoty funkcie je nahradený odhadom modulu jej odchýlky od presná hodnota spôsobené chybami v argumentácii. V tomto prípade je odchýlka funkcie nahradená jej celkovým diferenciálom, v ktorom sú prírastky argumentov nahradené ich absolútnymi chybami. Potom je limitná absolútna chyba hodnoty funkcie určená vzťahom
d=
0,02
0,01
= 2.
D(a*b*) = | b * | D(a *) + | a * | D(b*),
d(a*b*) = d(a*) + d(b*),
(1.7)
D(a*/b*) =
| b*|D(a*)+| a*|D(b*)| b * | 2
d(a*/b*) = d(a*) + d(b*).
1.7 Chyba funkcie
Pre hraničnú relatívnu chybu máme rovnosť
Pomocou vzorcov (1.11) je možné určiť presnosť argumentov, čo zaisťuje danú presnosť funkčnej hodnoty.
Príklad 1.5.1. Treba merať s presnosťou d = 1 % plocha bočného povrchu zrezaného kužeľa, ktorého polomery základne sú r 1 » 2 m, r 2" 1 m a generatrix l» 5 m.
S akou absolútnou chybou je potrebné merať polomery a tvoriacu čiaru a s koľkými znamienkami správne v širšom zmysle treba brať číslo p?
Ak D(a*) nepresahuje jednu číslicu vyjadrenú n-tou platnou číslicou, potom sa * nazýva číslo s n platnými číslicami v širokom zmysle.)
Riešenie. Plocha bočného povrchu zrezaného kužeľa sa vypočíta podľa vzorca:
S = π l(r 1 + r 2).
Máme teda funkciu štyroch argumentov S = S(p , l, r 1, r 2).
Nájdite parciálne derivácie a vydeľte S .
Zo vzorcov (1.11) vyjadríme absolútne chyby argumentov:
z toho vyplýva, že číslo p treba brať s počtom znakov n = 3 .
PRESVEDČTE SA
Dané približné číslo a * = 1,0754327 a jeho limitná absolútna chyba D(a*)=0,0005.
Zaokrúhlite toto číslo na správne čísla. Berte do úvahy chybu zaokrúhľovania.
Krajčírskym krajčírskym metrom zmerajte obvod poludníka, delovú guľu Car Cannon a tenisovú loptičku. Ktoré meranie poskytne najväčšiu relatívnu chybu?
Pri meraní polomeru kruhu s presnosťou 0,5 cm vyšlo číslo 12 cm. Nájdite absolútne a relatívne chyby oblasti kruhu.
Dokončiť aritmetické operácie nad približné čísla, ktorých všetky číslice sú správne:
130,6 + 0,255 + 1,15224 + 41,84 + 11,8216;
35,2 1,748;
Hodnota to, čo možno vyjadriť číslom v určitých jednotkách, sa nazýva. Napríklad dĺžka, plocha, objem sú veličiny. Hodnota veličiny, o ktorej pravdivosti nepochybujeme, sa nazýva exaktná. (ďalej x je presné číslo). Ale zvyčajne sa v praxi pri hľadaní hodnoty veličiny získa len jej približná hodnota. (ďalej a je približné číslo ). Napríklad pri meraní fyzikálnych veličín pomocou meracích prístrojov.
Modul rozdielu medzi presnými a približnými hodnotami množstva sa nazýva absolútna chyba
aproximácia Limitná absolútna chyba aproximácie alebo hranice chyby resp absolútne
chyby
zavolal na číslo 
. Takéto hodnotenia môžu byť nekonečné číslo. najlepší odhad chybovosť je najmenší odhad.
Skratka pre presné číslo:
Pomer absolútnej chyby aproximácie k modulu presnej hodnoty veličiny sa nazýva relatívna chyba . V praxi sa používa Pre limitnú relatívnu chybu (odhad relatívnej chyby): . Relatívna chyba sa zvyčajne vyjadruje v %.
Neskôr slovo stupňa ide dole.
PRÍKLAD. Nájdite absolútnu a relatívnu chybu aproximácie a = 3,14 pre x=π.
To je známe 3,14 <π<3,15 .
Z toho vyplýva, že t.j.
Zvažujem to 3,14 <π<3,142, potom dostaneme najlepší odhad
Číslica v desiatkovom zápise približnej hodnoty veličiny X volal pravda v širokom zmysle , ak absolútna chyba aproximácie nepresiahne jednotku tejto číslice r, ku ktorému táto číslica patrí (Nulová číslica sa považuje za číslicu jednotiek, desatinné číslice sa považujú za záporné číslice). Existuje ďalší koncept pravdivý údaj v užšom zmysle : . V budúcnosti budeme uvažovať o správnych číslach v širšom zmysle. Zvyšné číslice sú tzv pochybný . Zmysluplné číslice čísla zapísaného v desiatkovej forme sú všetky správne číslice čísla, počnúc prvým vľavo, okrem 0. Všetky nuly vľavo sú nevýznamné. Podľa počtu platných číslic možno ľahko odhadnúť absolútnu chybu približného čísla. Na odhad absolútnej chyby môžete použiť 0,5 číslice za poslednou platnou číslicou. Limitná relatívna chyba sa môže rovnať zlomku, ktorého čitateľ je 1 a menovateľom je dvojité celé číslo, zapísané pomocou všetkých platných číslic daného čísla.
PRÍKLAD. a = 0,065;
ÚLOHA 1.1. Objem miestnosti V určené s obmedzujúcou relatívnou chybou δ Koľko platných číslic obsahuje V ?
ÚLOHA 1.2. Je známe, že približná hodnota a Má n významné číslice. Odhadnite absolútnu a relatívnu chybu.
Pri riešení úloh súvisiacich s výpočtami sa získavajú číselné výsledky, ktoré často nie sú presné, pretože. chyby vznikajú pri formulácii problému a v priebehu výpočtov.
Zdroje chýb sú:
1) chyby v počiatočných údajoch;
2) chyby zaokrúhľovania priebežných a konečných výsledkov;
3) chyby približnej metódy riešenia problému.
Pri vykonávaní operácií s približnými číslami musíte:
1) poznať presnosť počiatočných údajov, byť schopný vyhodnotiť presnosť výsledku;
2) vziať počiatočné údaje s takou presnosťou, aby sa zabezpečila špecifikovaná presnosť výsledku.
2.1 Chyby v približných číslach
Nech číslo x je presná hodnota a číslo a je približná hodnota nejakej veličiny.
Definícia. Rozdiel medzi číslom x a jeho približnou hodnotou a sa nazýva chyba približného čísla a: Δ = |x-a |.
Nech x=10,5, a=10, potom Δ=10,5-10=0,5.
Nech x=9,5, a=10, potom Δ=9,5-10=-0,5.
Definícia. Absolútna hodnota rozdielu medzi číslom x a jeho približnou hodnotou a sa nazýva absolútna chyba približného čísla a: Δа = |х-а|
Nech x=10,5, a=10, potom Δa=|10,5-10|=0,5.
Nech x=9,5, a=10, potom Δa=|9,5-10|=0,5.
Často nie je známe presné číslo x. Potom nie je možné nájsť Δа = |х-а|, preto sa použije odhad absolútnej chyby - limitná absolútna chyba Δа ≥ Δа =x-а|. V tomto prípade je číslo x uzavreté v hraniciach:
a - Δ a x a + Δ a alebo stručne: x = a ± Δ a.
Znie: x sa rovná a s presnosťou Δ a.
Na určenie kvality vykonaných výpočtov je potrebné určiť, aký podiel tvorí absolútna chyba nameranej hodnoty. Na tento účel použite relatívnu chybu.
Definícia. Relatívna chyba δа približného čísla a je pomer absolútnej chyby Δа k modulu čísla x:
alebo 
.
Odhad relatívnej chyby ba je limitná relatívna chyba: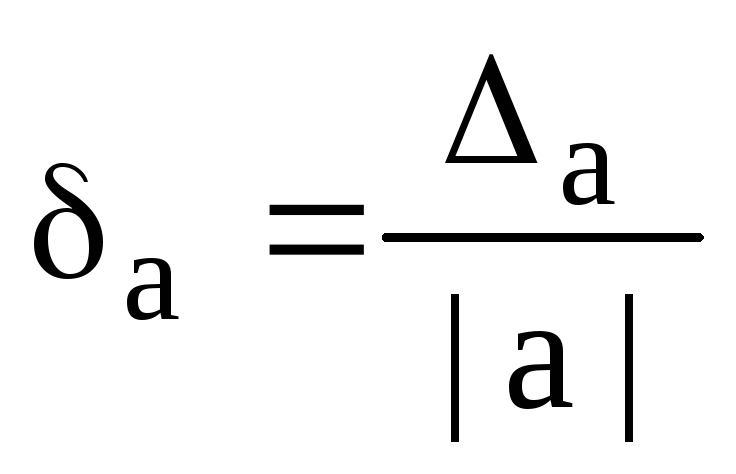 
Príklad. Dané číslo x=0,4287 a jeho približná hodnota a=0,4264. Nájdite absolútne a relatívne chyby čísla a.
Riešenie. Vypočítajme absolútnu chybu čísla a:
Δa=|0,4287-0,4264| = 0,0023.
Vypočítajme relatívnu chybu čísla a:
alebo 5,4 %.
Poznámky. 1. Pri zaznamenávaní chyby je zvykom ponechať 1-2 platné číslice. Chyby sú vždy zaokrúhlené nahor. V tomto prípade sa hranice presného čísla x rozširujú.
2. Ak číslo x nie je známe, potom sa na nájdenie relatívnej chyby použije číslo a.
3. Relatívna chyba sa často vyjadruje v percentách vynásobením 100 %.
2.2. Významné a pravdivé číslice približného čísla
Na posúdenie presnosti približného čísla a je zvykom písať ho ako desatinný zlomok. Presnosť výpočtov nie je určená počtom desatinných miest (číslice za desatinnou čiarkou), ale počtom platných platných číslic výsledku.
Definícia. Významné číslice čísla a sú všetky jeho číslice okrem núl napísaných pred prvou nenulovou číslicou a núl na konci záznamu, ak slúžia na zachovanie číslice alebo presnosti čísla.
Príklad. Nájdite platné číslice a.
a = 0,02701 => platné číslice: 2.7.0.1.
a = 0,0270 => platné číslice: 2,7.0.
a = 2700 => platné číslice: 2.7.0.0.
Definícia.Číslica α i približného čísla a sa nazýva skutočná platná číslica v širšom zmysle (v užšom zmysle), ak medzná absolútna chyba čísla a nepresahuje jednu (polovicu) číslice, v ktorej je číslica α i sa píše: Δ a 10 i (Δ a 0,5∙10 i).
Príklad. Určte správne čísla približného čísla a = 0,7264, ak absolútna chyba je Δ a = 0,0023.
Riešenie. Absolútna chyba Δ a \u003d 0,0023 0,005 \u003d 0,5 ∙ 10 -2. Preto sú čísla 7 a 2 správne v užšom zmysle, čísla 6 a 4 sú nesprávne (pochybné). Keďže Δ a = 0,0023< 0,01 = 10 -2 , то цифры 7 и 2 являются верными в широком смысле.
Poznámky. 1. V matematických tabuľkách sú všetky platné číslice správne v užšom slova zmysle.
2. V konečnom výsledku je zvykom nechať len správne čísla. Potom je limitná absolútna chyba čísla a určená jednotkou najmenšej významnej číslice. Napríklad nech a = 127,38, potom Δ a = 0,01, ak sú všetky čísla správne v užšom zmysle slova, a Δ a = 0,5 ∙ 0,01 = 0,005, ak sú všetky čísla správne v širšom zmysle.
Príklad. Určte, ktorá rovnosť je presnejšia 13/19=0,684 resp 
=7,21?
Riešenie. Označme a = 0,684, b = 7,21. Nájdime absolútne chyby týchto čísel. Ak to chcete urobiť, vezmite 19. 13. a s veľkým počtom desatinných miest: 13/39=0,68421..., =7,2111...
Potom Δ a =|0,68421...-0,684|< 0,00022, Δ в = |7,2111...-7,21| < 0,0012.
Poďme nájsť relatívne chyby:
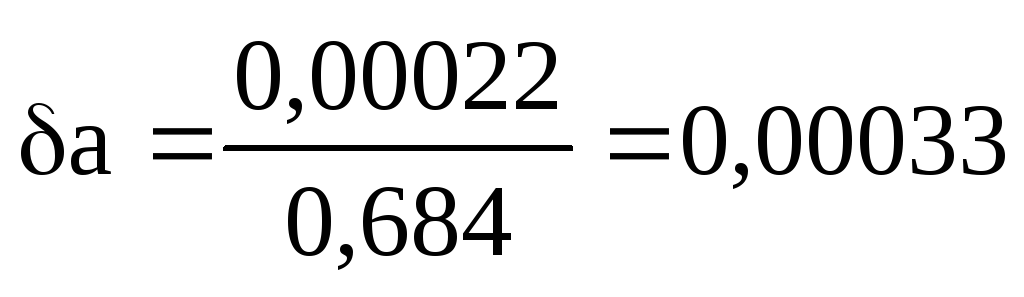alebo 0,033 %.
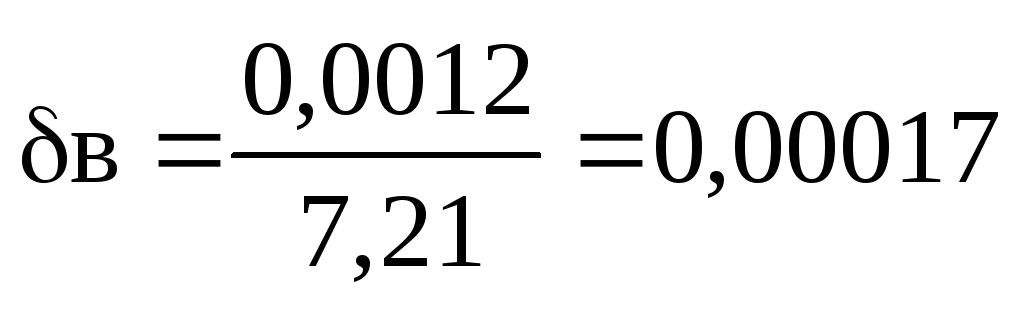alebo 0,017 %.
Druhá rovnica je presnejšia, keďže 
.
2.3. Zaokrúhľovanie čísel
Pri približných výpočtoch je často potrebné zaokrúhliť čísla, približné aj presné, to znamená vyradiť jednu alebo viac posledných číslic. Pri zaokrúhľovaní čísla ho nahrádzame približným číslom s menším počtom platných číslic, výsledkom čoho je chyba zaokrúhľovania. Aby bola táto chyba minimálna, treba dodržať niektoré pravidlá zaokrúhľovania.
pravidlo ja. Ak je prvá číslica naľavo od vyradených číslic väčšia ako 5, potom sa zosilní posledná ponechaná číslica, t.j. zvýši o jednu. Zosilnenie sa vykoná aj vtedy, keď prvá ľavá z vyradených číslic je 5, po ktorej nasledujú nenulové číslice.
Príklad. Zaokrúhlením na desatiny čísla 73,473 dostaneme 73,5. Posledná zostávajúca číslica je posilnená, pretože 7 > 5.
pravidlo II. Ak je prvá z vyradených číslic menšia ako 5, potom sa posledná zo zostávajúcich číslic nezvýši, t.j. zostane nezmenená.
Príklad. Zaokrúhlením na stotiny čísla 73,473 nahor dostaneme 73,47.
pravidloIII. Ak je prvá číslica naľavo od vyradených číslic 5 a nenasledujú po nej žiadne nenulové číslice, posledná zostávajúca číslica sa zvýši, ak je nepárna, a zostane nezmenená, ak je párna (pravidlo párnych číslic).
Príklad. Zaokrúhlením čísla 5,785 na stotiny dostaneme 5,78. Nerobíme zosilnenia, pretože posledná uložená číslica 8 je párna. Zaokrúhlením čísla 5,775 na druhé desatinné miesto dostaneme 5,78. Posledná uložená číslica, 7, sa zvýši o jednu, pretože je nepárna.
Pri aplikácii pravidla III na zaokrúhľovanie jedného čísla v skutočnosti nezvyšujeme presnosť výpočtov, ale pri početnom zaokrúhľovaní sa prečíslenia vyskytujú približne rovnako často ako podčíslenia. Dochádza k vzájomnej kompenzácii chýb, výsledok je presnejší.
Pri použití vyššie uvedených pravidiel zaokrúhľovania teda absolútna chyba zaokrúhľovania nepresahuje polovicu jednotky číslice určenej poslednou platnou číslicou, ktorá zostala.
Ak je presné číslo x zaokrúhlené na n platných číslic, potom výsledné približné číslo a má absolútnu chybu rovnajúcu sa chybe zaokrúhľovania. V tomto prípade má približné číslo a n správnych platných číslic v užšom zmysle.
Príklad. Zaokrúhlením čísla x=26,837 na tri platné číslice dostaneme a =26,8, odkiaľ Δ a = |x-a | = | 26,837-26,8 |=0,037< 0,05, т. е. число а имеет три верные значащие цифры в узком смысле.
Pri zaokrúhlení približného čísla a dostaneme nové približné číslo a 1 .
Definícia.Číslo Δ a1 \u003d Δ a + Δ env sa nazýva chyba zaokrúhľovania.
Absolútna chyba čísla a 1 je súčtom absolútnej chyby pôvodného čísla Δ a a chyby zaokrúhľovania Δ env, t.j.
Δ a1 = Δ a + Δ env.
Príklad. Zaokrúhlite pochybné číslice čísla x = 34,124 ± 0,021. Určte absolútnu chybu výsledku.
Riešenie. Približné číslo a=34,124 má tri správne čísla v užšom zmysle: 3, 4, 1, pretože Δ a = 0,021< 0,05. Применяя правила округления, найдем приближенное значение а 1 , сохранив десятые доли: а 1 = 34,1. Погрешность округления Δ окр =|34,124-34,1|=0,024. Тогда абсолютная погрешность числа а 1 равна Δ а1 =Δ а +Δ окр =0,021+0,024 = 0,045 < 0,05.
Všetky platné číslice čísla a 2 sú teda správne (v užšom zmysle).
Takže x = 34,1 ± 0,045.
Pri zaokrúhľovaní približného čísla a, ktoré má n správnych platných číslic (v užšom zmysle), na n platných číslic sa však môže ukázať, že zaokrúhlené číslo a 1 bude mať n správnych platných číslic v širšom zmysle.
Príklad. Približné číslo a=15,3654 (± 0,0018) má štyri správne platné číslice v užšom zmysle (1, 5, 3, 6), keďže Δ a = 0,0018< 0,005. При округлении до четырех значащих цифр получим а 1 = 15,37 и Δ а1 =Δ а +Δ окр =0,0018+|15,3654-15,37|=0,0064.
Samozrejme, 0,005< 0,0064 < 0,01. Следовательно, число 15,37 (± 0,0064) má štyri správne číslice v širšom zmysle.
Takže x = 15,37 ± 0,0064.
Príklad. Pochybné čísla čísla a = 26,7245 (± 0,0026) zaokrúhlite a ponechajte správne znamienka v užšom zmysle. Určte absolútnu chybu výsledku.
Riešenie. Podľa podmienky Δ a = 0,0026< 0,005, следовательно, в числе 26,7245 верными в узком смысле являются цифры 2, 6, 7, 2. Используя правила округления, найдем приближенное значение а 1 , сохранив сотые доли:
Výsledná chyba je väčšia ako 0,005 (0,005< 0,0071), поэтому уменьшим число цифр в приближенном числе до трех; а 2 = 26,7. Nájdeme Δ a2 = = Δ a + Δ env = 0,0026 + | 26,7245-26,7 | = 0,0271< 0,05. Следовательно, оставшиеся три цифры верны в узком смысле.
Takže x=26,7 ±0,0271 => x=26,7 ±0,03, zaokrúhlenie chyby na dve desatinné miesta.
Príklad. Zaokrúhlite pochybné číslice čísla a = 22,7314 a ponechajte správne znamienka v užšom zmysle. Určte absolútnu chybu čísla, ak δ a = 0,2 %.
Riešenie. Píšeme δ a v tvare desatinného zlomku: δа=0,002 a určte absolútnu chybu . Od Δ a \u003d \u003d 0,0455< 0,05, то верными в этом числе будут три цифры: 2, 2, 7. Округлим число 22,7314, сохранив в нем десятые доли: а 1 = 22,73. Potom Δ a1 = = Δ a + Δ env = 0,0455 + | 22,7314-22,73 | = 0,0769> 0,05, preto znížime počet číslic v približnom čísle na dve: a 2 = 23. Nájdeme Δ a2 = = Δ a + Δ env = 0,0455 + | 22,7314-23 | = 0,3141< 0,05. Следовательно, оставшиеся две цифры верны в узком смысле.
Takže x=23±0,3141 => x=23±0,32.
2.3. Pravidlá pre operácie s približnými číslami
Pravidlo 1 Absolútna chyba algebraického súčtu niekoľkých približných čísel sa rovná súčtu absolútnych chýb týchto čísel:
Δ a ± b = Δ a + Δ b
Pravidlo 2 Relatívna chyba súčinu niekoľkých približných čísel sa rovná súčtu relatívnych chýb týchto čísel:
δ av \u003d δ a + δ c.
Pravidlo 3 Relatívna chyba čiastočných približných čísel sa rovná súčtu týchto relatívnych čísel: δ a / b \u003d δ a + δ c.
Pravidlo 4 Relatívna chyba stupňa približného čísla a je: δa n = nδ a.
Pravidlo 5 Relatívna chyba koreňa približného čísla a je: 
.
Pravidlo 6 Ak sa pri výpočte nevykoná prísny výpočet chýb, odporúča sa použiť pravidlá počítania čísel. Tieto pravidlá špecifikujú, ako by sa mali výsledky zaokrúhľovať, aby sa zabezpečilo, že výsledok bude čo najpresnejší bez prečíslovania.
Pravidlá predpokladajú, že operované čísla obsahujú iba platné číslice a počet operácií je malý.
I. Pri sčítaní a odčítaní približných čísel by si mal výsledok zachovať toľko desatinných miest, koľko je v čísle, ktoré má najmenší počet desatinných miest.
II. Pri násobení a delení by si výsledok mal zachovať toľko platných číslic, koľko je v čísle s najmenším počtom platných číslic.
III. Pri zvyšovaní približného čísla na mocninu by výsledkom malo byť ponechať toľko platných číslic, koľko je v základe mocniny.
IV. Pri extrakcii odmocniny z približného čísla by ste mali ponechať toľko platných číslic, koľko je v koreňovom čísle.
V. V medzivýsledkoch by ste mali ponechať o 1-2 číslice viac, ako odporúčajú pravidlá I-IV. V konečnom výsledku sa „náhradné číslice“ vyradia so zaokrúhlením čísla.
VI. Ak majú niektoré zdrojové údaje viac desatinných miest (pre sčítanie a odčítanie) alebo viac platných číslic (pre iné operácie) ako iné, mali by sa najskôr zaokrúhliť nahor a ponechať iba jedno „bezpečné číslo“.
VII. Ak chcete získať výsledok s N správnymi číslicami, zdrojové údaje by sa mali brať s takým počtom číslic, aby podľa predchádzajúcich pravidiel poskytli vo výsledku N + 1 číslic.
Príklad. Nájdite s=2,35+11,8 bez zohľadnenia chýb. Aplikovaním pravidla I dostaneme s=14,15. Výsledok bude zaokrúhlený na číslo 11,8 s najmenším počtom desatinných miest. Dostávame: s \u003d 14.2.
Vyriešme problém s prihliadnutím na chyby. V čísle s=14,15 by mali byť ponechané iba správne čísla. Aby sme to dosiahli, nájdeme limitnú absolútnu chybu súčtu s pomocou pravidla 1. Vzhľadom na to, že všetky čísla v číslach 2,35 a 11,8 sú správne, dostaneme: Δ 14,15 = Δ 2,35 + Δ 11,8 = 0,01 +0,1=0,11< 0,5. Последняя верная цифра в числе 14,15 находится в разряде единиц. Поэтому число s=14,15 надо округлить: s=14 и найти абсолютную погрешность округленного числа. Погрешность округления равна: |14,15-14|=0,15. Тогда абсолютная погрешность округленного числа Δ 14 =0,11+0,15=0,26 <0,5. Окончательный результат примет вид: s=14 ± 0,26.
Problémy sa riešia podobne pri vykonávaní iných operácií na približných číslach.
Odoslanie dobrej práce do databázy znalostí je jednoduché. Použite nižšie uvedený formulár
Študenti, postgraduálni študenti, mladí vedci, ktorí pri štúdiu a práci využívajú vedomostnú základňu, vám budú veľmi vďační.
Uverejnené dňa http://www.allbest.ru/
Uverejnené dňa http://www.allbest.ru/
Moskovský ekonomický inštitút,manažment a právo
abstraktné
podľa disciplíny:
« Vyššiematematika»
« Ppribližné výpočty aodhad chybyopobyt»
Hotovo: študent
Yanchuk Lyudmila Alexandrovna
vedecký poradca Piterceva Galina Alexandrovna
Moskva, 2000
Plán
Úvod. Výpočtová technika v modernej vede a technike
1. Približné hodnoty a chyby aproximácie
2. Zaokrúhľovanie čísel. Chyba zaokrúhľovania
Záver. Niektoré informácie o výpočtovej technike
Literatúra
Úvod. Výpočtová technika v modernej vede a technike
Merania a výpočty zohrávali dôležitú úlohu v živote spoločnosti už od staroveku. Potreba vypočítať úrodu, merať kapacitu plavidiel, veľkosť pozemkov, robiť výpočty pri výstavbe veľkých stavieb, vykonávať rôzne astronomické výpočty - to je neúplný zoznam úloh, ktoré museli ľudia v dávnych dobách riešiť.
Za jednu z najvýznamnejších udalostí poslednej doby treba považovať prieskum vesmíru ľudstvom. S napätím sledujeme lety na Mesiac, Venušu, Mars, vznik pilotovaných orbitálnych staníc. Štart kozmickej lode by bol nemysliteľný, keby nešlo o presný výpočet pohybu lode, a to si vyžaduje kolosálnu a zložitú výpočtovú prácu.
V modernom období, v období vedecko-technickej revolúcie, narastá úloha matematických metód. Matematické metódy sa využívajú nielen vo fyzike, ale aj v chémii, biológii, medicíne, ekonómii, histórii a lingvistike
Veľa výpočtovej práce musia vykonať matematici a inžinieri v každodennej, súčasnej činnosti priemyselných podnikov, vedeckých ústavov, vládnych agentúr, fariem a kolektívnych fariem.
Výpočtové metódy sú dnes široko používané v ekonomických výpočtoch, pri plánovaní práce jednotlivého podniku, regiónu a celého hospodárstva krajiny.
Existuje veľa problémov, pri ktorých sú na získanie číselného výsledku potrebné výpočty, ktoré presahujú možnosti jednej osoby. Výpočet elastických napätí v priehrade, výpočet odporu, ktorému lietadlo čelí počas letu, alebo trajektórie projektilov sú príklady takýchto problémov. Túto zložitú výpočtovú prácu vykonávajú desiatky počítačových inžinierov, ktorí využívajú rôzne počítače.
Príchod počítača spôsobil revolúciu vo výpočtovej technike. Aby sa však riešenie matematických problémov dostalo do štádia, po ktorom ich možno preniesť do počítača na získanie numerických výsledkov, je potrebná aj práca mnohých kalkulačiek. Vytvorenie počítačov podnietilo rozvoj samotnej matematiky, najmä jej aplikovaných oblastí, výpočty teraz nehrajú pomocnú, ale hlavnú úlohu v mnohých vedeckých a technických úspechoch. Vo všetkých prípadoch, keď je potrebné dokončiť riešenie akéhokoľvek matematického problému praktického charakteru, je potrebné získať číselný výsledok. Ak sú počiatočné údaje približné, potom nie je možné dosiahnuť akýkoľvek stupeň presnosti výsledku. Človek musí vedieť vyhodnotiť presnosť počiatočných údajov, ako aj určiť, akú presnosť výsledku možno dosiahnuť a aká presnosť výsledku je potrebná pri praktickom využití získaných numerických výsledkov. Niektoré výpočty vyžadujú veľmi vysokú presnosť, zatiaľ čo iné nie. Z toho je zrejmé, že je potrebné organizovať výpočty tak, aby sa získali výsledky s požadovanou presnosťou s minimálnym vynaložením výpočtovej práce.
Na dosiahnutie tohto cieľa je potrebné:
študovať princípy a pravidlá výpočtov s približnými údajmi;
osvojiť si potrebné zručnosti racionálnych výpočtov pomocou dostupných prostriedkov, medzi ktoré patria rôzne metódy ústnych výpočtov, matematické tabuľky, administratívne účty, logaritmické pravítka, aritmometre, poloautomatické a automatické počítače.
1. Približné hodnoty a chyby aproximácie
Pri praktických činnostiach musí človek merať rôzne veličiny, brať do úvahy materiály a produkty práce a vykonávať rôzne výpočty. Výsledky rôznych meraní, počtov a výpočtov sú čísla. Čísla získané ako výsledok merania len približne, s určitým stupňom presnosti, charakterizujú požadované hodnoty. Presné merania sú nemožné pre nepresnosť meracích prístrojov, nedokonalosť našich zrakových orgánov a samotné merané objekty nám niekedy neumožňujú určiť ich hodnotu s nejakou presnosťou.
Napríklad je známe, že dĺžka Suezského prieplavu je 160 km, vzdialenosť po železnici z Moskvy do Leningradu je 651 km. Tu máme výsledky meraní vykonaných s presnosťou až na kilometer. Ak je napríklad dĺžka obdĺžnikového úseku 29 m, šírka je 12 m, potom sa pravdepodobne merania vykonali s presnosťou až na meter a zanedbali sa zlomky metra,
Pred vykonaním akéhokoľvek merania je potrebné rozhodnúť, s akou presnosťou je potrebné ho vykonať, t.j. ktoré zlomky mernej jednotky by sa mali brať do úvahy a ktoré by sa mali zanedbať.
Ak existuje nejaká hodnota a, ktorého skutočná hodnota je neznáma a približná hodnota (aproximácia) tejto hodnoty sa rovná X, oni píšu a X.
Rôznymi meraniami tej istej veličiny získame rôzne aproximácie. Každá z týchto aproximácií sa bude líšiť od skutočnej hodnoty nameranej hodnoty, rovná sa napr. a, o nejakú sumu, ktorú zavoláme chyba. Definícia. Ak je číslo x približná hodnota (aproximácia) nejakej veličiny, ktorej skutočná hodnota sa rovná číslu a, potom modul rozdielu čísel, a a X volal absolútna chyba daná aproximácia a označená aX: alebo jednoducho a. Teda podľa definície
aX = a- X (1)
Z tejto definície vyplýva, že
a = X aX (2)
Ak je známe o akej veličine hovoríme, tak v zápise aX index a je vynechaná a rovnosť (2) je napísaná takto:
a = X X (3)
Keďže skutočná hodnota požadovanej hodnoty je najčastejšie neznáma, nie je možné nájsť absolútnu chybu v aproximácii tejto hodnoty. V každom konkrétnom prípade možno uviesť iba kladné číslo, nad ktoré táto absolútna chyba nemôže byť. Toto číslo sa nazýva hranica absolútnej chyby aproximácie množstva a a označené h a. Teda ak X je ľubovoľná aproximácia hodnoty a pre daný postup získavania aproximácií, potom
aX = a- X h a (4)
Z uvedeného vyplýva, že ak h a je hranica absolútnej chyby aproximácie veličiny a, potom akékoľvek číslo väčšie ako h a, bude aj hranica absolútnej chyby aproximácie množstva a.
V praxi je zvykom zvoliť ako hranicu absolútnej chyby najmenšie číslo, ktoré spĺňa nerovnosť (4).
Riešenie nerovnosti a- X h a dostaneme to a obsiahnuté v medziach
X-h a a X+ h a (5)
Presnejšiu koncepciu hranice absolútnej chyby možno uviesť nasledovne.
Nechaj X- veľa možných aproximácií X množstvá a pre daný postup na získanie aproximácie. Potom ľubovoľné číslo h, splnenie podmienky a- X h a pre akékoľvek X X, sa nazýva hranica absolútnej chyby aproximácií z množiny X. Označiť podľa h a najmenšie známe číslo h. Toto číslo h a a je v praxi zvolený ako hranica absolútnej chyby.
Absolútna chyba aproximácie necharakterizuje kvalitu meraní. Skutočne, ak nameriame akúkoľvek dĺžku s presnosťou 1 cm, potom pri určovaní dĺžky ceruzky to bude slabá presnosť. Ak s presnosťou na 1 cm určíte dĺžku alebo šírku volejbalového ihriska, bude to vysoká presnosť.
Na charakterizáciu presnosti merania sa zavádza pojem relatívnej chyby.
Definícia. Ak aX: vyskytla sa absolútna chyba aproximácie X nejaká veličina, ktorej skutočná hodnota sa rovná číslu a, potom pomer aX na modul čísla X sa nazýva relatívna chyba aproximácie a označuje sa aX alebo X.
Teda podľa definície
Relatívna chyba sa zvyčajne vyjadruje v percentách.
Na rozdiel od absolútnej chyby, ktorá je najčastejšie rozmerovou veličinou, je relatívna chyba bezrozmerná veličina.
V praxi sa neberie do úvahy relatívna chyba, ale takzvaný limit relatívnej chyby: také číslo E a, ktorá nemôže byť väčšia ako relatívna chyba aproximácie požadovanej hodnoty.
Touto cestou, aX E a.
Ak h a-- hranica absolútnej chyby aproximácií veličiny a, potom aX h a a preto
Samozrejme, akékoľvek číslo E, splnenie podmienky, bude hranicou relatívnej chyby. V praxi je zvyčajne známa určitá aproximácia X množstvá a a limit absolútnej chyby. Potom číslo
2. Zaokrúhľovanie čísel. Chyba zaokrúhľovania
Pri vykonávaní výpočtov sa často stáva nevyhnutnosťou čísla zaokrúhľovať, t.j. ich nahradením číslami s menším počtom platných číslic.
Existujú tri spôsoby zaokrúhľovania čísel:
Zaokrúhľuje sa nadol na k platná číslica znamená zrušenie všetkých číslic začínajúcich na (k+1) th.
Zaokrúhľovanie nahor sa líši od zaokrúhľovania nadol v tom, že posledná uložená číslica sa zvýši o jednu.
Zaokrúhľovanie s najmenšou chybou sa líši od zaokrúhľovania s prebytkom v tom, že zvýšenie o jednu z posledných uložených číslic sa vykoná len vtedy, ak je prvá z vyradených číslic väčšia ako 4.
Výnimka: ak má zaokrúhľovanie s najmenšou chybou vyradiť iba jednu číslicu 5, posledná uložená číslica sa nezmení, ak je párna, a zvýši sa o 1, ak je nepárna.
Z vyššie uvedených pravidiel pre zaokrúhľovanie približných čísel vyplýva, že chyba spôsobená zaokrúhľovaním s najmenšou chybou nepresahuje polovicu jednotky poslednej uloženej číslice a pri zaokrúhľovaní s nedostatkom alebo nadbytkom môže byť chyba aj viac ako polovica jednotka poslednej uloženej číslice, ale nie viac ako celá jednotka tohto vybitia.
Pozrime sa na to v nasledujúcich príkladoch.
1. Chyba sumy. Nechaj X a, pri-- nejaká aproximácia hodnoty b. Nechaj X a pri-- absolútne chyby zodpovedajúcich aproximácií X a pri. Poďme nájsť absolútnu hranicu chýb h a+b sumy x+y, čo je približná suma a+b.
a = X + X,
b = r + r.
Pridaním týchto dvoch rovností dostaneme
a + b = X + r + x + r.
Je zrejmé, že chyba súčtu aproximácií X a pri sa rovná súčtu chýb pojmov, t.j.
(X + r) = X + r
Je známe, že modul súčtu je menší alebo rovný súčtu modulov členov. Preto
(X + r) = X + r X + r
To znamená, že absolútna chyba súčtu aproximácií nepresahuje súčet absolútnych chýb členov. Preto možno súčet limitov absolútnych chýb členov brať ako limitu absolútnej chyby súčtu.
Označenie hranice absolútnej chyby veličiny a cez h a, a b cez h b bude mať
h a + b = h a + h b
2. Chyba rozdielu. Nechaj X a pri-- chyby v aproximácii X a pri resp a a b.
a = X + X,
b = r + r.
Odčítajte druhú od prvej rovnosti, dostaneme
a - b = (X - r) + ( X - r)
Je zrejmé, že chyba rozdielu aproximácií sa rovná rozdielu medzi chybami minuendu a subtrahendu, t.j.
(X - r) = X - r) ,
(X - r) = X + (- r)
A potom, argumentovať rovnakým spôsobom ako v prípade sčítania, máme
(X - r) = X + (- r) X + r
Z toho vyplýva, že absolútna chyba rozdielu nepresahuje súčet absolútnych chýb minuendu a subtrahendu.
Pre hranicu absolútnej chyby rozdielu môžete vziať súčet hraníc absolútnych chýb redukovaného a subtrahendu. Touto cestou.
h a - b = h a + h b (9)
Zo vzorca (9) vyplýva, že limit absolútnej chyby rozdielu nemôže byť menší ako limit absolútnej chyby každej aproximácie. Z toho vyplýva pravidlo pre odčítanie aproximácií, ktoré sa niekedy používa pri výpočtoch.
Pri odčítaní čísel, ktoré sú aproximáciou niektorých veličín, by malo byť výsledkom toľko číslic za desatinnou čiarkou, koľko má aproximácia s najmenším počtom číslic za desatinnou čiarkou.
3. Chyba produktu. Zvážte súčin čísel X a pri, čo sú približné hodnoty množstiev a a b. Označiť podľa X chyba aproximácie X a cez pri-- chyba aproximácie pri,
a = X + X,
b = r + r.
Vynásobením týchto dvoch rovností dostaneme
Absolútna chyba produktu hu rovná sa
A preto
Delenie oboch strán výslednej nerovnosti o hu, dostaneme
Ak vezmeme do úvahy, že modul produktu sa rovná súčinu modulov faktorov, budeme mať
Tu je ľavá strana nerovnosti relatívna chyba produktu hu, -- relatívna chyba aproximácie X a je to relatívna chyba aproximácie pri. Preto, keď tu malú hodnotu zahodíme, dostaneme nerovnosť
Relatívna chyba súčinu aproximácií teda nepresahuje súčet relatívnych chýb faktorov. Z toho vyplýva, že súčet limitov relatívnych chýb faktorov je limitom relatívnej chyby súčinu, t.j.
E ab = E a + E b (10)
Zo vzorca (10) vyplýva, že limit relatívnej chyby súčinu nemôže byť menší ako limit relatívnej chyby najmenej presného z faktorov. Preto tu, rovnako ako v predchádzajúcich krokoch, nemá zmysel ponechať vo faktoroch nadmerný počet platných číslic.
Niekedy je užitočné použiť pri výpočtoch na zníženie množstva práce nasledujúce pravidlo: Pri násobení aproximácií rôznym počtom platných číslic by si mal výsledok zachovať toľko platných číslic, koľko má aproximácia s najmenším počtom platných číslic.
4. Chyba kvocientu. Ak X-- aproximácia hodnoty a, ktorého chyba X, a pri-- aproximácia hodnoty b s chybou r, potom
Najprv vypočítame absolútnu chybu kvocientu:
a potom relatívna chyba:
Berúc do úvahy to r málo v porovnaní s r, absolútnu hodnotu zlomku možno považovať za rovnú jednej. Potom
z posledného vzorca vyplýva, že relatívna chyba kvocientu nepresahuje súčet relatívnych chýb deliteľa a deliteľa. Preto môžeme predpokladať, že limita relatívnej chyby kvocientu sa rovná súčtu limitov relatívnych chýb deliteľa a deliteľa, t.j.
5. Chyba stupňa a koreňa. 1) Nechajte u = a n, kde n je prirodzené číslo a nech x. Potom ak E a-- hranica relatívnej chyby aproximácie X množstvá a, potom
a preto
Hranica relatívnej chyby stupňa sa teda rovná súčinu limity relatívnej chyby základu exponentom, t.j.
E u = n E a (11)
2) Nechaj kde n je prirodzené číslo a nech a X.
Podľa vzorca (11)
a preto
chyba odpočítateľný výpočet
Teda hranica relatívnej chyby koreňa n stupeň v n krát menej ako je limit relatívnej chyby radikálového čísla.
6. Inverzná úloha približných výpočtov. V priamom probléme je potrebné nájsť približnú hodnotu funkcie u =f(x, y, ...,n) podľa daných približných hodnôt argumentov
a tolerancia chyby h a, ktorý je vyjadrený chybami argumentov nejakej funkcie
h u = (h X, h r, …, h z) (12)
V praxi je často potrebné riešiť inverzný problém, v ktorom je potrebné zistiť, s akou presnosťou by sa mali uvádzať hodnoty argumentov x, y, …, z na výpočet zodpovedajúcich funkčných hodnôt u = f(x, y, ...,z) s vopred stanovenou presnosťou h u .
Pri riešení inverznej úlohy sa teda hľadajú limity chýb argumentov spojených s danou limitou chyby funkcie. h u rovnice (12) a riešenie inverznej úlohy sa redukuje na zostavenie a riešenie rovnice h u = (h X, h r, …, h z) pomerne h X, h r, …, h z. Takáto rovnica má buď nekonečný počet riešení, alebo nemá žiadne riešenia. Úloha sa považuje za vyriešenú, ak sa nájde aspoň jedno riešenie takejto rovnice.
Na vyriešenie inverzného problému, ktorý je často neurčitý, je potrebné zaviesť ďalšie podmienky týkajúce sa pomerov neznámych chýb, napríklad ich považovať za rovnaké, a tým zredukovať problém na rovnicu s jednou neznámou.
Záver. Niektoré informácie opočítajúc ichXnike
V závislosti od presnosti počiatočných údajov a účelu výpočtov sa používajú rôzne výpočtové nástroje. Pracovníci v mnohých masových profesiách výrazne uľahčujú výpočty a šetria čas a prácu pri výrobe rôznych výpočtov ruským počítadlom, počítacími logickými pravidlami, aritmometrami a všetkými druhmi vreckových a stolných elektronických kalkulačiek (mikro- a minikalkulačky).
Do triedy minikalkulačiek v súčasnosti u nás patrí rodina elektronických stolných kalkulačiek Iskra a rodina kalkulačiek Elektronika, do ktorej patrí aj niekoľko typov vreckových kalkulačiek. Zo zrejmých dôvodov sú tieto kalkulačky zastarané, ale napriek tomu sú to jediné modely vyrábané domácim priemyslom.
Stroje rodiny Elektronika a Iskra sú určené najmä na riešenie jednoduchého strojárskeho účtovníctva a účtovných úloh s presnosťou rádovo 8-10 platných číslic. Mnohé z nich poskytujú možnosť automatického výpočtu hodnôt elementárnych funkcií a existujú prvky ovládania programu.
S rýchlym rastom technického vybavenia nášho priemyslu a poľnohospodárstva, s rozvojom vedy sa čoraz viac zvyšuje potreba všemožných výpočtov. S vysokorýchlostnými elektronickými počítačmi (počítačmi) môže výskumník teraz riešiť problémy, ktoré predtým ani neexistovali, pretože ich riešenie si vyžadovalo príliš veľa času.
Elektronické počítače sa používajú napríklad na numerické riešenie rovníc. Prvé počítače boli navrhnuté špeciálne pre tento druh výpočtov.
V súčasnosti sa počítače úspešne využívajú na riadenie technologických procesov. Ak riadenie rýchlo plynúceho procesu vyžaduje zložité výpočty založené na údajoch získaných počas tohto procesu, potom by takáto úloha bez počítača bola vo všeobecnosti nemožná.
Literatúra
Algebra a začiatky analýzy. Časť 1. Ed. G.N. Jakovlev. - M.: Nauka, 1981. 336 s.
Vygotsky M.Ya. Príručka vyššej matematiky. M.: 1987.
Úvod do metrológie. Tyurin N.I., M., Publishing House of Standards, 1976, 304 s.
Hostené na Allbest.ru
...Podobné dokumenty
Stanovenie absolútnych a relatívnych chýb približných čísel. Odhad chýb vo výsledku. Interpolácia a extrapolácia dát, Lagrangeov a Newtonov interpolačný polynóm, ich hlavné charakteristiky a komparatívny popis.
laboratórne práce, doplnené 08.06.2013
Podstata a matematická interpretácia absolútnych a relatívnych chýb, spôsoby zápisu hodnoty spolu s nimi. Pojem približná hodnota a chyba aproximácie, smer analýzy týchto kategórií. Pravidlo pre zaokrúhľovanie desatinných miest.
abstrakt, pridaný 13.09.2014
Charakteristika a vlastnosti hlavných typov chýb vznikajúcich pri numerickom riešení matematických a aplikovaných úloh: úlohy, metódy, zaokrúhľovanie. Pojem a príčiny chýb merania. Popis náhodných chýb, momentov.
test, pridaný 13.01.2012
Klasická teória meraní o skutočnej hodnote fyzikálnej veličiny, jej hlavné postuláty. Klasifikácia chýb podľa spôsobu vyjadrenia, jej druhov: absolútne, redukované a relatívne. Náhodné chyby, zákon ich rozdelenia.
abstrakt, pridaný 07.06.2014
Zaokrúhlenie daného čísla na šesť, päť, štyri a tri desatinné miesta. Výpočet chýb po každom zaokrúhlení. Určenie absolútnej a relatívnej chyby pri výpočte hodnôt funkcie u, berúc do úvahy skutočnosť, že všetky znaky operandov a, b, c a d sú správne.
test, pridané 5.2.2012
Skúmanie metód na určovanie chýb a štatistické vyhodnotenie rozdelení. Konštrukcia empirickej funkcie, ktorá určuje konkrétnosť udalosti pre každú hodnotu náhodnej premennej. Výpočty pre danú vzorku, jej rozbor a stanovenie parametrov.
ročníková práca, pridaná 13.01.2011
Úvod do numerických metód, plán konštrukcie výpočtového experimentu. Presnosť výpočtov, klasifikácia chýb. Prehľad metód numerickej integrácie a diferenciácie, odhad aposteriórnej chyby. Riešenie sústav lineárnych rovníc.
tréningový manuál, pridaný 23.09.2010
Určenie počtu a hodnoty členov progresie pre nekonečne klesajúcu geometrickú progresiu. Výpočet relatívnej chyby veličiny. Určenie hodnôt stroja nula a nekonečno. Správanie chýb v závislosti od argumentu.
laboratórne práce, doplnené 15.11.2014
Skúmanie závislosti chyby riešenia na chybách pravej strany systému. Určenie koreňa rovnice s danou presnosťou. Výpočet odhadov presnosti metód podľa súradníc. Spline interpolácia a riešenie diferenciálnych rovníc.
test, pridané 26.04.2011
Riešenie Cauchyho úlohy pre diferenciálnu rovnicu. Chyba približných riešení. Funkcia, ktorá implementuje explicitnú Eulerovu metódu. Výpočet chyby podľa pravidla Runge. Riešenie diferenciálnych rovníc druhého rádu. Podmienka stability matrice.