مفاهيم القيمة التقريبية للخطأ النسبي والمطلق. الحسابات التقريبية وتقدير الأخطاء

القسم 1. الأعداد التقريبية والعمليات عليها

1.1 أنواع الأخطاء في الحسابات التقريبية

لا يمكن الحصول على حل دقيق لبعض المشاكل الرياضية بالطرق التقليدية ، أو يمكن الحصول على هذا الحل بهذه الطريقة. شكل معقد، وهو أمر غير مقبول لمزيد من الاستخدام العملي. بالإضافة إلى ذلك ، قد يتطلب الحل الدقيق للمشكلة للغاية عدد كبير(من عدة عشرات إلى عدة مليارات) إجراءات. في مثل هذه الحالات ، لجأ إلى الطرق التقريبية والرقمية للحل.

أدى ظهور أجهزة الكمبيوتر إلى توسيع نطاق هذه الأساليب بشكل كبير. في الوقت الحاضر ، من الصعب تخيل مهندس لا يمتلك جهاز كمبيوتر وطرق الحسابات التقريبية.

لاحظ أن أي جهاز كمبيوتر قادر على حفظ مصفوفات كبيرة ولكن محدودة من الأرقام وإجراء العمليات الحسابية والمقارنات عليها بسرعة كبيرة ولكن محدودة. أي أن الآلة قادرة على أداء عدد كبير جدًا ولكن محدود من العمليات. لذلك ، عند العمل على جهاز كمبيوتر ، يمكنك فقط استخدام تلك النماذج الرياضية الموصوفة بواسطة مجموعة محدودة من الأرقام ، واستخدام التسلسلات المحدودة فقط من العمليات الحسابية.

النماذج الرياضية لمختلف الظواهر هي الدوال ، المشتقات ، التكاملات ، المعادلات التفاضليةوما إلى ذلك وهلم جرا. عند العمل على جهاز كمبيوتر ، يجب استبدال هذه النماذج الأولية بتلك الموصوفة بمجموعات محدودة من الأرقام التي تشير إلى التسلسل النهائي للإجراءات لمعالجتها. للقيام بذلك ، يتم استبدال الوظيفة بجدول ، لا يتجزأ- المبلغ ، إلخ. بالإضافة إلى ذلك ، يمتلك الكمبيوتر ذاكرة محدودة ويمكنه العمل بأعداد محدودة الطول ، لذلك يتم تقريب النتائج الوسيطة. نتيجة لذلك ، حتى الطريقة الدقيقة التي لها عدد محدود من الخطوات تصبح تقريبية.

وبالتالي ، فإن الحل الذي تم الحصول عليه بالطريقة العددية تقريبي.

أسباب الأخطاء هي:

تضارب النموذج الرياضي مع الظاهرة الحقيقية المدروسة
خطأ في البيانات الأولية.
خطأ طريقة الحل.
أخطاء التقريب في العمليات الحسابية وغيرها من العمليات على الأرقام.

يتم استدعاء خطأ القرار الناجم عن أول سببين مميت- لا تعتمد على عالم الرياضيات.

خطأ في الأسلوبتنشأ لأن الطريقة العددية ، كقاعدة عامة ، لا تحل المشكلة الأصلية ، بل تحل مشكلة أبسط. بالإضافة إلى ذلك ، عادةً ما تعتمد الطريقة العددية على عملية لا نهائية يجب إنهاؤها في خطوة ما.

تعتمد معظم الطرق العددية على معلمة واحدة أو أكثر. يتيح لك اختيار معلمات الطريقة ضبط خطأ الطريقة.

خطأ التقريبلا ينبغي أن تكون كبيرة المزيد من الخطأطريقة. وينصح باختيار خطأ الطريقة 2-5 مرات أقل من الخطأ الفادح.

1.2 الأعداد التقريبية

في الممارسة العملية ، غالبًا ما يتعين على المرء أن يتعامل مع الأرقام التي تعبر عن القيمة الحقيقية ليس بالضبط ، ولكن تقريبًا. تسمى هذه الأرقام تقريبي.

دعنا نشير إلى القيمة العددية الدقيقة لبعض القيمة أ ، القيمة العددية التقريبية لنفس القيمة أ *. ثم أ »أ *.

استبدال الرقم الدقيق أ برقم تقريبي أ * ، نرتكب خطأ (خطأ).

تعريف 1.1. الخطأ المطلق للرقم التقريبي أ * هو القيمة المطلقة للفرق بين هذا الرقم وقيمته الدقيقة | a * |.

نظرًا لأن القيمة الدقيقة للكمية غير معروفة عادةً ، فمن المستحيل حسابها و الخطأ المطلق. لكن يمكنك تحديد رقم موجب د (أ *)، إرضاء عدم المساواة:

أي رقم د (أ *) ، إرضاء عدم المساواة

لاحظ أن هناك العديد من الأرقام التي ترضي التفاوتات (1.2) و (1.3). لذلك ، فإن قيمة الخطأ الهامشي ليست مؤكدة تمامًا.

في الممارسة العملية ، عادة ما يتم أخذ أصغر قيمة ممكنة للخطأ الهامشي. لكل رقم تقريبي ، يتم تحديد الخطأ الهامشي (المطلق أو النسبي) بالضرورة. يسمح لك الخطأ المطلق المحدد بتعيين الحدود التي يقع فيها الرقم a ، أي

يميز الخطأ النسبي المحدد دقة الحسابات أو القياسات.

أمثلة.

1.2.1 . عند حل المشكلات ، بدلاً من الرقم الدقيق ع = 3.14159265 ...نستخدم قيمته التقريبية 3.14 ونخطئ:

ص - 3.14> 0.00159265

1.2.2 . عند قياس طول المسار تم الحصول على نتيجة 25.2 كم بدقة 2 م. احسب الحد من الأخطاء النسبية المطلقة والمحدودة.

حل. في حالتنا ، الحد من الخطأ المطلق يساوي د = 0.002كم ، والخطأ النسبي المحدد

وبالمثل نحسب

يعني أن * هي قيمة تقريبية للرقم a مع وجود خطأ مطلق د (أ *). إذا كانت * قيمة تقريبية للرقم a بها خطأ نسبي د (أ *) ،ثم يكتبون هكذا:

1.4 أرقام مهمة ، أرقام حقيقية ومشكوك فيها

في الممارسة العملية ، يتم استخدام تقنيات مختلفة ، والتي تجعل من الممكن الحكم على خطأها فقط من خلال تسجيل الرقم التقريبي.

تسجيل الأرقام التقريبية والأخطاء المطلقة يخضع لقواعد معينة.

في التدوين العشري شخصية هامةيتم استدعاء أي رقم لا يساوي الصفر. يعتبر الصفر رقمًا مهمًا إذا كان يقع بين أرقام مميزة أو على يمين جميع الأرقام المهمة.

مثال 1.3.1.العدد التقريبي 0 ، 38 يتكون من رقمين معنويين ، 0 ، 308 - ثلاثة ، 0 ، 3080 - أربعة ، 0.00 308 - ثلاثة. الأرقام المهمة هي الأرقام التي تحتها خط.

التعريف 1.3.الرقم المميز يسمى صحيح بالمعنى الواسعإذا كان الخطأ المطلق للرقم لا يتجاوز وحدة واحدة من الرقم المقابل لهذا الرقم.
الرقم المميز يسمى صحيح بالمعنى الضيقإذا كان الخطأ المطلق للرقم لا يتجاوز نصف وحدة الرقم المقابل لهذا الرقم.
خلاف ذلك ، يعتبر الرقم متردد.

إذا تمت كتابة رقم تقريبي دون تحديد الخطأ المطلق (المطلق) ، فسيتم كتابة الأرقام الصحيحة فقط. في هذه الحالة ، لا يتم تجاهل الأصفار الحقيقية الموجودة في الطرف الأيمن من الرقم. الأرقام 0.25 و 0.250 مختلفة كتقريب. إذا استخدمنا سجلات من النموذج (1.4) أو (1.5) ، فيجب كتابة الأرقام الموجودة على الجانب الأيمن من هذه المعادلات بنفس عدد المنازل العشرية.

مطلق أو خطأ نسبيمن المعتاد كتابته كرقم يحتوي على رقم واحد أو رقمين مهمين. في هذه الحالة ، يتم التقريب بفائض.

قد يتضح أن الرقم التقريبي في جزءه الصحيح يحتوي على أرقام أكثر أهمية من العلامات الصحيحة. في هذه الحالة ، يتم استخدام الترميز في الشكل المقيس a * = m 10 n ، بينما يجب أن يحتوي الرقم m ≤ 1 على أرقام صالحة فقط. في التدوين المقيس ، يسمى الرقم م العشري، ن - الأس

لاحظ أن الحد من الخطأ المطلق يتحدد بعدد المنازل العشرية بعد الفاصلة العشرية: كلما قل عدد المنازل العشرية بعد العلامة العشرية ، زاد عدد هذه المنازل د (أ *).

يتم تحديد الخطأ النسبي المحدد من خلال عدد الأرقام المهمة: كلما قل عدد الأرقام المهمة ، زادت د (أ *).

1.5 التقريب

لكتابة أرقام تقريبية بالأرقام الصحيحة ، يتم استخدامها التقريب.

يجب أيضًا تقريب الأرقام الدقيقة إذا كان عدد الأرقام المستخدمة محدودًا.

التقريب (بالمكمل)يُطلق على الرقم كتابة هذا الرقم بأرقام أقل وفقًا للقاعدة التالية: إذا كان الرقم الأول المهمل أكبر من أو يساوي 5 ، فسيتم زيادة آخر رقم متبقٍ بمقدار واحد. عند تقريب الأرقام ، يحدث خطأ ، يجب أيضًا مراعاته.

خطأ التقريب بالمكمللا تتجاوز نصف وحدة أقل رقم ذي دلالة في القيمة المطلقة. عند حساب الخطأ الناتج ، يجب إضافة خطأ التقريب إلى الخطأ المطلق الأصلي للرقم.

مثال 1.3.2.الرقم * = 413287.51 به خطأ نسبي د (أ *) = 0.01. من (1.3) يتبع ذلك د (أ *) = | * | د (أ *).

لذلك ، فإن الخطأ المطلق لهذا الرقم هو 4133. وهذا يعني أن الرقم الرابع من الرقم * قد يحتوي بالفعل على خطأ. لذلك ، فإن أول رقمين فقط صحيحان. ثم في شكل موحد ، يتم كتابة هذا الرقم على النحو التالي: أ * = 0.41 · 10 6.

يجادل بالمثل ، الرقم التقريبي ب * = 0.0794 في د (ب *) = 2٪اكتب بالصيغة الطبيعية ب * = 0.8 10 - 1 .

لاحظ أننا هنا نحتاج لتقريب الرقم.

عند إجراء عمليات حسابية بأرقام تقريبية ، تظهر مشكلتان متعاكستان:

1. بقلم معروف الأخطاءإدخال البيانات لتقدير خطأ النتيجة.

2. تحديد دقة البيانات الأولية التي توفر الدقة المحددة للنتيجة.

بالإضافة إلى ذلك ، عند العمل بأرقام تقريبية ، من الضروري التوفيق بين دقة بيانات الإدخال المختلفة حتى لا يضيع الوقت في كتابة أرقام غير ضرورية وغير صحيحة.

في عملية الحسابات ، من الضروري أيضًا مراقبة دقة النتائج الوسيطة.

قبل أن تبدأ العمليات الحسابية ، يتم تطبيق التقريب بحيث تتم كتابة جميع الأرقام المتضمنة في هذه العمليات بنفس عدد المنازل العشرية. يتم تحديد عدد المنازل العشرية المتبقية من خلال أصغر عدد من الأرقام الصالحة في البيانات الأصلية.

عند جمع وطرح الأرقام التقريبية التي لها نفس عدد الأرقام الصحيحة بعد الفاصلة العشرية ، لا يتم التقريب.

عند جمع وطرح أرقام تقريبية بعدد مختلف من الأرقام الصحيحة بعد الفاصلة العشرية ، يتم تقريب النتيجة إلى أصغر عدد من الأرقام الصحيحة بعد الفاصلة العشرية في البيانات الأصلية.

عند ضرب وقسمة الأرقام التقريبية بعدد مختلف من الأرقام الصحيحة ، يتم تقريب النتيجة بالحد الأدنى لعدد الأرقام الصحيحة في البيانات الأصلية.

1.6 أخطاء حسابية

لنفترض أن أ * و ب * رقمان تقريبيان ، فإن مجموعهما ج * = أ * + ب * هو أيضًا رقم تقريبي.

إذا أشرنا إلى الأخطاء المطلقة للشروط د (أ *)و د (ب *)، على التوالي ، يتم تحديد الخطأ المطلق للرقم ج * بواسطة الصيغة

د (ج *) = د (أ *) + د (ب *).

لذلك ، عند إضافة رقمين تقريبيين ، تتم إضافة أخطائهم المطلقة المحددة.

هذه القاعدة صحيحة لأي عدد محدود من المصطلحات. بالإضافة إلى ذلك ، فإن الصيغة (1.6) صالحة أيضًا للاختلاف بين رقمين.

في الواقع ، يمكن تمثيل الفرق بين عددين كمجموع

أ * - ب * = أ * + (- ب *) ،

والخطأ المطلق في الرقم ( -ب*)يساوي الخطأ المطلق للرقم ب *.

تعليقعند طرح رقمين من نفس العلامة ، يمكن أن يكون الخطأ النسبي للفرق أكبر بكثير من الخطأ النسبي لكل مصطلح. يحدث فقدان كبير في الدقة بشكل خاص عند طرح الأرقام القريبة من بعضها البعض.

مثال 1.4.1. فليكن مطلوبًا للعثور على الفرق 61.32 - 61,31 .

الأخطاء المطلقة لهذه الأرقام ، على التوالي ، هي D1 = 0.01و D2 = 0.01.دعونا الآن نجد الأخطاء النسبية لهذه الأرقام:

عند الطرح ، سيتم الحصول على الرقم 0.01 (نلاحظ أن هناك خسارة بثلاثة أرقام معنوية). خطأها المطلق يساوي مجموع الأخطاء المطلقة للشروط D1 + د 2 \ u003d 0.02.

ثم الخطأ النسبي للنتيجة هو

د =

0,02 0,01

= 2.

بمقارنة أخطاء البيانات الأولية والنتيجة ، نجد زيادة حادة في الخطأ النسبي.

من المثال 1.4.1. ويترتب على ذلك أنه ينبغي على المرء أن يحاول تجنب طرح الأرقام القريبة من القيمة المطلقة. في بعض الأحيان يمكن تحقيق ذلك عن طريق تحويل صيغة الحساب. إذا كان من المستحيل تجنب مثل هذا الطرح ، فمن الضروري زيادة دقة الحسابات الوسيطة ، مع مراعاة فقدان الأرقام المهمة.

عند ضرب وقسمة رقمين تقريبيين أ * وب * ، يتم تحديد الأخطاء بواسطة الصيغ:

د (أ * ب *) = | ب * | د (أ *) + | * | د (ب *) ،

د (أ * ب *) = د (أ *) + د (ب *) ،

(1.7)

د (أ * / ب *) =

| ب * | د (أ *) + | أ * | د (ب *) | ب * | 2

د (أ * / ب *) = د (أ *) + د (ب *).

وهكذا ، عند ضرب وقسمة الأرقام التقريبية ، تتم إضافة أخطائها النسبية المحددة.

ملاحظة.إذا كان الخطأ المطلق للعدد التقريبي Δ (أ *) لا يتجاوز وحدة الرقم المعبر عنها بالرقم n من الرقم المهم في التدوين العشري لهذا الرقم ، فإن عدم المساواة التالية صحيحة بالنسبة للخطأ النسبي المحدد:

δ (أ *) ≤ 1 / ك 10 ن - 1

أين ك - أول رقم مهم من الرقمأ * .

إذا كان الخطأ المطلق للرقم التقريبي د (أ *)لا يتجاوز نصف وحدة الرقم ، معبراً عنه بالرقم المهم رقم n في التدوين العشري لهذا الرقم ، فإن عدم المساواة التالية صحيحة بالنسبة للخطأ النسبي المحدد:

δ (أ *) ≤ 1/2 ك 10 ن - 1

حيث k هو أول رقم مميز في a *.

في الحالة الأخيرة ، يكون العكس أيضًا صحيحًا: إذا

د (أ *) ي 1/2 (ك + 1) 10 ن - 1 ،

إذن ، a * هو رقم تقريبي به n من الأرقام الصالحة.

1.7 خطأ وظيفي

دع وظيفة قابلة للتفاضل باستمرار في مجال G يتم إعطاؤها

u \ u003d f (x 1 ، x 2 ، j ، x n).

يتم استبدال تقدير الخطأ في الحساب التقريبي لقيمة الوظيفة بتقدير معامل انحرافها عن القيمة الدقيقةبسبب أخطاء الحجة.

في هذه الحالة ، يتم استبدال انحراف الدالة بفارقها الكلي ، حيث يتم استبدال زيادات الوسيطات بأخطاءها المطلقة. ثم يتم تحديد الخطأ المطلق المحدد لقيمة الوظيفة من خلال العلاقة

بالنسبة للخطأ النسبي المحدد ، لدينا المساواة

باستخدام الصيغ (1.11) ، يمكن تحديد دقة الوسيطات ، مما يضمن الدقة المعطاة لقيمة الوظيفة.

مثال 1.5.1.يجب أن تقاس بدقة د = 1٪مساحة السطح الجانبية لمخروط مقطوع نصف قطر قاعدته ص 1 »2 م ، ص 2 "1 م، والمولدات ل»5 م.
ما هو الخطأ المطلق الضروري لقياس نصف القطر والمصفوفة ، وكم عدد العلامات ، الصحيحة بالمعنى الواسع ، هل يجب أخذ الرقم p؟

لو د (أ *) لا يتجاوز رقمًا واحدًا ، معبرًا عنه بالرقم nth المعنوي ، ثم يُطلق على * رقمًا يحتوي على n من الأرقام الصالحة بمعنى واسع.)

حل. يتم حساب مساحة السطح الجانبي للمخروط المقطوع بالصيغة التالية:

س = π ل(ص 1 + ص 2).

وبالتالي ، لدينا وظيفة من أربع حجج س = س(ص ل, ص 1 ، ص 2).
أوجد المشتقات الجزئية واقسم على S.

من الصيغ (1.11) نعبر عن الأخطاء المطلقة للوسيطات:

يتبع ذلك الرقم صيجب أن تؤخذ مع عدد الأحرف ن = 3.

تحقق من نفسك

إعطاء رقم تقريبي أ * = 1.0754327 والخطأ المطلق المحدد له د (أ *) = 0.0005.

قرّب هذا الرقم للأرقام الصحيحة. ضع في الاعتبار خطأ التقريب.

باستخدام شريط القياس الخاص بالخياط ، قم بقياس محيط خط الزوال وقذيفة مدفع القيصر وكرة التنس. ما هو القياس الذي سيعطي أكبر خطأ نسبي؟

عند قياس نصف قطر دائرة بدقة 0.5 سم ، تم الحصول على الرقم 12 سم. أوجد الأخطاء المطلقة والنسبية لمساحة الدائرة.

مكتمل عمليات حسابيةأكثر من الأرقام التقريبية ، وجميع أرقامها صحيحة:

130,6 + 0,255 + 1,15224 + 41,84 + 11,8216;

35.2 1.748 ؛

قيمةما يمكن التعبير عنه برقم في وحدات معينة يسمى. على سبيل المثال ، الطول والمساحة والحجم هي كميات. تسمى قيمة الكمية ، التي لا نشك في حقيقتها ، بالدقة. (إضافي x هو الرقم الدقيق). ولكن في الممارسة العملية ، عند البحث عن قيمة كمية ما ، يتم الحصول على قيمتها التقريبية فقط. (إضافي أ هو رقم تقريبي ). على سبيل المثال ، عند القياس كميات فيزيائيةباستخدام أدوات القياس.

يُطلق على معامل الاختلاف بين القيم الدقيقة والتقريبية للكمية الخطأ المطلق التقريب الحد من الخطأ التقريبي المطلق أو هامش الخطأ أو مطلق أخطاء يسمى رقم . يمكن أن تكون هذه التصنيفات عدد لا حصر له. أفضل تقديرهامش الخطأ هو أصغر تقدير.

اختصار للرقم الدقيق:

يتم استدعاء نسبة الخطأ المطلق للتقريب إلى معامل القيمة الدقيقة للكمية خطأ نسبي . في الممارسة العملية ، يتم استخدامه للخطأ النسبي المحدد (تقدير الخطأ النسبي):. عادة ما يتم التعبير عن الخطأ النسبي في المائة.

في وقت لاحق الكلمة درجةيذهب للأسفل.

مثال. أوجد الخطأ التقريبي المطلق والنسبي أ = 3.14ل س = π.

ومن المعروف أن 3,14 <π<3,15 .

ويترتب على ذلك من هنا أن ، أي.

معتبرا أن 3,14 <π<3,142, ثم نحصل على أفضل تقدير

الرقم في التدوين العشري للقيمة التقريبية للكمية Xمُسَمًّى حقيقي بمعنى واسع ، إذا كان خطأ التقريب المطلق لا يتجاوز وحدة هذا الرقم ص، الذي ينتمي إليه هذا الرقم (يعتبر الرقم صفر رقمًا للوحدات ، بينما تعتبر الأرقام العشرية أرقامًا سالبة). هناك مفهوم آخر الرقم الحقيقي بالمعنى الضيق :. في المستقبل ، سننظر في الأرقام الصحيحة بمعنى واسع. يتم استدعاء باقي الأرقام متردد . ذو معنى أرقام الرقم المكتوبة بشكل عشري هي جميع الأرقام الصحيحة من الرقم ، بدءًا من الأول على اليسار ، بخلاف 0. جميع الأصفار الموجودة على اليسار غير ذات أهمية. من خلال عدد الأرقام المهمة ، يمكن للمرء بسهولة تقدير الخطأ المطلق لرقم تقريبي. لتقدير الخطأ المطلق ، يمكنك أن تأخذ 0.5 رقم بعد آخر رقم مهم. يمكن اعتبار الخطأ النسبي المحدد مساويًا لكسر ، بسطه هو 1 ، والمقام هو عدد صحيح مزدوج ، مكتوب باستخدام جميع الأرقام المعنوية لرقم معين.

مثال. أ = 0.065 ؛

مهمة 1.1. حجم الغرفة الخامس تحدد بخطأ نسبي محدود δ كم عدد الأرقام المهمة في الخامس ?

مهمة 1.2. ومن المعروف أن القيمة التقريبية أ لديها ن أرقام هامة. تقدير الخطأ المطلق والنسبي.

عند حل المشكلات المتعلقة بالحسابات ، يتم الحصول على نتائج رقمية ، والتي غالبًا ما تكون غير دقيقة ، لأن. تحدث أخطاء في صياغة المشكلة وفي سياق العمليات الحسابية.

مصادر الأخطاء هي:

1) أخطاء في البيانات الأولية ؛

2) أخطاء التقريب للنتائج الوسيطة والنهائية ؛

3) أخطاء الطريقة التقريبية لحل المشكلة.

عند إجراء عمليات على أرقام تقريبية ، فأنت بحاجة إلى:

1) معرفة دقة البيانات الأولية ، تكون قادرة على تقييم دقة النتيجة ؛

2) أخذ البيانات الأولية بهذه الدقة لضمان الدقة المحددة للنتيجة.

2.1 أخطاء في الأرقام التقريبية

اجعل الرقم x هو القيمة الدقيقة ، والرقم a هو القيمة التقريبية لبعض الكمية.

تعريف.يسمى الفرق بين الرقم x وقيمته التقريبية a خطأ الرقم التقريبي a: Δ = | x-a |.

دع x = 10.5 ، a = 10 ، ثم Δ = 10.5-10 = 0.5.

دع x = 9.5 ، a = 10 ، ثم Δ = 9.5-10 = -0.5.

تعريف.تسمى القيمة المطلقة للفرق بين الرقم x وقيمته التقريبية a الخطأ المطلق للرقم التقريبي a: Δа = |-а |

دع x = 10.5 ، a = 10 ، ثم Δa = | 10.5-10 | = 0.5.

دع x = 9.5 ، a = 10 ، ثم Δa = | 9.5-10 | = 0.5.

في كثير من الأحيان لا يعرف الرقم الدقيق س. ثم من المستحيل العثور على Δа = | х-а | ، لذلك ، يتم استخدام تقدير الخطأ المطلق - الحد من الخطأ المطلق Δа ≥ Δа = x-а |. في هذه الحالة ، يتم وضع الرقم x داخل الحدود:

أ - أ  س  أ + أ أو باختصار: س = أ ± Δ أ.

يقرؤون: x يساوي a بدقة Δ a.

من أجل تحديد جودة الحسابات التي يتم إجراؤها ، من الضروري تحديد نسبة الخطأ المطلق للقيمة المقاسة. للقيام بذلك ، استخدم الخطأ النسبي.

تعريف.الخطأ النسبي δA للعدد التقريبي a هو نسبة الخطأ المطلق Δа إلى معامل الرقم x:

أو

.

تقدير الخطأ النسبي ba هو الخطأ النسبي المحدد: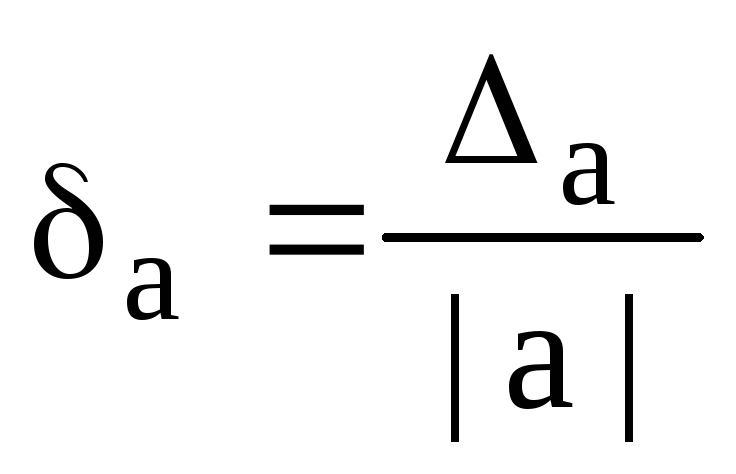

مثال.إذا كان الرقم x = 0.4287 وقيمته التقريبية a = 0.4264. أوجد الأخطاء المطلقة والنسبية للرقم أ.

حل.دعونا نحسب الخطأ المطلق للرقم أ:

Δa = | 0.4287-0.4264 | = 0.0023.

دعونا نحسب الخطأ النسبي للرقم أ:

أو 5.4٪.

ملاحظات. 1. عند تسجيل خطأ ما ، من المعتاد ترك رقم أو رقمين مهمين. يتم دائمًا تقريب الأخطاء. في هذه الحالة ، يتم توسيع حدود العدد المحدد x.

2. إذا كان الرقم x غير معروف ، فسيتم استخدام الرقم a للعثور على الخطأ النسبي.

3. غالبًا ما يتم التعبير عن الخطأ النسبي كنسبة مئوية بضربه في 100٪.

2.2. أرقام مهمة وصحيحة لرقم تقريبي

لتقييم دقة الرقم التقريبي أ ، من المعتاد كتابته في صورة كسر عشري. لا يتم تحديد دقة العمليات الحسابية بعدد المنازل العشرية (الأرقام بعد الفاصلة العشرية) ، ولكن من خلال عدد الأرقام المهمة الصالحة للنتيجة.

تعريف.الأرقام المهمة في الرقم a هي جميع أرقامه ، باستثناء الأصفار المكتوبة قبل الرقم الأول غير الصفري ، والأصفار في نهاية الإدخال ، إذا كانت تعمل على الحفاظ على الرقم أو دقة الرقم.

مثال.أوجد الخانات ذات الدلالة a.

أ = 0.02701 => أرقام معنوية: 2.7.0.1.

أ = 0.0270 => أرقام معنوية: 2.7.0.

أ = 2700 => أرقام معنوية: 2.7.0.0.

تعريف.يُطلق على الرقم α i للرقم التقريبي a رقمًا مهمًا حقيقيًا بالمعنى الواسع (بالمعنى الدقيق للكلمة) إذا كان الخطأ المطلق المحدد للرقم a لا يتجاوز واحدًا (نصف واحد) من الرقم الذي فيه الرقم α أنا مكتوب: Δ أ 10 أنا (Δ أ  0.5 ∙ 10 أنا).

مثال.حدد الأعداد الصحيحة للعدد التقريبي أ = 0.7264 إذا كان الخطأ المطلق Δ أ = 0.0023.

حل.خطأ مطلق Δ أ = 0.0023  0.005 = 0.5 ∙ 10 -2. لذلك ، فإن الرقمين 7 و 2 صحيحان بالمعنى الدقيق للكلمة ، والأرقام 6 و 4 غير صحيحة (مشكوك فيها). منذ Δ أ  = 0.0023< 0,01 = 10 -2 , то цифры 7 и 2 являются верными в широком смысле.

ملاحظات. 1. في الجداول الرياضية ، جميع الأرقام المعنوية صحيحة بالمعنى الدقيق للكلمة.

2. في النتيجة النهائية ، من المعتاد ترك الأرقام الصحيحة فقط. ثم يتم تحديد الخطأ المطلق المحدد للرقم أ بوحدة أقل رقم ذي دلالة. على سبيل المثال ، لنفترض أن a = 127.38 ، ثم Δ a = 0.01 إذا كانت جميع الأرقام صحيحة بالمعنى الدقيق للكلمة ، و Δ a = 0.5 0.01 = 0.005 إذا كانت جميع الأرقام صحيحة بالمعنى الواسع.

مثال.حدد المساواة الأكثر دقة 13/19 = 0.684 أو

=7,21?

حل.دعونا نشير إلى أ = 0.684 ، ب = 7.21. دعونا نجد الأخطاء المطلقة لهذه الأرقام. للقيام بذلك ، خذ 13/19 و

بعدد كبير من المنازل العشرية: 13/39 = 0.68421 ... ،

=7,2111...

ثم Δ a = | 0.68421 ...- 0.684 |< 0,00022, Δ в = |7,2111...-7,21| < 0,0012.

لنجد الأخطاء النسبية:

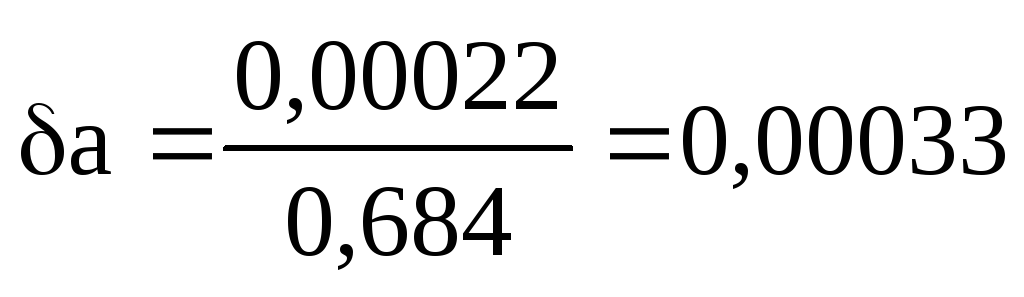أو 0.033٪.

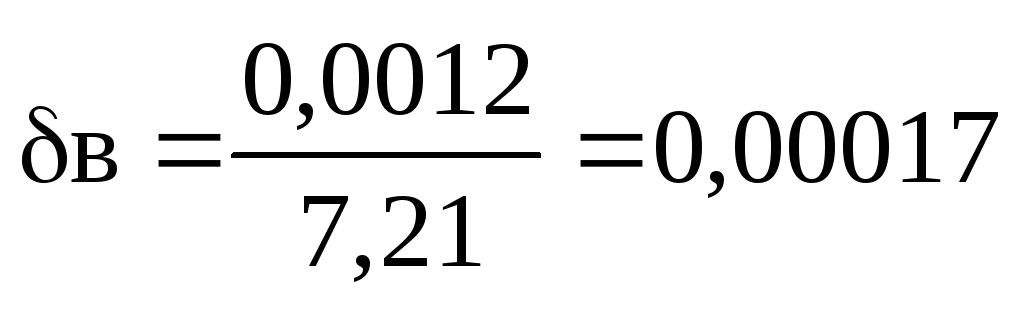أو 0.017٪.

المعادلة الثانية أكثر دقة ، منذ ذلك الحين

.

2.3 تقريب الأرقام

في الحسابات التقريبية ، غالبًا ما يكون من الضروري تقريب الأرقام ، التقريبية والدقيقة ، أي تجاهل واحد أو أكثر من الأرقام الأخيرة. عند تقريب رقم ، نستبدله برقم تقريبي به عدد أقل من الخانات المهمة ، مما يؤدي إلى حدوث خطأ في التقريب. لكي يكون هذا الخطأ في حده الأدنى ، يجب اتباع بعض قواعد التقريب.

قاعدة أنا. إذا كان أول على يسار الأرقام المهملة أكبر من 5 ، فسيتم تضخيم آخر الأرقام المحتجزة ، أي يزيد بمقدار واحد. يتم إجراء التضخيم أيضًا عندما يكون أول يسار من الأرقام المهملة هو 5 ، متبوعًا بأرقام غير صفرية.

مثال.بالتقريب لأعشار الرقم 73.473 ، نحصل على 73.5. الرقم الأخير المتبقي مقوى لأن 7> 5.

قاعدة ثانيًا. إذا كان الرقم الأول من الأرقام المهملة أقل من 5 ، فلن يتم تحسين آخر الأرقام المتبقية ، أي يظل دون تغيير.

مثال.بالتقريب حتى المئات من الرقم 73.473 ، نحصل على 73.47.

قاعدةثالثا. إذا كان الأول على يسار الأرقام المهملة هو 5 ولم يتبعه أي أرقام غير صفرية ، فسيتم تعزيز آخر رقم متبقٍ إذا كان فرديًا ولم يتغير إذا كان زوجيًا (قاعدة الأرقام الزوجية).

مثال.عند تقريب الرقم 5.785 إلى جزء من مائة ، نحصل على 5.78. نحن لا نجري تضخمات ، لأن آخر رقم محفوظ 8 هو زوجي. عند تقريب الرقم 5.775 إلى المكان العشري الثاني ، نحصل على 5.78. يتم زيادة آخر رقم مخزن ، 7 ، بمقدار واحد لأنه فردي.

عند تطبيق القاعدة 3 لتقريب رقم واحد ، فإننا لا نزيد فعليًا دقة الحسابات ، ولكن مع العديد من عمليات التقريب ، تحدث الأعداد الزائدة تقريبًا مثل الأرقام الأقل. هناك تعويض متبادل للأخطاء ، والنتيجة أكثر دقة.

وبالتالي ، عند تطبيق قواعد التقريب المذكورة أعلاه ، لا يتجاوز خطأ التقريب المطلق نصف وحدة الرقم ، التي يحددها آخر رقم مهم متبقٍ.

إذا تم تقريب العدد الدقيق x إلى n من الخانات ذات الدلالة ، فإن الرقم التقريبي الناتج يحتوي على خطأ مطلق يساوي خطأ التقريب. في هذه الحالة ، العدد التقريبي a يحتوي على n من الأرقام المهمة الصحيحة بالمعنى الضيق.

مثال.عند تقريب العدد x = 26.837 إلى ثلاثة أرقام معنوية ، نحصل على a = 26.8 ، ومن أين Δ a = | x-a | = | 26.837-26.8 | = 0.037< 0,05, т. е. число а имеет три верные значащие цифры в узком смысле.

عند تقريب الرقم التقريبي أ ، نحصل على رقم تقريبي جديد أ 1.

تعريف.الرقم Δ a1 \ u003d Δ a + env يسمى خطأ التقريب.

الخطأ المطلق للرقم أ 1 هو مجموع الخطأ المطلق للرقم الأصلي Δ أ وخطأ التقريب Δ إنف ، أي

Δ a1 = Δ a + env.

مثال.قرّب الأرقام المشكوك في تحصيلها من العدد x = 34.124 ± 0.021. تحديد الخطأ المطلق للنتيجة.

حل.الرقم التقريبي أ = 34.124 يحتوي على ثلاثة أرقام صحيحة بالمعنى الضيق: 3 ، 4 ، 1 ، لأن Δ أ = 0.021< 0,05. Применяя правила округления, найдем приближенное значение а 1 , сохранив десятые доли: а 1 = 34,1. Погрешность округления Δ окр =|34,124-34,1|=0,024. Тогда абсолютная погрешность числа а 1 равна Δ а1 =Δ а +Δ окр =0,021+0,024 = 0,045 < 0,05.

وبالتالي ، فإن جميع الأرقام المهمة في الرقم a 2 صحيحة (بالمعنى الضيق).

إذن x = 34.1 ± 0.045.

ومع ذلك ، عند تقريب رقم تقريبي a ، والذي يحتوي على عدد n من الأرقام المعنوية الصحيحة (بالمعنى الضيق) ، إلى n من الأرقام المهمة ، فقد يتضح أن الرقم المقرب 1 سيحتوي على n من الأرقام المعنوية الصحيحة بالمعنى الواسع.

مثال.يحتوي الرقم التقريبي أ = 15.3654 (± 0.0018) على أربعة أرقام معنوية صحيحة بالمعنى الضيق (1 ، 5 ، 3 ، 6) ، حيث أن Δ أ = 0.0018< 0,005. При округлении до четырех значащих цифр получим а 1 = 15,37 и Δ а1 =Δ а +Δ окр =0,0018+|15,3654-15,37|=0,0064.

من الواضح أن 0.005< 0,0064 < 0,01. Следовательно, число 15,37 (± 0.0064) بأربعة أرقام صحيحة بالمعنى الأوسع.

إذن x = 15.37 ± 0.0064.

مثال.قم بتقريب الأرقام المشكوك فيها للرقم أ = 26.7245 (± 0.0026) ، تاركًا الإشارات الصحيحة بالمعنى الضيق. تحديد الخطأ المطلق للنتيجة.

حل.حسب الشرط Δ أ = 0.0026< 0,005, следовательно, в числе 26,7245 верными в узком смысле являются цифры 2, 6, 7, 2. Используя правила округления, найдем приближенное значение а 1 , сохранив сотые доли:

الخطأ الناتج أكبر من 0.005 (0.005< 0,0071), поэтому уменьшим число цифр в приближенном числе до трех; а 2 = 26.7. نجد Δ a2 = = a + Δ env = 0.0026 + | 26.7245-26.7 | = 0.0271< 0,05. Следовательно, оставшиеся три цифры верны в узком смысле.

إذن ، x = 26.7 ± 0.0271 => x = 26.7 ± 0.03 ، لتقريب الخطأ إلى منزلتين عشريتين.

مثال.تقريب الأرقام المشكوك في تحصيلها من الرقم أ = 22.7314 ، تاركًا الإشارات الصحيحة بالمعنى الضيق. أوجد الخطأ المطلق للعدد إذا كانت أ = 0.2٪.

حل.نكتب δ أ في صورة كسر عشري: δа = 0.002 وحدد الخطأ المطلق. منذ Δ أ \ u003d = 0.0455< 0,05, то верными в этом числе будут три цифры: 2, 2, 7. Округлим число 22,7314, сохранив в нем десятые доли: а 1 = 22.73. ثم Δ a1 = = Δ a + Δ env = 0.0455 + | 22.7314-22.73 | = 0.0769> 0.05 ، لذلك سنقلل عدد الأرقام في العدد التقريبي إلى اثنين: a 2 = 23. نجد Δ a2 = = a + env = 0.0455 + | 22.7314-23 | = 0.3141< 0,05. Следовательно, оставшиеся две цифры верны в узком смысле.

إذن x = 23 ± 0.3141 => x = 23 ± 0.32.

2.3 قواعد العمليات على الأرقام التقريبية

المادة 1الخطأ المطلق في المجموع الجبري لعدة أرقام تقريبية يساوي مجموع الأخطاء المطلقة لهذه الأرقام:

Δ أ ± ب = Δ أ + Δ ب

القاعدة 2الخطأ النسبي لحاصل ضرب عدة أرقام تقريبية يساوي مجموع الأخطاء النسبية لهذه الأرقام:

δ av \ u003d δ a + c.

القاعدة 3الخطأ النسبي للأرقام التقريبية الجزئية يساوي مجموع هذه الأرقام النسبية: δ أ / ب \ u003d δ أ + δ ج.

القاعدة 4الخطأ النسبي لدرجة الرقم التقريبي أ هو: δa n = nδ a.

القاعدة 5الخطأ النسبي لجذر الرقم التقريبي أ هو:

.

القاعدة 6عند الحساب ، إذا لم يتم إجراء حساب صارم للأخطاء ، يوصى باستخدام قواعد حساب الأرقام. تحدد هذه القواعد كيفية تقريب النتائج للتأكد من أن النتيجة دقيقة قدر الإمكان بدون عمليات حسابية تزيد عن الأرقام.

تفترض القواعد أن الأرقام التي يتم العمل عليها تحتوي فقط على أرقام صالحة وأن عدد العمليات صغير.

1- عند إضافة وطرح الأرقام التقريبية ، يجب أن تحتفظ النتيجة بعدد من المنازل العشرية كما هو الحال في الرقم الذي يحتوي على أصغر عدد من المنازل العشرية.

ثانيًا. عند الضرب والقسمة ، يجب أن تحتفظ النتيجة بعدد من الأرقام المهمة كما هو الحال في العدد الذي يحتوي على أقل عدد من الأرقام المعنوية.

ثالثا. عند رفع رقم تقريبي إلى أس ، يجب أن تكون النتيجة الحفاظ على أكبر عدد من الأرقام المعنوية الموجودة في قاعدة الأس.

رابعا. عند استخراج جذر من رقم تقريبي ، يجب أن تحتفظ بعدد كبير من الأرقام المهمة كما هو الحال في رقم الجذر.

V. في النتائج الوسيطة ، يجب أن تحتفظ برقمين أو رقمين أكثر مما توصي به القواعد من الأول إلى الرابع. في النتيجة النهائية ، يتم تجاهل "الأرقام الاحتياطية" مع تقريب الرقم.

السادس. إذا كانت بعض بيانات المصدر تحتوي على منازل عشرية أكثر (للجمع والطرح) أو أرقام أكثر أهمية (لعمليات أخرى) من غيرها ، فيجب تقريبها أولاً ، مع الاحتفاظ بـ "رقم آمن" واحد فقط.

سابعا. للحصول على نتيجة مع N من الأرقام الصحيحة ، يجب أخذ بيانات المصدر مع مثل هذا العدد من الأرقام التي ، وفقًا للقواعد السابقة ، توفر N + 1 رقمًا في النتيجة.

مثال.لنجد s = 2.35 + 11.8 دون مراعاة الأخطاء. بتطبيق القاعدة الأولى نحصل على s = 14.15. سيتم تقريب النتيجة إلى الرقم 11.8 بأقل عدد من المنازل العشرية. نحصل على: s \ u003d 14.2.

دعونا نحل المشكلة مع مراعاة الأخطاء. في الرقم s = 14.15 ، يجب ترك الأرقام الصحيحة فقط. للقيام بذلك ، نجد الخطأ المطلق المحدد لمجموع s باستخدام القاعدة 1. نظرًا لأن جميع الأرقام في العددين 2.35 و 11.8 صحيحة ، نحصل على: Δ 14.15 = Δ 2.35 + Δ 11.8 = 0.01 + 0.1 = 0.11< 0,5. Последняя верная цифра в числе 14,15 находится в разряде единиц. Поэтому число s=14,15 надо округлить: s=14 и найти абсолютную погрешность округленного числа. Погрешность округления равна: |14,15-14|=0,15. Тогда абсолютная погрешность округленного числа Δ 14 =0,11+0,15=0,26 <0,5. Окончательный результат примет вид: s=14 ± 0,26.

يتم حل المشكلات بالمثل عند إجراء عمليات أخرى على أرقام تقريبية.

إرسال عملك الجيد في قاعدة المعرفة أمر بسيط. استخدم النموذج أدناه

سيكون الطلاب وطلاب الدراسات العليا والعلماء الشباب الذين يستخدمون قاعدة المعرفة في دراساتهم وعملهم ممتنين جدًا لك.

نشر على http://www.allbest.ru/

معهد موسكو للاقتصاد ،الإدارة والقانون

مقال

عن طريق الانضباط:

« أعلىمفي الرياضيات»

« صحسابات تقريبية وتقدير الخطأايقضي»

تم: الطالب

يانتشوك لودميلا الكسندروفنا

المدير العلمي بيتيرتسيفا غالينا الكسندروفنا

موسكو 2000

يخطط

مقدمة. الحوسبة في العلوم والتكنولوجيا الحديثة

1. القيم التقريبية وأخطاء التقريب

2. تقريب الأرقام. خطأ التقريب

خاتمة. بعض المعلومات عن الحوسبة

الأدب

مقدمة. الحوسبة في العلوم والتكنولوجيا الحديثة

لعبت القياسات والحسابات دورًا مهمًا في حياة المجتمع منذ العصور القديمة. الحاجة إلى حساب الحصاد ، وقياس سعة السفن ، وحجم قطع الأرض ، وإجراء الحسابات أثناء بناء الهياكل الكبيرة ، وإجراء حسابات فلكية مختلفة - هذه قائمة غير كاملة من المهام التي كان على الناس حلها في العصور القديمة.

يجب اعتبار استكشاف الفضاء من قبل البشرية أحد أهم الأحداث في الآونة الأخيرة. نحن نتابع بقلق الرحلات الجوية إلى القمر والزهرة والمريخ وإنشاء محطات مدارية مأهولة. إن إطلاق مركبة فضائية لن يكون من الممكن تصوره لولا الحساب الدقيق لحركة السفينة ، وهذا يتطلب عملاً حاسوبيًا ضخمًا ومعقدًا.

في العصر الحديث ، فترة الثورة العلمية والتكنولوجية ، يتزايد دور الأساليب الرياضية. تستخدم الأساليب الرياضية ليس فقط في الفيزياء ، ولكن أيضًا في الكيمياء والبيولوجيا والطب والاقتصاد والتاريخ واللغويات

يجب أن يقوم علماء الرياضيات والمهندسون بالكثير من الأعمال الحسابية في الأنشطة اليومية والحالية للمؤسسات الصناعية والمعاهد العلمية والوكالات الحكومية والمزارع والمزارع الجماعية.

تُستخدم الأساليب الحسابية الآن على نطاق واسع في الحسابات الاقتصادية ، في تخطيط عمل مؤسسة فردية ، ومنطقة واقتصاد البلد بأكمله.

هناك العديد من المشاكل التي تتطلب ، من أجل الحصول على نتيجة عددية ، حسابات تتجاوز قدرات شخص واحد. ومن الأمثلة على هذه المشاكل حساب الضغوط المرنة في السد ، أو حساب المقاومة التي تتعرض لها الطائرات أثناء الطيران ، أو مسارات المقذوفات. يقوم العشرات من مهندسي الكمبيوتر ، باستخدام أجهزة كمبيوتر مختلفة ، بتنفيذ هذا العمل الحسابي المعقد.

تسبب ظهور الكمبيوتر في حدوث ثورة في تكنولوجيا الحوسبة. ولكن من أجل إحضار حل المشكلات الرياضية إلى المرحلة التي يمكن بعدها نقلها إلى جهاز كمبيوتر للحصول على نتائج عددية ، فإن عمل العديد من الآلات الحاسبة ضروري أيضًا. حفز إنشاء أجهزة الكمبيوتر على تطوير الرياضيات نفسها ، وخاصة مجالاتها التطبيقية ؛ لا تلعب الحسابات الآن دورًا مساعدًا ، بل تلعب دورًا رئيسيًا في العديد من الإنجازات العلمية والتقنية. في جميع الحالات عندما يكون من الضروري إكمال حل أي مشكلة رياضية ذات طبيعة عملية ، من الضروري الحصول على نتيجة عددية. إذا كانت البيانات الأولية تقريبية ، فمن المستحيل تحقيق أي درجة من دقة النتيجة. يجب أن يكون المرء قادرًا على تقييم دقة البيانات الأولية ، وكذلك تحديد دقة النتيجة التي يمكن تحقيقها ودقة النتيجة المطلوبة في الاستخدام العملي للنتائج الرقمية التي تم الحصول عليها. تتطلب بعض العمليات الحسابية دقة عالية جدًا ، بينما لا يتطلب البعض الآخر ذلك. من هذا يتضح أنه من الضروري تنظيم الحسابات بطريقة للحصول على النتائج بالدقة المطلوبة مع الحد الأدنى من إنفاق العمل الحسابي.

لتحقيق هذا الهدف ، من الضروري:

دراسة مبادئ وقواعد الحسابات ببيانات تقريبية ؛

لإتقان المهارات اللازمة للحسابات العقلانية بمساعدة الوسائل المتاحة ، والتي تشمل طرقًا مختلفة للحسابات الشفوية ، والجداول الرياضية ، والحسابات الكتابية ، وقواعد الشرائح ، والمقاييس الحسابية ، وأجهزة الكمبيوتر شبه الآلية والآلية.

1. القيم التقريبية وأخطاء التقريب

في الأنشطة العملية ، يجب على الشخص قياس كميات مختلفة ، ومراعاة مواد ومنتجات العمل ، وإجراء حسابات مختلفة. نتائج القياسات والتعدادات والحسابات المختلفة عبارة عن أرقام. الأرقام التي تم الحصول عليها نتيجة القياس ، فقط تقريبًا ، بدرجة معينة من الدقة ، تميز القيم المرغوبة. القياسات الدقيقة مستحيلة بسبب عدم دقة أدوات القياس ، ونقص أعضائنا في الرؤية ، والأشياء المقاسة نفسها في بعض الأحيان لا تسمح لنا بتحديد قيمتها بأي دقة.

لذلك ، على سبيل المثال ، من المعروف أن طول قناة السويس يبلغ 160 كيلومترًا ، والمسافة بالسكك الحديدية من موسكو إلى لينينغراد 651 كيلومترًا. هنا لدينا نتائج القياسات التي تم إجراؤها بدقة تصل إلى كيلومتر واحد. على سبيل المثال ، إذا كان طول المقطع المستطيل 29 مترًا ، والعرض 12 مترًا ، فمن المحتمل أن القياسات تم إجراؤها بدقة تصل إلى متر ، وتم إهمال أجزاء من المتر ،

قبل إجراء أي قياس ، من الضروري تحديد الدقة التي يجب إجراؤها ، أي أي كسور من وحدة القياس يجب أن تؤخذ بعين الاعتبار وأيها يجب إهمالها.

إذا كان هناك بعض القيمة أ،القيمة الحقيقية غير معروفة ، والقيمة التقريبية (التقريبية) لهذه القيمة تساوي X ،يكتبون أ X.

بقياسات مختلفة من نفس الكمية ، سوف نحصل على تقديرات تقريبية مختلفة. سيختلف كل من هذه التقديرات التقريبية عن القيمة الحقيقية للقيمة المقاسة ، على سبيل المثال ، أ،بقدر ما سوف نسميه خطأ.تعريف. إذا كان الرقم x قيمة تقريبية (تقريبية) لبعض الكمية ، فإن القيمة الحقيقية لها تساوي الرقم أ،ثم معامل اختلاف الأعداد ، أو Xمُسَمًّى الخطأ المطلقالتقريب والمشار إليه أx: أو ببساطة أ. وهكذا ، بحكم التعريف ،

أx = أ- x (1)

من هذا التعريف يتبع ذلك

أ = x أx (2)

إذا كان معروفًا ما هي الكمية التي نتحدث عنها ، فعندئذٍ في التدوين أxفِهرِس أتم حذفه والمساواة (2) مكتوبة على النحو التالي:

أ = x x (3)

نظرًا لأن القيمة الحقيقية للقيمة المطلوبة غالبًا ما تكون غير معروفة ، فمن المستحيل العثور على الخطأ المطلق في تقريب هذه القيمة. يمكن للمرء أن يشير فقط في كل حالة محددة إلى رقم موجب ، أكثر مما لا يمكن أن يكون هذا الخطأ المطلق. يسمى هذا الرقم بحد الخطأ المطلق لتقريب الكمية أوالمشار إليها ح أ. وهكذا ، إذا xهو تقريب تعسفي للقيمة أ لإجراء معين للحصول على تقديرات تقريبية ، إذن

أx = أ- x ح أ (4)

ويترتب على ما سبق أنه إذا ح أهي حدود الخطأ المطلق لتقريب الكمية أ، ثم أي رقم أكبر من ح أ، سيكون أيضًا حد الخطأ المطلق لتقريب الكمية أ.

من الناحية العملية ، من المعتاد اختيار أصغر رقم يرضي عدم المساواة (4) كحد للخطأ المطلق.

حل المتباينة أ- x ح أحصلنا على ذلك أالواردة داخل الحدود

x-ح أ أ x+ ح أ (5)

يمكن إعطاء مفهوم أكثر صرامة لحد الخطأ المطلق على النحو التالي.

يترك X- العديد من التقريبات الممكنة Xكميات ألإجراء معين للحصول على تقريب. ثم أي رقم ح، تلبية الشرط أ- x ح ألأي X X، يسمى حد الخطأ المطلق للتقديرات من المجموعة X. للدلالة به ح أأصغر رقم معروف ح. هذا العدد ح أويتم اختياره في الممارسة العملية كحدود للخطأ المطلق.

خطأ التقريب المطلق لا يميز جودة القياسات. في الواقع ، إذا قمنا بقياس أي طول بدقة 1 سم ، فعندما يتعلق الأمر بتحديد طول قلم رصاص ، ستكون هذه دقة ضعيفة. إذا حددت بدقة 1 سم طول أو عرض ملعب الكرة الطائرة ، فسيكون ذلك دقة عالية.

لتوصيف دقة القياس ، يتم تقديم مفهوم الخطأ النسبي.

تعريف. لو أx: يوجد خطأ تقريبي مطلق Xبعض الكمية ، القيمة الحقيقية لها تساوي الرقم أثم النسبة أxلمعامل العدد Xيسمى الخطأ النسبي للتقريب ويشار إليه أxأو x.

وهكذا ، بحكم التعريف ،

عادة ما يتم التعبير عن الخطأ النسبي كنسبة مئوية.

على عكس الخطأ المطلق ، والذي غالبًا ما يكون كمية أبعاد ، فإن الخطأ النسبي هو كمية بلا أبعاد.

في الممارسة العملية ، ليس الخطأ النسبي هو الذي يؤخذ في الاعتبار ، ولكن ما يسمى بحد الخطأ النسبي: مثل هذا الرقم ه أ، والتي لا يمكن أن تكون أكبر من الخطأ النسبي لتقريب القيمة المطلوبة.

هكذا، أx ه أ.

لو ح أ- حد الخطأ المطلق لتقريب الكمية أ، الذي - التي أx ح أوبالتالي

من الواضح ، أي رقم ه، تلبية الشرط ، سيكون حدود الخطأ النسبي. في الممارسة العملية ، عادة ما يكون بعض التقريب معروفًا Xكميات أوحد الخطأ المطلق. ثم الرقم

2. تقريب الأرقام. خطأ التقريب

عند إجراء العمليات الحسابية ، غالبًا ما يكون من الضروري تقريب الأرقام ، أي في استبدالها بأرقام ذات أرقام معنوية أقل.

هناك ثلاث طرق لتقريب الأرقام:

التقريب إلى كالرقم المعنوي هو تجاهل كل الأرقام التي تبدأ بـ (ك+1) ذ.

يختلف التقريب لأعلى عن التقريب لأسفل في أن آخر رقم مخزن يتم زيادته بواحد.

يختلف التقريب مع أصغر خطأ عن التقريب مع زيادة في أن الزيادة بأحد آخر رقم مخزن يتم إجراؤها فقط إذا كان أول رقم من الخانات المهملة أكبر من 4.

استثناء: إذا كان التقريب مع أصغر خطأ هو تجاهل رقم واحد فقط 5 ، فلن يتغير الرقم الأخير المخزن إذا كان زوجيًا ، ويزيد بمقدار 1 إذا كان فرديًا.

من القواعد المذكورة أعلاه لتقريب الأرقام التقريبية ، فإن الخطأ الناتج عن التقريب مع أصغر خطأ لا يتجاوز نصف وحدة آخر رقم مخزن ، وعند التقريب بنقص أو زيادة ، قد يكون الخطأ أكثر من نصف وحدة من آخر رقم مخزن ، ولكن ليس أكثر من وحدة كاملة من هذا التفريغ.

لنلق نظرة على هذا في الأمثلة التالية.

1. الخطأ في المبلغ.يترك x أ, في- بعض التقريب للقيمة ب. يترك Xو في- الأخطاء المطلقة في التقديرات المقابلة Xو في. لنجد حد الخطأ المطلق ح أ + بكميات س + ص، وهو تقريب للمبلغ أ + ب.

أ = x + X ،

ب = ذ + ذ.

بجمع هاتين المتعادلتين ، نحصل على

أ + ب = x + ذ + x + ذ.

من الواضح أن الخطأ في مجموع التقريبات xو فييساوي مجموع أخطاء المصطلحات ، أي

(x + ذ) = x + ذ

من المعروف أن معامل المجموع أقل من أو يساوي مجموع معاملات المصطلحات. لهذا

(x + ذ) = x + ذ x + ذ

هذا يعني أن الخطأ المطلق لمجموع التقديرات التقريبية لا يتجاوز مجموع الأخطاء المطلقة للمصطلحات. لذلك ، يمكن اعتبار مجموع حدود الأخطاء المطلقة للشروط حدًا للخطأ المطلق في المجموع.

دلالة على حدود الخطأ المطلق للكمية أخلال ح أ، وب من خلال ح بسوف نحصل على

ح أ + ب = ح أ + ح ب

2. خطأ الاختلاف.يترك Xو في- أخطاء التقريب x و فيعلى التوالى أو ب.

أ = x + X ،

ب = ذ + ذ.

نطرح الثانية من المساواة الأولى ، نحصل عليها

أ - ب = (x - ذ) + ( x - ذ)

من الواضح أن خطأ فرق التقريب يساوي الفرق بين أخطاء المطروح والمطروح ، أي

(x - ذ) = x - ذ) ,

(x - ذ) = x + (- ذ)

وبعد ذلك ، نجادل بالطريقة نفسها كما في حالة الجمع

(x - ذ) = x + (- ذ) x + ذ

ويترتب على ذلك أن الخطأ المطلق للاختلاف لا يتجاوز مجموع الأخطاء المطلقة في الحد الأدنى والمطروح.

بالنسبة لحدود الخطأ المطلق للاختلاف ، يمكنك أن تأخذ مجموع حدود الأخطاء المطلقة للمطروح المصغر والمطروح الفرعي. هكذا.

ح أ - ب = ح أ + ح ب (9)

من الصيغة (9) يترتب على ذلك أن حد الخطأ المطلق للاختلاف لا يمكن أن يكون أقل من حد الخطأ المطلق لكل تقريب. يشير هذا إلى قاعدة طرح التقديرات التقريبية ، والتي تُستخدم أحيانًا في العمليات الحسابية.

عند طرح أرقام تقريبية لبعض الكميات ، يجب أن تكون النتيجة أكبر عدد من الأرقام بعد الفاصلة العشرية مثل التقريب مع أصغر عدد من الأرقام بعد الفاصلة العشرية.

3. خطأ في المنتج.ضع في اعتبارك ناتج الأعداد Xو في، وهي تقديرات تقريبية للكميات أ و ب. للدلالة به xخطأ تقريبي X، ومن خلال في- خطأ تقريبي في,

أ = x + X ،

ب = ذ + ذ.

بضرب هاتين المتعادلتين ، نحصل على

خطأ منتج مطلق هومساوي ل

وبالتالي

قسمة طرفي عدم المساواة الناتج على هو، نحن نحصل

مع الأخذ في الاعتبار أن مقياس المنتج يساوي حاصل ضرب معاملات العوامل ، فسنحصل على

هنا الجانب الأيسر من المتباينة هو الخطأ النسبي للمنتج هو، - خطأ تقريب نسبي X، وهو خطأ التقريب النسبي في. لذلك ، بغض النظر عن القيمة الصغيرة هنا ، نحصل على المتباينة

وبالتالي ، فإن الخطأ النسبي لمنتج التقريب لا يتجاوز مجموع الأخطاء النسبية للعوامل. ويترتب على ذلك أن مجموع حدود الأخطاء النسبية للعوامل هو حد الخطأ النسبي للمنتج ، أي

ه أب = ه أ + ه ب (10)

من الصيغة (10) يترتب على ذلك أن حد الخطأ النسبي للمنتج لا يمكن أن يكون أقل من حد الخطأ النسبي لأقل العوامل دقة. لذلك ، هنا ، كما في الخطوات السابقة ، ليس من المنطقي الاحتفاظ بعدد كبير من الأرقام المهمة في العوامل.

من المفيد أحيانًا استخدام القاعدة التالية في العمليات الحسابية لتقليل مقدار العمل: عند ضرب التقديرات التقريبية بأعداد مختلفة من الأرقام المعنوية ، يجب أن تحتفظ النتيجة بالعديد من الأرقام المهمة مثل التقريب مع أصغر عدد من الأرقام المعنوية.

4. خطأ حاصل القسمة.لو x- تقريب القيمة أالذي خطأه x، أ في- تقريب القيمة بمع وجود خطأ ذ، الذي - التي

دعونا أولاً نحسب الخطأ المطلق في حاصل القسمة:

ثم الخطأ النسبي:

مع الأخذ بعين الاعتبار أن ذقليلا بالمقارنة مع ذ، يمكن اعتبار القيمة المطلقة للكسر مساوية لواحد. ثم

ويترتب على الصيغة الأخيرة أن الخطأ النسبي للحاصل لا يتجاوز مجموع الأخطاء النسبية للمقسوم والمقسوم عليه. لذلك ، يمكننا أن نفترض أن حد الخطأ النسبي للحاصل يساوي مجموع حدود الأخطاء النسبية للمقسوم والمقسوم عليه ، أي

5. خطأ في الدرجة والجذر. 1) دع ش = أ ن، أين نهو عدد طبيعي ، ودع x. ثم إذا ه أ- حدود خطأ التقريب النسبي xكميات أ، الذي - التي

وبالتالي

وبالتالي ، فإن حد الخطأ النسبي للدرجة يساوي حاصل ضرب حد الخطأ النسبي للقاعدة بواسطة الأس ، أي

ه ش = ن ه أ (11)

2) دع أين نهو عدد طبيعي ، واسمحوا أ X.

حسب الصيغة (11)

وبالتالي

حساب للخصم من الخطأ

وبالتالي ، فإن حدود الخطأ النسبي للجذر نالدرجة في نمرات أقل من حد الخطأ النسبي للعدد الجذري.

6. مشكلة عكسية في الحسابات التقريبية.في المشكلة المباشرة ، يلزم إيجاد القيمة التقريبية للدالة ش =F(س ، ص ، ... ،ن) وفقًا للقيم التقريبية المعطاة للوسيطات

وهامش الخطأ ح أ، والتي يتم التعبير عنها من حيث أخطاء حجج بعض الوظائف

ح ش = (ح x, ح ذ, …, ح ض) (12)

من الناحية العملية ، غالبًا ما يكون من الضروري حل مشكلة عكسية ، حيث يلزم معرفة الدقة التي يجب أن تُعطى بها قيم الحجج س ، ص ، ... ، ضلحساب قيم الوظيفة المقابلة ش = F(س ، ص ، ... ،ض) بدقة محددة مسبقًا h ش.

وبالتالي ، عند حل المشكلة العكسية ، فإن المطلوب هو حدود الخطأ للوسيطات المرتبطة بحد خطأ معين للوظيفة ح شالمعادلة (12) ، ويتم تقليل حل المسألة العكسية إلى تجميع وحل المعادلة ح ش = (ح x, ح ذ, …, ح ض) نسبياً ح x, ح ذ, …, ح ض. مثل هذه المعادلة إما لها عدد لا حصر له من الحلول ، أو ليس لها حلول على الإطلاق. تعتبر المشكلة محلولة إذا تم إيجاد حل واحد على الأقل لهذه المعادلة.

لحل المشكلة العكسية ، التي غالبًا ما تكون غير محددة ، يتعين على المرء إدخال شروط إضافية على نسب الأخطاء غير المعروفة ، على سبيل المثال ، اعتبارها متساوية وبالتالي تقليل المشكلة إلى معادلة واحدة غير معروفة.

خاتمة. بعض المعلومات حولحساب هؤلاءXنايك

اعتمادًا على دقة البيانات الأولية والغرض من الحسابات ، يتم استخدام أدوات الحوسبة المختلفة. يعمل العاملون في العديد من المهن الجماعية بشكل كبير على تسهيل العمليات الحسابية وتوفير الوقت والجهد المبذول في إجراء عمليات حسابية مختلفة بواسطة العداد الروسي ، وحساب قواعد الشرائح ، وأجهزة القياس الحسابية وجميع أنواع الآلات الحاسبة الإلكترونية للجيب وسطح المكتب (الآلات الحاسبة الدقيقة والصغيرة).

تشتمل فئة الآلات الحاسبة الصغيرة الموجودة حاليًا في بلدنا على عائلة Iskra للآلات الحاسبة المكتبية الإلكترونية وعائلة الآلات الحاسبة Elektronika ، والتي تتضمن أيضًا عدة أنواع من حاسبات الجيب. لأسباب واضحة ، فإن هذه الآلات الحاسبة عفا عليها الزمن ، ولكن ، مع ذلك ، فهذه هي النماذج الوحيدة التي تنتجها الصناعة المحلية.

تم تصميم آلات عائلات Elektronika و Iskra بشكل أساسي لحل مشاكل المحاسبة والمحاسبة الهندسية البسيطة بدقة تتراوح من 8 إلى 10 أرقام مهمة. يوفر العديد منها إمكانية الحساب التلقائي لقيم الوظائف الأولية وهناك عناصر للتحكم في البرنامج.

مع النمو السريع للمعدات التقنية في صناعتنا وزراعتنا ، مع تطور العلم ، تزداد الحاجة إلى جميع أنواع الحسابات أكثر فأكثر. باستخدام أجهزة الكمبيوتر الإلكترونية عالية السرعة (أجهزة الكمبيوتر) ، يمكن للباحث الآن حل المشكلات التي لم يتم طرحها من قبل ، لأن حلها يتطلب الكثير من الوقت.

تستخدم أجهزة الكمبيوتر الإلكترونية ، على سبيل المثال ، في الحل العددي للمعادلات. تم تصميم أجهزة الكمبيوتر الأولى خصيصًا لهذا النوع من الحسابات.

حاليًا ، يتم استخدام أجهزة الكمبيوتر بنجاح للتحكم في العمليات التكنولوجية. إذا كان التحكم في عملية سريعة التدفق يتطلب حسابات معقدة بناءً على البيانات التي تم الحصول عليها أثناء هذه العملية ، فبدون جهاز كمبيوتر ، ستكون هذه المهمة مستحيلة بشكل عام.

الأدب

الجبر وبدايات التحليل. الجزء 1. إد. ج. ياكوفليف. - م: نوكا ، 1981. 336 ص.

فيجوتسكي م. كتيب الرياضيات العليا. م: 1987.

مقدمة في علم القياس. Tyurin NI، M.، Publishing House of Standards، 1976، 304 p.

استضافت على Allbest.ru

...

وثائق مماثلة

تحديد الأخطاء المطلقة والنسبية للأرقام التقريبية. تقدير الأخطاء في النتيجة. استيفاء واستقراء البيانات ، وكثيرات حدود لاغرانج ونيوتن ، خصائصها الرئيسية ووصفها المقارن.

العمل المخبري ، تم الإضافة في 08/06/2013

الجوهر والتفسير الرياضي للأخطاء المطلقة والنسبية وطرق كتابة القيمة معها. مفهوم القيمة التقريبية والخطأ التقريبي ، اتجاه تحليل هذه الفئات. حكم لتقريب الكسور العشرية.

الملخص ، تمت إضافة 09/13/2014

خصائص وخصائص الأنواع الرئيسية للأخطاء الناشئة في الحل العددي للمسائل الرياضية والتطبيقية: المشكلات والطرق والتقريب. مفهوم وأسباب أخطاء القياس. وصف الأخطاء العشوائية ، اللحظات.

الاختبار ، تمت إضافة 01/13/2012

النظرية الكلاسيكية للقياسات حول القيمة الحقيقية للكمية المادية ، مسلماتها الرئيسية. تصنيف الأخطاء حسب أسلوب التعبير وأنواعها: مطلقة ومختزلة ونسبية. الأخطاء العشوائية ، قانون توزيعها.

الملخص ، تمت الإضافة في 07/06/2014

تقريب رقم معيّن لأقرب رقم إلى ستة وخمسة وأربعة وثلاثة منازل عشرية. حساب الأخطاء بعد كل تقريب. تحديد الخطأ المطلق والنسبي في حساب قيم الدالة u ، مع الأخذ في الاعتبار حقيقة أن جميع علامات المعاملات a و b و c و d صحيحة.

اختبار ، تمت إضافة 05/02/2012

التحقيق في طرق تحديد الأخطاء والتقييم الإحصائي للتوزيعات. بناء دالة تجريبية تحدد خصوصية الحدث لكل قيمة لمتغير عشوائي. حسابات لعينة معينة وتحليلها وتحديد المعلمات.

ورقة المصطلح ، تمت إضافة 01/13/2011

مقدمة في الأساليب العددية ، خطة لبناء تجربة حسابية. دقة الحسابات وتصنيف الأخطاء. مراجعة طرق التكامل والتفاضل العددي وتقدير الخطأ اللاحق. حل أنظمة المعادلات الخطية.

دليل التدريب ، تمت إضافة 09/23/2010

تحديد عدد وقيمة أعضاء التقدم لتقدم هندسي متناقص بشكل لا نهائي. حساب الخطأ النسبي للكمية. تحديد قيم الآلة صفر ولانهاية. سلوك الأخطاء يعتمد على الحجة.

العمل المخبري ، تمت إضافة 11/15/2014

التحقيق في اعتماد خطأ الحل على أخطاء الجانب الأيمن من النظام. تحديد جذر المعادلة بدقة معينة. حساب تقديرات دقة الطرق بالإحداثيات. استيفاء المفتاح وحل المعادلة التفاضلية.

الاختبار ، تمت إضافة 2011/04/26

حل مسألة كوشي لمعادلة تفاضلية. خطأ في الحلول التقريبية. وظيفة تنفذ طريقة أويلر الصريحة. حساب الخطأ وفقًا لقاعدة Runge. حل المعادلات التفاضلية من الدرجة الثانية. شرط الاستقرار للمصفوفة.