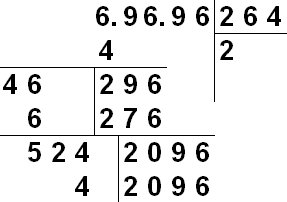Pomerne často sa pri riešení problémov stretávame s veľkými číslami, z ktorých musíme vyťažiť Odmocnina . Mnohí žiaci sa rozhodnú, že ide o omyl a začnú riešiť celý príklad. V žiadnom prípade by sa to nemalo robiť! Sú na to dva dôvody:
- Korene z veľké čísla skutočne vyskytujú v úlohách. Najmä v texte;
- Existuje algoritmus, podľa ktorého sa tieto korene zvažujú takmer verbálne.
Tento algoritmus dnes zvážime. Možno sa vám niektoré veci budú zdať nepochopiteľné. Ale ak budete venovať pozornosť tejto lekcii, dostanete najmocnejšia zbraň proti odmocniny .
Takže algoritmus:
- Obmedzte požadovaný koreň nad a pod na násobky 10. Takto zmenšíme rozsah vyhľadávania na 10 čísel;
- Z týchto 10 čísel vyraďte tie, ktoré rozhodne nemôžu byť koreňmi. V dôsledku toho zostanú 1-2 čísla;
- Odmocni tieto 1-2 čísla. Tá z nich, ktorých druhá mocnina sa rovná pôvodnému číslu, bude odmocninou.
Pred aplikáciou tohto algoritmu v praxi sa pozrime na každý jednotlivý krok.
Koreňové obmedzenie
V prvom rade musíme zistiť, medzi ktorými číslami sa nachádza náš koreň. Je veľmi žiaduce, aby čísla boli násobkom desiatich:
10 2 = 100;
20 2 = 400;
30 2 = 900;
40 2 = 1600;
...
90 2 = 8100;
100 2 = 10 000.
Dostaneme sériu čísel:
100; 400; 900; 1600; 2500; 3600; 4900; 6400; 8100; 10 000.
Čo nám tieto čísla dávajú? Je to jednoduché: dostávame hranice. Vezmime si napríklad číslo 1296. Leží medzi 900 a 1600. Preto jeho koreň nemôže byť menší ako 30 a väčší ako 40:
[Titul obrázku]
To isté platí pre akékoľvek iné číslo, z ktorého môžete nájsť druhú odmocninu. Napríklad 3364:
[Titul obrázku]Namiesto nezrozumiteľného čísla tak dostaneme veľmi špecifický rozsah, v ktorom leží pôvodný koreň. Ak chcete ďalej zúžiť rozsah vyhľadávania, prejdite na druhý krok.
Eliminácia zjavne nadbytočných čísel
Takže máme 10 čísel - kandidátov na koreň. Dostali sme ich veľmi rýchlo, bez zložitého premýšľania a násobenia v kolónke. Je čas pohnúť sa.
Verte či neverte, teraz zredukujeme počet kandidátskych čísel na dve – a opäť bez zložitých výpočtov! Stačí poznať špeciálne pravidlo. Tu je:
Posledná číslica štvorca závisí len od poslednej číslice pôvodné číslo.
Inými slovami, stačí sa pozrieť posledná číslicaštvorec - a hneď pochopíme, kde končí pôvodné číslo.
Na poslednom mieste môže byť iba 10 číslic. Pokúsme sa zistiť, na čo sa premenia, keď sú štvorcové. Pozrite sa na tabuľku:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 |
| 1 | 4 | 9 | 6 | 5 | 6 | 9 | 4 | 1 | 0 |
Táto tabuľka je ďalším krokom k výpočtu koreňa. Ako vidíte, čísla v druhom riadku sa ukázali ako symetrické vzhľadom na päť. Napríklad:
2 2 = 4;
8 2 = 64 → 4.
Ako vidíte, posledná číslica je v oboch prípadoch rovnaká. A to znamená, že napríklad koreň 3364 nevyhnutne končí na 2 alebo 8. Na druhej strane si pamätáme obmedzenie z predchádzajúceho odseku. Dostaneme:
 [Titul obrázku]
[Titul obrázku] Červené štvorce ukazujú, že tento údaj ešte nepoznáme. Ale koniec koncov, koreň leží medzi 50 a 60, na ktorých sú len dve čísla končiace na 2 a 8:
[Titul obrázku]To je všetko! Zo všetkých možných koreňov sme nechali len dve možnosti! A to je v najťažšom prípade, pretože posledná číslica môže byť 5 alebo 0. A potom zostane jediným kandidátom na korene!
Záverečné výpočty
Zostali nám teda 2 čísla kandidátov. Ako viete, ktorý z nich je koreň? Odpoveď je zrejmá: odmocni obe čísla. Ten, ktorý odmocni, dá pôvodné číslo a bude odmocninou.
Napríklad pre číslo 3364 sme našli dve kandidátske čísla: 52 a 58. Odmocnime ich:
52 2 \u003d (50 +2) 2 \u003d 2500 + 2 50 2 + 4 \u003d 2704;
58 2 \u003d (60 - 2) 2 \u003d 3600 - 2 60 2 + 4 \u003d 3364.
To je všetko! Ukázalo sa, že koreň je 58! Zároveň som pre zjednodušenie výpočtov použil vzorec druhých mocnín súčtu a rozdielu. Vďaka tomu ste ani nemuseli násobiť čísla v stĺpci! Toto je ďalšia úroveň optimalizácie výpočtov, ale, samozrejme, je úplne voliteľná :)
Príklady výpočtu koreňa
Teória je dobrá, samozrejme. Poďme si to však vyskúšať v praxi.
[Titul obrázku]
Najprv zistíme, medzi ktorými číslami leží číslo 576:
400 < 576 < 900
20 2 < 576 < 30 2
Teraz sa pozrime na posledné číslo. Rovná sa 6. Kedy sa to stane? Iba ak koreň končí na 4 alebo 6. Získame dve čísla:
Zostáva odmocniť každé číslo a porovnať s originálom:
24 2 = (20 + 4) 2 = 576
Skvelé! Ukázalo sa, že prvý štvorec sa rovná pôvodnému číslu. Takže toto je koreň.
Úloha. Vypočítajte druhú odmocninu:
[Titul obrázku]
900 < 1369 < 1600;
30 2 < 1369 < 40 2;
Pozrime sa na posledné číslo:
1369 → 9;
33; 37.
Urobme to na druhú:
33 2 \u003d (30 + 3) 2 \u003d 900 + 2 30 3 + 9 \u003d 1089 ≠ 1369;
37 2 \u003d (40 - 3) 2 \u003d 1600 - 2 40 3 + 9 \u003d 1369.
Tu je odpoveď: 37.
Úloha. Vypočítajte druhú odmocninu:
[Titul obrázku]
Obmedzujeme počet:
2500 < 2704 < 3600;
50 2 < 2704 < 60 2;
Pozrime sa na posledné číslo:
2704 → 4;
52; 58.
Urobme to na druhú:
52 2 = (50 + 2) 2 = 2500 + 2 50 2 + 4 = 2704;
Dostali sme odpoveď: 52. Druhé číslo už nebude potrebné odmocňovať.
Úloha. Vypočítajte druhú odmocninu:
[Titul obrázku]
Obmedzujeme počet:
3600 < 4225 < 4900;
60 2 < 4225 < 70 2;
Pozrime sa na posledné číslo:
4225 → 5;
65.
Ako vidíte, po druhom kroku zostáva iba jedna možnosť: 65. Toto je požadovaný koreň. Ale dajme si to na druhú a skontrolujte:
65 2 = (60 + 5) 2 = 3600 + 2 60 5 + 25 = 4225;
Všetko je správne. Odpoveď zapíšeme.
Záver
Bohužiaľ, o nič lepšie. Poďme sa pozrieť na dôvody. Sú dve z nich:
- Je zakázané používať kalkulačky pri akejkoľvek bežnej matematickej skúške, či už ide o GIA alebo jednotnú štátnu skúšku. A za nosenie kalkulačky do triedy môžu byť ľahko vyhodení zo skúšky.
- Nebuďte ako hlúpi Američania. Ktoré nie sú ako korene – sú dva základné čísla nedá sa zložiť. A pri pohľade na zlomky sú vo všeobecnosti hysterické.
Študenti sa vždy pýtajú: „Prečo nemôžem na skúške z matematiky použiť kalkulačku? Ako extrahovať druhú odmocninu čísla bez kalkulačky? Skúsme si na túto otázku odpovedať.
Ako extrahovať druhú odmocninu čísla bez pomoci kalkulačky?
Akcia extrakcia druhej odmocniny opak kvadratúry.
√81= 9 9 2 =81
Ak od kladné číslo vezmite druhú odmocninu a odmocnite výsledok, dostaneme rovnaké číslo.
Z malých čísel, ktoré sú presnými druhými mocninami prirodzených čísel, napríklad 1, 4, 9, 16, 25, ..., 100, je možné získať odmocniny slovne. Zvyčajne v škole učia tabuľku druhých mocnín prirodzených čísel do dvadsať. Keď poznáte túto tabuľku, je ľahké extrahovať druhé odmocniny z čísel 121, 144, 169, 196, 225, 256, 289, 324, 361, 400. Z čísel väčších ako 400 môžete extrahovať pomocou metódy výberu pomocou niekoľkých tipov. Skúsme príklad na zváženie tejto metódy.
Príklad: Extrahujte koreň čísla 676.
Všimli sme si, že 20 2 \u003d 400 a 30 2 \u003d 900, čo znamená 20< √676 < 900.
Presné druhé mocniny prirodzených čísel končia 0; 1; 4; 5; 6; 9.
Číslo 6 je dané 4 2 a 6 2 .
Takže, ak je koreň prevzatý z 676, potom je to buď 24 alebo 26.
Zostáva skontrolovať: 24 2 = 576, 26 2 = 676.
odpoveď: √676 = 26 .
Viac príklad: √6889 .
Od 80 2 \u003d 6400 a 90 2 \u003d 8100, potom 80< √6889 < 90.
Číslo 9 je dané 3 2 a 7 2, potom √6889 je buď 83 alebo 87.
Kontrola: 83 2 = 6889.
odpoveď: √6889 = 83 .
Ak zistíte, že je to ťažké vyriešiť metódou výberu, môžete koreňový výraz rozložiť na faktor.
Napríklad, nájsť √893025.
Rozložme číslo 893025, pamätajte, že ste to robili v šiestej triede.
Získame: √893025 = √3 6 ∙5 2 ∙7 2 = 3 3 ∙5 ∙7 = 945.
Viac príklad: √20736. Rozložme číslo 20736 na faktor:

Získame √20736 = √2 8 ∙3 4 = 2 4 ∙3 2 = 144.
Faktoring si samozrejme vyžaduje znalosť kritérií deliteľnosti a faktoringové zručnosti.
A nakoniec, existuje pravidlo druhej odmocniny. Pozrime sa na toto pravidlo na príklade.
Vypočítajte √279841.
Aby sme extrahovali odmocninu z viacciferného celého čísla, rozdelili sme ho sprava doľava na plochy obsahujúce 2 číslice (v ľavej krajnej strane môže byť jedna číslica). Napíšte takto 27'98'41

Aby sme získali prvú číslicu odmocniny (5), extrahujeme druhú odmocninu najväčšieho presného štvorca obsiahnutého v prvej ľavej strane (27).
Potom sa druhá mocnina prvej číslice odmocniny (25) odčíta od prvej plochy a ďalšia plocha (98) sa pripíše (zničí) rozdielu.
Naľavo od výsledného čísla 298 napíšu dvojcifernú odmocninu (10), vydelia ňou počet všetkých desiatok predtým získaného čísla (29/2 ≈ 2), zažijú kvocient (102 ∙ 2 = 204 by nemalo byť väčšie ako 298) a napíšte (2) za prvú číslicu koreňa.
Potom sa výsledný kvocient 204 odpočíta od 298 a rozdielu (94) sa pripíše (demoluje) ďalšia fazeta (41).
Naľavo od výsledného čísla 9441 napíšu dvojitý súčin číslic odmocniny (52 ∙ 2 = 104), týmto súčinom vydelia počet všetkých desiatok čísla 9441 (944/104 ≈ 9), skúsenosť podiel (1049 ∙ 9 = 9441) by mal byť 9441 a zapísať ho (9) za druhú číslicu odmocniny.
Dostali sme odpoveď √279841 = 529.
Podobne extrahujte korene desatinných miest. Iba radikálne číslo musí byť rozdelené na tváre tak, aby bola čiarka medzi tvárami.
Príklad. Nájdite hodnotu √0,00956484.

Len si to musíte zapamätať, ak desiatkový má nepárny počet desatinných miest, neberie presne druhú odmocninu.
Takže teraz ste videli tri spôsoby, ako extrahovať koreň. Vyberte si ten, ktorý vám najviac vyhovuje a cvičte. Aby ste sa naučili riešiť problémy, musíte ich vyriešiť. A ak máte nejaké otázky, prihláste sa na moje lekcie.
stránky, s úplným alebo čiastočným kopírovaním materiálu, je potrebný odkaz na zdroj.
Plocha štvorcového pozemku je 81 dm². Nájdite jeho stranu. Predpokladajme, že dĺžka strany štvorca je X decimetre. Potom je plocha pozemku X² štvorcových decimetrov. Keďže podľa stavu je táto plocha 81 dm², tak X² = 81. Dĺžka strany štvorca je kladné číslo. Kladné číslo, ktorého druhá mocnina je 81, je číslo 9. Pri riešení úlohy bolo potrebné nájsť číslo x, ktorého druhá mocnina je 81, teda vyriešiť rovnicu X² = 81. Táto rovnica má dva korene: X 1 = 9 a X 2 \u003d - 9, pretože 9² \u003d 81 a (- 9)² \u003d 81. Obidve čísla 9 a - 9 sa nazývajú odmocniny čísla 81.
Všimnite si, že jedna odmocnina X= 9 je kladné číslo. Nazýva sa aritmetická druhá odmocnina z 81 a označuje sa √81, teda √81 = 9.
Aritmetická druhá odmocnina čísla A je nezáporné číslo, ktorého druhá mocnina sa rovná A.
Napríklad čísla 6 a -6 sú odmocniny z 36. Číslo 6 je aritmetická odmocnina z 36, pretože 6 je nezáporné číslo a 6² = 36. Číslo -6 nie je aritmetická odmocnina.
Aritmetická druhá odmocnina čísla A označené takto: √ A.
Znamienko sa nazýva aritmetická odmocnina; A sa nazýva koreňový výraz. Výraz √ Ačítať takto: aritmetická druhá odmocnina čísla A. Napríklad √36 = 6, √0 = 0, √0,49 = 0,7. V prípadoch, keď je jasné, že hovoríme o aritmetickej odmocnine, stručne hovoria: „druhá odmocnina z A«.
Akt hľadania druhej odmocniny čísla sa nazýva branie druhej odmocniny. Táto akcia je opakom kvadratúry.
Každé číslo môže byť odmocnené, ale nie každé číslo môže byť odmocninou. Napríklad nie je možné extrahovať druhú odmocninu čísla - 4. Ak takýto odmocninec existoval, potom ho označte písmenom X, dostali by sme nesprávnu rovnosť x² \u003d - 4, pretože vľavo je nezáporné číslo a vpravo záporné číslo.
Výraz √ A dáva zmysel len vtedy a ≥ 0. Definíciu druhej odmocniny možno stručne zapísať ako: √ a ≥ 0, (√A)² = A. Rovnosť (√ A)² = A platný na a ≥ 0. Aby sme sa uistili, že druhá odmocnina nezáporného čísla A rovná sa b, teda že √ A =b, musíte skontrolovať, či sú splnené nasledujúce dve podmienky: b ≥ 0, b² = A.
Druhá odmocnina zlomku
Poďme počítať. Všimnite si, že √25 = 5, √36 = 6 a skontrolujte, či platí rovnosť.
Pretože  a potom platí rovnosť. takže,
a potom platí rovnosť. takže,  .
.
Veta: Ak A≥ 0 a b> 0, to znamená, že koreň zlomku sa rovná koreňu čitateľa vydelenému odmocninou menovateľa. Je potrebné preukázať, že: a  .
.
Od √ A≥0 a √ b> 0, potom .
Vlastnosťou zvýšiť zlomok na mocninu a určiť druhú odmocninu  veta je dokázaná. Pozrime sa na pár príkladov.
veta je dokázaná. Pozrime sa na pár príkladov.
Vypočítajte podľa osvedčenej vety  .
.
Druhý príklad: Dokážte to  , Ak A ≤ 0, b < 0.
, Ak A ≤ 0, b < 0.  .
.
Ďalší príklad: Vypočítajte .
 .
.
Transformácia druhej odmocniny
Vytiahnutie multiplikátora spod znamenia koreňa. Nech je daný výraz. Ak A≥ 0 a b≥ 0, potom pomocou vety o koreni súčinu môžeme napísať:
Takáto transformácia sa nazýva vylúčenie koreňového znamienka. Zvážte príklad;
Vypočítajte pri X= 2. Priama substitúcia X= 2 v radikálnom výraze vedie ku komplikovaným výpočtom. Tieto výpočty je možné zjednodušiť, ak najprv odstránime faktory pod koreňovým znakom: . Ak teraz dosadíme x = 2, dostaneme:.
Takže, keď vyberieme faktor spod koreňového znamienka, radikálny výraz je reprezentovaný ako súčin, v ktorom jeden alebo viac faktorov sú druhé mocniny nezáporných čísel. Potom sa použije teorém koreňového produktu a vezme sa koreň každého faktora. Uvažujme o príklade: Zjednodušte výraz A = √8 + √18 - 4√2 tak, že v prvých dvoch členoch vytiahnete faktory pod znamienkom odmocniny, dostaneme:. Zdôrazňujeme, že rovnosť ![]() platí len vtedy A≥ 0 a b≥ 0. ak A < 0, то .
platí len vtedy A≥ 0 a b≥ 0. ak A < 0, то .
Koreňové vzorce. vlastnosti odmocnin.
Pozor!
Existujú ďalšie
materiál v osobitnom oddiele 555.
Pre tých, ktorí silne „nie veľmi...“
A pre tých, ktorí „veľmi...“)
V predchádzajúcej lekcii sme zistili, čo je druhá odmocnina. Je čas zistiť, čo sú vzorce pre korene, čo sú koreňové vlastnosti a čo sa s tým všetkým dá robiť.
Koreňové vzorce, koreňové vlastnosti a pravidlá pre akcie s koreňmi- je to v podstate to isté. Existuje prekvapivo málo vzorcov pre druhé odmocniny. Čo, samozrejme, poteší! Skôr sa dá napísať množstvo všelijakých vzorcov, no na praktickú a sebavedomú prácu s koreňmi stačia len tri. Všetko ostatné plynie z týchto troch. Hoci mnohí blúdia v troch vzorcoch koreňov, áno ...
Začnime tým najjednoduchším. Tu je:
Ak sa vám táto stránka páči...
Mimochodom, mám pre vás niekoľko ďalších zaujímavých stránok.)
Môžete si precvičiť riešenie príkladov a zistiť svoju úroveň. Testovanie s okamžitým overením. Učenie - so záujmom!)
môžete sa zoznámiť s funkciami a deriváciami.
Racionálne číslaNezáporná druhá odmocnina kladného čísla sa nazýva aritmetická druhá odmocnina a označuje sa pomocou radikálneho znamienka.
Komplexné čísla
Nad oborom komplexných čísel existujú vždy dve riešenia, ktoré sa líšia iba znamienkom (okrem druhej odmocniny nuly). koreň z komplexné čísločasto označované ako, toto označenie sa však musí používať opatrne. Častá chyba:
Na extrakciu druhej odmocniny komplexného čísla je vhodné použiť exponenciálny zápis komplexného čísla: ak
,kde koreň modulu sa chápe v zmysle aritmetická hodnota a k môže nadobúdať hodnoty k=0 a k=1, takže výsledkom sú dva rôzne výsledky v odpovedi.
Zovšeobecnenia
Druhé odmocniny sa zavádzajú ako riešenia rovníc tvaru a pre iné objekty: matice, funkcie, operátory atď. V tomto prípade možno použiť celkom ľubovoľné multiplikatívne operácie, napríklad superpozíciu.
Druhá odmocnina v informatike
V mnohých programovacích jazykoch na funkčnej úrovni (ako aj v značkovacích jazykoch ako LaTeX) sa funkcia druhej odmocniny označuje ako sqrt(z angličtiny. odmocnina"Odmocnina").
Algoritmy na nájdenie druhej odmocniny
Nájdenie alebo výpočet druhej odmocniny daného čísla sa nazýva extrakcia(odmocnina.
Rozšírenie Taylorovho radu
v .Aritmetická druhá odmocnina
Pre druhé mocniny čísel platia nasledujúce rovnosti:
To znamená, že môžete zistiť celú časť druhej odmocniny čísla tak, že od nej postupne odčítate všetky nepárne čísla, kým zvyšok nie je menší ako nasledujúce odpočítané číslo alebo sa rovná nule, a spočítate počet vykonaných akcií. Napríklad takto:
Vykonané 3 kroky, druhá odmocnina z 9 je 3.
Nevýhodou tejto metódy je, že ak extrahovaný koreň nie je celé číslo, potom môžete zistiť iba jeho celočíselnú časť, ale nie presnejšie. Zároveň je táto metóda celkom prístupná deťom, ktoré riešia najjednoduchšie matematické problémy vyžadujúce extrakciu druhej odmocniny.
Hrubý odhad
Mnoho algoritmov na výpočet druhej odmocniny kladného reálneho čísla S vyžadujú určitú počiatočnú hodnotu. Ak je počiatočná hodnota príliš vzdialená od skutočnej hodnoty koreňa, výpočty sa spomalia. Preto je užitočné mať hrubý odhad, ktorý môže byť veľmi nepresný, ale dá sa ľahko vypočítať. Ak S≥ 1, let D bude počet číslic S naľavo od desatinnej čiarky. Ak S < 1, пусть D bude počet po sebe idúcich núl napravo od desatinnej čiarky, braných so znamienkom mínus. Potom hrubý odhad vyzerá takto:
Ak D zvláštny, D = 2n+ 1, potom použijeme ![]() Ak D dokonca, D = 2n+ 2, potom použijeme
Ak D dokonca, D = 2n+ 2, potom použijeme ![]()
Dva a šesť sa používajú, pretože ![]() A
A
Pri práci v binárnom systéme (ako v počítačoch) by sa mal použiť iný odhad (tu D je počet binárnych číslic).
Geometrická druhá odmocnina
Na manuálne extrahovanie koreňa sa používa zápis podobný deleniu stĺpcov. Číslo, ktorého koreň hľadáme, je vypísané. Napravo od neho postupne dostaneme čísla požadovaného koreňa. Nech je koreň extrahovaný z čísla s konečným počtom desatinných miest. Na začiatok, v duchu alebo s menovkami, rozdelíme číslo N do skupín po dvoch čísliciach vľavo a vpravo od desatinnej čiarky. V prípade potreby sú skupiny doplnené nulami - celočíselná časť je doplnená vľavo, zlomková vpravo. Takže 31234.567 môže byť reprezentované ako 03 12 34 . 56 70. Na rozdiel od delenia sa demolácia vykonáva v takýchto skupinách po 2 číslach.
Vizuálny popis algoritmu: