Bölüm 1. Yaklaşık sayılar ve bunlarla ilgili işlemler
1.1 Yaklaşık hesaplamalardaki hata türleri
Bazı matematiksel problemlerin kesin çözümü klasik yöntemlerle elde edilemez veya bu çözüm bu şekilde elde edilebilir. karmaşık biçim, daha fazla pratik kullanım için kabul edilemez. Ayrıca sorunun kesin çözümü çok fazla zaman gerektirebilir. Büyük bir sayı(onlardan milyarlara kadar) eylemler. Bu gibi durumlarda yaklaşık ve sayısal çözüm yöntemlerine başvurunuz.
Bilgisayarların ortaya çıkışı, bu yöntemlerin kapsamını büyük ölçüde genişletti. Şu anda, bilgisayarı ve yaklaşık hesaplama yöntemleri olmayan bir mühendis hayal etmek zor.
Herhangi bir bilgisayarın büyük ancak sonlu sayı dizilerini ezberleyebileceğini ve bunlar üzerinde büyük ancak sınırlı bir hızla aritmetik işlemler ve karşılaştırmalar yapabileceğini unutmayın. Yani, makine çok büyük ama sınırlı sayıda işlemi gerçekleştirebilir. Bu nedenle, bir bilgisayarda çalışırken, yalnızca sonlu bir sayı kümesiyle açıklanan matematiksel modelleri kullanabilir ve yalnızca sonlu aritmetik işlem dizilerini kullanabilirsiniz.
Çeşitli fenomenlerin matematiksel modelleri, fonksiyonlar, türevler, integraller, diferansiyel denklemler vb. Bir bilgisayarda çalışırken, bu ilk modeller, işlenmesi için son eylem sırasını gösteren sonlu sayı kümeleriyle açıklananlarla değiştirilmelidir. Bunu yapmak için, işlev bir tablo ile değiştirilir, kesin integral- miktar vb. Ek olarak, bilgisayar sonlu belleğe sahiptir ve sonlu uzunluktaki sayılarla çalışabilir, bu nedenle ara sonuçlar yuvarlanır. Sonuç olarak, sonlu sayıda adıma sahip kesin bir yöntem bile yaklaşık olur.
Böylece sayısal yöntemle elde edilen çözüm yaklaşıktır.
Hataların nedenleri şunlardır:
- Matematiksel modelin çalışılan gerçek fenomenle tutarsızlığı
- İlk veri hatası.
- Çözüm yönteminin hatası.
- Sayılarla ilgili aritmetik ve diğer işlemlerde yuvarlama hataları.
İlk iki nedenden kaynaklanan karar hatası denir. ölümcül- matematikçiye bağlı değildir.
Yöntem hatası sayısal yöntem, kural olarak, orijinal sorunu değil, daha basit bir sorunu çözdüğü için ortaya çıkar. Ek olarak, genellikle sayısal yöntem, bir adımda sonlandırılması gereken sonsuz bir sürece dayanır.
Çoğu sayısal yöntem bir veya daha fazla parametreye bağlıdır. Yöntem parametrelerinin seçimi, yöntemin hatasını ayarlamanıza olanak tanır.
Yuvarlama hatasıönemli olmamalı daha fazla hata yöntem. Ve yöntemin hatasını ölümcül hatadan 2-5 kat daha az seçmeniz önerilir.
1.2 Yaklaşık sayılar
Pratikte, çoğu zaman gerçek değeri tam olarak değil, yaklaşık olarak ifade eden sayılarla uğraşmak gerekir. Böyle sayılar denir yaklaşık.
Bazı a değerlerinin tam sayısal değerini, aynı değerin yaklaşık sayısal değerini a * gösterelim. Ardından a » a * .
Tam a sayısını yaklaşık a * sayısıyla değiştirerek bir hata yaparız (hata).
Tanım 1.1. Yaklaşık a* sayısının mutlak hatası, bu sayı ile tam değeri arasındaki farkın mutlak değeridir. | a-a* |.
Miktarın tam değeri genellikle bilinmediğinden, hesaplanması imkansızdır ve mutlak hata. Ancak pozitif bir sayı belirtebilirsiniz D(a*), eşitsizliği sağlayan:
Herhangi bir numara d(a*) eşitsizliği sağlayan
(1.2) ve (1.3) eşitsizliklerini karşılayan birçok sayı olduğuna dikkat edin. Bu nedenle, marjinal hatanın değeri tam olarak kesin değildir.
Pratikte genellikle marjinal hatanın mümkün olan en küçük değeri alınır. Her yaklaşık sayı için, marjinal hatası (mutlak veya göreli) mutlaka belirlenir. Sınırlayıcı mutlak hata, a sayısının içinde bulunduğu sınırları belirlemenizi sağlar, yani.
Sınırlayıcı bağıl hata, hesaplamaların veya ölçümlerin doğruluğunu karakterize eder.
Örnekler.
1.2.1 . Problemleri çözerken tam sayı yerine p = 3.14159265... yaklaşık 3.14 değerini kullanıyoruz ve bir hata yapıyoruz:
p - 3.14 > 0.00159265
1.2.2 . Yolun uzunluğunu ölçerken, 2m hassasiyetle 25.2 km'lik bir sonuç elde edildi. Sınırlayıcı mutlak ve sınırlayıcı bağıl hataları hesaplayın.
Çözüm. Bizim durumumuzda, sınırlayıcı mutlak hata eşittir D = 0,002 km ve sınırlayıcı bağıl hata
Benzer şekilde, hesaplıyoruz
a * , a sayısının mutlak bir hata ile yaklaşık bir değeri olduğu anlamına gelir D(a*). Bir *, a sayısının göreceli bir hataya sahip yaklaşık bir değeriyse d(a*), sonra şöyle yazıyorlar:
1.4 Önemli rakamlar, doğru ve şüpheli rakamlar
Uygulamada, hatasını yalnızca en yaklaşık sayıyı kaydederek yargılamayı mümkün kılan çeşitli teknikler kullanılır.
Yaklaşık sayıların ve mutlak hataların kaydedilmesi belirli kurallara tabidir.
ondalık gösterimde önemli şahsiyet Sıfıra eşit olmayan herhangi bir rakam denir. Sıfır, anlamlı basamaklar arasında yer alıyorsa veya tüm anlamlı basamakların sağındaysa, anlamlı bir basamak olarak kabul edilir.
Örnek 1.3.1. Yaklaşık sayı 0, 38 2 anlamlı basamağı var, 0, 308 - üç, 0, 3080 - dört, 0,00 308 - üç. Anlamlı rakamlar altı çizili rakamlardır.
Tanım 1.3. anlamlı rakam denir geniş anlamda doğru sayının mutlak hatası, bu rakama karşılık gelen basamağın bir birimini geçmiyorsa.
anlamlı rakam denir dar anlamda doğru sayının mutlak hatası, bu rakama karşılık gelen basamağın biriminin yarısını geçmiyorsa.
Aksi takdirde, sayı kabul edilir şüpheli.
Mutlak (nihai mutlak) hatası belirtilmeden yaklaşık bir sayı yazılırsa, yalnızca doğru sayıları yazılır. Bu durumda, sayının sağ ucundaki gerçek sıfırlar atılmaz. 0.25 ve 0.250 sayıları yaklaşık olarak farklıdır. (1.4) veya (1.5) biçimindeki kayıtları kullanırsak, bu eşitliklerin sağ tarafındaki sayılar aynı sayıda ondalık basamakla yazılmalıdır.
Mutlak veya göreceli hata Bir veya iki anlamlı basamak içeren bir sayı olarak yazmak gelenekseldir. Bu durumda, fazlalık ile yuvarlama yapılır.
Tamsayı kısmındaki yaklaşık bir sayının, doğru işaretlerden daha anlamlı basamaklara sahip olduğu ortaya çıkabilir. Bu durumda, notasyon normalleştirilmiş biçimde a * = m 10 n kullanılırken, m ≤ 1 sayısı yalnızca geçerli rakamları içermelidir. Normalleştirilmiş gösterimde, m sayısı denir mantis, n - üs
Sınırlayıcı mutlak hatanın, ondalık noktadan sonraki ondalık basamak sayısıyla belirlendiğini unutmayın: ondalık noktadan sonra ne kadar az ondalık basamak varsa, o kadar fazla D(a*).
Sınırlayıcı bağıl hata, anlamlı basamak sayısı ile belirlenir: daha az anlamlı basamak, daha fazla d(a*).
1.5 Yuvarlama
Yaklaşık sayıları doğru sayılarla yazmak için kullanılır yuvarlama.
Kullanılan basamak sayısı sınırlıysa, tam sayıların da yuvarlanması gerekir.
Yuvarlama (tamamlayıcıya göre) Bu sayıyı daha az basamakla yazmaya aşağıdaki kurala göre numara denir: İlk atılan rakam 5'e eşit veya büyükse, kalan son rakam bir artırılır. Rakamları yuvarlarken, dikkate alınması gereken bir hata oluşur.
Tamamlayıcıya göre yuvarlama hatası mutlak değerdeki en az anlamlı basamağın biriminin yarısını aşamaz. Ortaya çıkan hata hesaplanırken, sayının orijinal mutlak hatasına yuvarlama hatası eklenmelidir.
Örnek 1.3.2. a * = 413287.51 sayısının göreli bir hatası var d(a*) = 0.01. (1.3)'den şu sonuç çıkar: D(a*)=| bir * | d(a*).
Bu nedenle, bu sayının mutlak hatası 4133'tür. Bu, a * sayısının dördüncü hanesinin zaten bir hata içerebileceği anlamına gelir. Bu nedenle, sayının yalnızca ilk iki basamağı doğrudur. Daha sonra normalleştirilmiş biçimde bu sayı şu şekilde yazılır: a * = 0.41 ·10 6 .
Benzer şekilde tartışarak, yaklaşık b * = 0.0794 sayısı d(b*) = %2 normalleştirilmiş biçimde yazın * = 0.8 10 - 1 .
Burada sayıyı yuvarlamamız gerektiğini unutmayın.
Yaklaşık sayılarla aritmetik işlemler yaparken, birbirinin tersi olan iki problem ortaya çıkar:
1. Tarafından bilinen hatalar sonucun hatasını tahmin etmek için verileri girin.
2. Sonucun belirtilen doğruluğunu sağlayan ilk verilerin doğruluğunu belirleyin.
Ek olarak, yaklaşık sayılarla çalışırken, gereksiz ve yanlış sayıları yazarak zaman kaybetmemek için çeşitli giriş verilerinin doğruluğunu uzlaştırmak gerekir.
Hesaplama sürecinde, ara sonuçların doğruluğunu izlemek de gereklidir.
Aritmetik işlemlere başlamadan önce, bu işlemlerde yer alan tüm sayıların aynı sayıda ondalık basamakla yazılması için yuvarlama yapılır. Kalan ondalık basamak sayısı, orijinal verilerdeki en küçük geçerli basamak sayısıyla belirlenir.
Ondalık noktadan sonra aynı sayıda doğru basamağa sahip yaklaşık sayılar toplanırken ve çıkarılırken yuvarlama yapılmaz.
Ondalık noktadan sonra farklı sayıda doğru basamağa sahip yaklaşık sayılar toplanırken ve çıkarılırken, sonuç, orijinal verilerdeki ondalık noktadan sonraki en küçük doğru basamak sayısına yuvarlanır.
Yaklaşık sayıları farklı sayıda doğru basamakla çarparken ve bölerken, sonuç orijinal verilerdeki minimum doğru basamak sayısına yuvarlanır.
1.6 Aritmetik hatalar
a * ve b * yaklaşık sayılar olsun, o zaman toplamları c * = a * + b * de yaklaşık bir sayıdır.
Terimlerin mutlak hatalarını belirtirsek D(a*) ve D(b*) sırasıyla, c * sayısının mutlak hatası formülle belirlenir
|
Bu nedenle, iki yaklaşık sayı eklenirken, bunların sınırlayıcı mutlak hataları eklenir.
Bu kural sonlu sayıda terim için geçerlidir. Ayrıca formül (1.6) iki sayının farkı için de geçerlidir.
Gerçekten de, iki sayının farkı bir toplam olarak temsil edilebilir.
a * - b * = a * + ( - b *),
ve sayının mutlak hatası ( -b*) b* sayısının mutlak hatasına eşittir.
Yorum Aynı işaretli iki sayı çıkarıldığında, farkın göreli hatası, her terimin göreli hatasından çok daha büyük olabilir. Birbirine yakın sayıları çıkarırken özellikle büyük bir doğruluk kaybı meydana gelir.
Örnek 1.4.1. Farkı bulmak istensin 61.32 - 61,31 .
Bu sayıların mutlak hataları sırasıyla, D1 = 0.01 ve D2 = 0.01.Şimdi bu sayıların göreli hatalarını bulalım:
Çıkarırken, 0,01 sayısı elde edilecektir (üç önemli basamakta bir kayıp olduğunu fark ettik). Mutlak hatası, terimlerin mutlak hatalarının toplamına eşittir. D1+ D2 \u003d 0.02. O zaman sonucun göreli hatası İlk verilerin hatalarını ve sonucu karşılaştırdığımızda, göreceli hatada keskin bir artış buluyoruz. Örnek 1.4.1'den. Mutlak değere yakın sayıların çıkarılmasından kaçınılması gerektiği sonucu çıkar. Bazen bu, hesaplama formülünü dönüştürerek başarılabilir. Böyle bir çıkarmadan kaçınmak mümkün değilse, önemli rakamların kaybını hesaba katarak ara hesaplamaların doğruluğunu artırmak gerekir. İki yaklaşık a * ve b * sayısını çarparken ve bölerken, hatalar formüllerle belirlenir: Böylece, yaklaşık sayıları çarparken ve bölerken, sınırlayıcı göreli hataları eklenir. Açıklama . Yaklaşık Δ (a *) sayısının mutlak hatası, bu sayının ondalık gösteriminde n'inci anlamlı basamağın ifade ettiği basamağın birimini aşmıyorsa, sınırlayıcı göreli hata için aşağıdaki eşitsizlik doğrudur: δ(a *) ≤ 1 / k 10 n - 1 nerede - sayının ilk anlamlı basamağı a * . Yaklaşık sayının mutlak hatası ise D(a*) Bu sayının ondalık gösteriminde n'inci anlamlı basamağı ile ifade edilen basamağın biriminin yarısını geçmez, sınırlayıcı göreli hata için aşağıdaki eşitsizlik doğrudur: δ(a *) ≤ 1 / 2 k 10 n − 1 burada k, a * öğesinin ilk önemli basamağıdır. İkinci durumda, tersi de doğrudur: eğer d (a *) J 1/2 (k + 1)10 n - 1 , o zaman *, n geçerli basamak içeren yaklaşık bir sayıdır. G bölgesinde sürekli türevlenebilen bir fonksiyon verilsin u \u003d f (x 1, x 2, j, x n). Fonksiyonun değerinin yaklaşık hesaplanmasındaki hatanın tahmini, sapma modülünün bir tahmini ile değiştirilir. Kesin değer argüman hatalarından kaynaklanır. Bu durumda, fonksiyonun sapması, argümanların artışlarının mutlak hatalarıyla değiştirildiği toplam diferansiyeli ile değiştirilir. Daha sonra fonksiyonun değerinin sınırlayıcı mutlak hatası, ilişki tarafından belirlenir.
d=
0,02
0,01
= 2.
D(a*b*) = | b* | D(a *) + | bir * | D(b*),
d(a*b*) = d(a*) + d(b*),
(1.7)
D(a*/b*) =
| b*|D(a*)+| a*|D(b*)| b* | 2
d(a*/b*) = d(a*) + d(b*).
1.7 İşlev hatası
Sınırlayıcı bağıl hata için, eşitliğimiz var
Formüller (1.11) kullanılarak, fonksiyon değerinin verilen doğruluğunu sağlayan argümanların doğruluğu belirlenebilir.
Örnek 1.5.1. Hassas bir şekilde ölçülmesi gerekiyor d=1% taban yarıçapları olan kesik bir koninin yan yüzey alanı r 1 » 2m, r 2" 1m, ve generatrix ben» 5m.
Yarıçapları ve generatrisi ölçmek için hangi mutlak hatayla ve geniş anlamda doğru olan kaç işaretle p sayısı alınmalıdır?
Eğer bir D(bir*) bir basamağı geçmez, n. anlamlı basamağı ile ifade edilirse, * n geçerli basamağa sahip bir sayı olarak adlandırılır. geniş anlamda.)
Çözüm. Kesik bir koninin yan yüzeyinin alanı aşağıdaki formülle hesaplanır:
S = π ben(r 1 + r 2).
Böylece, dört argümanlı bir fonksiyonumuz var. S = S(p , ben, r 1 , r 2).
Kısmi türevleri bulun ve S'ye bölün.
Formüllerden (1.11) argümanların mutlak hatalarını ifade ediyoruz:
bu sayıyı takip eder p n = 3 karakter sayısı ile alınmalıdır.
KENDİNİ KONTROL ET
Yaklaşık bir sayı a * = 1.0754327 ve bunun sınırlayıcı mutlak hatası verildiğinde D(a*)=0.0005.
Bu sayıyı doğru sayılara yuvarlayın. Yuvarlama hatasını dikkate alın.
Bir terzi mezurasıyla meridyenin çevresini, Çar Cannon'un güllesini ve tenis topunu ölçün. Hangi ölçüm en büyük bağıl hatayı verecektir?
Bir dairenin yarıçapı 0,5 cm doğrulukla ölçülürken 12 cm sayısı elde edildi. Daire alanının mutlak ve göreli hatalarını bulun.
Tamamlamak Aritmetik işlemler tüm basamakları doğru olan yaklaşık sayıların üzerinde:
130,6 + 0,255 + 1,15224 + 41,84 + 11,8216;
35.2 1.748;
Değer Belirli birimlerde bir sayı ile ifade edilebilen şeye denir. Örneğin uzunluk, alan, hacim miktarlardır. Doğruluğundan şüphe duymadığımız bir miktarın değerine kesin denir. (daha öte x tam sayıdır). Ancak genellikle uygulamada, bir miktarın değeri aranırken, yalnızca yaklaşık değeri elde edilir. (daha öte a yaklaşık bir sayıdır ). Örneğin, ölçüm yaparken fiziksel özelliklerölçü aletlerini kullanmak.
Bir miktarın kesin ve yaklaşık değerleri arasındaki farkın modülüne denir. mutlak hata
yaklaşıklık Mutlak yaklaşıklık hatasını veya hata payını sınırlayan veya mutlak
hatalar
bir numara aradı 
. Bu tür derecelendirmeler olabilir sonsuz sayı. en iyi tahmin hata payı en küçük tahmindir.
Kesin sayının kısaltması:
Mutlak yaklaşım hatasının bir miktarın tam değerinin modülüne oranına denir. göreceli hata . Pratikte, bağıl hatayı sınırlandırmak için kullanılır (göreceli hatayı tahmin etmek): . Göreceli hata genellikle % olarak ifade edilir.
daha sonra kelime seviye iner.
ÖRNEK. Mutlak ve bağıl yaklaşım hatasını bulun a=3.14 için x=π.
Biliniyor ki 3,14 <π<3,15 .
Buradan şu sonuç çıkıyor, yani.
Hesaba katıldığında 3,14 <π<3,142, o zaman en iyi tahmini alırız
Miktarın yaklaşık değerinin ondalık gösterimindeki rakam X aranan doğru geniş anlamda , mutlak yaklaşım hatası o basamağın birliğini aşmıyorsa r, bu basamağın ait olduğu (Sıfır basamak, birimlerin basamağı olarak kabul edilir, ondalık basamaklar negatif basamaklar olarak kabul edilir). başka bir kavram var dar anlamda gerçek rakam : . Gelecekte, doğru sayıları geniş anlamda ele alacağız. Kalan rakamlar denir şüpheli . Anlamlı ondalık olarak yazılan bir sayının basamaklarının tümü, sayının 0 hariç, soldaki ilkinden başlayarak doğru basamaklarıdır. Soldaki tüm sıfırlar önemsizdir. Önemli basamakların sayısıyla, yaklaşık bir sayının mutlak hatası kolayca tahmin edilebilir. Mutlak hatanın bir tahmini için, son önemli basamaktan sonra 0,5 basamak alabilirsiniz. Sınırlayıcı göreli hata, payı 1 olan bir kesre eşit alınabilir ve payda, belirli bir sayının tüm önemli basamakları kullanılarak yazılmış bir çift tam sayıdır.
ÖRNEK. a=0.065;
GÖREV 1.1. Oda hacmi V sınırlayıcı bağıl hata ile belirlenir δ İçinde kaç tane anlamlı rakam var V ?
GÖREV 1.2. yaklaşık değer olduğu bilinmektedir. a sahip n önemli rakamlar Mutlak ve bağıl hatayı tahmin edin.
Hesaplamalarla ilgili problemleri çözerken, genellikle doğru olmayan sayısal sonuçlar elde edilir, çünkü. problemin formülasyonunda ve hesaplamalar sırasında hatalar meydana gelir.
Hata kaynakları şunlardır:
1) ilk verilerdeki hatalar;
2) ara ve nihai sonuçların yuvarlama hataları;
3) sorunu çözmek için yaklaşık yöntemin hataları.
Yaklaşık sayılar üzerinde işlem yaparken şunları yapmanız gerekir:
1) ilk verilerin doğruluğunu bilmek, sonucun doğruluğunu değerlendirebilmek;
2) sonucun belirtilen doğruluğunu sağlamak için ilk verileri böyle bir doğrulukla alın.
2.1 Yaklaşık sayılardaki hatalar
x sayısı tam değer ve a sayısı da bir miktarın yaklaşık değeri olsun.
Tanım. x sayısı ile yaklaşık değeri a arasındaki fark, yaklaşık a sayısının hatası olarak adlandırılır: Δ = |x-a |.
x=10.5, a=10, sonra Δ=10.5-10=0.5 olsun.
x=9.5, a=10 olsun, sonra Δ=9.5-10=-0.5 olsun.
Tanım. x sayısı ile yaklaşık değeri a arasındaki farkın mutlak değerine, a yaklaşık sayısının mutlak hatası denir: Δа = |х-а|
x=10.5, a=10, sonra Δa=|10.5-10|=0.5 olsun.
x=9.5, a=10, sonra Δa=|9.5-10|=0.5 olsun.
Çoğu zaman tam sayı x bilinmemektedir. O zaman Δа = |х-а| bulmak imkansızdır, bu nedenle, mutlak hata tahmini kullanılır - sınırlayıcı mutlak hata Δа ≥ Δа =x-а|. Bu durumda, x sayısı sınırlar içine alınır:
a - Δ a x a + Δ a veya kısaca: x = a ± Δ a.
Okurlar: x, Δ a doğruluğu ile a'ya eşittir.
Yapılan hesaplamaların kalitesini belirlemek için ölçülen değerin mutlak hatasının ne oranda olduğunu belirlemek gerekir. Bunu yapmak için göreli hatayı kullanın.
Tanım. Yaklaşık a sayısının göreli hatası δа, mutlak hata Δа'nın x sayısının modülüne oranıdır:
veya 
.
Bağıl hata ba'nın tahmini, sınırlayıcı bağıl hatadır: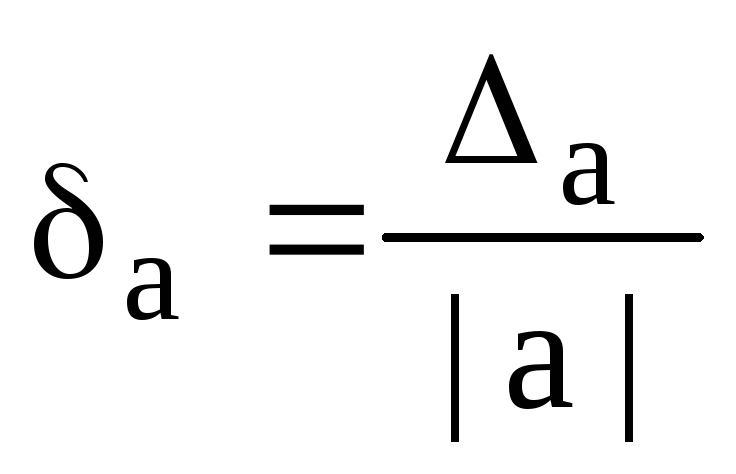 
Örnek. x=0.4287 sayısı ve yaklaşık değeri a=0.4264. a sayısının mutlak ve göreli hatalarını bulunuz.
Çözüm. a sayısının mutlak hatasını hesaplayalım:
Δa=|0.4287-0.4264| = 0.0023.
a sayısının göreli hatasını hesaplayalım:
veya %5,4.
Notlar. 1. Bir hatayı kaydederken, 1-2 anlamlı rakam bırakmak gelenekseldir. Hatalar her zaman yuvarlanır. Bu durumda, x tam sayısının sınırları genişler.
2. Eğer x sayısı bilinmiyorsa, ilgili hatayı bulmak için a sayısı kullanılır.
3. Göreceli hata, genellikle %100 ile çarpılarak yüzde olarak ifade edilir.
2.2. Yaklaşık bir sayının anlamlı ve gerçek basamakları
Yaklaşık bir a sayısının doğruluğunu değerlendirmek için, onu ondalık kesir olarak yazmak gelenekseldir. Hesaplamaların doğruluğu, ondalık basamakların sayısıyla (ondalık noktadan sonraki basamaklar) değil, sonucun geçerli anlamlı basamaklarının sayısıyla belirlenir.
Tanım. a sayısının anlamlı basamakları, ilk sıfır olmayan basamaktan önce yazılan sıfırlar ve sayının basamağını veya kesinliğini korumaya hizmet ediyorsa girişin sonundaki sıfırlar hariç, tüm basamaklarıdır.
Örnek. a'nın anlamlı rakamlarını bulunuz.
a = 0.02701 => anlamlı rakamlar: 2.7.0.1.
a = 0.0270 => anlamlı rakamlar: 2.7.0.
a = 2700 => anlamlı rakamlar: 2.7.0.0.
Tanım. Yaklaşık bir a sayısının α i basamağı, a sayısının sınırlayıcı mutlak hatası, α basamağının bir (yarım birini) geçmiyorsa, geniş anlamda (katı anlamda) gerçek bir anlamlı rakam olarak adlandırılır. i yazılır: Δ a 10 i (Δ a 0,5∙10 i).
Örnek. Mutlak hata Δ a = 0.0023 ise, yaklaşık a = 0.7264 sayısının doğru sayılarını belirleyin.
Çözüm. Mutlak hata Δ a \u003d 0,0023 0,005 \u003d 0,5 ∙ 10 -2. Bu nedenle, 7 ve 2 sayıları tam anlamıyla doğru, 6 ve 4 sayıları yanlış (şüpheli). Δ a = 0.0023 olduğundan< 0,01 = 10 -2 , то цифры 7 и 2 являются верными в широком смысле.
Notlar. 1. Matematiksel tablolarda tüm anlamlı rakamlar tam anlamıyla doğrudur.
2. Nihai sonuçta, yalnızca doğru sayıları bırakmak gelenekseldir. Daha sonra a sayısının sınırlayıcı mutlak hatası, en az anlamlı basamağın birimi tarafından belirlenir. Örneğin, tüm sayılar tam anlamıyla doğruysa a = 127,38, sonra Δ a = 0,01 ve tüm sayılar geniş anlamda doğruysa Δ a = 0,5 ∙ 0,01 = 0,005 olsun.
Örnek. Hangi eşitliğin daha doğru olduğunu belirleyin 13/19=0.684 veya 
=7,21?
Çözüm. a = 0.684, b = 7.21 olarak gösterelim. Bu sayıların mutlak hatalarını bulalım. Bunu yapmak için 13/19'u alın ve çok sayıda ondalık basamakla: 13/39=0.68421..., =7,2111...
O zaman Δ a =|0.68421...-0.684|< 0,00022, Δ в = |7,2111...-7,21| < 0,0012.
Göreli hataları bulalım:
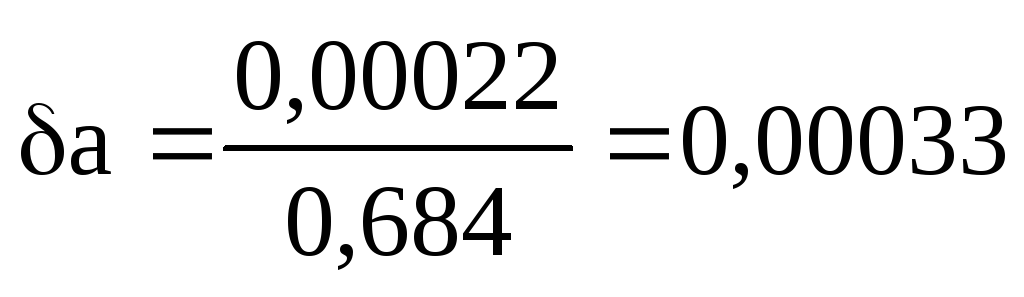veya %0.033.
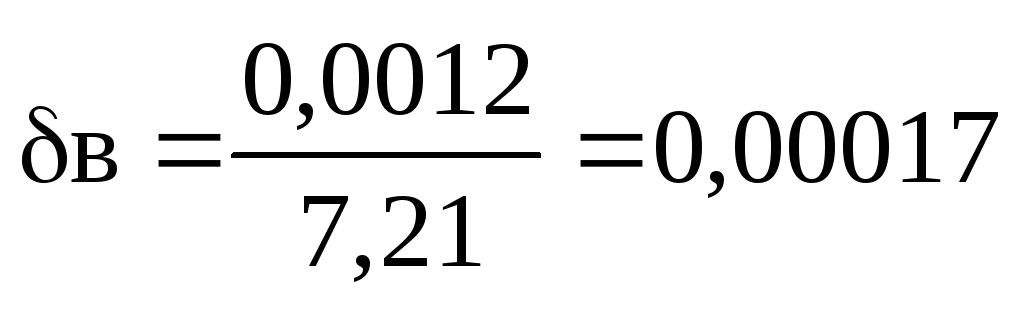veya %0.017.
İkinci denklem daha kesindir, çünkü 
.
2.3. Yuvarlama sayıları
Yaklaşık hesaplamalarda, genellikle hem yaklaşık hem de tam sayıları yuvarlamak, yani son basamaklardan bir veya daha fazlasını atmak gerekir. Bir sayıyı yuvarlarken, daha az anlamlı basamağa sahip yaklaşık bir sayı ile değiştiririz ve bu da yuvarlama hatasına neden olur. Bu hatanın minimum olması için bazı yuvarlama kurallarına uyulması gerekir.
kural ben. Atılan rakamların solundaki ilk rakam 5'ten büyükse, tutulan rakamların sonuncusu büyütülür, yani. bir artar. Amplifikasyon, atılan rakamların ilk solu 5 olduğunda ve ardından sıfır olmayan rakamlar geldiğinde de gerçekleştirilir.
Örnek. 73.473 sayısının onda birine yuvarlayarak 73.5 elde ederiz. 7 > 5 olduğu için son kalan basamak pekiştirilir.
kural II. Atılan basamaklardan ilki 5'ten küçükse, kalan basamakların sonuncusu geliştirilmez, yani değişmeden kalır.
Örnek. 73.473 sayısının yüzde birine yuvarlayarak 73.47 elde ederiz.
kuralIII. Atılan rakamların solundaki ilk rakam 5 ise ve ardından sıfır olmayan herhangi bir rakam gelmiyorsa, kalan son rakam tek ise artırılır ve çift ise değişmeden bırakılır (çift basamak kuralı).
Örnek. 5.785 sayısını yüzde bire yuvarlayarak 5.78 elde ederiz. Son kaydedilen 8 rakamı çift olduğu için amplifikasyon yapmıyoruz. 5.775 sayısını ikinci ondalık basamağa yuvarlayarak 5.78 elde ederiz. Son saklanan rakam olan 7, tek olduğu için bir artırılır.
Tek bir sayıyı yuvarlamak için Kural III'ü uygularken, aslında hesaplamaların doğruluğunu arttırmıyoruz, ancak çok sayıda yuvarlama ile, fazla sayılar, az sayılar kadar sık olur. Karşılıklı bir hata telafisi var, sonuç daha doğru.
Bu nedenle, yukarıdaki yuvarlama kurallarını uygularken, mutlak yuvarlama hatası, kalan son anlamlı basamağa göre belirlenen basamağın biriminin yarısını geçmez.
Tam sayı x, n anlamlı basamağa yuvarlanırsa, elde edilen yaklaşık a sayısı, yuvarlama hatasına eşit bir mutlak hataya sahiptir. Bu durumda, yaklaşık a sayısı dar anlamda n tane doğru anlamlı basamağa sahiptir.
Örnek. x=26.837 sayısını üç anlamlı basamağa yuvarlayarak, a =26.8 elde ederiz, buradan Δ a = |x-a | = | 26.837-26.8 |=0.037< 0,05, т. е. число а имеет три верные значащие цифры в узком смысле.
Yaklaşık a sayısını yuvarlarken, yeni bir yaklaşık sayı a 1 elde ederiz.
Tanım.Δ a1 \u003d Δ a + Δ env sayısına yuvarlama hatası denir.
a 1 sayısının mutlak hatası, orijinal sayı Δ a'nın mutlak hatası ile Δ env yuvarlama hatasının toplamıdır, yani.
Δ a1 = Δ bir + Δ env.
Örnek. x = 34.124 ± 0.021 sayısının şüpheli rakamlarını yuvarlayın. Sonucun mutlak hatasını belirleyin.
Çözüm. Yaklaşık a=34.124 sayısı dar anlamda üç doğru sayıya sahiptir: Δ a = 0.021 olduğundan 3, 4, 1< 0,05. Применяя правила округления, найдем приближенное значение а 1 , сохранив десятые доли: а 1 = 34,1. Погрешность округления Δ окр =|34,124-34,1|=0,024. Тогда абсолютная погрешность числа а 1 равна Δ а1 =Δ а +Δ окр =0,021+0,024 = 0,045 < 0,05.
Böylece, a 2 sayısının tüm önemli basamakları doğrudur (dar anlamda).
Yani x=34,1±0,045.
Bununla birlikte, (dar anlamda) n doğru anlamlı basamağa sahip yaklaşık bir a sayısını n anlamlı basamağa yuvarlarken, yuvarlatılmış a 1 sayısının geniş anlamda n tane doğru anlamlı basamağa sahip olacağı ortaya çıkabilir.
Örnek. Yaklaşık a=15.3654 (± 0.0018) sayısının dar anlamda (1, 5, 3, 6) dört doğru anlamlı rakamı vardır, çünkü Δ a = 0.0018< 0,005. При округлении до четырех значащих цифр получим а 1 = 15,37 и Δ а1 =Δ а +Δ окр =0,0018+|15,3654-15,37|=0,0064.
Açıkçası, 0.005< 0,0064 < 0,01. Следовательно, число 15,37 (± 0.0064) en geniş anlamda dört doğru basamağa sahiptir.
Yani x=15.37±0.0064.
Örnek. a = 26.7245 (± 0.0026) sayısının şüpheli rakamlarını, dar anlamda doğru işaretleri bırakarak tamamlayın. Sonucun mutlak hatasını belirleyin.
Çözüm.Δ a = 0.0026 koşuluna göre< 0,005, следовательно, в числе 26,7245 верными в узком смысле являются цифры 2, 6, 7, 2. Используя правила округления, найдем приближенное значение а 1 , сохранив сотые доли:
Ortaya çıkan hata 0,005'ten (0,005< 0,0071), поэтому уменьшим число цифр в приближенном числе до трех; а 2 = 26.7. Δ a2 = = Δ a + Δ env = 0.0026 + | 26.7245-26.7 | = 0.0271 buluyoruz< 0,05. Следовательно, оставшиеся три цифры верны в узком смысле.
Yani, x=26.7 ±0.0271 => x=26.7 ±0.03, hatayı iki ondalık basamağa yuvarlayarak.
Örnek. a = 22.7314 sayısının şüpheli basamaklarını, dar anlamda doğru işaretleri bırakarak tamamlayın. δ a = %0,2 ise sayının mutlak hatasını belirleyin.
Çözüm.δ yazıyoruz ondalık kesir biçiminde: δа=0,002 ve mutlak hatayı belirleyin. Δ a \u003d \u003d 0.0455'ten beri< 0,05, то верными в этом числе будут три цифры: 2, 2, 7. Округлим число 22,7314, сохранив в нем десятые доли: а 1 = 22.73. O zaman Δ a1 = = Δ a + Δ env = 0.0455 + | 22.7314-22.73 | = 0.0769> 0.05, bu nedenle, yaklaşık sayıdaki basamak sayısını ikiye indireceğiz: a 2 = 23. Δ a2 = = Δ a + Δ env = 0.0455 + | 22.7314-23 | = 0.3141 buluyoruz< 0,05. Следовательно, оставшиеся две цифры верны в узком смысле.
Yani x=23±0.3141 => x=23±0.32.
2.3. Yaklaşık sayılarla ilgili işlemler için kurallar
Kural 1 Birkaç yaklaşık sayının cebirsel toplamının mutlak hatası, bu sayıların mutlak hatalarının toplamına eşittir:
Δ bir ± b = Δ bir + Δ b
Kural 2 Birkaç yaklaşık sayının çarpımının göreli hatası, bu sayıların göreli hatalarının toplamına eşittir:
δ av \u003d δ bir + δ c.
Kural 3 Kısmi yaklaşık sayıların göreli hatası, bu göreli sayıların toplamına eşittir: δ a / b \u003d δ a + δ c.
Kural 4 Yaklaşık a sayısının derecesinin göreli hatası: δa n = nδ a.
Kural 5 Yaklaşık a sayısının kökünün bağıl hatası: 
.
Kural 6 Hesaplarken, katı bir hata hesaplaması yapılmazsa, sayı sayma kurallarının kullanılması önerilir. Bu kurallar, sonucun fazla basamaklı hesaplamalar olmadan mümkün olduğunca doğru olmasını sağlamak için sonuçların nasıl yuvarlanması gerektiğini belirtir.
Kurallar, üzerinde işlem yapılan sayıların yalnızca geçerli rakamlar içerdiğini ve işlem sayısının az olduğunu varsayar.
I. Yaklaşık sayıları toplarken ve çıkarırken, sonuç, en az ondalık basamağa sahip sayıda olduğu kadar ondalık basamak tutmalıdır.
II. Çarpma ve bölme yaparken, sonuç, en az anlamlı basamağa sahip sayıdaki kadar anlamlı basamağı tutmalıdır.
III. Yaklaşık bir sayıyı bir kuvvete yükseltirken, sonuç, kuvvetin tabanında olduğu kadar çok sayıda anlamlı basamak tutmak olmalıdır.
IV. Yaklaşık bir sayıdan kök çıkarırken, kök numarada olduğu kadar anlamlı basamak tutmalısınız.
V. Ara sonuçlarda, I-IV kurallarında önerilenden 1-2 basamak fazla tutmalısınız. Nihai sonuçta, sayının yuvarlanmasıyla "yedek rakamlar" atılır.
VI. Bazı kaynak veriler diğerlerinden daha fazla ondalık basamak (toplama ve çıkarma için) veya daha önemli rakamlara (diğer işlemler için) sahipse, önce bunlar yalnızca bir "güvenli rakam" tutularak yuvarlanmalıdır.
VII. N doğru basamaklı bir sonuç elde etmek için, kaynak veriler, önceki kurallara göre sonuçta N + 1 basamak sağlayacak kadar çok sayıda basamakla alınmalıdır.
Örnek. Hataları hesaba katmadan s=2.35+11.8'i bulalım. Kural I'i uygulayarak s=14.15 elde ederiz. Sonuç, en az ondalık basamaklı 11.8 sayısına yuvarlanacaktır. Şunu elde ederiz: s \u003d 14.2.
Hataları dikkate alarak sorunu çözelim. s=14.15 sayısında sadece doğru sayılar bırakılmalıdır. Bunu yapmak için, kural 1'i kullanarak toplam s'nin sınırlayıcı mutlak hatasını buluruz. 2.35 ve 11.8 sayılarındaki tüm sayıların doğru olduğu göz önüne alındığında, şunu elde ederiz: Δ 14.15 = Δ 2.35 + Δ 11.8 = 0.01 +0.1=0.11< 0,5. Последняя верная цифра в числе 14,15 находится в разряде единиц. Поэтому число s=14,15 надо округлить: s=14 и найти абсолютную погрешность округленного числа. Погрешность округления равна: |14,15-14|=0,15. Тогда абсолютная погрешность округленного числа Δ 14 =0,11+0,15=0,26 <0,5. Окончательный результат примет вид: s=14 ± 0,26.
Yaklaşık sayılar üzerinde diğer işlemler yapılırken problemler benzer şekilde çözülür.
İyi çalışmalarınızı bilgi tabanına gönderin basittir. Aşağıdaki formu kullanın
Bilgi tabanını çalışmalarında ve çalışmalarında kullanan öğrenciler, yüksek lisans öğrencileri, genç bilim adamları size çok minnettar olacaktır.
Yayınlanan http://www.allbest.ru/
Yayınlanan http://www.allbest.ru/
moskova Ekonomi Enstitüsü,yönetim ve hukuk
Öz
disipline göre:
« Daha yüksekmmatematik»
« Pyaklaşık hesaplamalar vehata tahminihakkındakalmak»
bitti: öğrenci
Yançuk Lyudmila Aleksandrovna
Bilim danışmanı Piterseva Galina Aleksandrovna
Moskova, 2000
Plan
Giriiş. Modern bilim ve teknolojide hesaplama
1. Yaklaşık değerler ve yaklaşım hataları
2. Yuvarlama sayıları. Yuvarlama hatası
Çözüm. Bilgisayar hakkında bazı bilgiler
Edebiyat
Giriiş. Modern bilim ve teknolojide hesaplama
Ölçümler ve hesaplamalar, eski çağlardan beri toplum yaşamında önemli bir rol oynamıştır. Hasadı hesaplamak, gemilerin kapasitesini ölçmek, arsaların büyüklüğünü ölçmek, büyük yapıların inşası sırasında hesaplamalar yapmak, çeşitli astronomik hesaplamalar yapmak - bu, eski zamanlarda insanların çözmesi gereken eksik bir görevler listesidir.
Son zamanların en önemli olaylarından biri, insanlığın uzayı keşfetmesi olarak kabul edilmelidir. Ay, Venüs, Mars uçuşlarını, insanlı yörünge istasyonlarının oluşturulmasını heyecanla takip ediyoruz. Geminin hareketinin tam olarak hesaplanması olmasaydı, bir uzay aracının fırlatılması düşünülemezdi ve bu, muazzam ve karmaşık bir hesaplama çalışmasını gerektirir.
Modern dönemde, bilimsel ve teknolojik devrim döneminde, matematiksel yöntemlerin rolü artmaktadır. Matematiksel yöntemler sadece fizikte değil, kimya, biyoloji, tıp, ekonomi, tarih ve dilbilimde de kullanılmaktadır.
Sanayi işletmelerinin, bilimsel enstitülerin, devlet kurumlarının, çiftliklerin ve kollektif çiftliklerin günlük, güncel faaliyetlerinde matematikçiler ve mühendisler tarafından birçok hesaplama çalışması yapılması gerekmektedir.
Hesaplamalı yöntemler artık ekonomik hesaplamalarda, bireysel bir işletmenin, bölgenin ve ülkenin tüm ekonomisinin çalışmasının planlanmasında yaygın olarak kullanılmaktadır.
Sayısal bir sonuç elde etmek için bir kişinin yeteneklerini aşan hesaplamaların gerekli olduğu birçok sorun vardır. Bir barajdaki elastik gerilmelerin hesaplanması, uçuş sırasında uçağın maruz kaldığı direncin hesaplanması veya mermilerin yörüngeleri bu tür problemlere örnektir. Düzinelerce bilgisayar mühendisi, çeşitli bilgisayarları kullanarak bu karmaşık hesaplama işini gerçekleştirir.
Bilgisayarın gelişi, bilgisayar teknolojisinde bir devrime neden oldu. Ancak matematiksel problemlerin çözümünü, sayısal sonuçlar elde etmek üzere bir bilgisayara aktarılabilecekleri aşamaya getirmek için, birçok hesap makinesinin çalışması da gereklidir. Bilgisayarların yaratılması, matematiğin kendisinin, özellikle de uygulamalı alanlarının gelişimini teşvik etti; hesaplamalar artık yardımcı değil, birçok bilimsel ve teknik başarıda ana rol oynuyor. Pratik nitelikteki herhangi bir matematiksel problemin çözümünü tamamlamanın gerekli olduğu her durumda, sayısal bir sonuç elde etmek gerekir. İlk veriler yaklaşıksa, sonucun herhangi bir doğruluk derecesini elde etmek imkansızdır. Elde edilen sayısal sonuçların pratik kullanımında, ilk verilerin doğruluğunu değerlendirebilmenin yanı sıra, sonucun hangi doğruluğuna ulaşılabileceğini ve sonucun hangi doğruluğuna ihtiyaç duyulduğunu belirleyebilmelidir. Bazı hesaplamalar çok yüksek hassasiyet gerektirirken diğerleri gerektirmez. Buradan, minimum hesaplama emeği harcaması ile gerekli doğrulukta sonuçları elde edecek şekilde hesaplamaları organize etmenin gerekli olduğu açıktır.
Bu hedefe ulaşmak için gereklidir:
yaklaşık verilerle hesaplama ilke ve kurallarını incelemek;
çeşitli sözlü hesaplama yöntemleri, matematiksel tablolar, büro hesapları, slayt kuralları, aritmometreler, yarı otomatik ve otomatik bilgisayarlar içeren mevcut araçların yardımıyla gerekli rasyonel hesaplama becerilerine hakim olmak.
1. Yaklaşık değerler ve yaklaşım hataları
Pratik faaliyetlerde, bir kişinin çeşitli miktarları ölçmesi, malzeme ve emek ürünlerini hesaba katması ve çeşitli hesaplamalar yapması gerekir. Çeşitli ölçüm, sayım ve hesaplamaların sonuçları sayılardır. Ölçüm sonucunda elde edilen sayılar, yalnızca yaklaşık olarak, belirli bir doğruluk derecesi ile istenen değerleri karakterize eder. Ölçüm cihazlarının yanlış olması, görme organlarımızın kusurlu olması nedeniyle doğru ölçümler imkansızdır ve ölçülen nesnelerin kendileri bazen değerlerini herhangi bir doğrulukla belirlememize izin vermez.
Örneğin, Süveyş Kanalı'nın uzunluğunun 160 km, Moskova'dan Leningrad'a demiryolu mesafesinin 651 km olduğu bilinmektedir. Burada bir kilometreye kadar doğrulukla yapılan ölçümlerin sonuçları var. Örneğin, dikdörtgen bir bölümün uzunluğu 29 m, genişliği 12 m ise, muhtemelen ölçümler bir metreye kadar doğrulukla yapıldı ve bir metrenin kesirleri ihmal edildi,
Herhangi bir ölçüm yapmadan önce, hangi doğrulukta yapılması gerektiğine karar vermek gerekir, yani. ölçü biriminin hangi kesirlerinin dikkate alınması ve hangilerinin ihmal edilmesi gerektiği.
bir değer varsa a, gerçek değeri bilinmeyen ve bu değerin yaklaşık değeri (yaklaşık) X, Onlar yazar a X.
Aynı miktarın farklı ölçümleri ile farklı yaklaşımlar elde edeceğiz. Bu yaklaşımların her biri ölçülen değerin gerçek değerinden farklı olacaktır, örneğin, a, diyeceğimiz bir miktar hata. Tanım. x sayısı, gerçek değeri sayıya eşit olan bir miktarın yaklaşık değeri (yaklaşık) ise a, sonra sayıların farkının modülü, a ve X aranan mutlak hata verilen yaklaşıklık ve gösterilen ax: ya da sadece a. Böylece, tanım gereği,
ax = a- x (1)
Bu tanımdan şu sonuç çıkar
a = x ax (2)
Hangi miktardan bahsettiğimiz biliniyorsa, gösterimde ax dizin a atlanır ve eşitlik (2) aşağıdaki gibi yazılır:
a = x x (3)
İstenen değerin gerçek değeri çoğu zaman bilinmediğinden, bu değerin yaklaşıklığında mutlak hatayı bulmak imkansızdır. Her özel durumda yalnızca pozitif bir sayı gösterilebilir, bu mutlak hatadan fazlası olamaz. Bu sayı, miktarın yaklaşıklığının mutlak hatasının sınırı olarak adlandırılır. a ve belirtilen h a. Böylece, eğer x yaklaşımları elde etmek için belirli bir prosedür için a değerinin keyfi bir yaklaşımıdır, o zaman
ax = a- x h a (4)
Yukarıdakilerden anlaşılacağı gibi, eğer h a miktarın yaklaşıklığının mutlak hatasının sınırıdır a, bundan büyük herhangi bir sayı h a, aynı zamanda miktarın yaklaşıklığının mutlak hatasının sınırı olacaktır. a.
Pratikte, mutlak hatanın limiti olarak eşitsizliği (4) sağlayan en küçük sayıyı seçmek gelenekseldir.
eşitsizliği çözme a- x h a anladık a sınırları içinde yer alan
x-h a a x+h a (5)
Mutlak hata sınırının daha kesin bir kavramı aşağıdaki gibi verilebilir.
İzin vermek X- birçok olası yaklaşım X miktarları a bir yaklaşım elde etmek için belirli bir prosedür için. sonra herhangi bir sayı h, koşulu sağlayan a- x h a herhangi X X, kümeden yaklaşıklıkların mutlak hatasının sınırı olarak adlandırılır. X. ile belirtmek h a bilinen en küçük sayı h. Bu numara h a ve pratikte mutlak hatanın sınırı olarak seçilir.
Mutlak yaklaşım hatası, ölçümlerin kalitesini karakterize etmez. Gerçekten de, herhangi bir uzunluğu 1 cm doğrulukla ölçersek, o zaman bir kalemin uzunluğunu belirlemeye gelince, bu zayıf bir doğruluk olacaktır. Voleybol sahasının uzunluğunu veya genişliğini 1 cm doğrulukla belirlerseniz, bu yüksek bir doğruluk olacaktır.
Ölçüm doğruluğunu karakterize etmek için bağıl hata kavramı tanıtılır.
Tanım. Eğer bir ax: mutlak bir yaklaşım hatası var X gerçek değeri sayıya eşit olan bir miktar a, sonra oran ax bir sayının modülüne X göreceli yaklaşım hatası denir ve gösterilir ax veya x.
Böylece, tanım gereği,
Göreceli hata genellikle yüzde olarak ifade edilir.
Çoğunlukla boyutsal bir nicelik olan mutlak hatanın aksine, bağıl hata boyutsuz bir niceliktir.
Pratikte, dikkate alınan göreceli hata değil, sözde bağıl hata sınırıdır: böyle bir sayı E a, istenen değerin tahmininin göreli hatasından büyük olamaz.
Böylece, ax E a.
Eğer bir h a-- miktarın yaklaşık değerlerinin mutlak hatasının sınırı a, sonra ax h a ve dolayısıyla
Açıkçası, herhangi bir sayı E koşulu sağlayan, bağıl hatanın sınırı olacaktır. Uygulamada, genellikle bazı yaklaşımlar bilinmektedir. X miktarları a ve mutlak hata sınırı. sonra numara
2. Yuvarlama sayıları. Yuvarlama hatası
Hesaplamalar yapılırken, genellikle sayıları yuvarlamak gerekir, yani. onları daha az anlamlı basamaklı sayılarla değiştirmek.
Sayıları yuvarlamanın üç yolu vardır:
Aşağı yuvarlama k th önemli basamak, ile başlayan tüm basamakları atmaktır. (k+1) th.
Yuvarlama, saklanan son basamağın bir artmasıyla aşağı yuvarlamadan farklıdır.
En küçük hatayla yuvarlama, fazlalıklı yuvarlamadan farklıdır, çünkü depolanan son basamaktan birindeki artış, yalnızca atılan basamaklardan ilki 4'ten büyükse gerçekleştirilir.
İstisna: En küçük hata ile yuvarlama sadece bir rakam 5'i atmak ise, o zaman saklanan son rakam çift ise değiştirilmez ve tek ise 1 arttırılır.
Yukarıdaki yaklaşık sayıları yuvarlama kurallarından, en küçük hatayla yuvarlamanın neden olduğu hatanın, saklanan son basamağın biriminin yarısını geçmediği ve eksik veya fazla yuvarlama yaparken hatanın yarısından fazla olabileceği sonucu çıkar. son saklanan basamağın birimi, ancak bu deşarjın tam bir biriminden fazla değil.
Aşağıdaki örneklerde buna bakalım.
1. Miktarın hatası.İzin vermek x a, de-- değerin bir tahmini b. İzin vermek X ve de-- ilgili yaklaşımların mutlak hataları X ve de. Mutlak hata sınırını bulalım h a+b miktarlar x+y toplamının bir tahmini olan a+b.
a = x + X,
b = y + y.
Bu iki eşitliği toplarsak,
a + b = x + y + x + y.
Açıkçası, yaklaşımların toplamının hatası x ve de terimlerin hatalarının toplamına eşittir, yani.
(x + y) = x + y
Toplamın modülünün, terimlerin modüllerinin toplamından küçük veya ona eşit olduğu bilinmektedir. Bu yüzden
(x + y) = x + y x + y
Bu, yaklaşımların toplamının mutlak hatasının, terimlerin mutlak hatalarının toplamını aşmadığı anlamına gelir. Bu nedenle, terimlerin mutlak hatalarının limitlerinin toplamı, toplamın mutlak hatasının limiti olarak alınabilir.
Miktarın mutlak hatasının sınırını belirtmek a vasıtasıyla h a, ve b aracılığıyla h b sahip olacak
h a + b = h a + h b
2. Fark hatası.İzin vermek X ve de-- yaklaşım hataları x ve de sırasıyla a ve b.
a = x + X,
b = y + y.
İlk eşitlikten ikinciyi çıkar,
a - b = (x - y) + ( x - y)
Açıkçası, yaklaşımlar farkının hatası, eksi ile çıkanın hataları arasındaki farka eşittir, yani.
(x - y) = x - y) ,
(x - y) = x + (- y)
Ve sonra, toplama durumundakiyle aynı şekilde tartışarak,
(x - y) = x + (- y) x + y
Farkın mutlak hatasının, eksi ve çıkarılanın mutlak hatalarının toplamını aşmadığı sonucu çıkar.
Farkın mutlak hatasının sınırı için, indirgenmiş ve çıkarılanın mutlak hatalarının sınırlarının toplamını alabilirsiniz. Böylece.
h a - b = h a + h b (9)
Formül (9)'dan, farkın mutlak hatasının sınırının, her bir yaklaşımın mutlak hatasının sınırından daha az olamayacağı sonucu çıkar. Bu, bazen hesaplamalarda kullanılan yaklaşımları çıkarma kuralını ifade eder.
Bazı büyüklüklerin yaklaşıkları olan sayıları çıkarırken, sonuç, ondalık noktadan sonraki en az basamaklı yaklaşık sayı kadar, ondalık noktadan sonraki basamak kadar olmalıdır.
3. Ürün hatası. Sayıların çarpımını düşünün X ve de, miktarların yaklaşık değerleri a ve b. ile belirtmek x yaklaşıklık hatası X, Ve aracılığıyla de-- yaklaşıklık hatası de,
a = x + X,
b = y + y.
Bu iki eşitliği çarparsak,
Mutlak ürün hatası hu eşittir
Ve bu nedenle
Elde edilen eşitsizliğin her iki tarafını da bölerek hu, alırız
Çarpım modülünün, çarpanların modülünün çarpımına eşit olduğu göz önüne alındığında,
Burada eşitsizliğin sol tarafı, ürünün göreli hatasıdır. hu, -- bağıl yaklaşım hatası X, ve göreli yaklaşım hatasıdır de. Bu nedenle, buradaki küçük değeri atarak eşitsizliği elde ederiz.
Böylece, yaklaşımların çarpımının göreli hatası, faktörlerin göreli hatalarının toplamını aşmaz. Faktörlerin nispi hatalarının limitlerinin toplamının, ürünün nispi hatasının limiti olduğu, yani.
E ab = E a + E b (10)
Formül (10)'dan, ürünün bağıl hatasının sınırının, faktörlerin en az doğru olanının göreli hatasının sınırından daha az olamayacağı sonucu çıkar. Bu nedenle, burada, önceki adımlarda olduğu gibi, faktörlerde aşırı sayıda anlamlı basamak tutmanın bir anlamı yoktur.
İş miktarını azaltmak için hesaplamalarda bazen aşağıdaki kuralı kullanmak yararlıdır: Farklı sayıda anlamlı basamaklı yaklaşımları çarparken, sonuç, en küçük anlamlı basamaklı yaklaşıklık kadar çok sayıda anlamlı basamağı tutmalıdır.
4. Bölümün hatası. Eğer bir x-- değer yaklaşımı a, kimin hatası x, a de-- değer yaklaşımı b bir hata ile y, sonra
Önce bölümün mutlak hatasını hesaplayalım:
ve ardından göreli hata:
Dikkate alınarak y karşılaştırıldığında çok az y, kesrin mutlak değeri bire eşit kabul edilebilir. O zamanlar
son formülden, bölümün göreli hatasının, bölünen ve bölenin göreli hatalarının toplamını geçmediği sonucu çıkar. Bu nedenle, bölümün göreli hatasının sınırının, temettü ve bölenin göreli hatalarının sınırlarının toplamına eşit olduğunu varsayabiliriz, yani.
5. Derece ve kök hatası. 1) İzin ver sen = a n, nerede n bir doğal sayıdır ve a x olsun. O zaman eğer E a-- bağıl yaklaşım hatasının sınırı x miktarları a, sonra
ve bu nedenle
Böylece, derecenin göreli hatasının sınırı, üssün göreli hatasının sınırının çarpımına eşittir, yani.
E sen = n E a (11)
2) Nereye n bir doğal sayıdır ve a X.
Formüle göre (11)
ve dolayısıyla
hatadan düşülebilir hesaplama
Böylece, kökün bağıl hatasının sınırı n inci derece n radikal sayının bağıl hatasının sınırından kat daha azdır.
6. Yaklaşık hesaplamaların ters problemi. Doğrudan problemde, fonksiyonun yaklaşık değerini bulmak gerekir. u=f(x, y, ...,n) argümanların verilen yaklaşık değerlerine göre
ve hata payı h a bazı işlevlerin argümanlarının hataları olarak ifade edilen
h sen = (h x, h y, …, h z) (12)
Uygulamada, genellikle, argümanların değerlerinin hangi doğrulukla verilmesi gerektiğini bulmanın gerekli olduğu bir ters problemi çözmek gerekir. x, y, …, z karşılık gelen fonksiyon değerlerini hesaplamak için sen = f(x, y, ...,z) önceden belirlenmiş doğrulukla h u .
Böylece, ters problemi çözerken aranan, fonksiyonun verilen hata limiti ile ilişkili argümanların hata limitleridir. h sen denklem (12) ve ters problemin çözümü, denklemi derlemeye ve çözmeye indirgenir h sen = (h x, h y, …, h z) Nispeten h x, h y, …, h z. Böyle bir denklemin ya sonsuz sayıda çözümü vardır ya da hiç çözümü yoktur. Böyle bir denklemin en az bir çözümü bulunursa problem çözülmüş olarak kabul edilir.
Genellikle belirsiz olan ters problemi çözmek için, bilinmeyen hataların oranlarına ek koşullar getirmek, örneğin onları eşit kabul etmek ve böylece problemi bir bilinmeyenli bir denkleme indirgemek gerekir.
Çözüm. hakkında bazı bilgilerbunları hesaplamakXnike
İlk verilerin doğruluğuna ve hesaplamaların amacına bağlı olarak çeşitli hesaplama araçları kullanılır. Birçok toplu meslekte çalışanlar, hesaplamaları büyük ölçüde kolaylaştırır ve Rus abaküsü ile çeşitli hesaplamaların üretilmesi, slayt kuralları, aritmometreler ve her türlü cep ve masaüstü elektronik hesap makineleri (mikro ve mini hesap makineleri) ile zamandan ve emekten tasarruf sağlar.
Şu anda ülkemizde bulunan mini hesap makineleri sınıfı, elektronik masaüstü hesap makinelerinin Iskra ailesini ve ayrıca çeşitli cep hesaplayıcılarını da içeren Elektronika hesap makineleri ailesini içerir. Açık nedenlerden dolayı, bu hesap makineleri eskidir, ancak yine de, bunlar yerli endüstri tarafından üretilen tek modellerdir.
Elektronika ve Iskra ailelerinin makineleri, temel olarak basit mühendislik muhasebesi ve muhasebe problemlerini 8-10 önemli rakam sırası doğruluğu ile çözmek için tasarlanmıştır. Birçoğu, temel fonksiyonların değerlerinin otomatik olarak hesaplanmasını sağlar ve program kontrolünün unsurları vardır.
Sanayimizin ve tarımımızın teknik donanımının hızla büyümesi, bilimin gelişmesiyle birlikte her türlü hesaba duyulan ihtiyaç giderek artmaktadır. Yüksek hızlı elektronik bilgisayarlar (bilgisayarlar) ile, araştırmacı, çözümleri çok fazla zaman gerektirdiğinden, daha önce ortaya bile çıkmamış olan problemleri çözebilir.
Elektronik bilgisayarlar örneğin denklemlerin sayısal çözümü için kullanılır. İlk bilgisayarlar özellikle bu tür hesaplamalar için tasarlandı.
Şu anda, bilgisayarlar teknolojik süreçleri kontrol etmek için başarıyla kullanılmaktadır. Hızlı akan bir işlemin kontrolü, bu işlem sırasında elde edilen verilere dayalı karmaşık hesaplamalar gerektiriyorsa, bilgisayar olmadan böyle bir görev genellikle imkansız olacaktır.
Edebiyat
Cebir ve analizin başlangıcı. Bölüm 1. Ed. G.N. Yakovlev. - E.: Nauka, 1981. 336 s.
Vygotsky M.Ya. Yüksek matematik el kitabı. M.: 1987.
Metrolojiye giriş. Tyurin N.I., M., Standartlar Yayınevi, 1976, 304 s.
Allbest.ru'da barındırılıyor
...Benzer Belgeler
Yaklaşık sayıların mutlak ve bağıl hatalarının belirlenmesi. Sonuçlardaki hataların tahmini. Verilerin enterpolasyonu ve ekstrapolasyonu, Lagrange ve Newton interpolasyon polinomu, temel özellikleri ve karşılaştırmalı açıklama.
laboratuvar çalışması, eklendi 08/06/2013
Mutlak ve bağıl hataların özü ve matematiksel yorumu, bunlarla birlikte değer yazma yolları. Yaklaşık değer kavramı ve yaklaşıklık hatası, bu kategorilerin analiz yönü. Ondalık sayıları yuvarlama kuralı.
özet, 13/09/2014 eklendi
Matematiksel ve uygulamalı problemlerin sayısal çözümünde ortaya çıkan ana hata türlerinin özellikleri ve özellikleri: problemler, yöntemler, yuvarlama. Ölçüm hataları kavramı ve nedenleri. Rastgele hataların açıklaması, anlar.
test, 13/01/2012 eklendi
Fiziksel bir miktarın gerçek değeri hakkındaki klasik ölçüm teorisi, ana varsayımları. İfade yöntemine göre hataların sınıflandırılması, türleri: mutlak, indirgenmiş ve bağıl. Rastgele hatalar, dağılımlarının kanunu.
özet, eklendi 07/06/2014
Belirli bir sayıyı altı, beş, dört ve üç ondalık basamağa yuvarlama. Her yuvarlamadan sonra hataların hesaplanması. a, b, c ve d işlenenlerinin tüm işaretlerinin doğru olduğu dikkate alınarak, u fonksiyonunun değerlerinin hesaplanmasında mutlak ve bağıl hatanın belirlenmesi.
deneme, 05/02/2012 eklendi
Hata belirleme yöntemlerinin araştırılması ve dağılımların istatistiksel olarak değerlendirilmesi. Rastgele bir değişkenin her değeri için bir olayın özelliğini belirleyen ampirik bir fonksiyonun oluşturulması. Belirli bir numune için hesaplamalar, analizi ve parametrelerin belirlenmesi.
dönem ödevi, eklendi 01/13/2011
Sayısal yöntemlere giriş, bir hesaplama deneyi oluşturma planı. Hesaplamaların doğruluğu, hataların sınıflandırılması. Sayısal entegrasyon ve türev yöntemlerinin gözden geçirilmesi, bir posteriori hatanın tahmini. Lineer denklem sistemlerini çözme.
eğitim kılavuzu, 23/09/2010 eklendi
Sonsuz azalan bir geometrik dizilim için dizinin elemanlarının sayısı ve değerinin belirlenmesi. Bir miktarın göreli hatasının hesaplanması. Makine sıfır ve sonsuz değerlerinin belirlenmesi. Argümana bağlı olarak hataların davranışı.
laboratuvar çalışması, eklendi 11/15/2014
Çözüm hatasının sistemin sağ tarafındaki hatalara bağımlılığının araştırılması. Belirli bir doğrulukla bir denklemin kökünü belirleme. Metotların Doğruluk Tahminlerinin Koordinatlara Göre Hesaplanması. Spline interpolasyonu ve diferansiyel denklem çözümü.
test, 26/04/2011 eklendi
Bir diferansiyel denklem için Cauchy probleminin çözümü. Yaklaşık çözümler hatası. Açık Euler yöntemini uygulayan bir işlev. Runge kuralına göre hatanın hesaplanması. İkinci mertebeden diferansiyel denklemlerin çözümü. Matris için kararlılık koşulu.