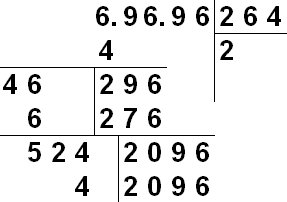Çoğu zaman, problemleri çözerken, çıkarmamız gereken büyük sayılarla karşı karşıya kalırız. Kare kök . Pek çok öğrenci bunun bir hata olduğuna karar verir ve tüm örneği çözmeye başlar. Hiçbir koşulda bu yapılmamalıdır! Bunun iki nedeni var:
- kökleri büyük sayılar aslında görevlerde ortaya çıkar. Özellikle metinde;
- Bu köklerin neredeyse sözlü olarak kabul edildiği bir algoritma var.
Bugün bu algoritmayı ele alacağız. Belki bazı şeyler size anlaşılmaz görünecektir. Ama bu derse dikkat ederseniz, en güçlü silah aykırı Karekök .
Yani algoritma:
- İstenilen kökü yukarıda ve aşağıda 10'un katları ile sınırlayın. Böylece, arama aralığını 10 sayıya indireceğiz;
- Bu 10 sayıdan kesinlikle kök olamayacakları ayıklayın. Sonuç olarak 1-2 sayı kalacak;
- Bu 1-2 sayıların karesini alın. Karesi orijinal sayıya eşit olan kök olacaktır.
Bu algoritmayı pratikte uygulamadan önce, her bir adıma bakalım.
Kök kısıtlaması
Öncelikle kökümüzün hangi sayılar arasında yer aldığını bulmamız gerekiyor. Sayıların onun katı olması çok arzu edilir:
10 2 = 100;
20 2 = 400;
30 2 = 900;
40 2 = 1600;
...
90 2 = 8100;
100 2 = 10 000.
Bir dizi sayı alıyoruz:
100; 400; 900; 1600; 2500; 3600; 4900; 6400; 8100; 10 000.
Bu rakamlar bize ne veriyor? Çok basit: sınırlar elde ederiz. Örneğin 1296 sayısını ele alalım. 900 ile 1600 arasındadır. Bu nedenle kökü 30'dan küçük ve 40'tan büyük olamaz:
[Şekil yazısı]
Aynısı, karekökü bulabileceğiniz diğer tüm sayılar için de geçerlidir. Örneğin, 3364:
[Şekil yazısı]Böylece anlaşılmaz bir sayı yerine orijinal kökün bulunduğu çok özel bir aralık elde ederiz. Aramanın kapsamını daha da daraltmak için ikinci adıma geçin.
Açıkça gereksiz sayıların ortadan kaldırılması
Yani, 10 numaramız var - kök için adaylar. Onları bir sütunda karmaşık düşünme ve çarpma olmadan çok hızlı bir şekilde aldık. Devam etme zamanı.
İster inanın ister inanmayın, şimdi aday sayısını ikiye indireceğiz - ve yine karmaşık hesaplamalar olmadan! Özel kuralı bilmek yeterlidir. İşte burada:
Karenin son basamağı yalnızca son basamağa bağlıdır orijinal numara.
Başka bir deyişle, sadece bakın son rakam kare - ve orijinal sayının nerede bittiğini hemen anlayacağız.
Son sırada olabilecek sadece 10 hane vardır. Kareleri alındığında neye dönüştüklerini bulmaya çalışalım. Tabloya bir göz atın:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 |
| 1 | 4 | 9 | 6 | 5 | 6 | 9 | 4 | 1 | 0 |
Bu tablo kökü hesaplamaya yönelik başka bir adımdır. Gördüğünüz gibi, ikinci satırdaki sayıların beşe göre simetrik olduğu ortaya çıktı. Örneğin:
2 2 = 4;
8 2 = 64 → 4.
Gördüğünüz gibi, her iki durumda da son rakam aynıdır. Ve bu, örneğin 3364'ün kökünün zorunlu olarak 2 veya 8 ile bittiği anlamına gelir. Öte yandan, önceki paragraftaki kısıtlamayı hatırlıyoruz. Biz:
 [Şekil yazısı]
[Şekil yazısı] Kırmızı kareler bu rakamı henüz bilmediğimizi gösteriyor. Ancak kök 50 ile 60 arasında yer alır ve üzerinde 2 ve 8 ile biten yalnızca iki sayı vardır:
[Şekil yazısı]Bu kadar! Tüm olası köklerden sadece iki seçenek bıraktık! Ve bu en zor durumda çünkü son basamak 5 veya 0 olabilir. Ve sonra kökler için tek aday kalacak!
Son Hesaplamalar
Yani 2 aday sayımız kaldı. Hangisinin kök olduğunu nasıl anlarsınız? Cevap açık: her iki sayının da karesini alın. Karesi olan orijinal sayıyı verecek ve kök olacaktır.
Örneğin 3364 sayısı için iki aday sayı bulduk: 52 ve 58. Karelerini alalım:
52 2 \u003d (50 +2) 2 \u003d 2500 + 2 50 2 + 4 \u003d 2704;
58 2 \u003d (60 - 2) 2 \u003d 3600 - 2 60 2 + 4 \u003d 3364.
Bu kadar! Kökün 58 olduğu ortaya çıktı! Aynı zamanda hesaplamaları basitleştirmek için toplamın ve farkın karelerinin formülünü kullandım. Bu sayede bir sütundaki sayıları çarpmanıza bile gerek kalmadı! Bu, hesaplamaların başka bir optimizasyon düzeyidir, ancak elbette tamamen isteğe bağlıdır :)
Kök Hesaplama Örnekleri
Teori elbette iyidir. Ama pratikte test edelim.
[Şekil yazısı]
Öncelikle 576 sayısının hangi sayılar arasında olduğunu bulalım:
400 < 576 < 900
20 2 < 576 < 30 2
Şimdi son sayıya bakalım. 6'ya eşittir. Bu ne zaman olur? Yalnızca kök 4 veya 6 ile bitiyorsa. İki sayı elde ederiz:
Her sayının karesini almak ve orijinaliyle karşılaştırmak kalır:
24 2 = (20 + 4) 2 = 576
Harika! İlk karenin orijinal sayıya eşit olduğu ortaya çıktı. Yani bu kök.
Görev. Karekökü hesaplayın:
[Şekil yazısı]
900 < 1369 < 1600;
30 2 < 1369 < 40 2;
Son sayıya bakalım:
1369 → 9;
33; 37.
Karesini alalım:
33 2 \u003d (30 + 3) 2 \u003d 900 + 2 30 3 + 9 \u003d 1089 ≠ 1369;
37 2 \u003d (40 - 3) 2 \u003d 1600 - 2 40 3 + 9 \u003d 1369.
İşte cevap: 37.
Görev. Karekökü hesaplayın:
[Şekil yazısı]
Sayıyı sınırlıyoruz:
2500 < 2704 < 3600;
50 2 < 2704 < 60 2;
Son sayıya bakalım:
2704 → 4;
52; 58.
Karesini alalım:
52 2 = (50 + 2) 2 = 2500 + 2 50 2 + 4 = 2704;
Cevabı aldık: 52. Artık ikinci sayının karesini almanıza gerek kalmayacak.
Görev. Karekökü hesaplayın:
[Şekil yazısı]
Sayıyı sınırlıyoruz:
3600 < 4225 < 4900;
60 2 < 4225 < 70 2;
Son sayıya bakalım:
4225 → 5;
65.
Gördüğünüz gibi ikinci adımdan sonra geriye sadece bir seçenek kalıyor: 65. Bu istenen kök. Ama yine de karesini alalım ve kontrol edelim:
65 2 = (60 + 5) 2 = 3600 + 2 60 5 + 25 = 4225;
Her şey doğru. Cevabı yazıyoruz.
Çözüm
Ne yazık ki, daha iyisi yok. Nedenlerine bir göz atalım. İki tane var:
- İster GIA ister Birleşik Devlet Sınavı olsun, herhangi bir normal matematik sınavında hesap makinesi kullanmak yasaktır. Ve sınıfa hesap makinesi taşıdıkları için kolayca sınavdan atılabilirler.
- Aptal Amerikalılar gibi olmayın. Hangisi kök gibi değildir - onlar ikidir asal sayılar katlanamaz. Ve kesirleri görünce genellikle histerikleşirler.
Öğrenciler her zaman şunu sorar: “Matematik sınavında neden hesap makinesi kullanamıyorum? Hesap makinesi olmadan bir sayının karekökü nasıl çıkarılır? Bu soruyu cevaplamaya çalışalım.
Hesap makinesinin yardımı olmadan bir sayının karekökü nasıl çıkarılır?
Aksiyon karekök çıkarma kare almanın tersi.
√81= 9 9 2 =81
Eğer pozitif sayı sonucun karekökünü alıp karesini alırsak aynı sayıyı elde ederiz.
Doğal sayıların tam kareleri olan küçük sayılardan, örneğin 1, 4, 9, 16, 25, ..., 100, sözel olarak karekökler alınabilir. Genellikle okulda yirmiye kadar doğal sayılardan oluşan bir kareler tablosu öğretilir. Bu tabloyu bilerek 121,144, 169, 196, 225, 256, 289, 324, 361, 400 sayılarından karekök çıkarmak kolaydır. 400'den büyük sayılardan bazı ipuçlarını kullanarak seçim yöntemini kullanarak çıkarabilirsiniz. Bu yöntemi ele almak için bir örnek deneyelim.
Örnek: 676 sayısının kökünü çıkarın.
20 2 \u003d 400 ve 30 2 \u003d 900'ün 20 anlamına geldiğini fark ettik.< √676 < 900.
Doğal sayıların tam kareleri 0 ile biter; 1; 4; 5; 6; 9.
6 sayısı 4 2 ve 6 2 tarafından verilir.
Yani, kök 676'dan alınırsa, o zaman ya 24 ya da 26'dır.
Kontrol etmek için kalır: 24 2 = 576, 26 2 = 676.
Cevap: √676 = 26 .
Daha örnek: √6889 .
80 2 \u003d 6400 ve 90 2 \u003d 8100 olduğundan, 80< √6889 < 90.
9 sayısı 3 2 ve 7 2 ile verilir, bu durumda √6889 83 veya 87'dir.
Kontrol edin: 83 2 = 6889.
Cevap: √6889 = 83 .
Seçim yöntemiyle çözmeyi zor bulursanız, kök ifadeyi çarpanlara ayırabilirsiniz.
Örneğin, √893025'i bul.
893025 sayısını çarpanlarına ayıralım, unutmayın altıncı sınıfta yapmıştınız.
Şunu elde ederiz: √893025 = √3 6 ∙5 2 ∙7 2 = 3 3 ∙5 ∙7 = 945.
Daha örnek: √20736. 20736 sayısını çarpanlarına ayıralım:

√20736 = √2 8 ∙3 4 = 2 4 ∙3 2 = 144 elde ederiz.
Elbette faktoring, bölünebilme kriterleri hakkında bilgi ve faktoring becerisi gerektirir.
Ve son olarak, var karekök kuralı. Bu kuralı bir örnekle inceleyelim.
Hesapla √279841.
Çok basamaklı bir tam sayının kökünü çıkarmak için, onu sağdan sola her biri 2 basamak içeren yüzlere böleriz (sol uç yüzde bir basamak olabilir). Böyle yaz 27'98'41

Kökün (5) ilk basamağını elde etmek için, ilk sol yüzde (27) bulunan en büyük tam karenin karekökünü alırız.
Daha sonra kökün (25) ilk basamağının karesi birinci yüzden çıkarılır ve sonraki yüz (98) farka atfedilir (yıkılır).
Ortaya çıkan 298 sayısının soluna, kökün (10) çift hanesini yazarlar, daha önce elde edilen sayının onluk sayısını (29/2 ≈ 2) bölerler, bölümü deneyimlerler (102 ∙ 2 = 204, 298'den büyük olmamalıdır) ve kökün ilk basamağından sonra (2) yazınız.
Daha sonra ortaya çıkan bölüm 204, 298'den çıkarılır ve sonraki yön (41) farka (94) atfedilir (yıkılır).
Ortaya çıkan 9441 sayısının soluna, kök rakamlarının çift çarpımını yazarlar (52 ∙ 2 = 104), 9441 sayısının onluklarının sayısını bu ürüne bölün (944/104 ≈ 9), deneyim bölüm (1049 ∙ 9 = 9441) 9441 olmalı ve kökün ikinci basamağından sonra (9) yazılmalıdır.
√279841 = 529 cevabını aldık.
Benzer şekilde ayıklayın ondalık sayıların kökleri. Virgül yüzler arasında olacak şekilde sadece kök sayı yüzlere bölünmelidir.
Örnek. √0.00956484 değerini bulun.

Sadece şunu hatırlamalısın, eğer ondalık tek sayıda ondalık basamak vardır, tam olarak karekök almaz.
Şimdi kökü çıkarmanın üç yolunu gördünüz. Size en uygun olanı seçin ve uygulayın. Sorunları nasıl çözeceğinizi öğrenmek için onları çözmeniz gerekir. Herhangi bir sorunuz varsa, derslerime kaydolun.
site, malzemenin tamamen veya kısmen kopyalanmasıyla, kaynağa bir bağlantı gereklidir.
Kare bir arsanın alanı 81 dm²'dir. Onun tarafını bul. Diyelim ki karenin bir kenarının uzunluğu X desimetre. O zaman arsanın alanı X² desimetrekare. Duruma göre bu alan 81 dm² olduğuna göre, X² = 81. Karenin kenar uzunluğu pozitif bir sayıdır. Karesi 81 olan pozitif bir sayı 9 sayısıdır. Problemi çözerken karesi 81 olan x sayısını bulmak yani denklemi çözmek istenmiştir. X² = 81. Bu denklemin iki kökü vardır: X 1 = 9 ve X 2 \u003d - 9, çünkü 9² \u003d 81 ve (- 9)² \u003d 81. Hem 9 hem de - 9 sayılarına 81 sayısının karekökleri denir.
Dikkat edin, kareköklerden biri X= 9 pozitif bir sayıdır. 81'in aritmetik karekökü olarak adlandırılır ve √81 ile gösterilir, dolayısıyla √81 = 9'dur.
Bir sayının aritmetik karekökü A karesi eşit olan negatif olmayan bir sayıdır A.
Örneğin, 6 ve -6 sayıları 36'nın kareköküdür. 6 sayısı 36'nın aritmetik kareköküdür, çünkü 6 negatif olmayan bir sayıdır ve 6² = 36'dır. -6 sayısı aritmetik kök değildir.
Bir sayının aritmetik karekökü A aşağıdaki gibi gösterilir: √ A.
İşarete aritmetik karekök işareti denir; A kök ifadesi denir. İfade √ A Okumak bunun gibi: bir sayının aritmetik karekökü A.Örneğin, √36 = 6, √0 = 0, √0,49 = 0,7. Bir aritmetik kökten bahsettiğimizin açık olduğu durumlarda kısaca şöyle derler: "kökün karekökü A«.
Bir sayının karekökünü bulma işlemine karekök alma denir. Bu eylem, kare almanın tersidir.
Herhangi bir sayının karesi alınabilir, ancak her sayının karekökü olamaz. Örneğin, - 4 sayısının karekökünü çıkarmak imkansızdır. Eğer böyle bir kök varsa, o zaman onu harfle belirtmek X, solda negatif olmayan bir sayı ve sağda negatif bir sayı olduğu için yanlış x² \u003d - 4 eşitliğini alırdık.
İfade √ A sadece ne zaman mantıklı bir ≥ 0. Karekökün tanımı kısaca şu şekilde yazılabilir: √ bir ≥ 0, (√A)² = A. Eşitlik (√ A)² = AŞunun için geçerli bir ≥ 0. Böylece, negatif olmayan bir sayının karekökünün olduğundan emin olmak için A eşittir B, yani bu √ A =B, aşağıdaki iki koşulun karşılanıp karşılanmadığını kontrol etmeniz gerekir: b ≥ 0, B² = A.
Bir kesrin karekökü
Hesaplayalım. √25 = 5, √36 = 6 olduğuna dikkat edin ve eşitliğin sağlanıp sağlanmadığını kontrol edin.
Çünkü  ve , o zaman eşitlik doğrudur. Bu yüzden,
ve , o zaman eşitlik doğrudur. Bu yüzden,  .
.
teorem: Eğer A≥ 0 ve B> 0, yani kesrin kökü, payın kökü bölü paydanın köküne eşittir. Aşağıdakileri kanıtlamak gerekir: ve  .
.
√'den beri A≥0 ve √ B> 0, ardından .
Bir kesri bir kuvvete yükseltme ve karekökü belirleme özelliği ile  teorem kanıtlanmıştır. Birkaç örneğe bakalım.
teorem kanıtlanmıştır. Birkaç örneğe bakalım.
Kanıtlanmış teoreme göre hesaplayın  .
.
İkinci örnek: Bunu kanıtlayın  , Eğer A ≤ 0, B < 0.
, Eğer A ≤ 0, B < 0.  .
.
Başka bir örnek: Hesapla .
 .
.
Karekök dönüşümü
Çarpanı kökün işaretinin altından çıkarmak. Bir ifade verilsin. Eğer A≥ 0 ve B≥ 0, o zaman çarpımın köküne ilişkin teorem ile şunu yazabiliriz:
Böyle bir dönüşüme kök işaretinin çarpanlarına ayrılması denir. Bir örnek düşünün;
hesapla X= 2. Doğrudan ikame X= 2 radikal ifadesinde karmaşık hesaplamalara yol açar. Bu hesaplamalar, önce kök işaretinin altındaki faktörleri kaldırırsak basitleştirilebilir: . Şimdi x = 2'yi yerine koyarsak: elde ederiz.
Bu nedenle, kök işaretinin altından çarpanı çıkarırken, kök ifadesi, bir veya daha fazla çarpanın negatif olmayan sayıların kareleri olduğu bir çarpım olarak temsil edilir. Daha sonra kök çarpım teoremi uygulanır ve her faktörün kökü alınır. Bir örnek ele alalım: A = √8 + √18 - 4√2 ifadesini ilk iki terimde kök işaretinin altındaki çarpanları çıkararak sadeleştirirsek şunu elde ederiz:. eşitliği vurguluyoruz. ![]() sadece ne zaman geçerlidir A≥ 0 ve B≥ 0. eğer A < 0, то .
sadece ne zaman geçerlidir A≥ 0 ve B≥ 0. eğer A < 0, то .
Kök formüller. kareköklerin özellikleri.
Dikkat!
ek var
Özel Bölüm 555'teki malzeme.
Kesinlikle "çok değil ..." olanlar için
Ve "çok fazla..." olanlar için)
Bir önceki derste karekökün ne olduğunu bulmuştuk. ne olduğunu anlamanın zamanı geldi kökler için formüller, neler kök özellikleri ve tüm bunlar hakkında ne yapılabilir?
Kök Formülleri, Kök Özellikleri ve Köklü İşlemler İçin Kurallar- temelde aynı şey. Karekökler için şaşırtıcı derecede az sayıda formül vardır. Hangisi, elbette memnun! Aksine, her türden pek çok formül yazabilirsiniz, ancak köklerle pratik ve kendinden emin çalışma için yalnızca üçü yeterlidir. Diğer her şey bu üçünden akar. Köklerin üç formülünde başıboş olsa da, evet ...
En basitinden başlayalım. İşte burada:
Bu siteyi beğendiyseniz...
Bu arada, sizin için birkaç ilginç sitem daha var.)
Örnek çözme alıştırmaları yapabilir ve seviyenizi öğrenebilirsiniz. Anında doğrulama ile test etme. Öğrenmek - ilgiyle!)
fonksiyonlar ve türevler hakkında bilgi sahibi olabilirsiniz.
Rasyonel sayılarPozitif bir sayının negatif olmayan kareköküne ne ad verilir? aritmetik karekök ve kök işareti kullanılarak gösterilir.
Karışık sayılar
Karmaşık sayılar alanı üzerinde, her zaman yalnızca işaret bakımından farklı olan (sıfırın karekökü hariç) iki çözüm vardır. in kökü karmaşık sayı genellikle olarak belirtilir, ancak bu atama dikkatle kullanılmalıdır. Yaygın hata:
Karmaşık bir sayının karekökünü çıkarmak için, karmaşık sayının üstel gösterimini kullanmak uygundur:
,modülün kökü anlamında anlaşıldığı yer aritmetik değer, ve k k=0 ve k=1 değerlerini alabilir yani cevapta iki farklı sonuç olur.
genellemeler
Karekökler, formun denklemlerine ve diğer nesnelere çözümler olarak sunulur: matrisler, fonksiyonlar, operatörler, vb. Bu durumda, örneğin süperpozisyon gibi oldukça keyfi çarpma işlemleri kullanılabilir.
Bilgisayar biliminde karekök
İşlevsel düzeydeki birçok programlama dilinde (LaTeX gibi biçimlendirme dillerinin yanı sıra), karekök işlevi şu şekilde gösterilir: sqrt(İngilizceden. kare kök"Kare kök").
Karekökü bulmak için algoritmalar
Verilen bir sayının karekökünü bulma veya hesaplama işlemine ne ad verilir? çıkarma(kare kök.
Taylor serisi açılımı
.aritmetik karekök
Sayıların kareleri için aşağıdaki eşitlikler doğrudur:
Yani, bir sayının karekökünün tamsayı kısmını, kalan bir sonraki çıkarılan sayıdan küçük veya sıfıra eşit olana kadar tüm tek sayıları ondan sırayla çıkararak ve gerçekleştirilen eylemlerin sayısını sayarak öğrenebilirsiniz. Örneğin, bunun gibi:
3 adım gerçekleştirilen, 9'un karekökü 3'tür.
Bu yöntemin dezavantajı, çıkarılan kök bir tamsayı değilse, o zaman yalnızca tamsayı kısmını bulabilmeniz, ancak daha doğru bir şekilde öğrenememenizdir. Aynı zamanda, bu yöntem, bir karekökün çıkarılmasını gerektiren en basit matematik problemlerini çözen çocuklar için oldukça erişilebilirdir.
Kabaca tahmin
Pozitif bir gerçek sayının kareköklerini hesaplamak için birçok algoritma S bazı başlangıç değerleri gerektirir. Başlangıç değeri kökün gerçek değerinden çok uzaksa hesaplamalar yavaşlar. Bu nedenle, çok yanlış olabilen ancak hesaplaması kolay olan kaba bir tahmine sahip olmak faydalıdır. Eğer S≥ 1, izin ver D basamak sayısı olacak S ondalık noktanın solunda. Eğer S < 1, пусть D eksi işaretiyle alınan ondalık virgülün sağındaki ardışık sıfırların sayısı olacaktır. O zaman kabaca bir tahmin şuna benzer:
Eğer D garip, D = 2N+ 1, sonra kullanırız ![]() Eğer D eşit, D = 2N+ 2, sonra kullanırız
Eğer D eşit, D = 2N+ 2, sonra kullanırız ![]()
İki ve altı kullanılır çünkü ![]() Ve
Ve
İkili bir sistemde çalışırken (bilgisayarların içindeki gibi), farklı bir tahmin kullanılmalıdır (burada D ikili basamak sayısıdır).
geometrik karekök
Kökü manuel olarak çıkarmak için, sütun bölmesine benzer bir notasyon kullanılır. Kökünü aradığımız sayı yazılır. Sağında, istenen kökün numaralarını yavaş yavaş alacağız. Kök, sonlu sayıda ondalık basamaklı bir sayıdan çıkarılsın. Başlamak için, zihinsel olarak veya etiketlerle, N sayısını ondalık noktanın solunda ve sağında iki basamaklı gruplara ayırırız. Gerekirse, gruplar sıfırlarla doldurulur - tamsayı kısmı solda, kesirli kısım sağda doldurulur. Böylece 31234.567, 03 12 34 olarak gösterilebilir. 56 70. Bölmeden farklı olarak yıkım 2 haneli gruplar halinde yapılır.
Algoritmanın görsel açıklaması: