قسمة رقم عادي على عدد عشري. القسمة العشرية

§ 107. إضافة الكسور العشرية.

تتم عملية جمع الكسور العشرية بنفس طريقة جمع الأعداد الصحيحة. دعونا نرى هذا مع الأمثلة.

1) 0.132 + 2.354. دعونا نوقع الشروط أحدهما تحت الآخر.

هنا ، من إضافة 2 من الألف إلى 4 آلاف ، تم الحصول على 6 آلاف ؛
من إضافة ثلاث مائة بخمس مائة تحولت إلى ثمان مائة ؛
من جمع 1 على 3 أعشار و 4 أعشار و
من إضافة 0 أعداد صحيحة مع 2 أعداد صحيحة - 2 أعداد صحيحة.

2) 5,065 + 7,83.

لا يوجد جزء من الألف في المصطلح الثاني ، لذلك من المهم عدم ارتكاب أخطاء عند التوقيع على الشروط تحت بعضها البعض.

3) 1,2357 + 0,469 + 2,08 + 3,90701.

هنا ، عند جمع جزء من الألف ، نحصل على 21 جزءًا من الألف ؛ كتبنا 1 تحت جزء من الألف ، و 2 مضافًا إلى جزء من مائة ، لذلك في خانة المائة حصلنا على المصطلحات التالية: 2 + 3 + 6 + 8 + 0 ؛ باختصار ، يعطون 19 جزءًا من مائة ، ووقعنا على 9 أقل من مائة ، و 1 تم حسابه على أنه أعشار ، إلخ.

وبالتالي ، عند إضافة الكسور العشرية ، يجب مراعاة الترتيب التالي: يتم وضع علامة على الكسور واحدة تحت الأخرى بحيث تكون جميع الأرقام نفسها تحت بعضها البعض وجميع الفواصل في نفس العمود الرأسي ؛ على يمين المنازل العشرية لبعض المصطلحات ، ينسبون ، على الأقل عقليًا ، عددًا من الأصفار بحيث تحتوي جميع المصطلحات بعد الفاصلة العشرية على نفس عدد الأرقام. ثم قم بإجراء الجمع بالأرقام ، بدءًا من الجانب الأيمن، وفي المقدار الناتج ضع فاصلة في نفس العمود الرأسي الذي توجد فيه بهذه الشروط.

§ 108. طرح الكسور العشرية.

يتم طرح الكسور العشرية بنفس طريقة طرح الأعداد الصحيحة. دعنا نظهر هذا مع الأمثلة.

1) 9.87 - 7.32. دعنا نوقع المطروح أسفل المصغر بحيث تكون الوحدات من نفس الرقم تحت بعضها البعض:

2) 16.29 - 4.75. دعنا نوقع المطروح تحت الحد الأدنى ، كما في المثال الأول:

لطرح أعشار ، كان على المرء أن يأخذ وحدة كاملة من 6 ويقسمها إلى أجزاء من عشرة.

3) 14.0213-5.350712. دعنا نوقع المطروح تحت الحد الأدنى:

تم إجراء الطرح على النحو التالي: نظرًا لأنه لا يمكننا طرح 2 من المليون من 0 ، يجب أن نشير إلى أقرب رقم إلى اليسار ، أي إلى مائة من الألف ، ولكن هناك أيضًا صفر بدلاً من مائة من الألف ، لذلك نأخذ 1 عشرة آلاف من ثلاثة إلى عشرة آلاف ونقسمها إلى مائة ألف ، نحصل على 10 مائة ألف ، منها 9 مائة ألف تبقى في فئة مائة ألف ، ومئة ألف سحق إلى جزء من المليون ، نحصل على 10 مليون. وهكذا ، في الأرقام الثلاثة الأخيرة ، حصلنا على: 10 من المليون ، ومئات من المئات من الألف ، وعشرة آلاف من 2. لمزيد من الوضوح والراحة (دون أن ننسى) ، تمت كتابة هذه الأرقام أعلى الكسور الكسرية المقابلة للمختصر. الآن يمكننا البدء في الطرح. نطرح 2 من المليون من 10 من المليون ، ونحصل على 8 من المليون ؛ اطرح مائة ألف من 9 مائة ألف ، نحصل على 8 مائة ألف ، إلخ.

وبالتالي ، عند طرح الكسور العشرية ، يتم ملاحظة الترتيب التالي: يتم توقيع المخصوم أسفل الرقم المصغر بحيث تكون نفس الأرقام واحدة تحت الأخرى وتكون جميع الفواصل في نفس العمود الرأسي ؛ على اليمين ، ينسبون ، على الأقل عقليًا ، عددًا كبيرًا من الأصفار مخفضة أو مطروحة بحيث يكون لديهم نفس عدد الأرقام ، ثم يطرحون بالأرقام ، بدءًا من الجانب الأيمن ، وفي الفرق الناتج ضع فاصلة في نفس العمود الرأسي الذي يتم فيه تقليله وطرحه.

109. ضرب الكسور العشرية.

ضع في اعتبارك بعض الأمثلة على ضرب الكسور العشرية.

لإيجاد حاصل ضرب هذه الأرقام ، يمكننا أن نفكر على النحو التالي: إذا زاد العامل بمقدار 10 مرات ، فسيكون كلا العاملين عددًا صحيحًا ويمكننا بعد ذلك ضربهما وفقًا لقواعد ضرب الأعداد الصحيحة. لكننا نعلم أنه عند زيادة أحد العوامل عدة مرات ، يزيد المنتج بنفس المقدار. هذا يعني أن الرقم الذي سيتم الحصول عليه من ضرب عوامل الأعداد الصحيحة ، أي 28 في 23 ، هو 10 مرات أكبر من المنتج الحقيقي ، ومن أجل الحصول على عمل حقيقي، تحتاج إلى تقليل المنتج الذي تم العثور عليه بمقدار 10 مرات. لذلك ، عليك هنا إجراء عملية الضرب على 10 مرة والقسمة على 10 مرة واحدة ، ولكن يتم تنفيذ الضرب والقسمة على 10 عن طريق تحريك الفاصلة إلى اليمين واليسار بعلامة واحدة. لذلك ، عليك القيام بذلك: في المضاعف ، انقل الفاصلة إلى اليمين بعلامة واحدة ، ومن هذا ستكون 23 ، ثم تحتاج إلى مضاعفة الأعداد الصحيحة الناتجة:

هذا المنتج أكبر 10 مرات من المنتج الحقيقي. لذلك ، يجب تقليله بمقدار 10 مرات ، حيث ننقل الفاصلة حرفًا واحدًا إلى اليسار. وهكذا نحصل

28 2,3 = 64,4.

لأغراض التحقق ، يمكنك كتابة كسر عشري بمقام وتنفيذ إجراء وفقًا لقاعدة ضرب الكسور العادية ، أي

2) 12,27 0,021.

الفرق بين هذا المثال والمثال السابق هو أنه هنا يتم تمثيل كلا العاملين بكسور عشرية. لكن هنا ، في عملية الضرب ، لن ننتبه للفواصل ، أي سنزيد المضاعف مؤقتًا بمقدار 100 مرة ، والمضاعف بمقدار 1000 مرة ، مما سيزيد الناتج بمقدار 100000 مرة. وهكذا ، بضرب 1227 في 21 ، نحصل على:

1 227 21 = 25 767.

مع الأخذ في الاعتبار أن المنتج الناتج أكبر 100000 مرة من المنتج الحقيقي ، يجب علينا الآن تقليله بمقدار 100000 مرة عن طريق وضع فاصلة فيه بشكل صحيح ، ثم نحصل على:

32,27 0,021 = 0,25767.

دعونا تحقق:

وبالتالي ، من أجل ضرب كسرين عشريين ، يكفي ، دون الالتفات إلى الفاصلات ، ضربهما كأعداد صحيحة وفي حاصل الضرب للفصل بفاصلة على الجانب الأيمن بعدد المنازل العشرية كما هو الحال في المضاعف وفي العامل معا.

في المثال الأخير ، تكون النتيجة منتجًا بخمس منازل عشرية. إذا لم تكن هذه الدقة الأكبر مطلوبة ، فسيتم تقريب الكسر العشري. عند التقريب ، يجب استخدام نفس القاعدة المشار إليها للأعداد الصحيحة.

110. الضرب باستخدام الجداول.

يمكن أحيانًا ضرب الكسور العشرية باستخدام الجداول. لهذا الغرض ، يمكنك ، على سبيل المثال ، استخدام جداول الضرب هذه للأرقام المكونة من رقمين ، والتي تم وصفها مسبقًا.

1) اضرب 53 في 1.5.

سنضرب 53 في 15. في الجدول ، هذا حاصل الضرب يساوي 795. وجدنا حاصل ضرب 53 في 15 ، لكن العامل الثاني كان أقل 10 مرات ، مما يعني أنه يجب تقليل حاصل الضرب بمقدار 10 مرات ، أي

53 1,5 = 79,5.

2) اضرب 5.3 في 4.7.

أولاً ، لنجد حاصل ضرب 53 في 47 في الجدول ، فسيكون 2491. ولكن نظرًا لأننا زدنا المضاعف والمضاعف بما مجموعه 100 مرة ، فإن الناتج الناتج يكون أكبر بمئة مرة مما ينبغي ؛ لذلك علينا تقليل هذا المنتج بمعامل 100:

5,3 4,7 = 24,91.

3) اضرب 0.53 في 7.4.

أولًا نجد في الجدول حاصل ضرب 53 × 74 ؛ سيكون هذا 3922. ولكن بما أننا قمنا بزيادة المضاعف بمقدار 100 مرة والمضاعف بمقدار 10 مرات ، فقد زاد المنتج بمقدار 1000 مرة ؛ لذلك علينا الآن تقليله بمقدار 1000:

0,53 7,4 = 3,922.

§ 111. قسمة الكسور العشرية.

سننظر في القسمة العشرية بهذا الترتيب:

1. القسمة العشرية على عدد صحيح,

1. قسمة الكسر العشري على عدد صحيح.

1) قسّم 2.46 على 2.

قسمنا على أول رقمين صحيحين ، ثم على عشرة وأخيرًا على مئات.

2) قسّم 32.46 على 3.

32,46: 3 = 10,82.

قسمنا 3 عشرات على 3 ، ثم بدأنا في قسمة وحدتين على 3 ؛ نظرًا لأن عدد وحدات المقسوم (2) أقل من المقسوم عليه (3) ، كان علينا وضع 0 في حاصل القسمة ؛ علاوة على ذلك ، هدمنا الباقي 4 أعشار وقسمنا 24 على 3 ؛ حصلوا على 8 أعشار وقسموا أخيرًا على 6 أجزاء.

3) قسّم 1.2345 على 5.

1,2345: 5 = 0,2469.

هنا ، في حاصل القسمة في المقام الأول ، تحولت الأعداد الصحيحة الصفرية ، لأن عددًا صحيحًا واحدًا لا يقبل القسمة على 5.

4) قسّم 13.58 على 4.

تكمن خصوصية هذا المثال في أنه عندما حصلنا على 9 أجزاء من المئات على انفراد ، ثم تم العثور على الباقي الذي يساوي 2 من مائة ، وقمنا بتقسيم الباقي إلى أجزاء من الألف ، وحصلنا على 20 جزءًا من الألف ، وأكملنا القسمة.

قاعدة.يتم تنفيذ قسمة الكسر العشري على عدد صحيح بنفس طريقة تقسيم الأعداد الصحيحة ، ويتم تحويل الباقي الناتج إلى كسور عشرية ، صغيرة أكثر فأكثر ؛ تستمر القسمة حتى يصبح الباقي صفرًا.

2. قسمة الكسر العشري على كسر عشري.

1) قسّم 2.46 على 0.2.

نحن نعلم بالفعل كيفية قسمة كسر عشري على عدد صحيح. لنفكر فيما إذا كان من الممكن أيضًا اختزال حالة القسمة الجديدة هذه إلى الحالة السابقة؟ في وقت ما ، اعتبرنا خاصية رائعة للحاصل ، والتي تتمثل في حقيقة أنها تظل دون تغيير مع زيادة أو تقليل المقسوم والمقسوم عليه بنفس العدد من المرات. من السهل إجراء قسمة الأعداد المعروضة علينا إذا كان المقسوم عليه عددًا صحيحًا. للقيام بذلك ، يكفي زيادته 10 مرات ، وللحصول على حاصل القسمة الصحيح ، من الضروري زيادة الأرباح بنفس عدد المرات ، أي 10 مرات. ثم يتم استبدال قسمة هذه الأرقام بقسمة هذه الأرقام:

ولا داعي لإجراء أي تعديلات على انفراد.

لنقم بهذا التقسيم:

إذن 2.46: 0.2 = 12.3.

2) قسّم 1.25 على 1.6.

نزيد المقسوم عليه (1.6) بمقدار 10 مرات ؛ حتى لا يتغير حاصل القسمة ، نزيد العائد بمقدار 10 مرات ؛ 12 عددًا صحيحًا لا يقبل القسمة على 16 ، لذلك نكتب في حاصل القسمة 0 ونقسم 125 جزءًا من 10 على 16 ، ونحصل على 7 أعشار في حاصل القسمة والباقي هو 13. نقسم 13 جزءًا من المئات عن طريق تخصيص صفر وقسمة 130 جزءًا من مائة على 16 ، إلخ. .. انتبه إلى ما يلي:

أ) عندما لا يتم الحصول على الأعداد الصحيحة في حاصل القسمة ، فإن الأعداد الصفرية تكتب مكانها ؛

ب) عندما يتم الحصول على رقم لا يقبل القسمة على المقسوم عليه بعد أخذ رقم المقسوم إلى الباقي ، ثم يتم كتابة الصفر في حاصل القسمة ؛

ج) بعد الهدم آخر رقملا تنتهي القسمة القابلة للقسمة ، ثم ، مع تخصيص الأصفار للباقي ، استمر في التقسيم ؛

د) إذا كان المقسوم عددًا صحيحًا ، فعند تقسيمه على كسر عشري ، تتم زيادته عن طريق تخصيص أصفار له.

وبالتالي ، من أجل قسمة رقم على كسر عشري ، تحتاج إلى تجاهل فاصلة في المقسوم عليه ، ثم زيادة المقسوم عدة مرات كلما زاد المقسوم عليه عندما تم إسقاط الفاصلة فيه ، ثم قم بإجراء القسمة وفقًا لـ قاعدة قسمة الكسر العشري على عدد صحيح.

§ 112. الحاصل التقريبي.

في الفقرة السابقة ، درسنا قسمة الكسور العشرية ، وفي جميع الأمثلة التي حللناها ، تم إنهاء القسمة ، أي تم الحصول على حاصل قسمة دقيق. ومع ذلك ، في معظم الحالات ، لا يمكن الحصول على حاصل القسمة الدقيق ، بغض النظر عن مدى توسيع القسمة. إليك إحدى هذه الحالات: قسّم 53 على 101.

لقد تلقينا بالفعل خمسة أرقام في حاصل القسمة ، لكن القسمة لم تنته بعد ولا أمل في أن تنتهي أبدًا ، لأن الأرقام التي التقيناها من قبل تبدأ في الظهور في الباقي. سيتم أيضًا تكرار الأرقام في حاصل القسمة: من الواضح أنه بعد الرقم 7 ، سيظهر الرقم 5 ، ثم 2 ، وهكذا بدون نهاية. في مثل هذه الحالات ، تتم مقاطعة القسمة وتقتصر على الأرقام القليلة الأولى من حاصل القسمة. هذا خاص يسمى تقريبي.كيفية إجراء القسمة في هذه الحالة ، سنعرض مع الأمثلة.

دعنا نطلب قسمة 25 على 3. من الواضح أن حاصل القسمة الدقيق ، معبرًا عنه بعدد صحيح أو كسر عشري ، لا يمكن الحصول عليه من هذا القسمة. لذلك سنبحث عن حاصل قسمة تقريبي:

25: 3 = 8 والباقي 1

الحاصل التقريبي هو 8 ؛ إنه ، بالطبع ، أقل من حاصل القسمة بالضبط ، لأن هناك الباقي 1. للحصول على حاصل القسمة الدقيق ، تحتاج إلى إضافة إلى حاصل القسمة التقريبي الموجود ، أي إلى 8 ، الكسر الناتج من قسمة الباقي ، يساوي 1 في 3 ؛ سيكون كسر 1/3. لذلك يتم التعبير عن حاصل القسمة الدقيق عدد كسري 8 1/3. بما أن 1/3 كسر صحيح ، أي كسر ، أقل من واحد، إذن ، نبذها ، نفترض خطأ، أيّ أقل من واحد. 8 سوف الخاص الحاصل التقريبي يصل إلى واحد مع وجود عيب.إذا أخذنا 9 بدلاً من 8 ، فإننا نسمح أيضًا بخطأ أقل من واحد ، لأننا لن نضيف وحدة كاملة ، بل 2/3. هذه إرادة خاصة حاصل قسمة تقريبي يصل إلى واحد مع فائض.

لنأخذ مثالاً آخر الآن. دعنا نطلب قسمة 27 على 8. نظرًا لأننا هنا لن نحصل على حاصل قسمة دقيق معبرًا عنه بعدد صحيح ، فسنبحث عن حاصل قسمة تقريبي:

27: 8 = 3 والباقي 3.

الخطأ هنا هو 3/8 ، وهو أقل من واحد ، مما يعني أن الحاصل التقريبي (3) تم العثور عليه حتى يصل إلى واحد به عيب. نواصل القسمة: قسمنا ما تبقى من 3 إلى أعشار ، نحصل على 30 من عشرة ؛ دعونا نقسمهم على 8.

حصلنا على خصوصية في البقعة أعشار 3 وفي الجزء المتبقي ب من عشرة. إذا قصرنا أنفسنا على الرقم 3.3 على وجه الخصوص ، وتجاهلنا الباقي 6 ، فسنسمح بخطأ أقل من عُشر. لماذا؟ لأنه سيتم الحصول على حاصل القسمة الدقيق عندما أضفنا إلى 3.3 نتيجة قسمة 6 أعشار على 8 ؛ من هذه القسمة تساوي 80/6 ، وهو أقل من واحد على عشرة. (تحقق!) وبالتالي ، إذا حددنا أنفسنا بعشر في حاصل القسمة ، فيمكننا القول إننا وجدنا حاصل القسمة دقيقة حتى عُشر(مع عيب).

فلنواصل القسمة لإيجاد منزلة عشرية أخرى. للقيام بذلك ، قسمنا 6 أعشار إلى أجزاء من مائة ونحصل على 60 جزءًا من مائة ؛ دعونا نقسمهم على 8.

في المركز الثالث ، ظهر 7 وفي الباقي 4 مائة ؛ إذا تجاهلناها ، فإننا نسمح بخطأ أقل من جزء من مائة ، لأن 4 من مائة مقسومة على 8 أقل من مائة. في مثل هذه الحالات ، يُقال أن حاصل القسمة موجود. دقيقة حتى المئة(مع عيب).

في المثال الذي ندرسه الآن ، يمكنك الحصول على حاصل القسمة الدقيق ، معبرًا عنه في صورة كسر عشري. للقيام بذلك ، يكفي تقسيم الباقي الأخير ، 4 أجزاء من المائة ، إلى أجزاء من الألف وقسمته على 8.

ومع ذلك ، في الغالبية العظمى من الحالات ، من المستحيل الحصول على حاصل دقيق ويجب على المرء أن يقتصر على قيمه التقريبية. سننظر الآن في مثل هذا المثال:

40: 7 = 5,71428571...

تشير النقاط الموجودة في نهاية الرقم إلى أن التقسيم لم يكتمل ، أي أن المساواة تقريبية. عادة ما يتم كتابة المساواة التقريبية على النحو التالي:

40: 7 = 5,71428571.

أخذنا خارج القسمة بثمانية منازل عشرية. ولكن إذا لم تكن هذه الدقة الكبيرة مطلوبة ، فيمكن للمرء أن يحصر نفسه في الجزء الكامل من حاصل القسمة ، أي الرقم 5 (بتعبير أدق ، 6) ؛ لمزيد من الدقة ، يمكن أخذ الأعشار في الاعتبار وحاصل القسمة يساوي 5.7 ؛ إذا كانت هذه الدقة غير كافية لسبب ما ، فيمكننا التوقف عند المئات وأخذ 5.71 ، إلخ. دعونا نكتب حاصل القسمة الفردية ونسميها.

الحاصل التقريبي الأول حتى 6 واحد.

والثاني »» »إلى العُشر 5.7.

الثالثة »» حتى 5.71 مائة.

الرابع »» حتى الألف من 5.714.

وبالتالي ، من أجل العثور على حاصل تقريبي يصل إلى بعض ، على سبيل المثال ، المكان العشري الثالث (أي ما يصل إلى ألف واحد) ، يتم إيقاف القسمة بمجرد العثور على هذه العلامة. في هذه الحالة ، يجب على المرء أن يتذكر القاعدة المنصوص عليها في الفقرة 40.

§ 113. أبسط المشاكل للفائدة.

بعد دراسة الكسور العشرية ، سنحل بعض مسائل النسبة المئوية.

تشبه هذه المشكلات تلك التي تم حلها في قسم الكسور العادية ؛ لكننا الآن سنكتب المئات في صورة كسور عشرية ، أي بدون مقام محدد بشكل صريح.

بادئ ذي بدء ، يجب أن تكون قادرًا على التبديل بسهولة من جزء مشتركإلى رقم عشري بمقامه 100. للقيام بذلك ، اقسم البسط على المقام:

يوضح الجدول أدناه كيفية استبدال رقم برمز٪ (نسبة مئوية) برقم عشري بمقامه 100:

دعنا الآن نفكر في بعض المشاكل.

1. إيجاد النسب المئوية لعدد معين.

مهمة 1.يعيش 1600 شخص فقط في قرية واحدة. عدد الاطفال سن الدراسة 25٪ من الرقم الإجماليسكان. كم عدد الأطفال في سن المدرسة في هذه القرية؟

في هذه المسألة ، تحتاج إلى إيجاد 25٪ ، أو 0.25 ، من 1600. يتم حل المشكلة بضرب:

1600 0.25 = 400 (أطفال).

لذلك ، 25٪ من 1600 تساوي 400.

لفهم هذه المهمة بشكل واضح ، من المفيد أن نتذكر أنه لكل مائة من السكان هناك 25 طفلاً في سن المدرسة. لذلك ، لمعرفة عدد جميع الأطفال في سن المدرسة ، يمكنك أولاً معرفة عدد المئات في الرقم 1600 (16) ، ثم ضرب 25 في عدد المئات (25 × 16 = 400). بهذه الطريقة يمكنك التحقق من صحة الحل.

المهمة 2.تمنح بنوك التوفير المودعين 2٪ من الدخل سنويًا. ما مقدار الدخل السنوي الذي سيحصل عليه المودع الذي قام بإيداع: أ) 200 روبل؟ ب) 500 روبل؟ ج) 750 روبل؟ د) 1000 روبل؟

في جميع الحالات الأربع ، لحل المشكلة ، سيكون من الضروري حساب 0.02 من المبالغ المشار إليها ، أي يجب ضرب كل رقم من هذه الأرقام في 0.02. دعنا نقوم به:

أ) 200 0.02 = 4 (روبل) ،

ب) 500 0.02 = 10 (روبل) ،

ج) 750 0.02 = 15 (روبل) ،

د) 1000 0.02 = 20 روبل.

يمكن التحقق من كل من هذه الحالات من خلال الاعتبارات التالية. تمنح بنوك التوفير المودعين 2٪ من الدخل ، أي 0.02 من المبلغ المدخرات. إذا كان المبلغ 100 روبل ، فسيكون 0.02 روبل منه. هذا يعني أن كل مائة يجلب المودع 2 روبل. دخل. لذلك ، في كل حالة من الحالات التي تم النظر فيها ، يكفي معرفة عدد المئات في رقم معين ، وضرب 2 روبل في هذا العدد من المئات. في المثال أ) مئات من 2 ، لذلك

2 2 = 4 (روبل).

في المثال د) المئات هي 10 ، مما يعني

2 10 \ u003d 20 (روبل).

2. إيجاد رقم بنسبته المئوية.

مهمة 1.في الربيع ، تخرجت المدرسة 54 طالبًا ، أي ما نسبته 6٪ من إجمالي عدد الطلاب. كم عدد الطلاب في المدرسة خلال العام الدراسي الماضي؟

دعونا أولا نوضح معنى هذه المشكلة. تخرجت المدرسة 54 طالبًا ، وهو ما يمثل 6٪ من إجمالي عدد الطلاب ، أو بعبارة أخرى ، ستمائة (0.06) من جميع الطلاب في المدرسة. هذا يعني أننا نعرف جزء الطلاب المعبر عنه بالرقم (54) والكسر (0.06) ، ومن هذا الكسر علينا إيجاد العدد الصحيح. وبالتالي ، أمامنا مشكلة عادية لإيجاد رقم من كسره (§ 90 p.6). يتم حل مشاكل هذا النوع عن طريق القسمة:

هذا يعني أنه كان هناك 900 طالب في المدرسة.

من المفيد التحقق من هذه المشكلات عن طريق حل المشكلة العكسية ، أي بعد حل المشكلة ، يجب ، على الأقل في عقلك ، حل مشكلة النوع الأول (إيجاد النسبة المئوية لرقم معين): خذ الرقم الموجود ( 900) على النحو المعطى وإيجاد النسبة المئوية المشار إليها في المشكلة المحلولة منه وهي:

900 0,06 = 54.

المهمة 2.تنفق الأسرة 780 روبل على الطعام خلال الشهر ، أي 65٪ من الدخل الشهري للأب. تحديد دخله الشهري.

هذه المهمة لها نفس معنى المهمة السابقة. يعطي جزءًا من الأرباح الشهرية ، معبرًا عنه بالروبل (780 روبل) ، ويشير إلى أن هذا الجزء يمثل 65٪ ، أو 0.65 ، من إجمالي الأرباح. والمطلوب هو كامل المكاسب:

780: 0,65 = 1 200.

لذلك ، فإن الأرباح المرغوبة هي 1200 روبل.

3. إيجاد النسبة المئوية للأرقام.

مهمة 1.تحتوي مكتبة المدرسة على 6000 كتاب. من بينها 1200 كتاب في الرياضيات. ما النسبة المئوية لكتب الرياضيات التي تشكل العدد الإجمالي للكتب في المكتبة؟

لقد درسنا بالفعل (§97) هذا النوع من المشاكل وتوصلنا إلى استنتاج مفاده أنه لحساب النسبة المئوية لرقمين ، تحتاج إلى إيجاد نسبة هذه الأرقام وضربها في 100.

في مهمتنا ، علينا إيجاد النسبة المئوية للأعداد 1200 و 6000.

نحسب النسبة أولاً ، ثم نضربها في 100:

وبالتالي ، فإن النسبة المئوية للأعداد 1200 و 6000 هي 20. بمعنى آخر ، تشكل كتب الرياضيات 20٪ من العدد الإجمالي لجميع الكتب.

للتحقق من ذلك ، قمنا بحل المسألة العكسية: أوجد 20٪ من 6000:

6 000 0,2 = 1 200.

المهمة 2.يجب أن يستقبل المصنع 200 طن من الفحم. تم تسليم 80 طناً ، ما هي نسبة الفحم التي تم تسليمها إلى المحطة؟

تسأل هذه المسألة عن النسبة المئوية لرقم واحد (80) لرقم آخر (200). ستكون نسبة هذه الأرقام 80/200. لنضربها في 100:

هذا يعني أنه تم تسليم 40٪ من الفحم.

في الدرس الأخير ، تعلمنا كيفية جمع الكسور العشرية وطرحها (انظر الدرس "جمع الكسور العشرية وطرحها"). في الوقت نفسه ، قدّروا مقدار تبسيط الحسابات مقارنةً بالكسور "المكونة من طابقين" المعتادة.

لسوء الحظ ، مع ضرب الكسور العشرية وتقسيمها ، لا يحدث هذا التأثير. في بعض الحالات ، يؤدي التدوين العشري إلى تعقيد هذه العمليات.

أولاً ، دعنا نقدم تعريفًا جديدًا. سنلتقي به كثيرًا ، وليس فقط في هذا الدرس.

الجزء المهم من الرقم هو كل شيء يقع بين أول وآخر رقم غير صفري ، بما في ذلك المقطورات. نحن نتحدث فقط عن الأرقام ، الفاصلة العشرية لا تؤخذ بعين الاعتبار.

الأرقام المدرجة في جزء كبيرتسمى الأرقام أرقامًا ذات دلالة. يمكن تكرارها وحتى تساوي الصفر.

على سبيل المثال ، ضع في اعتبارك عدة كسور عشرية واكتب الأجزاء المهمة المقابلة لها:

1. 91.25 - 9125 (أرقام ذات دلالة: 9 ؛ 1 ؛ 2 ؛ 5) ؛
2. 0.008241 - 8241 (أرقام معنوية: 8 ؛ 2 ؛ 4 ؛ 1) ؛
3. 15.0075 - 150075 (أرقام ذات دلالة: 1 ؛ 5 ؛ 0 ؛ 0 ؛ 7 ؛ 5) ؛
4. 0.0304 - 304 (أرقام معنوية: 3 ؛ 0 ؛ 4) ؛
5. 3000 → 3 (هناك رقم واحد مهم فقط: 3).

يرجى ملاحظة: الأصفار الموجودة داخل الجزء المهم من الرقم لا تذهب إلى أي مكان. لقد واجهنا بالفعل شيئًا مشابهًا عندما تعلمنا تحويل الكسور العشرية إلى الكسور العادية (انظر الدرس "الكسور العشرية").

هذه النقطة مهمة للغاية ، وهناك أخطاء تحدث هنا كثيرًا لدرجة أنني سأقوم بنشر اختبار حول هذا الموضوع في المستقبل القريب. تأكد من الممارسة! ونحن ، مسلحين بمفهوم جزء كبير ، سننتقل ، في الواقع ، إلى موضوع الدرس.

الضرب العشري

تتكون عملية الضرب من ثلاث خطوات متتالية:

1. اكتب الجزء المهم لكل كسر. سوف تحصل على رقمين صحيحين عاديين - بدون أي قواسم ونقاط عشرية ؛
2. اضرب هذه الأرقام بأي طريقة مناسبة. مباشرة ، إذا كانت الأرقام صغيرة أو في عمود. نحصل على جزء كبير من الكسر المطلوب ؛
3. اكتشف مكان إزاحة الفاصلة العشرية في الكسور الأصلية وعددها للحصول على الجزء المهم المقابل. قم بإجراء نوبات عكسية على الجزء الهام الذي تم الحصول عليه في الخطوة السابقة.

اسمحوا لي أن أذكركم مرة أخرى بأن الأصفار على جوانب الجزء المهم لا تؤخذ في الاعتبار أبدًا. تجاهل هذه القاعدة يؤدي إلى أخطاء.

1. 0.28 12.5 ؛
2. 6.3 1.08
3. 132.5 0.0034 ؛
4. 0.0108 1600.5 ؛
5. 5.25 10000.

نتعامل مع التعبير الأول: 0.28 12.5.

1. لنكتب الأجزاء المهمة للأرقام من هذا التعبير: 28 و 125 ؛
2. منتجهم: 28125 = 3500 ؛
3. في المضاعف الأول ، يتم إزاحة الفاصلة العشرية رقمين إلى اليمين (0.28 → 28) ، وفي الثانية - برقم واحد آخر. في المجموع ، هناك حاجة إلى التحول إلى اليسار بثلاثة أرقام: 3500 → 3.500 = 3.5.

الآن دعونا نتعامل مع التعبير 6.3 1.08.

1. لنكتب الأجزاء المهمة: 63 و 108 ؛
2. منتجهم: 63108 = 6804 ؛
3. مرة أخرى ، نوبتان إلى اليمين: بمقدار رقمين ورقم واحد ، على التوالي. في المجموع - مرة أخرى 3 أرقام إلى اليمين ، وبالتالي فإن التحول العكسي سيكون 3 أرقام إلى اليسار: 6804 - 6.804. هذه المرة لا توجد أصفار في النهاية.

وصلنا إلى التعبير الثالث: 132.5 0.0034.

1. أجزاء مهمة: 1325 و 34 ؛
2. منتجهم: 1325 34 = 45.050 ؛
3. في الكسر الأول ، تنتقل العلامة العشرية إلى اليمين بمقدار رقم واحد ، وفي الثانية - بما يصل إلى 4. المجموع: 5 على اليمين. نقوم بإجراء تحول بمقدار 5 إلى اليسار: 45050 → .45050 = 0.4505. تمت إزالة الصفر في النهاية ، وإضافته إلى المقدمة حتى لا تترك فاصلة عشرية "عارية".

التعبير التالي: 1600.5 0.0108.

1. نكتب أجزاء مهمة: 108 و 16 005 ؛
2. نضربهم: 108 16005 = 1728540 ؛
3. نحسب الأرقام بعد الفاصلة العشرية: في الرقم الأول هناك 4 ، في الثاني - 1. في المجموع - مرة أخرى 5. لدينا: 1،728،540 → 17.28540 = 17.2854. في النهاية ، تمت إزالة الصفر "الإضافي".

أخيرًا ، التعبير الأخير: 5.25 10000.

1. أجزاء مهمة: 525 و 1 ؛
2. نضربهم: 525 1 = 525 ؛
3. يتم إزاحة الكسر الأول بمقدار رقمين إلى اليمين ، ويتم إزاحة الكسر الثاني بمقدار 4 أرقام إلى اليسار (10000 → 1.0000 = 1). المجموع 4-2 = رقمان إلى اليسار. نقوم بإجراء إزاحة عكسية بمقدار رقمين إلى اليمين: 525 ، → 52500 (كان علينا إضافة الأصفار).

انتبه إلى المثال الأخير: نظرًا لأن الفاصلة العشرية تتحرك في اتجاهات مختلفة ، فإن التحول الكلي يكون من خلال الاختلاف. هذا جدا نقطة مهمة! إليك مثال آخر:

النظر في الأرقام 1.5 و 12500. لدينا: 1.5 → 15 (التحول بمقدار 1 إلى اليمين) ؛ 12500 - 125 (انقل 2 إلى اليسار). نحن "نخطو" رقمًا واحدًا إلى اليمين ، ثم رقمين إلى اليسار. نتيجة لذلك ، صعدنا 2-1 = رقم واحد إلى اليسار.

القسمة العشرية

ربما يكون التقسيم هو الأكثر عملية معقدة. بالطبع ، هنا يمكنك العمل عن طريق القياس مع الضرب: اقسم الأجزاء المهمة ، ثم "حرك" الفاصلة العشرية. ولكن في هذه الحالة ، هناك العديد من التفاصيل الدقيقة التي تنفي المدخرات المحتملة.

لذلك دعونا نلقي نظرة على خوارزمية عامة أطول قليلاً ولكنها أكثر موثوقية:

1. حول كل الكسور العشرية إلى كسور مشتركة. مع القليل من الممارسة ، سوف تستغرق هذه الخطوة بضع ثوان ؛
2. اقسم الكسور الناتجة بالطريقة الكلاسيكية. بمعنى آخر ، اضرب الكسر الأول في الثانية "المقلوبة" (انظر الدرس "الضرب والقسمة للكسور العددية") ؛
3. إذا أمكن ، قم بإرجاع النتيجة في صورة رقم عشري. هذه الخطوة سريعة أيضًا ، لأنه غالبًا ما يكون للمقام بالفعل قوة عشرة.

مهمة. أوجد قيمة التعبير:

1. 3,51: 3,9;
2. 1,47: 2,1;
3. 6,4: 25,6:
4. 0,0425: 2,5;
5. 0,25: 0,002.

نحن نعتبر التعبير الأول. أولاً ، دعنا نحول كسور obi إلى كسور عشرية:

نفعل الشيء نفسه مع التعبير الثاني. يتحلل بسط الكسر الأول مرة أخرى إلى عوامل:

هناك نقطة مهمة في المثالين الثالث والرابع: بعد التخلص من التدوين العشري ، تظهر الكسور القابلة للإلغاء. ومع ذلك ، لن نقوم بإجراء هذا التخفيض.

المثال الأخير مثير للاهتمام لأن بسط الكسر الثاني هو رقم أولي. ببساطة لا يوجد شيء يمكن تحليله هنا ، لذلك نعتبره "فارغًا من خلال":

ينتج عن القسمة أحيانًا عددًا صحيحًا (أتحدث عن المثال الأخير). في هذه الحالة ، لا يتم تنفيذ الخطوة الثالثة على الإطلاق.

بالإضافة إلى ذلك ، عند القسمة ، غالبًا ما تظهر الكسور "القبيحة" التي لا يمكن تحويلها إلى كسور عشرية. هذا هو المكان الذي تختلف فيه القسمة عن الضرب ، حيث يتم التعبير عن النتائج دائمًا في شكل عشري. بالطبع ، في هذه الحالة ، لا يتم تنفيذ الخطوة الأخيرة مرة أخرى.

انتبه أيضًا إلى الأمثلة الثالثة والرابعة. في نفوسهم ، نحن عمدا لا تقلل الكسور المشتركةمشتق من الكسور العشرية. خلاف ذلك ، فإنه سيعقد المسألة العكسية - تمثيل الإجابة النهائية مرة أخرى في شكل عشري.

تذكر: الخاصية الأساسية للكسر (مثل أي قاعدة أخرى في الرياضيات) في حد ذاتها لا تعني أنه يجب تطبيقها في كل مكان ودائمًا ، وفي كل فرصة.

أنا. لقسمة كسر عشري على رقم طبيعي ، تحتاج إلى قسمة الكسر على هذا الرقم ، حيث يتم تقسيم الأرقام الطبيعية ووضعها في فاصلة خاصة عند انتهاء قسمة الجزء بالكامل.

أمثلة.

تنفيذ التقسيم: 1) 96,25: 5; 2) 4,78: 4; 3) 183,06: 45.

حل.

مثال 1) 96,25: 5.

نقسم على "ركن" بنفس طريقة قسمة الأعداد الطبيعية. بعد أن نزيل الرقم 2 (عدد الأعشار هو الرقم الأول بعد الفاصلة العشرية في سجل المقسوم 96 ، 2 5) ، ضع فاصلة في حاصل القسمة واستمر في القسمة.

إجابة: 19,25.

مثال 2) 4,78: 4.

نقسم عندما نقسم الأعداد الطبيعية. على انفراد ، ضع فاصلة بمجرد أن نهدم 7 - الرقم الأول بعد الفاصلة العشرية في المقسوم 4 ، 7 8. نواصل التقسيم أكثر. عند طرح 38-36 ، نحصل على 2 ، لكن القسمة لم تنته بعد. كيف نفعل؟ نعلم أنه يمكن إضافة الأصفار في نهاية الكسر العشري - وهذا لن يغير قيمة الكسر. نسند صفرًا ونقسم 20 على 4. نحصل على 5 - انتهت عملية القسمة.

إجابة: 1,195.

مثال 3) 183,06: 45.

اقسم 18306 على 45. في حاصل القسمة ، ضع فاصلة بمجرد أن نحذف الرقم 0 - الرقم الأول بعد الفاصلة العشرية في المقسوم 183 ، 0 6. كما في المثال 2) ، كان علينا تعيين صفر للرقم 36 - الفرق بين العددين 306 و 270.

إجابة: 4,068.

خاتمة: عند قسمة كسر عشري على رقم طبيعي في وضع خاص فاصلة مباشرة بعد هدم الرقم في مكان أعشار المقسوم. يرجى ملاحظة ما يلي: تم تمييز كل شيء أرقام باللون الأحمر في هذه الأمثلة الثلاثة تنتمي إلى الفئة أعشار المقسوم.

ثانيًا. لتقسيم رقم عشري على 10 ، 100 ، 1000 ، إلخ ، تحتاج إلى تحريك الفاصلة إلى اليسار بمقدار 1 ، 2 ، 3 ، إلخ.

أمثلة.

أداء القسم: 1) 41,56: 10; 2) 123,45: 100; 3) 0,47: 100; 4) 8,5: 1000; 5) 631,2: 10000.

حل.

يعتمد تحريك الفاصلة إلى اليسار على عدد الأصفار بعد الواحد في المقسوم عليه. لذلك ، عند قسمة الكسر العشري على 10 سنحمل في القسمة فاصلة على اليسار برقم واحد؛ عند القسمة على 100 - حرك الفاصلة تُركت برقمين؛ عند القسمة على 1000 نقل في كسر عشري معين فاصلة ثلاثة أرقام إلى اليسار.

في هذا البرنامج التعليمي ، سنلقي نظرة على كل من هذه العمليات واحدة تلو الأخرى.

محتوى الدرس

جمع الكسور العشرية

كما نعلم ، يحتوي الكسر العشري على جزء صحيح وجزء كسري. عند إضافة الكسور العشرية ، تتم إضافة الأعداد الصحيحة والكسور بشكل منفصل.

على سبيل المثال ، لنجمع الكسور العشرية 3.2 و 5.3. من الأنسب إضافة كسور عشرية في عمود.

أولاً ، نكتب هذين الكسرين في عمود ، بينما يجب أن تكون الأجزاء الصحيحة تحت الأجزاء الصحيحة ، والأجزاء الكسرية تحت الأجزاء الكسرية. في المدرسة ، هذا الشرط يسمى "فاصلة تحت الفاصلة".

لنكتب الكسور في عمود بحيث تكون الفاصلة أسفل الفاصلة:

نبدأ في جمع الأجزاء الكسرية: 2 + 3 \ u003d 5. نكتب الخمسة في الجزء الكسري من إجابتنا:

الآن نجمع أجزاء الأعداد الصحيحة: 3 + 5 = 8. نكتب الثمانية في الجزء الصحيح من إجابتنا:

الآن نفصل الجزء الصحيح من الجزء الكسري بفاصلة. للقيام بذلك ، نتبع القاعدة مرة أخرى "فاصلة تحت الفاصلة":

حصلت على الجواب 8.5. إذن التعبير 3.2 + 5.3 يساوي 8.5

في الواقع ، ليس كل شيء بهذه البساطة كما يبدو للوهلة الأولى. هنا أيضًا ، هناك مطبات سنتحدث عنها الآن.

الأماكن في الكسور العشرية

الأعداد العشرية ، مثل الأعداد العادية ، لها أرقامها الخاصة. هذه هي المراكز العاشرة ، المئات ، المراتب الألف. في هذه الحالة ، تبدأ الأرقام بعد الفاصلة العشرية.

الرقم الأول بعد الفاصلة العشرية مسؤول عن خانة الجزء من عشرة ، والرقم الثاني بعد العلامة العشرية لخانة المئات ، والرقم الثالث بعد العلامة العشرية لخانة الجزء من الألف.

يتم تخزين بعض الأرقام في الكسور العشرية معلومات مفيدة. على وجه الخصوص ، يبلغون عن عدد الأعشار والمئات والألف في النظام العشري.

على سبيل المثال ، ضع في الاعتبار الرقم العشري 0.345

الموضع الذي يوجد فيه الثلاثي يسمى المركز العاشر

يسمى الموضع الذي يقع فيه الأربعة مكان المئات

يسمى الموضع الذي يقع فيه الخمسة جزء من الألف

دعونا نلقي نظرة على هذا الرقم. نلاحظ أنه في فئة الجزء من عشرة ، يوجد ثلاثة. يشير هذا إلى وجود ثلاثة أعشار في الكسر العشري 0.345.

إذا جمعنا الكسور ، فسنحصل على الكسر العشري الأصلي 0.345

يمكن ملاحظة أننا حصلنا على الإجابة في البداية ، لكننا حولناها إلى كسر عشري وحصلنا على 0.345.

عند إضافة الكسور العشرية ، يتم اتباع نفس المبادئ والقواعد كما هو الحال عند جمع الأرقام العادية. تتم إضافة الكسور العشرية بالأرقام: تتم إضافة الأعشار إلى الأعشار ، ومن المئات إلى المئات ، ومن الألف إلى الألف.

لذلك ، عند إضافة الكسور العشرية ، يلزم اتباع القاعدة "فاصلة تحت الفاصلة". توفر الفاصلة الموجودة أسفل الفاصلة نفس الترتيب الذي تتم به إضافة الأعشار إلى الأعشار ، والمئات إلى المئات ، والألف إلى الألف.

مثال 1أوجد قيمة التعبير 1.5 + 3.4

أولًا ، نجمع الأجزاء الكسرية 5 + 4 = 9. نكتب التسعة في الجزء الكسري من إجابتنا:

الآن نجمع الأجزاء الصحيحة 1 + 3 = 4. نكتب الأربعة في الجزء الصحيح من إجابتنا:

الآن نفصل الجزء الصحيح من الجزء الكسري بفاصلة. للقيام بذلك ، نلاحظ مرة أخرى القاعدة "الفاصلة تحت الفاصلة":

حصلت على الإجابة 4.9. إذن ، فإن قيمة التعبير 1.5 + 3.4 هي 4.9

مثال 2أوجد قيمة التعبير: 3.51 + 1.22

نكتب هذا التعبير في عمود ، مع مراعاة القاعدة "الفاصلة تحت الفاصلة"

اجمع أولًا الجزء الكسري ، أي 1 + 2 = 3. نكتب الثلاثية في الجزء المائة من إجابتنا:

أضف الآن أعشار 5 + 2 = 7. نكتب السبعة في الجزء العاشر من إجابتنا:

الآن أضف الأجزاء الكاملة 3 + 1 = 4. نكتب الأربعة في الجزء الكامل من إجابتنا:

نفصل الجزء الصحيح من الجزء الكسري بفاصلة ، مع ملاحظة قاعدة "الفاصلة تحت الفاصلة":

حصلت على الجواب 4.73. إذن ، فإن قيمة التعبير 3.51 + 1.22 هي 4.73

3,51 + 1,22 = 4,73

كما هو الحال مع الأرقام العادية ، عند جمع الكسور العشرية ،. في هذه الحالة ، يتم كتابة رقم واحد في الإجابة ، ويتم نقل الباقي إلى الرقم التالي.

مثال 3أوجد قيمة التعبير 2.65 + 3.27

نكتب هذا التعبير في عمود:

اجمع أجزاء من مائة 5 + 7 = 12. الرقم 12 لن يتناسب مع الجزء المائة من إجابتنا. لذلك ، في الجزء المائة ، نكتب الرقم 2 ، وننقل الوحدة إلى الجزء التالي:

نجمع الآن أعشار 6 + 2 = 8 زائد الوحدة التي حصلنا عليها من العملية السابقة ، نحصل على 9. نكتب الرقم 9 في الجزء العاشر من إجابتنا:

الآن أضف الأجزاء الكاملة 2 + 3 = 5. نكتب الرقم 5 في الجزء الصحيح من إجابتنا:

حصلت على الإجابة 5.92. إذن ، فإن قيمة التعبير 2.65 + 3.27 هي 5.92

2,65 + 3,27 = 5,92

مثال 4أوجد قيمة التعبير 9.5 + 2.8

اكتب هذا التعبير في عمود

نجمع الأجزاء الكسرية 5 + 8 = 13. العدد 13 لن يتناسب مع الجزء الكسري من إجابتنا ، لذلك نكتب الرقم 3 أولاً ، وننقل الوحدة إلى الرقم التالي ، أو بالأحرى ننقلها إلى العدد الصحيح جزء:

الآن نجمع الأجزاء الصحيحة 9 + 2 = 11 زائد الوحدة التي حصلنا عليها من العملية السابقة ، نحصل على 12. نكتب الرقم 12 في الجزء الصحيح من إجابتنا:

افصل الجزء الصحيح عن الجزء الكسري بفاصلة:

حصلت على الجواب 12.3. إذن ، فإن قيمة التعبير 9.5 + 2.8 هي 12.3

9,5 + 2,8 = 12,3

عند جمع الكسور العشرية ، يجب أن يكون عدد الأرقام بعد الفاصلة العشرية في كلا الكسرين متماثلاً. إذا لم تكن هناك أرقام كافية ، فإن هذه الأماكن في الجزء الكسري تمتلئ بالأصفار.

مثال 5. أوجد قيمة التعبير: 12.725 + 1.7

قبل كتابة هذا التعبير في عمود ، دعونا نجعل عدد الأرقام بعد الفاصلة العشرية في كلا الكسرين متماثلاً. يحتوي الكسر العشري 12.725 على ثلاثة أرقام بعد الفاصلة العشرية ، بينما يحتوي الكسر 1.7 على رقم واحد فقط. إذن في الكسر 1.7 في النهاية ، تحتاج إلى إضافة صفرين. ثم نحصل على الكسر 1700. يمكنك الآن كتابة هذا التعبير في عمود والبدء في الحساب:

اجمع أجزاء من الألف من 5 + 0 = 5. نكتب الرقم 5 في الجزء الألف من إجابتنا:

اجمع أجزاء من مائة 2 + 0 = 2. نكتب الرقم 2 في الجزء المائة من إجابتنا:

أضف أعشار 7 + 7 = 14. العدد 14 لن يتناسب مع عُشر إجابتنا. لذلك ، نكتب الرقم 4 أولاً ، وننقل الوحدة إلى البتة التالية:

نجمع الآن الأجزاء الصحيحة 12 + 1 = 13 زائد الوحدة التي حصلنا عليها من العملية السابقة ، نحصل على 14. نكتب الرقم 14 في الجزء الصحيح من إجابتنا:

افصل الجزء الصحيح عن الجزء الكسري بفاصلة:

حصلت على الاجابة 14،425. إذن ، فإن قيمة التعبير 12.725 + 1.700 هي 14.425

12,725+ 1,700 = 14,425

طرح الكسور العشرية

عند طرح الكسور العشرية ، يجب اتباع نفس القواعد المتبعة عند إضافة: "فاصلة تحت الفاصلة" و "عدد متساوٍ من الأرقام بعد الفاصلة العشرية".

مثال 1أوجد قيمة التعبير 2.5 - 2.2

نكتب هذا التعبير في عمود ، مع ملاحظة قاعدة "الفاصلة تحت الفاصلة":

نحسب الجزء الكسري 5−2 = 3. نكتب الرقم 3 في الجزء العاشر من إجابتنا:

احسب الجزء الصحيح 2−2 = 0. نكتب الصفر في الجزء الصحيح من إجابتنا:

افصل الجزء الصحيح عن الجزء الكسري بفاصلة:

حصلنا على الإجابة 0.3. إذن ، فإن قيمة التعبير 2.5 - 2.2 تساوي 0.3

2,5 − 2,2 = 0,3

مثال 2أوجد قيمة التعبير 7.353 - 3.1

في هذا التعبير كمية مختلفةبعد الفاصلة العشرية. يوجد في الكسر 7.353 ثلاثة أرقام بعد الفاصلة العشرية ، وفي الكسر 3.1 يوجد رقم واحد فقط. هذا يعني أنه في الكسر 3.1 ، يجب إضافة صفرين في النهاية لجعل عدد الأرقام في كلا الكسرين متماثلًا. ثم نحصل على 3100.

يمكنك الآن كتابة هذا التعبير في عمود وحسابه:

حصلت على إجابة 4،253. إذن ، فإن قيمة التعبير 7.353 - 3.1 تساوي 4.253

7,353 — 3,1 = 4,253

كما هو الحال مع الأرقام العادية ، سيتعين عليك أحيانًا استعارة واحدة من البتة المجاورة إذا أصبح الطرح مستحيلاً.

مثال 3أوجد قيمة التعبير 3.46 - 2.39

اطرح أجزاء من المئات من 6−9. من الرقم 6 لا تطرح الرقم 9. لذلك ، تحتاج إلى أخذ وحدة من الرقم المجاور. بعد استعارة واحد من الرقم المجاور ، يتحول الرقم 6 إلى الرقم 16. الآن يمكننا حساب المئات من 16−9 = 7. نكتب السبعة في الجزء المائة من إجابتنا:

الآن اطرح أجزاء من عشرة. نظرًا لأننا أخذنا وحدة واحدة من فئة أعشار ، فإن الرقم الموجود هناك انخفض بمقدار وحدة واحدة. بعبارة أخرى ، المكان العاشر الآن ليس الرقم 4 ، ولكن الرقم 3. دعونا نحسب أعشار 3−3 = 0. نكتب صفرًا في الجزء العاشر من إجابتنا:

الآن اطرح الأجزاء الصحيحة 3−2 = 1. نكتب الوحدة في الجزء الصحيح من إجابتنا:

افصل الجزء الصحيح عن الجزء الكسري بفاصلة:

حصلت على الجواب 1.07. إذن ، فإن قيمة التعبير 3.46−2.39 تساوي 1.07

3,46−2,39=1,07

مثال 4. أوجد قيمة التعبير 3−1.2

يطرح هذا المثال رقمًا عشريًا من عدد صحيح. لنكتب هذا التعبير في عمود بحيث يكون الجزء الصحيح من الكسر العشري 1.23 تحت الرقم 3

الآن لنجعل عدد الأرقام بعد الفاصلة العشرية كما هو. للقيام بذلك ، بعد الرقم 3 ، ضع فاصلة وأضف صفرًا واحدًا:

الآن اطرح أعشار: 0−2. لا تطرح الرقم 2 من الصفر ، لذلك عليك أن تأخذ وحدة من الرقم المجاور. من خلال استعارة واحد من الرقم المجاور ، يتحول 0 إلى الرقم 10. الآن يمكنك حساب أعشار 10−2 = 8. نكتب الثمانية في الجزء العاشر من إجابتنا:

الآن اطرح الأجزاء الكاملة. في السابق ، كان الرقم 3 موجودًا في عدد صحيح ، لكننا اقترضنا وحدة واحدة منه. نتيجة لذلك ، تحول إلى الرقم 2. لذلك ، نطرح 1 من 2. 2−1 = 1. نكتب الوحدة في الجزء الصحيح من إجابتنا:

افصل الجزء الصحيح عن الجزء الكسري بفاصلة:

حصلت على الجواب 1.8. إذن ، فإن قيمة التعبير 3−1.2 هي 1.8

الضرب العشري

يعد ضرب الكسور العشرية أمرًا سهلاً وممتعًا. لضرب الكسور العشرية ، تحتاج إلى ضربهم مثل الأعداد العادية ، مع تجاهل الفواصل.

بعد تلقي الإجابة ، من الضروري فصل الجزء الصحيح عن الجزء الكسري بفاصلة. للقيام بذلك ، تحتاج إلى حساب عدد الأرقام بعد الفاصلة العشرية في كلا الكسرين ، ثم عد نفس عدد الأرقام على اليمين في الإجابة ووضع فاصلة.

مثال 1أوجد قيمة التعبير 2.5 × 1.5

نضرب هذه الكسور العشرية كأرقام عادية ، متجاهلين الفواصل. لتجاهل الفواصل ، يمكنك أن تتخيل مؤقتًا أنها غائبة تمامًا:

حصلنا على 375. في هذا الرقم ، من الضروري فصل الجزء الكامل من الجزء الكسري بفاصلة. للقيام بذلك ، تحتاج إلى حساب عدد الأرقام بعد الفاصلة العشرية في كسرين 2.5 و 1.5. في الكسر الأول يوجد رقم واحد بعد الفاصلة العشرية ، وفي الكسر الثاني يوجد رقم واحد أيضًا. ما مجموعه رقمين.

نعود إلى الرقم 375 ونبدأ في التحرك من اليمين إلى اليسار. نحتاج إلى عد رقمين من اليمين ووضع فاصلة:

حصلت على الجواب 3.75. إذن ، فإن قيمة التعبير 2.5 × 1.5 هي 3.75

2.5 × 1.5 = 3.75

مثال 2أوجد قيمة التعبير 12.85 × 2.7

دعونا نضرب هذه الكسور العشرية ، متجاهلين الفواصل:

حصلنا على 34695. في هذا الرقم ، تحتاج إلى فصل الجزء الصحيح من الجزء الكسري بفاصلة. للقيام بذلك ، تحتاج إلى حساب عدد الأرقام بعد الفاصلة العشرية في كسور 12.85 و 2.7. في الكسر 12.85 يوجد رقمان بعد الفاصلة العشرية ، وفي الكسر 2.7 يوجد رقم واحد - إجمالي ثلاثة أرقام.

نعود إلى الرقم 34695 ونبدأ في التحرك من اليمين إلى اليسار. نحتاج إلى عد ثلاثة أرقام من اليمين ووضع فاصلة:

حصلت على إجابة 34695. إذن ، فإن قيمة التعبير 12.85 × 2.7 هي 34.695

12.85 × 2.7 = 34.695

ضرب عدد عشري في رقم عادي

في بعض الأحيان توجد مواقف تحتاج فيها إلى ضرب كسر عشري في رقم عادي.

لضرب رقم عشري ورقم عادي ، تحتاج إلى ضربهما ، بغض النظر عن الفاصلة في العلامة العشرية. بعد تلقي الإجابة ، من الضروري فصل الجزء الصحيح عن الجزء الكسري بفاصلة. للقيام بذلك ، تحتاج إلى حساب عدد الأرقام بعد الفاصلة العشرية في الكسر العشري ، ثم في الإجابة ، قم بحساب نفس عدد الأرقام إلى اليمين ووضع فاصلة.

على سبيل المثال ، اضرب 2.54 في 2

نضرب الكسر العشري 2.54 في الرقم المعتاد 2 ، مع تجاهل الفاصلة:

حصلنا على الرقم 508. في هذا الرقم ، تحتاج إلى فصل الجزء الصحيح من الجزء الكسري بفاصلة. للقيام بذلك ، تحتاج إلى حساب عدد الأرقام بعد الفاصلة العشرية في الكسر 2.54. يتكون الكسر 2.54 من رقمين بعد الفاصلة العشرية.

نعود إلى الرقم 508 ونبدأ في التحرك من اليمين إلى اليسار. نحتاج إلى عد رقمين من اليمين ووضع فاصلة:

حصلت على الجواب 5.08. إذن ، فإن قيمة التعبير 2.54 × 2 هي 5.08

2.54 × 2 = 5.08

ضرب الكسور العشرية بـ 10 ، 100 ، 1000

يتم ضرب الكسور العشرية في 10 أو 100 أو 1000 بنفس طريقة ضرب الكسور العشرية في الأعداد العادية. من الضروري إجراء الضرب ، وتجاهل الفاصلة في الكسر العشري ، ثم في الإجابة ، افصل الجزء الصحيح عن الجزء الكسري ، مع حساب نفس عدد الأرقام على اليمين حيث كانت هناك أرقام بعد الفاصلة العشرية جزء.

على سبيل المثال ، اضرب 2.88 في 10

لنضرب الكسر العشري 2.88 في 10 ، مع تجاهل الفاصلة في الكسر العشري:

حصلنا على 2880. في هذا الرقم ، تحتاج إلى فصل الجزء الكامل من الجزء الكسري بفاصلة. للقيام بذلك ، تحتاج إلى حساب عدد الأرقام بعد الفاصلة العشرية في الكسر 2.88. نرى أنه في الكسر 2.88 يوجد رقمان بعد الفاصلة العشرية.

نعود إلى الرقم 2880 ونبدأ في التحرك من اليمين إلى اليسار. نحتاج إلى عد رقمين من اليمين ووضع فاصلة:

حصلت على الاجابة 28.80. نتجاهل الصفر الأخير - نحصل على 28.8. إذن ، فإن قيمة التعبير 2.88 × 10 هي 28.8

2.88 × 10 = 28.8

هناك طريقة ثانية لضرب الكسور العشرية في 10 ، 100 ، 1000. هذه الطريقة أبسط بكثير وأكثر ملاءمة. وهو يتألف من حقيقة أن الفاصلة في الكسر العشري تتحرك إلى اليمين بعدد أرقام يساوي عدد الأصفار في المضاعف.

على سبيل المثال ، لنحل المثال السابق 2.88 × 10 بهذه الطريقة. دون إعطاء أي حسابات ، ننظر على الفور إلى العامل 10. نحن مهتمون بعدد الأصفار فيه. نرى أنه يحتوي على صفر واحد. الآن في الكسر 2.88 نقوم بتحريك الفاصلة العشرية إلى اليمين برقم واحد ، نحصل على 28.8.

2.88 × 10 = 28.8

دعنا نحاول ضرب 2.88 في 100. ننظر على الفور إلى العامل 100. نحن مهتمون بعدد الأصفار فيه. نرى أن لها صفرين. الآن في الكسر 2.88 نقوم بتحريك الفاصلة العشرية إلى اليمين بمقدار رقمين ، نحصل على 288

2.88 × 100 = 288

دعنا نحاول ضرب 2.88 في 1000. ننظر على الفور إلى العامل 1000. نحن مهتمون بعدد الأصفار فيه. نرى أن لها ثلاثة أصفار. الآن في الكسر 2.88 نقوم بتحريك الفاصلة العشرية إلى اليمين بثلاثة أرقام. الرقم الثالث غير موجود ، لذا نضيف صفرًا آخر. نتيجة لذلك ، نحصل على 2880.

2.88 × 1000 = 2880

ضرب الكسور العشرية في 0.1 0.01 و 0.001

يعمل ضرب الكسور العشرية في 0.1 و 0.01 و 0.001 بنفس طريقة ضرب رقم عشري في عدد عشري. من الضروري ضرب الكسور مثل الأعداد العادية ، ووضع فاصلة في الإجابة ، مع حساب عدد الأرقام على اليمين حيث توجد أرقام بعد الفاصلة العشرية في كلا الكسرين.

على سبيل المثال ، اضرب 3.25 في 0.1

نضرب هذه الكسور مثل الأعداد العادية ، متجاهلين الفواصل:

حصلنا على 325. في هذا الرقم ، تحتاج إلى فصل الجزء الكامل من الجزء الكسري بفاصلة. للقيام بذلك ، تحتاج إلى حساب عدد الأرقام بعد الفاصلة العشرية في كسور 3.25 و 0.1. في الكسر 3.25 يوجد رقمان بعد الفاصلة العشرية ، وفي الكسر 0.1 يوجد رقم واحد. ما مجموعه ثلاثة أرقام.

نعود إلى الرقم 325 ونبدأ في التحرك من اليمين إلى اليسار. نحتاج إلى عد ثلاثة أرقام على اليمين ووضع فاصلة. بعد عد ثلاثة أرقام ، نجد أن الأعداد قد انتهت. في هذه الحالة ، تحتاج إلى إضافة صفر ووضع فاصلة:

حصلنا على الإجابة 0.325. إذن ، فإن قيمة التعبير 3.25 × 0.1 هي 0.325

3.25 × 0.1 = 0.325

هناك طريقة ثانية لضرب الكسور العشرية في 0.1 و 0.01 و 0.001. هذه الطريقة أسهل بكثير وأكثر ملاءمة. وهو يتألف من حقيقة أن الفاصلة في الكسر العشري تتحرك إلى اليسار بمقدار عدد من الأرقام مثل الأصفار في المضاعف.

على سبيل المثال ، لنحل المثال السابق 3.25 × 0.1 بهذه الطريقة. دون إعطاء أي حسابات ، ننظر على الفور إلى العامل 0.1. نحن مهتمون بعدد الأصفار الموجودة فيه. نرى أنه يحتوي على صفر واحد. الآن في الكسر 3.25 نقوم بتحريك العلامة العشرية إلى اليسار بمقدار رقم واحد. عند تحريك الفاصلة رقمًا واحدًا إلى اليسار ، نرى أنه لا يوجد المزيد من الأرقام قبل الثلاثة. في هذه الحالة ، أضف صفرًا وضع فاصلة. نتيجة لذلك ، نحصل على 0.325

3.25 × 0.1 = 0.325

لنجرب ضرب 3.25 في 0.01. انظر على الفور إلى مضاعف 0.01. نحن مهتمون بعدد الأصفار الموجودة فيه. نرى أن لها صفرين. الآن في الكسر 3.25 نحرك الفاصلة إلى اليسار بمقدار رقمين ، نحصل على 0.0325

3.25 × 0.01 = 0.0325

لنجرب ضرب 3.25 في 0.001. انظر على الفور إلى مضاعف 0.001. نحن مهتمون بعدد الأصفار الموجودة فيه. نرى أن لها ثلاثة أصفار. الآن في الكسر 3.25 نقوم بتحريك العلامة العشرية إلى اليسار بمقدار ثلاثة أرقام ، نحصل على 0.00325

3.25 × 0.001 = 0.00325

لا تخلط بين ضرب الكسور العشرية في 0.1 و 0.001 و 0.001 مع الضرب في 10 و 100 و 1000. خطأ عاممعظم الناس.

عند الضرب في 10 ، 100 ، 1000 ، يتم نقل الفاصلة إلى اليمين من خلال العديد من الأرقام حيث توجد أصفار في المضاعف.

وعند الضرب في 0.1 و 0.01 و 0.001 ، يتم نقل الفاصلة إلى اليسار بعدد من الأرقام يساوي عدد الأصفار في المضاعف.

إذا كان من الصعب تذكر ذلك في البداية ، يمكنك استخدام الطريقة الأولى ، والتي يتم فيها الضرب كما هو الحال مع الأرقام العادية. في الإجابة ، ستحتاج إلى فصل الجزء الصحيح عن الجزء الكسري عن طريق حساب عدد الأرقام الموجودة على اليمين حيث توجد أرقام بعد الفاصلة العشرية في كلا الكسرين.

قسمة عدد أصغر على رقم أكبر. مستوى متقدم.

قلنا في أحد الدروس السابقة أنه عند قسمة عدد أصغر على عدد أكبر ، نحصل على كسر ، في بسطه المقسوم ، وفي المقام هو المقسوم عليه.

على سبيل المثال ، لتقسيم تفاحة واحدة إلى اثنتين ، عليك كتابة 1 (تفاحة واحدة) في البسط ، وكتابة 2 (صديقان) في المقام. النتيجة هي كسر. لذلك سيحصل كل صديق على تفاحة. بمعنى آخر ، نصف تفاحة. الكسر هو الحل لمشكلة ما كيفية تقسيم تفاحة واحدة بين اثنين

اتضح أنه يمكنك حل هذه المسألة أكثر إذا قسمت 1 على 2. بعد كل شيء ، الشريط الكسري في أي كسر يعني القسمة ، مما يعني أن هذه القسمة مسموح بها أيضًا في الكسر. ولكن كيف؟ تعودنا على حقيقة أن المقسوم أكبر دائمًا من المقسوم عليه. وهنا ، على العكس من ذلك ، المقسوم أقل من المقسوم عليه.

سيتضح كل شيء إذا تذكرنا أن الكسر يعني التكسير والقسمة والقسمة. هذا يعني أنه يمكن تقسيم الوحدة إلى أي عدد تريده من الأجزاء ، وليس إلى جزأين فقط.

عند قسمة عدد أصغر على رقم أكبر ، يتم الحصول على كسر عشري ، يكون فيه الجزء الصحيح 0 (صفر). يمكن أن يكون الجزء الكسري أي شيء.

لنقسم 1 على 2. لنحل هذا المثال بزاوية:

لا يمكن تقسيم المرء إلى قسمين بهذه الطريقة. إذا سألت سؤالا "كم عدد الثنائيات في واحد" ، إذن ستكون الإجابة 0. لذلك ، على انفراد نكتب 0 ونضع فاصلة:

الآن ، كالعادة ، نضرب حاصل القسمة في القاسم لنخرج الباقي:

حانت اللحظة التي يمكن فيها تقسيم الوحدة إلى قسمين. للقيام بذلك ، أضف صفرًا آخر إلى يمين المستلم:

حصلنا على 10. نقسم 10 على 2 ، ونحصل على 5. نكتب الخمسة في الجزء الكسري من إجابتنا:

الآن نخرج الباقي الأخير لإكمال الحساب. اضرب 5 في 2 ، نحصل على 10

حصلنا على 0.5 الإجابة. إذن ، الكسر يساوي 0.5

يمكن أيضًا كتابة نصف تفاحة باستخدام الكسر العشري 0.5. إذا أضفنا هذين النصفين (0.5 و 0.5) ، فسنحصل مرة أخرى على التفاحة الكاملة الأصلية:

يمكن أيضًا فهم هذه النقطة إذا تخيلنا كيفية تقسيم 1 سم إلى جزأين. إذا قسمت سنتيمترًا واحدًا إلى جزئين ، فستحصل على 0.5 سم

مثال 2أوجد قيمة التعبير 4: 5

كم عدد الخمسات في أربعة؟ مُطْلَقاً. نكتب 0 الخاص ونضع فاصلة:

نضرب 0 في 5 ، نحصل على 0. نكتب صفرًا تحت الأربعة. اطرح هذا الصفر على الفور من المقسوم:

لنبدأ الآن في تقسيم (تقسيم) الأربعة إلى 5 أجزاء. للقيام بذلك ، على يمين 4 ، نضيف صفرًا ونقسم 40 على 5 ، ونحصل على 8. نكتب الثمانية على انفراد.

نكمل المثال بضرب 8 في 5 ، ونحصل على 40:

حصلنا على الإجابة 0.8. إذن ، فإن قيمة التعبير 4: 5 هي 0.8

مثال 3أوجد قيمة التعبير 5: 125

كم عدد 125 في خمسة؟ مُطْلَقاً. نكتب 0 على انفراد ونضع فاصلة:

نضرب 0 في 5 ، نحصل على 0. نكتب 0 تحت الخمسة. اطرح فورًا من الخمسة 0

لنبدأ الآن في تقسيم (تقسيم) الخمسة إلى 125 جزءًا. للقيام بذلك ، على يمين هذه الخمسة ، نكتب صفرًا:

قسّم 50 على 125. كم عدد 125 في 50؟ مُطْلَقاً. لذا نكتب 0 مرة أخرى في حاصل القسمة

نضرب 0 في 125 ، نحصل على 0. نكتب هذا الصفر تحت 50. اطرح 0 من 50 على الفور

الآن نقسم الرقم 50 إلى 125 جزءًا. للقيام بذلك ، إلى يمين الرقم 50 ، نكتب صفرًا آخر:

قسّم 500 على 125. كم عدد الأرقام 125 في الرقم 500. في الرقم 500 هناك أربعة أعداد 125. نكتب الأربعة على انفراد:

نكمل المثال بضرب 4 في 125 ، ونحصل على 500

حصلنا على الإجابة 0.04. إذن ، فإن قيمة التعبير 5: 125 هي 0.04

قسمة الأعداد بدون باقي

لذلك ، دعونا نضع فاصلة في حاصل القسمة بعد الوحدة ، مما يشير إلى أن تقسيم الأجزاء الصحيحة قد انتهى وننتقل إلى الجزء الكسري:

أضف صفرًا إلى الباقي 4

الآن نقسم 40 على 5 ، نحصل على 8. نكتب الثمانية على انفراد:

40-40 = 0. تلقى 0 في الباقي. لذا فإن القسمة قد اكتملت بالكامل. ينتج عن قسمة 9 على 5 عدد عشري 1.8:

9: 5 = 1,8

مثال 2. قسّم 84 على 5 بدون الباقي

أولاً نقسم 84 على 5 كالمعتاد مع الباقي:

حصل على 16 خاص و 4 في الميزان. الآن نقسم الباقي على 5. نضع فاصلة في الخاص ، ونضيف 0 إلى الباقي 4

الآن نقسم 40 على 5 ، نحصل على 8. نكتب الثمانية في خارج القسمة بعد الفاصلة العشرية:

وأكمل المثال بالتحقق مما إذا كان لا يزال هناك باقي:

قسمة العلامة العشرية على رقم عادي

يتكون الكسر العشري ، كما نعلم ، من عدد صحيح وجزء كسري. عند قسمة كسر عشري على رقم عادي ، تحتاج أولاً إلى:

• قسّم الجزء الصحيح من الكسر العشري على هذا الرقم ؛
• بعد تقسيم الجزء الصحيح ، تحتاج إلى وضع فاصلة على الفور في الجزء الخاص ومتابعة الحساب ، كما هو الحال في القسمة العادية.

على سبيل المثال ، دعنا نقسم 4.8 على 2

لنكتب هذا المثال كزاوية:

الآن لنقسم الجزء كله على 2. أربعة على اثنين يساوي اثنين. نكتب الشيطان على انفراد ونضع فاصلة على الفور:

الآن نضرب حاصل القسمة في المقسوم عليه ونرى ما إذا كان هناك باقٍ من القسمة:

4−4 = 0. الباقي صفر. لم نكتب صفرًا بعد ، لأن الحل لم يكتمل. ثم نواصل الحساب ، كما هو الحال في القسمة العادية. انزل 8 وقسمه على 2

8: 2 = 4. نكتب الأربعة في حاصل القسمة ونضربها في القاسم على الفور:

حصلت على الجواب 2.4. قيمة التعبير 4.8: 2 تساوي 2.4

مثال 2أوجد قيمة التعبير 8.43: 3

نقسم 8 على 3 ، نحصل على 2. وضع فاصلة على الفور بعد الاثنين:

الآن نضرب حاصل القسمة في المقسوم عليه 2 × 3 = 6. نكتب الستة تحت الثمانية ونوجد الباقي:

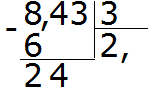
نقسم 24 على 3 ، نحصل على 8. نكتب الثمانية على انفراد. نضربه على الفور في المقسوم عليه لإيجاد باقي القسمة:

24−24 = 0. الباقي صفر. لم يتم تسجيل الصفر بعد. خذ الثلاثة الأخيرة من المقسوم واقسم على 3 ، نحصل على 1. اضرب 1 في 3 على الفور لإكمال هذا المثال:

حصلت على الإجابة 2.81. إذن ، فإن قيمة التعبير 8.43: 3 تساوي 2.81

قسمة عدد عشري على عدد عشري

لتقسيم كسر عشري إلى كسر عشري ، في المقسوم وفي المقسوم عليه ، انقل الفاصلة إلى اليمين بنفس عدد الأرقام الموجود بعد الفاصلة العشرية في المقسوم عليه ، ثم اقسم على رقم عادي.

على سبيل المثال ، قسّم 5.95 على 1.7

لنكتب هذا التعبير كزاوية

الآن ، في المقسوم والمقسوم عليه ، ننقل الفاصلة إلى اليمين بنفس عدد الأرقام الموجود بعد الفاصلة العشرية في المقسوم عليه. للمقسوم عليه رقم واحد بعد الفاصلة العشرية. لذا علينا تحريك الفاصلة إلى اليمين بمقدار رقم واحد في المقسوم وفي المقسوم عليه. التحويل:

بعد تحريك الفاصلة العشرية إلى اليمين برقم واحد ، تحول الكسر العشري 5.95 إلى كسر 59.5. والكسر العشري 1.7 ، بعد نقل الفاصلة العشرية إلى اليمين برقم واحد ، تحول إلى الرقم المعتاد 17. ونحن نعرف بالفعل كيفية قسمة الكسر العشري على العدد المعتاد. الحساب الإضافي ليس بالأمر الصعب:

يتم نقل الفاصلة إلى اليمين لتسهيل القسمة. هذا مسموح به نظرًا لحقيقة أنه عند ضرب أو قسمة المقسوم والمقسوم على نفس الرقم ، فإن حاصل القسمة لا يتغير. ماذا يعني ذلك؟

هذا هو واحد من ميزات مثيرة للاهتمامقسم. يطلق عليه الملكية الخاصة. ضع في اعتبارك التعبير 9: 3 = 3. إذا تم ضرب المقسوم والمقسوم عليه في هذا التعبير أو قسما على نفس الرقم ، فلن يتغير حاصل القسمة 3.

لنضرب المقسوم والمقسوم عليه في 2 ونرى ما سيحدث:

(9 × 2): (3 × 2) = 18: 6 = 3

كما يتضح من المثال ، لم يتغير حاصل القسمة.

يحدث الشيء نفسه عندما نحمل فاصلة في المقسوم والمقسوم عليه. في المثال السابق ، حيث قسمنا 5.91 على 1.7 ، نقلنا الفاصلة رقمًا واحدًا إلى اليمين في المقسوم والمقسوم عليه. بعد تحريك الفاصلة ، تم تحويل الكسر 5.91 إلى كسر 59.1 وتم تحويل الكسر 1.7 إلى الرقم المعتاد 17.

في الواقع ، حدثت عملية الضرب في 10 داخل هذه العملية ، وهذا ما بدا عليه الأمر:

5.91 × 10 = 59.1

لذلك ، فإن عدد الأرقام بعد الفاصلة العشرية في المقسوم عليه يعتمد على ما سيتم ضرب المقسوم عليه والمقسوم عليه. بمعنى آخر ، فإن عدد الأرقام بعد الفاصلة العشرية في المقسوم عليه سيحدد عدد الأرقام في المقسوم وفي المقسوم عليه ، سيتم نقل الفاصلة إلى اليمين.

القسمة العشرية على 10 ، 100 ، 1000

تتم قسمة العلامة العشرية على 10 أو 100 أو 1000 بنفس طريقة قسمة الكسر العشري على 10 أو 100 أو 1000. على سبيل المثال ، دعنا نقسم 2.1 على 10. لنحل هذا المثال بزاوية:

ولكن هناك أيضًا طريقة ثانية. إنه أخف وزنا. جوهر هذه الطريقة هو أن الفاصلة في المقسوم يتم نقلها إلى اليسار بمقدار عدد من الأرقام مثل الأصفار في المقسوم عليه.

لنحل المثال السابق بهذه الطريقة. 2.1: 10. ننظر إلى الحاجز. نحن مهتمون بعدد الأصفار الموجودة فيه. نرى أن هناك صفرًا واحدًا. لذا في الإصدار 2.1 القابل للقسمة ، تحتاج إلى تحريك الفاصلة إلى اليسار بمقدار رقم واحد. نحرك الفاصلة إلى اليسار برقم واحد ونرى أنه لم يعد هناك المزيد من الأرقام. في هذه الحالة ، نضيف صفرًا واحدًا قبل الرقم. نتيجة لذلك ، نحصل على 0.21

لنحاول قسمة 2.1 على 100. يوجد صفرين في العدد 100. لذا في الإصدار 2.1 القابل للقسمة ، تحتاج إلى تحريك الفاصلة إلى اليسار بمقدار رقمين:

2,1: 100 = 0,021

لنحاول قسمة 2.1 على 1000. يوجد ثلاثة أصفار في العدد 1000. لذا في الإصدار 2.1 القابل للقسمة ، تحتاج إلى تحريك الفاصلة إلى اليسار بثلاثة أرقام:

2,1: 1000 = 0,0021

القسمة العشرية على 0.1 و 0.01 و 0.001

يتم قسمة العلامة العشرية على 0.1 و 0.01 و 0.001 بنفس طريقة قسمة الكسر العشري على 0.1 و 0.01 و 0.001. في المقسوم والمقسوم عليه ، تحتاج إلى تحريك الفاصلة إلى اليمين بعدد من الأرقام كما هو موجود بعد الفاصلة العشرية في المقسوم عليه.

على سبيل المثال ، دعنا نقسم 6.3 على 0.1. بادئ ذي بدء ، نقوم بتحريك الفواصل في المقسوم وفي المقسوم عليه إلى اليمين بنفس عدد الأرقام الموجود بعد الفاصلة العشرية في المقسوم عليه. للمقسوم عليه رقم واحد بعد الفاصلة العشرية. لذلك ننقل الفاصلتين في المقسوم وفي المقسوم عليه إلى اليمين برقم واحد.

بعد نقل الفاصلة العشرية إلى اليمين برقم واحد ، يتحول الكسر العشري 6.3 إلى الرقم المعتاد 63 ، ويتحول الكسر العشري 0.1 ، بعد نقل الفاصلة العشرية إلى اليمين برقم واحد ، إلى واحد. وقسمة 63 على 1 بسيطة للغاية:

إذن ، فإن قيمة التعبير 6.3: 0.1 تساوي 63

ولكن هناك أيضًا طريقة ثانية. إنه أخف وزنا. جوهر هذه الطريقة هو أن الفاصلة في المقسوم يتم نقلها إلى اليمين من خلال عدد من الأرقام مثل الأصفار في المقسوم عليه.

لنحل المثال السابق بهذه الطريقة. 6.3: 0.1. لنلق نظرة على الحاجز. نحن مهتمون بعدد الأصفار الموجودة فيه. نرى أن هناك صفرًا واحدًا. لذا في 6.3 القابل للقسمة ، تحتاج إلى تحريك الفاصلة إلى اليمين بمقدار رقم واحد. نحرك الفاصلة إلى اليمين برقم واحد ونحصل على 63

لنحاول قسمة 6.3 على 0.01. المقسوم عليه 0.01 له صفرين. لذلك في 6.3 القابل للقسمة ، تحتاج إلى تحريك الفاصلة إلى اليمين بمقدار رقمين. ولكن في المقسوم يوجد رقم واحد فقط بعد الفاصلة العشرية. في هذه الحالة ، يجب إضافة صفر واحد في النهاية. نتيجة لذلك ، حصلنا على 630

لنجرب قسمة 6.3 على 0.001. للمقسوم عليه 0.001 ثلاثة أصفار. لذا في 6.3 القابل للقسمة ، تحتاج إلى تحريك الفاصلة إلى اليمين بثلاثة أرقام:

6,3: 0,001 = 6300

مهام الحل المستقل

هل أعجبك الدرس؟
انضم الينا مجموعة جديدةفكونتاكتي وابدأ في تلقي إشعارات حول الدروس الجديدة