Il problema è formulato come segue: lasciamo la quantità desiderata z determinato attraverso altre quantità a, b, c, ... ottenuti da misurazioni dirette
z = f (a, b, c,...) (1.11)
È necessario trovare il valore medio della funzione e l'errore delle sue misurazioni, ad es. trovare l'intervallo di confidenza
con affidabilità a e relativo errore .
Per quanto riguarda , si trova invece sostituendo nella parte destra di (11). a, b, c,...i loro valori medi
Errore assoluto misurazioni indiretteè una funzione degli errori assoluti delle misurazioni dirette ed è calcolata dalla formula
 (1.14)
(1.14)
Ecco le derivate parziali della funzione F da variabili un, b, …
Se i valori a, b, c,...in una funzione Z = f (a, b, c,...) sono inclusi sotto forma di fattori in varia misura, vale a dire se
![]() , (1.15)
, (1.15)
allora conviene calcolare prima l'errore relativo
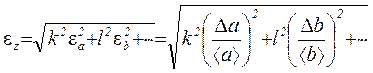 , (1.16)
, (1.16)
e quindi assoluto
Formule per D z ed ez sono forniti nella letteratura di riferimento.
Appunti
1. Per le misurazioni indirette, le formule di calcolo possono includere costanti fisiche note (accelerazione caduta libera G, velocità della luce nel vuoto Con ecc.), numeri come fattori frazionari... . Questi valori vengono arrotondati durante i calcoli. In questo caso, ovviamente, viene introdotto un errore nel calcolo ![]() - errore di arrotondamento nei calcoli, di cui occorre tenere conto.
- errore di arrotondamento nei calcoli, di cui occorre tenere conto.
È generalmente accettato che l'errore di arrotondamento di un numero approssimativo sia pari a mezza unità della cifra a cui questo numero è stato arrotondato. Ad esempio, pag = 3.14159... . Se prendiamo p = 3,1, allora Dp = 0,05, se p = 3,14, allora Dp = 0,005 ... ecc. La questione su quale cifra arrotondare un numero approssimativo si risolve come segue: l'errore relativo introdotto dall'arrotondamento deve essere dello stesso ordine o di un ordine di grandezza inferiore al massimo degli errori relativi di altro tipo. L'errore assoluto dei dati tabulari viene stimato allo stesso modo. Ad esempio, la tabella indica r = 13,6 × 10 3 kg/m 3, quindi Dr = 0,05 × 10 3 kg/m 3.
L'errore nei valori delle costanti universali viene spesso indicato insieme ai loro valori presi come media: ( Con = ![]() m/s, dove D Con= 0,3×10 3 m/s.
m/s, dove D Con= 0,3×10 3 m/s.
2. Talvolta, con le misurazioni indirette, le condizioni sperimentali non coincidono con le osservazioni ripetute. In questo caso, la funzione value z viene calcolato per ogni singola misurazione e l'intervallo di confidenza viene calcolato tra i valori z come per le misurazioni dirette (tutti gli errori qui sono inclusi in un errore di misurazione casuale z). I valori non misurati, ma specificati (se esistenti) devono essere indicati con una precisione sufficientemente elevata.
La procedura per l'elaborazione dei risultati delle misurazioni
Misurazioni dirette
1. Calcola il valore medio di N misurazioni
2. Trova gli errori delle singole misurazioni ![]() .
.
3. Calcola gli errori quadratici delle singole misurazioni e la loro somma: 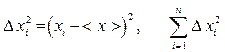 .
.
4. Imposta l'affidabilitàa (per i nostri scopi prendiamo a = 0,95) e utilizza la tabella per determinare i coefficienti di Student T UN, N e t a, ¥ .
5. Effettuare una valutazione errori sistematici: strumento D X errori di arrotondamento nelle misurazioniD X env = D/2 (D è il valore della divisione dello strumento) e trovare l'errore totale del risultato della misurazione (metà ampiezza dell'intervallo di confidenza):
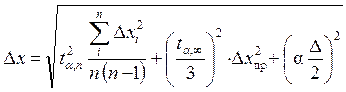 .
.
6. Stimare l'errore relativo
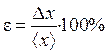 .
.
7. Scrivi il risultato finale nel modulo
![]() ε = … % per a = ...
ε = … % per a = ...
Misure indirette
1. Per ogni grandezza misurata direttamente, inserita nella formula per determinare la quantità desiderata ![]() , effettuare il trattamento come sopra indicato. Se tra le quantità a, b, c, ... ci sono costanti di tabella o numeri di tipo p, e,..., allora durante i calcoli dovrebbero essere arrotondati in modo (se possibile) che l'errore relativo introdotto sia un ordine di grandezza inferiore all'errore relativo più grande delle grandezze misurate direttamente.
, effettuare il trattamento come sopra indicato. Se tra le quantità a, b, c, ... ci sono costanti di tabella o numeri di tipo p, e,..., allora durante i calcoli dovrebbero essere arrotondati in modo (se possibile) che l'errore relativo introdotto sia un ordine di grandezza inferiore all'errore relativo più grande delle grandezze misurate direttamente.
Determinare il valore medio della quantità desiderata
z = f( ,,
3. Stimare la semiampiezza dell'intervallo di confidenza per il risultato delle misurazioni indirette
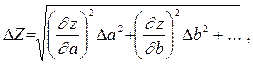 ,
,
dove i derivati ... sono calcolati a
4. Determinare l'errore relativo del risultato
![]()
5. Se la dipendenza di z da a, b, c,... ha la forma ![]() , Dove k, l, m‒ qualsiasi numero reale, devi prima trovarlo parente errore
, Dove k, l, m‒ qualsiasi numero reale, devi prima trovarlo parente errore
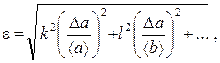
poi assoluto .
6. Scrivi il risultato finale nel modulo
z =
Nota:
Quando si elaborano i risultati delle misurazioni dirette, è necessario seguire la seguente regola: i valori numerici di tutte le quantità calcolate devono contenere una cifra in più rispetto alle quantità originali (determinate sperimentalmente).
Per le misurazioni indirette, i calcoli vengono effettuati secondo regole di calcolo approssimativo:
Regola 1. Quando aggiungi e sottrai numeri approssimativi, devi:
a) selezionare il termine in cui la cifra dubbia ha la cifra più alta;
b) arrotondare tutti gli altri termini alla cifra successiva (viene mantenuta una cifra di riserva);
c) eseguire addizioni (sottrazioni);
d) scartare di conseguenza ultima cifra mediante arrotondamento (la cifra della cifra dubbia del risultato coincide con la cifra più alta delle cifre dubbie dei termini).
Esempio: 5,4382·10 5 – 2,918·10 3 + 35,8 + 0,064.
In questi numeri le ultime cifre significative sono dubbie (quelle errate sono già state scartate). Scriviamoli nella forma 543820 – 2918 + 35,8 + 0,064.
Si può vedere che nel primo termine il numero dubbio 2 ha la cifra più alta (le decine). Arrotondando tutti gli altri numeri alla cifra successiva e sommando, otteniamo
543820 – 2918 + 36 + 0 = 540940 = 5,4094 10 5.
Regola 2. Quando moltiplichi (dividi) numeri approssimati devi:
a) selezionare il/i numero/i con il minor numero di cifre significative ( SIGNIFICATIVO – numeri diversi dallo zero e zeri tra di loro);
b) arrotondare i numeri rimanenti in modo che abbiano una cifra significativa in più (viene mantenuta una cifra di riserva) rispetto a quelle assegnate al passaggio a;
c) moltiplicare (dividere) i numeri risultanti;
d) lasciare di conseguenza tante cifre significative quante erano nel/i numero/i con meno cifre significative.
Esempio: .
Regola 3. Quando elevato a una potenza, quando si estrae una radice, il risultato conserva tante cifre significative quante sono nel numero originale.
Esempio: ![]() .
.
Regola 4. Quando si trova il logaritmo di un numero, la mantissa del logaritmo deve avere tante cifre significative quante sono il numero originale:
Esempio: ![]() .
.
Nella registrazione finale assoluto gli errori dovrebbero essere lasciati solo una cifra significativa. (Se questa cifra risulta essere 1, dopo di essa viene memorizzata un'altra cifra).
Il valore medio viene arrotondato alla stessa cifra dell'errore assoluto.
Per esempio: V= (375,21 0,03) cm 3 = (3,7521 0,0003) cm 3.
IO= (5,530 0,013) A, UN = ![]() J.
J.
Ordine di lavoro
Determinazione del diametro del cilindro.
1. Utilizzando un calibro, misurare 7 volte (in luoghi differenti e direzioni) diametro del cilindro. Registra i risultati in una tabella.
| NO. | d io, mm | d io- | (d io- | ciao io, mm E Informazioni correlate: |
STIME ELEMENTARI DELL'ERRORE DI MISURA
La misurazione consiste nel trovare il valore di una quantità fisica sperimentalmente utilizzando speciali mezzi tecnici- misure, strumenti di misura.
Una misura è un mezzo di misura che riproduce una quantità fisica di una determinata dimensione: un'unità di misura, il suo valore multiplo o frazionario. Ad esempio, pesa 1 kg, 5 kg, 10 kg.
Un dispositivo di misurazione è uno strumento di misurazione progettato per generare un segnale di misurazione delle informazioni in una forma accessibile alla percezione diretta da parte di un osservatore. Un dispositivo di misurazione consente di confrontare direttamente o indirettamente il valore misurato con le misure. Anche le misurazioni si dividono in dirette e indirette.
Nelle misurazioni dirette, il valore desiderato della quantità si trova direttamente dai dati di base (sperimentali).
Nelle misurazioni indirette, il valore desiderato di una grandezza si trova in base alla relazione nota tra tale grandezza e le grandezze sottoposte a misurazioni dirette. Il principio di misurazione è un insieme di fenomeni fisici su cui si basano le misurazioni.
Un metodo di misurazione è un insieme di tecniche per utilizzare principi e strumenti di misura. Senso quantità fisica, che idealmente rifletterebbe in termini qualitativi e quantitativi la corrispondente proprietà di un dato oggetto è il vero valore di una grandezza fisica. Il valore di una grandezza fisica trovato misurandola è il risultato della misurazione.
La deviazione del risultato della misurazione dal valore reale del valore misurato è l'errore di misurazione.
L'errore di misurazione assoluto è l'errore di misurazione, espresso in unità del valore misurato e pari alla differenza tra il risultato e il valore reale del valore misurato. Il rapporto tra l'errore assoluto e il valore reale della quantità misurata è l'errore di misurazione relativo.
Contributi all'errore di misurazione includono errori negli strumenti di misura (errore strumentale o strumentale), imperfezione del metodo di misurazione, errore nella lettura sulla scala dello strumento, influenze esterne su strumenti e oggetti di misura, ritardo nella reazione umana ai segnali luminosi e sonori.
In base alla natura della loro manifestazione, gli errori si dividono in sistematici e casuali. Un evento casuale è un evento che, dato un dato insieme di fattori, può verificarsi o meno.
L'errore casuale è una componente dell'errore di misurazione che cambia in modo casuale con misurazioni ripetute della stessa quantità. Un tratto caratteristico Gli errori casuali sono cambiamenti nell'entità e nel segno dell'errore in condizioni di misurazione costanti.
L'errore sistematico è una componente dell'errore di misurazione che rimane costante o cambia naturalmente con misurazioni ripetute della stessa quantità. Gli errori sistematici, in linea di principio, possono essere eliminati attraverso correzioni e l’uso di strumenti e metodi più accurati (anche se nella pratica non è sempre facile individuare errori sistematici). È impossibile escludere errori casuali nelle singole misurazioni; la teoria matematica dei fenomeni casuali (teoria della probabilità) consente solo di stabilire una stima ragionevole della loro grandezza.
Errori di misurazioni dirette
Supponiamo che gli errori sistematici siano esclusi e che gli errori nei risultati della misurazione siano solo casuali. Indichiamo con lettere i risultati delle misurazioni di una quantità fisica, vero significato che è uguale a ![]() . Sono indicati gli errori assoluti dei risultati delle singole misurazioni:
. Sono indicati gli errori assoluti dei risultati delle singole misurazioni:
Sommando i lati sinistro e destro dell’uguaglianza (1), otteniamo:
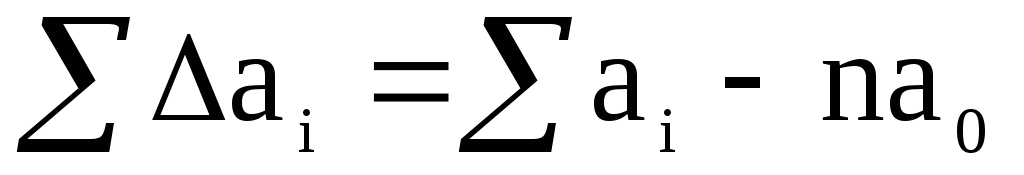 (2)
(2)
La teoria degli errori casuali si basa su ipotesi confermate dall’esperienza:
gli errori possono assumere una serie continua di valori;
A elevato numero misurazioni errori casuali della stessa grandezza, ma segno diverso si verificano altrettanto spesso;
la probabilità di un errore diminuisce all’aumentare della sua entità. È inoltre necessario che gli errori siano piccoli rispetto al valore misurato e indipendenti.
Secondo l'ipotesi (1), con il numero di misurazioni n otteniamo
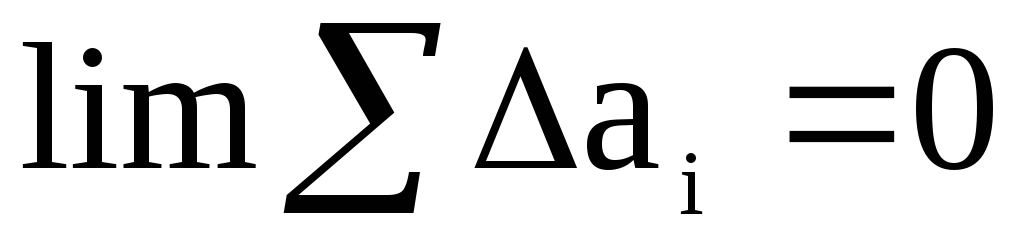
 ,
,
Tuttavia, il numero di dimensioni è sempre finito e ![]() rimane sconosciuto. Ma ai fini pratici è sufficiente trovare sperimentalmente il valore di una grandezza fisica così vicina a quella vera che
rimane sconosciuto. Ma ai fini pratici è sufficiente trovare sperimentalmente il valore di una grandezza fisica così vicina a quella vera che  può essere utilizzato invece di true. La domanda è: come valutare il grado di questa approssimazione?
può essere utilizzato invece di true. La domanda è: come valutare il grado di questa approssimazione?
Secondo la teoria della probabilità, la media aritmetica di una serie di misurazioni  più affidabile dei risultati delle singole misurazioni, perché sono ugualmente probabili deviazioni casuali dal valore reale in direzioni diverse. La probabilità della comparsa di un valore ai in un intervallo di larghezza 2a i è intesa come la frequenza relativa di occorrenza dei valori di a i che rientrano nell'intervallo 2a i rispetto al numero di tutti i valori che compaiono di a i con il numero di esperimenti (misure) tendente all'infinito. Ovviamente la probabilità di un evento affidabile è pari a uno, la probabilità di un evento impossibile è pari a zero, cioè 0 100%.
più affidabile dei risultati delle singole misurazioni, perché sono ugualmente probabili deviazioni casuali dal valore reale in direzioni diverse. La probabilità della comparsa di un valore ai in un intervallo di larghezza 2a i è intesa come la frequenza relativa di occorrenza dei valori di a i che rientrano nell'intervallo 2a i rispetto al numero di tutti i valori che compaiono di a i con il numero di esperimenti (misure) tendente all'infinito. Ovviamente la probabilità di un evento affidabile è pari a uno, la probabilità di un evento impossibile è pari a zero, cioè 0 100%.
La probabilità che il valore cercato (il suo vero valore) sia contenuto nell'intervallo (a - a, a + a) sarà chiamata probabilità di confidenza (affidabilità) , e il corrispondente intervallo (a - a, a + a) - intervallo di confidenza; Quanto più piccolo è l'errore a, tanto minore è la probabilità che il valore misurato sia contenuto nell'intervallo definito da questo errore. È vera anche l'affermazione opposta: meno affidabile è il risultato, più stretto è l'intervallo di confidenza del valore desiderato.
Per n grande (praticamente per n 100), la semiampiezza dell'intervallo di confidenza per una data affidabilità è uguale a
 ,
(3)
,
(3)
dove K() = 1 in = 0,68; K() = 2 in = 0,95; K() = 3 in = 0,997.
Con un numero limitato di misurazioni, che si riscontra più spesso nella pratica di laboratorio degli studenti, il coefficiente K() in (3) dipende non solo da , ma anche dal numero di misurazioni n. Pertanto, saremo sempre disponibili solo errore casuale trova la semiampiezza dell'intervallo di confidenza utilizzando la formula
 (4)
(4)
Nella (4), il coefficiente t n è chiamato coefficiente di Student. Per = 0,95 adottato nel lavoro pratico degli studenti, i valori di t n sono i seguenti:
Il valore è chiamato errore quadratico medio della media aritmetica di una serie di misurazioni.
L'errore di uno strumento o di una misura è solitamente indicato sul suo passaporto o da un simbolo sulla scala dello strumento. Solitamente per errore strumentale si intende la semiampiezza dell'intervallo entro il quale può essere contenuto il valore misurato con una probabilità di misura pari a 0,997, se l'errore di misura è dovuto solo all'errore strumentale. Come errore generale (totale) del risultato della misurazione, accetteremo con probabilità = 0,95
L'errore assoluto consente di determinare in quale segno del risultato ottenuto è contenuta l'imprecisione. L'errore relativo fornisce informazioni su quale proporzione (percentuale) del valore misurato è l'errore (metà ampiezza dell'intervallo di confidenza).
Scriviamo il risultato finale di una serie di misurazioni dirette del valore a 0 nel modulo
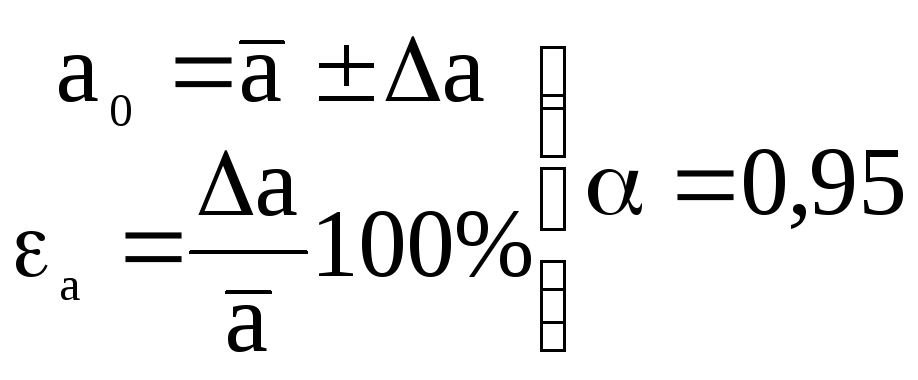 .
.
Per esempio
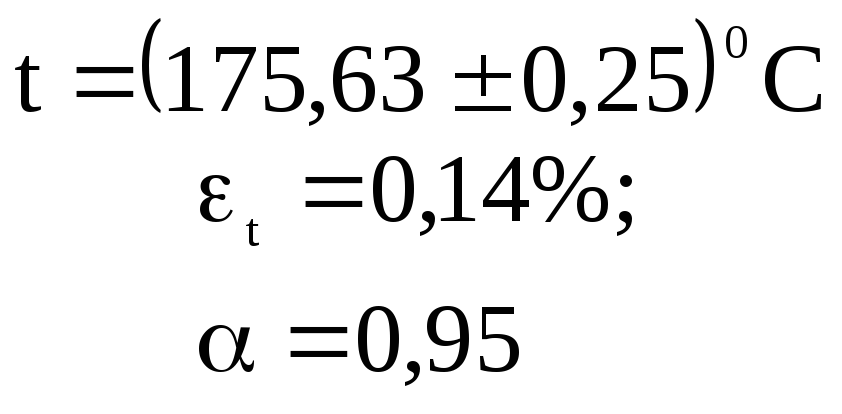 (6)
(6)
Pertanto, qualsiasi grandezza fisica trovata sperimentalmente deve essere rappresentata:

Errori nelle quantità misurate e tabulate determinano gli errori di DH avg del valore determinato indirettamente e il contributo maggiore a DH avg è dato dai valori meno accurati, che hanno l'errore relativo massimo D. Pertanto, per aumentare la precisione delle misurazioni indirette, è necessario raggiungere la stessa precisione delle misurazioni dirette
(d A, d B, d C, ...).
Regole per trovare errori nelle misurazioni indirette:
1. Trova il logaritmo naturale della funzione data
ln(X = f(A,B,C,…));
2. Trova il differenziale totale (su tutte le variabili) da quello trovato logaritmo naturale data funzione;
3. Sostituire il segno del differenziale d con il segno dell'errore assoluto D;
4. Sostituisci tutti gli "svantaggi" che comportano errori assoluti DA, DB, DC, ... ai "professionisti".
Il risultato è la formula per il più grande errore relativo dx valore misurato indirettamente X:
dx = = j (A medio, B medio, C medio, ..., DA medio, DB medio, DC medio, ...).(18)
Secondo l'errore relativo trovato dx determinare errore assoluto misurazione indiretta:
DX av = dx. X media . (19)
Il risultato delle misurazioni indirette è scritto in forma standard e rappresentato sull'asse numerico:
X = (X medio ± DХ medio), unità. (20)

Esempio:
Trova il parente e errore medio quantità fisica l, determinato indirettamente dalla formula:
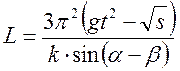 , (21)
, (21)
Dove π, g, t, k, α, β– grandezze i cui valori sono misurati o presi da tabelle di riferimento e inseriti in una tabella di risultati di misurazione e dati tabulati (simile alla Tabella 1).
1. Calcolare il valore medio Media, sostituendo i valori medi della tabella nella (21) – π medio, g medio, t medio, k medio, α medio, β medio.
2. Determinare l'errore relativo più grande δL:
UN). Formula del logaritmo (21):
B). L'espressione risultante (22) è differenziata:
c) Sostituisci il segno del differenziale d con Δ e i "meno" davanti agli errori assoluti con "più" e ottieni un'espressione per l'errore relativo più grande δL:
D). Sostituendo i valori medi delle quantità di input e i loro errori dalla tabella dei risultati di misurazione nell'espressione risultante, calcola δL.
3. Quindi calcolare l'errore assoluto ΔL medio:
![]()
Il risultato viene registrato in forma standard e rappresentato graficamente sull'asse l:
![]() , unità modifica
, unità modifica
