Per ridurre l'influenza degli errori casuali, è necessario misurare più volte questo valore. Supponiamo di misurare un valore x. Come risultato delle misurazioni, abbiamo ottenuto i seguenti valori:
x 1 , x 2 , x 3 , ... x n . (1.4)
Questa serie di valori x è chiamata campione. Avendo un tale campione, possiamo valutare il risultato della misurazione. Il valore che sarà tale stima, indicheremo . Ma poiché questo valore di valutazione dei risultati della misurazione non rappresenterà il vero valore della grandezza misurata, è necessario stimare il suo errore. Supponiamo di poter determinare la stima dell'errore Δx . In questo caso, possiamo scrivere il risultato della misurazione nel modulo
x = ±Δx. (1.5)
Poiché i valori stimati del risultato della misura e dell'errore Δx non sono esatti, la registrazione del risultato della misura deve essere accompagnata da un'indicazione della sua attendibilità P. Per affidabilità o probabilità di confidenza si intende la probabilità che vero valore del valore misurato è racchiuso nell'intervallo indicato dalla registrazione (3). Questo stesso intervallo è chiamato intervallo di confidenza.
Ad esempio, misurando la lunghezza di un certo segmento, abbiamo scritto il risultato finale come
l= (8,34 ± 0,02) mm,(P = 0,95). (1.6)
Ciò significa che su 100 possibilità - 95 che il vero valore della lunghezza del segmento risieda nell'intervallo da 8,32 a 8,36 mm.
Pertanto, il compito è, avendo un campione di misurazioni, trovare una stima del risultato della misurazione, il suo errore Δx e l'affidabilità P.
Questo problema può essere risolto usando la teoria della probabilità e statistica matematica.
Nella maggior parte dei casi, gli errori casuali seguono la normale legge di distribuzione stabilita da Gauss. La distribuzione normale degli errori è espressa dalla formula
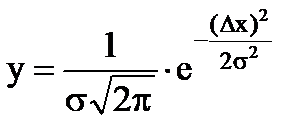, (1.7)
dove Δx è la deviazione dal valore vero;
σ è il vero errore quadratico medio;
σ 2 - dispersione, il cui valore caratterizza la diffusione di variabili casuali.
Come si può vedere dalla formula, la funzione y(x) ha valore massimo per x=0 , inoltre, è pari.
| si |
| X |
| ∆x 1 |
| ∆x2 |
| -Δx 1 |
| -Δx2 |
Fig.1.4. Curva di distribuzione normale gaussiana.
La Figura 1.4 mostra un grafico di questa funzione. L'area della figura racchiusa tra la curva, l'asse Δx e due ordinate dai punti Δx 1 e Δx 2 (area ombreggiata) è numericamente uguale alla probabilità con cui un qualsiasi campione rientri nell'intervallo (Δx 1 ,Δx 2 ).
Poiché la curva è distribuita simmetricamente attorno all'asse y, si può sostenere che gli errori di uguale entità ma di segno opposto sono ugualmente probabili. E questo rende possibile prendere il valore medio di tutti gli elementi del campione come stima dei risultati della misurazione:
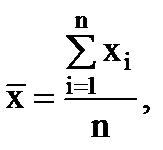(1.8)
dove – n è il numero di misurazioni.
Se n misurazioni vengono effettuate nelle stesse condizioni, allora la maggior parte probabile valore il valore misurato sarà il suo valore medio (aritmetico). Il valore tende al valore vero di x e al valore misurato come n → ∞.
L'errore quadratico medio di un singolo risultato di misurazione è il valore
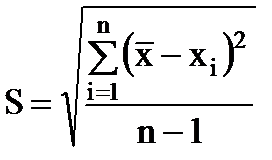(1.9)
Caratterizza l'errore di ogni singola misurazione. Poiché n → ∞, S tende a un limite costante σ:
σ = limS.
n → ∞ (1.10)
All'aumentare di σ, aumenta la dispersione delle letture, cioè, la precisione della misurazione diminuisce.
L'errore quadratico medio della media aritmetica è il valore
(1.11)
Questa è la legge fondamentale dell'aumento della precisione all'aumentare del numero di misurazioni.
L'errore caratterizza l'accuratezza con cui si ottiene il valore medio del valore misurato. Il risultato si scrive come:
x = ±Δx. (1.12)
Questa tecnica di calcolo degli errori dà buoni risultati(con un'affidabilità di 0,68) solo se lo stesso valore è stato misurato almeno 30 – 50 volte.
Nel 1908, William Sealy Gosset, noto statistico, meglio conosciuto con lo pseudonimo di Student, dimostrò che l'approccio statistico è valido anche per un piccolo numero di misurazioni. La distribuzione di Student per il numero di misure n → ∞ diventa la distribuzione gaussiana, e per un piccolo numero ne differisce.
Per calcolare l'errore assoluto per un piccolo numero di misurazioni, viene introdotto un coefficiente speciale che dipende dall'affidabilità P e dal numero di misurazioni n, chiamato coefficiente di Student t. Con l'introduzione di questo coefficiente
Tralasciando le giustificazioni teoriche per la sua introduzione, lo notiamo
Δx t = t, (1.13)
dove Δx t è l'errore assoluto per un dato livello di confidenza; è l'errore quadratico medio della media aritmetica.
I coefficienti degli studenti sono riportati nell'Appendice 1.
Da quanto detto segue:
1. Il valore dell'errore quadratico medio consente di calcolare la probabilità che il valore reale del valore misurato rientri in qualsiasi intervallo vicino alla media aritmetica.
2. Come n → ∞ → 0, cioè, l'intervallo in cui si trova il valore vero di x e con una data probabilità tende a zero all'aumentare del numero di misurazioni. Sembrerebbe che aumentando n si possa ottenere un risultato con qualsiasi grado di accuratezza. Tuttavia, l'accuratezza aumenta in modo significativo solo fino a quando l'errore casuale diventa confrontabile con quello sistematico. Un ulteriore aumento del numero di misurazioni è inopportuno, perché l'accuratezza finale del risultato dipenderà solo dall'errore sistematico. Conoscendo il valore dell'errore sistematico, è facile fissare il valore ammissibile dell'errore casuale, assumendolo, ad esempio, pari al 10% dell'errore sistematico. Chiedendo così il prescelto intervallo di confidenza un certo valore di P (ad esempio, P = 0,95), non è difficile trovare il numero richiesto di misurazioni, che garantisce un piccolo effetto dell'errore casuale sull'accuratezza del risultato.
Per fare ciò, è più conveniente utilizzare la tabella dell'Appendice 2, in cui gli intervalli sono dati in frazioni del valore σ, che è una misura dell'accuratezza di questo esperimento rispetto agli errori casuali.
Parte dei coefficienti di Student, con una colonna evidenziata per l'affidabilità P=95%, è riportata nella Tabella 1.6.
Coefficienti di studente Tabella 1.6
| N R | 0,9 | 0,95 | 0,999 |
| 6,31 2,92 2,35 2,13 2,02 1,94 1,89 1,86 1,83 | 12,7 4,30 3,18 2,78 2,57 2,45 2,36 2,31 2,26 | 636,6 31,6 12,9 8,61 6,37 5,96 5,41 5,04 4,78 | |
| ∞ | 1,96 |
Quando si elaborano i risultati di più misurazioni dirette, il seguente ordine di operazioni:
1. Registrare il risultato di ciascuna misurazione in una tabella.
2. Calcolare la media di n misure
(1.14)
3. Trova l'errore di una singola misurazione
(1.15)
4. Calcolare gli errori al quadrato delle singole misurazioni
(Δx 1) 2 , (Δx 2) 2 , ... , (Δx n) 2 . (1.16)
5. Determinare l'errore standard della media aritmetica
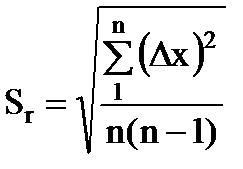. (1.17)
6. Impostare il valore di affidabilità (di solito si prende P = 0,95).
7. Determinare il coefficiente di Student t per una data affidabilità P e il numero di misurazioni n.
8. Trova l'intervallo di confidenza (errore di misurazione)
Δx t = t. (1.18)
Se l'errore del risultato della misurazione Δx risulta essere confrontabile con l'errore dello strumento Δx p, allora prendi come confine dell'intervallo di confidenza:
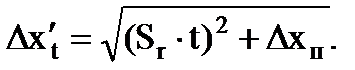(1.19)
Se uno degli errori è inferiore a tre o più volte l'altro, scartare l'errore minore.
9. Scrivi il risultato finale come
. (1.20)
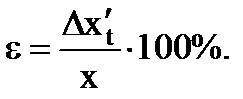(1.21)
Si consideri utilizzando l'esempio numerico l'applicazione delle formule di cui sopra.
Esempio. Il diametro d dell'asta è stato misurato con un micrometro (l'errore di misura sistematico è 0,005 mm). I risultati della misurazione sono inseriti nella seconda colonna della tabella, troviamo, e nella terza colonna di questa tabella scriviamo le differenze, e nella quarta - i loro quadrati della loro differenza (Tabella 1.7).
Tabella 1.7
| N | D, mm | ||
| 4.02 | + 0.01 | 0.0001 | |
| 3.98 | - 0.03 | 0.0009 | |
| 3.97 | - 0.04 | 0.0016 | |
| 4.01 | + 0 .00 | 0.0000 | |
| 4.05 | + 0.04 | 0.0016 | |
| 4.03 | + 0.02 | 0.0004 | |
| Σ | 24.06 | – | 0.0046 |
(1.22)
Data l'affidabilità di P = 0,95, troviamo t = 2,57 dalla tabella dei coefficienti di Student per sei misurazioni. L'errore assoluto può essere trovato dalla formula (10).
Δd = 0,01238 2,57 = 0,04 mm. (1.24)
Confrontiamo errori casuali e sistematici:
quindi, δ = 0,005 mm può essere scartato.
Scriviamo il risultato finale come:
d = (4,01 ± 0,04) mm a R = 0,95. (1.26)
Se il valore misurato UNè una funzione di più variabili: UN= F(X, si,..., T), Quello errore assoluto risultato misure indirette
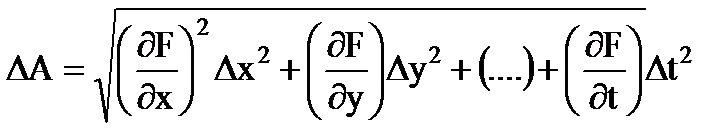(1.29)
Gli errori relativi parziali della misurazione indiretta sono determinati dalle formule
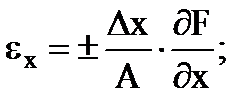
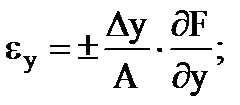…. e così via. (1.30)
Errore relativo risultato della misurazione
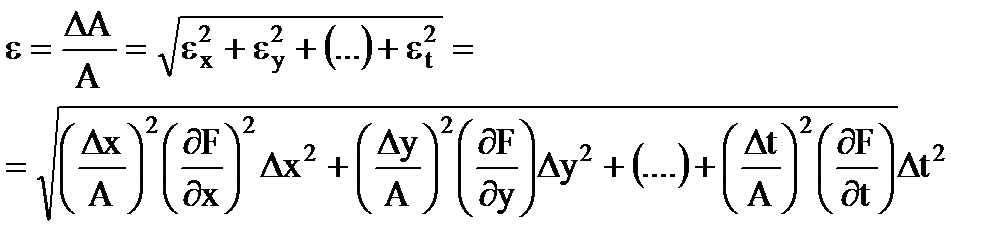(1.31)
Errore grossolano (miss)è un errore casuale del risultato di una singola osservazione inclusa in una serie di misurazioni, che per determinate condizioni differisce nettamente dal resto dei risultati di questa serie. Di norma, sorgono a causa di errori o azioni errate dell'operatore (il suo stato psico-fisiologico, lettura errata, letture di lettura dalla scala adiacente del dispositivo, errori di registrazione o calcoli, accensione errata di dispositivi o malfunzionamenti in il loro funzionamento, ecc.). Causa possibile il verificarsi di errori può anche essere un cambiamento brusco a breve termine delle condizioni delle misurazioni. Se durante il processo di misurazione vengono rilevati errori, i risultati che li contengono vengono scartati. Tuttavia, molto spesso, gli errori vengono rilevati solo durante l'elaborazione finale dei risultati della misurazione utilizzando criteri statistici speciali.
A seconda delle cause di accadimento si distinguono errori strumentali, metodologici e soggettivi.
Errore strumentaleè l'errore insito nello strumento di misura stesso, cioè il dispositivo o il trasduttore con cui viene eseguita la misurazione. Le cause dell'errore strumentale possono essere l'imperfezione del design dello strumento di misura, l'influenza ambiente sulle sue caratteristiche, deformazioni o usura di parti del dispositivo, ecc.
Errore metodologico appare a causa dell'imperfezione del metodo di misurazione; incongruenze tra la grandezza misurata e il suo modello adottato nello sviluppo dello strumento di misura; l'influenza dello strumento di misura sull'oggetto di misurazione e sui processi che si verificano in esso. Caratteristiche distintive errori metodologiciè che non possono essere specificati nella documentazione normativa e tecnica dello strumento di misura, poiché non dipendono da essa, ma devono essere determinati dall'operatore caso per caso.
Errore soggettivo (personale). la misura è dovuta all'errore di lettura dell'operatore sulle scale dello strumento di misura, le carte degli strumenti di registrazione. Sono causati dallo stato dell'operatore, dalla sua posizione durante il lavoro, dall'imperfezione degli organi di senso e dalle proprietà ergonomiche dello strumento di misura. Le caratteristiche di errore soggettivo sono determinate sulla base del valore nominale normalizzato della divisione di scala dello strumento di misura (o della carta cartografica dello strumento di registrazione), tenendo conto della capacità dell'"operatore medio" di interpolare entro i limiti di la divisione della scala. Questi errori diminuiscono man mano che gli strumenti migliorano, ad esempio: l'uso di un puntatore luminoso negli strumenti analogici elimina l'errore dovuto alla parallasse ( Parallasse(dal greco parallassi - deviazione), un cambiamento visibile nelle posizioni relative degli oggetti dovuto al movimento dell'occhio dell'osservatore) l'uso di un riferimento digitale elimina l'errore soggettivo.
Errore di misurazione oggettiva- un errore che non dipende dalle qualità personali di chi effettua la misurazione.
In base all'influenza delle condizioni esterne, si distinguono gli errori principali e aggiuntivi dello strumento di misura.
Il principale è chiamato l'errore dello strumento di misura definito in condizioni normali la sua applicazione. Per ogni strumento di misura, i documenti normativi e tecnici specificano le condizioni operative - un insieme di grandezze d'influenza (temperatura ambiente, umidità, pressione, tensione, frequenza di rete, ecc.), in base alle quali il suo errore è normalizzato (la grandezza d'influenza è quantità fisica, non misurata da questo strumento di misura, ma che ne influenza i risultati).
Ulteriori è chiamato l'errore dello strumento di misura derivante dalla deviazione di una qualsiasi delle grandezze d'influenza, vale a dire errore aggiuntivo, che aumenta l'errore complessivo del dispositivo, si verifica se il dispositivo opera in condizioni diverse dal normale.
A seconda della natura della variazione dell'entità dell'errore quando si modifica il valore misurato, gli errori vengono divisi in additivi e moltiplicativi.
Errori aggiuntivi a causa di uno spostamento della caratteristica statica del dispositivo verso l'alto o verso il basso (a destra oa sinistra), ad esempio, a causa dello spostamento della scala dello strumento (zero drift), attrito nei supporti, ecc. L'errore additivo non dipende dal valore della quantità misurata x, cioè costante su tutta la scala dello strumento.
Gli errori additivi dominano la maggior parte degli strumenti analogici.
Errori moltiplicativi sorgono a causa di errori nell'impostazione del coefficiente di trasferimento k della caratteristica statica y = kx. L'errore moltiplicativo dipende dal valore della grandezza misurata e aumenta verso la fine della scala dello strumento.
L'errore moltiplicativo (quando espresso come errore assoluto) è proporzionale al valore della quantità misurata.
Gli errori moltiplicativi prevalgono nei dispositivi relativi ai convertitori di scala (shunt, resistenze aggiuntive, amplificatori, divisori, trasformatori, ecc.).
Esistono dispositivi i cui errori additivi e moltiplicativi sono comparabili. Questa classe di dispositivi include dispositivi digitali.
Errori di misurazione casuali sorgono a causa dell'impatto simultaneo sull'oggetto di misurazione di diverse quantità indipendenti, i cui cambiamenti sono di natura fluttuante. Un certo contributo all'errore di misura casuale è dato anche dall'errore casuale dello strumento di misura.
Assumeremo che la componente sistematica dell'errore di misura sia esclusa e che l'errore casuale, in quanto variabile casuale, lo sia completamente
caratterizzato da una densità di distribuzione di probabilità (in altre parole, una densità di probabilità) dove è la funzione di distribuzione. Pertanto, non viene determinato un valore numerico errore casuale, ma solo la probabilità che si trovi in un certo intervallo o non superi un certo valore. Se la legge di distribuzione è nota, allora e sono noti La probabilità di trovare un errore casuale in un dato intervallo da a è trovata dalla formula
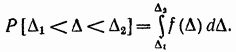
Il modello di variazione dell'errore casuale può essere stabilito da più osservazioni dei suoi valori e dall'elaborazione statistica dei risultati delle osservazioni.
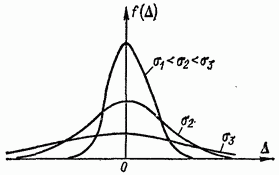
Riso. 2-1. Densità di probabilità degli errori casuali secondo la legge della distribuzione normale
Questo lavoro lungo e scrupoloso viene svolto con misurazioni accurate e consiste nel verificare la conformità dei dati ottenuti con la distribuzione prevista secondo un certo criterio.
Anche le fluttuazioni delle grandezze influenzanti sono casuali e sono caratterizzate dalle loro leggi di distribuzione (uniforme, triangolare, normale, ecc.). Tuttavia, a causa della commensurabilità delle loro dispersioni, già a 4-5 grandezze influenzanti, la risultante legge di distribuzione dell'errore di misura casuale concorda in modo soddisfacente con quella normale (Fig. 2-1).
Funzione di distribuzione normale
e densità di probabilità
dove è la varianza che caratterizza la dispersione di un errore casuale rispetto al centro di distribuzione e la sua deviazione standard.
Dispersione e deviazione standard caratterizzano l'accuratezza della misura: maggiore è, minore è l'accuratezza. Nella pratica della misurazione, viene utilizzata principalmente la deviazione standard c, poiché è espressa nelle stesse unità del valore misurato.
Riso. 2-2. Integrale di probabilità
La probabilità che si verifichi un errore casuale nell'intervallo da a secondo la formula
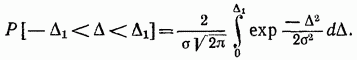
Se introduciamo una variabile casuale normalizzata, il lato destro dell'uguaglianza viene trasformato nella funzione di Laplace, spesso chiamata integrale di probabilità
Questa funzione è tabulata e i suoi valori sono riportati in Tabella. e il grafico è riportato in Fig. 2-2.
Se viene data una certa probabilità a, quindi, dopo averla trovata, è possibile determinare Secondo la normale legge di distribuzione, l'errore massimo Dmax è preso uguale a cui corrisponde alla probabilità di un errore superiore Ciò significa che in 369 su 370 osservazioni con una probabilità di 0,9973 l'errore si trova nell'intervallo ± 3a e solo in un'osservazione può superarlo.
Riso. 2-3. Densità di probabilità degli errori casuali con una legge di distribuzione uniforme
La legge di distribuzione uniforme si verifica anche nelle misurazioni. In particolare, è tipico per la misura di grandezze continue con il metodo del conteggio discreto. La densità di probabilità di errore nell'intervallo da a (Fig. 2-3) è scritta nella forma seguente;
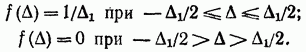
Pertanto, la varianza
e deviazione standard
Ad esempio, l'errore di quantizzazione, che di solito è compreso nella cifra meno significativa (da -1/2 a 1/2), è caratterizzato dalla deviazione standard
Torniamo alla legge della distribuzione normale. Questa legge è caratterizzata da parametri numerici: aspettativa matematica e dispersione. Definizione precisa questi parametri è quasi impossibile, poiché per questo è necessario disporre di un numero infinitamente elevato di valori variabile casuale, cioè eseguire osservazioni a . Nella pratica delle misurazioni è sempre finito, quindi vengono chiamati i valori calcolati come risultato dell'esperimento
stime aspettativa matematica e deviazione standard.
Consideriamo la procedura di misurazione statistica di un valore, il cui vero valore è prodotto da singole osservazioni, a seguito delle quali si ottengono un numero di valori casuali del valore misurato. In ogni errore assoluto della prima osservazione È impossibile determinare il valore di questo errore, poiché è sconosciuto.
La media aritmetica è considerata una stima dell'aspettativa matematica (valore vero)
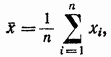
che è chiamato il valore effettivo A della quantità misurata a
Ora puoi calcolare la deviazione assoluta di ogni risultato dell'osservazione rispetto al valore medio: Ovviamente, a Per controllare la correttezza dei calcoli, puoi utilizzare le proprietà delle deviazioni dei risultati dell'osservazione dalla media aritmetica: la somma delle deviazioni è zero e la somma dei loro quadrati è minima:
La stima della deviazione standard delle deviazioni assolute di ciascuna delle singole osservazioni è determinata dalla formula
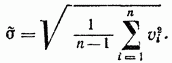
La precisione del risultato della misurazione sarà maggiore. È caratterizzato da una stima della deviazione standard del valore medio aritmetico (reale):
All'aumentare del numero di misurazioni (con risultati indipendenti), l'accuratezza aumenta proporzionalmente. Sembrerebbe che aumentando si possa ottenere qualsiasi aumento dell'accuratezza. Tuttavia, il buon senso e la pratica della misurazione suggeriscono che sia di scarsa utilità, poiché il misurando stesso può cambiare durante la misurazione.
Intervallo di confidenza e probabilità di confidenza. Come risultato delle osservazioni del valore misurato, otteniamo una stima del suo valore effettivo A, pari alla media aritmetica X, secondo la formula (2-11). Anche questa stima è una variabile casuale; la sua deviazione standard a - è determinata dalla formula (2-13), ovvero il risultato della misurazione contiene incertezza. È necessario scoprire entro quali limiti il valore effettivo di A può cambiare durante misurazioni ripetute di quantità (statistiche) nelle stesse condizioni, ovvero è necessario trovare un intervallo di valori che "copra" il vero valore di la quantità misurata con una data probabilità. Tale intervallo è chiamato intervallo di confidenza e una data probabilità (stabilita) è chiamata intervallo di confidenza. L'intervallo di confidenza e il livello di confidenza caratterizzano l'incertezza del risultato della misurazione. Analiticamente si scrive così:
L'espressione (2-14) recita come segue: il vero valore del valore misurato si trova all'interno dell'intervallo di confidenza da a con una probabilità di confidenza a.
Allo stesso modo per errore casuale
L'errore di misura casuale è compreso nell'intervallo di confidenza da a con una probabilità di confidenza a.
A seconda dello scopo della misurazione, il livello di confidenza è posto pari a . Nelle espressioni (2-14) e (2-15), gli intervalli di confidenza sono simmetrici. La metà dell'intervallo di confidenza è chiamata errore limite (massimo, ammissibile) con una probabilità di confidenza a. A volte l'intervallo di confidenza è asimmetrico e ha la forma
L'errore marginale e l'intervallo di confidenza sono espressi in termini di deviazione standard. Per una legge di distribuzione normale, l'intervallo di confidenza per una data probabilità di confidenza (e viceversa) è determinato utilizzando la tabella degli integrali di probabilità (tabella A4). Sono impostati con un livello di confidenza, ad esempio 0,95. Secondo la tabella, viene trovato anche il valore, che in questo caso è uguale a 2. Poiché questo è l'intervallo di confidenza
Ovviamente, sia l'intervallo di confidenza che il livello di confidenza sono correlati al numero di osservazioni, in quanto maggiore è l'intervallo più ristretto. Tuttavia, come accennato in precedenza, nella pratica delle misurazioni è raro. Per il numero di osservazioni, l'intervallo di confidenza è determinato non attraverso ma attraverso un certo coefficiente che dipende dal numero di osservazioni e dalla probabilità di confidenza a. La legge della variazione del coefficiente è determinata dalla distribuzione di Student della variabile casuale normalizzata calcolata con una distribuzione normale. Il coefficiente è determinato utilizzando la seguente formula:
non si tratta di miss, cioè errori non palesi commessi dall'operatore, occorre allora stabilire se si tratti di errori grossolani, anch'essi da escludere dall'elaborazione, come i miss. L'esclusione di un errore grossolano senza motivi sufficienti porta a un irragionevole miglioramento del risultato della misurazione. D'altra parte, la non esclusione di un errore grossolano, soprattutto con un numero ridotto di osservazioni, distorce sia il valore effettivo del valore misurato sia i limiti dell'intervallo di confidenza. Pertanto, gli errori grossolani devono essere rilevati ed eliminati.
Il modo più semplice per rilevare un errore grossolano in una distribuzione normale è confrontare l'errore assoluto dell'osservazione "sospetta" con l'errore massimo Se allora questo risultato dovrebbe essere scartato e i valori ricalcolati Questo metodo si basa sul fatto che la probabilità che un valore si discosti dalla media aritmetica è più che uguale a solo 0,003.
Tuttavia, va ricordato che se grandi numeri osservazioni, sebbene con una bassa probabilità, è possibile che il numero scartato non sia un errore grossolano, ma una deviazione statistica naturale di questo valore. Pertanto, nei casi critici, la determinazione di un errore grossolano viene effettuata sulla base della teoria della probabilità. Si stabilisce a quale numero di misurazioni con una data probabilità a è possibile scartare il risultato dell'osservazione che supera un dato numero o determinati limiti.
Gli errori di misurazione sono classificati nei seguenti tipi:
assoluto e relativo.
Positivo e negativo.
costante e proporzionale.
Approssimativo, casuale e sistematico.
Errore assoluto risultato di una singola misurazione (A si) è definito come la differenza tra i seguenti valori:
UN si = si io- si ist. » si io-` si.
Errore relativo risultato di una singola misurazione (B si) è calcolato come rapporto tra le seguenti grandezze:
Da questa formula risulta che l'entità dell'errore relativo dipende non solo dall'entità dell'errore assoluto, ma anche dal valore della quantità misurata. Quando il valore misurato rimane invariato ( si) l'errore di misura relativo può essere ridotto solo riducendo l'errore assoluto (A si). Quando l'errore di misurazione assoluto è costante, per ridurre l'errore di misurazione relativo, è possibile utilizzare il metodo per aumentare il valore della quantità misurata.
Esempio. Supponiamo che una bilancia commerciale in un negozio abbia un errore di misurazione della massa assoluta costante: A m = 10 g Se pesi 100 g di caramelle (m 1) su tali bilance, l'errore relativo nella misurazione della massa di caramelle sarà :
.
Quando si pesano 500 g di caramelle (m 2) sulla stessa bilancia, l'errore relativo sarà cinque volte inferiore:
.
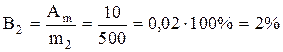Pertanto, se pesi cinque volte 100 g di caramelle, a causa di un errore di misurazione della massa, non riceverai un totale di 50 g di prodotto su 500 g. Con una singola pesata di una massa maggiore (500 g), perderai solo 10 g di caramelle, cioè cinque volte meno.
Ciò premesso, si può rilevare che, in primo luogo, occorre adoperarsi per ridurre i relativi errori di misura. Gli errori assoluti e relativi possono essere calcolati solo dopo aver determinato la media valore aritmetico risultato della misurazione.
Il segno dell'errore (positivo o negativo) è determinato dalla differenza tra il risultato della misurazione singola e quello effettivo:
si io-` si > 0 (l'errore è positivo);
si io-` si < 0 (l'errore è negativo).
Se l'errore di misurazione assoluto non dipende dal valore della quantità misurata, viene chiamato un tale errore permanente. Altrimenti, l'errore sarà proporzionale. La natura dell'errore di misurazione (costante o proporzionale) viene determinata dopo studi speciali.
Errore grossolano misurazione (miss) è un risultato di misurazione significativamente diverso dagli altri, che di solito si verifica quando viene violata una procedura di misurazione. La presenza di errori di misura grossolani nel campione è stabilita solo dai metodi della statistica matematica (per n>2). Acquisisci familiarità con i metodi per rilevare errori grossolani in te stesso.
La divisione degli errori in casuali e sistematici è piuttosto condizionata.
A errori casuali includere errori che non hanno valore e segno costanti. Tali errori si verificano sotto l'influenza dei seguenti fattori: sconosciuto al ricercatore; conosciuto ma non regolamentato; in continua evoluzione.
Gli errori casuali possono essere stimati solo dopo aver effettuato le misurazioni.
Quantificare il modulo dell'entità di un errore di misurazione casuale può essere i seguenti parametri: ecc.
Gli errori di misurazione casuali non possono essere esclusi, possono solo essere ridotti. Uno dei modi principali per ridurre l'entità di un errore di misurazione casuale è aumentare il numero di singole misurazioni (un aumento del valore di n). Ciò è spiegato dal fatto che l'entità degli errori casuali è inversamente proporzionale al valore di n, ad esempio:
Errori sistematici sono errori di entità e segno costanti o variabili secondo una legge nota. Questi errori sono causati da fattori costanti. Gli errori sistematici possono essere quantificati, ridotti e persino eliminati.
Gli errori sistematici sono classificati in errori di tipo I, II e III.
A sistematico errori di tipo I si riferiscono a errori di origine nota, che possono essere stimati mediante calcolo prima della misurazione. Questi errori possono essere eliminati introducendoli nel risultato della misurazione sotto forma di correzioni. Un esempio di questo tipo di errore è l'errore nella determinazione titrimetrica della concentrazione volumetrica di una soluzione se il titolante è stato preparato a una temperatura e la concentrazione è stata misurata a un'altra. Conoscendo la dipendenza della densità del titolante dalla temperatura, è possibile calcolare la variazione della concentrazione volumetrica del titolante associata a una variazione della sua temperatura prima della misurazione e tenere conto di questa differenza come correzione a seguito di la misurazione.
Sistematico errori di II tipo- si tratta di errori di origine nota, che possono essere valutati solo durante l'esperimento o come risultato di studi speciali. Questo tipo di errore include errori strumentali (strumentali), reattivi, di riferimento e di altro tipo. Acquisisci familiarità con le caratteristiche di tali errori.
Qualsiasi dispositivo, quando utilizzato nella procedura di misurazione, introduce i propri errori strumentali nel risultato della misurazione. Allo stesso tempo, alcuni di questi errori sono casuali e l'altra parte è sistematica. Gli errori strumentali casuali non vengono valutati separatamente, vengono valutati insieme a tutti gli altri errori di misurazione casuali.
Ogni istanza di qualsiasi strumento ha il suo personale errore sistematico. Per valutare questo errore, è necessario condurre studi speciali.
Maggior parte modo affidabile valutazione dell'errore sistematico strumentale di tipo II - questa è una riconciliazione del funzionamento degli strumenti rispetto agli standard. Per gli utensili di misurazione (pipette, burette, cilindri, ecc.), Viene eseguita una procedura speciale: la calibrazione.
In pratica, il più delle volte è necessario non stimare, ma ridurre o eliminare l'errore sistematico di tipo II. I metodi più comuni per ridurre gli errori sistematici sono metodi di relativizzazione e randomizzazione.Dai un'occhiata a questi metodi su .
A errori III tipo includere errori di origine sconosciuta. Questi errori possono essere rilevati solo dopo che tutti gli errori sistematici di tipo I e II sono stati eliminati.
A altri errori includeremo tutti gli altri tipi di errori non considerati sopra (ammissibili, eventuali errori marginali, ecc.). Il concetto di possibili errori marginali viene utilizzato nei casi di utilizzo di strumenti di misura e presuppone il massimo errore di misurazione strumentale possibile (il valore effettivo dell'errore può essere inferiore al valore del possibile errore marginale).
Quando si utilizzano strumenti di misura, è possibile calcolare il possibile limite assoluto (P` si, ecc.) o relativa (E` si, ecc.) errori di misura. Quindi, ad esempio, il possibile errore di misurazione assoluto limitante viene trovato come somma di possibili limiti casuali (x ` si, casuale, ecc.) e sistematica non esclusa (d` si, ecc.) errori:
P' si, es. = x ` si, casuale, pr.+d` si, eccetera.
Per piccoli campioni (n £ 20), l'ignoto popolazione, obbedendo alla legge della distribuzione normale, i possibili errori di misurazione limitanti casuali possono essere stimati come segue:
x' si, casuale, pr.= D` si=S' si½t P, n ½,
dove t P,n è il quantile della distribuzione di Student (test) per la probabilità P e la dimensione del campione n. L'errore di misurazione limite assoluto possibile in questo caso sarà pari a:
P' si,es.= S ` si½t P, n ½+ d` si, eccetera.
Se i risultati della misurazione non obbediscono alla legge della distribuzione normale, l'errore viene stimato utilizzando altre formule.
Determinazione del valore di d ` si,eccetera. dipende dal fatto che lo strumento di misura abbia o meno una classe di precisione. Se lo strumento di misura non ha una classe di precisione, quindi per il valore d ` si,eccetera. può essere accettato il valore minimo della divisione della scala misurazione. Per uno strumento di misura con una classe di precisione nota per il valore d ` si, ad esempio, si può accettare l'errore sistematico assoluto ammissibile dello strumento di misura (d si, aggiungere.):
d' si,eccetera." .
valore d si, aggiungere. è calcolato sulla base delle formule fornite nella Tabella 5.
Per molti strumenti di misura, la classe di precisione è indicata sotto forma di numeri a × 10 n, dove a è uguale a 1; 1,5; 2; 2,5; 4; 5; 6 en è 1; 0; -1; -2, ecc., che mostrano il valore del possibile errore sistematico massimo ammissibile (E si, add.) e segni speciali che ne indicano il tipo (relativo, ridotto, costante, proporzionale).
Tabella 5
Esempi di designazione delle classi di precisione degli strumenti di misura
Continuazione della tabella 5
Fine della tabella 5
Gli errori sistematici possono essere trascurati se la disuguaglianza
In questo caso si assume che:
P' si, eccetera." x' si, caso , ecc. » D` si»S« si½t P, n ½.
Gli errori casuali possono essere trascurati purché
Per questo caso P` si, eccetera." d' si,eccetera. .
Aumentare il numero di misurazioni singole è il metodo più comune per ridurre gli errori casuali (che aumenta anche il costo delle misurazioni). Si consiglia di aumentare n fino a quando l'errore di misura totale è determinato solo dall'errore sistematico. Il numero minimo di misurazioni parallele necessarie per questo (n min) può essere calcolato solo per valore noto la popolazione generale dei singoli risultati secondo la formula
.
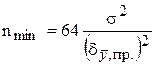Se i componenti (m - il numero di componenti) dell'errore sistematico assoluto della media aritmetica del risultato della misurazione () sono noti, allora può essere stimato dalla formula
,
dove k è un coefficiente determinato dalla probabilità P e dal numero m.
La stima degli errori di misurazione dipende non solo dai mezzi di misurazione e dalla dimensione del campione, ma anche dal tipo di misurazione (misurazione diretta o indiretta).
La divisione delle misurazioni in diretta e indiretta è piuttosto condizionata. Più tardi, sotto misure dirette lo capiremo quando il risultato della misurazione viene ottenuto direttamente, ad esempio, viene letto dalla scala dello strumento. A misure indirette attribuiremo tale quando il risultato della misurazione calcolato in funzione di (j) i risultati di una o più misurazioni dirette ( X 1 , X 2 , …, X J,. …, X K).
È necessario sapere che gli errori delle misurazioni indirette sono sempre maggiori degli errori delle singole misurazioni dirette. Gli errori delle misurazioni indirette sono stimati secondo le leggi pertinenti.
Errori casuali portano al fatto che i valori osservati della quantità misurata durante misurazioni ripetute sono sparsi casualmente rispetto al suo valore reale. Quindi il valore effettivo viene trovato come il più probabile di una serie di esperimenti e l'errore è caratterizzato dall'ampiezza dell'intervallo, che include il valore vero con una data probabilità. La fondatezza matematica di queste disposizioni è data nella teoria della probabilità, la cui applicazione per l'elaborazione dei risultati delle misurazioni è data in letteratura e l'applicazione diretta alle opere officina fisica nella letteratura.
Molto spesso, studenti e scolari trovano l'errore di misurazione utilizzando la formula
, (6.2)
dove è il valore medio della quantità ottenuta durante il processo di misurazione ed è il valore preso dal libro di riferimento o calcolato da concetti teorici. Una tale definizione dell'errore è un grave errore, poiché lo scopo dell'esperimento, come mostrato sopra, è testare i concetti teorici e perfezionare i dati tabulari.
Inoltre, spesso l'errore viene calcolato come valore medio delle deviazioni dei singoli risultati di misurazione dal valore medio utilizzando la formula
. (6.3)
Secondo questo approccio, qualsiasi valore di errore appare ugualmente spesso, ad es. errori di entità diversa sono considerati ugualmente probabili. Questo metodo può essere utilizzato in lavoro di laboratorio con un piccolo numero di misurazioni.
Tuttavia, gli errori casuali non sono ugualmente probabili. Richiedono l'elaborazione statistica dei risultati della misurazione per la loro definizione. Pertanto, sembra necessario considerare il contenuto dell'elaborazione statistica dei risultati della misurazione. La teoria statistica degli errori si basa sulle seguenti disposizioni:
1) con un numero elevato di misurazioni, si osservano errori casuali della stessa entità, ma segno diverso, cioè gli errori, sia nella direzione della diminuzione che in quella dell'aumento, si verificano ugualmente spesso;
2) gli errori grandi (in valore assoluto) sono meno comuni di quelli piccoli, ad es. la probabilità della comparsa di un errore diminuisce con un aumento dell'entità dell'errore;
3) gli errori di misura possono assumere una serie continua di valori.
La distribuzione di una variabile casuale che obbedisce alle proprietà elencate è chiamata distribuzione normale. Per stimare lo spread individuale vengono scelti i valori di una variabile casuale con una distribuzione normale o singoli campioni nella teoria della distribuzione normale campione deviazione standard delle letture, che si calcola con la formula:
. (6.4)
La stima del valore di errore di una misura, determinato dalla formula (6.4) è molto importante. Tuttavia, per la misurazione, un compito importante è determinare con quale precisione il valore medio del valore misurato corrisponde al valore desiderato. Questo problema sorge a causa del fatto che il valore medio può essere ottenuto da diverse dimensioni. Ad esempio, il valore medio può essere ottenuto da un diverso numero di misurazioni. Pertanto, anche la media empirica è una variabile casuale, che può anche essere descritta da una funzione di distribuzione. Il valore della deviazione standard corrispondente a questa funzione è determinato, come mostrato nella teoria della probabilità, dalla formula:
(6.5)
Questo valore è chiamato deviazione standard campionaria della media O errore standard.
Come si può vedere dalla formula dell'errore standard (6.5), diminuisce con l'aumentare del numero di misurazioni e aumenta l'accuratezza del risultato, che corrisponde al ragionamento precedente.
Le formule di cui sopra per determinare l'errore di misurazione utilizzano le caratteristiche della distribuzione normale di una variabile casuale. Tuttavia, non è noto in base a quale legge siano distribuiti i risultati della misurazione. Pertanto, queste stime sono approssimative. A questo proposito, è necessario analizzare questo approccio per determinare l'errore di misurazione. Per tale analisi, si può utilizzare il ben noto concetto di intervallo di confidenza nella teoria della probabilità. Sia il valore uguale alla probabilità che il risultato della misurazione - il valore medio - differisca dal valore vero di un valore non maggiore di . Nella teoria della probabilità, questa frase è scritta come segue:
Il valore è chiamato livello di confidenza (affidabilità) risultato di una serie di osservazioni. Mostra la probabilità con cui l'intervallo di confidenza include il vero valore del misurando.
Intervallo di confidenza chiamato intervallo di valori, che con un dato grado di certezza include il valore vero del valore misurato. La rappresentazione geometrica di questo intervallo è data in Figura 1.
Pertanto, per determinare l'errore casuale, è necessario trovare o impostare due numeri: vale a dire, il valore dell'errore casuale stesso o l'intervallo di confidenza e il valore della probabilità di confidenza.
Per qualsiasi valore dell'intervallo di confidenza, è possibile calcolare la probabilità di confidenza. Per questo viene utilizzata la funzione di Laplace, chiamata anche integrale di probabilità. La funzione di Laplace ha la forma:
,
Dove . Molto spesso, quando si risolvono i problemi, vengono utilizzati i valori tabulari della funzione di Laplace. Questi valori sono mostrati nella Tabella 1.
I risultati di questa tabella mostrano che un errore rms ha una probabilità di confidenza di 0,68, un errore 2x rms ha una probabilità di confidenza di 0,95 e un errore 3x rms di 3 ha una probabilità di confidenza di 0,997.
Tabella 1
Probabilità di fiducia
per l'intervallo di confidenza, espresso in frazioni dell'errore quadratico medio . Funzione di Laplace
| 1,2 | 0,77 | 2,6 | 0,990 | ||
| 0,05 | 0,04 | 1,3 | 0,80 | 2,7 | 0,993 |
| 0,1 | 0,08 | 1,4 | 0,84 | 2,8 | 0,995 |
| 0.15 | 0,12 | 1,5 | 0,87 | 2,9 | 0,996 |
| 0,2 | 0,16 | 1,6 | 0,89 | 3,0 | 0,997 |
| 0,3 | 0,24 | 1,7 | 0,91 | 3,1 | 0,9981 |
| 0,4 | 0,31 | 1,8 | 0,93 | 3,2 | 0,9986 |
| 0,5 | 0,38 | 1,9 | 0,94 | 3,3 | 0,9990 |
| 0,6 | 0,45 | 2,0 | 0,95 | 3,4 | 0,9993 |
| 0,7 | 0,51 | 2,1 | 0,964 | 3,5 | 0,9995 |
| 0,8 | 0,57 | 2,2 | 0,972 | 3,6 | 0,9997 |
| 0,9 | 0,63 | 2,3 | 0,978 | 3,7 | 0,9998 |
| 1,0 | 0,68 | 2,4 | 0,984 | 3,8 | 0,99986 |
| 1.1 | 0,73 | 2,5 | 0,988 | 3,9 | 0,99990 |
| 4,0 | 0,99993 |
Errore casualeÈ consuetudine definirlo come la metà dell'intervallo di confidenza. La dimensione dell'intervallo di confidenza è data come un multiplo della deviazione standard campionaria della media , che è determinato dalla formula (6.5). Poi errore casuale di misurazioni multipleè determinato dalla formula.