صيغة الخطأ المطلق العشوائية. أخطاء عشوائية ومنهجية

لتقليل تأثير الأخطاء العشوائية ، من الضروري قياس هذه القيمة عدة مرات. لنفترض أننا نقيس بعض القيمة x. نتيجة للقياسات ، حصلنا على القيم التالية:

x 1 ، x 2 ، x 3 ، ... x n. (1.4)

هذه السلسلة من قيم x تسمى عينة. بوجود مثل هذه العينة ، يمكننا تقييم نتيجة القياس. سوف نشير إلى القيمة التي ستكون مثل هذا التقدير. ولكن نظرًا لأن قيمة التقييم لنتائج القياس لن تمثل القيمة الحقيقية للكمية المقاسة ، فمن الضروري تقدير خطأها. لنفترض أنه يمكننا تحديد تقدير الخطأ Δx. في هذه الحالة ، يمكننا كتابة نتيجة القياس بالصيغة

س = ± Δx. (1.5)

نظرًا لأن القيم المقدرة لنتيجة القياس والخطأ x ليست دقيقة ، يجب أن يكون تسجيل نتيجة القياس مصحوبًا بإشارة إلى موثوقيتها P. تُفهم الموثوقية أو احتمالية الثقة على أنها احتمال أن قيمة حقيقيةمن القيمة المقاسة محاطًا بالفاصل الزمني المشار إليه بالسجل (3). هذه الفترة نفسها تسمى فاصل الثقة.

على سبيل المثال ، عند قياس طول مقطع معين ، كتبنا النتيجة النهائية على النحو التالي

ل= (8.34 ± 0.02) مم،(P = 0.95). (1.6)

هذا يعني أنه من بين 100 فرصة - 95 أن القيمة الحقيقية لطول المقطع تقع في الفترة من 8.32 إلى 8.36 مم.

وبالتالي ، فإن المهمة تتمثل في الحصول على عينة من القياسات ، وإيجاد تقدير لنتيجة القياس وخطأها Δx والموثوقية P.

يمكن حل هذه المشكلة باستخدام نظرية الاحتمالات و الإحصاء الرياضي.

في معظم الحالات ، تتبع الأخطاء العشوائية قانون التوزيع الطبيعي الذي وضعه غاوس. يتم التعبير عن التوزيع الطبيعي للأخطاء بواسطة الصيغة

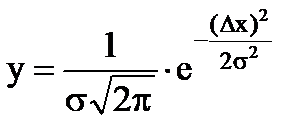, (1.7)

حيث Δx هو الانحراف عن القيمة الحقيقية ؛

σ هو متوسط ​​الخطأ التربيعي الحقيقي ؛

σ 2- التشتت ، قيمته تميز انتشار المتغيرات العشوائية.

كما يتضح من الصيغة ، فإن الوظيفة y (x) لها أقصى قيمةبالنسبة إلى x = 0 ، فهي زوجية.

ذ

x

∆x 1

∆x2

-x 1

-x2

الشكل 1.4. منحنى التوزيع الطبيعي الجاوسي.

يوضح الشكل 1.4 رسمًا بيانيًا لهذه الوظيفة. مساحة الشكل المحاطة بين المنحنى ومحور x والإحداثيات من النقطتين Δx 1 و Δx 2 (المنطقة المظللة) تساوي عدديًا الاحتمال الذي تقع به أي عينة في الفترة (Δx 1 ، Δx 2 ).

نظرًا لأن المنحنى موزع بشكل متماثل حول المحور y ، فيمكن القول بأن الأخطاء متساوية في الحجم ولكن العكس في الإشارة تكون محتملة بشكل متساوٍ. وهذا يجعل من الممكن أخذ متوسط ​​القيمة لجميع عناصر العينة كتقدير لنتائج القياس:

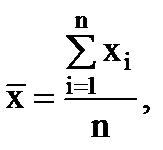(1.8)

حيث - n هو عدد القياسات.

إذا تم إجراء قياسات n في نفس الظروف ، فسيكون الأكثر شيوعًا القيمة المحتملةستكون القيمة المقاسة هي متوسط ​​قيمتها (حسابيًا). تميل القيمة إلى القيمة الحقيقية لـ x والقيمة المقاسة كـ n → ∞.

متوسط ​​الخطأ التربيعي لنتيجة قياس واحدة هو القيمة

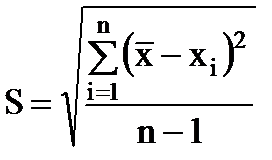(1.9)

يميز خطأ كل قياس على حدة. نظرًا لأن n → ∞ ، تميل S إلى حد ثابت σ:

σ = ليمس.
ن → ∞ (1.10)

كلما زاد ، يزداد تشتت القراءات ، أي ، تصبح دقة القياس أقل.

القيمة جذر متوسط ​​التربيع للمتوسط ​​الحسابي

(1.11)

هذا هو القانون الأساسي لزيادة الدقة مع زيادة عدد القياسات.

يميز الخطأ الدقة التي يتم بها الحصول على متوسط ​​قيمة القيمة المقاسة. النتيجة مكتوبة على النحو التالي:

س = ± Δx. (1.12)

يعطي أسلوب حساب الخطأ هذا نتائج جيدة(مع موثوقية 0.68) فقط إذا تم قياس نفس القيمة على الأقل 30-50 مرة.

في عام 1908 ، أظهر ويليام سيلي جوسيت ، وهو إحصائي مشهور معروف أكثر باسمه المستعار الطالب ، أن النهج الإحصائي صالح حتى لعدد صغير من القياسات. يصبح توزيع الطالب لعدد القياسات n → ∞ هو التوزيع الغاوسي ، ويختلف عنه بالنسبة لعدد صغير.

لحساب الخطأ المطلق لعدد صغير من القياسات ، يتم إدخال معامل خاص يعتمد على الموثوقية P وعدد القياسات n ، يسمى معامل الطالب t. مع إدخال هذا المعامل

بحذف المبررات النظرية لتقديمه ، نلاحظ ذلك

Δx t = t ، (1.13)

حيث Δx t هو الخطأ المطلق لمستوى ثقة معين ؛ هو جذر متوسط ​​الخطأ التربيعي للمتوسط ​​الحسابي.

ترد معاملات الطالب في الملحق 1.

ويتبع مما قيل:

1. تسمح لك قيمة خطأ الجذر التربيعي بحساب احتمال وقوع القيمة الحقيقية للقيمة المقاسة في أي فترة قريبة من المتوسط ​​الحسابي.

2. كـ n → ∞ → 0 ، أي الفترة التي تميل فيها القيمة الحقيقية لـ x والموجودة مع احتمال معين إلى الصفر مع زيادة عدد القياسات. يبدو أنه من خلال زيادة n ، يمكن للمرء الحصول على نتيجة بأي درجة من الدقة. ومع ذلك ، تزيد الدقة بشكل كبير فقط حتى يصبح الخطأ العشوائي مشابهًا للخطأ المنتظم. زيادة أخرى في عدد القياسات غير مجدية ، لأن الدقة النهائية للنتيجة ستعتمد فقط على الخطأ المنهجي. بمعرفة قيمة الخطأ المنهجي ، من السهل تحديد القيمة المقبولة للخطأ العشوائي ، مع الأخذ في الاعتبار ، على سبيل المثال ، ما يعادل 10٪ من الخطأ النظامي. بالسؤال عن المختار هكذا فاصل الثقةقيمة معينة لـ P (على سبيل المثال ، P = 0.95) ، ليس من الصعب العثور على العدد المطلوب من القياسات ، مما يضمن تأثيرًا بسيطًا للخطأ العشوائي على دقة النتيجة.

للقيام بذلك ، من الأنسب استخدام الجدول الموجود في الملحق 2 ، حيث يتم إعطاء الفواصل الزمنية في أجزاء من القيمة σ ، وهو مقياس لدقة هذه التجربة فيما يتعلق بالأخطاء العشوائية.

جزء من معاملات الطالب ، مع عمود مميز للاعتمادية P = 95٪ ، يرد في الجدول 1.6.

معاملات الطالب الجدول 1.6

نص	0,9	0,95	0,999
	6,31 2,92 2,35 2,13 2,02 1,94 1,89 1,86 1,83	12,7 4,30 3,18 2,78 2,57 2,45 2,36 2,31 2,26	636,6 31,6 12,9 8,61 6,37 5,96 5,41 5,04 4,78
∞		1,96

عند معالجة نتائج العديد من القياسات المباشرة ، يكون الترتيب التالي للعمليات:

1. سجل نتيجة كل قياس في جدول.

2. احسب متوسط ​​عدد ن القياسات

(1.14)

3. أوجد خطأ قياس واحد

(1.15)

4. احسب التربيعية للأخطاء للقياسات الفردية

(Δx 1) 2، (Δx 2) 2، ...، (Δx n) 2. (1.16)

5. تحديد الخطأ المعياري للمتوسط ​​الحسابي

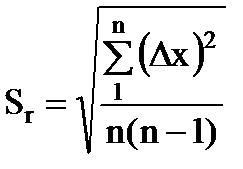. (1.17)

6. قم بتعيين قيمة الموثوقية (عادةً ما تأخذ P = 0.95).

7. حدد معامل الطالب t لموثوقية معينة P وعدد القياسات n.

8. أوجد فاصل الثقة (خطأ القياس)

Δx t = t. (1.18)

إذا تبين أن الخطأ في نتيجة القياس Δx يمكن مقارنته بخطأ الأداة Δx p ، فاخذ حدًا لفاصل الثقة:

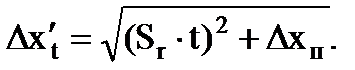(1.19)

إذا كان أحد الأخطاء أقل من ثلاث مرات أو أكثر في الآخر ، فتجاهل الخطأ الأصغر.

9. اكتب النتيجة النهائية على شكل

. (1.20)

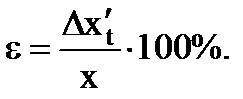(1.21)

ضع في اعتبارك استخدام المثال العددي لتطبيق الصيغ أعلاه.

مثال.تم قياس القطر d للقضيب بالميكرومتر (خطأ القياس المنتظم هو 0.005 مم). يتم إدخال نتائج القياس في العمود الثاني من الجدول ، ونجد ، وفي العمود الثالث من هذا الجدول نكتب الاختلافات ، وفي العمود الرابع - مربعات اختلافهم (الجدول 1.7).

الجدول 1.7

ن	د، مم
	4.02	+ 0.01	0.0001
	3.98	- 0.03	0.0009
	3.97	- 0.04	0.0016
	4.01	+ 0 .00	0.0000
	4.05	+ 0.04	0.0016
	4.03	+ 0.02	0.0004
Σ	24.06	–	0.0046

(1.22)

بالنظر إلى موثوقية P = 0.95 ، نجد أن t = 2.57 من جدول معاملات الطالب لستة قياسات. يمكن إيجاد الخطأ المطلق بالصيغة (10).

Δd = 0.01238 2.57 = 0.04 مم. (1.24)

دعنا نقارن الأخطاء العشوائية والمنهجية:

لذلك ، δ = 0.005 مميمكن التخلص منها.

نكتب النتيجة النهائية على النحو التالي:

د = (4.01 ± 0.04) ممعند Р = 0.95. (1.26)

إذا كانت القيمة المقاسة أهي دالة لعدة متغيرات: أ= F(x, ذ,..., ر), الذي - التي الخطأ المطلقنتيجة القياسات غير المباشرة

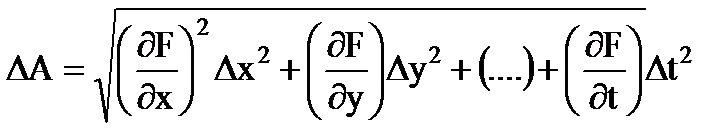(1.29)

يتم تحديد الأخطاء النسبية الجزئية للقياس غير المباشر بواسطة الصيغ

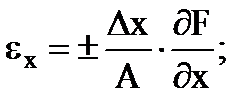
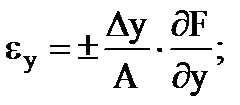…. وما إلى ذلك وهلم جرا. (1.30)

خطأ نسبينتيجة القياس

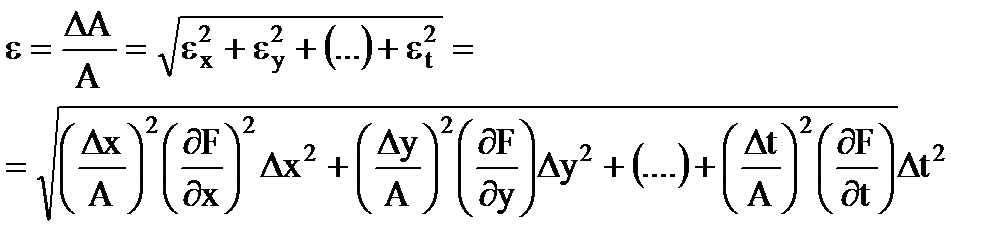(1.31)

الخطأ الإجمالي (Miss)هو خطأ عشوائي ناتج عن ملاحظة واحدة مدرجة في سلسلة من القياسات ، والتي تختلف اختلافًا حادًا عن بقية نتائج هذه السلسلة بالنسبة لظروف معينة. وهي ، كقاعدة عامة ، تنشأ بسبب أخطاء أو تصرفات غير صحيحة من جانب المشغل (حالته النفسية-الفسيولوجية ، القراءة غير الصحيحة ، قراءة القراءات من المقياس المجاور للجهاز ، أخطاء في السجلات أو الحسابات ، تشغيل غير صحيح للأجهزة أو أعطال في عملياتهم ، وما إلى ذلك). سبب محتمليمكن أن يكون حدوث الأخطاء أيضًا تغييرات مفاجئة قصيرة المدى في ظروف القياسات. إذا تم اكتشاف الأخطاء أثناء عملية القياس ، فسيتم تجاهل النتائج التي تحتوي عليها. ومع ذلك ، في أغلب الأحيان ، يتم اكتشاف الأخطاء فقط أثناء المعالجة النهائية لنتائج القياس باستخدام معايير إحصائية خاصة.

اعتمادًا على أسباب الحدوث ، يتم تمييز الأخطاء الآلية والمنهجية والذاتية.

خطأ آليهو الخطأ المتأصل في أداة القياس نفسها ، أي الجهاز أو محول الطاقة الذي يتم إجراء القياس به. قد تكون أسباب الخطأ الآلي هي النقص في تصميم أداة القياس ، التأثير بيئةبشأن خصائصه أو تشوهه أو تآكل أجزاء من الجهاز ، إلخ.

خطأ منهجييظهر بسبب النقص في طريقة القياس ؛ التناقضات بين الكمية المقاسة ونموذجها المعتمد في تطوير أداة القياس ؛ تأثير أداة القياس على موضوع القياس والعمليات التي تحدث فيه. السمات المميزة أخطاء منهجيةهي أنه لا يمكن تحديدها في الوثائق التنظيمية والفنية لأداة القياس ، لأنها لا تعتمد عليها ، ولكن يجب أن يحددها المشغل في كل حالة محددة.

خطأ شخصي (شخصي)القياس يرجع إلى خطأ قراءة المشغل في موازين أداة القياس ، مخططات أدوات التسجيل. وهي ناتجة عن حالة المشغل ، وموقعه أثناء العمل ، ونقص أعضاء الحس ، والخصائص المريحة لأداة القياس. يتم تحديد خصائص الخطأ الذاتي على أساس القيمة الاسمية المعيارية لتقسيم مقياس أداة القياس (أو ورقة الرسم البياني لأداة التسجيل) ، مع مراعاة قدرة "المشغل المتوسط" على الاستيفاء ضمن حدود تقسيم المقياس. تنخفض هذه الأخطاء مع تحسن الأدوات ، على سبيل المثال: استخدام مؤشر ضوئي في الأدوات التناظرية يزيل الخطأ بسبب اختلاف المنظر ( المنظر(من المنظر اليوناني - الانحراف) ، تغيير مرئي في المواضع النسبية للأشياء بسبب حركة عين المراقب) استخدام مرجع رقمي يزيل الخطأ الذاتي.

خطأ القياس الموضوعي- خطأ لا يعتمد على الصفات الشخصية للشخص الذي يقوم بالقياس.

وفقًا لتأثير الظروف الخارجية ، يتم تمييز الأخطاء الرئيسية والإضافية لأداة القياس.

يسمى الخطأ الرئيسي خطأ أداة القياسالمعرفة في الظروف الطبيعيةتطبيقه. لكل أداة قياس ، تحدد الوثائق التنظيمية والفنية ظروف التشغيل - مجموعة من الكميات المؤثرة (درجة الحرارة المحيطة ، الرطوبة ، الضغط ، الجهد ، تردد التيار الكهربائي ، إلخ) ، والتي بموجبها يتم تطبيع الخطأ (الكمية المؤثرة هي الكمية المادية، لا تقاس بأداة القياس هذه ، ولكنها تؤثر على نتائجه).

إضافي يسمىخطأ جهاز القياس الناتج عن انحراف أي من الكميات المؤثرة ، أي. خطأ إضافيمما يزيد من الخطأ الكلي للجهاز ، يحدث إذا كان الجهاز يعمل في ظروف غير طبيعية.

اعتمادًا على طبيعة التغيير في حجم الخطأ عند تغيير القيمة المقاسة ، يتم تقسيم الأخطاء إلى مضافة ومضاعفة.

أخطاء مضافةبسبب تحول في الخاصية الثابتة للجهاز لأعلى أو لأسفل (إلى اليمين أو اليسار) ، على سبيل المثال ، بسبب إزاحة مقياس الجهاز (انحراف صفري) ، والاحتكاك في الدعامات ، إلخ. لا يعتمد الخطأ الإضافي على قيمة الكمية المقاسة x ، أي ثابت على كامل مقياس الأداة.

تهيمن الأخطاء الإضافية على معظم الأدوات التناظرية.

أخطاء مضاعفةتنشأ بسبب أخطاء في تحديد معامل التحويل k للخاصية الثابتة y = kx. يعتمد الخطأ المضاعف على قيمة الكمية المقاسة ويزيد في نهاية مقياس الأداة.

يتناسب الخطأ المضاعف (عند التعبير عنه كخطأ مطلق) مع قيمة الكمية المقاسة.

تسود الأخطاء المضاعفة في الأجهزة المتعلقة بمحولات القياس (المحولات ، المقاومة الإضافية ، المكبرات ، المقسمات ، المحولات ، إلخ).

هناك أجهزة يمكن مقارنة أخطائها الإضافية والمضاعفة. تتضمن هذه الفئة من الأجهزة أجهزة رقمية.

تنشأ أخطاء القياس العشوائية بسبب التأثير المتزامن على كائن القياس للعديد من الكميات المستقلة ، والتي تتغير طبيعتها بشكل متقلب. يتم أيضًا تقديم مساهمة معينة في خطأ القياس العشوائي بواسطة الخطأ العشوائي لجهاز القياس.

سنفترض أن المكون النظامي لخطأ القياس مستبعد وأن الخطأ العشوائي ، كمتغير عشوائي ، مستبعد تمامًا

تتميز بكثافة توزيع الاحتمالية (بمعنى آخر ، كثافة الاحتمالية) حيث تكون دالة التوزيع. لذلك ، لم يتم تحديد قيمة عددية خطأ عشوائي، ولكن فقط احتمال أنها تقع في فترة معينة أو لا تتجاوز قيمة معينة. إذا كان قانون التوزيع معروفًا ، فعندئذٍ ومعروف. تم العثور على احتمالية العثور على خطأ عشوائي في فترة زمنية معينة من إلى بواسطة الصيغة

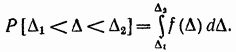
يمكن تحديد نمط التغيير في الخطأ العشوائي من خلال ملاحظات متعددة لقيمه والمعالجة الإحصائية لنتائج الملاحظات.

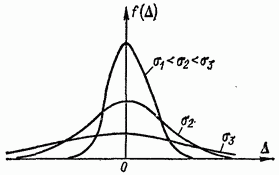
أرز. 2-1. الكثافة الاحتمالية للأخطاء العشوائية بموجب قانون التوزيع العادي

يتم تنفيذ هذا العمل الذي يستغرق وقتًا طويلاً ومضنيًا بقياسات دقيقة ويتكون من التحقق من توافق البيانات التي تم الحصول عليها مع التوزيع المتوقع وفقًا لبعض المعايير.

تقلبات الكميات المؤثرة هي أيضًا عشوائية وتتميز بقوانين التوزيع الخاصة بها (موحدة ، مثلثة ، عادية ، إلخ). ومع ذلك ، نظرًا لتناسب مشتتاتها ، بالفعل عند 4-5 كميات مؤثرة ، فإن قانون التوزيع الناتج لخطأ القياس العشوائي يتفق بشكل مرضٍ مع القانون العادي (الشكل 2-1).

دالة التوزيع الطبيعي

وكثافة الاحتمال

أين هو التباين الذي يميز تشتت الخطأ العشوائي بالنسبة لمركز التوزيع وانحرافه المعياري.

يميز التشتت والانحراف المعياري دقة القياس: كلما قلت الدقة. في ممارسة القياس ، يتم استخدام الانحراف المعياري c بشكل أساسي ، حيث يتم التعبير عنه بنفس الوحدات مثل القيمة المقاسة.

أرز. 2-2. تكامل الاحتمالية

احتمال حدوث خطأ عشوائي في النطاق من إلى وفقًا للصيغة

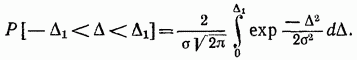
إذا أدخلنا متغيرًا عشوائيًا طبيعيًا ، فسيتم تحويل الجانب الأيمن من المساواة إلى وظيفة لابلاس ، والتي تسمى غالبًا احتمال التكامل

تم جدولة هذه الوظيفة ، وترد قيمها في الجدول. ويظهر الرسم البياني في الشكل. 2-2.

إذا تم إعطاء احتمال معين a ، فعندما وجدته ، من الممكن تحديده بموجب قانون التوزيع العادي ، يتم أخذ الحد الأقصى للخطأ Dmax والذي يتوافق مع احتمال حدوث خطأ يتجاوز هذا يعني أنه في 369 من أصل 370 الملاحظات مع احتمال 0.9973 يكمن الخطأ في الفاصل الزمني ± 3 أ وفقط في ملاحظة واحدة قد يتجاوزها.

أرز. 2-3. الكثافة الاحتمالية للأخطاء العشوائية مع قانون توزيع موحد

يحدث قانون التوزيع الموحد أيضًا في القياسات. على وجه الخصوص ، هو نموذجي لقياس الكميات المستمرة بطريقة العد المنفصل. كثافة احتمال الخطأ في المدى من (الشكل 2-3) مكتوبة بالشكل التالي ؛

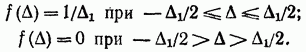
لذلك ، فإن التباين

والانحراف المعياري

على سبيل المثال ، يتسم خطأ التكميم ، والذي يكون عادةً ضمن الرقم الأقل دلالة (من -1/2 إلى 1/2) ، بالانحراف المعياري

لنعد إلى قانون التوزيع الطبيعي. يتميز هذا القانون بالمعلمات العددية: التوقع الرياضي والتشتت. تعريف دقيقتكاد تكون هذه المعلمات مستحيلة ، حيث يجب أن يكون لديك عدد لا نهائي من القيم لهذا الغرض متغير عشوائي، أي إجراء الملاحظات في. في ممارسة القياسات ، تكون دائمًا محدودة ، لذلك يتم استدعاء القيم المحسوبة نتيجة التجربة

التقديرات توقع رياضيوالانحراف المعياري.

دعنا نفكر في إجراء القياس الإحصائي لبعض القيمة ، والتي يتم إنتاج القيمة الحقيقية لها من خلال الملاحظات الفردية ، ونتيجة لذلك يتم الحصول على عدد من القيم العشوائية للقيمة المقاسة. في كل خطأ مطلق من الملاحظة الأولى ، من المستحيل تحديد قيمة هذا الخطأ ، لأنه غير معروف.

يؤخذ المتوسط ​​الحسابي كتقدير للتوقع الرياضي (القيمة الحقيقية)

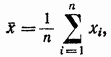
والتي تسمى القيمة الفعلية A للكمية المقاسة عند

يمكنك الآن حساب الانحراف المطلق لكل نتيجة ملاحظة بالنسبة إلى القيمة المتوسطة: من الواضح ، في للتحكم في صحة الحسابات ، يمكنك استخدام خصائص انحرافات نتائج الملاحظة من المتوسط ​​الحسابي: مجموع الانحرافات هو صفر ومجموع مربعاتهم ضئيل:

يتم تحديد تقدير الانحراف المعياري للانحرافات المطلقة لكل ملاحظة مفردة بواسطة الصيغة

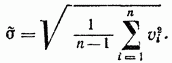
ستكون دقة نتيجة القياس أعلى. يتميز بتقدير الانحراف المعياري للقيمة الحسابية (الحقيقية):

مع زيادة عدد القياسات (مع نتائج مستقلة) ، تزداد الدقة بشكل متناسب. يبدو أنه من خلال الزيادة يمكنك الحصول على أي زيادة في الدقة. ومع ذلك ، فإن الفطرة السليمة وممارسة القياس تشير إلى أنها قليلة الفائدة ، حيث يمكن أن يتغير القياس نفسه أثناء القياس.

فاصل الثقة واحتمالية الثقة.نتيجة لملاحظات القيمة المقاسة ، نحصل على تقدير لقيمتها الفعلية A ، تساوي المتوسط ​​الحسابي X ، وفقًا للصيغة (2-11). هذا التقدير هو أيضا متغير عشوائي. يتم تحديد الانحراف المعياري أ - بواسطة الصيغة (2-13) ، أي أن نتيجة القياس تحتوي على عدم يقين. مطلوب معرفة ضمن الحدود التي يمكن أن تتغير فيها القيمة الفعلية لـ A أثناء القياسات المتكررة للكميات (الإحصائية) في ظل نفس الظروف ، أي أنه من الضروري العثور على فاصل من القيم "يغطي" القيمة الحقيقية لـ الكمية المقاسة باحتمالية معينة. يسمى هذا الفاصل الزمني بفاصل الثقة ، ويسمى الاحتمال المحدد (الثابت) بفاصل الثقة. فاصل الثقة ومستوى الثقة يميزان عدم التيقن من نتيجة القياس. تحليليًا ، يكتب هذا على النحو التالي:

يقرأ التعبير (2-14) على النحو التالي: القيمة الحقيقية للقيمة المقاسة تقع ضمن فاصل الثقة من إلى مع احتمال الثقة أ.

وبالمثل بالنسبة للخطأ العشوائي

يقع خطأ القياس العشوائي ضمن فاصل الثقة من إلى احتمال الثقة أ.

اعتمادًا على الغرض من القياس ، يتم تعيين مستوى الثقة على قدم المساواة. في التعبيرات (2-14) و (2-15) ، تكون فترات الثقة متماثلة. يُطلق على نصف فاصل الثقة اسم الخطأ المحدد (الحد الأقصى ، المسموح به) باحتمالية الثقة أ. في بعض الأحيان يكون فاصل الثقة غير متماثل وله الشكل

يتم التعبير عن الخطأ الهامشي وفاصل الثقة من حيث الانحراف المعياري. بالنسبة لقانون التوزيع العادي ، يتم تحديد فاصل الثقة لاحتمالية ثقة معينة (والعكس صحيح) باستخدام جدول الاحتمالات المتكامل (الجدول A4). تم تعيينها بمستوى ثقة ، على سبيل المثال ، 0.95. وفقًا للجدول ، تم العثور على القيمة أيضًا ، والتي في هذه الحالة تساوي 2. نظرًا لأن هذه هي فترة الثقة

من الواضح أن كلاً من فاصل الثقة ومستوى الثقة مرتبطان بعدد الملاحظات ، لأنه كلما كان الفاصل الزمني أكبر ، كان أضيق. ومع ذلك ، كما ذكر أعلاه ، في ممارسة القياسات أمر نادر الحدوث. بالنسبة لعدد الملاحظات ، يتم تحديد فاصل الثقة ليس من خلال ولكن من خلال معامل معين يعتمد على عدد الملاحظات واحتمال الثقة أ. يتم تحديد قانون تغيير المعامل من خلال توزيع الطالب للمتغير العشوائي العادي المحسوب بالتوزيع الطبيعي. يتم تحديد المعامل باستخدام الصيغة التالية:

هذه ليست أخطاء ، أي ليست أخطاء واضحة ارتكبها المشغل ، فمن الضروري تحديد ما إذا كانت أخطاء جسيمة ، والتي يجب استبعادها أيضًا من المعالجة ، مثل الأخطاء. يؤدي استبعاد الخطأ الجسيم دون أسباب كافية إلى تحسن غير معقول في نتيجة القياس. من ناحية أخرى ، فإن عدم استبعاد الخطأ الجسيم ، خاصة مع عدد قليل من الملاحظات ، سيشوه القيمة الفعلية للقيمة المقاسة وحدود فاصل الثقة. لذلك ، يجب اكتشاف الأخطاء الجسيمة والتخلص منها.

إن أبسط طريقة لاكتشاف الخطأ الإجمالي في التوزيع العادي هي مقارنة الخطأ المطلق للملاحظة "المشبوهة" مع الحد الأقصى للخطأ. حقيقة أن احتمالية انحراف القيمة عن المتوسط ​​الحسابي أكبر من تساوي 0.003 فقط.

ومع ذلك ، يجب أن نتذكر أنه إذا أعداد كبيرةالملاحظات ، على الرغم من وجود احتمال منخفض ، فمن الممكن أن الرقم المهمل ليس خطأ جسيمًا ، ولكنه انحراف إحصائي طبيعي لهذه القيمة. لذلك ، في الحالات الحرجة ، يتم تحديد الخطأ الجسيم على أساس نظرية الاحتمالات. يتم تحديد عدد القياسات ذات الاحتمالية المعينة التي يمكن تجاهلها نتيجة الملاحظة التي تتجاوز رقمًا معينًا أو حدودًا معينة.

تصنف أخطاء القياس إلى الأنواع التالية:

مطلق ونسبي.

ايجابي وسلبي.

ثابت ومتناسب.

خشن وعشوائي ومنهجي.

الخطأ المطلقنتيجة قياس واحدة (أ ذ) على أنه الفرق بين القيم التالية:

أ ذ = ذأنا- ذ IST. » ذأنا `` ذ.

خطأ نسبينتيجة قياس واحدة (ب ذ) تحسب كنسبة الكميات التالية:

ويترتب على هذه الصيغة أن حجم الخطأ النسبي لا يعتمد فقط على حجم الخطأ المطلق ، ولكن أيضًا على قيمة الكمية المقاسة. عندما تظل القيمة المقاسة دون تغيير ( ذ) لا يمكن تقليل خطأ القياس النسبي إلا عن طريق تقليل الخطأ المطلق (أ ذ). عندما يكون خطأ القياس المطلق ثابتًا ، لتقليل خطأ القياس النسبي ، يمكنك استخدام طريقة زيادة قيمة الكمية المقاسة.

مثال.لنفترض أن مقياس التجارة في متجر له خطأ ثابت مطلق في قياس الكتلة: أ م = 10 جم. إذا كنت تزن 100 جرام من الحلويات (م 1) على هذه المقاييس ، فسيكون الخطأ النسبي في قياس كتلة الحلويات هو :

.

عند وزن 500 جرام من الحلويات (م 2) على نفس الميزان ، سيكون الخطأ النسبي أقل بخمس مرات:

.

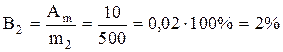وبالتالي ، إذا كنت تزن 100 جرام من الحلويات خمس مرات ، فبسبب خطأ في قياس الكتلة ، لن تحصل على إجمالي 50 جرام من المنتج من أصل 500 جرام. بوزن واحد بكتلة أكبر (500 جم) ، ستخسر 10 جم فقط من الحلويات ، أي خمس مرات أقل.

بالنظر إلى ما سبق ، يمكن ملاحظة أنه ، أولاً وقبل كل شيء ، من الضروري السعي لتقليل أخطاء القياس النسبية. لا يمكن حساب الأخطاء المطلقة والنسبية إلا بعد تحديد المتوسط قيمة حسابيةنتيجة القياس.

يتم تحديد علامة الخطأ (إيجابية أو سلبية) من خلال الفرق بين نتيجة القياس الفردية والفعلية:

ذأنا `` ذ > 0 (الخطأ موجب);

ذأنا `` ذ < 0 (الخطأ سلبي).

إذا كان خطأ القياس المطلق لا يعتمد على قيمة الكمية المقاسة ، فسيتم استدعاء هذا الخطأ دائم. خلاف ذلك ، سيكون الخطأ متناسب. يتم تحديد طبيعة خطأ القياس (ثابت أو متناسب) بعد دراسات خاصة.

خطأ جسيمالقياس (الخطأ) هو نتيجة قياس تختلف اختلافًا كبيرًا عن النتائج الأخرى ، والتي تحدث عادةً عند انتهاك إجراء القياس. يتم تحديد وجود أخطاء القياس الإجمالية في العينة فقط من خلال طرق الإحصاء الرياضي (لـ n> 2). تعرف على طرق اكتشاف الأخطاء الجسيمة بنفسك.

إن تقسيم الأخطاء إلى عشوائية ومنهجية أمر مشروط إلى حد ما.

ل أخطاء عشوائيةتتضمن الأخطاء التي ليس لها قيمة وعلامة ثابتة. تحدث مثل هذه الأخطاء تحت تأثير العوامل التالية: غير معروف للباحث. معروف لكن غير منظم ؛ يتغير باستمرار.

لا يمكن تقدير الأخطاء العشوائية إلا بعد أخذ القياسات.

التحديديمكن أن يكون معامل حجم خطأ القياس العشوائي هو المعلمات التالية: إلخ.

لا يمكن استبعاد أخطاء القياس العشوائية ، بل يمكن تقليلها فقط. تتمثل إحدى الطرق الرئيسية لتقليل حجم خطأ القياس العشوائي في زيادة عدد القياسات الفردية (زيادة قيمة n). يفسر ذلك حقيقة أن حجم الأخطاء العشوائية يتناسب عكسياً مع قيمة n ، على سبيل المثال:

أخطاء منهجيةهي أخطاء ذات حجم وعلامة ثابتة أو متغيرة وفقًا لقانون معروف. هذه الأخطاء ناتجة عن عوامل ثابتة. يمكن قياس الأخطاء المنهجية وتقليلها وحتى القضاء عليها.

تصنف الأخطاء المنهجية إلى أنواع الأخطاء الأول والثاني والثالث.

لمنهجية اكتب أنا الأخطاءتشير إلى أخطاء معروفة المنشأ ، والتي يمكن تقديرها بالحساب قبل القياس. يمكن التخلص من هذه الأخطاء عن طريق إدخالها في نتيجة القياس في شكل تصحيحات. مثال على هذا النوع من الخطأ هو الخطأ في تحديد القياس بالمعايرة للتركيز الحجمي للمحلول إذا تم تحضير المعاير عند درجة حرارة واحدة ، وتم قياس التركيز عند درجة حرارة أخرى. بمعرفة اعتماد كثافة المعاير على درجة الحرارة ، من الممكن حساب التغير في التركيز الحجمي للمعاير المرتبط بالتغير في درجة حرارته قبل القياس ، وأخذ هذا الاختلاف في الاعتبار كتصحيح نتيجة القياسات.

منهجي النوع الثاني من الأخطاء- هذه أخطاء معروفة المصدر ، والتي لا يمكن تقييمها إلا أثناء التجربة أو نتيجة لدراسات خاصة. يشتمل هذا النوع من الأخطاء على أخطاء مفيدة (آلية) وتفاعلية ومرجعية وأخطاء أخرى. تعرف على ميزات هذه الأخطاء بنفسك.

يُدخل أي جهاز ، عند استخدامه في إجراء القياس ، أخطاءه الآلية في نتيجة القياس. في الوقت نفسه ، تكون بعض هذه الأخطاء عشوائية ، والجزء الآخر منهجي. لا يتم تقييم أخطاء الجهاز العشوائية بشكل منفصل ، بل يتم تقييمها مع جميع أخطاء القياس العشوائية الأخرى.

كل مثيل لأي أداة له خطأ منهجي شخصي خاص به. لتقييم هذا الخطأ ، من الضروري إجراء دراسات خاصة.

معظم طريقة موثوقةتقييم الخطأ المنهجي الآلي من النوع الثاني - هذا هو التوفيق بين تشغيل الأدوات والمعايير. لأدوات القياس (الماصات ، السحاحات ، الأسطوانات ، إلخ) ، يتم تنفيذ إجراء خاص - المعايرة.

في الممارسة العملية ، غالبًا ما يكون مطلوبًا عدم التقدير ، ولكن تقليل أو إزالة الخطأ المنهجي من النوع الثاني. أكثر الطرق شيوعًا لتقليل الأخطاء المنهجية هي طرق النسبية والعشوائيةتحقق من هذه الأساليب بنفسك على.

ل اخطاء النوع الثالث تتضمن أخطاء من أصل غير معروف. لا يمكن اكتشاف هذه الأخطاء إلا بعد التخلص من جميع الأخطاء المنهجية من النوع الأول والثاني.

ل اخطاء اخرىسنقوم بتضمين جميع أنواع الأخطاء الأخرى التي لم يتم النظر فيها أعلاه (مقبولة ، أخطاء هامشية محتملة ، وما إلى ذلك). يتم استخدام مفهوم الأخطاء الهامشية المحتملة في حالات استخدام أدوات القياس ويفترض الحد الأقصى لخطأ القياس الآلي الممكن (قد تكون القيمة الفعلية للخطأ أقل من قيمة الخطأ الهامشي المحتمل).

عند استخدام أدوات القياس ، من الممكن حساب الحد المطلق المحتمل (P` ذ، إلخ) أو قريب (E` ذ، وما إلى ذلك) أخطاء القياس. لذلك ، على سبيل المثال ، تم العثور على خطأ القياس المطلق المحدد كمجموع العشوائية المحددة المحتملة (x ` ذ، العشوائية ، إلخ.) النظامية غير المستبعدة (d` ذ، وما إلى ذلك):

P` ذ، على سبيل المثال = x ` ذ، عشوائي، العلاقات العامة + d` ذ، إلخ.

بالنسبة للعينات الصغيرة (20 جنيهًا إسترلينيًا) ، فإن المجهول سكان، وفقًا لقانون التوزيع العادي ، يمكن تقدير أخطاء القياس العشوائية المحتملة على النحو التالي:

x` ذ، عشوائي ، العلاقات العامة = D` ذ= S ' ذ½t P ، n ½ ،
حيث t P، n هو مقدار توزيع الطالب (الاختبار) لاحتمال P وحجم العينة n. سيكون خطأ القياس المحدد المطلق في هذه الحالة مساويًا لـ:

P` ذ، على سبيل المثال = S ` ذ½t P ، n ½ + d` ذ، إلخ.

إذا كانت نتائج القياس لا تمتثل لقانون التوزيع العادي ، فسيتم تقدير الخطأ باستخدام معادلات أخرى.

تحديد قيمة د ذ،إلخ. يعتمد على ما إذا كانت أداة القياس بها فئة دقة. إذا لم يكن لأداة القياس فئة دقة ، فعندئذٍ للقيمة d ` ذ،إلخ. يمكن قبولها الحد الأدنى لقيمة تقسيم المقياسقياس . لأداة قياس ذات فئة دقة معروفة للقيمة d ` ذ، على سبيل المثال ، يمكن للمرء أن يقبل الخطأ المنهجي المطلق المسموح به لأداة القياس (د ذ، يضيف.):

د` ذ،إلخ." .

قيمة د ذ، يضيف. يتم حسابه بناءً على الصيغ الواردة في الجدول 5.

بالنسبة للعديد من أدوات القياس ، تتم الإشارة إلى فئة الدقة في شكل أرقام a × 10 n ، حيث a يساوي 1 ؛ 1.5 ؛ 2 ؛ 2.5 ؛ 4 ؛ 5 ؛ 6 و n هي 1 ؛ 0 ؛ -1 ؛ -2 ، وما إلى ذلك ، والتي توضح قيمة الحد الأقصى المسموح به للخطأ المنهجي (E ذ، add.) وعلامات خاصة تدل على نوعها (نسبي ، مختزل ، ثابت ، متناسب).

الجدول 5

أمثلة على تعيين فئات الدقة لأجهزة القياس

استمرار الجدول 5

نهاية الجدول 5

يمكن إهمال الأخطاء المنهجية إذا كان عدم المساواة

في هذه الحالة ، من المفترض أن:

P` ذ، إلخ." x` ذ، قضية ، إلخ. »D` ذ»S` ذ½t P ، n ½.

يمكن إهمال الأخطاء العشوائية المقدمة

لهذه الحالة P` ذ، إلخ." د` ذ،إلخ. .

تعد زيادة عدد القياسات الفردية الطريقة الأكثر شيوعًا لتقليل الأخطاء العشوائية (مما يؤدي أيضًا إلى زيادة تكلفة القياسات). يُنصح بزيادة n حتى يتم تحديد إجمالي خطأ القياس فقط من خلال الخطأ النظامي. لا يمكن حساب الحد الأدنى لعدد القياسات المتوازية المطلوبة لهذا (n min) إلا من أجل قيمة معروفةالعدد العام للنتائج الفردية وفقًا للصيغة

.

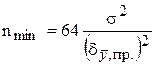إذا كانت مكونات (م - عدد المكونات) للخطأ المنهجي المطلق للمتوسط ​​الحسابي لنتيجة القياس () معروفة ، فيمكن تقديرها بالصيغة

,

حيث k هو معامل يحدده الاحتمال P والرقم m.

لا يعتمد تقدير أخطاء القياس على وسائل القياس وحجم العينة فحسب ، بل يعتمد أيضًا على نوع القياس (القياس المباشر أو غير المباشر).

تقسيم القياسات إلى مباشرة وغير مباشرة مشروط إلى حد ما. في وقت لاحق ، تحت القياسات المباشرةسوف نفهم ذلك عندما يتم الحصول على نتيجة القياس مباشرة ، على سبيل المثال ، يتم قراءتها من مقياس الجهاز. ل القياسات غير المباشرةسننسب مثل هذا عندما نتيجة القياس محسوبكدالة لـ (ي) نتائج قياس مباشر واحد أو أكثر ( x 1 , x 2 , …, xي. ... ، xك).

من الضروري معرفة أن أخطاء القياسات غير المباشرة دائمًا ما تكون أكبر من أخطاء القياسات الفردية المباشرة. يتم تقدير أخطاء القياسات غير المباشرة وفقًا للقوانين ذات الصلة.

تؤدي الأخطاء العشوائية إلى حقيقة أن القيم المرصودة للكمية المقاسة أثناء القياسات المتكررة مبعثرة عشوائيًا بالنسبة لقيمتها الحقيقية. ثم يتم العثور على القيمة الفعلية على أنها الأكثر احتمالًا في سلسلة من التجارب ، ويتسم الخطأ بعرض الفاصل الزمني ، والذي يتضمن القيمة الحقيقية مع احتمال معين. يتم تقديم الإثبات الرياضي لهذه الأحكام في نظرية الاحتمالية ، والتي يتم تقديم تطبيقها لمعالجة نتائج القياس في الأدبيات ، والتطبيق المباشر للأعمال ورشة عمل فيزيائيةفي الأدب.

في كثير من الأحيان ، يجد الطلاب وتلاميذ المدارس خطأ القياس باستخدام الصيغة

, (6.2)

أين هي متوسط ​​قيمة الكمية التي تم الحصول عليها أثناء عملية القياس ، وهي القيمة المأخوذة من الكتاب المرجعي ، أو محسوبة من المفاهيم النظرية. مثل هذا التعريف للخطأ هو خطأ جسيم ، لأن الغرض من التجربة ، كما هو موضح أعلاه ، هو اختبار المفاهيم النظرية وتنقيح البيانات الجدولية.

بالإضافة إلى ذلك ، غالبًا ما يتم حساب الخطأ على أنه متوسط ​​قيمة انحرافات نتائج القياس الفردية من متوسط ​​القيمة باستخدام الصيغة

. (6.3)

وفقًا لهذا النهج ، تظهر أي قيمة خطأ بشكل متساوٍ ، أي تعتبر الأخطاء ذات الأحجام المختلفة محتملة بنفس القدر. يمكن استخدام هذه الطريقة في العمل المخبريمع عدد قليل من القياسات.

ومع ذلك ، فإن الأخطاء العشوائية ليست محتملة بنفس القدر. تتطلب معالجة إحصائية لنتائج القياس لتعريفها. لذلك ، يبدو من الضروري النظر في محتوى المعالجة الإحصائية لنتائج القياس. تستند النظرية الإحصائية للأخطاء على الأحكام التالية:

1) مع عدد كبير من القياسات ، لوحظت أخطاء عشوائية من نفس الحجم ، ولكن علامة مختلفة، أي الأخطاء ، سواء في اتجاه الانخفاض أو الزيادة ، تحدث في كثير من الأحيان على حد سواء ؛

2) الأخطاء الكبيرة (بالقيمة المطلقة) أقل شيوعًا من الأخطاء الصغيرة ، أي يتناقص احتمال ظهور الخطأ مع زيادة حجم الخطأ ؛

3) يمكن أن تأخذ أخطاء القياس سلسلة متواصلة من القيم.

يسمى توزيع المتغير العشوائي الذي يخضع للخصائص المدرجة بالتوزيع العادي. لتقدير انتشار فردييتم اختيار قيم المتغير العشوائي مع التوزيع الطبيعي أو العينات الفردية في نظرية التوزيع الطبيعي عينة الانحراف المعياري للقراءات ،والتي يتم حسابها بواسطة الصيغة:

. (6.4)

تقدير قيمة الخطأ في قياس واحد ، التي تحددها الصيغة (6.4) مهم للغاية. ومع ذلك ، بالنسبة للقياس ، تتمثل المهمة المهمة في تحديد الدقة التي يتوافق بها متوسط ​​قيمة القيمة المقاسة مع القيمة المطلوبة. تنشأ هذه المشكلة بسبب حقيقة أنه يمكن الحصول على متوسط ​​القيمة أبعاد مختلفة. على سبيل المثال ، يمكن الحصول على متوسط ​​القيمة من عدد مختلف من القياسات. لذلك ، فإن المتوسط ​​التجريبي هو أيضًا متغير عشوائي ، يمكن أيضًا وصفه بواسطة دالة التوزيع. يتم تحديد قيمة الانحراف المعياري المقابل لهذه الوظيفة ، كما هو موضح في نظرية الاحتمالات ، من خلال الصيغة:

(6.5)

هذه القيمة تسمى عينة الانحراف المعياري للمتوسطأو خطأ تقليدي.

كما يتضح من معادلة الخطأ القياسية (6.5) ، فإنها تتناقص مع زيادة عدد القياسات وتزداد دقة النتيجة ، وهو ما يتوافق مع الاستدلال السابق.

تستخدم الصيغ المذكورة أعلاه لتحديد خطأ القياس خصائص التوزيع الطبيعي لمتغير عشوائي. ومع ذلك ، لا يعرف القانون الذي توزع فيه نتائج القياس. لذلك ، هذه التقديرات تقريبية. في هذا الصدد ، هناك حاجة لتحليل هذا النهج لتحديد خطأ القياس. لمثل هذا التحليل ، يمكن للمرء استخدام المفهوم المعروف لفاصل الثقة في نظرية الاحتمالات. دع القيمة تساوي احتمال أن نتيجة القياس - القيمة المتوسطة - تختلف عن القيمة الحقيقية بقيمة لا تزيد عن. في نظرية الاحتمالات ، تتم كتابة هذه العبارة على النحو التالي:

القيمة تسمى مستوى الثقة (الموثوقية)نتيجة سلسلة من الملاحظات. يوضح الاحتمال الذي يتضمن به فاصل الثقة القيمة الحقيقية للمقياس.

فاصل الثقةيسمى فاصل القيم ، والذي يتضمن بدرجة معينة من اليقين القيمة الحقيقية للقيمة المقاسة. التمثيل الهندسي لهذه الفترة الزمنية موضح في الشكل 1.

وبالتالي ، لتحديد الخطأ العشوائي ، من الضروري إيجاد أو تعيين رقمين: أي قيمة الخطأ العشوائي نفسه أو فاصل الثقة وقيمة احتمال الثقة.

لأي قيمة لفاصل الثقة ، يمكنك حساب احتمال الثقة. لهذا ، يتم استخدام دالة لابلاس ، والتي تسمى أيضًا تكامل الاحتمال. وظيفة لابلاس لها الشكل:

,

أين . في أغلب الأحيان ، عند حل المشكلات ، يتم استخدام القيم المجدولة لوظيفة لابلاس. هذه القيم موضحة في الجدول 1.

تظهر نتائج هذا الجدول أن خطأ جذر متوسط ​​التربيع له احتمالية ثقة تبلغ 0.68 ، وخطأ 2x جذر متوسط ​​التربيع له احتمالية ثقة 0.95 ، وخطأ 3x جذر متوسط ​​التربيع له احتمالية ثقة 0.997.

الجدول 1

احتمالات الثقة لفاصل الثقة ، معبراً عنه في كسور متوسط ​​الخطأ التربيعي . وظيفة لابلاس

		1,2	0,77	2,6	0,990
0,05	0,04	1,3	0,80	2,7	0,993
0,1	0,08	1,4	0,84	2,8	0,995
0.15	0,12	1,5	0,87	2,9	0,996
0,2	0,16	1,6	0,89	3,0	0,997
0,3	0,24	1,7	0,91	3,1	0,9981
0,4	0,31	1,8	0,93	3,2	0,9986
0,5	0,38	1,9	0,94	3,3	0,9990
0,6	0,45	2,0	0,95	3,4	0,9993
0,7	0,51	2,1	0,964	3,5	0,9995
0,8	0,57	2,2	0,972	3,6	0,9997
0,9	0,63	2,3	0,978	3,7	0,9998
1,0	0,68	2,4	0,984	3,8	0,99986
1.1	0,73	2,5	0,988	3,9	0,99990
				4,0	0,99993

خطأ عشوائيمن المعتاد تعريفه على أنه نصف عرض فاصل الثقة. يتم إعطاء حجم فاصل الثقة كمضاعف للانحراف المعياري للعينة للمتوسط ، والتي تحددها الصيغة (6.5).ثم خطأ عشوائي في قياسات متعددةيتم تحديده من خلال الصيغة.