Problém je položený nasledovne: nechajte požadovanú hodnotu z určené z hľadiska iných veličín a, b, c, ... získané z priamych meraní
z = f(a,b,c,...) (1.11)
Je potrebné nájsť strednú hodnotu funkcie a chybu jej meraní, t.j. nájsť interval spoľahlivosti
so spoľahlivosťou a a relatívnou chybou .
Pokiaľ ide o , nájde sa dosadením do pravej strany (11) namiesto a, b, c,... ich priemerné hodnoty
Absolútna chyba nepriame merania je funkciou absolútnych chýb priamych meraní a vypočíta sa podľa vzorca
 (1.14)
(1.14)
Tu sú parciálne derivácie funkcií f podľa premenných a, b, …
Ak množstvá a, b, c,... do funkcie Z = f(a,b,c,...) vstupujú vo forme faktorov v tej či onej miere, t.j
![]() , (1.15)
, (1.15)
potom je vhodné najskôr vypočítať relatívnu chybu
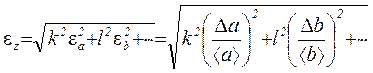 , (1.16)
, (1.16)
a potom absolútne
Vzorce pre D z a ez sú uvedené v referenčnej literatúre.
Poznámky.
1. Pre nepriame merania môžu výpočtové vzorce obsahovať známe fyzikálne konštanty (zrýchlenie voľný pád g, rýchlosť svetla vo vákuu s atď.), čísla ako zlomkové faktory ... . Tieto hodnoty sú vo výpočtoch zaokrúhlené. V tomto prípade sa samozrejme do výpočtu vnáša chyba ![]() - chyba zaokrúhľovania vo výpočtoch, s ktorou je potrebné počítať.
- chyba zaokrúhľovania vo výpočtoch, s ktorou je potrebné počítať.
Všeobecne sa uznáva, že chyba zaokrúhľovania približného čísla sa rovná polovici jednotky číslice, na ktorú bolo toto číslo zaokrúhlené. Napríklad p = 3,14159... . Ak vezmeme p=3,1, tak Dp=0,05, ak p=3,14, tak Dp=0,005...atď. Otázka, na akú číslicu zaokrúhliť približné číslo, sa rieši nasledovne: relatívna chyba spôsobená zaokrúhľovaním musí byť rovnakého rádu alebo rádovo menšia ako maximum relatívnych chýb iných typov. Rovnakým spôsobom sa vyhodnocuje absolútna chyba tabuľkových údajov. Napríklad tabuľka uvádza r = 13,6 × 103 kg / m3, teda Dr = 0,05 × 103 kg / m3.
Chyba v hodnotách univerzálnych konštánt sa často uvádza spolu s ich priemernými hodnotami: ( s = ![]() m/s, kde D s= 0,3 x 103 m/s.
m/s, kde D s= 0,3 x 103 m/s.
2. Niekedy sa pri nepriamych meraniach experimentálne podmienky nezhodujú s opakovanými pozorovaniami. V tomto prípade hodnota funkcie z sa vypočíta pre každé jednotlivé meranie a interval spoľahlivosti sa vypočíta z hodnôt z rovnakým spôsobom ako pri priamych meraniach (všetky chyby sú tu zahrnuté do jednej náhodnej chyby merania z). Hodnoty, ktoré sa nemerajú, ale sú uvedené (ak nejaké existujú), musia byť uvedené s dostatočne vysokou presnosťou.
Postup spracovania výsledkov merania
Priame merania
1. Vypočítajte priemernú hodnotu pre n merania
2. Nájdite chyby jednotlivých meraní ![]() .
.
3. Vypočítajte druhú mocninu chýb jednotlivých meraní a ich súčet: 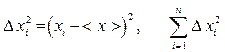 .
.
4. Nastavte spoľahlivosť a (pre naše účely berieme a = 0,95) a určte Studentove koeficienty z tabuľky t a, n a ta, ¥ .
5. Urobte hodnotenie systematické chyby: nástroj D X pr a chyby zaokrúhľovania v meraniach D X env \u003d D / 2 (D je dielik mierky zariadenia) a nájdite celkovú chybu výsledku merania (polovičná šírka intervalu spoľahlivosti):
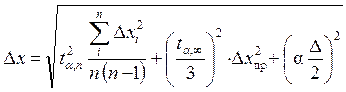 .
.
6. Odhadnite relatívnu chybu
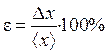 .
.
7. Konečný výsledok zapíšte ako
![]() ε = … % pre a = ...
ε = … % pre a = ...
Nepriame merania
1. Pre každú veličinu meranú priamym spôsobom, zahrnutú do vzorca na určenie požadovanej hodnoty ![]() , spracujte ako je uvedené vyššie. Ak medzi množstvá a, b, c, ... sú tabuľkové konštanty alebo čísla typu p, e,..., potom by sa mali vo výpočtoch zaokrúhliť tak (ak je to možné), aby relatívna chyba zavedená v tomto prípade bola rádovo menšia ako najväčšia relatívna chyba priamo nameraných hodnôt.
, spracujte ako je uvedené vyššie. Ak medzi množstvá a, b, c, ... sú tabuľkové konštanty alebo čísla typu p, e,..., potom by sa mali vo výpočtoch zaokrúhliť tak (ak je to možné), aby relatívna chyba zavedená v tomto prípade bola rádovo menšia ako najväčšia relatívna chyba priamo nameraných hodnôt.
Určte priemernú hodnotu požadovanej hodnoty
z = f( ,,
3. Odhadnite polovičnú šírku intervalu spoľahlivosti pre výsledok nepriamych meraní
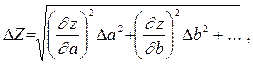 ,
,
kde sa deriváty ... počítajú na
4. Určte relatívnu chybu výsledku
![]()
5. Ak je závislosť z na a, b, c,... má podobu ![]() , kde k,l,m sú nejaké reálne čísla, musíte najprv nájsť príbuzný omyl
, kde k,l,m sú nejaké reálne čísla, musíte najprv nájsť príbuzný omyl
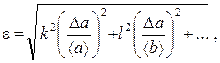
a potom absolútne .
6. Konečný výsledok zapíšte ako
z=
Poznámka:
Pri spracovaní výsledkov priamych meraní je potrebné dodržať nasledujúce pravidlo: číselné hodnoty všetkých vypočítaných hodnôt musia obsahovať o jednu číslicu viac ako počiatočné (experimentálne stanovené) hodnoty.
Pri nepriamych meraniach by sa mali výpočty robiť podľa pravidlá aproximácie:
Pravidlo 1 Pri pridávaní a odčítaní približných čísel musíte:
a) zvýrazniť pojem, v ktorom má pochybná postava najvyššie postavenie;
b) zaokrúhliť všetky ostatné výrazy na ďalšiu číslicu (ponecháva sa jedna náhradná číslica);
c) vykonať sčítanie (odčítanie);
d) v dôsledku toho vyradiť posledná číslica zaokrúhľovaním (číslica pochybnej číslice výsledku sa zhoduje s najvyššou z číslic pochybných číslic výrazov).
Príklad: 5,4382 10 5 – 2,918 10 3 + 35,8 + 0,064.
V týchto číslach sú posledné platné číslice pochybné (nesprávne už boli vyradené). Zapisujeme ich v tvare 543820 - 2918 + 35,8 + 0,064.
Je vidieť, že v prvom termíne má najvyššiu cifru (desiatky) pochybné číslo 2. Zaokrúhlením všetkých ostatných čísel nahor na ďalšiu číslicu a sčítaním dostaneme
543820 – 2918 + 36 + 0 = 540940 = 5,4094 10 5 .
Pravidlo 2 Pri násobení (delení) približných čísel musíte:
a) vyberte číslo (čísla) s najmenším počtom platných číslic ( VÝZNAMNÉ - čísla iné ako nula a nuly medzi nimi);
b) zaokrúhliť zvyšné čísla tak, aby mali o jednu platnú číslicu viac (uchová sa jedna náhradná číslica), ako je priradené v odseku a;
c) vynásobte (rozdeľte) výsledné čísla;
d) v dôsledku toho ponechajte toľko platných číslic, koľko ich bolo v čísle (číslach) s najmenším počtom platných číslic.
Príklad: .
Pravidlo 3 Pri zvýšení na mocninu, pri extrakcii odmocniny sa v dôsledku toho uloží toľko platných číslic, koľko je v pôvodnom čísle.
Príklad: ![]() .
.
Pravidlo 4 Pri hľadaní logaritmu čísla musí mať mantisa logaritmu toľko platných číslic, koľko je v pôvodnom čísle:
Príklad: ![]() .
.
V záverečnom vstupe absolútne mali by sa ponechať iba chyby jedna významná číslica. (Ak sa ukáže, že táto číslica je 1, potom sa za ňou uloží ďalšia číslica).
Stredná hodnota sa zaokrúhli na rovnakú číslicu ako absolútna chyba.
Napríklad: V\u003d (375,21 0,03) cm 3 \u003d (3,7521 0,0003) cm 3.
ja\u003d (5,530 0,013) A, A = ![]() J.
J.
Zákazka
Určenie priemeru valca.
1. Odmerajte posuvným meradlom 7-krát (in rôzne miesta a smeroch) priemer valca. Výsledky zapíšte do tabuľky.
| č. p / p | dj, mm | d i- | (d i- | h i, mm a Súvisiace informácie: |
ZÁKLADNÉ ODHADY CHYB MERANIA
Meranie je zisťovanie hodnoty fyzikálnej veličiny empiricky pomocou špeciálnych technických prostriedkov - mier, meracích prístrojov.
Miera je prostriedok merania, ktorý reprodukuje fyzikálnu veličinu danej veľkosti – mernú jednotku, jej násobok alebo zlomkovú hodnotu. Napríklad hmotnosti 1 kg, 5 kg, 10 kg.
Meracie zariadenie je merací prístroj určený na generovanie signálu meranej informácie vo forme dostupnej pre priame vnímanie pozorovateľom. Merací prístroj umožňuje priamo alebo nepriamo porovnávať nameranú hodnotu s mierami. Merania sa tiež delia na priame a nepriame.
Pri priamych meraniach sa požadovaná hodnota veličiny zistí priamo z hlavných (experimentálnych) údajov.
Pri nepriamych meraniach sa požadovaná hodnota veličiny zisťuje na základe známeho vzťahu medzi touto veličinou a veličinami podrobenými priamym meraniam. Princíp merania je súhrn fyzikálnych javov, na ktorých sú merania založené.
Metóda merania - súbor metód na využitie princípov a prostriedkov merania. Význam fyzikálne množstvo, čo by v ideálnom prípade z kvalitatívneho a kvantitatívneho hľadiska odrážalo zodpovedajúcu vlastnosť daného objektu skutočnú hodnotu fyzikálnej veličiny. Hodnota fyzikálnej veličiny zistená jej meraním je výsledkom merania.
Chybou merania je odchýlka výsledku merania od skutočnej hodnoty meranej veličiny.
Absolútna chyba merania je chyba merania, vyjadrená v jednotkách meranej veličiny a rovná sa rozdielu medzi výsledkom a skutočnou hodnotou meranej veličiny. Pomer absolútnej chyby k skutočnej hodnote meranej veličiny je relatívna chyba merania.
Na chybe merania sa podieľajú chyby meracích prístrojov (prístrojová alebo prístrojová chyba), nedokonalosť metódy merania, chyba odčítania na stupnici prístroja, vonkajšie vplyvy o prostriedkoch a predmetoch merania oneskorenie reakcie človeka na svetelné a zvukové signály.
Podľa charakteru prejavu chýb sa delia na systematické a náhodné. Náhodná udalosť je taká, ktorá sa vzhľadom na súbor faktorov môže alebo nemusí vyskytnúť.
Náhodná chyba – zložka chyby merania, ktorá sa náhodne mení pri opakovaných meraniach rovnakej hodnoty. charakteristický znak náhodné chyby je zmena veľkosti a znamienka chyby pri konštantných podmienkach merania.
Systematická chyba - zložka chyby merania, ktorá zostáva konštantná alebo sa pravidelne mení pri opakovaných meraniach rovnakej hodnoty. Systematické chyby možno v zásade odstrániť pomocou opráv, s použitím presnejších nástrojov a metód (hoci v praxi nie je vždy ľahké systematickú chybu odhaliť). Nie je možné vylúčiť náhodné chyby jednotlivých meraní, matematická teória náhodných javov (teória pravdepodobnosti) umožňuje iba rozumne odhadnúť ich veľkosť.
Chyby priamych meraní
Predpokladajme, že systematické chyby sú vylúčené a chyby výsledkov meraní sú len náhodné. Písmenami označujeme výsledky meraní fyzikálnej veličiny, skutočnú hodnotučo sa rovná ![]() . Sú uvedené absolútne chyby výsledkov jednotlivých meraní:
. Sú uvedené absolútne chyby výsledkov jednotlivých meraní:
Zhrnutím získanej ľavej a pravej strany rovnosti (1) dostaneme:
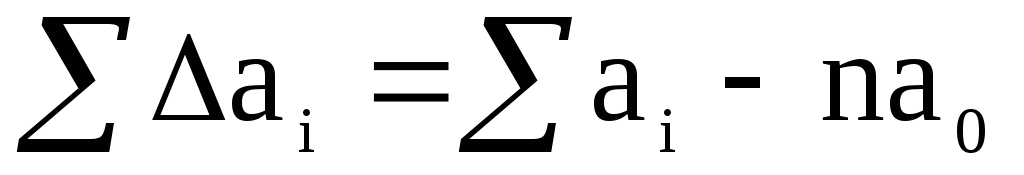 (2)
(2)
Teória náhodných chýb je založená na experimentálne potvrdených predpokladoch:
chyby môžu nadobúdať súvislý rad hodnôt;
pri veľké čísla merania náhodné chyby rovnakej veľkosti, ale iné znamenie stretávať sa rovnako často;
pravdepodobnosť výskytu chyby klesá so zvyšujúcou sa jej veľkosťou. Je tiež potrebné, aby chyby boli malé v porovnaní s nameranou hodnotou a nezávislé.
Podľa predpokladu (1) s počtom meraní n dostaneme
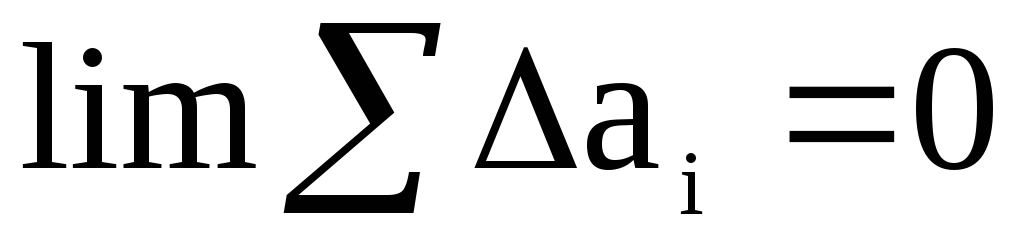
 ,
,
Počet rozmerov je však vždy konečný a ![]() zostáva neznámy. Ale na praktické účely postačí experimentálne nájsť hodnotu fyzikálnej veličiny tak blízku skutočnej hodnote, že
zostáva neznámy. Ale na praktické účely postačí experimentálne nájsť hodnotu fyzikálnej veličiny tak blízku skutočnej hodnote, že  možno použiť namiesto toho pravého. Otázkou je, ako odhadnúť mieru tejto aproximácie?
možno použiť namiesto toho pravého. Otázkou je, ako odhadnúť mieru tejto aproximácie?
Podľa teórie pravdepodobnosti aritmetický priemer série meraní  spoľahlivejšie ako výsledky jednotlivých meraní, pretože náhodné odchýlky od skutočnej hodnoty v rôznych smeroch sú rovnako pravdepodobné. Pravdepodobnosťou výskytu hodnoty a i v intervale šírky 2a rozumiem relatívnu frekvenciu výskytu hodnôt a i spadajúcich do intervalu 2a i k počtu všetkých vyskytujúcich sa hodnôt a i s číslom experimentov (meraní) smerujúcich do nekonečna. Je zrejmé, že pravdepodobnosť určitej udalosti sa rovná jednej, pravdepodobnosť nemožnej udalosti je nulová, t.j. 0 100 %.
spoľahlivejšie ako výsledky jednotlivých meraní, pretože náhodné odchýlky od skutočnej hodnoty v rôznych smeroch sú rovnako pravdepodobné. Pravdepodobnosťou výskytu hodnoty a i v intervale šírky 2a rozumiem relatívnu frekvenciu výskytu hodnôt a i spadajúcich do intervalu 2a i k počtu všetkých vyskytujúcich sa hodnôt a i s číslom experimentov (meraní) smerujúcich do nekonečna. Je zrejmé, že pravdepodobnosť určitej udalosti sa rovná jednej, pravdepodobnosť nemožnej udalosti je nulová, t.j. 0 100 %.
Pravdepodobnosť, že požadovaná hodnota (jej skutočná hodnota) je obsiahnutá v intervale (a - a, a + a), sa nazýva pravdepodobnosť (spoľahlivosť) a príslušný interval (a - a, a + a) - interval spoľahlivosti; čím menšia je hodnota chyby a, tým menšia je pravdepodobnosť, že nameraná hodnota sa nachádza v intervale definovanom touto chybou. Platí aj opačné tvrdenie: čím nižšia je spoľahlivosť výsledku, tým užší je interval spoľahlivosti požadovanej hodnoty.
Pre veľké n (prakticky pre n 100) sa polovičná šírka intervalu spoľahlivosti pre danú spoľahlivosť rovná
 ,
(3)
,
(3)
kde K() = 1 pri = 0,68; K() = 2 pri = 0,95; K() = 3 s = 0,997.
Pri malom počte meraní, ktoré sa najčastejšie vyskytujú v študentskej laboratórnej praxi, závisí koeficient K() v (3) nielen od , ale aj od počtu meraní n. Preto budeme vždy závisieť iba od dostupnosti náhodná chyba polovičná šírka intervalu spoľahlivosti sa zistí pomocou vzorca
 (4)
(4)
V (4) sa koeficient t n nazýva Studentov koeficient. Pre = 0,95 prijaté v študentskej praxi sú hodnoty t n nasledovné:
Hodnota sa nazýva efektívna chyba aritmetického priemeru zo série meraní.
Chybu prístroja alebo miery zvyčajne označuje v pase alebo symbolom na stupnici prístroja. Chybou prístroja sa zvyčajne rozumie polovičná šírka intervalu, v ktorom sa môže nameraná hodnota nachádzať s pravdepodobnosťou merania 0,997, ak je chyba merania spôsobená len chybou prístroja. Ako celkovú (celkovú) chybu výsledku merania akceptujeme s pravdepodobnosťou = 0,95
Absolútna chyba vám umožňuje určiť, ktoré znamienko výsledku obsahuje nepresnosť. Relatívna chyba dáva informáciu o tom, aký podiel (percento) nameranej hodnoty je chyba (polovičná šírka intervalu spoľahlivosti).
Konečný výsledok série priamych meraní nuly zapíšeme do formulára
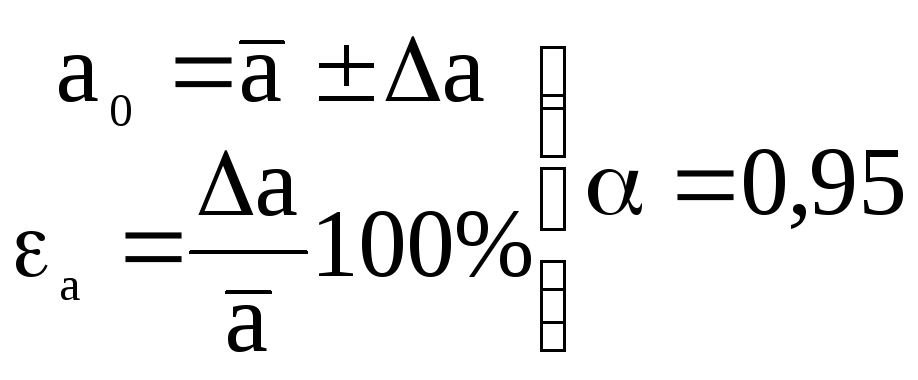 .
.
Napríklad
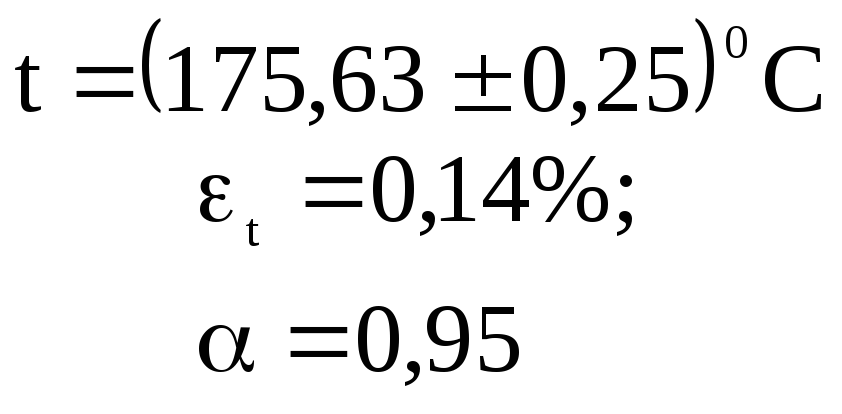 (6)
(6)
Akákoľvek fyzikálna veličina zistená empiricky musí byť teda reprezentovaná:

Chyby v nameraných a tabuľkových hodnotách spôsobujú chyby DX avg nepriamo určenej hodnoty a najväčší príspevok k DX avg majú najmenej presné hodnoty s maximálnou relatívnou chybou d. Preto na zlepšenie presnosti nepriamych meraní je potrebné dosiahnuť rovnakú presnosť priamych meraní.
(d A, d B, d C, ...).
Pravidlá zisťovania chýb nepriamych meraní:
1. Nájdite prirodzený logaritmus danej funkcie
log(X = f(A,B,C,...));
2. Nájdite celkový diferenciál (cez všetky premenné) z nájdených prirodzený logaritmus daná funkcia;
3. Nahraďte znamienko diferenciálu d znamienkom absolútnej chyby D;
4. Vymeňte všetky "mínusy", ktoré čelia absolútnym chybám DA, DB, DC, ... k "profíkom".
Výsledkom je vzorec pre najväčšie relatívna chyba d x nepriamo nameraná hodnota X:
d x = = j (A av, B av, Ca av, …, DA av, DB av, DC av, …).(18)
Podľa zistenej relatívnej chyby d x určiť absolútna chyba nepriame meranie:
DX cf \u003d d x. X porov . (19)
Výsledok nepriamych meraní sa zaznamenáva v štandardnej forme a zobrazuje sa na číselnej osi:
X \u003d (X sr ± DX sr), jednotka. (dvadsať)

Príklad:
Nájdite príbuzného a priemerné chyby fyzikálne množstvo L, určený nepriamo vzorcom:
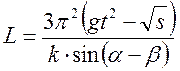 , (21)
, (21)
kde π, g, t, k, α, β- veličiny, ktorých hodnoty sú namerané alebo prevzaté z referenčných tabuliek a zapísané do tabuľky výsledkov meraní a tabuľkových údajov (podobne ako v tabuľke 1).
1. Vypočítajte priemernú hodnotu L porov, pričom do (21) nahradíme priemerné hodnoty z tabuľky - π cf, g cf, t cf, k cf, α cf, β cf.
2. Určte najväčšiu relatívnu chybu δ L:
a). Vzorec (21) je logaritmizovaný:
b). Výsledný výraz (22) je diferencovaný:
c) Nahraďte znamienko diferenciálu d za Δ a "mínusy" pred absolútnymi chybami - za "plusy" a získajte výraz pre najväčšiu relatívnu chybu δ L:
d). Nahradením výsledného výrazu priemernými hodnotami vstupných veličín a ich chybami z tabuľky výsledkov merania vypočítajte δ L.
3. Potom vypočítajte absolútnu chybu ΔLav:
![]()
Výsledok sa zaznamená v štandardnej forme a graficky sa vynesie na os L:
![]() , Jednotky rev.
, Jednotky rev.
