Na zníženie vplyvu náhodných chýb je potrebné túto hodnotu zmerať niekoľkokrát. Predpokladajme, že meriame nejakú hodnotu x. Ako výsledok meraní sme získali nasledujúce hodnoty:
x 1 , x 2 , x 3 , ... x n . (1,4)
Tento rad hodnôt x sa nazýva vzorka. S takouto vzorkou môžeme vyhodnotiť výsledok merania. Hodnotu, ktorá bude takýmto odhadom, označíme . Ale keďže táto vyhodnocovacia hodnota výsledkov merania nebude predstavovať skutočnú hodnotu meranej veličiny, je potrebné odhadnúť jej chybu. Predpokladajme, že vieme určiť odhad chyby Δx . V tomto prípade môžeme výsledok merania zapísať do formulára
x = ± Δx. (1,5)
Keďže odhadované hodnoty výsledku merania a chyby Δx nie sú presné, záznam výsledku merania musí byť sprevádzaný údajom o jeho spoľahlivosti P. Reliabilita alebo spoľahlivosť pravdepodobnosťou sa rozumie pravdepodobnosť, že skutočnú hodnotu nameranej hodnoty je uzavretý v intervale uvedenom v zázname (3). Tento interval sa nazýva interval spoľahlivosti.
Napríklad pri meraní dĺžky určitého segmentu sme zapísali konečný výsledok ako
l= (8,34 ± 0,02) mm,(P = 0,95). (1,6)
To znamená, že zo 100 šancí - 95, že skutočná hodnota dĺžky segmentu leží v intervale od 8,32 do 8,36 mm.
Úlohou je teda na vzorke meraní nájsť odhad výsledku merania, jeho chybu Δx a spoľahlivosť P.
Tento problém možno vyriešiť pomocou teórie pravdepodobnosti a matematickej štatistiky.
Vo väčšine prípadov sa náhodné chyby riadia zákonom normálneho rozdelenia, ktorý stanovil Gauss. Normálne rozdelenie chýb je vyjadrené vzorcom
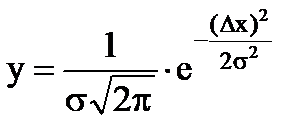, (1.7)
kde Δx je odchýlka od skutočnej hodnoty;
σ je skutočná stredná kvadratická chyba;
σ 2 - disperzia, ktorej hodnota charakterizuje šírenie náhodných veličín.
Ako vidno zo vzorca, funkcia y(x) má maximálna hodnota pre x=0 je navyše párne.
| r |
| X |
| ∆x 1 |
| ∆x2 |
| -Δx 1 |
| -Δx2 |
Obr.1.4. Krivka Gaussovho normálneho rozdelenia.
Obrázok 1.4 ukazuje graf tejto funkcie. Plocha obrázku uzavretá medzi krivkou, osou Δx a dvomi ordinátami z bodov Δx 1 a Δx 2 (tieňovaná oblasť) sa číselne rovná pravdepodobnosti, s akou ktorákoľvek vzorka spadá do intervalu (Δx 1 ,Δx 2 ).
Keďže krivka je rozložená symetricky okolo osi y, možno tvrdiť, že chyby rovnakej veľkosti, ale opačného znamienka sú rovnako pravdepodobné. A to umožňuje vziať priemernú hodnotu všetkých prvkov vzorky ako odhad výsledkov merania:
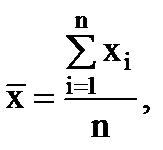(1.8)
kde – n je počet meraní.
Ak sa vykoná n meraní za rovnakých podmienok, potom najviac pravdepodobná hodnota nameraná hodnota bude jej priemerná hodnota (aritmetická). Hodnota smeruje k skutočnej hodnote x a nameraná hodnota ako n → ∞.
Stredná kvadratická chyba jedného výsledku merania je hodnota
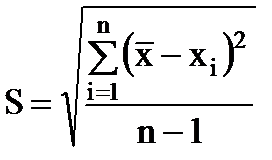(1.9)
Charakterizuje chybu každého jednotlivého merania. Ako n → ∞, S má tendenciu ku konštantnému limitu σ:
σ = limS.
n → ∞ (1,10)
Ako sa σ zvyšuje, rozptyl nameraných hodnôt sa zvyšuje, t.j. presnosť merania sa zníži.
Kvadratická chyba aritmetického priemeru je hodnota
(1.11)
Toto je základný zákon zvyšovania presnosti so zvyšujúcim sa počtom meraní.
Chyba charakterizuje presnosť, s akou sa získa priemerná hodnota nameranej hodnoty. Výsledok je napísaný takto:
x = ± Δx. (1,12)
Táto technika výpočtu chýb dáva pekné výsledky(so spoľahlivosťou 0,68) len vtedy, ak bola rovnaká hodnota nameraná aspoň 30 – 50-krát.
V roku 1908 William Sealy Gosset, známy štatistik, známy skôr pod pseudonymom Student, ukázal, že štatistický prístup platí aj pre malý počet meraní. Študentovo rozdelenie pre počet meraní n → ∞ sa stáva Gaussovým rozdelením a pre malé číslo sa od neho líši.
Na výpočet absolútnej chyby pre malý počet meraní sa zavádza špeciálny koeficient, ktorý závisí od spoľahlivosti P a počtu meraní n, nazývaný Studentov koeficient t. So zavedením tohto koeficientu
Poznamenávame, že vynecháme teoretické zdôvodnenia jeho zavedenia
Δx t = t, (1,13)
kde Δxt je absolútna chyba pre danú úroveň spoľahlivosti; je stredná kvadratická chyba aritmetického priemeru.
Študentské koeficienty sú uvedené v prílohe 1.
Z toho, čo bolo povedané, vyplýva:
1. Hodnota strednej kvadratúry chyby vám umožňuje vypočítať pravdepodobnosť, že skutočná hodnota nameranej hodnoty bude spadať do akéhokoľvek intervalu blízkeho aritmetického priemeru.
2. Ako n → ∞ → 0, t.j. interval, v ktorom sa skutočná hodnota x a nachádza s danou pravdepodobnosťou, má tendenciu k nule s nárastom počtu meraní. Zdá sa, že zvýšením n možno získať výsledok s ľubovoľným stupňom presnosti. Presnosť sa však výrazne zvyšuje len dovtedy, kým sa náhodná chyba nestane porovnateľnou so systematickou. Ďalšie zvyšovanie počtu meraní je neúčelné, pretože konečná presnosť výsledku bude závisieť len od systematickej chyby. Keď poznáme hodnotu systematickej chyby, je ľahké nastaviť prípustnú hodnotu náhodnej chyby, napríklad rovnajúcu sa 10 % systematickej chyby. Požiadaním o vyvolených tak interval spoľahlivosti určitú hodnotu P (napríklad P = 0,95), nie je ťažké nájsť potrebný počet meraní, čo zaručuje malý vplyv náhodnej chyby na presnosť výsledku.
Na to je vhodnejšie použiť tabuľku v prílohe 2, v ktorej sú intervaly uvedené v zlomkoch hodnoty σ, ktorá je mierou presnosti tohto experimentu vzhľadom na náhodné chyby.
Časť Studentových koeficientov so zvýrazneným stĺpcom pre spoľahlivosť P=95% je uvedená v tabuľke 1.6.
Študentské koeficienty Tabuľka 1.6
| n R | 0,9 | 0,95 | 0,999 |
| 6,31 2,92 2,35 2,13 2,02 1,94 1,89 1,86 1,83 | 12,7 4,30 3,18 2,78 2,57 2,45 2,36 2,31 2,26 | 636,6 31,6 12,9 8,61 6,37 5,96 5,41 5,04 4,78 | |
| ∞ | 1,96 |
Pri spracovaní výsledkov viacerých priamych meraní postupujte v nasledujúcom poradí:
1. Zaznamenajte výsledok každého merania do tabuľky.
2. Vypočítajte priemer n meraní
(1.14)
3. Nájdite chybu jedného merania
(1.15)
4. Vypočítajte druhú mocninu chýb jednotlivých meraní
(Ax1)2, (Ax2)2, ..., (Axn)2. (1,16)
5. Určite smerodajnú chybu aritmetického priemeru
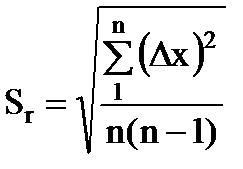. (1.17)
6. Nastavte hodnotu spoľahlivosti (zvyčajne berte P = 0,95).
7. Určte Studentov koeficient t pre danú spoľahlivosť P a počet meraní n.
8. Nájdite interval spoľahlivosti (chyba merania)
Δx t = t. (1,18)
Ak sa ukáže, že chyba výsledku merania Δx je porovnateľná s chybou prístroja Δx p, potom berte ako hranicu intervalu spoľahlivosti:
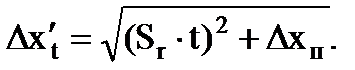(1.19)
Ak je jedna z chýb menšia ako trojnásobok alebo viacnásobok druhej, zahoďte menšiu chybu.
9. Konečný výsledok zapíšte ako
. (1.20)
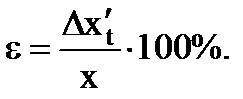(1.21)
Zvážte použitie numerického príkladu použitia vyššie uvedených vzorcov.
Príklad. Priemer d tyče sa meral mikrometrom (systematická chyba merania je 0,005 mm). Výsledky meraní sa zapisujú do druhého stĺpca tabuľky, nájdeme, a do tretieho stĺpca tejto tabuľky zapíšeme rozdiely a do štvrtého - ich štvorce ich rozdielu (tabuľka 1.7).
Tabuľka 1.7
| n | d, mm | ||
| 4.02 | + 0.01 | 0.0001 | |
| 3.98 | - 0.03 | 0.0009 | |
| 3.97 | - 0.04 | 0.0016 | |
| 4.01 | + 0 .00 | 0.0000 | |
| 4.05 | + 0.04 | 0.0016 | |
| 4.03 | + 0.02 | 0.0004 | |
| Σ | 24.06 | – | 0.0046 |
(1.22)
Vzhľadom na spoľahlivosť P = 0,95 zistíme z tabuľky Studentových koeficientov pre šesť meraní t = 2,57. Absolútnu chybu možno nájsť podľa vzorca (10).
Ad = 0,01238 2,57 = 0,04 mm. (1.24)
Porovnajme náhodné a systematické chyby:
preto 5 = 0,005 mm možno zlikvidovať.
Konečný výsledok zapíšeme takto:
d = (4,01 ± 0,04) mm pri Р = 0,95. (1,26)
Ak je nameraná hodnota ALE je funkciou niekoľkých premenných: A= F(X, r,..., t), potom absolútna chyba výsledok nepriame merania
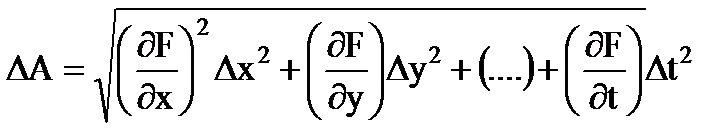(1.29)
Čiastočné relatívne chyby nepriameho merania sú určené vzorcami
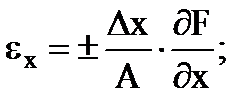
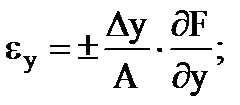…. a tak ďalej. (1,30)
Relatívna chyba výsledok merania
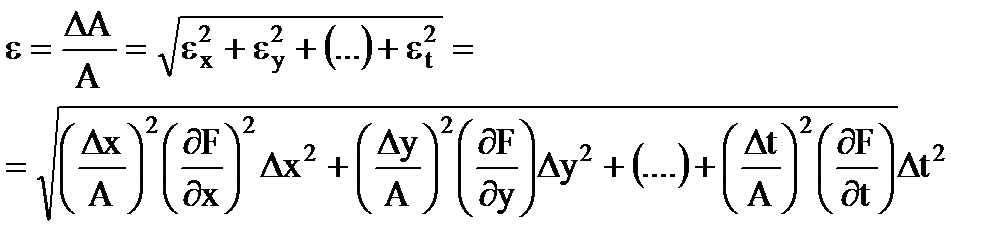(1.31)
Hrubá chyba (minúť) je náhodná chyba výsledku jedného pozorovania zaradeného do série meraní, ktorá sa pre dané podmienky výrazne líši od ostatných výsledkov tejto série. Spravidla vznikajú v dôsledku chýb alebo nesprávnych činností operátora (jeho psychofyziologický stav, nesprávne čítanie, čítanie hodnôt zo susednej stupnice prístroja, chyby v záznamoch alebo výpočtoch, nesprávne zapnutie prístrojov alebo poruchy v ich prevádzka a pod.). Možná príčina výskyt chýb môže byť aj krátkodobými náhlymi zmenami podmienok meraní. Ak sa počas procesu merania zistia chyby, výsledky, ktoré ich obsahujú, sa zahodia. Najčastejšie sa však chyby zistia až pri konečnom spracovaní výsledkov meraní pomocou špeciálnych štatistických kritérií.
V závislosti od príčin výskytu sa rozlišujú inštrumentálne, metodologické a subjektívne chyby.
Inštrumentálna chyba je chyba vlastná samotnému meraciemu prístroju, t.j. zariadenie alebo prevodník, ktorým sa meranie vykonáva. Príčinami prístrojovej chyby môže byť nedokonalosť konštrukcie meracieho prístroja, vplyv životné prostredie na jeho vlastnostiach, deformácii alebo opotrebovaní častí zariadenia a pod.
Metodologická chyba objavuje sa v dôsledku nedokonalosti metódy merania; nezrovnalosti medzi meranou veličinou a jej modelom prijatým pri vývoji meracieho prístroja; vplyv meracieho prístroja na objekt merania a procesy v ňom prebiehajúce. Charakteristické rysy metodologické chyby je, že ich nemožno špecifikovať v regulačnej a technickej dokumentácii meradla, keďže od nej nezávisia, ale v každom konkrétnom prípade ich musí určiť prevádzkovateľ.
Subjektívna (osobná) chyba meranie je spôsobené chybou čítania operátora na stupniciach meracieho prístroja, tabuliek záznamových prístrojov. Sú spôsobené stavom operátora, jeho polohou pri práci, nedokonalosťou zmyslových orgánov, ergonomickými vlastnosťami meracieho prístroja. Charakteristiky subjektívnej chyby sa určujú na základe normalizovanej nominálnej hodnoty dielika stupnice meracieho prístroja (alebo tabuľkového papiera záznamového prístroja), pričom sa berie do úvahy schopnosť „priemerného operátora“ interpolovať v medziach stupnicové rozdelenie. Tieto chyby sa znižujú, keď sa prístroje zlepšujú, napríklad: použitie svetelného ukazovateľa v analógových prístrojoch eliminuje chybu spôsobenú paralaxou ( Paralaxa(z gréckeho paralaxa - odchýlka), viditeľná zmena relatívnych polôh predmetov v dôsledku pohybu oka pozorovateľa) použitie digitálnej referencie eliminuje subjektívnu chybu.
Objektívna chyba merania- chyba, ktorá nezávisí od osobných kvalít osoby, ktorá meranie vykonáva.
Podľa vplyvu vonkajších podmienok sa rozlišujú hlavné a dodatočné chyby meracieho prístroja.
Hlavná sa nazýva chyba meracieho prístroja definované v normálnych podmienkach jeho uplatnenie. Pre každé meradlo sú v regulačných a technických dokumentoch uvedené prevádzkové podmienky - súbor ovplyvňujúcich veličín (okolitá teplota, vlhkosť, tlak, napätie, sieťová frekvencia atď.), pri ktorých sa normalizuje jeho chyba (ovplyvňujúca veličina je fyzikálne množstvo nemerané týmto meracím prístrojom, ale ovplyvňujúce jeho výsledky).
Doplnkové je tzv chyba meracieho prístroja vyplývajúca z odchýlky niektorej z ovplyvňujúcich veličín, t.j. dodatočná chyba, ktorá zvyšuje celkovú chybu zariadenia, nastáva, ak zariadenie pracuje v iných ako normálnych podmienkach.
Podľa charakteru zmeny veľkosti chyby pri zmene nameranej hodnoty sa chyby delia na aditívne a multiplikatívne.
Aditívne chyby v dôsledku posunu statickej charakteristiky zariadenia nahor alebo nadol (doprava alebo doľava), napríklad v dôsledku posunutia stupnice prístroja (drift nuly), trenia v podperách atď. Aditívna chyba nezávisí od hodnoty meranej veličiny x, t.j. konštantná v celej škále prístroja.
Aditívne chyby dominujú väčšine analógových prístrojov.
Multiplikatívne chyby vznikajú v dôsledku chýb v nastavení koeficientu prenosu k statickej charakteristiky y = kx. Multiplikačná chyba závisí od hodnoty meranej veličiny a narastá ku koncu stupnice prístroja.
Multiplikatívna chyba (ak je vyjadrená ako absolútna chyba) je úmerná hodnote meranej veličiny.
Multiplikatívne chyby prevládajú v zariadeniach súvisiacich so škálovacími meničmi (bočníky, prídavné odpory, zosilňovače, deliče, transformátory atď.).
Existujú zariadenia, ktorých aditívne a multiplikatívne chyby sú porovnateľné. Táto trieda zariadení zahŕňa digitálne zariadenia.
Náhodné chyby merania vznikajú súčasným dopadom viacerých nezávislých veličín na objekt merania, ktorých zmeny majú kolísavý charakter. Určitý podiel na náhodnej chybe merania má aj náhodná chyba meracieho prístroja.
Budeme predpokladať, že systematická zložka chyby merania je vylúčená a náhodná chyba ako náhodná premenná úplne
charakterizované hustotou rozdelenia pravdepodobnosti (inými slovami hustotou pravdepodobnosti), kde je distribučná funkcia. Preto nie je určená číselná hodnota náhodná chyba, ale iba pravdepodobnosť, že leží v určitom intervale alebo nepresahuje určitú hodnotu. Ak je známy distribučný zákon, potom a sú známe Pravdepodobnosť nájdenia náhodnej chyby v danom intervale od do sa zistí podľa vzorca
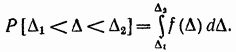
Vzorec zmeny náhodnej chyby môže byť stanovený viacnásobným pozorovaním jej hodnôt a štatistickým spracovaním výsledkov pozorovaní.
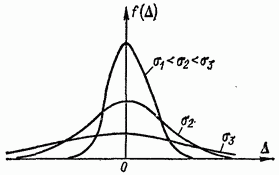
Ryža. 2-1. Hustota pravdepodobnosti náhodných chýb podľa zákona normálneho rozdelenia
Táto časovo náročná a starostlivá práca sa vykonáva s presnými meraniami a spočíva v kontrole súladu získaných údajov s očakávaným rozdelením podľa nejakého kritéria.
Kolísanie ovplyvňujúcich veličín je tiež náhodné a je charakterizované zákonitosťami ich rozdelenia (rovnomerné, trojuholníkové, normálne atď.). Vzhľadom na porovnateľnosť ich rozptylov však už pri 4-5 ovplyvňujúcich veličinách výsledný zákon rozdelenia náhodnej chyby merania uspokojivo súhlasí s normálnym (obr. 2-1).
Funkcia normálneho rozdelenia
a hustota pravdepodobnosti
kde je rozptyl charakterizujúci rozptyl náhodnej chyby vo vzťahu k distribučnému centru a jeho štandardná odchýlka.
Disperzia a štandardná odchýlka charakterizujú presnosť merania: čím viac, tým menšia presnosť. V praxi merania sa používa hlavne smerodajná odchýlka c, pretože je vyjadrená v rovnakých jednotkách ako nameraná hodnota.
Ryža. 2-2. Integrál pravdepodobnosti
Pravdepodobnosť výskytu náhodnej chyby v rozsahu od do v súlade so vzorcom
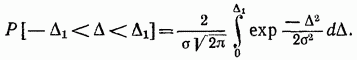
Ak zavedieme normalizovanú náhodnú premennú, pravá strana rovnosti sa transformuje na Laplaceovu funkciu, často nazývanú integrál pravdepodobnosti
Táto funkcia je uvedená v tabuľke a jej hodnoty sú uvedené v tabuľke. a graf je znázornený na obr. 2-2.
Ak je daná určitá pravdepodobnosť a, potom po jej nájdení je možné určiť Podľa zákona normálneho rozdelenia sa maximálna chyba Dmax rovná, čo zodpovedá pravdepodobnosti prekročenia chyby To znamená, že v 369 z 370 pozorovaní s pravdepodobnosťou 0,9973 chyba leží v intervale ± 3a a iba v jednom pozorovaní ho môže prekročiť.
Ryža. 2-3. Hustota pravdepodobnosti náhodných chýb so zákonom rovnomerného rozdelenia
Zákon rovnomerného rozdelenia sa vyskytuje aj pri meraniach. Typické je najmä meranie spojitých veličín metódou diskrétneho počítania. Hustota pravdepodobnosti chyby v rozsahu od do (obr. 2-3) sa zapisuje v nasledujúcom tvare;
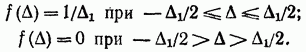
Preto ten rozptyl
a štandardná odchýlka
Napríklad kvantizačná chyba, ktorá je zvyčajne v rámci najmenej významnej číslice (od -1/2 do 1/2), je charakterizovaná štandardnou odchýlkou
Vráťme sa k zákonu normálneho rozdelenia. Tento zákon je charakterizovaný numerickými parametrami: matematickým očakávaním a disperziou. Presná definícia tieto parametre sú takmer nemožné, pretože na to musíte mať nekonečne veľké množstvo hodnôt náhodná premenná, t.j. vykonávať pozorovania na . V praxi meraní je vždy konečný, preto sa hodnoty vypočítané ako výsledok experimentu nazývajú
odhady matematické očakávanie a štandardná odchýlka.
Uvažujme o postupe štatistického merania nejakej hodnoty, ktorej skutočnú hodnotu vytvárajú jednotlivé pozorovania, v dôsledku ktorých sa získa množstvo náhodných hodnôt nameranej hodnoty. V každej absolútnej chybe 1. pozorovania nie je možné určiť hodnotu tejto chyby, pretože nie je známa.
Aritmetický priemer sa berie ako odhad matematického očakávania (skutočná hodnota)
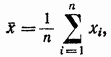
ktorá sa nazýva skutočná hodnota A meranej veličiny pri
Teraz môžete vypočítať absolútnu odchýlku každého výsledku pozorovania vzhľadom na strednú hodnotu: Je zrejmé, že na kontrolu správnosti výpočtov môžete použiť vlastnosti odchýlok výsledkov pozorovania od aritmetického priemeru: súčet odchýlok je nula a súčet ich štvorcov je minimálny:
Odhad štandardnej odchýlky absolútnych odchýlok každého z jednotlivých pozorovaní je určený vzorcom
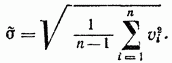
Presnosť výsledku merania bude vyššia. Je charakterizovaná odhadom smerodajnej odchýlky aritmetického priemeru (reálnej) hodnoty:
S nárastom počtu meraní (s nezávislými výsledkami) sa presnosť úmerne zvyšuje Zdá sa, že zvýšením môžete dosiahnuť akékoľvek zvýšenie presnosti. Zdravý rozum a prax merania však naznačujú, že je to málo užitočné, pretože samotná meraná veličina sa môže počas merania meniť.
Interval spoľahlivosti a pravdepodobnosť spoľahlivosti. Ako výsledok pozorovania nameranej hodnoty získame odhad jej skutočnej hodnoty A, rovný aritmetického priemeru X, podľa vzorca (2-11). Tento odhad je tiež náhodná premenná; jeho smerodajná odchýlka a - je určená vzorcom (2-13), t.j. výsledok merania obsahuje neistotu. Je potrebné zistiť, v akých medziach sa môže skutočná hodnota A meniť pri opakovanom meraní (štatistických) veličín za rovnakých podmienok, t.j. je potrebné nájsť interval hodnôt, ktorý „pokryje“ skutočnú hodnotu meraná veličina s danou pravdepodobnosťou. Takýto interval sa nazýva interval spoľahlivosti a daná (stanovená) pravdepodobnosť sa nazýva interval spoľahlivosti. Interval spoľahlivosti a úroveň spoľahlivosti charakterizujú neistotu výsledku merania. Analyticky je to napísané takto:
Výraz (2-14) znie takto: skutočná hodnota nameranej hodnoty leží v intervale spoľahlivosti od do s pravdepodobnosťou spoľahlivosti a.
Podobne pre náhodnú chybu
Náhodná chyba merania leží v intervale spoľahlivosti od do s pravdepodobnosťou spoľahlivosti a.
V závislosti od účelu merania sa úroveň spoľahlivosti nastaví na . Vo výrazoch (2-14) a (2-15) sú intervaly spoľahlivosti symetrické. Polovica intervalu spoľahlivosti sa nazýva hraničná (maximálna, dovolená) chyba s pravdepodobnosťou spoľahlivosti a. Niekedy je interval spoľahlivosti asymetrický a má tvar
Hraničná chyba a interval spoľahlivosti sú vyjadrené ako štandardná odchýlka. Pre zákon normálneho rozdelenia je interval spoľahlivosti pre danú pravdepodobnosť spoľahlivosti (a naopak) určený pomocou integrálnej tabuľky pravdepodobnosti (tabuľka A4). Sú nastavené s úrovňou spoľahlivosti, napríklad 0,95. Podľa tabuľky sa zistí aj hodnota, ktorá sa v tomto prípade rovná 2. Keďže ide o interval spoľahlivosti
Je zrejmé, že interval spoľahlivosti aj úroveň spoľahlivosti súvisia s počtom pozorovaní, pretože čím väčší, tým užší je interval. Ako je však uvedené vyššie, v praxi meraní je to zriedkavé. Pre počet pozorovaní sa interval spoľahlivosti neurčuje prostredníctvom, ale prostredníctvom určitého koeficientu, ktorý závisí od počtu pozorovaní a pravdepodobnosti spoľahlivosti a. Zákon zmeny koeficientu je určený Studentovým rozdelením normalizovanej náhodnej premennej vypočítanej s normálnym rozdelením. Koeficient sa určuje podľa vzorca:
nejde o omyly, t. j. o zjavné chyby prevádzkovateľa, potom je potrebné zistiť, či ide o hrubé chyby, ktoré by tiež mali byť vylúčené zo spracovania, ako napríklad chyby. Vylúčenie hrubej chyby bez dostatočného odôvodnenia vedie k neprimeranému zlepšeniu výsledku merania. Na druhej strane, nevylúčenie hrubej chyby, najmä pri malom počte pozorovaní, skreslí tak skutočnú hodnotu nameranej hodnoty, ako aj hranice intervalu spoľahlivosti. Preto je potrebné odhaliť a odstrániť hrubé chyby.
Najjednoduchší spôsob, ako zistiť hrubú chybu v normálnom rozdelení, je porovnať absolútnu chybu "podozrivého" pozorovania s maximálnou chybou. Ak potom tento výsledok zahodiť a hodnoty prepočítať skutočnosť, že pravdepodobnosť odchýlky hodnoty od aritmetického priemeru je viac ako rovná iba 0,003.
Treba však pripomenúť, že ak veľké čísla pozorovaní, aj keď s nízkou pravdepodobnosťou je možné, že vyradené číslo nie je hrubou chybou, ale prirodzenou štatistickou odchýlkou tejto hodnoty. Preto sa v kritických prípadoch určuje hrubá chyba na základe teórie pravdepodobnosti. Stanovuje sa, pri akom počte meraní s danou pravdepodobnosťou a je možné vyradiť výsledok pozorovania, ktorý prekračuje daný počet alebo dané limity.
Chyby merania sú rozdelené do nasledujúcich typov:
absolútne a relatívne.
Pozitívne aj negatívne.
konštantné a proporcionálne.
Drsné, náhodné a systematické.
Absolútna chyba výsledok jedného merania (A r) je definovaný ako rozdiel medzi nasledujúcimi hodnotami:
A r = r ja- r ist. » r i-` r.
Relatívna chyba výsledok jedného merania (B r) sa vypočíta ako podiel týchto veličín:
Z tohto vzorca vyplýva, že veľkosť relatívnej chyby závisí nielen od veľkosti absolútnej chyby, ale aj od hodnoty meranej veličiny. Keď nameraná hodnota zostane nezmenená ( r) relatívnu chybu merania možno znížiť iba znížením absolútnej chyby (A r). Keď je absolútna chyba merania konštantná, na zníženie relatívnej chyby merania môžete použiť metódu zvýšenia hodnoty meranej veličiny.
Príklad. Predpokladajme, že obchodná váha v obchode má konštantnú absolútnu chybu merania hmotnosti: A m = 10 g Ak na takýchto váhach odvážite 100 g sladkostí (m 1), potom bude relatívna chyba merania hmotnosti sladkostí :
.
Pri vážení 500 g sladkostí (m 2) na rovnakých váhach bude relatívna chyba päťkrát menšia:
.
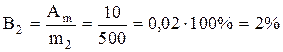Ak teda päťkrát odvážite 100 g sladkostí, z 500 g kvôli chybe merania hmotnosti nedostanete celkovo 50 g výrobku. Jediným vážením väčšej hmoty (500 g) stratíte len 10 g sladkostí, t.j. päťkrát menej.
Vzhľadom na vyššie uvedené možno poznamenať, že v prvom rade je potrebné usilovať sa o zníženie relatívnych chýb merania. Absolútne a relatívne chyby možno vypočítať až po určení priemeru aritmetická hodnota výsledok merania.
Znamienko chyby (kladné alebo záporné) je určené rozdielom medzi jedným a skutočným výsledkom merania:
r i-` r > 0 (chyba je pozitívna);
r i-` r < 0 (chyba je negatívna).
Ak absolútna chyba merania nezávisí od hodnoty meranej veličiny, potom sa takáto chyba nazýva konštantný. V opačnom prípade bude chyba proporcionálne. Povaha chyby merania (konštantná alebo proporcionálna) sa určuje po špeciálnych štúdiách.
Hrubá chyba meranie (miss) je výsledok merania, ktorý sa výrazne líši od ostatných, ku ktorému zvyčajne dochádza pri porušení meracieho postupu. Prítomnosť hrubých chýb merania vo vzorke zisťujú iba metódy matematickej štatistiky (pre n>2). Zoznámte sa s metódami zisťovania hrubých chýb sami v.
Rozdelenie chýb na náhodné a systematické je skôr podmienené.
Komu náhodné chyby zahŕňajú chyby, ktoré nemajú konštantnú hodnotu a znamienko. K takýmto chybám dochádza pod vplyvom nasledujúcich faktorov: výskumníkovi neznáme; známe, ale neregulované; neustále sa mení.
Náhodné chyby možno odhadnúť až po vykonaní meraní.
Kvantifikácia modulom veľkosti náhodnej chyby merania môžu byť tieto parametre: atď.
Náhodné chyby merania nemožno vylúčiť, možno ich len znížiť. Jedným z hlavných spôsobov zníženia veľkosti náhodnej chyby merania je zvýšenie počtu jednotlivých meraní (zvýšenie hodnoty n). Vysvetľuje to skutočnosť, že veľkosť náhodných chýb je nepriamo úmerná hodnote n, napríklad:
Systematické chyby sú chyby s konštantnou veľkosťou a znamienkom alebo meniace sa podľa známeho zákona. Tieto chyby sú spôsobené konštantnými faktormi. Systematické chyby sa dajú kvantifikovať, redukovať a dokonca eliminovať.
Systematické chyby sa zaraďujú do chýb typu I, II a III.
K systematickému chyby typu I sa vzťahujú na chyby známeho pôvodu, ktoré možno odhadnúť výpočtom pred meraním. Tieto chyby je možné eliminovať ich zavedením do výsledku merania vo forme opráv. Príkladom tohto typu chyby je chyba v titrimetrickom stanovení objemovej koncentrácie roztoku, ak sa titračné činidlo pripravilo pri jednej teplote a koncentrácia sa merala pri inej. Pri znalosti závislosti hustoty titrantu od teploty je možné vypočítať zmenu objemovej koncentrácie titrantu spojenú so zmenou jeho teploty pred meraním a tento rozdiel vziať do úvahy ako korekciu v dôsledku meranie.
Systematický chyby typu II- ide o chyby známeho pôvodu, ktoré možno posúdiť len počas experimentu alebo ako výsledok špeciálnych štúdií. Tento typ chyby zahŕňa inštrumentálne (inštrumentálne), reaktívne, referenčné a iné chyby. Zoznámte sa s vlastnosťami takýchto chýb sami.
Akékoľvek zariadenie, keď sa používa v postupe merania, vnáša do výsledku merania svoje inštrumentálne chyby. Niektoré z týchto chýb sú zároveň náhodné a druhá časť je systematická. Náhodné chyby prístroja sa nevyhodnocujú samostatne, vyhodnocujú sa spolu so všetkými ostatnými náhodnými chybami merania.
Každý prípad akéhokoľvek nástroja má svoju vlastnú osobnú systematickú chybu. Na vyhodnotenie tejto chyby je potrebné vykonať špeciálne štúdie.
Väčšina spoľahlivým spôsobom hodnotenie prístrojovej systematickej chyby typu II - ide o zosúladenie činnosti prístrojov s normami. Pre meracie pomôcky (pipety, byrety, valce atď.) sa vykonáva špeciálny postup - kalibrácia.
V praxi sa najčastejšie vyžaduje nie odhadovať, ale redukovať alebo eliminovať systematickú chybu typu II. Najbežnejšie metódy na zníženie systematických chýb sú relativizačné a randomizačné metódy.Presvedčte sa sami o týchto metódach na .
Komu chyby III typ obsahuje chyby neznámeho pôvodu. Tieto chyby možno odhaliť až po odstránení všetkých systematických chýb I. a II. typu.
Komu iné chyby zahrnieme všetky ostatné typy chýb, ktoré nie sú uvedené vyššie (prípustné, možné okrajové chyby atď.). Koncept možných hraničných chýb sa používa v prípadoch použitia meracích prístrojov a predpokladá maximálnu možnú chybu prístrojového merania (skutočná hodnota chyby môže byť menšia ako hodnota možnej hraničnej chyby).
Pri použití meracích prístrojov je možné vypočítať možný absolútny limit (P` r atď.) alebo príbuzný (E r, atď.) chyby merania. Takže napríklad možná limitná absolútna chyba merania sa zistí ako súčet možných limitujúcich náhodných (x ` r, náhodné atď.) a nevylúčené systematické (d` r, atď.) chyby:
P` r, napr. = x ` r, náhodný, pr. + d` r, atď.
Pre malé vzorky (n £ 20) neznáma populácia v súlade so zákonom normálneho rozdelenia možno náhodné možné obmedzujúce chyby merania odhadnúť takto:
x' r, náhodný, pr. = D` r=S' r½t P, n ½,
kde t P,n je kvantil Studentovho rozdelenia (testu) pre pravdepodobnosť P a veľkosť vzorky n. Absolútna možná medzná chyba merania sa v tomto prípade bude rovnať:
P` r,napr.= S ` r½ t P, n ½ + d` r, atď.
Ak výsledky merania nezodpovedajú zákonu normálneho rozdelenia, potom sa chyba odhadne pomocou iných vzorcov.
Určenie hodnoty d` r,atď. závisí od toho, či má merací prístroj triedu presnosti. Ak merací prístroj nemá triedu presnosti, potom pre hodnotu d ` r,atď. možno prijať minimálna hodnota dielika stupnice meranie . Pre meradlo so známou triedou presnosti pre hodnotu d` r možno akceptovať absolútnu prípustnú systematickú chybu meracieho prístroja (d r, pridaj.):
d` r,atď." .
hodnota d r, pridajte. sa vypočíta na základe vzorcov uvedených v tabuľke 5.
Pre mnohé meracie prístroje sa trieda presnosti uvádza vo forme čísel a × 10 n, kde a sa rovná 1; 1,5; 2; 2,5; štyri; 5; 6 a n je 1; 0; - jeden; -2 atď., ktoré ukazujú hodnotu možnej najväčšej dovolenej systematickej chyby (E r, príp.) a špeciálne znaky označujúce jeho typ (relatívny, redukovaný, konštantný, proporcionálny).
Tabuľka 5
Príklady označovania tried presnosti meracích prístrojov
Pokračovanie tabuľky 5
Koniec tabuľky 5
Systematické chyby možno zanedbať, ak nerovnosť
V tomto prípade sa predpokladá, že:
P` r, atď." x' r, prípad atď. »D' r»S' r½ t P, n ½.
Náhodné chyby je možné zanedbať
V tomto prípade P` r, atď." d` r,atď. .
Zvýšenie počtu jednotlivých meraní je najbežnejšou metódou na zníženie náhodných chýb (čo tiež zvyšuje náklady na merania). Odporúča sa zvyšovať n, až kým celková chyba merania nebude určená iba systematickou chybou. Minimálny počet paralelných meraní potrebných na to (n min) možno vypočítať len pre známa hodnota všeobecná populácia jednotlivých výsledkov podľa vzorca
.
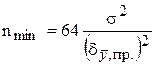Ak sú známe zložky (m - počet zložiek) absolútnej systematickej chyby aritmetického priemeru výsledku merania (), možno ich odhadnúť podľa vzorca
,
kde k je koeficient určený pravdepodobnosťou P a číslom m.
Odhad chýb merania závisí nielen od prostriedkov merania a veľkosti vzorky, ale aj od typu merania (priame meranie alebo nepriame).
Rozdelenie meraní na priame a nepriame je skôr podmienené. Neskôr, pod priame merania takému budeme rozumieť, keď sa výsledok merania získa priamo, napríklad sa odčíta zo stupnice prístroja. Komu nepriame merania pripíšeme také, keď výsledok merania vypočítané ako funkcia j) výsledkov jedného alebo viacerých priamych meraní ( X 1 , X 2 , …, X j,. …, X k).
Je potrebné vedieť, že chyby nepriamych meraní sú vždy väčšie ako chyby jednotlivých priamych meraní. Chyby nepriamych meraní sa odhadujú podľa príslušných zákonov.
Náhodné chyby vedú k tomu, že pozorované hodnoty meranej veličiny pri opakovaných meraniach sú náhodne rozptýlené vzhľadom na jej skutočnú hodnotu. Potom sa zistí skutočná hodnota ako najpravdepodobnejšia zo série experimentov a chyba sa charakterizuje šírkou intervalu, ktorý zahŕňa skutočnú hodnotu s danou pravdepodobnosťou. Matematické zdôvodnenie týchto ustanovení je dané v teórii pravdepodobnosti, ktorej aplikácia na spracovanie výsledkov meraní je uvedená v literatúre, a priama aplikácia na prac. fyzická dielňa v literatúre.
Študenti a školáci veľmi často nájdu chybu merania pomocou vzorca
, (6.2)
kde je priemerná hodnota veličiny získaná počas procesu merania a je hodnota prevzatá z referenčnej knihy alebo vypočítaná z teoretických konceptov. Takáto definícia chyby je hrubou chybou, pretože účelom experimentu, ako je uvedené vyššie, je otestovať teoretické koncepty a spresniť tabuľkové údaje.
Okrem toho sa často chyba vypočíta ako priemerná hodnota odchýlok jednotlivých výsledkov merania od priemernej hodnoty pomocou vzorca
. (6.3)
Podľa tohto prístupu sa akákoľvek chybová hodnota objavuje rovnako často, t.j. chyby rôznej veľkosti sa považujú za rovnako pravdepodobné. Túto metódu je možné použiť v laboratórne práce s malým počtom meraní.
Náhodné chyby však nie sú rovnako pravdepodobné. Pre svoju definíciu vyžadujú štatistické spracovanie výsledkov meraní. Preto sa javí ako potrebné zvážiť obsah štatistického spracovania výsledkov meraní. Štatistická teória chýb je založená na týchto ustanoveniach:
1) pri veľkom počte meraní sa pozorujú náhodné chyby rovnakej veľkosti, ale iné znamenie t.j. chyby v smere poklesu aj nárastu sa vyskytujú rovnako často;
2) veľké (v absolútnej hodnote) chyby sú menej časté ako malé, t.j. pravdepodobnosť výskytu chyby klesá so zvyšujúcou sa veľkosťou chyby;
3) chyby merania môžu mať súvislý rad hodnôt.
Rozdelenie náhodnej premennej, ktorá sa riadi uvedenými vlastnosťami, sa nazýva normálne rozdelenie. Na odhad rozptylu individuálne sa vyberú hodnoty náhodnej premennej s normálnym rozdelením alebo jednotlivé vzorky v teórii normálneho rozdelenia vzorová štandardná odchýlka odčítania, ktorý sa vypočíta podľa vzorca:
. (6.4)
Veľmi dôležitý je odhad hodnoty chyby jedného merania, určený vzorcom (6.4). Pre meranie je však dôležitou úlohou určiť, s akou presnosťou zodpovedá priemerná hodnota nameranej hodnoty požadovanej hodnote. Tento problém vzniká v dôsledku skutočnosti, že priemernú hodnotu možno získať z rôzne rozmery. Napríklad priemernú hodnotu možno získať z iného počtu meraní. Empirický priemer je preto tiež náhodná premenná, ktorú možno opísať aj distribučnou funkciou. Hodnota štandardnej odchýlky zodpovedajúcej tejto funkcii je určená, ako ukazuje teória pravdepodobnosti, podľa vzorca:
(6.5)
Táto hodnota sa nazýva vzorová smerodajná odchýlka priemeru alebo štandardná chyba.
Ako je zrejmé zo vzorca pre štandardnú chybu (6.5), s narastajúcim počtom meraní klesá a presnosť výsledku sa zvyšuje, čo zodpovedá predchádzajúcej úvahe.
Vyššie uvedené vzorce na určenie chyby merania využívajú charakteristiky normálneho rozdelenia náhodnej veličiny. Nie je však známe, akým zákonom sa rozdeľujú výsledky meraní. Preto sú tieto odhady približné. V tejto súvislosti je potrebné analyzovať tento prístup na určenie chyby merania. Na takúto analýzu možno použiť dobre známy koncept intervalu spoľahlivosti v teórii pravdepodobnosti. Nech sa hodnota rovná pravdepodobnosti, že výsledok merania - stredná hodnota - sa líši od skutočnej hodnoty o hodnotu nie väčšiu ako . V teórii pravdepodobnosti je táto fráza napísaná takto:
Hodnota sa volá úroveň spoľahlivosti (spoľahlivosť) výsledkom série pozorovaní. Ukazuje pravdepodobnosť, s ktorou interval spoľahlivosti zahŕňa skutočnú hodnotu meranej veličiny.
Interval spoľahlivosti nazývaný interval hodnôt, ktorý s daným stupňom istoty zahŕňa skutočnú hodnotu nameranej hodnoty. Geometrické znázornenie tohto intervalu je uvedené na obrázku 1.
Na určenie náhodnej chyby je teda potrebné nájsť alebo nastaviť dve čísla: a to hodnotu samotnej náhodnej chyby alebo interval spoľahlivosti a hodnotu pravdepodobnosti spoľahlivosti.
Pre akúkoľvek hodnotu intervalu spoľahlivosti môžete vypočítať pravdepodobnosť spoľahlivosti. Na tento účel sa používa Laplaceova funkcia, ktorá sa nazýva aj pravdepodobnostný integrál. Laplaceova funkcia má tvar:
,
kde . Najčastejšie sa pri riešení problémov používajú tabuľkové hodnoty funkcie Laplace. Tieto hodnoty sú uvedené v tabuľke 1.
Výsledky tejto tabuľky ukazujú, že rms chyba má pravdepodobnosť spoľahlivosti 0,68, 2x rms chyba má pravdepodobnosť spoľahlivosti 0,95 a 3x rms chyba 3 má pravdepodobnosť spoľahlivosti 0,997.
stôl 1
Pravdepodobnosť spoľahlivosti
pre interval spoľahlivosti vyjadrený v zlomkoch strednej štvorcovej chyby . Laplaceova funkcia
| 1,2 | 0,77 | 2,6 | 0,990 | ||
| 0,05 | 0,04 | 1,3 | 0,80 | 2,7 | 0,993 |
| 0,1 | 0,08 | 1,4 | 0,84 | 2,8 | 0,995 |
| 0.15 | 0,12 | 1,5 | 0,87 | 2,9 | 0,996 |
| 0,2 | 0,16 | 1,6 | 0,89 | 3,0 | 0,997 |
| 0,3 | 0,24 | 1,7 | 0,91 | 3,1 | 0,9981 |
| 0,4 | 0,31 | 1,8 | 0,93 | 3,2 | 0,9986 |
| 0,5 | 0,38 | 1,9 | 0,94 | 3,3 | 0,9990 |
| 0,6 | 0,45 | 2,0 | 0,95 | 3,4 | 0,9993 |
| 0,7 | 0,51 | 2,1 | 0,964 | 3,5 | 0,9995 |
| 0,8 | 0,57 | 2,2 | 0,972 | 3,6 | 0,9997 |
| 0,9 | 0,63 | 2,3 | 0,978 | 3,7 | 0,9998 |
| 1,0 | 0,68 | 2,4 | 0,984 | 3,8 | 0,99986 |
| 1.1 | 0,73 | 2,5 | 0,988 | 3,9 | 0,99990 |
| 4,0 | 0,99993 |
Náhodná chyba Je zvykom definovať ho ako polovičnú šírku intervalu spoľahlivosti. Veľkosť intervalu spoľahlivosti je uvedená ako násobok štandardnej odchýlky vzorky od priemeru , ktorý je určený vzorcom (6.5). Potom náhodná chyba viacerých meraní sa určuje podľa vzorca.