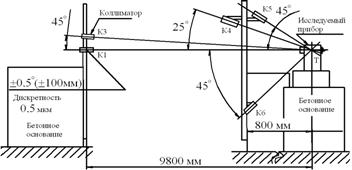
3.2 تصنيف أخطاء القياس الجيوديسية. متوسط مربع الخطأ. أشكال غاوس وبسل لحسابها
أجريت القياسات الجيوديسية حتى في غاية ظروف جيدة، مصحوبة بأخطاء، أي. انحراف نتيجة القياس L عن القيمة الحقيقية X للكمية المرقمة:
صحيح هي قيمة الكمية المقاسة التي تعكس بشكل مثالي الخصائص الكمية للكائن. حالة لا يمكن الوصول إليها - المعنى الحقيقي- مفهوم افتراضي. هذه قيمة يمكن الاقتراب منها إلى ما لا نهاية، ولا يمكن تحقيقها.
دقة القياس هي درجة تقريب نتيجته إلى القيمة الحقيقية. كلما انخفض الخطأ، زادت الدقة.
يتم التعبير عن الخطأ المطلق بالفرق بين القيمة التي تم الحصول عليها نتيجة القياس والقياس الحقيقي للكمية. على سبيل المثال، القيمة الحقيقية ل = 100 م، ولكن عند قياس نفس الخط كانت النتيجة 100.05 م، فالخطأ المطلق هو:
E = X مقاس - X
ه = 100.05 – 100 = 0.05 (م)
للحصول على القيمة، يكفي إجراء قياس واحد. يطلق عليه أنه ضروري، ولكن في كثير من الأحيان لا يقتصر على قياس واحد، بل يتكرر مرتين على الأقل. تسمى القياسات التي يتم أخذها بما يتجاوز ما هو ضروري زائدة عن الحاجة (إضافية)، فهي وسيلة مهمة جدًا لمراقبة نتيجة القياس.
الخطأ المطلق لا يعطي فكرة عن دقة النتيجة التي تم الحصول عليها. على سبيل المثال، يمكن الحصول على خطأ قدره 0.06 م عند قياس l = 100 m أو l = 1000 m، ولذلك يتم حساب الخطأ النسبي:
C = 0.06 / 100 = 1/1667، أي عند 1667 م من القياس l يوجد خطأ قدره 1 متر.
الخطأ النسبي هو نسبة الخطأ المطلق إلى القيمة الحقيقية أو المقاسة. يتم التعبير عنها ككسر. وفقًا للتعليمات، يجب ألا يزيد قياس خط التضاريس عن 1/1000.
تسمى الأخطاء الناشئة عن العوامل الفردية بالابتدائية. الخطأ المعمم هو مجموع الأخطاء الأولية.
هناك:
· الخام (س)،
· منهجي (O)،
· عشوائي (∆).
تنشأ أخطاء القياس الإجمالية نتيجة للأخطاء الجسيمة أو سوء التقدير من قبل المؤدي أو عدم انتباهه أو الأعطال التي لم يتم اكتشافها. الوسائل التقنية. الأخطاء الجسيمة غير مقبولة تمامًا ويجب إزالتها تمامًا من نتائج القياس عن طريق إجراء قياسات إضافية متكررة.
تعد أخطاء القياس المنهجية مكونًا ثابتًا مرتبطًا بالعيوب: الرؤية، وعطل المعدات التقنية، ودرجة الحرارة. يمكن أن تكون الأخطاء المنهجية إما أحادية أو متغيرة (أخطاء دورية). إنهم يسعون جاهدين، إن أمكن، لأخذها في الاعتبار أو استبعادها من نتائج القياس عند تنظيم وتنفيذ العمل.
أخطاء القياس العشوائية تصاحب حتما جميع القياسات. لا يمكن استبعاد الأخطاء العشوائية، ولكن يمكن إضعاف تأثيرها على النتيجة المرجوة عن طريق إجراء قياسات إضافية. هذه هي الأخطاء الأكثر غدرا التي تصاحب جميع القياسات. يمكن أن تكون مختلفة في الحجم والعلامة.
وإذا كان من الممكن دراسة الأخطاء الجسيمة والمنهجية واستبعادها من نتيجة القياس، فيمكن أخذ الأخطاء العشوائية بعين الاعتبار بناءً على القياسات العميقة. الدراسة على أساس نظرية الاحتمالات.
في الممارسة العملية، تكمن الصعوبة في حقيقة أن بعض القياسات يتم إجراؤها كمية محدودةمرات ولذلك، لتقييم دقة القياسات، يتم استخدام تقدير تقريبي للانحراف المعياري، وهو ما يسمى خطأ الجذر المتوسط التربيعي (RMS).
اقترح غاوس صيغة لخطأ الجذر المتوسط التربيعي:
∆ 2 أف = (∆ 2 1 + ∆ 2 2 +… +∆ 2 ن) / ن,
∆ 2 = م 2 = (∆ 2 1 + ∆ 2 2 +… +∆ 2 ن) / ن,
∆ أف = م = √(∑∆ 2 ط / ن)
يتم تطبيق الصيغة عند حساب الأخطاء من القيم الحقيقية.
صيغة بيسل:
م = √(∑V 2 ط / (ن-1))
جذر متوسط مربع الخطأ للوسط الحسابي أقل بـ 10 مرات من جذر متوسط مربع خطأ القياس الفردي
عند التقييم، يتم استخدام متوسط مربع الخطأ بوزن يساوي واحدًا كوحدة للدقة. ويسمى متوسط مربع الخطأ لوحدة الوزن.
μ 2 = P×m 2 – μ = m√P, m = μ / √P، أي جذر متوسط مربع الخطأ لأي نتيجة قياس يساوي خطأ القياس بوزن 1 (μ) مقسوما على الجذر التربيعي لوزن هذه النتيجة (P).
مع عدد كبير بما فيه الكفاية من القياسات، يمكننا كتابة ∑m 2 P=∑∆ 2 P (بما أن ∆ = m):
μ = √(∑(∆ 2 ×P)/n)، أي متوسط الخطأ التربيعي لقياس بوزن يساوي 1 يساوي الجذر التربيعي للكسر الذي في بسطه مجموع منتجات مربعات الأخطاء المطلقة للقياسات غير المتساوية وأوزانها، وفي المقام هو عدد القياسات غير المتكافئة.
جذر متوسط مربع الخطأ للوسط الحسابي العام وفقا للصيغة:
م 0 = μ / √∑P
وبتعويض قيمته بدل μ نحصل على:
M 0 = √(∑∆ 2 ×P/n) / (√∑P) = √[(∑∆ 2 ×P) / n×(∑P)]
M 0 = √[ (∆ 1 2 P 1 + ∆ 2 2 P 2 +… + ∆ n 2 P n) / n×(P 1 + P 2 + … + P n) ] – صيغة غاوس، متوسط مربع الخطأ لـ مجموع الوسط الحسابي يساوي الجذر التربيعي لكسر، بسطه هو مجموع حاصل ضرب مربعات أخطاء القياسات غير المتساوية وأوزانها، والمقام هو حاصل ضرب عدد القياسات و مجموع أوزانهم.
μ = √ [∑(V 2 ×P) / (n-1)] هذه هي صيغة بيسل لحساب المتوسط خطأ حسابيبقياس وزني يساوي 1 لعدد من القياسات غير المتكافئة حسب احتمال أخطائها. وهي صالحة لعدد كبير من القياسات، ولكنها تحتوي على أخطاء لعدد محدود (غالبًا في الممارسة العملية): m μ = μ / هي موثوقية التقدير μ.
مهمة الاختبار 1
لدراسة المزواة، قام بقياس نفس الزاوية بشكل متكرر. وكانت النتائج على النحو التالي: 39˚17.4 بوصة؛ 39˚16.8 بوصة؛ 39˚16.6 بوصة؛ 39˚16.2 بوصة؛ 39˚15.5 بوصة; 39˚15.8 بوصة; 39˚16.3 بوصة؛ 39˚16.2 بوصة. تم قياس نفس الزاوية بمقياس الزوايا عالي الدقة، والذي أعطى نتيجة 39˚16"42". بأخذ هذه القيمة على أنها دقيقة، قم بحساب متوسط مربع الخطأ، وحدد موثوقية SKP، وابحث عن الحد الأقصى للخطأ.
| رقم القياس | نتائج القياس، ل | أخطاء | ∆2 |
| 1 | 39˚17.4" | +0.7" | 0.49 |
| 2 | 16.8 | +0.1 | 0.01 |
| 3 | 16.6 | -0.1 | 0.01 |
| 4 | 16.2 | -0.5 | 0.25 |
| 5 | 15.5 | -1.2 | 1.44 |
| 6 | 15.8 | -0.9 | 0.81 |
| 7 | 16.3 | -0.4 | 0.16 |
| 8 | 16.2 | -0.5 | 0.25 |
| مجموع | 3.42 |
39˚16"42" = 39˚16.7"
جذر متوسط مربع الخطأ: m = √([∆ 2 ]/n),
م = √(3.42/8) = 0.65".
تقييم موثوقية SKP: m m = m / √2n،
م م = 0.65 / √16=0.1625≈0.16".
خطأ الحد: ∆pr = 3×m،
∆ العلاقات العامة = 3×0.65" = 1.96"
مهمة الاختبار 2
يتم إعطاء مجموعة من بقايا مثلثات التثليث بحجم 50 وحدة. مع الأخذ بعين الاعتبار أن البقايا أخطاء حقيقية، وحساب متوسط مربع الخطأ وإنتاج موثوقية SKP، وحساب الحد الأقصى للخطأ. باستخدام هذا المجتمع، تحقق من خاصية الأخطاء العشوائية:
Lim[∆] / n =0، حيث يتم حساب W = [W] / n.
| ن | دبليو | ن | دبليو | ن | دبليو | ن | دبليو | ن | دبليو |
| 1 | +1,02 | 11 | -1,72 | 21 | -0,90 | 31 | +2,80 | 41 | -0,44 |
| 2 | +0,41 | 12 | +1,29 | 22 | +1,22 | 32 | -0,81 | 42 | -0,28 |
| 3 | +0,02 | 13 | -1,81 | 23 | -1,84 | 33 | +1,04 | 43 | -0,75 |
| 4 | -1,88 | 14 | -0,08 | 24 | -0,44 | 34 | +0,42 | 44 | -0,80 |
| 5 | -1,44 | 15 | -0,50 | 25 | +0,18 | 35 | +0,68 | 45 | -0,95 |
| 6 | -0,25 | 16 | -1,89 | 26 | -0,08 | 36 | +0,55 | 46 | -0,58 |
| 7 | +0,12 | 17 | +0,72 | 27 | -1,11 | 37 | +0,22 | 47 | +1,60 |
| 8 | +0,22 | 18 | +0,24 | 28 | +2,51 | 38 | +1,67 | 48 | +1,85 |
| 9 | -1,05 | 19 | -0,13 | 29 | -1,16 | 39 | +0,11 | 49 | +2,22 |
| 10 | +0,56 | 20 | +0,59 | 30 | +1,65 | 40 | +2,08 | 50 | -2,59 |
W = [W] / n، W = +2.51 / 50 = 0.05
في هذه الحالة، من المستحسن حساب جذر متوسط مربع الخطأ باستخدام الصيغة: m = √( – [W] 2 /n) ÷ (n-1)،
م = √(76.5703 – (2.51 2)/50) ÷ 49 = 1.249
تقييم موثوقية SKP باستخدام الصيغة: m m = m / √2(n-1)،
م م = 1.249/ √(2×49) = 0.13.
الحد الأقصى للخطأ وفقًا للصيغة: ∆ pr = 3×m,
∆ العلاقات العامة = 3×1.249= 3.747.
مهمة الاختبار 5 تحديد مسافة SKP المحسوبة بواسطة الصيغة
ص = √(س ٢ – س ١) ٢ + (ص ٢ – ص ١) ٢
إذا س 2 = 6,068,740 م؛ ص 2 = 431,295 م؛
× 1 = 6,068,500 م؛ ص 2 = 431248 م؛
م س = م ص = 0.1 م.
س = √(6,068,740 - 6,068,500) 2 + (431,295 - 431,248) 2 =235.36
م م = 0.1/ √4 = 0.05
مهمة الاختبار 6
تم قياس الزاوية نفسها 5 مرات وكانت النتائج: 60˚41"; 60˚40"; 60˚40"; 60˚42"; 60˚41". إنتاج المعالجة الرياضيةهذه السلسلة من نتائج القياس.
| نب / ص | ل، ˚ | ε, " | الخامس،" | الإصدار الثاني،" |
| 1 | 60˚41" | 1 | -0,2 | 0,04 |
| 2 | 60˚40" | 0 | +0,8 | 0,64 |
| 3 | 60˚40" | 0 | +0,8 | 0,64 |
| 4 | 60˚42" | 2 | -1,2 | 1,44 |
| 5 | 60˚41" | 1 | -0,2 | 0,04 |
| مجموع | 4 | 0 | 2,8 |
l 0 - القيمة الدنيا للكمية المقاسة، l 0 = 60˚40"؛ ε - الباقي، يتم الحصول عليه كـ ε = l 1 - l 0؛ L - القيمة الأفضلالكمية المقاسة,
ل = [ل]/ن؛ m = √([ v 2 ]/(n – 1)، حيث v هو الانحراف عن الوسط الحسابي. M هو تقدير لدقة الوسط الحسابي، M = m/√n.
ل = 60˚40" + 4/5 = 60˚40.8"
م = √2.8 / 4 = 0.7"
م = 0.7"/√5 = 0.313"
مهمة الاختبار 7
إجراء معالجة رياضية لنتائج قياس مساحة نفس الكفاف باستخدام مقياس التخطيط: 26.31؛ 26.28؛ 26.32؛ 26.26؛ 26.31 هكتار.
| نب / ص | ل، ها | ε، ها | الخامس، ها | v2، ها |
| 1 | 26,31 | 0,05 | -0,014 | 0,000196 |
| 2 | 26,28 | 0,02 | +0,016 | 0,000256 |
| 3 | 26,32 | 0,06 | -0,024 | 0,000576 |
| 4 | 26,26 | 0 | 0,036 | 0,001296 |
| 5 | 26,31 | 0,05 | -0,014 | 0,000576 |
| مجموع | 0,18 | 0 | 0,0029 |
ل = 26.26 + 0.18/5 = 26.296 هكتار
م = √0.0029/ 4 = 0.0269 هكتار
م = 0.0269/√5 = 0.01204 هكتار
مهمة الاختبار 8
عند دراسة تقسيمات السنتيمترات لقضيب التسوية باستخدام مسطرة جنيف، تم تحديد درجة الحرارة وقت أخذ التقرير. لقطاعات خمسة سنتيمترات تم الحصول على القيم التالية: 20.3˚؛ 19.9 درجة؛ 20.1˚; 20.2˚; 20.3˚. إجراء المعالجة الرياضية لنتائج القياس.
| نب / ص | ل، ˚ | ε, ˚ | الخامس | v2، ˚ |
| 1 | 20,3 | 0,4 | -0,14 | 0,0196 |
| 2 | 19,9 | 0 | -0,26 | 0,0676 |
| 3 | 20,1 | 0,2 | -0,06 | 0,0036 |
| 4 | 20,2 | 0,3 | 0,04 | 0,0024 |
| 5
لم يتبين أنها ضرورية، فيجب تطوير الأداة يدويًا، إذا كان ذلك مبررًا من حيث الوقت المستغرق و الموارد المادية. 2. معالجة القياسات الجيوديسية باستخدام جداول البيانات للمعالجة الأولية للمعلومات التي تم الحصول عليها نتيجة لمجموعة معقدة من الأعمال الطبوغرافية والجيوديسية، استخدمت برنامج "TOGI" وهو عبارة عن حزمة...
في موقع البناء، من الضروري الامتثال لمتطلبات معايير ولوائح السلامة المنصوص عليها في الفصل SNiP Sh-4-80 "السلامة في البناء" وتعليمات الإدارات. يُسمح للأشخاص الذين خضعوا للتعليمات الصادرة بأمر من إدارة الإنشاءات بمزاولة الأعمال الجيوديسية. يعتمد خطر الإصابة أو الإصابة على ظروف العمل...
الأجهزة الإلكترونية بمشاركة مباشرة من المؤلف. الفصل الثاني. ويناقش الفصل الثاني الأساليب المطورة لإجراء البحوث على المنشآت المترولوجية ويقف على فحص ومعايرة الأجهزة الجيوديسية لقياس الارتفاعات. طريقة لدراسة خطأ الفترة القصيرة في قياس الزوايا الرأسية للأجهزة الجيوديسية. مهمة مهمة عند البحث... |
هنا متوسط آخر، وهو مرتبط بالأخطاء.
متوسط مربع الخطأ(SKP) هو مقياس لدقة نتائج القياس أو وظائف الكميات المقاسة وهي خاصية احتمالية.
أرز. 3.1. قانون التوزيع الطبيعي
أخطاء عشوائية.
لنفترض أننا نعرف قيمة متوسط مربع الخطأ م. وفقًا لقانون التوزيع الطبيعي، سيكون الرسم البياني لتوزيع الأخطاء الحقيقية حسب النوع مشابهًا للرسم البياني في الشكل. 3.1. معامل صيميز التردد (أو التردد) لحدوث أخطاء عشوائية بحجم وعلامة واحدة أو أخرى. في هذه الحالة، احتمال حدوث أخطاء في نطاق محدد مسبقًا، على سبيل المثال، ± م، يتم تحديده بمساحة الشكل، ويقتصر على منحنى التوزيع والقطاعات الإحداثية عند القيم + مو - م. بالنسبة لقانون التوزيع الطبيعي، فإن احتمال حدوث الأخطاء في النطاقات المحددة يساوي القيم التالية:
للنطاق ± م ® ر= 68.3% (»68%);
للنطاق ±2 م® ر= 95.5% (»95%);
للنطاق ±3 م® ر= 99.7% (100%) تقريباً.
وبالتالي، في 3 حالات فقط من أصل 1000 يمكن أن يتجاوز الخطأ قيمة 3 م. أخطاء تتجاوز 3 في القيمة المطلقة م(الحد الأقصى للخطأ) تعتبر تقريبية، ويتم استبعاد نتائج القياس التي تحتوي على هذا الخطأ الجسيم من المعالجة الإضافية. في بعض الحالات، لتشديد متطلبات دقة القياس، يتم تعيين الحد الأقصى للخطأ في النطاق من 2 محتى 3 م.
الجدول 3.1
قيم معامل الطالب ( ر) لاحتمالات مختلفة ( ر)
| ر | ص% | ر | ص% | ر | ص% |
| 0,1 | 8,0 | 1,1 | 72,9 | 2,1 | 96,4 |
| 0,2 | 15,9 | 1,2 | 77,0 | 2,2 | 97,2 |
| 0,3 | 23,6 | 1,3 | 80,6 | 2,3 | 97,9 |
| 0,4 | 31,1 | 1,4 | 83,8 | 2,4 | 98,4 |
| 0,5 | 38,3 | 1,5 | 86,6 | 2,5 | 98,8 |
| 0,6 | 45,1 | 1,6 | 89,0 | 2,6 | 99,1 |
| 0,7 | 51,6 | 1,7 | 91,1 | 2,7 | 99,3 |
| 0,8 | 57,6 | 1,8 | 92,8 | 2,8 | 99,5 |
| 0,9 | 63,2 | 1,9 | 94,3 | 2,9 | 99,6 |
| 1,0 | 68,3 | 2,0 | 95,5 | 3,0 | 99,7 |
غالبًا ما تتم الإشارة إلى قيمة SKP بمعامل ر (معامل الطالب) ، الذي يحدد فاصل احتمال الثقة ( X± tm) نتيجة القياس عند مستوى احتمال محدد ر. لهذا فمن المناسب استخدام الجدول. 3.1.
على سبيل المثال، لا بد من تحديد فاصل الثقةللقيمة Xمع احتمال 90٪. من الجدول، عن طريق الاستيفاء نجد أن ل ص 1 = 89,0% ر 1= 1.6 ل ص 2 = 91,1% ر 2 = 1,7: ر س= 1.6476 » 1.65.
وهذا يعني أن نتيجة القياس باحتمال 90% تقع ضمن ( X± 1.65 م).
إذا كانت الكمية المقاسة Xمعروفة، ثم يتم تحديد قيمة SKP بواسطة صيغة غاوس:
حيث Δ - أخطاء القياس الحقيقية.
تذكر أن العلامة [...] هي علامة المجموع الغوسي.
في الحالات التي تكون فيها الكمية المقاسة غير معروفة، استخدم صيغة بيسل:
أين الخامس- انحراف نتائج القياس عن الوسط الحسابي.
وكما يتبين من الصيغتين (3.9) و(3.10)، في حالة معرفة الكمية المقاسة، يكفي قياس واحد لتقييم الدقة (ضروري). كما سبق ذكره أعلاه، غالبا ما يتم استخدام صيغة غاوس لتقييم دقة الأدوات القياسية عند قياس الكميات المعروفة (المعايير). لتقييم الدقة باستخدام صيغة بيسل، من الضروري إجراء قياسين على الأقل. تُستخدم صيغة بيسل لتقييم دقة نتائج قياسات الكتلة (المتعددة) لكمية واحدة غير معروفة مسبقًا.
مع زيادة عدد القياسات، تصبح قيم SCP التي تم الحصول عليها باستخدام صيغ Gauss و Bessel متطابقة تقريبًا (مع ما يقرب من ن³ 20). في هذه الحالة، تميل قيمة SCP لبعد واحد إلى الحد الأقصى م السابقوالتي تتحدد من خلال دقة الجهاز أو دقة طريقة القياس أو البرنامج. من الواضح أنه سبق أن قيل أعلاه أنه من المستحيل عمليًا، وحتى غير المناسب لعدد من الأسباب، توفير عدد كبير جدًا من القياسات لكمية واحدة. وفي هذه الحالة، يجب أن يضمن العدد العملي للقياسات الحصول على نتيجة القياس بدقة معينة عند مستوى ثقة محدد.
نظرًا لأن عدد القياسات محدود، فإن SCP نفسه يحتوي على خطأ تحدده الصيغة التقريبية:
وهذا ما يطلق عليه - متوسط مربع الخطأ لمتوسط مربع الخطأ (RMSE).
ومن المناسب هنا العودة إلى تصنيف الأخطاء. لم تتم مناقشة جميع أنواع الأخطاء أعلاه.
في كثير من الأحيان، عند دراسة سلسلة من أخطاء القياس، ما يسمى خطأ محتمل، وهو ما يُشار إليه بالحرف ص. يمكن تقدير حجم الخطأ المحتمل باستخدام الصيغة التقريبية
على افتراض، بالطبع، أن توزيع الأخطاء يخضع للقانون الطبيعي.
ويسمى الخطأ المحتمل أيضا خطأ متوسط. إذا كنت لا تريد إجراء العمليات الحسابية باستخدام الصيغة (3.12)، لأنها تتضمن القيمة م، والتي يجب الحصول عليها باستخدام صيغة بيسل، فيمكن تحديد الخطأ المحتمل أو المتوسط من خلال ترتيب سلسلة من الأخطاء بترتيب متزايد للقيم المطلقة. سيتم تحديد موقع قيمة هذا الخطأ في منتصف السلسلة الناتجة. هذا إذا كان عدد الأخطاء فرديًا. وإذا كان زوجيًا، فسيكون الخطأ المتوسط هو متوسط قيمة الأخطاء المجاورة في منتصف السلسلة.
لا ينبغي الخلط بينه وبين الخطأ المتوسط متوسط الخطأ v oوالتي يمكن الحصول عليها أيضًا باستخدام صيغة بسيطة:
هنا، مطلوب أيضًا شرط لعدد من القياسات (الأخطاء) للامتثال للقانون العادي.
الخطأ المتوسط هو توقع رياضي القيم المطلقةانحرافات نتائج القياس لأي قيمة عن التوقع الرياضي لهذه النتائج. يمكن تقدير القيمة التقريبية لمتوسط الخطأ باستخدام الصيغة:
أين السادس- انحراف نتائج القياس عن وسطها الحسابي.
تُستخدم الصيغة (3.13) غالبًا لتقدير أولي لمتوسط مربع الخطأ.
الأخطاء العشوائية هي تلك الأخطاء التي يظل حجمها وطبيعة تأثيرها على كل نتيجة قياس فردية غير معروفة. لا يمكن تحديد حجم وعلامة الأخطاء العشوائية مسبقًا. فهي لا مفر منها وتصاحب كل قياس، لأننا نجري القياسات فقط بالدقة التي يمكن تحقيقها باستخدام الأدوات المستخدمة. من المستحيل استبعاد نتائج القياس تمامًا من الأخطاء العشوائية. ولكن بناءً على دراسة خصائصها، من الممكن استخلاص قواعد حول كيفية الحصول على النتائج الأكثر موثوقية من عدد من القياسات وتقييم دقتها. وتتعامل نظرية أخطاء القياس مع هذه القضايا.
في نظرية الأخطاء، يتم التمييز بين قياسات الدقة المتساوية وغير المتساوية. تسمى القياسات التي يتم إجراؤها في نفس الظروف، وباستخدام أدوات بنفس الدقة، ونفس عدد المرات، وبواسطة مراقبين من نفس المؤهلات، قياسات متكافئة. إذا لم يتم استيفاء أحد هذه الشروط، فإن هذه القياسات ستكون غير دقيقة.
خصائص الأخطاء العشوائية. يمكن تعريف الأخطاء العشوائية على أنها الفرق بين القيم المقاسة والقيم الحقيقية لنفس الكمية. بناءً على الدراسة النظرية والعملية للعديد من سلاسل الأخطاء العشوائية، تم استخلاص خصائصها العامة:
1 في ظل هذه الظروف، لا يمكن أن تتجاوز الأخطاء العشوائية حدًا معينًا.
2 الأخطاء الموجبة والسالبة لنفس القيمة المطلقة ممكنة على قدم المساواة.
3 الأخطاء الأصغر في القيمة المطلقة أكثر شيوعًا من الأخطاء الأكبر.
4- يميل الوسط الحسابي للأخطاء العشوائية لقياسات متساوية الدقة لنفس الكمية إلى الاقتراب من الصفر مع زيادة غير محدودة في عدد القياسات.
4.2 مبدأ الوسط الحسابي
دع إجراء قياسات متساوية الدقة l 1، l 2، ...، l n من نفس الكمية، وقيمتها الحقيقية هي X. ثم يمكننا حساب قيم n للأخطاء العشوائية:
Δ 1 = ل 1 – X;
Δ 2 = ل 2 – X; (4.1)
Δ ن = ل ن – X.
وبجمع الطرفين الأيسر والأيمن لهذه المتساويات، نحصل على ذلك
Δ 1 + Δ 2 +…+ Δ n = ل 1 + ل 2 +…+ ل ن – nX. (4.2)
من المعتاد في نظرية الخطأ الإشارة إلى مجموع الكميات بين قوسين مربعين، على سبيل المثال:
Δ 1 + Δ 2 + … + Δ n = [Δ]; ل 1 + ل 2 + … + ل ن = [ل]، الخ.
وبهذه الرموز، تأخذ المساواة (4.2) الشكل
[Δ] = [l] – nX، حيث X = [l] / n – [Δ] / n. (4.3)
ووفقاً للخاصية الرابعة للأخطاء العشوائية فإن القيمة [Δ] / n في التساوي (4.3) تميل إلى الصفر مع زيادة غير محدودة في عدد القياسات. وبالتالي فإن القيمة [l] / n في ظل هذه الظروف ستقترب من القيمة الحقيقية لـ X. وبناء على ذلك، يعتبر الوسط الحسابي (الوسط الحسابي لنتائج القياس) هو النتيجة الأكثر موثوقية أو الأكثر احتمالا من القياسات المكافئة بنفس الكمية لأي عدد من القياسات.
ل = [ل] / ن = (ل 1 + ل 2 + ل 3 + … + ل ن) / ن. (4.4)
4.3 متوسط مربع الخطأ لقياس واحد.
صيغ غاوس وبسل
في نظرية الأخطاء، تتميز دقة القياس بمتوسط مربع الخطأ، الذي قدمه عالم الرياضيات الألماني الشهير والمساح K. F. Gauss (1777–1855) ويشار إليه بالحرف m:
______________________ ______
م = ± √ (Δ 1 2 + Δ 2 2 + .. + Δ n 2) / n = ± √ [Δ 2 ] / n, (4.5)
حيث Δ 1، Δ 2، …، Δ n – أخطاء عشوائية؛
ن – عدد القياسات.
يعد جذر متوسط مربع الخطأ معيارًا موثوقًا لتقييم دقة القياسات. إنه مستقر تمامًا حتى مع وجود عدد صغير من القياسات ويعكس جيدًا وجود عدد كبير أخطاء عشوائيةوالتي تحدد بشكل أساسي جودة القياسات.
تستخدم الصيغة (4.5) لحساب متوسط مربع الخطأ عندما تكون القيمة الحقيقية للقيمة المقاسة معروفة. هذه الحالات نادرة جدًا في الممارسة العملية. كقاعدة عامة، القيمة الحقيقية للقيمة المقاسة غير معروفة، ولكن من القياسات يمكن الحصول على النتيجة الأكثر موثوقية - الوسط الحسابي. دعونا نحصل على صيغة لحساب متوسط مربع الخطأ باستخدام انحراف النتائج الفردية عن الوسط الحسابي باستخدام ما يسمى الأخطاء الأكثر احتمالا V.
دع l 1, l 2, ..., l n تكون نتائج قياسات متكافئة لنفس الكمية، قيمتها الحقيقية هي X، والوسط الحسابي هو L. ثم يمكن حساب الأخطاء العشوائية أو الحقيقية
Δ أنا = ل أنا – X (4.6)
والأخطاء الأكثر احتمالا
V i = l i - L. (4.7)
مجموع ن للمساواة (4.7)
[V] = [ل] – nL. (4.8)
ولكن وفقا للمساواة (4.4) nL = [l]، وبالتالي
أي أن مجموع الأخطاء المحتملة يجب أن يكون دائمًا مساويًا للصفر.
بطرح المساواة (4.7) من المساواة (4.6) نحصل على
Δ i – V i = L – X. (4.10)
على الجانب الأيمن من المساواة (4.10) لدينا خطأ عشوائي في الوسط الحسابي. دعونا نشير إليها بـ ε. ثم
Δi = V i + ε. (4.11)
دعونا نقوم بتربيع المساواة (4.11)، ونأخذ مجموعها ونقسمها على n:
[Δ 2 ] / n = / n + nε 2 / n + 2ε[V] / n. (4.12)
الجانب الأيسر من هذه المساواة ليس أكثر من م 2 . ونظرًا للمساواة (4.9)، فإن الحد الأخير في الطرف الأيمن يساوي صفرًا.
م 2 = / ن + ε 2. (4.13)
دعونا نستبدل الخطأ العشوائي ε بمتوسط قيمته، أي متوسط مربع الخطأ للوسط الحسابي. وسيثبت أدناه ذلك متوسط مربع الخطأ للوسط الحسابي
م 2 = ε 2 = م 2 / ن. (4.14)
م 2 – م 2 / ن = / ن أو م 2 (ن – 1) / ن = / ن,
أين ___________
م 2 = / (ن – 1)، أو م = √ / (ن – 1). (4.15)
تسمى الصيغة (4.15). صيغة بيسلولها عظيم أهمية عملية. يسمح لك بحساب جذر متوسط مربع الخطأ بناءً على الانحرافات الأكثر احتمالية لنتائج القياس عن المتوسط الحسابي.
بالإضافة إلى متوسط مربع الخطأ، هناك أيضًا أخطاء متوسطة ومحتملة ونسبية.
متوسط الخطأ (Θ) هو الوسط الحسابي للقيم المطلقة للأخطاء العشوائية، أي.
Θ = (|Δ 1 | + |Δ 2 | + … + |Δ n |) / n = [|Δ|] / n. (4.16)
ثبت في نظرية الخطأ أنه عندما يكون n → ∞ Θ = 0.8 م، أو m = 1.25Θ.
في بعض الأحيان في الأسئلة التطبيقية يستخدمونها خطأ محتملص. الخطأ المحتمل هو قيمة الخطأ العشوائي في سلسلة واحدة من القياسات المتساوية الدقة، والتي فيما يتعلق بها من الممكن حدوث خطأ أكبر أو أقل من هذه القيمة، في القيمة المطلقة. للعثور على r، يتم ترتيب جميع الأخطاء في سلسلة معينة بترتيب تصاعدي في القيمة المطلقة ويتم تحديد القيمة التي تشغل الموضع الأوسط، أي أن هناك عددًا من الأخطاء أقل منها كما يوجد المزيد. يرتبط الخطأ المحتمل بمتوسط مربع الخطأ بنسبة r = 2/3 m = 0.67 m أو m = 1.5 r.
كما يمكن أن يرى، m > Θ و m > r، مما يوضح أن متوسط الخطأ المربع يميز دقة القياسات بشكل أفضل من الأخطاء المتوسطة والمحتملة.
غالبًا ما يتم تقييم دقة الكميات المقاسة مثل الخطوط والمساحات والأحجام باستخدام خطأ نسبي. الخطأ النسبي هو نسبة الخطأ المطلق إلى قيمة الكمية المقاسة. يتم كتابة الخطأ النسبي ككسر، بسطه واحد، والمقام هو رقم يشير إلى نسبة القيمة المقاسة التي يجب أن تكون الخطأ المسموح به. على سبيل المثال، طول الضلع D = 150 م مقاسًا من الخطأ المطلقم د = 0.05 م ثم الخطأ النسبي لنتيجة القياس سيكون م د / د = 0.05 م / 150 م = 1/3000.
وتعني القيمة 1/3000 أنه يمكن السماح بخطأ قدره 1 متر على مسافة 3000 متر، وكلما زاد مقام الخطأ النسبي، زادت دقة القياسات. يتم دائمًا تحديد دقة جميع القياسات الخطية في الجيوديسيا خطأ نسبي، والتي ترد في التعليمات والأدلة ذات الصلة لإنتاج هذا النوع من الأعمال الجيوديسية.
4.4 قانون التوزيع الطبيعي للأخطاء.
الحد الأقصى للخطأ
من النظر السابق لخصائص الأخطاء العشوائية، يتبع أنه من المستحيل قول أي شيء محدد مقدما حول ظهور خطأ منفصل. ومع ذلك، عندما يزيد عدد هذه الأخطاء، فمن الممكن إنشاء أنماط معينة لمجموعة الأخطاء الكاملة لسلسلة معينة من القياسات. يمكن التعبير عن هذه الأنماط بالمعادلة التي حصل عليها K. F. Gauss. يبدو الأمر كذلك
ص = (1 / σ √2π) ه – (ل i – أ) / 2 σ = (1 /σ √2π) ه – Δ ج / 2 σ , (4.17)
حيث y هي كثافة توزيع الخطأ؛
σ - معلمة المعادلة، التي تسمى المعيار، مرتبطة بالمتوسط
نسبة الخطأ المربع
a هي معلمة معادلة تسمى التوقع الرياضي،
يرتبط بالوسط الحسابي بالعلاقة
ه - القاعدة اللوغاريتمات الطبيعية;
Δ أنا = ل أنا – أ – خطأ عشوائي.
تسمى هذه المعادلة قانون التوزيع الطبيعيأخطاء.
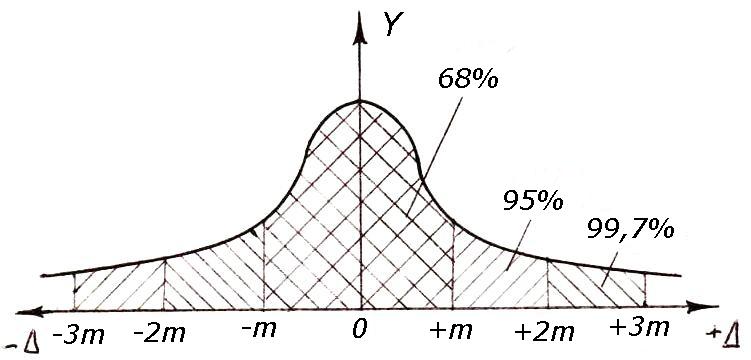
المعادلة (4.17) تتوافق مع منحنى على شكل جرس يسمى منحنى التوزيع الطبيعي (منحنى غاوسي) (الشكل 4.1)
الشكل 4.1 - منحنى غاوسي
المساحة الموجودة أسفل المنحنى، والتي يحدها المنحنى والمحور السيني، تساوي واحدًا. إن جزء هذه المنطقة المقابل لأي جزء من محور الإحداثي السيني يعطي احتمال حدوث خطأ عشوائي في فترة زمنية معينة. بالنسبة لـ l i = a أو Δ = 0 نحصل عليها القيمة القصوىإحداثيات المنحنى __
ص = 1/σ √2π.
يتضح من الشكل 4.1 أن الجزء الأكبر من الأخطاء يتم تجميعه حول قيمة الخطأ الأكثر احتمالية Δ i = 0 (وفقًا للخاصية الرابعة للأخطاء العشوائية، يميل المتوسط الحسابي للأخطاء العشوائية إلى الصفر). يبرر هذا الموضع الخاصية الثالثة للأخطاء العشوائية (الأخطاء الصغيرة تحدث أكثر من الأخطاء الكبيرة). الخاصية الثانية للأخطاء العشوائية - التكرار المتساوي للأخطاء الإيجابية والسلبية - تتميز بتماثل منحنى التوزيع الطبيعي بالنسبة لمحور OY.
يُظهر البحث النظري وممارسة القياسات الجيوديسية أن 68% من جميع الأخطاء العشوائية تقع في الفواصل الزمنية من –m إلى +m (انظر الشكل 4.1)، و95% من الأخطاء تقع في الفاصل الزمني بمقدار الضعف (من –2m إلى +2m) ، وفي الفاصل الزمني الأكبر بثلاث مرات (من -3 م إلى +3 م) يقع ضمن 99.73٪ من الأخطاء. وهذا يعني أنه من بين 100 خطأ في القياس، فإن 32 فقط في القيمة المطلقة ستتجاوز جذر متوسط مربع الخطأ m، و3 من 1000 خطأ ستتجاوز قيمة ثلاثة أضعاف جذر متوسط مربع الخطأ ±3m. وبالتالي، فإن 0.27% فقط من أخطاء القياس تتجاوز ±3 م. لذلك، يتم اعتبار ثلاثة أضعاف متوسط مربع الخطأ بمثابة الحد الأقصى للخطأ Δ، أي.
Δقبل = 3 م. (4.18)
دعونا الآن نفكر في جوهر المعلمتين a و σ في المعادلة (4.17). تسمى المعلمة a بالتوقع الرياضي وتميز مركز التجميع على المنحنى الغاوسي، أي إزاحة مركز التجميع على طول محور الإحداثي السيني (الشكل 4.2، أ) مع الحفاظ على شكل المنحنى. إذا قمنا، عند قيمة ثابتة للمعلمة a، بتغيير معلمة أخرى σ (تسمى المعيار)، والتي تميز دقة القياسات، وهذا ممكن إذا قمنا بتغيير طريقة القياس أو إجرائها باستخدام أدوات أخرى. ثم يظل مركز التجميع دون تغيير، ولكن يتغير شكل المنحنى. وسوف يصبح مسطحًا إذا انخفضت دقة القياس، وسيصبح أكثر انحدارًا مع زيادة الدقة (الشكل 4.2، ب).
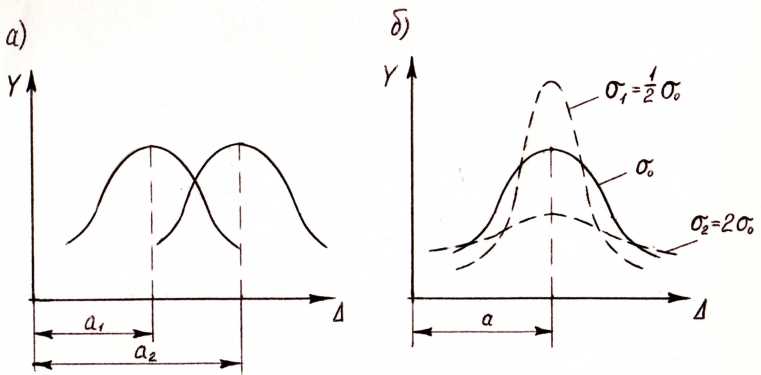
الشكل 4.2 - الإزاحة والتغير في شكل المنحنى الطبيعي
المعلمتان a وσ غير معروفتين مسبقًا، قبل القياسات. يتم الحصول عليها نتيجة لذلك عدد كبيرقياسات. من الناحية العملية، بدلاً من المعلمتين a وσ، نحصل على قيمهما التقريبية: المتوسط الحسابي L، المحسوب باستخدام الصيغة (4.4)، ومتوسط مربع الخطأ m، المحسوب باستخدام الصيغ (4.5) أو (4.15).
4.5 جذر متوسط مربع خطأ الدالة
قياس الكميات
في الجيوديسيا، غالبًا ما يكون من الضروري تحديد دقة ليس فقط الكميات المقاسة نفسها، ولكن أيضًا وظائفها. على سبيل المثال، الموقع الأفقي للخط هو دالة لميل المسافة وزاوية الميل، والمساحة التي يحددها المقياس هي دالة للقراءات على المقياس، وما إلى ذلك. لذلك، من المهم أن تكون قادرًا لحساب متوسط الأخطاء المربعة للوظائف. دعونا نلقي نظرة على بعض أنواع الوظائف.
م = نانومتر 2 أو م φ = م√ ن، (4.27)
أي أن متوسط مربع الخطأ لمجموع القيم المقاسة بدقة متساوية أكبر بمقدار √n مرة من متوسط مربع الخطأ للقياس الفردي.
مثال أوجد جذر متوسط مربع الخطأ لمجموع الزوايا المقاسة في شكل رباعي إذا كان جذر متوسط مربع خطأ زاوية واحدة هو ±30 "" . باستخدام الصيغة (4.27) نجد
م φ = ± 30 "" √ 4 = ±60 "" = 1 " .
2دالة خطية
حيث K هو رقم ثابت؛
X هي وسيطة تم الحصول عليها من القياسات.
إذا تم قياس X بخطأ عشوائي Δ X، فسيكون للدالة خطأ عشوائي
Δ φ = ك Δ X . (4.29)
بعد قياس الوسيطة n مرات، يمكنك إنشاء معادلات n (4.29)، وأخذ مجموع مربعاتها وتقسيمها على n. وبعد ذلك نحصل
[Δ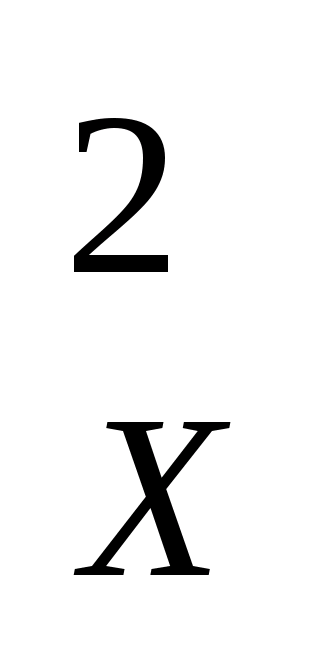 
] / ن = ك 2 [Δ] / ن أو م = ك 2 م، (4.30)
م φ = ك م X . (4.31)
على غرار ما سبق، يمكن إظهار ذلك بالنسبة للوظيفة
φ = ± K 1 X ± K 2 Y ± … ± K n U (4.32)
Δ φ = K 1 Δ X ± K 2 Δ Y ± … ± K n Δ U (4.33)
م= (ك 1 م X) 2 + (ك 2 م ص) 2 + … + (ك ن م يو) 2 . (4.34)
مثال حدد متوسط مربع الخطأ M للوسط الحسابي L، إذا كان متوسط مربع الخطأ لقياس فردي يساوي m. لنكتب الصيغة (4.4) للوسط الحسابي بالشكل التالي:
ل = ل 1 / ن + ل 2 / ن + … + ل ن / ن. (4.35)
كما ترون، هنا يمكنك تطبيق الصيغة (4.34) للوظيفة (4.35):
م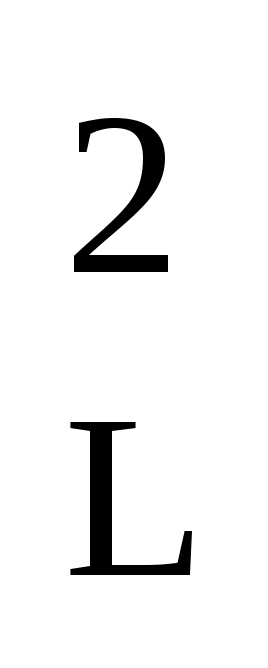 
= م 2 = (م 1 / ن) 2 + (م 2 / ن) 2 + ... + (م ن / ن) 2.
بالنظر إلى أن القياسات l 1, l 2,…, l n متساوية في الدقة، أي m 1 = m 2 = … = m n، نحصل على
م 2 = ن(م / ن) 2 = م 2 / ن,
م = م / √ن، (4.36)
أي أن متوسط مربع الخطأ للوسط الحسابي أقل بمقدار √n من متوسط مربع الخطأ للقياس الفردي.
3وظيفة منظر عام
φ = و (X، Y، Z، …، U)، (4.37)
حيث X، Y، Z، …، U هي قيم يتم قياسها بشكل مستقل.
مع الأخذ في الاعتبار الأخطاء العشوائية، فإن الدالة (4.37) ستأخذ الشكل
φ + Δ φ = f (X + Δ X ; Y + Δ Y ; Z + Δ Z ; …; U + Δ U). (4.38)
بتوسيع الدالة (4.38) إلى متسلسلة تايلور وقصر أنفسنا على الدرجات الأولى فقط من الأخطاء العشوائية، نحصل على الدالة
Δ φ = (∂f/∂x) Δ X + (∂f/∂y) Δ Y + (∂f/∂z) Δ Z + … + (∂f/∂u) Δ U , (4.39)
حيث (∂f/∂x)، (∂f/∂y)، …، (∂f/∂u) هي مشتقات جزئية، وهي للدالة
(4.39) كميات ثابتة.
وكما يتبين، فإن الدالة (4.39) تشبه الدالة (4.33). وبالتالي فإن مربع متوسط مربع الخطأ
= (∂f/∂x ∙ m X) 2 + (∂f/∂y ∙ m Y) 2 + (∂f/∂z ∙ m Z) 2 + … + (∂f/∂u ∙ m U) 2 . (4.40)
مثال يتم قياس الجانبين في مستطيل - X = 200 م وY = 100 م مع جذر متوسط الأخطاء المربعة m X = +0.20 م وm Y = +0.10 م.
تحديد مساحة المستطيل P ومتوسط مربع خطأه m P .
.م = √ / 2ن. (4.43)
الصيغة (4.43) تعطي تعبيرا عن جذر متوسط مربع الخطأ لقياس واحد من قياسات مزدوجة n.
4.7 قياسات متفاوتة
في الأقسام السابقة، تمت مناقشة قياسات متساوية الدقة. ومع ذلك، من الناحية العملية، غالبًا ما يتم إجراء قياسات غير متساوية، والتي يتم إجراؤها في ظل ظروف مختلفة أو باستخدام أدوات متفاوتة الدقة وبعدد مختلف من الخطوات. وفي هذه الحالة، لم يعد من الممكن أن نقتصر على متوسط حسابي بسيط، وهنا يجب أن نأخذ في الاعتبار درجة موثوقية كل نتيجة قياس.
وتسمى درجة موثوقية نتيجة القياس، معبرا عنها برقم، بوزن هذا القياس. كلما كانت النتيجة أكثر موثوقية، كلما زاد وزنها. دعونا نحصل على سلسلة من القيم المتوسطة: L 1، L 2، ...، L n - قيمة واحدة تم الحصول عليها من P 1، P 2، ...، P n القياسات الفردية.
وفقًا للصيغة (4.4)، سيكون المنتج L i P i مساويًا لمجموع القياسات الفردية l i في سلسلة معينة، وسيكون مجموع جميع القياسات في جميع السلاسل مساويًا لـ L 1 P 1 + L 2 P 2 + … + ل ن ف ن. سيكون عدد جميع القياسات مساوياً لـ P 1 + P 2 +…+ P n.
ومن هنا، وباستخدام قاعدة الوسط الحسابي، نحصل على القيمة المتوسطة من جميع سلاسل القياسات:
ل س = (ل 1 ف 1 + ل 2 ف 2 + … + ل ن ف ن ) / ( ف 1 + ف 2 + … + ف ن ) = / [ ف ]. (4.44)
يتم استدعاء التعبير (4.44). صيغة متوسط الوزنأو المتوسط الحسابي المشترك. هنا عدد القياسات P 1, P 2, ..., P n في كل صف هو وزن متوسط النتائج L 1, L 2, ..., L n، ومجموع الأوزان هو وزن الوسط الحسابي المشترك L o. وفي جميع الحالات التي تكون فيها نتائج القياس وأوزانها معروفة، المعنى على الأرجحيتم حساب القيمة المقاسة باستخدام الصيغة (4.44).
دعونا نشير إلى متوسط الخطأ المربع لقياس واحد بواسطة μ، ومتوسط الأخطاء المربعة للكميات L 1، L 2 .... L n، على التوالي، بواسطة m 1، m 2، ...، m n. ثم، وفقا للمساواة (4.36)، يمكننا أن نكتب أن ___ __ __
م 1 = μ / √ ف 1 ; م 2 = μ / √ ص 2 ; ...; م n = μ / √ P n . (4.45)
إذا أخذنا في الصيغة (4.45) P i = 1، إذن μ = m i. ويترتب على ذلك أن μ هو جذر متوسط مربع الخطأ لقياس وزنه يساوي واحدًا، أو ما يسمى جذر متوسط مربع خطأ وحدة الوزن.
الدورات الدراسيةأنواع الأخطاء.دائمًا ما يشتمل الخطأ على مكونين: منهجي وعشوائي.
Δa = Δasystem + Δaran.
منهجييسمى خطأ، والذي يظل ثابتًا في ظل ظروف معينة (أو يتغير، ولكن وفقًا لقانون معروف).
تحدث مثل هذه الأخطاء باستمرار أسباب فعالةونتيجة لذلك، عند القياس، "نخطئ" بنفس المقدار في كل مرة. في كثير من الأحيان تكون هذه الأخطاء ناتجة عن التصنيع غير الدقيق للجهاز (أخطاء الآلات) أو الثابتة عامل خارجي. على سبيل المثال، يتسبب المجال المغناطيسي الخاص بالطائرة في حدوث خطأ في قياس المسار المغناطيسي (الانحراف)، والذي له قيمة محددة جدًا في كل مسار.
الأخطاء المنهجية، حيث أنها متماثلة في كل قياس، يمكن تحديدها مرة واحدة باستخدام أدوات أكثر دقة، ثم يتم حذفها من نتائج القياس عن طريق إدخال التصحيحات.
لا تسبب الأخطاء المنهجية الكثير من المتاعب أثناء التنقل، لأنها بعد إزالتها لم تعد موجودة. لذلك، سنفترض أيضًا أنه لا توجد أخطاء منهجية (تم أخذها في الاعتبار بالفعل).
خطأ عشوائيلكل قياس يأخذ معنى مختلف، ولا يُعرف مسبقًا أيهما.
لكن الأخطاء العشوائية، من حيث المبدأ، لا يمكن القضاء عليها، لأنها مختلفة لكل قياس. ويظلون مجهولين دائمًا.
من المستحيل تحديد القيم العددية للأخطاء العشوائية، ولكن يجب على الطيار أن يضع في اعتباره دائمًا أن هذه الأخطاء موجودة وأن تكون لديه فكرة عن قيمها المحتملة. يعد وجود عدم اليقين في نتائج القياس أحد العوامل الرئيسية التي تعقد عملية الملاحة وتجعلها ليس علمًا فحسب، بل فنًا أيضًا.
الحدث العشوائي هو حدث قد يحدث أو لا يحدث في ظل ظروف معينة. يتم تحديد درجة احتمال حدوث مثل هذا الحدث عدديًا بقيمة الاحتمال. الاحتمال P هو رقم يمكن أن يتراوح من 0 إلى 1. إذا لم يحدث حدث مطلقًا، في ظل ظروف معينة، فإنه يسمى حدثًا مستحيلًا ويكون احتماله صفرًا. إذا حدث دائمًا في ظل ظروف معينة، فإنه يسمى موثوقًا وينسب إليه الاحتمال. يساوي واحد. إذا، على سبيل المثال، P = 0.3، فهذا يعني أنه في المتوسط، في 30 حالة من أصل 100، سيحدث الحدث. إنه في المتوسط، لأن الحدث عشوائي. إذا قمت بتهيئة الظروف اللازمة لحدوث حدث ما وقمت بإجراء سلسلة من 100 تجربة، فمن الممكن أن يقع الحدث مثلاً 23 مرة، أو 32 مرة... إذا قمت بإجراء عدة سلاسل من هذه التجارب، أو سلسلة واحدة من ألف، عشرة آلاف، مليون تجربة، فكلما زاد عدد التجارب التي تم تنفيذها، كلما اقترب متوسط عدد مرات حدوث الحدث من 30% من إجمالي عدد التجارب (إذا كانت P = 0.3).
كيف يمكننا وصف الأخطاء العشوائية إذا لم يكن لها أي معنى محدد؟ وهي تتميز غالبًا بقيمة متوسط مربع الخطأ (MSE)، والذي يُشار إليه بالحرف σ (سيجما). لذلك، على سبيل المثال، سوف نشير إلى قياس SKP للكمية a بواسطة σa.
SKP هي خاصية لدرجة تشتت القيمة المقاسة لكمية ما حول قيمتها الفعلية. كلما كانت σa أكبر، كانت القياسات أكثر تشتتًا (مبعثرة). تجارب مختلفةقيم حول القيمة الفعلية للكمية.
في التين. يتم تمثيل 2.19 هندسيًا كمحور رقم القيم الممكنةالكمية المقاسة أويلاحظ معناها الحقيقي. تشير الصلبان على المقياس إلى القيم المقاسة التي تم الحصول عليها نتيجة لعدة تجارب. في الحالة الأولى، يكون انتشار القيم المقاسة حول القيمة الفعلية أكبر منه في الحالة الثانية، وبالتالي فإن “سيجما” الذي يميز درجة الانتشار، يكون أصغر في الحالة الثانية.
أرز. 2.19. متوسط مربع الخطأ
من خلال قيمة SKP، يمكنك الحكم على احتمالات أن القيمة المقاسة سوف تأخذ قيمة أو أخرى. ولكن لهذا لا يكفي معرفة SKP، بل تحتاج أيضًا إلى معرفة قانون التوزيع الذي يخضع له هذا الخطأ العشوائي. تخضع العديد من المتغيرات العشوائية لقانون التوزيع الطبيعي (الغاوسي). ومن المفيد لهذا القانون أن نتذكر المعاني التالية.
لو خطأ منهجيغائبة ونتيجة للقياس تم الحصول على القيمة، فإن القيمة الفعلية للكمية تقع ضمن الحدود (الشكل 2.20):
Aism ± σa مع احتمال P = 0.68؛
نطاقات ± 2σa مع احتمال Р=0.95؛
Aism ± 3σa مع احتمال P = 0.997.
أرز. 2.20. بعض الاحتمالات لقانون التوزيع الطبيعي
على سبيل المثال، بمساعدة البوصلة يتم قياس المسار γ = 100 درجة، وتتميز دقة البوصلة بـ SKP σγ = 2 درجة. وهذا يعني أن سعر الصرف الفعلي (الذي سيبقى مجهولاً بالنسبة لنا) متوسط:
وفي 68 حالة من أصل 100 تقع ضمن 100° ±2°، أي في النطاق 98°...102°؛
وفي 95 حالة من أصل 100 تقع ضمن 100° ±4°، أي في النطاق 96°...104°؛
في 997 حالة من أصل 1000، تقع ضمن 100 درجة ±6 درجة، أي في النطاق 94 درجة ... 106 درجة.
قيمة الاحتمال ر=0.997 قريب جدًا من الوحدة لدرجة أن قيمة خطأ سيجما الثلاثة المقابلة غالبًا ما تسمى الحد الأقصى للخطأ. وفي الواقع قد يتجاوز الخطأ ذلك. صحيح، نادرا - في المتوسط \u200b\u200bفي ثلاث حالات من أصل ألف.
في الأوصاف الفنيةالأدوات والمعدات، يمكن الإشارة إلى دقتها مباشرة في شكل UPC ومن ثم يصبح كل شيء واضحًا. لكن في بعض الأحيان يشار إليه، على سبيل المثال، على النحو التالي: "خطأ قياس المحمل ±1.5 درجة". بالطبع، هذا لا يعني أن أداة تحديد الاتجاه هذه تكون "خاطئة" بمقدار 1.5 درجة في كل مرة. وهذا لا يعني أيضًا أنه لا يستطيع ارتكاب الأخطاء. أكثر، بمقدار 1.5 درجة مئوية. كقاعدة عامة، تتوافق قيمة الخطأ المشار إليها بهذه الطريقة مع الاحتمال ر=0.95. وهذا يعني، في المتوسط، في 95 حالة من أصل 100، لن يتجاوز الخطأ (لأعلى أو لأسفل) قيمة 1.5 درجة.
وعليه، ففي خمس حالات من أصل مائة قد يكون الخطأ أكبر. بالنسبة لقانون توزيع الأخطاء الطبيعي، فإن احتمال 0.95 يتوافق مع تضاعف UPC. ولذلك، فإن UPC لقياس المحمل في هذا المثال سيكون 0.75 درجة.