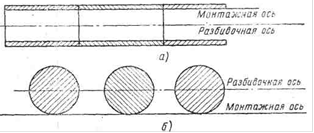
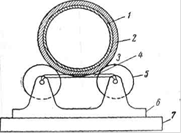
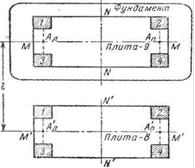
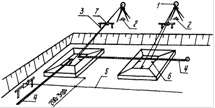
3.2 طبقه بندی خطاهای اندازه گیری ژئودتیک. میانگین مربعات خطا فرم های گاوس و بسل برای محاسبه آن
اندازه گیری های ژئودتیکی حتی در بسیار شرایط خوب، با خطاهایی همراه هستند، i.e. انحراف نتیجه اندازه گیری L از مقدار واقعی X کمیت شماره گذاری شده:
True مقدار کمیت اندازه گیری شده است که به طور ایده آل ویژگی های کمی جسم را منعکس می کند. شرایط دست نیافتنی - معنی واقعی- یک مفهوم فرضی این ارزشی است که می توان بی نهایت نزدیک به آن نزدیک شد، دست یافتنی نیست.
دقت اندازه گیری درجه تقریب نتیجه آن به مقدار واقعی است. هر چه خطا کمتر باشد، دقت بالاتر است.
خطای مطلق با تفاوت بین مقدار به دست آمده در نتیجه اندازه گیری و اندازه گیری واقعی کمیت بیان می شود. به عنوان مثال، مقدار واقعی l = 100 m، با این حال، هنگام اندازه گیری همان خط، نتیجه 100.05 متر بود، پس خطای مطلق این است:
E = X اندازه گیری شده - X
E = 100.05 - 100 = 0.05 (m)
برای بدست آوردن مقدار کافی است یک اندازه گیری انجام دهید. لازم نامیده می شود، اما اغلب به یک اندازه گیری محدود نمی شود، بلکه حداقل دو بار تکرار می شود. اندازه‌گیری‌هایی که فراتر از حد ضروری انجام می‌شوند، اضافی (اضافی) نامیده می‌شوند؛ آنها ابزار بسیار مهمی برای نظارت بر نتیجه اندازه‌گیری هستند.
خطای مطلق ایده ای از صحت نتیجه به دست آمده نمی دهد. به عنوان مثال، هنگام اندازه گیری l = 100 m یا l = 1000 m، خطای 0.06 m را می توان به دست آورد. بنابراین، خطای نسبی محاسبه می شود:
C = 0.06 / 100 = 1/1667، یعنی در 1667 متر از L اندازه گیری شده خطای 1 متر وجود دارد.
خطای نسبی نسبت خطای مطلق به مقدار واقعی یا اندازه گیری شده است. به صورت کسری بیان می شود. طبق دستورالعمل، خط زمین نباید ناهموارتر از 1/1000 اندازه گیری شود.
خطاهای ناشی از عوامل فردی را ابتدایی می نامند. خطای تعمیم یافته مجموع خطاهای ابتدایی است.
وجود دارد:
· خشن (Q)،
· سیستماتیک (O)،
· تصادفی (∆).
خطاهای اندازه گیری فاحش در نتیجه اشتباهات فاحش، محاسبات اشتباه توسط مجری، بی توجهی وی یا نقص های شناسایی نشده به وجود می آیند. وسایل فنی. خطاهای فاحش کاملاً غیرقابل قبول هستند و باید با انجام اندازه گیری های مکرر و اضافی کاملاً از نتایج اندازه گیری حذف شوند.
خطاهای اندازه گیری سیستماتیک یک جزء ثابت همراه با نقص است: بینایی، نقص تجهیزات فنی، دما. خطاهای سیستماتیک می توانند یک طرفه یا متغیر (خطاهای دوره ای) باشند. آنها در صورت امکان تلاش می کنند تا هنگام سازماندهی و انجام کار، آنها را در نظر بگیرند یا از نتایج اندازه گیری حذف کنند.
خطاهای اندازه گیری تصادفی ناگزیر با تمام اندازه گیری ها همراه است. خطاهای تصادفی را نمی توان حذف کرد، اما تأثیر آنها بر نتیجه مطلوب را می توان با انجام اندازه گیری های اضافی تضعیف کرد. اینها موذیانه ترین خطاهایی هستند که همه اندازه گیری ها را همراهی می کنند. آنها می توانند هم از نظر اندازه و هم از نظر علامت متفاوت باشند.
اگر بتوان خطاهای فاحش و سیستماتیک را مطالعه کرد و از نتیجه اندازه گیری حذف کرد، آنگاه می توان خطاهای تصادفی را بر اساس اندازه گیری های عمیق در نظر گرفت. مطالعه بر اساس نظریه احتمال.
در عمل، مشکل در این واقعیت است که اندازه‌گیری‌ها تا حدی انجام می‌شوند تعداد محدودبارها و بنابراین، برای ارزیابی دقت اندازه‌گیری‌ها، از تخمین تقریبی انحراف استاندارد استفاده می‌شود که به آن خطای ریشه میانگین مربع (RMS) می‌گویند.
گاوس فرمولی را برای خطای ریشه میانگین مربع پیشنهاد کرد:
∆ 2 av = (∆ 2 1 + ∆ 2 2 +… +∆ 2 n) / n،
∆ 2 = m 2 = (∆ 2 1 + ∆ 2 2 +... +∆ 2 n) / n،
∆ av = m = √(∑∆ 2 i / n)
این فرمول زمانی اعمال می شود که خطاها از مقادیر واقعی محاسبه شوند.
فرمول بسل:
m = √(∑V 2 i / (n-1))
ریشه میانگین مربعات خطای میانگین حسابی یک بار کمتر از ریشه میانگین مربعات خطای یک اندازه گیری فردی است.
هنگام ارزیابی، میانگین مربعات خطا با وزن برابر یک به عنوان واحد دقت استفاده می شود. به آن میانگین مربعات خطای واحد وزن می گویند.
µ2 = P×m 2 – µ = m√P، m = µ / √P، یعنی. ریشه میانگین مربعات خطای هر نتیجه اندازه گیری برابر است با خطای اندازه گیری با وزن 1 (μ) تقسیم بر ریشه دوم وزن این نتیجه (P).
با تعداد کافی اندازه گیری، می توانیم ∑m 2 P=∑∆ 2 P بنویسیم (زیرا ∆ = m):
µ = √(∑(∆ 2 ×P)/n)، یعنی. میانگین مربعات خطای اندازه گیری با وزنی برابر با 1 برابر است با جذر کسری که در صورت شمار آن مجموع حاصل ضرب مجذور خطاهای مطلق اندازه گیری های نابرابر و وزن آنها است و در عدد مخرج تعداد اندازه گیری های نابرابر است.
ریشه میانگین مربعات خطای میانگین حسابی طبق فرمول:
M 0 = µ / √∑P
با جایگزینی مقدار آن به جای µ، دریافت می کنیم:
M 0 = √(∑∆ 2 ×P/n) / (√∑P) = √[(∑∆ 2 ×P) / n×(∑P)]
M 0 = √[ (∆ 1 2 P 1 + ∆ 2 2 P 2 +… + ∆ n 2 P n) / n×(P 1 + P 2 + … + P n) ] - فرمول گاوس، میانگین مربعات خطای مجموع میانگین حسابی برابر است با جذر کسری که صورت آن مجموع حاصل ضرب مجذور خطاهای اندازه گیری های نامساوی و وزن آنها و مخرج حاصل ضرب تعداد اندازه گیری ها و مجموع وزن آنها
μ = √ [∑(V 2 ×P) / (n-1)] این فرمول بسل برای محاسبه میانگین است. خطای حسابیبا اندازه گیری وزن برابر با 1 برای تعدادی از اندازه گیری های نابرابر با توجه به محتمل ترین خطاهای آنها. این برای تعداد زیادی اندازه گیری معتبر است، اما برای تعداد محدودی (اغلب در عمل) دارای خطاهایی است: m μ = µ / قابلیت اطمینان تخمین µ است.
تکلیف تست 1
برای مطالعه تئودولیت، او بارها و بارها همان زاویه را اندازه گرفت. نتایج به شرح زیر بود: 39˚17.4 اینچ؛ 39˚16.8 اینچ؛ 39˚16.6"؛ 39˚16.2"؛ 39˚15.5"؛ 39˚15.8"؛ 39˚16.3 اینچ؛ 39˚16.2 اینچ همین زاویه با یک گونیومتر با دقت بالا اندازه گیری شد که نتیجه آن 39˚16 "42" بود. با در نظر گرفتن این مقدار به عنوان دقیق، میانگین مربع خطا را محاسبه کنید، قابلیت اطمینان SKP را تعیین کنید و حداکثر خطا را پیدا کنید.
| شماره اندازه گیری | نتایج اندازه گیری، l | خطاها | ∆2 |
| 1 | 39˚17.4 اینچ | +0.7" | 0.49 |
| 2 | 16.8 | +0.1 | 0.01 |
| 3 | 16.6 | -0.1 | 0.01 |
| 4 | 16.2 | -0.5 | 0.25 |
| 5 | 15.5 | -1.2 | 1.44 |
| 6 | 15.8 | -0.9 | 0.81 |
| 7 | 16.3 | -0.4 | 0.16 |
| 8 | 16.2 | -0.5 | 0.25 |
| مجموع | 3.42 |
39˚16"42" = 39˚16.7"
ریشه میانگین مربعات خطا: m = √([∆ 2 ]/n)،
m = √(3.42/8) = 0.65 اینچ
ارزیابی قابلیت اطمینان SKP: m m = m / √2n،
m m = 0.65 / √16=0.1625≈0.16 اینچ
خطای حد: ∆pr = 3×m،
∆ pr = 3×0.65" = 1.96"
تکلیف تست 2
مجموعه ای از باقیمانده مثلث های مثلثی با حجم 50 واحد آورده شده است. با در نظر گرفتن باقیمانده ها به عنوان خطاهای واقعی، میانگین مربع خطا را محاسبه کنید و قابلیت اطمینان SKP را تولید کنید، حداکثر خطا را محاسبه کنید. با استفاده از این جمعیت، ویژگی خطاهای تصادفی را بررسی کنید:
Lim[∆] / n = 0، که W = [W] / n را محاسبه کنید.
| ن | دبلیو | ن | دبلیو | ن | دبلیو | ن | دبلیو | ن | دبلیو |
| 1 | +1,02 | 11 | -1,72 | 21 | -0,90 | 31 | +2,80 | 41 | -0,44 |
| 2 | +0,41 | 12 | +1,29 | 22 | +1,22 | 32 | -0,81 | 42 | -0,28 |
| 3 | +0,02 | 13 | -1,81 | 23 | -1,84 | 33 | +1,04 | 43 | -0,75 |
| 4 | -1,88 | 14 | -0,08 | 24 | -0,44 | 34 | +0,42 | 44 | -0,80 |
| 5 | -1,44 | 15 | -0,50 | 25 | +0,18 | 35 | +0,68 | 45 | -0,95 |
| 6 | -0,25 | 16 | -1,89 | 26 | -0,08 | 36 | +0,55 | 46 | -0,58 |
| 7 | +0,12 | 17 | +0,72 | 27 | -1,11 | 37 | +0,22 | 47 | +1,60 |
| 8 | +0,22 | 18 | +0,24 | 28 | +2,51 | 38 | +1,67 | 48 | +1,85 |
| 9 | -1,05 | 19 | -0,13 | 29 | -1,16 | 39 | +0,11 | 49 | +2,22 |
| 10 | +0,56 | 20 | +0,59 | 30 | +1,65 | 40 | +2,08 | 50 | -2,59 |
W = [W] / n، W = +2.51 / 50 = 0.05
در این مورد، توصیه می شود ریشه میانگین مربعات خطا را با استفاده از فرمول محاسبه کنید: m = √( – [W] 2 /n) ÷ (n-1)،
m = √(76.5703 - (2.51 2)/50) ÷ 49 = 1.249
ارزیابی قابلیت اطمینان SKP با استفاده از فرمول: m m = m / √2 (n-1)،
m m = 1.249/ √(2×49) = 0.13.
حداکثر خطا طبق فرمول: ∆ pr = 3×m،
∆ pr = 3×1.249= 3.747.
کار تست 5 فاصله SKP محاسبه شده با فرمول را تعیین کنید
S = √(x 2 - x 1) 2 + (y 2 - y 1) 2
اگر x 2 = 6,068,740 متر؛ y 2 = 431,295 متر;
x 1 = 6,068,500 متر؛ y 2 = 431 248 m;
m x = m y = 0.1 متر.
S =√(6,068,740 - 6,068,500) 2 + (431,295 - 431,248) 2 =235.36
m m = 0.1 / √4 = 0.05
تکلیف آزمایشی 6
همان زاویه 5 بار با نتایج: 60˚41"; 60˚40" اندازه گیری شد. 60˚40"؛ 60˚42"؛ 60˚41". تولید کنید پردازش ریاضیاین سری از نتایج اندازه گیری
| Np/p | ل، ˚ | ε, " | v" | v2" |
| 1 | 60˚41" | 1 | -0,2 | 0,04 |
| 2 | 60˚40" | 0 | +0,8 | 0,64 |
| 3 | 60˚40" | 0 | +0,8 | 0,64 |
| 4 | 60˚42" | 2 | -1,2 | 1,44 |
| 5 | 60˚41" | 1 | -0,2 | 0,04 |
| مجموع | 4 | 0 | 2,8 |
l 0 - حداقل مقدار کمیت اندازه گیری شده، l 0 = 60˚40"؛ ε - باقیمانده، به دست آمده به صورت ε = l 1 - l 0؛ L - بهترین ارزشکمیت اندازه گیری شده
L = [l]/n; m = √([ v 2 ]/(n – 1)، که در آن v انحراف از میانگین حسابی است. M تخمینی از دقت میانگین حسابی است، M = m/√n.
L = 60˚40 اینچ + 4/5 = 60˚40.8 اینچ
m = √2.8 / 4 = 0.7 اینچ
M = 0.7"/√5 = 0.313"
تکلیف تست 7
پردازش ریاضی نتایج اندازه گیری مساحت همان کانتور را با پلان متر انجام دهید: 26.31. 26.28; 26.32; 26.26; 26.31 هکتار.
| Np/p | ل، ها | ε، ها | v، ha | v2, ha |
| 1 | 26,31 | 0,05 | -0,014 | 0,000196 |
| 2 | 26,28 | 0,02 | +0,016 | 0,000256 |
| 3 | 26,32 | 0,06 | -0,024 | 0,000576 |
| 4 | 26,26 | 0 | 0,036 | 0,001296 |
| 5 | 26,31 | 0,05 | -0,014 | 0,000576 |
| مجموع | 0,18 | 0 | 0,0029 |
L = 26.26 + 0.18/5 = 26.296 هکتار
m = √0.0029/ 4 = 0.0269 هکتار
M = 0.0269/√5 = 0.01204 هکتار
تکلیف تست 8
هنگام مطالعه تقسیمات سانتی متری یک میله تسطیح با استفاده از خط کش ژنو، دما در زمان تهیه گزارش تعیین شد. برای بخش های پنج سانتی متری مقادیر زیر به دست آمد: 20.3˚; 19.9˚; 20.1˚; 20.2˚; 20.3 درجه پردازش ریاضی نتایج اندازه گیری را انجام دهید.
| Np/p | ل، ˚ | ε, ˚ | v، ˚ | v2، ˚ |
| 1 | 20,3 | 0,4 | -0,14 | 0,0196 |
| 2 | 19,9 | 0 | -0,26 | 0,0676 |
| 3 | 20,1 | 0,2 | -0,06 | 0,0036 |
| 4 | 20,2 | 0,3 | 0,04 | 0,0024 |
| 5
آنها ضروری به نظر نمی رسند ، اگر این از نظر زمان صرف شده توجیه شود ، ابزار باید به صورت دستی توسعه یابد منابع مادی. 2. پردازش اندازه گیری های ژئودزی با استفاده از صفحات گسترده برای پردازش اولیه اطلاعات به دست آمده در نتیجه مجموعه ای از کارهای توپوگرافی و ژئودزی از برنامه “TOGI” استفاده کردم که یک بسته ...
در محل ساخت و ساز، رعایت الزامات استانداردها و مقررات ایمنی مندرج در فصل SNiP Sh-4-80 "ایمنی در ساخت و ساز" و دستورالعمل های بخش ضروری است. افرادی که تحت دستورات صادره از بخش ساخت و ساز قرار گرفته اند مجاز به انجام کارهای ژئودتیکی هستند. خطر آسیب یا آسیب به شرایط کار بستگی دارد...
دستگاه های الکترونیکی با مشارکت مستقیم نویسنده. فصل دوم. فصل دوم روش‌های توسعه‌یافته برای انجام تحقیقات بر روی تاسیسات اندازه‌شناسی و مخفف بررسی و کالیبره کردن ابزارهای ژئودزیکی برای اندازه‌گیری ارتفاعات را مورد بحث قرار می‌دهد. روش بررسی خطای دوره کوتاه در اندازه گیری زوایای عمودی ابزارهای ژئودزی. یک کار مهم هنگام تحقیق ... |
در اینجا میانگین دیگری وجود دارد که با خطا همراه است.
میانگین مربعات خطا(SKP) اندازه گیری دقت نتایج اندازه گیری یا توابع کمیت های اندازه گیری شده است و یک مشخصه احتمالی است.
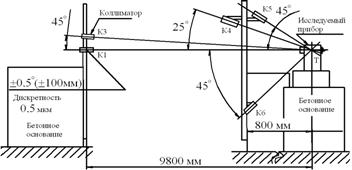
برنج. 3.1. قانون توزیع عادی
خطاهای تصادفی
بیایید فرض کنیم که مقدار میانگین مربعات خطا را می دانیم متر. مطابق با قانون توزیع نرمال، نمودار توزیع خطاهای واقعی بر اساس نوع مشابه نمودار در شکل 1 خواهد بود. 3.1. پارامتر rفراوانی (یا فرکانس) وقوع خطاهای تصادفی یک یا آن بزرگی و علامت را مشخص می کند. در این مورد، احتمال وقوع خطا در یک محدوده از پیش تعیین شده، به عنوان مثال، ± متر، توسط مساحت شکل تعیین می شود که توسط منحنی توزیع و قطعات ارتین در مقادیر + محدود می شود. مترو - متر. برای یک قانون توزیع نرمال، احتمال وقوع خطا در محدوده های تعیین شده برابر با مقادیر زیر است:
برای محدوده ± متر ® آر= 68.3% (» 68%);
برای محدوده 2± متر® آر= 95.5% (» 95%);
برای محدوده 3± متر® آر= 99.7٪ (تقریباً 100٪).
بنابراین، تنها در 3 مورد از 1000 می تواند یک خطا از مقدار 3 بیشتر شود متر. خطاهای بیش از 3 در مقدار مطلق متر(حداکثر خطا) خشن در نظر گرفته می شود و نتایج اندازه گیری حاوی این خطای فاحش از پردازش بیشتر حذف می شود. در برخی موارد، برای سخت تر کردن الزامات دقت اندازه گیری، حداکثر خطا در محدوده 2 تنظیم می شود. مترتا 3 متر.
جدول 3.1
مقادیر ضرایب دانش آموز ( تی) برای احتمالات مختلف ( آر)
| تی | پ% | تی | پ% | تی | پ% |
| 0,1 | 8,0 | 1,1 | 72,9 | 2,1 | 96,4 |
| 0,2 | 15,9 | 1,2 | 77,0 | 2,2 | 97,2 |
| 0,3 | 23,6 | 1,3 | 80,6 | 2,3 | 97,9 |
| 0,4 | 31,1 | 1,4 | 83,8 | 2,4 | 98,4 |
| 0,5 | 38,3 | 1,5 | 86,6 | 2,5 | 98,8 |
| 0,6 | 45,1 | 1,6 | 89,0 | 2,6 | 99,1 |
| 0,7 | 51,6 | 1,7 | 91,1 | 2,7 | 99,3 |
| 0,8 | 57,6 | 1,8 | 92,8 | 2,8 | 99,5 |
| 0,9 | 63,2 | 1,9 | 94,3 | 2,9 | 99,6 |
| 1,0 | 68,3 | 2,0 | 95,5 | 3,0 | 99,7 |
اغلب مقدار SKP با یک ضریب نشان داده می شود تی (ضریب دانش آموزی) که فاصله احتمال اطمینان را تعیین می کند ( ایکس± tm) نتیجه اندازه گیری در سطح مشخصی از احتمال آر. برای این کار استفاده از جدول راحت است. 3.1.
مثلاً باید تعیین کرد فاصله اطمینانبرای ارزش ایکسبا احتمال 90 درصد. از جدول، با درون یابی می یابیم که برای P 1 = 89,0% t 1= 1.6، برای R 2 = 91,1% t 2 = 1,7: t x= 1.6476 » 1.65.
این بدان معنی است که نتیجه اندازه گیری با احتمال 90٪ در محدوده ( ایکس 1.65 ± متر).
اگر کمیت اندازه گیری شده ایکسشناخته شده است، سپس مقدار SKP توسط تعیین می شود فرمول گاوس:
جایی که Δ - خطاهای اندازه گیری واقعی.
به یاد بیاورید که علامت [...] علامت مجموع گاوسی است.
برای مواردی که کمیت اندازه گیری شده ناشناخته است، استفاده کنید فرمول بسل:
جایی که v- انحراف نتایج اندازه گیری از میانگین حسابی.
همانطور که از فرمول های (3.9) و (3.10) مشاهده می شود، در صورتی که کمیت اندازه گیری شده مشخص باشد، یک اندازه گیری برای ارزیابی دقت کافی است (الزامی است). همانطور که در بالا ذکر شد، اغلب از فرمول گاوس برای ارزیابی دقت ابزار استاندارد هنگام اندازه گیری مقادیر شناخته شده (استاندارد) استفاده می شود. برای ارزیابی دقت با استفاده از فرمول بسل، حداقل دو اندازه گیری لازم است. فرمول بسل برای ارزیابی دقت نتایج اندازه گیری جرم (چندین) یک کمیت که از قبل ناشناخته است استفاده می شود.
با افزایش تعداد اندازه گیری ها، مقادیر SCP به دست آمده با استفاده از فرمول های گاوس و بسل تقریباً یکسان می شوند (با تقریباً n³ 20). در این حالت، مقدار SCP یک بعد به سمت حد میل می کند متر قبل، که با دقت دستگاه، دقت روش اندازه گیری یا برنامه مشخص می شود. بدیهی است که قبلاً در بالا گفته شد که در عمل به دلایلی غیرممکن و حتی نامناسب است که بتوان تعداد بسیار زیادی اندازه گیری از یک کمیت را ارائه داد. در این حالت، تعداد عملی اندازه‌گیری‌ها باید تضمین کند که نتیجه اندازه‌گیری با دقت معین در سطح اطمینان مشخص به دست می‌آید.
از آنجایی که تعداد اندازه‌گیری‌ها محدود است، SCP خود حاوی خطایی است که با فرمول تقریبی تعیین می‌شود:
این همان چیزی است که به آن می گویند - میانگین مربعات خطای میانگین مربعات خطا (RMSE).
در اینجا مناسب است که به طبقه بندی خطاها برگردیم. همه انواع خطاها در بالا مورد بحث قرار نگرفته اند.
اغلب، هنگام مطالعه مجموعه ای از خطاهای اندازه گیری، به اصطلاح خطای احتمالی، که با حرف مشخص می شود r. بزرگی خطای احتمالی را می توان با استفاده از فرمول تقریبی تخمین زد
البته با این فرض که توزیع خطاها از قانون عادی تبعیت می کند.
خطای احتمالی نیز نامیده می شود خطای میانه. اگر نمی خواهید محاسبات را با استفاده از فرمول (3.12) انجام دهید، زیرا شامل مقدار است متر، که باید با استفاده از فرمول بسل به دست آید، سپس با مرتب کردن یک سری خطا به ترتیب افزایش مقادیر مطلق می توان خطای احتمالی یا میانه را تعیین کرد. مقدار این خطا در وسط سری حاصل قرار خواهد گرفت. این در صورتی است که تعداد خطاها فرد باشد. و اگر زوج باشد، خطای میانه میانگین مقدار خطاهای مجاور در وسط سری خواهد بود.
خطای میانه را نباید با اشتباه گرفت میانگین خطای v o، که با استفاده از یک فرمول ساده نیز می توان به دست آورد:
در اینجا، برای تعدادی از اندازه‌گیری‌ها (خطاها) برای رعایت قانون عادی شرطی نیز لازم است.
میانگین خطا است انتظارات ریاضی ارزش های مطلقانحراف نتایج اندازه گیری با هر مقدار از انتظارات ریاضی برای این نتایج. مقدار تقریبی میانگین خطا را می توان با استفاده از فرمول تخمین زد:
جایی که v i- انحراف نتایج اندازه گیری از میانگین حسابی آنها.
فرمول (3.13) اغلب برای برآورد اولیه میانگین مربعات خطا استفاده می شود.
خطاهای تصادفی آن دسته از خطاهایی هستند که اندازه و ماهیت تأثیر آنها بر هر نتیجه اندازه گیری مجزا ناشناخته باقی می ماند. بزرگی و علامت خطاهای تصادفی را نمی توان از قبل تعیین کرد. آنها اجتناب ناپذیر هستند و هر اندازه گیری را همراهی می کنند، زیرا ما اندازه گیری ها را فقط با چنان دقتی انجام می دهیم که می توان با ابزارهای مورد استفاده به دست آورد. حذف کامل نتایج اندازه گیری از خطاهای تصادفی غیرممکن است. اما بر اساس مطالعه خواص آنها، می توان قوانینی را در مورد چگونگی به دست آوردن مطمئن ترین نتایج از تعدادی از اندازه گیری ها استخراج کرد و دقت آنها را ارزیابی کرد. تئوری خطاهای اندازه گیری به این مسائل می پردازد.
در تئوری خطاها، بین اندازه گیری های دقیق یکسان و نابرابر تمایز قائل می شوند. اندازه‌گیری‌هایی که در شرایط یکسان، با ابزارهایی با دقت یکسان، تعداد دفعات یکسان و توسط ناظرانی با شرایط یکسان انجام می‌شوند، اندازه‌گیری‌های معادل نامیده می‌شوند. اگر یکی از این شرایط برآورده نشود، این اندازه گیری ها نادرست خواهند بود.
ویژگی های خطاهای تصادفی خطاهای تصادفی را می توان به عنوان تفاوت بین مقادیر اندازه گیری شده و واقعی همان کمیت تعریف کرد. بر اساس مطالعه نظری و عملی بسیاری از سری از خطاهای تصادفی، ویژگی های کلی آنها به دست می آید:
1 در این شرایط، خطاهای تصادفی نمی توانند از حد معینی تجاوز کنند.
2 خطاهای مثبت و منفی با مقدار مطلق یکسان به یک اندازه امکان پذیر است.
3 خطاهایی که از نظر قدر مطلق کوچکتر هستند نسبت به خطاهای بزرگتر رایج هستند.
4 میانگین حسابی خطاهای تصادفی اندازه گیری های به همان اندازه دقیق با همان کمیت با افزایش نامحدود در تعداد اندازه گیری ها به صفر نزدیک می شود.
4.2 اصل میانگین حسابی
اجازه دهید اندازه گیری های دقیق برابر با l 1، l 2، ...، l n از همان کمیت انجام شود که مقدار واقعی آن X است. سپس می توانیم n مقدار خطای تصادفی را محاسبه کنیم:
Δ 1 = l 1 - X;
Δ 2 = l 2 - X; (4.1)
Δ n = l n – X.
با اضافه کردن سمت چپ و راست این برابری ها، به دست می آوریم
Δ 1 + Δ 2 +…+ Δ n = l 1 + l 2 +…+ l n – nX. (4.2)
در تئوری خطا، مرسوم است که مجموع مقادیر را از طریق کروشه نشان دهیم، به عنوان مثال:
Δ 1 + Δ 2 + … + Δ n = [Δ]; l 1 + l 2 + … + l n = [l] و غیره.
با این نمادها، برابری (4.2) شکل می گیرد
[Δ] = [l] – nX، از آنجا X = [l] / n – [Δ] / n. (4.3)
با توجه به ویژگی چهارم خطاهای تصادفی، مقدار [Δ] / n در برابری (4.3) با افزایش نامحدود در تعداد اندازه‌گیری‌ها به صفر می‌رود. در نتیجه، مقدار [l] / n در این شرایط به مقدار واقعی X نزدیک می شود. بر این اساس، میانگین حسابی (میانگین حسابی نتایج اندازه گیری) قابل اطمینان ترین یا محتمل ترین نتیجه از اندازه گیری های معادل در نظر گرفته می شود. به همان مقدار برای هر تعداد اندازه گیری.
L = [l] / n = (l 1 + l 2 + l 3 + … + l n) / n. (4.4)
4.3 میانگین مربعات خطای یک اندازه گیری.
فرمول های گاوس و بسل
در تئوری خطاها، دقت اندازه گیری با میانگین مربعات خطا مشخص می شود که توسط ریاضیدان و نقشه بردار مشهور آلمانی K. F. Gauss (1777-1855) معرفی شد و با m نشان داده می شود:
______________________ ______
m = ± √ (Δ 1 2 + Δ 2 2 + .. + Δ n 2) / n = ± √ [Δ 2 ] / n، (4.5)
که در آن Δ 1، Δ 2، ...، Δ n - خطاهای تصادفی.
n - تعداد اندازه گیری ها.
ریشه میانگین مربعات خطا یک معیار قابل اعتماد برای ارزیابی دقت اندازه گیری است. حتی با تعداد کمی از اندازه گیری ها کاملاً پایدار است و حضور بزرگ را به خوبی نشان می دهد خطاهای تصادفی، که اساساً کیفیت اندازه گیری ها را تعیین می کند.
زمانی که مقدار واقعی مقدار اندازه گیری شده مشخص باشد، از فرمول (4.5) برای محاسبه میانگین مربعات خطا استفاده می شود. این موارد در عمل بسیار نادر است. به عنوان یک قاعده، مقدار واقعی مقدار اندازه گیری شده ناشناخته است، اما از اندازه گیری ها می توان مطمئن ترین نتیجه را به دست آورد - میانگین حسابی. اجازه دهید فرمولی برای محاسبه میانگین مربعات خطا با استفاده از انحراف نتایج فردی از میانگین حسابی با استفاده از به اصطلاح محتمل ترین خطاهای V بدست آوریم.
فرض کنید l 1، l 2، ...، l n نتایج اندازه گیری های معادل با همان کمیت باشد که مقدار واقعی آن X و میانگین حسابی L است. سپس n خطای تصادفی یا واقعی را می توان محاسبه کرد.
Δ i = l i – X (4.6)
و n خطای محتمل
V i = l i – L. (4.7)
جمع n برابری (4.7)
[V] = [l] - nL. (4.8)
اما، با توجه به برابری (4.4) nL = [l]، بنابراین
یعنی مجموع محتمل ترین خطاها همیشه باید برابر با صفر باشد.
با کم کردن برابری (4.7) از برابری (4.6)، به دست می‌آییم
Δ i – V i = L – X. (4.10)
در سمت راست برابری (4.10) یک خطای تصادفی در میانگین حسابی داریم. اجازه دهید آن را با ε نشان دهیم. سپس
Δi = V i + ε. (4.11)
اجازه دهید برابری (4.11) را مجذور کنیم، مجموع آنها را گرفته و بر n تقسیم کنیم:
[Δ 2 ] / n = / n + nε 2 / n + 2ε[V] / n. (4.12)
سمت چپ این برابری چیزی بیش از m 2 نیست. به دلیل برابری (4.9)، آخرین جمله در سمت راست برابر با صفر است.
m 2 = / n + ε 2. (4.13)
اجازه دهید خطای تصادفی ε را با مقدار میانگین آن جایگزین کنیم، یعنی میانگین مربعات خطای میانگین حسابی. در ذیل آن ثابت خواهد شد میانگین مربعات خطای میانگین حسابی
M 2 = ε 2 = m 2 / n. (4.14)
m 2 - m 2 / n = / n یا m 2 (n - 1) / n = / n،
جایی که ___________
m 2 = / (n – 1)، یا m = √ / (n – 1). (4.15)
فرمول (4.15) نامیده می شود فرمول بسلو عالی دارد اهمیت عملی. این به شما امکان می دهد ریشه میانگین مربعات خطا را بر اساس محتمل ترین انحرافات نتایج اندازه گیری از میانگین حسابی محاسبه کنید.
علاوه بر میانگین مربعات خطا، خطاهای متوسط، احتمالی و نسبی نیز وجود دارد.
میانگین خطای (Θ) میانگین حسابی مقادیر مطلق خطاهای تصادفی است، یعنی.
Θ = (|Δ 1 | + |Δ 2 | + … + |Δ n |) / n = [|Δ|] / n. (4.16)
در تئوری خطا ثابت شده است که وقتی n → ∞ Θ = 0.8 m، یا m = 1.25Θ.
گاهی در سوالات کاربردی استفاده می کنند خطای احتمالی r خطای احتمالی مقدار یک خطای تصادفی در یک سری اندازه گیری با دقت برابر است که در رابطه با آن خطای بزرگتر و کمتر از این مقدار در مقدار مطلق به همان اندازه ممکن است. برای یافتن r، تمام خطاهای یک سری داده شده به ترتیب صعودی در مقدار مطلق مرتب می شوند و مقداری که موقعیت وسط را اشغال می کند انتخاب می شود، یعنی به تعداد خطاها کمتر از آن وجود دارد. خطای احتمالی با نسبت r = 2/3 m = 0.67 m یا m = 1.5 r به میانگین مربعات خطا مربوط می شود.
همانطور که مشاهده می شود m > Θ و m > r که نشان می دهد میانگین مربعات خطا بهتر از خطاهای متوسط و احتمالی دقت اندازه گیری ها را مشخص می کند.
دقت کمیت های اندازه گیری شده مانند خطوط، مساحت ها و حجم ها اغلب با استفاده از آن ارزیابی می شود خطای مربوطه. خطای نسبی نسبت خطای مطلق به مقدار کمیت اندازه گیری شده است. خطای نسبی به صورت کسری نوشته می شود که صورت آن یک است و مخرج عددی است که نشان می دهد چه نسبتی از مقدار اندازه گیری شده باید خطای مجاز باشد. به عنوان مثال، طول ضلع D = 150 متر از اندازه گیری شده است خطای مطلق m d = 0.05 m. سپس خطای نسبی نتیجه اندازه گیری m d / D = 0.05 m / 150 m = 1 / 3000 خواهد بود.
مقدار 1/3000 به این معنی است که در فاصله 3000 متری می توان خطای 1 متری را مجاز دانست، هر چه مخرج خطای نسبی بزرگتر باشد، دقت اندازه گیری ها بیشتر می شود. دقت تمام اندازه گیری های خطی در ژئودزی همیشه مشخص است خطای مربوطه، که در دستورالعمل ها و دستورالعمل های مربوطه برای تولید این نوع کارهای ژئودزی آورده شده است.
4.4 قانون توزیع نرمال خطاها.
حداکثر خطا
از بررسی قبلی در مورد ویژگی های خطاهای تصادفی، نتیجه می شود که نمی توان از قبل چیزی قطعی در مورد ظاهر یک خطای جداگانه گفت. با این حال، هنگامی که تعداد این خطاها افزایش می یابد، می توان الگوهای خاصی را برای کل مجموعه خطاهای یک سری اندازه گیری معین ایجاد کرد. این الگوها را می توان با معادله به دست آمده توسط K. F. Gauss بیان کرد. به نظر می رسد
y = (1 / σ √2π) e – (l i – a) / 2 σ = (1 /σ √2π) e – Δ c / 2 σ، (4.17)
که در آن y چگالی توزیع خطا است.
σ – پارامتر معادله که استاندارد نامیده می شود به میانگین مربوط می شود
نسبت خطای مربعی
a پارامتر معادله ای است به نام انتظار ریاضی،
با رابطه به میانگین حسابی مربوط می شود
e – پایه لگاریتم های طبیعی;
Δ i = l i – a – خطای تصادفی.
این معادله نامیده می شود قانون توزیع نرمالخطاها
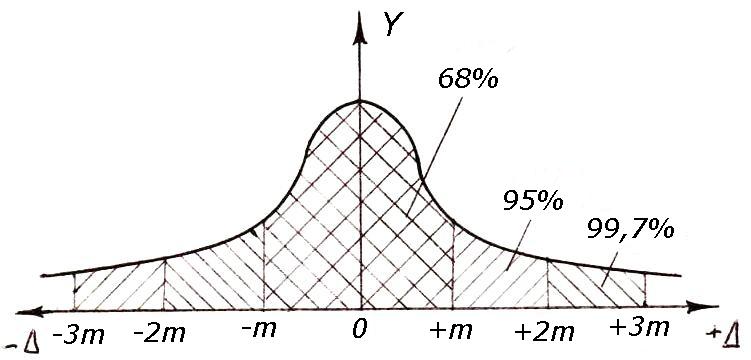
معادله (4.17) مربوط به یک منحنی زنگی شکل است که منحنی توزیع نرمال (منحنی گاوسی) نامیده می شود (شکل 4.1).
شکل 4.1 - منحنی گاوسی
مساحت زیر منحنی، محدود به منحنی و محور x، برابر با یک در نظر گرفته می شود. بخشی از این ناحیه که مربوط به هر بخش از محور آبسیسا است، احتمال سقوط یک خطای تصادفی در یک بازه معین را می دهد. برای l i = a یا Δ = 0 به دست می آوریم حداکثر مقدارمختصات منحنی __
Y = 1/σ √2π.
از شکل 4.1 واضح است که عمده خطاها حول محتمل ترین مقدار خطا Δ i = 0 گروه بندی می شوند (طبق ویژگی چهارم خطاهای تصادفی، میانگین حسابی خطاهای تصادفی به صفر میل می کند). این موقعیت سومین ویژگی خطاهای تصادفی را توجیه می کند (خطاهای کوچک بیشتر از خطاهای بزرگ رخ می دهند). ویژگی دوم خطاهای تصادفی - وقوع مساوی خطاهای مثبت و منفی - با تقارن منحنی توزیع نرمال نسبت به محور OY مشخص می شود.
تحقیقات نظری و عملی اندازه‌گیری‌های زمین‌شناسی نشان می‌دهد که 68٪ از تمام خطاهای تصادفی در فواصل از -m تا +m رخ می‌دهند (شکل 4.1 را ببینید)، 95٪ خطاها در فاصله دو برابر بزرگتر (از -2m تا +2m) قرار می‌گیرند. و در فاصله سه برابر بزرگتر (از -3 متر تا +3 متر) در 99.73٪ از خطاها قرار می گیرد. این به این معنی است که از 100 خطای اندازه گیری، تنها 32 خطای قدر مطلق از ریشه میانگین مربعات خطای m بیشتر خواهد شد، 3 خطا از 1000 خطا از مقدار سه برابر خطای ریشه میانگین مربع ± 3 متر بیشتر خواهد شد. بنابراین، تنها 0.27٪ از خطاهای اندازه گیری فراتر از ± 3 متر است. بنابراین، سه برابر میانگین مربعات خطا به عنوان حداکثر خطا Δ در نظر گرفته می شود، یعنی.
Δpre = 3m. (4.18)
حال اجازه دهید ماهیت پارامترهای a و σ را در رابطه (4.17) در نظر بگیریم. پارامتر a انتظار ریاضی نامیده می شود و مرکز گروه بندی را در منحنی گاوس مشخص می کند، به عنوان مثال، جابجایی مرکز گروه بندی در امتداد محور آبسیسا (شکل 4.2، a) در حالی که شکل منحنی را حفظ می کند. اگر در مقدار ثابت پارامتر a، پارامتر دیگری σ (به نام استاندارد) را تغییر دهیم که دقت اندازه‌گیری‌ها را مشخص می‌کند و این در صورتی امکان‌پذیر است که روش اندازه‌گیری را تغییر دهیم یا آنها را با ابزارهای دیگر انجام دهیم. سپس مرکز گروه بندی بدون تغییر باقی می ماند، اما شکل منحنی تغییر می کند. اگر دقت اندازه گیری کاهش یابد صاف تر می شود و با افزایش دقت تندتر می شود (شکل 4.2، ب).
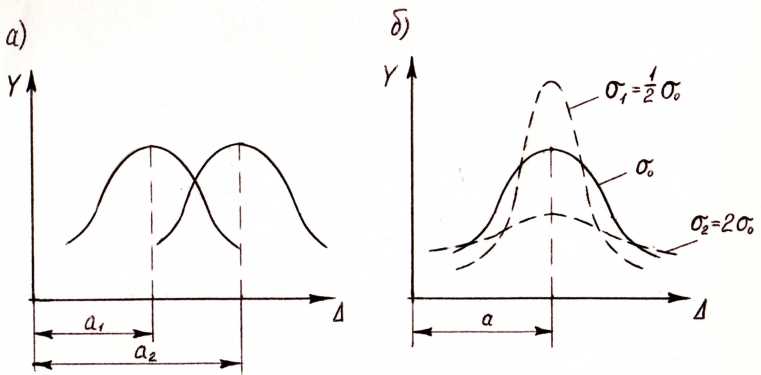
شکل 4.2 - تغییر مکان و تغییر شکل منحنی نرمال
پارامترهای a و σ از قبل، قبل از اندازه گیری ناشناخته هستند. در نتیجه به دست می آیند تعداد زیادیاندازه گیری ها در عمل، به جای پارامترهای a و σ، مقادیر تقریبی آنها را به دست می آوریم: میانگین حسابی L، محاسبه شده با استفاده از فرمول (4.4)، و میانگین مربع خطای m، محاسبه شده با استفاده از فرمول (4.5) یا (4.15).
4.5 ریشه میانگین مربعات خطای تابع
اندازه گیری کمیت ها
در ژئودزی، اغلب لازم است که دقت نه تنها خود مقادیر اندازه گیری شده، بلکه عملکرد آنها نیز تعیین شود. به عنوان مثال، موقعیت افقی یک خط تابعی از شیب فاصله و زاویه میل است، مساحت تعیین شده توسط پلان متر تابعی از قرائت های روی صفحه سنج و غیره است، بنابراین مهم است که بتوانیم برای محاسبه میانگین مربعات خطای توابع. بیایید به برخی از انواع توابع نگاه کنیم.
m = nm 2 یا m φ = m√ n، (4.27)
به عنوان مثال، میانگین مربعات خطای مجموع مقادیر به طور دقیق اندازه گیری شده √n برابر بیشتر از میانگین مربع خطای یک اندازه گیری فردی است.
مثال جذر میانگین مربعات خطای مجموع زوایای اندازه گیری شده در یک چهارضلعی را بیابید اگر ریشه میانگین مربعات خطای یک زاویه ± 30 "" باشد. با استفاده از فرمول (4.27) پیدا می کنیم
m φ = ± 30 "" √ 4 = ± 60 "" = 1 " .
2تابع خطی
که در آن K یک عدد ثابت است.
X آرگومانی است که از اندازه گیری ها به دست می آید.
اگر X با خطای تصادفی Δ X اندازه گیری شود، تابع یک خطای تصادفی خواهد داشت
Δ φ = K Δ X . (4.29)
پس از اندازه گیری آرگومان n بار، می توانید n معادله (4.29) ایجاد کنید، مجموع مربع های آنها را بگیرید و بر n تقسیم کنید. پس از آن می گیریم
[Δ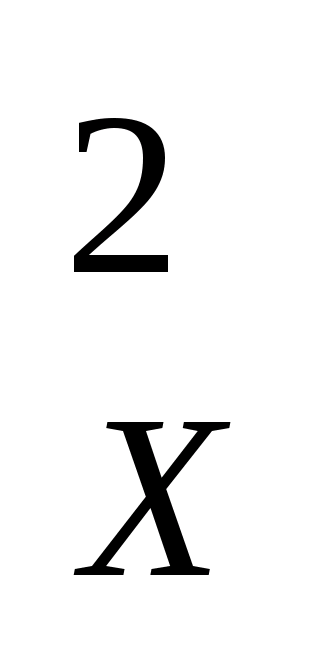 
] / n = K 2 [Δ] / n یا m = K 2 m، (4.30)
m φ = K m X . (4.31)
مشابه مورد قبلی، می توان نشان داد که برای تابع
φ = ± K 1 X ± K 2 Y ± … ± K n U (4.32)
Δφ = K 1 Δ X ± K 2 Δ Y ± … ± K n Δ U (4.33)
m= (K 1 m X) 2 + (K 2 m Y) 2 + … + (K n m U) 2 . (4.34)
مثال اگر میانگین مربعات خطای یک اندازه گیری منفرد برابر با m باشد، میانگین مربعات خطای M میانگین حسابی L را تعیین کنید. اجازه دهید فرمول (4.4) را برای میانگین حسابی به شکل زیر بنویسیم:
L = l 1 / n + l 2 / n + … + l n / n. (4.35)
همانطور که می بینید، در اینجا می توانید فرمول (4.34) را برای تابع (4.35) اعمال کنید:
متر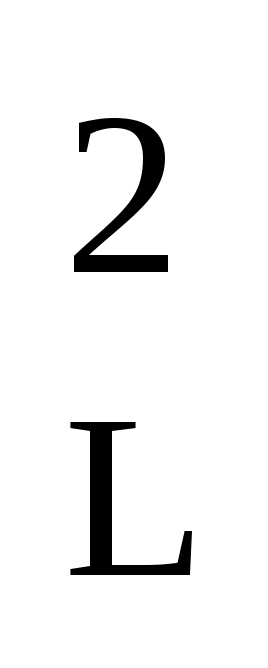 
= M 2 = (m 1 / n) 2 + (m 2 / n) 2 + ... + (m n / n) 2.
با توجه به اینکه اندازه گیری های l 1، l 2، ...، l n به یک اندازه دقیق هستند، یعنی m 1 = m 2 = … = m n، به دست می آوریم
M 2 = n(m / n) 2 = m 2 / n،
M = m / √n، (4.36)
یعنی میانگین مربعات خطای میانگین حسابی √n برابر کمتر از میانگین مربعات خطای یک اندازه گیری فردی است.
3تابع نمای کلی
φ = f (X، Y، Z، …، U)، (4.37)
که در آن X، Y، Z، …، U مقادیر مستقل اندازه گیری می شوند.
با در نظر گرفتن خطاهای تصادفی، تابع (4.37) شکل خواهد گرفت
φ + Δ φ = f (X + Δ X ؛ Y + Δ Y ؛ Z + Δ Z ؛ ...؛ U + Δ U). (4.38)
با گسترش تابع (4.38) به یک سری تیلور و محدود کردن خود به تنها قدرت های اولیه خطاهای تصادفی، تابع را به دست می آوریم.
Δ φ = (∂f/∂x) Δ X + (∂f/∂y) Δ Y + (∂f/∂z) Δ Z + … + (∂f/∂u) Δ U , (4.39)
که در آن (∂f/∂x)، (∂f/∂y)، …، (∂f/∂u) مشتقات جزئی هستند که برای تابع
(4.39) کمیت های ثابت هستند.
همانطور که مشاهده می شود، تابع (4.39) مشابه تابع (4.33) است. بنابراین، مربع میانگین مربعات خطای آن
= (∂f/∂x ∙ m X) 2 + (∂f/∂y ∙ m Y) 2 + (∂f/∂z ∙ m Z) 2 + … + (∂f/∂u ∙ m U) 2 . (4.40)
مثال دو ضلع در یک مستطیل اندازه گیری می شوند - X = 200 m و Y = 100 m با ریشه میانگین مربعات خطا m X = +0.20 m و m Y = + 0.10 m.
مساحت مستطیل P و میانگین مربع خطای آن را m P تعیین کنید.
.m = √ / 2n. (4.43)
فرمول (4.43) بیانی برای ریشه میانگین مربعات خطای یک اندازه گیری منفرد از n اندازه گیری دو برابری می دهد.
4.7 اندازه گیری های ناهموار
در بخش های قبل، اندازه گیری های با دقت برابر مورد بحث قرار گرفت. با این حال، در عمل، اغلب اندازه گیری های نابرابر انجام می شود که در شرایط مختلف یا با ابزارهایی با دقت متفاوت، با تعداد مراحل متفاوت انجام می شود. در این حالت، دیگر نمی توان خود را به یک میانگین حسابی ساده محدود کرد؛ در اینجا باید درجه قابلیت اطمینان هر نتیجه اندازه گیری را در نظر گرفت.
درجه قابلیت اطمینان یک نتیجه اندازه گیری که به صورت عدد بیان می شود، وزن این اندازه گیری نامیده می شود. هر چه نتیجه قابل اطمینان تر باشد، وزن آن بیشتر است. اجازه دهید یک سری مقادیر متوسط داشته باشیم: L 1، L 2، ...، L n - یک مقدار به دست آمده از اندازه گیری های فردی P 1، P 2، ...، Pn.
بر اساس فرمول (4.4)، حاصلضرب L i P i برابر با مجموع اندازه گیری های منفرد l i در یک سری معین خواهد بود و مجموع تمام اندازه گیری ها در همه سری ها برابر با L 1 P 1 + L 2 P 2 خواهد بود. + … + L n P n. تعداد تمام اندازه گیری ها برابر با P 1 + P 2 +… + P n خواهد بود.
از اینجا، با استفاده از قانون میانگین حسابی، مقدار میانگین را از تمام سری های اندازه گیری به دست می آوریم:
L o = (L 1 P 1 + L 2 P 2 + … + L n P n) / (P 1 + P 2 + … + P n) = / [P]. (4.44)
عبارت (4.44) نامیده می شود فرمول میانگین وزنیا میانگین حسابی رایج. در اینجا تعداد اندازه گیری های P 1، P 2، ...، P n در هر ردیف وزن میانگین نتایج L 1، L 2، ...، L n است و مجموع اوزان وزن است. حساب مشترک L o. در تمام مواردی که نتایج اندازه گیری و وزن آنها مشخص است، به احتمال زیاد معنیمقدار اندازه گیری شده با استفاده از فرمول (4.44) محاسبه می شود.
اجازه دهید ریشه میانگین مربعات خطای یک اندازه گیری را با μ و ریشه میانگین مربعات خطاهای مقادیر L 1 , L 2 ....L n را به ترتیب با m 1 , m 2 , …, m n نشان دهیم. سپس با توجه به برابری (4.36) می توان نوشت که ___ __ __
m 1 = μ / √ P 1 ; m 2 = μ / √ P 2 ; ...; m n = μ / √ P n . (4.45)
اگر در فرمول (4.45) P i = 1 را بگیریم، پس μ = m i. نتیجه می شود که μ ریشه میانگین مربعات خطای اندازه گیری است که وزن آن برابر با یک است یا به اصطلاح ریشه میانگین مربعات خطای یک واحد وزنی است.
کار درسیانواع خطاها.تقریباً همیشه، خطا شامل دو جزء است: سیستماتیک و تصادفی.
Δa= Δasystem + Δaran.
نظامخطا نامیده می شود که در شرایط معین ثابت می ماند (یا تغییر می کند، اما طبق یک قانون شناخته شده).
چنین خطاهایی دائما ایجاد می شود دلایل موثر، در نتیجه ، هنگام اندازه گیری ، هر بار به همان میزان "اشتباه" می کنیم. اغلب چنین خطاهایی ناشی از ساخت نادرست دستگاه (خطاهای ابزاری) یا ثابت است. عامل خارجی. به عنوان مثال میدان مغناطیسی خود هواپیما باعث ایجاد خطا در اندازه گیری مسیر مغناطیسی (انحراف) می شود که در هر مسیر مقدار بسیار خاصی دارد.
خطاهای سیستماتیک، از آنجایی که در هر اندازه گیری یکسان است، می توان یک بار با استفاده از ابزار دقیق تر تعیین کرد و سپس با انجام اصلاحات، از نتایج اندازه گیری حذف شد.
خطاهای سیستماتیک در هنگام ناوبری مشکل زیادی ایجاد نمی کنند، زیرا پس از حذف آنها دیگر وجود ندارند. بنابراین، ما بیشتر فرض خواهیم کرد که هیچ خطای سیستماتیک وجود ندارد (که قبلاً در نظر گرفته شده است).
خطای تصادفیبرای هر اندازه گیری می گیرد معنی متفاوت، و از قبل معلوم نیست کدام یک.
اما خطاهای تصادفی، در اصل، قابل حذف نیستند، زیرا برای هر اندازه گیری متفاوت هستند. و همیشه ناشناخته می مانند.
تعیین مقادیر عددی خطاهای تصادفی غیرممکن است، اما خلبان باید همیشه در نظر داشته باشد که این خطاها وجود دارد و ایده ای از مقادیر احتمالی آنها داشته باشد. وجود عدم قطعیت در نتایج اندازه گیری یکی از عوامل اصلی است که ناوبری را پیچیده می کند و آن را نه تنها یک علم، بلکه یک هنر نیز می کند.
رویداد تصادفی رویدادی است که در شرایط معین ممکن است رخ دهد یا نباشد. درجه احتمال وقوع چنین رویدادی از نظر عددی با مقدار احتمال مشخص می شود. احتمال P عددی است که می تواند از 0 تا 1 متغیر باشد. اگر در شرایط معین، رویدادی هرگز رخ ندهد، آن را رویداد غیرممکن می نامند و احتمال آن صفر است. اگر همیشه در شرایط معین رخ دهد، آن را قابل اعتماد می نامند و یک احتمال به آن نسبت می دهند. برابر با یک. برای مثال اگر P = 0.3 باشد، این بدان معناست که به طور متوسط در 30 مورد از 100 مورد، رویداد رخ می دهد. به طور متوسط است، زیرا رویداد تصادفی است. اگر شرایط لازم برای وقوع یک رویداد را ایجاد کنید و یک سری از 100 آزمایش انجام دهید، آن رویداد می تواند مثلاً 23 بار یا 32 بار رخ دهد ... اگر چندین سری از این آزمایش ها یا یک سری انجام دهید. از هزار، ده هزار، میلیون آزمایش، سپس هرچه آزمایش‌های بیشتری انجام شود، میانگین تعداد وقوع رویداد نزدیک‌تر به 30٪ از تعداد کل آزمایش‌ها خواهد بود (اگر P = 0.3).
چگونه می توانیم خطاهای تصادفی را توصیف کنیم اگر معنای خاصی ندارند؟ آنها اغلب با مقدار میانگین مربعات خطا (MSE) مشخص می شوند که با حرف σ (سیگما) نشان داده می شود. بنابراین، برای مثال، اندازه گیری SKP کمیت a را با σa نشان می دهیم.
SKP مشخصه درجه پراکندگی مقدار اندازه گیری شده یک کمیت حول مقدار واقعی آن است. هرچه σa بزرگتر باشد، اندازه گیری ها پراکنده تر (پراکنده) هستند تجربیات مختلفمقادیر حول ارزش واقعی کمیت.
در شکل 2.19 از نظر هندسی به عنوان یک محور عددی نشان داده می شود مقادیر ممکنکمیت اندازه گیری شده آو معنای واقعی آن ذکر شده است. تلاقی های روی مقیاس مقادیر اندازه گیری شده را نشان می دهد که در نتیجه چندین آزمایش به دست آمده است. در حالت اول، گسترش مقادیر اندازه گیری شده حول مقدار واقعی بیشتر از حالت دوم است، بنابراین "سیگما" که درجه گسترش را مشخص می کند، در حالت دوم کوچکتر است.
برنج. 2.19. میانگین مربعات خطا
بر اساس مقدار SKP می توان احتمالاتی را قضاوت کرد که مقدار اندازه گیری شده این یا مقدار دیگری را می گیرد. اما برای این کار، دانستن SKP کافی نیست؛ همچنین باید بدانید که این خطای تصادفی از چه قانون توزیع تبعیت می کند. بسیاری از متغیرهای تصادفی از قانون توزیع نرمال (گاوسی) تبعیت می کنند. برای این قانون، یادآوری معانی زیر مفید است.
اگر خطای سیستماتیکوجود ندارد و در نتیجه اندازه گیری مقدار ameas به دست آمد، سپس مقدار واقعی کمیت در محدوده ها قرار دارد (شکل 2.20):
aism ± σa با احتمال P = 0.68;
ameas ± 2σa با احتمال Р=0.95.
aism ± 3σa با احتمال P = 0.997.
برنج. 2.20. برخی احتمالات برای قانون توزیع نرمال
به عنوان مثال، با کمک یک قطب نما، مسیر γ = 100 درجه اندازه گیری می شود، و دقت قطب نما با SKP σγ = 2º مشخص می شود. این بدان معنی است که نرخ واقعی ارز (که برای ما ناشناخته خواهد ماند) میانگین:
در 68 مورد از 100 مورد، در 100º ± 2º قرار دارد، یعنی در محدوده 98º...102º.
در 95 مورد از 100 مورد، در محدوده 100º ± 4º قرار دارد، یعنی در محدوده 96º...104º.
در 997 مورد از 1000 مورد در 100º ± º قرار دارد، یعنی در محدوده 94º ... 106º قرار دارد.
مقدار احتمال آر 0.997 = آنقدر به وحدت نزدیک است که مقدار خطای سه سیگما مربوطه را اغلب حداکثر خطا می نامند. در واقع، خطا ممکن است از آن بیشتر باشد. درست است، به ندرت - به طور متوسط در سه مورد از هزار.
که در توضیحات فنیابزار و تجهیزات، دقت آنها را می توان مستقیماً در قالب UPC نشان داد و سپس همه چیز مشخص است. اما گاهی اوقات به عنوان مثال نشان داده می شود: "خطای اندازه گیری بلبرینگ ± 1.5 درجه". البته، این بدان معنا نیست که چنین جهت یاب هر بار 1.5 درجه "اشتباه" می کند. این همچنین به این معنی نیست که او نمی تواند اشتباه کند. بیشتر، نسبت به 1.5 درجه. به عنوان یک قاعده، مقدار خطای نشان داده شده در این روش با احتمال مطابقت دارد آر= 0.95. یعنی به طور متوسط در 95 مورد از 100 مورد، خطا از مقدار 1.5 درجه (بالا یا پایین) تجاوز نمی کند.
بر این اساس، در پنج مورد از صد مورد ممکن است خطا بیشتر باشد. برای یک قانون توزیع خطای عادی، احتمال 0.95 مطابقت دارد دو برابر شد UPC. بنابراین، UPC اندازه گیری بلبرینگ در این مثال 0.75 درجه خواهد بود.