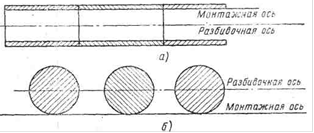
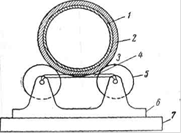
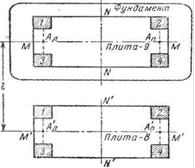
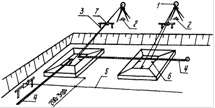
3.2 Klasifikácia chýb geodetických meraní. Priemerná štvorcová chyba. Gaussove a Besselove formy na jej výpočet
Geodetické merania vykonávané aj vo veľmi dobré podmienky, sú sprevádzané chybami, t.j. odchýlka výsledku merania L od skutočnej hodnoty X očíslovanej veličiny:
Pravda - taká hodnota meranej veličiny, ktorá by v ideálnom prípade odrážala kvantitatívne vlastnosti objektu. Nedosiahnuteľný stav - skutočnú hodnotu je hypotetický koncept. To je hodnota, ku ktorej sa možno nekonečne približovať, nie je dosiahnuteľná.
Presnosť meraní je miera priblíženia sa jeho výsledku k skutočnej hodnote. Čím nižšia je chyba, tým vyššia je presnosť.
Absolútna chyba je vyjadrená ako rozdiel medzi hodnotou získanou ako výsledok merania a skutočným meraním veličiny. Napríklad skutočná hodnota l = 100 m, avšak pri meraní tej istej čiary bol výsledok 100,05 m, potom je absolútna chyba:
E = X meas – X
E = 100,05 - 100 = 0,05 (m)
Na získanie hodnoty stačí vykonať jedno meranie. Nazýva sa to nevyhnutné, ale častejšie jedno meranie nie je obmedzené, ale opakuje sa aspoň dvakrát. Merania, ktoré sa robia nad rámec toho, čo je potrebné, sa nazývajú redundantné (dodatočné), sú veľmi dôležitým prostriedkom kontroly výsledku merania.
Absolútna chyba nedáva predstavu o presnosti výsledku. Napríklad chybu 0,06 m možno získať meraním l = 100 m alebo l = 1 000 m. Preto vypočítajte relatívnu chybu:
C \u003d 0,06 / 100 \u003d 1/1667, t.j. pri 1667 m nameraného l bola povolená chyba 1 meter.
Relatívna chyba je pomer absolútnej chyby k skutočnej alebo nameranej hodnote. Vyjadrené ako zlomok. Podľa pokynov by čiara terénu nemala byť hrubšia ako 1/1000.
Chyby vyplývajúce z jednotlivých faktorov sa nazývajú elementárne. Zovšeobecnená chyba je súčtom základných.
Vstať:
hrubý (Q),
systematický (O),
náhodný (∆).
Hrubé chyby merania vznikajú v dôsledku hrubých chýb, nesprávnych výpočtov interpreta, jeho nepozornosti, nepozorovaných porúch technických prostriedkov. Hrubé chyby sú úplne neakceptovateľné a musia byť úplne vylúčené z výsledkov merania opakovanými dodatočnými meraniami.
Systematické chyby merania sú stálou zložkou spojenou s poruchami: zrak, nefunkčnosť technických prostriedkov, teplota. Systematické chyby môžu byť jednostranné aj premenlivé (periodické chyby). Snažíme sa, aby boli zohľadnené, ak je to možné, alebo vylúčené z výsledkov meraní pri organizácii a vykonávaní práce.
Náhodné chyby merania nevyhnutne sprevádzajú všetky merania. Náhodné chyby nemožno vylúčiť, ale ich vplyv na požadovaný výsledok možno oslabiť dodatočnými meraniami. Toto sú najzákernejšie chyby sprevádzajúce všetky merania. Môžu sa líšiť veľkosťou aj znakom.
Ak je možné študovať hrubé a systematické chyby a vylúčiť ich z výsledku merania, potom je možné na základe hĺbkového merania vziať do úvahy náhodné. Štúdia založená na teórii pravdepodobnosti.
V praxi problém spočíva v tom, že pre niektorých sa vykonávajú merania obmedzené množstvo krát a preto sa na posúdenie presnosti meraní používa približný odhad smerodajnej odchýlky, ktorý sa nazýva koreňová stredná štvorcová chyba (RMS).
Gauss navrhol vzorec pre strednú odmocninu chyby:
∆ 2 cf = (∆ 2 1 + ∆ 2 2 +… + ∆ 2 n) / n,
∆ 2 \u003d m 2 \u003d (∆ 2 1 + ∆ 2 2 + ... + ∆ 2 n) / n,
∆ cf = m = √(∑∆ 2 i / n)
Vzorec sa použije, keď sa chyby vypočítajú zo skutočných hodnôt.
Besselov vzorec:
m = √(∑V 2 i / (n-1))
Stredná kvadratická chyba aritmetického priemeru je Ön-krát menšia ako kvadratická chyba jedného merania
Pri vyhodnocovaní ako mernej jednotky presnosti sa používa stredná kvadratická chyba s váhou rovnajúcou sa jednej. Nazýva sa to stredná kvadratická chyba jednotky hmotnosti.
µ 2 = P×m 2 – µ = m√P, m = µ / √P, t.j. Stredná kvadratická chyba akéhokoľvek výsledku merania sa rovná chybe merania s váhou 1 (µ) vydelenej druhou odmocninou váhy tohto výsledku (P).
Pri dostatočne veľkom počte meraní môžeme zapísať ∑m 2 P=∑∆ 2 P (keďže ∆ = m):
µ = √(∑(∆ 2 ×P)/n), t.j. stredná kvadratická chyba merania s váhou rovnou 1 sa rovná druhej odmocnine zlomku, v čitateľovi ktorého je súčet súčinov druhých mocnín absolútnych chýb nerovnakých meraní ich váhami a v menovateli je počet nerovnakých meraní.
Stredná kvadratická chyba spoločného aritmetického priemeru podľa vzorca:
M° = µ / √∑P
Nahradením jeho hodnoty namiesto µ dostaneme:
M 0 = √(∑∆ 2 ×P/n) / (√∑P) = √[(∑∆ 2 ×P) / n×(∑P)]
M 0 = √[ (∆ 1 2 P 1 + ∆ 2 2 P 2 +… + ∆ n 2 P n) / n×(P 1 + P 2 + … + P n) ] je Gaussov vzorec, odmocnina štvorcová chyba súčtu aritmetický priemer sa rovná druhej odmocnine zlomku, v čitateľovi ktorého je súčet súčinov štvorcov chýb nerovnakých meraní ich váhami a menovateľ je súčinom počet meraní súčtom ich váh.
µ = √ [∑(V 2 ×P) / (n-1)] Toto je Besselov vzorec na výpočet priemeru aritmetická chyba s meraním hmotnosti rovným 1 pre množstvo nerovnakých meraní z hľadiska ich najpravdepodobnejších chýb. Platí pre veľký počet meraní, ale pre obmedzené (často v praxi) obsahuje chyby: m µ = µ / je spoľahlivosť odhadu µ.
Kontrolná úloha 1
Na štúdium teodolitu opakovane meral rovnaký uhol. Výsledky boli nasledovné: 39˚17,4"; 39˚16,8"; 39˚16,6"; 39˚16,2"; 39˚15,5"; 39˚15,8"; 39˚16,3"; 39˚16,2". Rovnaký uhol bol nameraný pomocou vysoko presného goniometra, ktorý dal výsledok 39˚16"42". Berte túto hodnotu ako presnú, vypočítajte odmocninu, určte spoľahlivosť SCP a nájdite hraničnú chybu.
| Meranie č. | Výsledky merania, l | Chyby | ∆2 |
| 1 | 39˚17,4" | +0.7" | 0.49 |
| 2 | 16.8 | +0.1 | 0.01 |
| 3 | 16.6 | -0.1 | 0.01 |
| 4 | 16.2 | -0.5 | 0.25 |
| 5 | 15.5 | -1.2 | 1.44 |
| 6 | 15.8 | -0.9 | 0.81 |
| 7 | 16.3 | -0.4 | 0.16 |
| 8 | 16.2 | -0.5 | 0.25 |
| Sum | 3.42 |
39˚16"42" = 39˚16,7"
Odmocninová chyba: m = √([∆ 2 ]/n),
m = √(3,42/8) = 0,65".
Odhad spoľahlivosti SKP: m m = m / √2n,
m m = 0,65 / √16=0,1625≈0,16".
Chyba limitu: ∆ pr \u003d 3 × m,
∆ pr = 3 × 0,65" = 1,96"
Kontrolná úloha 2
Je uvedený súbor zvyškov triangulačných trojuholníkov s objemom 50 jednotiek. Za predpokladu, že rezíduá sú skutočné chyby, vypočítajte strednú kvadratúru chyby a vytvorte spoľahlivosť SCP, vypočítajte hraničnú chybu. Na tejto množine skontrolujte vlastnosť náhodných chýb:
Lim[∆] / n =0, pre ktoré vypočítame W = [W] / n.
| N | W | N | W | N | W | N | W | N | W |
| 1 | +1,02 | 11 | -1,72 | 21 | -0,90 | 31 | +2,80 | 41 | -0,44 |
| 2 | +0,41 | 12 | +1,29 | 22 | +1,22 | 32 | -0,81 | 42 | -0,28 |
| 3 | +0,02 | 13 | -1,81 | 23 | -1,84 | 33 | +1,04 | 43 | -0,75 |
| 4 | -1,88 | 14 | -0,08 | 24 | -0,44 | 34 | +0,42 | 44 | -0,80 |
| 5 | -1,44 | 15 | -0,50 | 25 | +0,18 | 35 | +0,68 | 45 | -0,95 |
| 6 | -0,25 | 16 | -1,89 | 26 | -0,08 | 36 | +0,55 | 46 | -0,58 |
| 7 | +0,12 | 17 | +0,72 | 27 | -1,11 | 37 | +0,22 | 47 | +1,60 |
| 8 | +0,22 | 18 | +0,24 | 28 | +2,51 | 38 | +1,67 | 48 | +1,85 |
| 9 | -1,05 | 19 | -0,13 | 29 | -1,16 | 39 | +0,11 | 49 | +2,22 |
| 10 | +0,56 | 20 | +0,59 | 30 | +1,65 | 40 | +2,08 | 50 | -2,59 |
W = [W]/n, W = +2,51/50 = 0,05
V tomto prípade je vhodné vypočítať strednú odmocninu podľa vzorca: m = √ ( - [W] 2 / n) ÷ (n-1),
m = √(76,5703 - (2,51 2)/50) ÷ 49 = 1,249
Hodnotenie spoľahlivosti SCP podľa vzorca: m m = m / √2(n-1),
mm = 1,249/ √(2x49) = 0,13.
Limitná chyba podľa vzorca: ∆ pr \u003d 3 × m,
∆ pr \u003d 3 × 1,249 \u003d 3,747.
Kontrolná úloha 5 Určte vzdialenosť UPC vypočítanú podľa vzorca
S \u003d √ (x 2 - x 1) 2 + (y 2 - y 1) 2
ak x 2 \u003d 6 068 740 m; y 2 \u003d 431 295 m;
x 1 \u003d 6 068 500 m; y 2 \u003d 431 248 m;
m x \u003d m y \u003d 0,1 m.
S =√(6 068 740 - 6 068 500) 2 + (431 295 - 431 248) 2 = 235,36
mm = 0,1/√4 = 0,05
Kontrolná úloha 6
Rovnaký uhol bol meraný 5-krát s výsledkami: 60˚41"; 60˚40"; 60˚40"; 60˚42"; 60˚41". matematické spracovanie túto sériu meraní.
| Np/p | l, ˚ | ε, " | v," | v2," |
| 1 | 60˚41" | 1 | -0,2 | 0,04 |
| 2 | 60˚40" | 0 | +0,8 | 0,64 |
| 3 | 60˚40" | 0 | +0,8 | 0,64 |
| 4 | 60˚42" | 2 | -1,2 | 1,44 |
| 5 | 60˚41" | 1 | -0,2 | 0,04 |
| Sum | 4 | 0 | 2,8 |
l 0 - minimálna hodnota nameranej hodnoty, l 0 \u003d 60˚40 "; ε - zvyšok získaný ako ε \u003d l 1 - l 0; L - najlepšia hodnota nameranej hodnoty,
L = [l]/n; m = √([ v 2 ]/(n - 1), kde v je odchýlka od aritmetického priemeru. M je odhad presnosti aritmetického priemeru, M = m/√n.
L = 60˚40" + 4/5 = 60˚40,8"
m = √2,8 / 4 = 0,7"
M = 0,7"/√5 = 0,313"
Kontrolná úloha 7
Vykonajte matematické spracovanie výsledkov merania plochy toho istého obrysu pomocou planimetra: 26,31; 26,28; 26,32; 26,26; 26,31 ha.
| Np/p | l, ha | ε, ha | v, ha | v2, ha |
| 1 | 26,31 | 0,05 | -0,014 | 0,000196 |
| 2 | 26,28 | 0,02 | +0,016 | 0,000256 |
| 3 | 26,32 | 0,06 | -0,024 | 0,000576 |
| 4 | 26,26 | 0 | 0,036 | 0,001296 |
| 5 | 26,31 | 0,05 | -0,014 | 0,000576 |
| Sum | 0,18 | 0 | 0,0029 |
L = 26,26 + 0,18/5 = 26,296 ha
m = √0,0029/ 4 = 0,0269 ha
М = 0,0269/√5 = 0,01204 ha
Benchmark 8
Pri štúdiu centimetrových dielikov nivelačnej tyče pomocou ženevského pravítka bola teplota stanovená v čase vyhotovenia správy. Pre päťcentimetrové segmenty sa získali nasledujúce hodnoty: 20,3˚; 19,9˚; 20,1˚; 20,2˚; 20,3˚. Vykonajte matematické spracovanie výsledkov merania.
| Np/p | l, ˚ | ε, ˚ | v, ˚ | v2, ˚ |
| 1 | 20,3 | 0,4 | -0,14 | 0,0196 |
| 2 | 19,9 | 0 | -0,26 | 0,0676 |
| 3 | 20,1 | 0,2 | -0,06 | 0,0036 |
| 4 | 20,2 | 0,3 | 0,04 | 0,0024 |
| 5
Nebudú potrebné, potom sa musí nástroj vyvinúť ručne, ak je to opodstatnené z hľadiska vynaloženého času a materiálnych zdrojov. 2. Spracovanie geodetických meraní pomocou tabuľkových procesorov Na prvotné spracovanie informácií získaných ako výsledok komplexu topografických a geodetických prác som použil program TOGI, čo je balík ...
Na stavenisku je potrebné dodržiavať požiadavky bezpečnostných noriem a predpisov uvedených v kapitole SNiP Sh-4-80 "Bezpečnosť vo výstavbe" a pokyny rezortu. Geodetické práce môžu vykonávať osoby, ktoré boli poučené, vydané príkazom stavebného odboru. Riziko úrazu alebo úrazu sa určuje v závislosti od pracovných podmienok...
Elektronické zariadenia s priamou účasťou autora. Druhá kapitola. Druhá kapitola rozoberá vyvinuté metódy na vykonávanie výskumu na metrologických zariadeniach a stojany na kontrolu a kalibráciu geodetických prístrojov na meranie výšok. Metóda na štúdium krátkodobej chyby pri meraní vertikálnych uhlov geodetických prístrojov. Dôležitá úloha v štúdiu... |
Tu je ďalší priemer, ktorý je spojený s chybami.
Odmocnina so štvorcovou chybou(SKP) je mierou presnosti výsledkov merania alebo funkcií nameraných hodnôt a je pravdepodobnostnou charakteristikou.
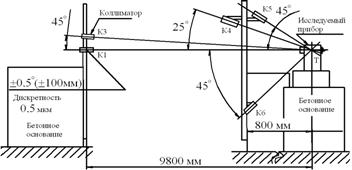
Ryža. 3.1. Zákon normálneho rozdelenia
náhodné chyby.
Predpokladajme, že poznáme hodnotu strednej kvadratickej chyby m. V súlade so zákonom normálneho rozdelenia bude graf rozdelenia skutočných chýb vzhľadu podobný grafu na obr. 3.1. Parameter r charakterizuje frekvenciu (alebo frekvenciu) výskytu náhodných chýb tej či onej veľkosti a znamienka. V tomto prípade je pravdepodobnosť výskytu chýb vo vopred určenom rozsahu, napríklad ± m, je určená oblasťou obrázku ohraničenou distribučnou krivkou a ordinátami na hodnotách + m a - m. Pre zákon normálneho rozdelenia sa pravdepodobnosť výskytu chýb v stanovených rozsahoch rovná nasledujúcim hodnotám:
Pre rozsah ± m ® R= 68,3 % (» 68 %);
Pre rozsah ±2 m® R= 95,5 % (» 95 %);
Pre rozsah ±3 m® R= 99,7 % (prakticky 100 %).
Teda len v 3 prípadoch z 1000 môže byť chyba presahujúca hodnotu 3 m. Chyby väčšie ako 3 v absolútnej hodnote m(medzná chyba), považuje sa za hrubý a výsledky merania obsahujúce túto hrubú chybu sú vylúčené z ďalšieho spracovania. V niektorých prípadoch sa kvôli sprísneniu požiadaviek na presnosť merania nastavuje medzná chyba v rozsahu od 2 m do 3 m.
Tabuľka 3.1
Hodnoty študentského koeficientu ( t) pre rôzne pravdepodobnosti ( R)
| t | P% | t | P% | t | P% |
| 0,1 | 8,0 | 1,1 | 72,9 | 2,1 | 96,4 |
| 0,2 | 15,9 | 1,2 | 77,0 | 2,2 | 97,2 |
| 0,3 | 23,6 | 1,3 | 80,6 | 2,3 | 97,9 |
| 0,4 | 31,1 | 1,4 | 83,8 | 2,4 | 98,4 |
| 0,5 | 38,3 | 1,5 | 86,6 | 2,5 | 98,8 |
| 0,6 | 45,1 | 1,6 | 89,0 | 2,6 | 99,1 |
| 0,7 | 51,6 | 1,7 | 91,1 | 2,7 | 99,3 |
| 0,8 | 57,6 | 1,8 | 92,8 | 2,8 | 99,5 |
| 0,9 | 63,2 | 1,9 | 94,3 | 2,9 | 99,6 |
| 1,0 | 68,3 | 2,0 | 95,5 | 3,0 | 99,7 |
Často je hodnota UPC označená koeficientom t (Študentský koeficient), ktorý určuje interval spoľahlivosti ( X± tm) výsledok merania na stanovenej úrovni pravdepodobnosti R. Na tento účel je vhodné použiť tabuľku. 3.1.
Napríklad musíte definovať interval spoľahlivosti pre množstvo X s 90% šancou. Z tabuľky interpoláciou zistíme, že pre R 1 = 89,0% t1= 1,6, pre R 2 = 91,1% t2 = 1,7: t x= 1,6476 » 1,65.
To znamená, že výsledok merania s pravdepodobnosťou 90 % je v rámci ( X±1,65 m).
Ak je nameraná hodnota X známe, potom sa hodnota SCP určuje podľa Gaussov vzorec:
kde Δ - skutočné chyby merania.
Pripomeňme, že znak [...] je znakom Gaussovej sumy.
V prípadoch, keď nameraná hodnota nie je známa, použite Besselov vzorec:
Kde v- odchýlka výsledkov merania od aritmetického priemeru.
Ako je zrejmé zo vzorcov (3.9) a (3.10), v prípade, keď je nameraná hodnota známa, na odhad presnosti stačí jedno meranie (je potrebné). Ako bolo uvedené vyššie, najčastejšie sa Gaussov vzorec používa pri posudzovaní presnosti štandardizovaných prístrojov pri meraní známych veličín (etalónov). Na vyhodnotenie presnosti pomocou Besselovho vzorca sú potrebné aspoň dve merania. Besselov vzorec sa používa pri odhade presnosti výsledkov hmotnostných (viacnásobných) meraní jednej vopred neznámej veličiny.
S nárastom počtu meraní sa hodnoty SQL získané pomocou Gaussových a Besselových vzorcov takmer zhodujú (približne n³ 20). V tomto prípade sa hodnota SCP jedného merania blíži k limitu m predtým, ktorá je určená presnosťou prístroja, presnosťou meracej metódy alebo programu. Je zrejmé, že už bolo povedané vyššie, že v praxi je nemožné a z mnohých dôvodov neúčelné poskytovať veľmi veľký počet meraní jednej veličiny. V tomto prípade by mal praktický počet meraní zabezpečiť, že výsledok merania sa získa s danou presnosťou a špecifikovanou úrovňou spoľahlivosti.
Keďže počet meraní je obmedzený, samotný SCP obsahuje chybu určenú približným vzorcom:
Hovorí sa tomu tak - stredná kvadratická chyba strednej kvadratúry chyby (SKP SKP).
Tu je vhodné vrátiť sa ku klasifikácii chýb. Nie všetky typy chýb zvažujeme vyššie.
Často sa pri skúmaní sérií chýb merania, tzv. pravdepodobná chyba, ktorý sa označuje písmenom r. Hodnotu pravdepodobnej chyby možno odhadnúť podľa približného vzorca
samozrejme za predpokladu, že rozdelenie chýb sa riadi normálnym zákonom.
Pravdepodobná chyba je tiež tzv chyba mediánu. Ak nechcete robiť výpočty pomocou vzorca (3.12), pretože obsahuje hodnotu m, ktorý je potrebné získať pomocou Besselovho vzorca, potom je možné určiť pravdepodobnú alebo strednú chybu zoradením počtu chýb v poradí ich nárastu v absolútnych hodnotách. V strede výslednej série bude hodnota tejto chyby. Toto je, ak je počet chýb nepárny. A ak je párny, potom stredná chyba bude priemerná hodnota susedných chýb v strede série.
Nezamieňajte strednú chybu s priemerná chyba v o, ktorý možno získať aj jednoduchým vzorcom:
Vyžaduje tiež podmienku, že množstvo meraní (chýb) podlieha bežnému zákonu.
Priemerná chyba je matematické očakávanie absolútne hodnoty odchýlky výsledkov merania akejkoľvek hodnoty od matematického očakávania pre tieto výsledky. Približne hodnotu priemernej chyby možno odhadnúť podľa vzorca:
Kde v i– odchýlka výsledkov merania od ich aritmetického priemeru.
Na predbežný odhad strednej kvadratickej chyby sa často používa vzorec (3.13).
Náhodné chyby sa nazývajú také chyby, ktorých veľkosť a povaha vplyvu na každý jednotlivý výsledok merania zostáva neznáma. Veľkosť a znamienko náhodných chýb nie je možné vopred určiť. Sú nevyhnutné a sprevádzajú každé meranie, keďže meranie vykonávame len s takou presnosťou, akú je možné dosiahnuť s použitými prístrojmi. Nie je možné úplne zbaviť výsledky merania náhodných chýb. Ale na základe štúdia ich vlastností je možné odvodiť pravidlá, ako zo série meraní získať čo najspoľahlivejšie výsledky a vyhodnotiť ich presnosť. Týmito otázkami sa zaoberá teória chýb merania.
V teórii chýb sa rozlišujú rovnaké a nerovnaké merania. Ekvivalentné merania sú merania vykonané za rovnakých podmienok, so zariadeniami s rovnakou presnosťou, rovnakým počtom krát, pozorovateľmi s rovnakou kvalifikáciou. Ak jedna z týchto podmienok nie je splnená, takéto merania budú nerovnaké.
Vlastnosti náhodných chýb. Náhodné chyby možno definovať ako rozdiel medzi nameranými a skutočnými hodnotami tej istej veličiny. Na základe teoretického a praktického štúdia mnohých sérií náhodných chýb sú odvodené ich všeobecné vlastnosti:
1 Za týchto podmienok náhodné chyby nemôžu prekročiť určitú hranicu.
2 Pozitívne a negatívne chyby rovnakej absolútnej hodnoty sú rovnako možné.
3 Menšie chyby sú bežnejšie ako väčšie.
4 Aritmetický priemer náhodných chýb rovnako presných meraní rovnakej hodnoty má tendenciu k nule s neobmedzeným nárastom počtu meraní.
4.2 Princíp aritmetického priemeru
Nech sa urobia rovnaké merania l 1 , l 2 , ... , l n tej istej veličiny, ktorej skutočná hodnota je X. Potom možno vypočítať n hodnôt náhodných chýb:
Δ 1 \u003d l 1 - X;
Δ 2 \u003d l 2 - X; (4.1)
Δ n \u003d l n - X.
Pridaním ľavej a pravej časti týchto rovníc dostaneme
Δ 1 + Δ 2 +…+ Δ n = l 1 + l 2 +…+ l n – nX. (4.2)
V teórii chýb je obvyklé označovať súčet veličín pomocou hranatých zátvoriek, napríklad:
A 1 + A 2 + ... + A n = [A]; l 1 + l 2 + … + l n = [l] atď.
Pri týchto zápisoch nadobúda tvar rovnosť (4.2).
[A] = [l] - nX, odkiaľ X = [l] / n - [A] / n. (4.3)
Podľa štvrtej vlastnosti náhodných chýb má hodnota [Δ] / n v rovnosti (4.3) tendenciu k nule s neobmedzeným nárastom počtu meraní. Následne sa hodnota [l] / n za týchto podmienok priblíži skutočnej hodnote X. Na základe toho sa aritmetický priemer (aritmetický priemer výsledkov meraní) považuje za najspoľahlivejší alebo najpravdepodobnejší výsledok rovnako presných meraní. rovnakej hodnoty pre ľubovoľný počet meraní.
L \u003d [l] / n \u003d (l 1 + l 2 + l 3 + ... + l n) / n. (4.4)
4.3 Kvadratická chyba jedného merania.
Gaussove a Besselove vzorce
V teórii chýb je presnosť meraní charakterizovaná strednou štvorcovou chybou, ktorú zaviedol slávny nemecký matematik a geodet K. F. Gauss (1777–1855) a označuje sa m:
______________________ ______
m = ± √ (Δ 1 2 + Δ 2 2 + .. + Δ n 2) / n = ± √ [Δ 2 ] / n, (4,5)
kde A 1 , A 2, ..., Δ n sú náhodné chyby;
n je počet meraní.
Stredná kvadratická chyba je spoľahlivým kritériom na posúdenie presnosti meraní. Aj pri malom počte meraní je celkom stabilný a dobre odráža prítomnosť veľkých náhodných chýb, ktoré v podstate určujú kvalitu meraní.
Vzorec (4.5) sa používa na výpočet strednej kvadratickej chyby, keď je známa skutočná hodnota meranej veličiny. Tieto prípady sú v praxi veľmi zriedkavé. Skutočná hodnota meranej veličiny je spravidla neznáma, ale najspoľahlivejší výsledok, aritmetický priemer, možno získať z meraní. Vzorec na výpočet strednej kvadratickej chyby získame tak, že jednotlivé výsledky odchýlime od aritmetického priemeru v zmysle takzvaných najpravdepodobnejších chýb V.
Nech l 1 , l 2 , ..., l n sú výsledky rovnako presných meraní tej istej veličiny, ktorej skutočná hodnota je X a aritmetický priemer je L. Potom môžete vypočítať n náhodných alebo skutočných chýb
Δ i = l i – X (4,6)
a n najpravdepodobnejšie chyby
V i = l i – L. (4,7)
Súčet n k rovnosti (4.7)
[V] = [l] - nL. (4,8)
Ale podľa rovnosti (4.4) nL = [l] teda
t.j. súčet najpravdepodobnejších chýb sa musí vždy rovnať nule.
Odčítaním rovnosti (4.7) od rovnosti (4.6) dostaneme
Δ i – V i = L – X. (4.10)
Na pravej strane rovnosti (4.10) máme náhodnú chybu aritmetického priemeru. Označujeme ho ε. Potom
Ai = Vi + ε. (4.11)
Odmocnime rovnosť (4.11), vezmeme ich súčet a vydelíme n:
[A2]/n = / n + nε2/n + 2ε[V]/n. (4.12)
Ľavá strana tejto rovnosti nie je nič iné ako m 2 . Posledný člen na pravej strane sa vzhľadom na rovnosť (4.9) rovná nule.
m2 = / n + e2. (4,13)
Náhodnú chybu ε nahradíme jej strednou hodnotou, t.j. strednou kvadratickou chybou aritmetického priemeru. Nižšie to bude dokázané stredná kvadratická chyba aritmetického priemeru
M 2 \u003d ε 2 \u003d m 2 / n. (4,14)
m2 - m2 / n = / n alebo m2 (n - 1) / n = / n,
kde ___________
m 2 \u003d / (n - 1) alebo m \u003d √ / (n - 1). (4,15)
Vzorec (4.15) sa nazýva Besselov vzorec a má skvelú praktickú hodnotu. Umožňuje vám vypočítať kvadratickú chybu z najpravdepodobnejších odchýlok výsledkov merania od aritmetického priemeru.
Okrem strednej štvorcovej chyby existujú aj priemerné, pravdepodobné a relatívne chyby.
Priemerná chyba (Θ) je aritmetický priemer absolútnych hodnôt náhodných chýb, t.j.
Θ = (|Δ 1 | + |Δ 2 | + … + |Δ n |) / n = [|Δ|] / n. (4,16)
V teórii chyby je dokázané, že ako n → ∞ Θ = 0,8 m, alebo m = 1,25Θ.
Niekedy v aplikovaných otázkach, ktoré používajú pravdepodobná chyba r. Pravdepodobná chyba je taká hodnota náhodnej chyby v jednej sérii rovnako presných meraní, vo vzťahu ku ktorej je rovnako možná chyba väčšia aj menšia ako táto hodnota, v absolútnej hodnote. Na nájdenie r sú všetky chyby tohto radu usporiadané vo vzostupnom poradí v absolútnej hodnote a je zvolená hodnota, ktorá zaberá strednú pozíciu, to znamená, že chýb je menej ako viac. Pravdepodobná chyba súvisí so strednou kvadratickou chybou vzťahom r = 2/3 m = 0,67 m alebo m = 1,5 r.
Ako je možné vidieť, m > Θ a m > r, čo ukazuje, že stredná kvadratická chyba charakterizuje presnosť merania lepšie ako priemerné a pravdepodobné chyby.
Presnosť meraných veličín, ako sú čiary, plochy a objemy, sa často posudzuje pomocou relatívna chyba. Relatívna chyba je pomer absolútnej chyby k hodnote nameranej hodnoty. Relatívna chyba sa zapisuje ako zlomok, ktorého čitateľ je jedna a menovateľ je číslo, ktoré ukazuje, aký podiel na nameranej hodnote má byť prípustná chyba. Napríklad dĺžka strany D = 150 m meraná s absolútna chyba m d = 0,05 m Potom bude relatívna chyba výsledku merania m d / D = 0,05 m / 150 m = 1/3000.
Hodnota 1 / 3000 znamená, že na vzdialenosť 3000 m je možné pripustiť chybu 1 m. Čím väčší je menovateľ relatívnej chyby, tým vyššia je presnosť merania. Presnosť všetkých lineárnych meraní v geodézii je vždy špecifikovaná relatívna chyba, ktorý je uvedený v príslušných návodoch a návodoch na zhotovenie tohto druhu geodetických prác.
4.4 Zákon normálneho rozdelenia chýb.
Chyba limitu
Z predchádzajúcej úvahy o vlastnostiach náhodných chýb vyplýva, že o výskyte samostatnej chyby nemožno vopred nič konkrétne povedať. Keď sa však počet týchto chýb zvýši, môžu sa vytvoriť určité vzory pre celý súbor chýb v danej sérii meraní. Tieto zákonitosti možno vyjadriť rovnicou, ktorú získal K. F. Gauss. Vyzerá to ako
y = (1 / σ √2π) e – (l i – a) / 2 σ = (1 /σ √2π) e – Δ c / 2 σ , (4.17)
kde y je hustota distribúcie chýb;
σ je parameter rovnice, nazývaný štandard, spojený s priemerom
pomer kvadratických chýb
a je parameter rovnice nazývaný matematické očakávanie,
súvisí s aritmetickým priemerom vzťahom
e - základňa prirodzené logaritmy;
Δ i = l i - a - náhodná chyba.
Táto rovnica sa nazýva zákon normálneho rozdelenia chyby.
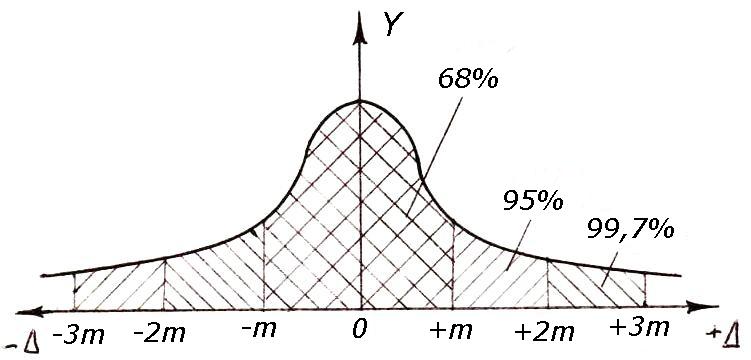
Rovnica (4.17) zodpovedá krivke v tvare zvona nazývanej krivka normálneho rozdelenia (Gaussova krivka) (obrázok 4.1)
Obrázok 4.1 - Gaussova krivka
Plocha pod krivkou, ohraničená krivkou a osou x, sa rovná jednej. Časť tejto oblasti zodpovedajúca ľubovoľnému segmentu osi x udáva pravdepodobnosť náhodnej chyby spadajúcej do tohto intervalu. Pre l i = a alebo Δ = 0 dostaneme maximálna hodnota súradnice krivky __
Y = 1 / σ √2π.
Obrázok 4.1 ukazuje, že väčšina chýb je zoskupená okolo najpravdepodobnejšej hodnoty chyby Δ i = 0 (podľa štvrtej vlastnosti náhodných chýb má aritmetický priemer náhodných chýb tendenciu k nule). Toto ustanovenie odôvodňuje tretiu vlastnosť náhodných chýb (malé chyby sú bežnejšie ako veľké). Druhá vlastnosť náhodných chýb o rovnakom výskyte pozitívnych a negatívnych chýb je charakterizovaná symetriou krivky normálneho rozdelenia okolo osi OY.
Teoretické štúdie a prax geodetických meraní ukazujú, že 68 % všetkých náhodných chýb spadá do intervalov od –m do +m (pozri obrázok 4.1), 95 % chýb spadá do intervalu dvakrát väčšieho (od –2m do +2m). ) a 95 % chýb spadá do intervalu trikrát väčšieho (od –3 m do +3 m) nájdených 99,73 % chýb. To znamená, že zo 100 chýb merania iba 32 v absolútnej hodnote prekročí strednú odmocninu m, 3 z 1000 chýb prekročí trojnásobnú odmocninu ±3 m. Len 0,27 % chýb merania teda presahuje ±3 m. Preto sa ako limitná chyba Δ berie trojnásobná stredná kvadratická chyba, t.j.
Δ pre = 3 m. (4,18)
Uvažujme teraz o podstate parametrov a a σ v rovnici (4.17). Parameter a sa nazýva matematické očakávanie a charakterizuje stred zoskupenia na Gaussovej krivke, t.j. posunutie stredu zoskupenia pozdĺž osi x (obrázok 4.2, a) pri zachovaní tvaru krivky. Ak pri konštantnej hodnote parametra a zmeníme ďalší parameter σ (nazývaný etalón), ktorý charakterizuje presnosť meraní, a to je možné, ak zmeníme spôsob merania alebo ich vykonáme inými prístrojmi. Potom zostane stred zoskupenia nezmenený a tvar krivky sa zmení. Ak sa presnosť merania zníži, bude plochejšia a so zvyšovaním presnosti bude strmšia (obrázok 4.2, b).
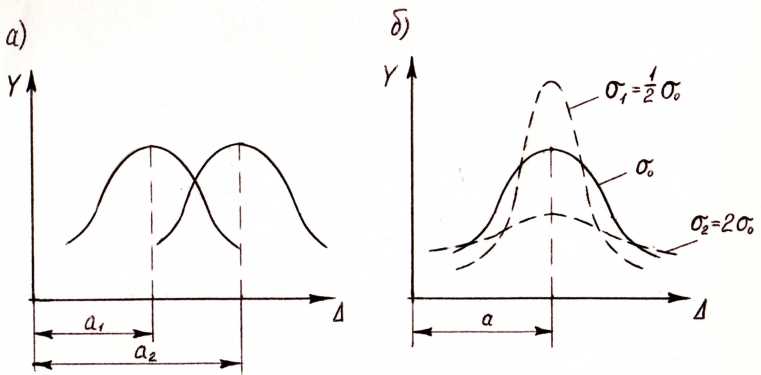
Obrázok 4.2 - Posun a zmena tvaru normálnej krivky
Parametre a a σ sú pred meraním neznáme. Získajú sa ako výsledok Vysoké číslo merania. V praxi namiesto parametrov a a σ získame ich približné hodnoty: aritmetický priemer L vypočítaný podľa vzorca (4.4) a kvadratúru m vypočítanú podľa vzorcov (4.5) alebo (4.15).
4.5 RMS chyba funkcie
merania veličín
V geodézii je často potrebné určiť presnosť nielen samotných meraných veličín, ale aj ich funkcií. Napríklad horizontálne položenie čiary je funkciou sklonu vzdialenosti a uhla sklonu, plocha určená planimetrom je funkciou odčítania na planimetri atď. Preto je dôležité mať možnosť na výpočet stredných kvadratických chýb funkcií. Pozrime sa na niektoré typy funkcií.
m = nm2 alebo mφ = m√n, (4.27)
t.j. kvadratická chyba súčtu rovnako presných nameraných hodnôt je √n-krát väčšia ako kvadratická chyba jedného merania.
PRÍKLAD Nájdite strednú odmocninu zo súčtu nameraných uhlov v štvoruholníku, ak stredná odmocnina jedného rohu je ±30 "". Podľa vzorca (4.27) nájdeme
m φ \u003d ± 30 "" √ 4 \u003d ± 60 "" \u003d 1 ".
2Funkcia riadkového zobrazenia
kde K je konštantné číslo;
X je argument získaný z meraní.
Ak sa X meria s náhodnou chybou ΔX, funkcia bude mať náhodnú chybu
Δ φ \u003d K Δ X. (4,29)
Po zmeraní argumentu n-krát je možné zostaviť n rovníc (4.29), vziať súčet ich štvorcov a vydeliť n. Po ktorom dostaneme
[Δ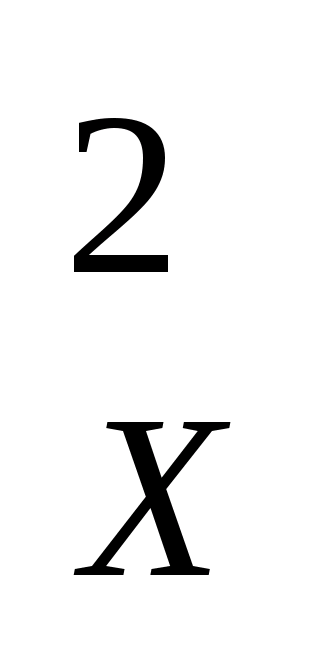 
] / n = K2 [Δ] / n alebo m = K2 m, (4,30)
mφ = KmX. (4,31)
Podobne ako v predchádzajúcom možno ukázať, že pre funkciu
φ = ± K 1 X ± K 2 Y ± … ± K n U (4.32)
Δ φ \u003d K 1 Δ X ± K 2 Δ Y ± ... ± K n Δ U (4.33)
m= (K1mX)2+ (K2mY)2+...+ (KnmU)2. (4,34)
PRÍKLAD Určte kvadratúru M aritmetického priemeru L, ak sa kvadratická chyba jedného merania rovná m. Vzorec (4.4) aritmetického priemeru zapíšeme v tomto tvare:
L \u003d l 1 / n + l 2 / n + ... + l n / n. (4,35)
Ako vidíte, vzorec (4.34) pre funkciu (4.35) možno použiť tu:
m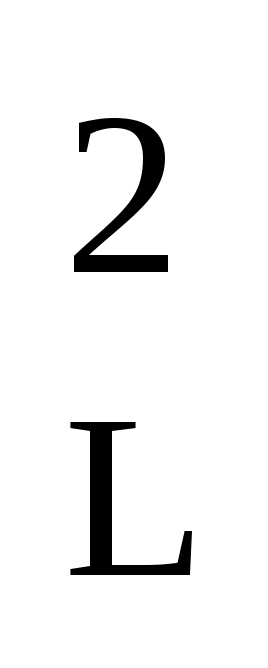 
\u003d M2 \u003d (m 1 / n) 2 + (m 2 / n) 2 + ... + (m n / n) 2.
Ak vezmeme do úvahy, že merania l 1 , l 2 ,…, l n sú rovnaké, t. j. m 1 = m 2 = … = m n , dostaneme
M 2 \u003d n (m / n) 2 \u003d m 2 / n,
M = m / √n, (4,36)
t.j. kvadratická chyba aritmetického priemeru je √n-krát menšia ako kvadratická chyba jedného merania.
3Funkcia všeobecný pohľad
φ = f (X, Y, Z, … ,U), (4,37)
kde X, Y, Z, …, U sú nezávisle merané veličiny.
Ak vezmeme do úvahy náhodné chyby, funkcia (4.37) má tvar
φ + Δ φ \u003d f (X + Δ X; Y + Δ Y; Z + Δ Z; ...; U + Δ U). (4,38)
Rozšírením funkcie (4.38) v Taylorovom rade a obmedzením sa iba na prvé mocniny náhodných chýb získame funkciu
Δ φ = (∂f/∂x) Δ X + (∂f/∂y) Δ Y + (∂f/∂z) Δ Z + … + (∂f/∂u) Δ U , (4,39)
kde (∂f/∂x), (∂f/∂y), …, (∂f/∂u) sú parciálne derivácie, ktoré pre funkciu
(4.39) sú konštanty.
Ako vidno, funkcia (4.39) je podobná funkcii (4.33). Preto druhá mocnina jeho odmocniny je stredná kvadratická chyba
= (∂f/∂x ∙ m X) 2 + (∂f/∂y ∙ m Y) 2 + (∂f/∂z ∙ m Z) 2 + … + (∂f/∂u ∙ m U) 2 . (4,40)
PRÍKLAD V obdĺžniku sa merajú dve strany - X = 200 m a Y = 100 m s chybami odmocniny m X = +0,20 ma m Y = +0,10 m.
Určte plochu obdĺžnika P a jeho strednú kvadratúru chybu m P.
.m = √ / 2n. (4,43)
Vzorec (4.43) poskytuje vyjadrenie pre odmocninu chyby jedného merania z n dvojitých meraní.
4.7 Nerovnaké miery
V predchádzajúcich častiach boli uvažované ekvivalentné merania. V praxi sa však často robia nerovnaké merania, ktoré sa vykonávajú za iných podmienok alebo prístrojmi rôznej presnosti, s rôznym počtom krokov. V tomto prípade už nie je možné obmedziť sa na jednoduchý aritmetický priemer, tu treba brať do úvahy mieru spoľahlivosti každého výsledku merania.
Miera spoľahlivosti výsledku merania vyjadrená ako číslo sa nazýva hmotnosť tohto merania. Čím je výsledok spoľahlivejší, tým väčšia je jeho hmotnosť. Majme sériu priemerných hodnôt: L 1 , L 2 , …, L n - jedna hodnota získaná z Р 1 , Р 2, …, Р n jednotlivých meraní.
Podľa vzorca (4.4) sa súčin L i P i bude rovnať súčtu jednotlivých meraní l i v tejto sérii a súčet všetkých meraní všetkých sérií sa bude rovnať L 1 P 1 + L 2 P 2 + ... + L n P n . Počet všetkých meraní sa bude rovnať P 1 + P 2 +…+ P n .
Odtiaľ, podľa pravidla aritmetického priemeru, získame priemernú hodnotu zo všetkých sérií meraní:
Lo = (L1P1 + L2P2 + ... + L n P n) / (P 1 + P 2 + ... + P n) = / [P]. (4,44)
Zavolá sa výraz (4.44). vzorec pre priemernú hmotnosť alebo spoločný aritmetický priemer. Počet meraní P 1 , P 2, ..., P n v každom riadku je váha priemerných výsledkov L 1 , L 2, ..., L n a súčet váh je váha celkového aritmetického priemeru L o . Vo všetkých prípadoch, keď sú známe výsledky merania a ich hmotnosti, pravdepodobná hodnota nameraná hodnota sa vypočíta podľa vzorca (4.44).
Označme strednú kvadratúru jedného merania cez μ a stredné kvadratické chyby hodnôt L 1 ,L 2 ….L n v tomto poradí cez m 1 , m 2 , …, m n . Potom podľa rovnosti (4.36) môžeme napísať, že ___ __ __
m1 = μ/√P1; m2 \u003d μ / √ P 2; …; m n = μ / √ P n. (4,45)
Ak vo vzorci (4.45) vezmeme P i = 1, potom μ = m i. Z toho vyplýva, že μ je stredná kvadratická chyba merania, ktorej váha sa rovná jednej alebo takzvaná kvadratická chyba váhovej jednotky.
ročníková prácaTypy chýb. Takmer vždy chyba zahŕňa dve jej zložky: systematickú a náhodnú.
Δa= Δasyst + Δaran.
Systematický nazývaná chyba, ktorá za daných podmienok zostáva konštantná (alebo sa mení, ale podľa známeho zákona).
Takéto chyby sú neustále spôsobené prevádzkových dôvodov, v dôsledku čoho sa pri meraní zakaždým „mýlime“ o rovnakú sumu. Veľmi často sú takéto chyby spôsobené nepresnou výrobou zariadenia (inštrumentálne chyby), alebo konštantné vonkajší faktor. Napríklad vlastné magnetické pole lietadla spôsobuje chybu v meraní magnetického kurzu (odchýlku), ktorá má na každom kurze presne definovanú hodnotu.
Systematické chyby, keďže sú pre každé meranie rovnaké, je možné určiť raz presnejšími prístrojmi a potom ich z výsledkov merania odstrániť zavedením opráv.
Systematické chyby nespôsobujú pri navigácii veľké problémy, pretože po ich odstránení sa už nevyskytujú. Preto budeme ďalej predpokladať, že neexistujú žiadne systematické chyby (už zohľadnené).
náhodná chyba pre každé meranie iný význam, ktorý nie je vopred známy.
Náhodné chyby však v zásade nemožno odstrániť, pretože sú pre každé meranie iné. A vždy zostávajú neznámi.
Nie je možné určiť číselné hodnoty náhodných chýb, ale pilot musí mať vždy na pamäti, že tieto chyby existujú a byť si vedomý ich možných hodnôt. Prítomnosť neistoty vo výsledkoch merania je jedným z hlavných faktorov, ktoré komplikujú navigáciu a robia z nej nielen vedu, ale aj umenie.
Náhodná udalosť je udalosť, ktorá za daných podmienok môže, ale nemusí nastať. Miera možnosti výskytu takejto udalosti je číselne charakterizovaná veľkosťou pravdepodobnosti. Pravdepodobnosť P je číslo, ktoré sa môže pohybovať od 0 do 1. Ak za daných podmienok k udalosti nikdy nedôjde, nazýva sa nemožná udalosť a jej pravdepodobnosť je nulová. Ak sa vyskytuje vždy za daných podmienok, potom sa nazýva spoľahlivý a pripisuje sa mu pravdepodobnosť. rovný jednej. Ak je napríklad P = 0,3, potom to znamená, že v priemere v 30 prípadoch zo 100 dôjde k udalosti. Je to v priemere, pretože udalosť je náhodná. Ak vytvoríte podmienky potrebné na výskyt udalosti a vykonáte sériu 100 experimentov, udalosť sa môže vyskytnúť napríklad 23-krát alebo 32-krát... Ak vykonáte niekoľko sérií takýchto experimentov alebo jednu sériu z tisíc, desaťtisíc, miliónov experimentov, čím väčší je počet vykonaných experimentov, tým bližšie bude priemerný počet výskytov udalosti bližšie k 30 % z celkového počtu experimentov (ak P = 0,3).
Ako teda možno opísať náhodné chyby, ak nemajú žiadny konkrétny význam? Často sú charakterizované hodnotou strednej kvadratickej chyby (MSE), ktorá sa označuje písmenom σ (sigma). Takže napríklad SQL merania veličiny a budeme označovať σa.
SCP je charakteristika stupňa rozptylu nameranej hodnoty veličiny okolo jej skutočnej hodnoty. Čím väčšie σa, tým viac rozptýlené (rozptýlené) merané v rôzne skúsenosti hodnoty okolo skutočnej hodnoty množstva.
Na obr. 2.19 geometricky znázornené ako číselná os možné hodnoty merané množstvo a a zaznamená sa jeho skutočná hodnota. Krížiky na stupnici označujú namerané hodnoty získané ako výsledok niekoľkých experimentov. V prvom prípade je rozptyl nameraných hodnôt okolo skutočnej hodnoty väčší ako v druhom prípade, preto je „sigma“, ktorá charakterizuje stupeň rozptylu, v druhom prípade menšia.
Ryža. 2.19. Odmocnina so štvorcovou chybou
Hodnotu SCP možno použiť na posúdenie pravdepodobnosti, že nameraná hodnota nadobudne jednu alebo druhú hodnotu. Na to však nestačí poznať SCP, musíte tiež vedieť, aký distribučný zákon dodržiava táto náhodná chyba. Mnoho náhodných premenných sa riadi zákonom normálneho (Gaussovho) rozdelenia. Pre tento zákon je užitočné zapamätať si nasledujúce hodnoty.
Ak systematická chyba chýba a ako výsledok merania sa získa hodnota ameas, potom skutočná hodnota veličiny leží v (obr. 2.20):
ameas ± σa s pravdepodobnosťou Р=0,68;
ameas ± 2σa s pravdepodobnosťou Р=0,95;
ameas ± 3σa s pravdepodobnosťou Р=0,997.
Ryža. 2.20. Niektoré pravdepodobnosti pre normálne rozdelenie
Napríklad pomocou kompasu sa meria kurz γ=100º a presnosť kompasu je charakterizovaná SCP σγ =2º. To znamená, že skutočná sadzba (ktorá nám zostane neznáma) priemer:
v 68 prípadoch zo 100 leží v rozmedzí 100º ± 2º, to znamená v rozmedzí 98º ... 102º;
v 95 prípadoch zo 100 leží v rozmedzí 100º ±4º, to znamená v rozmedzí 96º ... 104º;
v 997 prípadoch z 1000 leží v rozmedzí 100º ±6º, to znamená v rozsahu 94º ... 106º.
Hodnota pravdepodobnosti R=0,997 je tak blízko k jednote, že zodpovedajúca chyba troch sigma sa často označuje ako maximálna chyba. V skutočnosti ju môže chyba prekročiť. Pravda, zriedkavo - v priemere v troch prípadoch z tisíc.
IN technické popisy prístrojov a zariadení, ich presnosť je možné uviesť priamo v tvare UPC a potom je všetko jasné. Niekedy sa však uvádza napríklad takto: „chyba merania ložiska ± 1,5º“. To samozrejme neznamená, že sa takýto zameriavač "pomýli" zakaždým o 1,5º. To tiež neznamená, že nemôže urobiť chybu. viac ako 1,5º. Takto označená hodnota chyby spravidla zodpovedá pravdepodobnosti R= 0,95. To znamená, že v priemere v 95 prípadoch zo 100 chyba nepresiahne (nahor alebo nadol) hodnotu 1,5º.
Preto v piatich prípadoch zo sto môže byť chyba väčšia. Pre normálne rozdelenie chýb zodpovedá pravdepodobnosť 0,95 zdvojnásobil UPC. Preto je miera merania SCP v tomto príklade 0,75º.