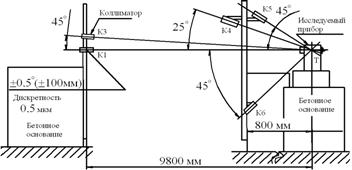
3.2 Jeodezik ölçümlerdeki hataların sınıflandırılması. Ortalama kare hatası. Hesaplanması için Gauss ve Bessel formları
Jeodezik ölçümler çok iyi koşullar, hatalar eşlik eder, yani L ölçüm sonucunun numaralandırılmış miktarın gerçek X değerinden sapması:
Doğru - ölçülen miktarın, nesnenin nicel özelliklerini ideal olarak yansıtacak böyle bir değeri. Ulaşılamaz durum - gerçek değer varsayımsal bir kavramdır. Bu sonsuz yaklaşılabilecek bir değerdir, ulaşılamaz.
Ölçümlerin doğruluğu, sonucunun gerçek değere yaklaşma derecesidir. Hata ne kadar düşükse, doğruluk o kadar yüksek olur.
Mutlak hata, ölçüm sonucunda elde edilen değer ile miktarın gerçek ölçümü arasındaki fark olarak ifade edilir. Örneğin, l = 100 m'nin gerçek değeri, ancak aynı çizgiyi ölçerken sonuç 100,05 m idi, o zaman mutlak hata:
E = X ölçümü – X
E = 100,05 - 100 = 0,05 (m)
Değeri elde etmek için bir ölçüm yapmak yeterlidir. Buna gerekli denir, ancak daha sıklıkla bir ölçüm sınırlı değildir ve en az iki kez tekrarlanır. Gereğinden fazla yapılan ölçümlere fazlalık (ilave) denir, bunlar ölçüm sonucunu kontrol etmenin çok önemli bir yoludur.
Mutlak hata, sonucun doğruluğu hakkında bir fikir vermez. Örneğin, l = 100 m veya l = 1000 m ölçülerek 0,06 m'lik bir hata elde edilebilir, bu nedenle bağıl hatayı hesaplayın:
C \u003d 0,06 / 100 \u003d 1/1667, yani 1667 m ölçülen l'de 1 metrelik bir hataya izin verildi.
Bağıl hata, mutlak hatanın gerçek veya ölçülen değere oranıdır. Kesir olarak ifade edilir. Talimatlara göre, arazi çizgisi 1/1000'den daha kaba ölçülmemelidir.
Bireysel faktörlerden kaynaklanan hatalara temel denir. Genelleştirilmiş hata, temel olanların toplamıdır.
Kalkmak:
kaba (Q),
sistematik (O),
rastgele (∆).
Brüt ölçüm hataları, icracının büyük hataları, yanlış hesaplamaları, dikkatsizliği, fark edilmeyen arızalar sonucunda ortaya çıkar. teknik araçlar. Büyük hatalar kesinlikle kabul edilemez ve tekrarlanan ek ölçümlerle ölçüm sonuçlarından tamamen çıkarılmalıdır.
Sistematik ölçüm hataları, kusurlarla ilişkili sabit bir bileşendir: görüş, teknik araçların arızası, sıcaklık. Sistematik hatalar hem tek taraflı hem de değişken olabilir (periyodik hatalar). İşin organizasyonunda ve yürütülmesinde mümkünse dikkate alınmaları veya ölçüm sonuçlarının dışında tutulmaları istenir.
Rastgele ölçüm hataları kaçınılmaz olarak tüm ölçümlere eşlik eder. Rastgele hatalar göz ardı edilemez, ancak bunların istenen sonuç üzerindeki etkisi ek ölçümlerle zayıflatılabilir. Bunlar, tüm ölçümlere eşlik eden en sinsi hatalardır. Hem boyut hem de işaret olarak farklı olabilirler.
Büyük ve sistematik hatalar incelenebilir ve ölçüm sonucundan hariç tutulabilirse, derin ölçüm temelinde rastgele olanlar dikkate alınabilir. Olasılık teorisine dayalı çalışma.
Uygulamada zorluk, ölçümlerin bazıları için gerçekleştirilmesinde yatmaktadır. sınırlı miktar kez ve bu nedenle, ölçümlerin doğruluğunu değerlendirmek için, ortalama karekök hatası (RMS) adı verilen yaklaşık bir standart sapma tahmini kullanılır.
Gauss, ortalama karekök hatası için formülü önerdi:
∆ 2 cf = (∆ 2 1 + ∆ 2 2 +… +∆ 2 n) / n,
∆ 2 \u003d m 2 \u003d (∆ 2 1 + ∆ 2 2 + ... + ∆ 2 n) / n,
∆ cf = m = √(∑∆ 2 ben / n)
Formül, hatalar gerçek değerlerden hesaplandığında uygulanır.
Besel formülü:
m = √(∑V 2 ben / (n-1))
Aritmetik ortalamanın kök ortalama kare hatası, tek bir ölçümün kök ortalama kare hatasından Ön kat daha azdır
Bir doğruluk ölçü birimi olarak değerlendirilirken, bire eşit ağırlığa sahip ortalama karekök hatası kullanılır. Bir ağırlık biriminin kök ortalama kare hatası olarak adlandırılır.
µ 2 = P×m 2 – µ = m√P, m = µ / √P, yani Herhangi bir ölçüm sonucunun ortalama karekök hatası, 1 (µ) ağırlığındaki ölçüm hatasının o sonucun ağırlığının (P) kareköküne bölünmesine eşittir.
Yeterli sayıda ölçümle ∑m 2 P=∑∆ 2 P yazabiliriz (çünkü ∆ = m):
µ = √(∑(∆ 2 ×P)/n), yani 1'e eşit bir ağırlığa sahip ortalama kare ölçüm hatası, payda eşit olmayan ölçümlerin mutlak hatalarının karelerinin ağırlıklarına göre çarpımlarının toplamı olan payın kareköküne eşittir ve paydada eşit olmayan ölçümlerin sayısı.
Aşağıdaki formüle göre ortak aritmetik ortalamanın kök ortalama kare hatası:
M 0 = µ / √∑P
µ yerine değerini değiştirerek şunu elde ederiz:
M 0 = √(∑∆ 2 ×P/n) / (√∑P) = √[(∑∆ 2 ×P) / n×(∑P)]
M 0 = √[ (∆ 1 2 P 1 + ∆ 2 2 P 2 +… + ∆ n 2 P n) / n×(P 1 + P 2 + … + P n) ] Gauss formülüdür, kök ortalama toplamın kare hatası aritmetik ortalama, payda eşit olmayan ölçüm hatalarının karelerinin ağırlıklarının çarpımının toplamı olan bir kesrin kareköküne eşittir ve payda, ağırlıklarının toplamına göre ölçüm sayısı.
µ = √ [∑(V 2 ×P) / (n-1)] Bu, ortalamayı hesaplamak için kullanılan Bessel formülüdür. aritmetik hata en olası hataları açısından eşit olmayan bir dizi ölçüm için 1'e eşit bir ağırlık ölçümü ile. Çok sayıda ölçüm için geçerlidir, ancak sınırlı bir ölçüm için (genellikle pratikte) hatalar içerir: m µ = µ / µ tahmininin güvenilirliğidir.
Kontrol görevi 1
Teodoliti incelemek için aynı açıyı defalarca ölçtü. Sonuçlar şu şekildeydi: 39˚17,4"; 39˚16,8"; 39˚16,6"; 39˚16,2"; 39˚15,5"; 39˚15,8"; 39˚16,3"; 39˚16,2". Aynı açı, 39˚16"42" sonucunu veren yüksek hassasiyetli bir gonyometre ile ölçülmüştür. Bu değeri tam olarak alarak, kök ortalama kare hatasını hesaplayın, SCP'nin güvenilirliğini belirleyin ve marjinal hatayı bulun.
| Ölçüm numarası | Ölçüm sonuçları, l | Hatalar | ∆2 |
| 1 | 39˚17.4" | +0.7" | 0.49 |
| 2 | 16.8 | +0.1 | 0.01 |
| 3 | 16.6 | -0.1 | 0.01 |
| 4 | 16.2 | -0.5 | 0.25 |
| 5 | 15.5 | -1.2 | 1.44 |
| 6 | 15.8 | -0.9 | 0.81 |
| 7 | 16.3 | -0.4 | 0.16 |
| 8 | 16.2 | -0.5 | 0.25 |
| toplam | 3.42 |
39˚16"42" = 39˚16.7"
Kök ortalama kare hatası: m = √([∆ 2 ]/n),
m = √(3,42/8) = 0,65".
SKP güvenilirliğinin tahmini: m m = m / √2n,
m m = 0,65 / √16=0,1625≈0,16".
Sınır hatası: ∆ pr \u003d 3 × m,
∆ pr = 3×0,65" = 1,96"
Kontrol görevi 2
Hacmi 50 birim olan üçgenleme üçgenlerinin artıkları verilmiştir. Artıkların gerçek hatalar olduğunu varsayarak, kök ortalama kare hatasını hesaplayın ve SCP'nin güvenilirliğini üretin, marjinal hatayı hesaplayın. Bu kümede rastgele hataların özelliğini kontrol edin:
Lim[∆] / n =0, bunun için W = [W] / n hesaplıyoruz.
| N | W | N | W | N | W | N | W | N | W |
| 1 | +1,02 | 11 | -1,72 | 21 | -0,90 | 31 | +2,80 | 41 | -0,44 |
| 2 | +0,41 | 12 | +1,29 | 22 | +1,22 | 32 | -0,81 | 42 | -0,28 |
| 3 | +0,02 | 13 | -1,81 | 23 | -1,84 | 33 | +1,04 | 43 | -0,75 |
| 4 | -1,88 | 14 | -0,08 | 24 | -0,44 | 34 | +0,42 | 44 | -0,80 |
| 5 | -1,44 | 15 | -0,50 | 25 | +0,18 | 35 | +0,68 | 45 | -0,95 |
| 6 | -0,25 | 16 | -1,89 | 26 | -0,08 | 36 | +0,55 | 46 | -0,58 |
| 7 | +0,12 | 17 | +0,72 | 27 | -1,11 | 37 | +0,22 | 47 | +1,60 |
| 8 | +0,22 | 18 | +0,24 | 28 | +2,51 | 38 | +1,67 | 48 | +1,85 |
| 9 | -1,05 | 19 | -0,13 | 29 | -1,16 | 39 | +0,11 | 49 | +2,22 |
| 10 | +0,56 | 20 | +0,59 | 30 | +1,65 | 40 | +2,08 | 50 | -2,59 |
W = [W] / n, W = +2,51 / 50 = 0,05
Bu durumda, kök ortalama kare hatasının aşağıdaki formüle göre hesaplanması tavsiye edilir: m = √ ( - [W] 2 / n) ÷ (n-1),
m = √(76,5703 - (2,51 2)/50) ÷ 49 = 1,249
SCP'nin güvenilirliğinin aşağıdaki formüle göre değerlendirilmesi: m m = m / √2(n-1),
m m = 1,249/ √(2×49) = 0,13.
Aşağıdaki formüle göre hatayı sınırlayın: ∆ pr \u003d 3 × m,
∆ pr \u003d 3 × 1,249 \u003d 3,747.
Kontrol görevi 5 Formülle hesaplanan UPC mesafesini belirleyin
S \u003d √ (x 2 - x 1) 2 + (y 2 - y 1) 2
x 2 \u003d 6.068.740 m ise; y 2 \u003d 431 295 m;
x 1 \u003d 6 068 500 m; y 2 \u003d 431 248 m;
m x \u003d m y \u003d 0,1 m.
S =√(6.068.740 - 6.068.500) 2 + (431.295 - 431.248) 2 = 235,36
m m = 0,1/ √4 = 0,05
Kontrol görevi 6
Aynı açı 5 kez ölçüldü ve sonuçlar: 60˚41"; 60˚40"; 60˚40"; 60˚42"; 60˚41". matematiksel işlem bu ölçüm serisi
| Np/n | l, ˚ | ε, " | " | v2, " |
| 1 | 60˚41" | 1 | -0,2 | 0,04 |
| 2 | 60˚40" | 0 | +0,8 | 0,64 |
| 3 | 60˚40" | 0 | +0,8 | 0,64 |
| 4 | 60˚42" | 2 | -1,2 | 1,44 |
| 5 | 60˚41" | 1 | -0,2 | 0,04 |
| toplam | 4 | 0 | 2,8 |
l 0 - ölçülen değerin minimum değeri, l 0 \u003d 60˚40 "; ε - ε \u003d l 1 - l 0 olarak elde edilen kalan; L - En iyi değeriölçülmüş değer,
L = [1]/n; m = √([ v 2 ]/(n - 1), burada v, aritmetik ortalamadan sapmadır M, aritmetik ortalamanın doğruluğunun tahminidir, M = m/√n.
L = 60˚40" + 4/5 = 60˚40,8"
m = √2,8 / 4 = 0,7"
M = 0,7"/√5 = 0,313"
Kontrol görevi 7
Aynı konturun alanını bir planimetre ile ölçme sonuçlarının matematiksel olarak işlenmesini gerçekleştirin: 26.31; 26.28; 26.32; 26.26; 26.31 ha.
| Np/n | ben ha | ε, ha | v, ha | v2, ha |
| 1 | 26,31 | 0,05 | -0,014 | 0,000196 |
| 2 | 26,28 | 0,02 | +0,016 | 0,000256 |
| 3 | 26,32 | 0,06 | -0,024 | 0,000576 |
| 4 | 26,26 | 0 | 0,036 | 0,001296 |
| 5 | 26,31 | 0,05 | -0,014 | 0,000576 |
| toplam | 0,18 | 0 | 0,0029 |
L = 26,26 + 0,18/5 = 26,296 ha
m = √0,0029/ 4 = 0,0269 ha
М = 0,0269/√5 = 0,01204 ha
Kıyaslama 8
Bir Cenevre cetveli kullanılarak tesviye çubuğunun santimetre bölümlerinin incelenmesinde, raporun alındığı andaki sıcaklık belirlendi. Beş santimetre segment için aşağıdaki değerler elde edildi: 20.3˚; 19.9˚; 20.1˚; 20.2˚; 20.3˚. Ölçüm sonuçlarının matematiksel işlemlerini gerçekleştirin.
| Np/n | l, ˚ | ε, ˚ | v, ˚ | v2, ˚ |
| 1 | 20,3 | 0,4 | -0,14 | 0,0196 |
| 2 | 19,9 | 0 | -0,26 | 0,0676 |
| 3 | 20,1 | 0,2 | -0,06 | 0,0036 |
| 4 | 20,2 | 0,3 | 0,04 | 0,0024 |
| 5
Bunlara ihtiyaç yoktur, o zaman harcanan zaman açısından gerekçelendirilirse araç manuel olarak geliştirilmelidir ve maddi kaynaklar. 2. Elektronik tabloları kullanarak jeodezik ölçümlerin işlenmesi Bir topografik ve jeodezik çalışma kompleksi sonucunda elde edilen bilgilerin ilk işlenmesi için, bir paket olan TOGI programını kullandım ...
Şantiyede, SNiP Sh-4-80 "İnşaatta güvenlik" bölümünde ve departman talimatlarında belirtilen güvenlik standartları ve yönetmeliklerinin gerekliliklerine uyulması gerekir. İnşaat departmanının emriyle talimat verilen kişilerin jeodezik çalışmaları yapmasına izin verilir. Yaralanma veya yaralanma riski çalışma koşullarına bağlı olarak belirlenir...
Yazarın doğrudan katılımıyla elektronik cihazlar. İkinci bölüm. İkinci bölüm, metrolojik tesisler hakkında araştırma yapmak için geliştirilen yöntemleri tartışır ve yükseklikleri ölçmek için jeodezik aletleri kontrol etmek ve kalibre etmek için kullanılır. Jeodezik aletlerin düşey açılarının ölçülmesindeki kısa dönemli hatayı incelemek için bir yöntem. Çalışmada önemli bir görev... |
İşte hatalarla ilişkili başka bir ortalama.
Kök ortalama kare hatası(SKP), ölçüm sonuçlarının doğruluğunun veya ölçülen değerlerin fonksiyonlarının bir ölçüsüdür ve olasılıksal bir özelliktir.
Pirinç. 3.1. Normal dağılım yasası
rastgele hatalar
Kök ortalama kare hatasının değerini bildiğimizi varsayalım. M. Normal dağılım yasasına göre, görünüşteki gerçek hataların dağılımının grafiği, Şekil 1'deki grafiğe benzer olacaktır. 3.1. Parametre R bir veya daha fazla büyüklükte ve işarette rastgele hataların meydana gelme sıklığını (veya sıklığını) karakterize eder. Bu durumda, önceden belirlenmiş bir aralıkta meydana gelen hataların olasılığı, örneğin, ± M, dağılım eğrisi ile sınırlanan şeklin alanı ve değerler üzerindeki ordinat bölümleri tarafından belirlenir + M Ve - M. Normal bir dağılım yasası için, belirlenen aralıklarda meydana gelen hataların olasılığı aşağıdaki değerlere eşittir:
Aralık için ± M ® R= %68,3 (» %68);
±2 aralığı için M® R= %95,5 (» %95);
±3 aralığı için M® R= %99,7 (neredeyse %100).
Böylece 1000 vakadan sadece 3'ünde 3 değerini aşan bir hata olabilir. M. Mutlak değerde 3'ten büyük hatalar M(sınırlama hatası), kaba olarak kabul edilir ve bu kaba hatayı içeren ölçüm sonuçları daha sonraki işlemlerden hariç tutulur. Bazı durumlarda, ölçüm doğruluğu gereksinimlerini sıkılaştırmak için, 2 aralığında bir marjinal hata ayarlanır. M 3'e kadar M.
Tablo 3.1
Öğrenci katsayısı değerleri ( T) farklı olasılıklar için ( R)
| T | P% | T | P% | T | P% |
| 0,1 | 8,0 | 1,1 | 72,9 | 2,1 | 96,4 |
| 0,2 | 15,9 | 1,2 | 77,0 | 2,2 | 97,2 |
| 0,3 | 23,6 | 1,3 | 80,6 | 2,3 | 97,9 |
| 0,4 | 31,1 | 1,4 | 83,8 | 2,4 | 98,4 |
| 0,5 | 38,3 | 1,5 | 86,6 | 2,5 | 98,8 |
| 0,6 | 45,1 | 1,6 | 89,0 | 2,6 | 99,1 |
| 0,7 | 51,6 | 1,7 | 91,1 | 2,7 | 99,3 |
| 0,8 | 57,6 | 1,8 | 92,8 | 2,8 | 99,5 |
| 0,9 | 63,2 | 1,9 | 94,3 | 2,9 | 99,6 |
| 1,0 | 68,3 | 2,0 | 95,5 | 3,0 | 99,7 |
Genellikle UPC'nin değeri bir katsayı ile gösterilir. T (Öğrenci katsayısı), güven aralığını belirleyen ( X± tm) belirlenen olasılık düzeyinde ölçüm sonucu R. Bunun için tabloyu kullanmak uygundur. 3.1.
Örneğin, tanımlamanız gerekir güven aralığı miktar için X%90 şansla. Tablodan, enterpolasyon yoluyla şunu buluruz: R 1 = 89,0% t1= 1.6, için R 2 = 91,1% t2 = 1,7: t x= 1,6476 » 1,65.
Bu, %90 olasılıkla ölçüm sonucunun ( X±1,65 M).
Ölçülen değer ise X biliniyorsa, SCP'nin değeri şu şekilde belirlenir: Gauss formülü:
nerede Δ - gerçek ölçüm hataları.
[...] işaretinin bir Gauss toplamının işareti olduğunu hatırlayın.
Ölçülen değerin bilinmediği durumlarda, Bessel formülü:
Nerede v- ölçüm sonuçlarının aritmetik ortalamadan sapması.
Formül (3.9) ve (3.10)'dan da görülebileceği gibi, ölçülen değerin bilinmesi durumunda, doğruluğu tahmin etmek için bir ölçüm yeterlidir (gerekli). Yukarıda bahsedildiği gibi, bilinen miktarları (standartları) ölçerken standartlaştırılmış aletlerin doğruluğunu değerlendirmede çoğunlukla Gauss formülü kullanılır. Bessel formülünü kullanarak doğruluğu değerlendirmek için en az iki ölçüm gereklidir. Bessel formülü, önceden bilinmeyen bir niceliğin kütle (çoklu) ölçümlerinin sonuçlarının doğruluğunu tahmin etmede kullanılır.
Ölçüm sayısının artması ile Gauss ve Bessel formüllerinin elde ettiği SQL değerleri hemen hemen aynı hale gelmektedir (yaklaşık olarak N³ 20). Bu durumda, bir ölçümün SCP'sinin değeri sınıra yönelir. m önce, aletin doğruluğu, ölçüm yönteminin veya programın doğruluğu ile belirlenir. Açıkçası, pratikte bir niceliğin çok sayıda ölçümünü sağlamanın imkansız ve birkaç nedenden dolayı uygun olmadığı yukarıda zaten söylenmişti. Bu durumda pratik ölçüm sayısı, ölçüm sonucunun belirli bir doğruluk düzeyinde ve belirli bir güven seviyesinde elde edilmesini sağlamalıdır.
Ölçüm sayısı sınırlı olduğundan, SCP'nin kendisi yaklaşık formül tarafından belirlenen bir hata içerir:
Buna şöyle denir - kök ortalama kare hatasının (SKP SKP) kök ortalama kare hatası.
Burada hataların sınıflandırılmasına geri dönmek uygun olacaktır. Yukarıda her tür hata bizim tarafımızdan dikkate alınmamaktadır.
Genellikle, sözde bir dizi ölçüm hatası çalışmasında. olası hata, harfle gösterilir R. Muhtemel hatanın değeri, yaklaşık formülle tahmin edilebilir.
tabii ki hataların dağılımının normal yasaya uyduğunu varsayarsak.
Muhtemel hata da denir medyan hata. (3.12) formülünü kullanarak hesaplamalar yapmak istemiyorsanız, çünkü bu değer içerir. M Bessel formülü ile elde edilmesi gereken, o zaman bir dizi hatayı mutlak değerlerdeki artış sırasına göre düzenleyerek olası veya medyan hatayı belirlemek mümkündür. Ortaya çıkan serinin ortasında bu hatanın değeri olacaktır. Bu, hata sayısı tek ise. Ve eğer çift ise, medyan hata, satırın ortasındaki komşu hataların ortalama değeri olacaktır.
Medyan hata ile karıştırmayın ortalama hata, basit bir formülle de elde edilebilir:
Ayrıca bir takım ölçümlerin (hataların) normal yasaya tabi olması koşulunu da gerektirir.
ortalama hata matematiksel beklenti mutlak değerler herhangi bir değerin ölçüm sonuçlarının bu sonuçlar için matematiksel beklentiden sapmaları. Ortalama hatanın yaklaşık değeri aşağıdaki formülle tahmin edilebilir:
Nerede v ben– ölçüm sonuçlarının aritmetik ortalamalarından sapması.
Genellikle formül (3.13), kök ortalama kare hatasının bir ön tahmini için kullanılır.
Rastgele hatalar, her bir ölçüm sonucu üzerindeki etkisinin boyutu ve doğası bilinmeyen hatalar olarak adlandırılır. Rastgele hataların büyüklüğü ve işareti önceden belirlenemez. Ölçümü yalnızca kullanılan aletlerle elde edilebilecek doğrulukta gerçekleştirdiğimiz için kaçınılmazdır ve her ölçüme eşlik ederler. Ölçüm sonuçlarını rastgele hatalardan tamamen kurtarmak imkansızdır. Ancak özelliklerini inceleme temelinde, bir dizi ölçümden en güvenilir sonuçların nasıl elde edileceğine ve bunların doğruluğunun nasıl değerlendirileceğine dair kurallar çıkarmak mümkündür. Bu sorular, ölçüm hataları teorisi tarafından ele alınmaktadır.
Hata teorisinde, eşit ve eşit olmayan ölçümler ayırt edilir. Eşdeğer ölçümler, aynı koşullar altında, aynı hassasiyete sahip cihazlarla, aynı sayıda, aynı niteliklere sahip gözlemciler tarafından yapılan ölçümlerdir. Bu koşullardan biri karşılanmazsa, bu tür ölçümler eşit olmayacaktır.
Rastgele hataların özellikleri. Rastgele hatalar, aynı miktarın ölçülen ve gerçek değerleri arasındaki fark olarak tanımlanabilir. Birçok rasgele hata dizisinin teorik ve pratik çalışmasına dayanarak, bunların genel özellikleri türetilmiştir:
1 Bu koşullar altında rastgele hatalar belirli bir sınırı aşamaz.
2 Aynı mutlak değerin pozitif ve negatif hataları eşit derecede mümkündür.
3 Küçük hatalar, büyük hatalardan daha yaygındır.
4 Aynı değerin eşit derecede doğru ölçümlerinin rastgele hatalarının aritmetik ortalaması, ölçüm sayısındaki sınırsız artışla birlikte sıfır olma eğilimindedir.
4.2 Aritmetik ortalama ilkesi
Gerçek değeri X olan aynı miktarın l 1 , l 2 , ... , l n'nin eşit ölçümlerinin yapılmasına izin verin.Daha sonra rastgele hataların n değerleri hesaplanabilir:
Δ 1 \u003d l 1 - X;
Δ 2 \u003d l 2 - X; (4.1)
Δ n \u003d ln - X.
Bu eşitliklerin sol ve sağ kısımlarını toplayarak şunu elde ederiz:
Δ 1 + Δ 2 +…+ Δ n = l 1 + l 2 +…+ l n – nX. (4.2)
Hata teorisinde, miktarların toplamını köşeli parantezlerle belirtmek gelenekseldir, örneğin:
Δ 1 + Δ 2 + ... + Δ n = [Δ]; l 1 + l 2 + … + l n = [l], vb.
Bu gösterimlerle, eşitlik (4.2) şeklini alır.
[Δ] = [l] - nX , dolayısıyla X = [l] / n - [Δ] / n. (4.3)
Rastgele hataların dördüncü özelliğine göre, eşitlikteki (4.3) [Δ] / n değeri, ölçüm sayısındaki sınırsız artışla sıfıra meyleder. Sonuç olarak, bu koşullar altında [l] / n değeri, X'in gerçek değerine yaklaşacaktır. Buna dayanarak, aritmetik ortalama (ölçüm sonuçlarının aritmetik ortalaması), eşit derecede doğru ölçümlerin en güvenilir veya en olası sonucu olarak kabul edilir. herhangi bir sayıda ölçüm için aynı değerin.
L \u003d [l] / n \u003d (l 1 + l 2 + l 3 + ... + l n) / n. (4.4)
4.3 Bir ölçümün ortalama kare hatasının kökü.
Gauss ve Bessel formülleri
Hata teorisinde, ölçümlerin doğruluğu, ünlü Alman matematikçi ve araştırmacı K. F. Gauss (1777–1855) tarafından ortaya atılan ve m ile gösterilen ortalama karesel hata ile karakterize edilir:
______________________ ______
m = ± √ (Δ 1 2 + Δ 2 2 + .. + Δ n 2) / n = ± √ [Δ 2 ] / n, (4.5)
Δ 1 , Δ 2 , …, Δ n rastgele hatalardır;
n, ölçüm sayısıdır.
Kök ortalama kare hatası, ölçümlerin doğruluğunu değerlendirmek için güvenilir bir kriterdir. Az sayıda ölçümle bile oldukça kararlıdır ve büyük ölçümlerin varlığını iyi yansıtır. rastgele hatalar, esasen ölçümlerin kalitesini belirleyen.
Ölçülen niceliğin gerçek değeri bilindiğinde, formül (4.5) ortalama karesel hatanın kökünü hesaplamak için kullanılır. Bu durumlar pratikte çok nadirdir. Kural olarak, ölçülen niceliğin gerçek değeri bilinmemekle birlikte, en güvenilir sonuç olan aritmetik ortalama, ölçümlerden elde edilebilir. Bireysel sonuçları aritmetik ortalamadan sözde en olası hatalar V cinsinden saptırarak ortalama karesel hatanın kökünü hesaplamak için bir formül elde ederiz.
l 1 , l 2 , ..., l n gerçek değeri X ve aritmetik ortalaması L olan aynı niceliğin eşit derecede doğru ölçümlerinin sonuçları olsun. O zaman n rasgele veya gerçek hata hesaplayabilirsiniz.
Δ ben = l ben – X (4.6)
ve n en olası hatalar
V ben = l ben – L. (4.7)
Eşitlik için n'nin toplamı (4.7)
[V] = [l] - nL. (4.8)
Ancak, (4.4) eşitliğine göre nL = [l], dolayısıyla
yani, en olası hataların toplamı her zaman sıfıra eşit olmalıdır.
Eşitliği (4.7) eşitlikten (4.6) çıkararak şunu elde ederiz:
Δ ben – V ben = L – X. (4.10)
Eşitliğin (4.10) sağ tarafında, aritmetik ortalamanın rastgele bir hatası var. Bunu ε ile gösteriyoruz. Daha sonra
Δi = V ben + ε. (4.11)
Eşitliğin (4.11) karesini alır, toplamlarını alır ve n'ye böleriz:
[Δ 2 ] / n = / n + nε 2 / n + 2ε[V] / n. (4.12)
Bu eşitliğin sol tarafı m 2'den başka bir şey değildir. Eşitlik (4.9) açısından sağ taraftaki son terim sıfıra eşittir.
m 2 = / n + ε 2 . (4.13)
Rastgele hatayı ε ortalama değeriyle, yani aritmetik ortalamanın kök ortalama kare hatasıyla değiştiririz. Aşağıda kanıtlanacak aritmetik ortalamanın ortalama kare hatası
M 2 \u003d ε 2 \u003d m 2 / n. (4.14)
m 2 - m 2 / n = / n veya m 2 (n - 1) / n = / n,
Neresi ___________
m 2 \u003d / (n - 1) veya m \u003d √ / (n - 1). (4.15)
Formül (4.15) denir Bessel formülü ve harika pratik değer. Ölçüm sonuçlarının aritmetik ortalamadan en olası sapmalarından ortalama karesel hata kökünü hesaplamanıza olanak tanır.
Ortalama kare hatasına ek olarak, ortalama, olası ve göreceli hatalar da vardır.
Ortalama hata (Θ), rastgele hataların mutlak değerlerinin aritmetik ortalamasıdır, yani.
Θ = (|Δ 1 | + |Δ 2 | + … + |Δ n |) / n = [|Δ|] / n. (4.16)
Hata teorisinde, n → ∞ Θ = 0,8 m veya m = 1,25Θ olduğu kanıtlanmıştır.
Bazen uygulamalı sorularda kullandıkları olası hata R. Muhtemel bir hata, bir hatanın mutlak değer olarak bu değerden hem daha fazla hem de daha az eşit derecede olası olduğu, eşit derecede doğru ölçümlerin bir serisindeki rastgele bir hatanın böyle bir değeridir. r'yi bulmak için, bu dizinin tüm hataları mutlak değerde artan sırada düzenlenir ve ortadaki konumu işgal eden değer seçilir, yani ondan daha çok hata olduğu kadar az da vardır. Muhtemel hata, r = 2/3 m = 0,67 m veya m = 1,5 r ilişkisiyle ortalama karekök hatasıyla ilişkilidir.
Görüldüğü gibi, m > Θ ve m > r, ortalama karesel hatanın kökünün ölçüm doğruluğunu ortalama ve olası hatalardan daha iyi karakterize ettiğini gösterir.
Çizgiler, alanlar ve hacimler gibi ölçülen niceliklerin doğruluğu genellikle bağıl hata. Bağıl hata, mutlak hatanın ölçülen değerin değerine oranıdır. Bağıl hata, payı bir olan bir kesir olarak yazılır ve payda, ölçülen değerin hangi oranının izin verilen hata olması gerektiğini gösteren bir sayıdır. Örneğin, kenar uzunluğu D = 150 m ile ölçülen mutlak hata m d = 0,05 m O zaman ölçüm sonucunun bağıl hatası m d / D = 0,05 m / 150 m = 1/3000 olacaktır.
1 / 3000 değeri, 3000 m'lik bir mesafe için 1 m'lik bir hataya izin verilebileceği anlamına gelir Bağıl hatanın paydası ne kadar büyük olursa, ölçüm doğruluğu o kadar yüksek olur. Jeodezideki tüm doğrusal ölçümlerin doğruluğu her zaman belirtilir bağıl hata Bu tür jeodezik işlerin üretimi için ilgili talimat ve el kitaplarında verilen.
4.4 Hataların normal dağılım yasası.
sınır hatası
Rastgele hataların özelliklerinin önceki değerlendirmesinden, ayrı bir hatanın ortaya çıkması hakkında önceden kesin bir şey söylemenin imkansız olduğu sonucu çıkar. Bununla birlikte, bu hataların sayısı arttığında, belirli bir ölçüm serisindeki tüm hatalar için belirli modeller oluşturulabilir. Bu düzenlilikler, K. F. Gauss tarafından elde edilen denklemle ifade edilebilir. benziyor
y = (1 / σ √2π) e – (l ben – a) / 2 σ = (1 /σ √2π) e – Δ c / 2 σ , (4.17)
burada y, hata dağılım yoğunluğudur;
σ, standart olarak adlandırılan ve ortalama ile ilişkili denklemin parametresidir.
ikinci dereceden hata oranı
a matematiksel beklenti adı verilen denklemin bir parametresidir,
ilişki ile aritmetik ortalama ile ilgilidir
e - taban doğal logaritmalar;
Δ ben = l ben - bir - rastgele hata.
Bu denklem denir normal dağılım kanunu hatalar.
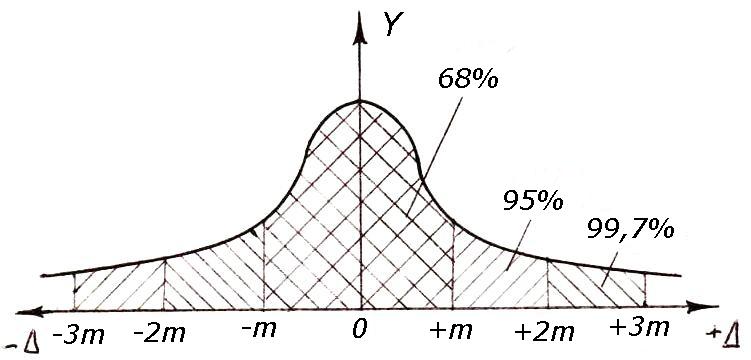
Denklem (4.17), normal dağılım eğrisi (Gauss eğrisi) adı verilen çan şeklindeki bir eğriye karşılık gelir (Şekil 4.1)
Şekil 4.1 - Gauss eğrisi
Eğri ve x ekseni ile sınırlı olan eğri altındaki alan bire eşit alınır. Bu alanın apsis ekseninin herhangi bir bölümüne karşılık gelen kısmı, bu aralığa düşen rastgele bir hata olasılığını verir. l ben = a veya Δ = 0 için şunu elde ederiz: maksimum değer eğri koordinatları __
Y = 1 / σ √2π.
Şekil 4.1, hataların büyük kısmının en olası hata değeri Δ i = 0 etrafında gruplandığını göstermektedir (rastgele hataların dördüncü özelliğine göre, rastgele hataların aritmetik ortalaması sıfıra eğilimlidir). Bu hüküm, rastgele hataların üçüncü özelliğini doğrular (küçük hatalar büyük olanlardan daha yaygındır). Pozitif ve negatif hataların eşit oluşumuyla ilgili rastgele hataların ikinci özelliği, normal dağılım eğrisinin OY ekseni etrafındaki simetrisi ile karakterize edilir.
Teorik çalışmalar ve jeodezik ölçüm uygulamaları, tüm rasgele hataların %68'inin -m ila +m arasındaki aralıklarda (bkz. Şekil 4.1), hataların %95'inin iki kat daha büyük aralıklarda (–2m'den +2m'ye) düştüğünü göstermektedir. ) ve hataların %95'i, hataların %99,73'üne isabet eden üç kat daha büyük (–3m'den +3m'ye) aralığa düşüyor. Bu, 100 ölçüm hatasından yalnızca 32'sinin mutlak değer olarak ortalama karekök hatası m'yi aşacağı, 1000 hatadan 3'ünün üçlü kök ortalama karesel hatayı ±3m aşacağı anlamına gelir. Böylece, ölçüm hatalarının yalnızca %0,27'si ±3 m'nin ötesine geçer. Bu nedenle, sınırlayıcı hata Δ olarak, üçlü ortalama karekök hatası alınır, yani
Δ ön = 3m. (4.18)
Şimdi (4.17) denklemindeki a ve σ parametrelerinin özünü düşünün. a parametresi matematiksel beklenti olarak adlandırılır ve Gauss eğrisi üzerindeki gruplama merkezini, yani gruplama merkezinin eğrinin şeklini korurken apsis ekseni boyunca yer değiştirmesini (Şekil 4.2, a) karakterize eder. a parametresinin sabit bir değerinde, ölçümlerin doğruluğunu karakterize eden başka bir parametreyi σ (standart olarak adlandırılır) değiştirirsek ve bu, ölçüm yöntemini değiştirirsek veya başka cihazlarla gerçekleştirirsek mümkündür. Daha sonra gruplama merkezi değişmeden kalır ve eğrinin şekli değişir. Ölçüm doğruluğu azalırsa düzleşir, doğruluk arttıkça dikleşir (Şekil 4.2, b).
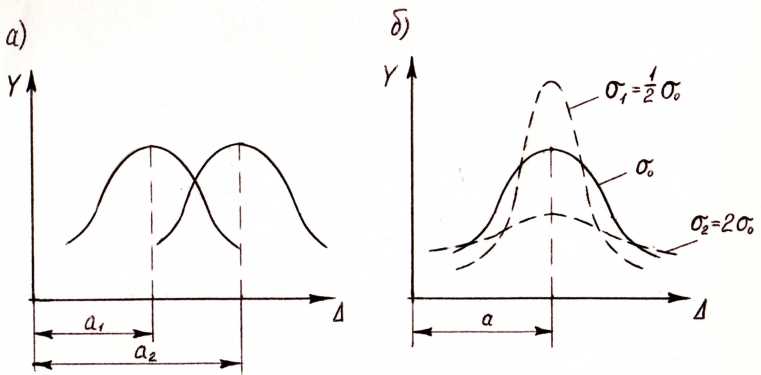
Şekil 4.2 - Normal eğrinin kaydırılması ve yeniden şekillendirilmesi
a ve σ parametreleri önceden, ölçümlerden önce bilinmemektedir. Sonuç olarak elde edilirler Büyük bir sayıölçümler. Uygulamada, a ve σ parametreleri yerine yaklaşık değerlerini elde ederiz: formül (4.4) ile hesaplanan aritmetik ortalama L ve formül (4.5) veya (4.15) ile hesaplanan kök ortalama kare hatası m.
4.5 Bir fonksiyonun RMS hatası
miktar ölçümleri
Jeodezide, yalnızca ölçülen niceliklerin değil, aynı zamanda işlevlerinin de doğruluğunu belirlemek genellikle gereklidir. Örneğin, bir çizginin yatay döşenmesi, mesafenin eğiminin ve eğim açısının bir fonksiyonudur, planimetre tarafından belirlenen alan, planimetre üzerindeki okumaların bir fonksiyonudur, vb. fonksiyonların kök ortalama kare hatalarını hesaplamak için. Bazı fonksiyon türlerini ele alalım.
m = nm 2 veya m φ = m√ n, (4.27)
yani, eşit derecede doğru ölçülen değerlerin toplamının kök ortalama kare hatası, tek bir ölçümün kök ortalama kare hatasının √n katıdır.
ÖRNEK Bir köşenin ortalama karekök hatası ±30 "" ise, bir dörtgende ölçülen açıların toplamının ortalama karesel hatasının kökünü bulun. Formül (4.27) ile buluruz
m φ \u003d ± 30 "" √ 4 \u003d ± 60 "" \u003d 1 ".
2Çizgi görünümü işlevi
burada K sabit bir sayıdır;
X, ölçümlerden elde edilen argümandır.
X, rasgele bir hata ΔX ile ölçülürse, fonksiyonun rasgele bir hatası olacaktır.
Δ φ \u003d K Δ X. (4.29)
Argümanı n kez ölçtükten sonra, n denklem (4.29) oluşturulabilir, karelerinin toplamı alınabilir ve n'ye bölünebilir. Bundan sonra alırız
[Δ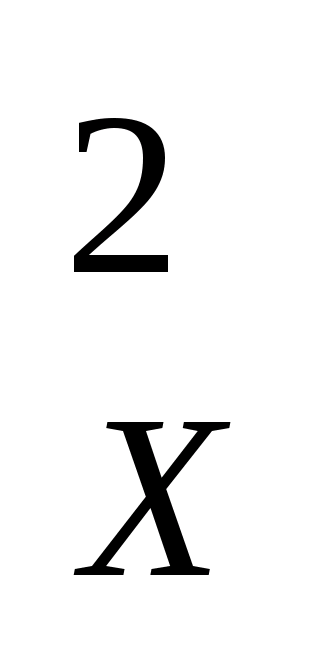 
] / n = K 2 [Δ] / n veya m = K 2 m, (4.30)
mφ = KmX . (4.31)
Bir öncekine benzer şekilde, fonksiyon için gösterilebilir.
φ = ± K 1 X ± K 2 Y ± … ± K n U (4.32)
Δ φ \u003d K 1 Δ X ± K 2 Δ Y ± ... ± K n Δ U (4.33)
m= (K 1 m X) 2 + (K 2 m Y) 2 + … + (K n m U) 2 . (4.34)
ÖRNEK Tek bir ölçümün kök ortalama kare hatası m'ye eşitse, aritmetik ortalama L'nin kök ortalama kare hatası M'yi belirleyin. Aritmetik ortalamanın formülünü (4.4) aşağıdaki biçimde yazıyoruz:
L \u003d l 1 / n + l 2 / n + ... + l n / n. (4.35)
Gördüğünüz gibi, fonksiyon (4.35) için formül (4.34) buraya uygulanabilir:
M 
\u003d M 2 \u003d (m 1 / n) 2 + (m 2 / n) 2 + ... + (m n / n) 2.
Ölçümlerin göz önüne alındığında l 1 , l 2 ,…, l n eşittir, yani m 1 = m 2 = … = m n , elde ederiz
M 2 \u003d n (m / n) 2 \u003d m 2 / n,
M = m / √n , (4.36)
yani, aritmetik ortalamanın ortalama karekök hatası, tek bir ölçümün kök ortalama karesel hatasından √n kat daha azdır.
3İşlev Genel görünüm
φ = f (X, Y, Z, … ,U), (4.37)
burada X, Y, Z, …, U bağımsız olarak ölçülen değerlerdir.
Rastgele hataları hesaba katan fonksiyon (4.37) şu formu alır:
φ + Δ φ \u003d f (X + Δ X; Y + Δ Y; Z + Δ Z; ...; U + Δ U). (4.38)
(4.38) fonksiyonunu bir Taylor serisinde genişleterek ve kendimizi sadece rasgele hataların ilk kuvvetleriyle sınırlayarak, fonksiyonu elde ederiz.
Δ φ = (∂f/∂x) Δ X + (∂f/∂y) Δ Y + (∂f/∂z) Δ Z + … + (∂f/∂u) Δ U , (4.39)
burada (∂f/∂x), (∂f/∂y), …, (∂f/∂u) fonksiyon için kısmi türevlerdir.
(4.39) sabittir.
Görüldüğü gibi (4.39) fonksiyonu (4.33) fonksiyonuna benzer. Bu nedenle, kökünün karesi ortalama kare hatası
= (∂f/∂x ∙ m X) 2 + (∂f/∂y ∙ m Y) 2 + (∂f/∂z ∙ m Z) 2 + … + (∂f/∂u ∙ m U) 2 . (4.40)
ÖRNEK Dikdörtgenin iki kenarı ölçülür - X = 200 m ve Y = 100 m, ortalama karekök hataları m X = +0,20 m ve m Y = +0,10 m.
Dikdörtgen P'nin alanını ve kök ortalama kare hatası m P'yi belirleyin.
.m = √ / 2n. (4.43)
Formül (4.43), n çift ölçümden tek bir ölçümün ortalama karekök hatası için bir ifade verir.
4.7 Eşit olmayan ölçümler
Önceki bölümlerde, eşdeğer ölçümler ele alındı. Bununla birlikte, pratikte, farklı koşullar altında veya farklı doğruluktaki aletlerle, farklı sayıda adımla gerçekleştirilen eşit olmayan ölçümler sıklıkla yapılır. Bu durumda, artık kendinizi basit bir aritmetik ortalama ile sınırlamak mümkün değildir, burada her bir ölçüm sonucunun güvenilirlik derecesi dikkate alınmalıdır.
Ölçüm sonucunun sayı olarak ifade edilen güvenilirlik derecesi, bu ölçümün ağırlığı olarak adlandırılır. Sonuç ne kadar güvenilir olursa, ağırlığı da o kadar büyük olur. Bir dizi ortalama değere sahip olalım: L 1 , L 2 , …, L n - Р 1 , Р 2 , …, Р n bireysel ölçümlerden elde edilen bir değer.
Formül (4.4)'e göre, L i P i ürünü, bu serideki bireysel ölçümlerin toplamına eşit olacaktır ve tüm serilerdeki tüm ölçümlerin toplamı L 1 P 1 + L 2 P 2 +'ya eşit olacaktır. ... + L n P n . Tüm ölçümlerin sayısı P 1 + P 2 +…+ Pn'ye eşit olacaktır.
Buradan, aritmetik ortalama kuralına göre, tüm ölçüm serilerinin ortalama değerini elde ederiz:
L o = (L 1 P 1 + L 2 P 2 + ... + L n P n) / (P 1 + P 2 + ... + P n) = / [P]. (4.44)
İfade (4.44) çağrılır ağırlık ortalama formülü veya ortak aritmetik ortalama. Burada her satırdaki ölçüm sayısı P 1 , P 2, ..., P n ortalama sonuçların ağırlığı L 1 , L 2 , ..., L n ve ağırlıkların toplamı ağırlıktır toplam aritmetik ortalamanın L o . Ölçüm sonuçlarının ve ağırlıklarının bilindiği tüm durumlarda, olası değerölçülen değer formül (4.44) ile hesaplanır.
Bir ölçümün kök ortalama kare hatasını μ ile ve L 1 ,L 2 ….L n değerlerinin ortalama kare hatalarını sırasıyla m 1 , m 2 , …, m n ile gösterelim. O halde (4.36) eşitliğine göre ___ __ __ yazabiliriz.
m 1 = μ / √ P 1 ; m2 \u003d μ / √ P2; …; m n = μ / √ P n . (4.45)
Formül (4.45)'te P ben = 1 alırsak, μ = m ben . Buradan, μ'nin, ağırlığı bire eşit olan ölçümün ortalama kare hatasının kökü veya ağırlık biriminin sözde kök ortalama kare hatası olduğu sonucu çıkar.
ödevHata türleri. Neredeyse her zaman, hata iki bileşeni içerir: sistematik ve rastgele.
Δa= Δasyst + Δaran.
Sistematik verilen koşullar altında sabit kalan (veya değişen, ancak bilinen bir yasaya göre değişen) hata olarak adlandırılır.
Bu tür hatalar sürekli olarak neden olur işletme nedenleri, bunun bir sonucu olarak, ölçerken her seferinde aynı miktarda "hata yaparız". Çoğu zaman, bu tür hatalara cihazın hatalı imalatı (enstrümantal hatalar) veya sürekli harici faktör. Örneğin, uçağın kendi manyetik alanı, her rotada iyi tanımlanmış bir değere sahip olan manyetik rotanın (sapma) ölçülmesinde bir hataya neden olur.
Sistematik hatalar, her ölçüm için aynı olduğundan, daha doğru cihazlarla bir kez belirlenebilir ve daha sonra düzeltmeler yapılarak ölçüm sonuçlarından elimine edilebilir.
Sistematik hatalar, navigasyon sırasında fazla sorun yaratmaz, çünkü ortadan kaldırıldıktan sonra artık mevcut değildirler. Bu nedenle, ayrıca hiçbir sistematik hata olmadığını varsayacağız (zaten dikkate alınmıştır).
rastgele hata her ölçüm için farklı anlam hangisi önceden bilinmez.
Ancak rastgele hatalar, her ölçüm için farklı oldukları için prensip olarak ortadan kaldırılamaz. Ve her zaman bilinmez kalırlar.
Rastgele hataların sayısal değerlerini belirlemek imkansızdır ancak pilot bu hataların var olduğunu daima akılda tutmalı ve olası değerlerinin farkında olmalıdır. Ölçüm sonuçlarındaki belirsizliğin varlığı, navigasyonu karmaşıklaştıran ve onu sadece bir bilim değil, bir sanat haline getiren ana faktörlerden biridir.
Rastgele bir olay, belirli koşullar altında meydana gelebilecek veya gelmeyebilecek bir olaydır. Böyle bir olayın meydana gelme olasılığının derecesi, olasılığın büyüklüğü ile sayısal olarak karakterize edilir. P olasılığı, 0 ile 1 arasında değişebilen bir sayıdır. Belirli koşullar altında bir olay asla gerçekleşmiyorsa, buna imkansız olay denir ve olasılığı sıfırdır. Her zaman belirli koşullar altında gerçekleşiyorsa, o zaman güvenilir olarak adlandırılır ve ona bir olasılık atfedilir. bire eşit. Örneğin, P = 0,3 ise, bu, ortalama olarak 100 vakadan 30'unda bir olayın meydana geleceği anlamına gelir. Olay rastgele olduğu için ortalamadır. Bir olayın meydana gelmesi için gerekli koşulları yaratır ve 100 deneylik bir dizi yürütürseniz, olay örneğin 23 kez veya 32 kez meydana gelebilir ... Bu tür birkaç deney serisi veya bir dizi yaparsanız bin, on bin, milyon deneyden, o zaman gerçekleştirilen deney sayısı ne kadar fazlaysa, olayın ortalama oluşum sayısı, toplam deney sayısının %30'una o kadar yakın olacaktır (eğer P = 0.3 ise).
O halde, herhangi bir kesin anlamı yoksa rastgele hatalar nasıl açıklanabilir? Genellikle, σ (sigma) harfi ile gösterilen ortalama karesel hatanın (MSE) değeri ile karakterize edilirler. Örneğin, a miktarının ölçüm SQL'i σa ile gösterilecektir.
SCP, bir niceliğin ölçülen değerinin gerçek değeri etrafındaki dağılım derecesinin bir özelliğidir. σa ne kadar büyükse, ölçülen daha fazla saçılmış (dağınık) farklı deneyimler miktarın gerçek değeri civarında değerler.
Şek. 2.19 sayısal eksen olarak geometrik olarak temsil edilir olası değerlerölçülmüş değer A ve gerçek değeri not edilir. Ölçek üzerindeki çarpılar, birkaç deney sonucunda elde edilen ölçülen değerleri gösterir. İlk durumda ölçülen değerlerin gerçek değer etrafındaki yayılımı ikinci duruma göre daha fazladır, bu nedenle yayılma derecesini karakterize eden “sigma” ikinci durumda daha küçüktür.
Pirinç. 2.19. Kök ortalama kare hatası
SCP'nin değeri, ölçülen değerin bir veya başka bir değer alma olasılıklarını yargılamak için kullanılabilir. Ancak bunun için SCP'yi bilmek yeterli değil, bu rastgele hatanın hangi dağıtım yasasına uyduğunu da bilmeniz gerekiyor. Birçok rasgele değişken, normal (Gauss) dağılım yasasına uyar. Bu yasa için aşağıdaki değerleri hatırlamakta fayda var.
Eğer Sistematik hata yoktur ve ölçüm sonucunda a değeri elde edilir, ardından miktarın gerçek değeri içinde bulunur (Şekil 2.20):
ameas ± σa, Р=0.68 olasılıkla;
ameas ± 2σa, Р=0.95 olasılıkla;
ameas ± 3σa, Р=0.997 olasılıkla.
Pirinç. 2.20. Normal dağılım için bazı olasılıklar
Örneğin, bir pusula yardımıyla rota γ=100º ölçülür ve pusulanın doğruluğu SCP σγ =2º ile karakterize edilir. Bu, gerçek oranın (bizim için bilinmeyen kalacak) anlamına gelir. ortalama:
100 vakadan 68'inde 100º ± 2º içinde, yani 98º ... 102º aralığında;
100 vakanın 95'inde 100º ±4º içinde, yani 96º ... 104º aralığında;
1000 vakadan 997'si 100º ±6º içinde, yani 94º ... 106º aralığındadır.
olasılık değeri R=0.997, bire o kadar yakındır ki, karşılık gelen üç-sigma hatası genellikle maksimum hata olarak anılır. Aslında, hata onu aşabilir. Doğru, nadiren - ortalama olarak bin vakadan üçünde.
İÇİNDE teknik açıklamalar aletler ve ekipman, doğrulukları doğrudan UPC şeklinde gösterilebilir ve ardından her şey netleşir. Ancak bazen, örneğin şu şekilde belirtilir: "rulman ölçüm hatası ± 1,5º". Elbette bu, böyle bir yön bulucunun her seferinde 1,5º "hata yaptığı" anlamına gelmez. Ayrıca hata yapamayacağı anlamına da gelmez. Daha 1,5º'den fazla. Kural olarak, bu şekilde belirtilen hata değeri, olasılığa karşılık gelir. R= 0.95. Yani, ortalama olarak, 100 vakanın 95'inde, hata (yukarı veya aşağı) 1,5º değerini geçmeyecektir.
Buna göre, yüz vakadan beşinde hata daha büyük olabilir. Normal bir hata dağılımı için, 0,95 olasılığı şuna karşılık gelir: ikiye katlandı UPC. Bu nedenle, bu örnekteki yön ölçümü SCP 0,75º'dir.